A theory of search with deadlines and uncertain recall

Abstract

We ask how the ability to recall past prices affects the dynamics of search and price formation. In the model, buyers have limited time to purchase a good and face uncertainty regarding the availability of past price quotes in the future. Sellers cannot observe a potential buyer’s remaining time until deadline nor her quote history, and hence post prices that weigh the probability of sale versus the profit once sold. We find that, in contrast to conventional wisdom, reducing the consumer’s recall ability may actually improve his expected utility because it lowers the average expected price in the market and reduces the duration of search.

1 Introduction

Quite frequently, the timing of a purchase is of crucial importance to the buyer. A husband might buy diamond earrings for his wife at any time before her birthday, but purchasing it thereafter would cause significant grief. For credit cards and home mortgages, consumers are often given an introductory rate that eventually expires; this gives the consumer incentive to search for a replacement provider as this deadline approaches.

Buyers face two complications in meeting this deadline. First, the item could be offered at a variety of prices, and the deadline limits how many quotes one may obtain. Second, past offers may not be valid later on, as sellers revise their prices or run out of inventory. Therefore, consumers have to weigh the possibility of getting better price offers in the future against the possibility of losing an offer that is unappealing today but may become acceptable later on.

We study endogenous price formation in an economy that incorporates anonymities that are typical in a market: sellers are uncertain how close any particular buyer is to his deadline or what other price quotes he has available. We examine how a buyer’s ability to recall previous offers affects the equilibrium timing of purchase, the distribution of prices, and sellers’ profits. We show that the presence of deadlines and uncertain recall offer a new channel for overcoming the Diamond Paradox, obtaining price dispersion even with ex ante identical consumers and firms.

In the model, buyers randomly encounter sellers of a homogeneous good. On meeting, the buyer learns the asking price and must decide whether to purchase now, or defer the offer and continue search. Recall is uncertain, meaning that with some probability, the offer deferred yesterday is not available for consideration today. Buyers enjoy a positive flow of utility during an initial grace period; after passing the deadline, however, they incur a penalty each period until the purchase is completed.¹ Thus, even though buyers identically value the good in question, they will be ex post heterogeneous in their willingness to pay for it, depending on how close they are to the deadline and how lucky they have been in securing quotes in the past.

Sellers explicitly consider this in choosing an asking price. A higher price generates greater profit if accepted, but also limits the pool of buyers who would accept the offer. In equilibrium, the higher markup exactly offsets the lower probability of acceptance, allowing identical sellers to offer different prices and yet have equal expected profit.

The resulting equilibrium displays several interesting characteristics. First, the equilibrium is unique and takes one of two forms. In a late equilibrium, buyers initially forgo any purchases, preferring to wait in hopes of comparing two offers. Since recall is uncertain, only some buyers will be able to comparison shop. In a full equilibrium, some of the offers are low enough to be accepted by buyers early in their search; higher prices are still turned down until the deadline, as in the late equilibrium.

Second, in a full equilibrium, our model generates a continuum of offered prices. This occurs because some fortunate buyers are able to compare their best prior quote to their new offer. Thus, sellers realize that a higher price has a greater chance of being undercut in such comparisons. This feature of our sequential model with recall mimics the behavior of simultaneous search models (as in Burdett and Judd 1983) where individuals get multiple quotes in a single period and choose the lowest price. Unlike that setting, though, our price distribution also includes an atom at the lowest price. This is because buyers also differ ex post in their time remaining to the deadline. This lowest price is specifically meant to entice those who have just entered the market, though any buyer offered this price accepts it immediately.

Third, the full equilibrium response to a change in parameters is often surprising. The anticipated direct effect is often overpowered by a larger indirect effect: changes in the number of buyers near their deadline who have no retained offers. This deadline concentration strongly influences sellers’ ability to extract consumer surplus. If more of the population is desperate, more sellers offer prices accepted only by the desperate. But this increases the average offered price; thus, all buyers face worse prospects and are willing to pay more.

For example, if buyers enjoy higher grace-period utility, they are inclined to delay their purchases and enjoy more of this utility flow. This increases deadline concentration and allows sellers to raise prices and capture most of this added utility.

Even more striking is how the recall of past offers affects consumers in changing the equilibrium prices. Typical intuition suggests that less recall gives more power to sellers to charge higher prices, because they would have less chance of being undercut. However, less recall also encourages more early purchases, decreasing deadline concentration, and weakening the market power of sellers. Indeed, we find that the latter effect dominates in a full equilibrium: the average expected price is lower when recall ability is reduced, raising ex ante utility of consumers.

Our work relates to three strands of literature: search with uncertain recall, equilibrium search theory, and bargaining on a deadline. We now provide a review of the literature to highlight our contributions.

1.1 Related literature: search with recall

Most search models have exclusively studied the extremes of either no recall or perfect recall; however, these may not capture the uncertainty a buyer faces. In consumer search, it is frequently possible to return to previously visited sellers, though there is a real possibility that the product may be sold or price may have changed in the interim. Only a few articles have considered some form of uncertain recall, and these have assumed an exogenous distribution of prices.

The closest analog to our work is Landsberger and Peled (1977). They depict uncertain recall as a constant probability that the best offer so far will be available in the next period.² In an approximation of a deadline, they impose a cap on the number of offers that may be received from an exogenous price distribution and conclude that reservation prices fall as the probability of recall increases. However, this will delay purchases and concentrate more buyers near their deadline. In our model of endogenous pricing, firms will exploit this desperation; as a consequence, greater recall leads to higher prices.

Janssen and Parakhonyak (2011) take an alternative approach to recall, assuming buyers have access to all prior quotes but incur an additional cost to return and purchase using a prior quote. When a finite number of stores are available, this results in a non-stationary problem; for an exogenous price distribution, they characterize the reservation price strategy which depends on the current best offer and the number of stores remaining. To obtain a non-degenerate, endogenous price distribution, they embed costly second visits in the Stahl (1989) shopping model, but the same equilibrium distribution emerges, which is not sensitive to the cost of second visits. We examine this in further detail in Sect. 5.2.

Some models endogenize recall, but in simpler environments. In Armstrong and Zhou (2010), sellers recognize buyers who return to their store and decide whether to honor the original quote. This typically results in no recall, in that new customers are offered a discount that is unavailable to returning customers. In our model, buyers see a price at a particular retailer and know that the seller commits to that price as long as it is open for business. In this sense, our model is more applicable to transactions in large retailers who cannot renege on announced prices contingent on the identity of the customers. In Daughety and Reinganum (1992), a seller has no knowledge of buyers’ history and is not guaranteed to have the item in stock. He offers a price and states how many periods he will hold the item. The buyer can then check the other seller (at a cost). If both sellers have the item, Bertrand competition drives price to marginal cost.

In contrast to these, our model produces a richer distribution of prices, making search more meaningful. Also, in our full equilibrium, buyers accept some offers immediately, rather than always deferring in hopes of sparking a price war. While we do not endogenize recall, our model indicates that industry profits are maximized with a moderate degree of recall, rather than banning it outright.

1.2 Related literature: equilibrium search theory

One objective of this paper is to demonstrate a channel, whereby price dispersion may exist even with ex ante identical buyers. The Diamond Paradox (1971) states that when firms sell a homogenous product, and consumers have identical unit demand and incur a constant search cost each round, all firms will charge the same monopoly price in equilibrium. Subsequent work has shown that price dispersion can arise if buyers are heterogeneous in their cost of search (Salop and Stiglitz 1976; Butters 1977; Wilde and Schwartz 1979; Rob 1985; Stahl 1989) or valuations (Diamond 1987). Burdett and Judd (1983) demonstrate this can also arise with simultaneous search.³

In our paper, all buyers are ex ante identical, yet the Diamond Paradox does not occur because ex post differences emerge during the search process. Those who defer high offers are closer to their deadline and hence willing to pay more. Even within their cohort, buyers differ in whether their offer was retained and which offer it was. This mechanism for generating ex post heterogeneity in willingness to pay is particularly interesting since these difference arise largely due to the buyers’ own choice to defer their first offer.

Hamalainen (2012) also studies equilibrium price distribution, building on Ellison and Ellison (2009, 2010). In her model, two sellers of a good each choose a price as well as the additional time it takes for a consumer to find out their price. As in Stahl (1989), some buyers enjoy shopping and do not incur a search cost, which plays a critical role in the results and produces a continuous price distribution on a connected support. Our full equilibrium also features a continuum of prices, but with a disconnected atom at the lowest price generated by some firms targeting the early buyers.

A large parallel literature has applied equilibrium search environments to labor markets with the intent to study wage formation and the effects of unemployment insurance; this literature is well surveyed in Rogerson et al. (2005). Burdett and Mortensen (1998) add on-the-job search as another source of dispersed wages.

Akın and Platt (2012) shows how limited duration of unemployment benefits might generate a continuum of wages in continuous time. However, that model assumes no recall, as is common in labor search. By relaxing that assumption, we provide a much richer and realistic model of consumer search, but this also adds technical complexity since past prices become additional state variables. Here, we show that in a discrete time environment, multiple prices emerge in equilibrium even when buyers have some ability to recall past offers.

Finally, Albrecht et al. (2007) studies an economy where both buyers and sellers become desperate at a given Poisson rate; that is, their “deadline” arrives randomly. Buyers and sellers can observe each others’ states on meeting and then determine prices via Nash bargaining.⁴ In essence, our incomplete information environment reverses these features. Buyer deadlines are deterministic, but unknown to sellers who randomize their pricing.

1.3 Related literature: bargaining on a deadline

Many papers study how two parties split a known surplus when bargaining must conclude in a fixed time frame or the surplus is lost.⁵ Fuchs and Skrzypacz (2012) is the closest analog to our environment, in that the seller is uncertain of the buyer’s valuation. Thus, the seller makes repeated offers until the buyer accepts. If the deadline is reached, both parties receive an exogenous fraction of the buyer’s valuation.⁶ The equilibrium strategy has the seller make a decreasing sequence of offers; if early offers are rejected, the buyer is revealed to have a lower valuation.

There are three important differences from our environment: first, the buyer’s valuation is not known but the deadline is. We reverse these, so that the seller cannot observe the time until deadline, but knows the buyer’s valuation. Second, rather than having a single buyer and seller negotiate, such as in labor or other contract disputes, our environment examines private deadlines in a market setting that is more appropriate for consumer transactions. While both environments result in dispersed prices, the dynamics differ. For us, the highest prices are paid by desperate buyers, while the earliest buyers do so in Fuchs and Skrzypacz (2012). Also, as the delay between offers goes to zero, the limit bargaining equilibrium has a continuum of prices, including an atom on the lowest price. Our price distribution has similar features that are caused by the comparison of retained and new offers, rather than learning the buyer’s type.

We proceed with the remainder of the paper as follows: in Sect. 2, we present the model and define equilibrium. In Sect. 3, we present the equilibrium solution for moderate parameter values and characterize its behavior through comparative statics. In Sect. 4, we examine special cases with extreme parameter values; these are particularly helpful in identifying which aspects of the model are most influential in its behavior. In Sect. 5, we discuss extended versions of our model. Finally, we conclude. Proofs are provided in the Appendix.

2 Model

Consider a dynamic discrete time environment, with measure $\delta$ of infinitesimal buyers entering the market each period. The good being sold is homogeneous, which provides utility $x$ to any buyer, but because sellers may quote different prices for the good, buyers may find it worthwhile to search. Buyers have unit demand and exit the market after their purchase.

Sellers are also infinitesimal and remain in the market forever; we normalize their measure to 1. Each firm is able to produce on demand, with a cost of $c < x$ for each unit of the good. In any period, fraction $\gamma$ of these firms will not be operational, meaning they neither produce nor offer quotes that period.

Each period, every buyer encounters an operational seller, who offers a price quote $p$, drawn from an endogenous distribution of offered prices, $F(p)$. The buyer can either make the purchase immediately or defer the offer to allow further search. However, the ability to recall this offer is uncertain: if an offer is deferred, with probability $\gamma$ the firm that offered it will not operate tomorrow and the opportunity is lost. If an offer is still available in the next period, we say a buyer has retained it. If retained, an offer can be deferred yet again with the same uncertainty of retaining it one more period. For simplicity of notation, we assume that only the best available offer can be deferred—all others are discarded. In Sect. 3.1, we show that the same equilibrium exists in the more general environment where all offers can be deferred.

2.1 The buyer’s search problem

On entering the market, a buyer automatically receives a price quote. If he chooses to obtain a second price quote, he receives utility $b > 0$ from the search process (i.e., a negative search cost). Thereafter, he incurs utility $d < 0$ for each additional quote. In each iteration, the buyer’s timing proceeds as follows:

• 1. Buyers receive a new quoted price $q$.

• 2. If a buyer has both a new and an old quote, the higher of these is discarded. Ties are broken by randomizing with equal probability on each offer. The lowest (or only) offer becomes the current offer.

• 3. Buyers with a current offer $p$ decide whether to accept it, obtaining utility $x - p$ and exiting the market.

• 4. If the buyer defers offer $p$, he receives utility $b$ or $d$ and then learns whether the offer was retained for tomorrow.

At the beginning of each iteration, one can summarize the buyer’s problem with two state variables: prior quote $p \in \mathbb R$ (if available) and search state $s \in \{ 0, 1\}$. For the latter, buyers can be divided in two groups: early buyers ($s = 1$) who have newly entered the market, and delayed buyers ($s = 0$) who have already completed at least one iteration. Note that $s$ identifies whether the buyer will incur utility $b$ or $d$, respectively, if he defers at the end of his current iteration.

Let $V_s$ denote the expected utility of a consumer entering search state $s$ with no past offers available, and $W_s(p)$ denote the same for a consumer who retained offer $p$. Thus, the expected utility of a delayed buyer with no prior offers is

$$\begin{aligned} V_0 = \int _{-\infty }^{\infty } \max \left\{ x - q, \; d + (1 - \gamma ) W_0(q) + \gamma V_0 \right\} dF(q). \end{aligned}$$

(1)

For any $q$ this buyer may be quoted, he must decide to either accept or defer the offer. If he does the latter, he incurs utility $d$ and he is not guaranteed that $q$ will be retained tomorrow. Thus, his continuation utility is $d + (1 - \gamma ) W_0(q) + \gamma V_0$. This is weighed against the utility $x - q$ received from making the purchase now. The reservation price $R_0$ is defined such that the delayed buyer is indifferent between the current purchase and further search:

$$\begin{aligned} x - R_0 = d+ (1-\gamma )W_0(R_0)+\gamma V_0. \end{aligned}$$

(2)

Next, consider delayed buyers who have a prior offer $p$:

$$\begin{aligned} W_0(p) = \int _{-\infty }^{\infty } \max \left\{ x - \min \{p,q\} , \; d + (1 - \gamma ) W_0( \min \{p,q\}) + \gamma V_0 \right\} dF(q).\qquad \end{aligned}$$

(3)

Here, $q$ is replaced with the lower offer $m = \min \{p,q\}$. Notably, the comparison of acceptance ($x - m$) and deferral ($d + (1 - \gamma ) W_0(m) + \gamma V_0$) proceeds for each value of $m$ as it did for each value of $q$ in Eq. 1. Thus, delayed buyers have the same indifference condition (Eq. 2) and reservation price ($R_0$) regardless of whether they have a prior offer available. The following result establishes that $R_0$ behaves as a typical stopping rule.

Lemma 1

Assuming $\gamma \in (0,1)$, for any $p$ where $0 < F(p) < 1$, $W_0^{\prime }(p) > -1$. Hence, delayed buyers will accept offer $p$ iff $p \le R_0$.

Finally, consider early buyers. As new entrants to the market, none of them have a prior offer available. Their expected utility is

$$\begin{aligned} V_1 = \int _{-\infty }^{\infty } \max \left\{ x - q, \; b + (1 - \gamma ) W_0(q) + \gamma V_0 \right\} dF(q). \end{aligned}$$

(4)

This is nearly identical to $V_0$ except for utility $b$ associated with deferring offer $q$; however, this creates a distinct indifference condition which defines the reservation price $R_1$ among early buyers:

$$\begin{aligned} x - R_1 = b + (1 - \gamma ) W_0(R_1) + \gamma V_0. \end{aligned}$$

(5)

The same reservation property in Lemma 1 applies to $R_1$. Moreover, the fact that $W_0^{\prime }(p) > -1$ also contributes to the following result.

Lemma 2

Since $b > d$, $R_1 < R_0$.

As an immediate consequence, this means that all buyers would immediately accept $R_1$ if offered it. Moreover, all buyers would defer a price above $R_0$ indefinitely.

2.2 The seller’s problem

Sellers are unable to observe the state of the buyers who approach them. Thus, quoting a higher price bears the risk of a lower likelihood of being accepted. At the same time, it results in higher realized profits if accepted. If a set of prices produce the same maximal expected profit, sellers can randomize over this set.

Let $H$ denote the total measure of buyers in the market (across all states). Since every buyer encounters an operational seller, $H/(1 - \gamma )$ provides the number of buyers per operational seller. Seller static profit is defined as:

$$\begin{aligned} \pi (p) \equiv \frac{H}{1 - \gamma } (p - c) S(p), \end{aligned}$$

(6)

where $S(p)$ is the expected fraction of buyers who will (eventually) purchase if offered price $p$. Informed by the preceding buyer’s problem, we can make several observations regarding the equilibrium price distribution, $F(p)$.

Lemma 3

Let $P$ denote the support of $F(p)$.

• 1. $P \cap (R_0,+\infty ) = \emptyset$.

• 2. $P \cap (-\infty ,R_1) = \emptyset$.

• 3. If $\gamma < 1$, no atoms⁷ can occur in $F(p)$ for any $p \in (R_1,R_0]$.

• 4. If $P \backslash \{R_1\} \ne \emptyset$ then $R_0 \in P$.

The first two claims are straightforward. For the first, no seller will charge more than $R_0$, because even the most desperate of buyers (those in search state 0) always defer such an offer, which results in zero profit. For the second, no seller will charge less than $R_1$ because every buyer in every state is willing to immediately purchase the good at price $R_1$. Charging less will decrease $p$ without any compensating increase in $S(p)$.

The third claim is slightly more subtle and is a consequence of buyers comparing retained offers to new offers. In essence, if an atom did occur at a given price, sellers would prefer to undercut that price to avoid a tie, much like Bertrand competition. The proof is provided in the appendix. Note that this does not apply when $\gamma = 1$, since no offers can be retained. Also, this does not rule out an atom at $R_1$, since no one defers a purchase when offered $R_1$.

Thus, let $a$ be the weight of the atom at $R_1$ (while still allowing that $a$ may be $0$). The remaining distribution is continuous. Let $\underline{p}$ denote the lower bound of $P \backslash \{R_1\}$, that is, the lowest price in the continuous portion of the distribution. This notation is needed because typically $\underline{p} > R_1$.

The fourth claim ensures that $R_0$ is in the support if anything besides $R_1$ is. The maximal price in the support only targets those who have reached their deadline and have no other offers. If some $\hat{p} < R_0$ were the maximal price, a firm could sell to the same population with either price, but have a higher markup using $R_0$.

When buyers are indifferent, equilibrium will direct them to make the purchase rather than defer. Indeed, this is necessary. Suppose instead that some fraction of early buyers deferred offers of $R_1$. A seller would then prefer to offer $R_1 - \epsilon$, with $\epsilon > 0$ arbitrarily small, as this would break the indifference of early buyers, strictly increasing sales and profits.

2.3 Steady state conditions

For sellers to choose a pricing strategy, it will be critical to know how many buyers there are in each state of the search process. We consider a steady state equilibrium, where the measure of buyers in each state stays constant over time. Let $h_s$ denote the measure of buyers in search state $s$ who have no retained offer, and let $g_0(p)$ denote the measure of buyers in search state $0$ who have retained offer $p$.

Early buyers enter the market at rate $\delta$. All of them either become delayed buyers or make their purchase and exit the market. Thus,

$$\begin{aligned} h_1 = \delta . \end{aligned}$$

(7)

Next, consider delayed buyers with no retained offers. Buyers arrive in this state because they deferred an offer and did not retain it, which occurs with probability $\gamma (1 - a)$, since early buyers defer any offer except $R_1$. All of the delayed buyers will exit, having purchased using their period 0 offer. Thus, the steady state requires

$$\begin{aligned} h_0= \gamma (1-a) h_1. \end{aligned}$$

(8)

On the other hand, those early buyers who deferred and retained an offer arrive in state $(0,p)$. All of these delayed buyers exit the market (accepting either their retained offer or their new offer). Their steady state condition is

$$\begin{aligned} g_0(p)= (1-\gamma ) F^{\prime }(p) h_1, \end{aligned}$$

(9)

for $\underline{p} \le p \le R_0$, with $g_0(p) = 0$ for all other prices.

The total measure of active buyers in the market must satisfy

$$\begin{aligned} H = h_1 + h_0 + \int _{\underline{p}}^{R_0} g_0(q)\mathrm{d}q \end{aligned}$$

(10)

These steady state conditions allow us to compute the expected sales $S(p)$ from quoting price $p$. First, if a seller offers $R_1$, any buyer immediately accepts it. Thus,

$$\begin{aligned} S(R_1) = 1. \end{aligned}$$

(11)

On the other hand, if a seller offers price $p \in [\underline{p}, R_0]$, there are three possibilities. First, delayed buyers with no retained offer will immediately accept the offer. Second, delayed buyers with retained offer $q$ will only accept new offer $p$ if $p < q$. Finally, early buyers will defer the offer $p$, and if it is retained, will exercise it only if their second quote is higher. Thus,

$$\begin{aligned} S(p) = \frac{h_0+\int _p^{R_0} g_0(q)\mathrm{d}q+ (1-\gamma )(1- F(p))h_1}{H}. \end{aligned}$$

(12)

2.4 Equilibrium definition

A steady state search equilibrium consists of seller profit $\pi ^*$, the distribution of sellers’ offered prices $F^*(p)$, reservation prices $R_0^*$ and $R_1^*$, and the measures of buyers in each state $h_0^*$, $h_1^*$, $g_0^*(p)$, and $H^*$, such that

• 1. $R_0^*$ and $R_1^*$ are consistent with Bellman Eqs. 1 through 5, given $F^*(p)$.

• 2. All prices in the support of $F^*$ produce the same profit $\pi ^*$, while all other prices produce no more than $\pi ^*$, using Eqs. 6, 11 and 12.

• 3. $h_0^*$, $h_1^*$, $g_0^*(p)$, and $H^*$ satisfy the steady state conditions in Eqs. 7 through 10.

In the next section, we characterize the equilibrium solution, describing its key features. Indeed, an equilibrium can take one of two forms.

In the first, sellers only offer prices between $\underline{p}$ and $R_0$, effectively ignoring early buyers. This occurs because early buyers are a relatively small portion of the market, and the price drop between $\underline{p}$ and $R_1$ is too large. We refer to this as a late equilibrium.

In the second form of equilibrium, some sellers also offer $R_1$, as this offers the same expected profit as any price between $\underline{p}$ and $R_0$. This we refer to as a full equilibrium.

In either equilibrium, the price distribution is typically not degenerate. In particular, prices are continuously distributed between $\underline{p}$ and $R_0$ because of the possibility of recall. Even though these prices are only accepted by delayed buyers, these buyers still differ in the retained offer they hold (if any) from their first draw. A higher price in this range reduces the likelihood of sale since there is a greater chance that the delayed buyer will favor his retained offer.

3 Equilibrium characterization

We begin by examining the main case of interest, in which $0 < \gamma < 1$ and $b > 0 > d$; other special cases are considered in Sect. 4. When a late equilibrium occurs, we can provide a closed-form solution. For the full equilibrium, we must implicitly solve for $a$, the size of the atom on $R_1$; all other equilibrium objects are expressed in terms of $a$. A numerical illustration of this equilibrium is provided in Sect. 3.3. Conveniently, both solutions can be expressed in the same equations presented below. The late equilibrium simply sets $a^* = 0$.

We begin by providing the equilibrium prices. We note that even in a late equilibrium, $R_1$ is still well defined (though not offered in equilibrium). In essence, this provides the hypothetical price at which early buyers would be willing to immediately accept an offer. In equilibrium, these prices (stated in terms of $a^*$) are

$$\begin{aligned} R_1^*&= \kappa (a^*) - \frac{b}{ \gamma }\end{aligned}$$

(13)

$$\begin{aligned} R_0^*&= \kappa (a^*) -d, \end{aligned}$$

(14)

where

$$\begin{aligned} \kappa (a) \equiv d + c - \frac{2(1 - \gamma )(a b + \gamma (1-a) d )}{(1 - a) \gamma \left( 2(1 - \gamma ) + \gamma \ln \left( \frac{\gamma }{2 - \gamma } \right) \right)}. \end{aligned}$$

(15)

The function $\kappa (a)$ is $E[p]$, the expected price from one draw out of the distribution $F(p)$ and is decreasing in $a$. Note that $\kappa (0)$ simplifies to $d + c - \frac{2(1 - \gamma ) d }{ 2(1 - \gamma ) + \gamma \ln \left( \frac{\gamma }{2 - \gamma } \right)}$, while $\kappa (a)$ approaches $-\infty$ as $a$ approaches 1.

Next, we turn to the equilibrium price distribution. In the continuous portion of the distribution, the lowest price is

$$\begin{aligned} \underline{p}^*&= c + \frac{\gamma }{2 - \gamma } (\kappa (a^*) - c - d). \end{aligned}$$

(16)

Even in the late equilibrium, $\underline{p}^* < R_0^*$, indicating that price dispersion occurs. This is because all households receive a quote upon entering the market, though none of them purchase at that time. Since $1 - \gamma$ of them retain this quote and compare it to their second draw, firms have an incentive to offer lower prices than $R_0^*$ to have a better chance of making the eventual sale.

In equilibrium, firms randomize their pricing with the following cumulative distribution:

$$\begin{aligned} F^*(p) = {\left\{ \begin{array}{ll} 0&\text{ if} \, p < R_1^* \\ a^*&\text{ if} \, p \in [R_1^*,\underline{p}^*) \\ 1 - \frac{\gamma (1 - a^*)}{2(1- \gamma )} \left( \frac{\kappa (a^*) - d - p}{p-c} \right)&\text{ if} \, p \in [\underline{p}^*,R_0^*) \\ 1&\text{ if} \, p \ge R_0^* \end{array}\right.}. \end{aligned}$$

(17)

As required from Lemma 3, $F^*(p)$ is continuous at $p = R_0^*$ since $R_0^* = \kappa (a^*) -d$. The steady state distribution of buyers is given by substituting $F^*$ into Eqs. 7 through 10.

The comparison of profits plays a pivotal role in equilibrium. Let $\varPi _s(a)$ denote the expected profit of a seller offering price $R_s$, given the distribution of prices and the steady state population of buyers implied by $a$. Thus, the expected profit from offering $R_1^*$ is

$$\begin{aligned} \varPi _1(a^*) = \frac{H}{1 - \gamma } (R_1^* - c) = \frac{\left(2 - a^*\right) \delta }{1 - \gamma } \left( \kappa (a^*)- \frac{b}{ \gamma } - c \right), \end{aligned}$$

(18)

while offering $p \in [\underline{p}^*,R_0^*]$ yields:

$$\begin{aligned} \varPi _0(a^*) = \left( 2(1 - F(p)) + \frac{ (1 - a) \gamma }{1 - \gamma } \right)\delta (p-c) = \frac{(1 - a^*) \gamma \delta }{1 - \gamma } ( \kappa (a^*) - d - c).\nonumber \\ \end{aligned}$$

(19)

The ability of a firm offering $R_1^*$ to extract profit depends on how nervous early buyers are about their future prospects. In particular, since $\kappa ^{\prime }(a) < 0$, profits will be lower if a large number of firms target the early buyers.

Proposition 1 establishes that any equilibrium must take this form, with the pivotal question being whether any sellers decide to target early buyers. For sellers to offer $R_1^*$, this must be at least as profitable as offering $R_0^*$. If not, then $a^* = 0$ will result.

Proposition 1

For all parameter values where $0 < \gamma < 1$ and $b > 0 > d$, an equilibrium exists. Any such equilibrium necessarily satisfies Eqs. 13 through 19, where

• 1. (Late) $a^* = 0$ only if $\varPi _1(0) \le \varPi _0(0)$, and

• 2. (Full) $a^* \in (0,1)$ only if $\varPi _1(a^*) = \varPi _0(a^*)$.

The proof (provided in the appendix) proceeds by construction and illuminates the genesis of this solution. Note that after substitution for $\kappa (a)$, the comparison of profits, $\varPi _1(a^*) \gtreqqless \varPi _0(a^*)$, simplifies to

$$\begin{aligned} \frac{b}{\gamma ^2}\left(\gamma + \frac{2 (1 - \gamma ) (2 - a^* - \gamma + \gamma a^*) }{(1 - a^*) \left( 2(1 - \gamma )( 1 - a^*) + (2 - a^*) \ln \left( \frac{\gamma }{2 - \gamma } \right) \right)} \right) \gtreqqless d. \end{aligned}$$

(20)

The parenthetical element in Eq. 20 is strictly negative for all $a \in [0,1]$ and $\gamma \in (0,1)$.

Proposition 1 rules out any equilibrium where firms only offer $R_1$ (i.e. $a^* = 1$). If all firms offered $R_1$, early buyers would have no reason to accept their first offer. Rather, they could defer and enjoy $b$, then purchase at price $R_1$ using either the retained offer or the new offer. But this in turn means that all buyers will compare two prices, giving firms a reason to offer a slightly lower price so as to secure more purchases from delayed buyers.⁸

When a late equilibrium emerges ($a^* = 0$), the resulting price distribution is the same as in the simultaneous search model presented in Burdett and Judd (1983). There, buyers choose the number of quotes to simultaneously request then choose the best offer received, with no option for additional search. In equilibrium, the buyers are indifferent between requesting one or two quotes and employ a mixed strategy with fraction $q$ requesting a single quote.

In our setting, a late equilibrium mimics a simultaneous search environment. All buyers defer on the first draw, hoping to choose the best of two, but $\gamma$ of them lose this draw and are stuck with their second (and only available) quote. While $\gamma$ plays the role of their $q$ here, the difference is that $\gamma$ is exogenously given. On the other hand, B&J take the maximum price as exogenous, while $R_0$ is endogenously determined in our model by the (off-equilibrium) possibility for an additional round of search.

The full equilibrium shares this flavor of simultaneous search; yet, it also permits an atom in the distribution, which could not occur in B&J. Despite having ex ante identical buyers, the impending deadline makes them differ ex post: early buyers have a different willingness to pay than delayed buyers. If a firm decides to target early buyers by offering $R_1$, they do not concern themselves with the likelihood of being undercut, since the offer will be accepted before a second draw is possible. This sidesteps the tiebreaking which leads to an atomless distribution in simultaneous search (and the upper price range in our model).

In addition to the equilibrium objects above, we also provide three useful measures of equilibrium behavior. First, the newly entered buyer can expect to conclude his search after one draw with probability $a^*$ and after two draws with probability $1 - a^*$; thus, the expected duration of search is $a^* + 2 (1 - a^*) = 2 - a^*$.

Second, welfare in this market amounts to the sum of buyer and seller surplus, per transaction. The transaction itself generates $x - c$, with the split between buyer and seller determined by the agreed upon price. In addition, buyers obtain $b$ utils from their second search (if reached). Thus, total welfare is $x - c + (1 - a^*) b$. Thus, exit by early buyers is actually inefficient, as they forego utility $b$ that they would have enjoyed as delayed buyers.

Finally, the aggregate industry profit is defined as $\varPi ^* = (1 - \gamma ) \varPi _0(a^*)$; that is, the $\gamma$ non-operational firms earn 0 profit, and the other $1 - \gamma$ firms earn $\varPi _0(a^*)$ (regardless of which price they charge, since profits equate in equilibrium).

3.1 Uniqueness

Next, we consider the uniqueness of equilibrium. Note that when $a = 0$ is imposed, Eqs. 13 through 19 provide a single solution; thus, for any given parameter values, there is at most one late equilibrium.

It is also the case that at most one full equilibrium can emerge. This occurs because $\varPi _1(a)$ shrinks faster than $\varPi _0(a)$ as $a$ increases; hence, these profits equate at most once.⁹ This same fact also rules out the simultaneous existence of a full and a late equilibrium.

Proposition 2

If there exists an $a^* \in (0,1)$ such that $\varPi _1(a^*) = \varPi _0(a^*)$, then $\varPi _1^{\prime }(a^*) - \varPi _0^{\prime }(a^*) < 0$. Thus, $a^*$ is unique. Furthermore, if $\varPi _1(0) \le \varPi _0(0)$, then $a^* = 0$ is the unique equilibrium.

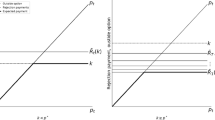
Applying this proposition to Equation 20 with $a^* = 0$, we see that a late equilibrium occurs iff $b (\frac{1}{\gamma } + \frac{1 - \gamma }{\gamma ^2} \cdot \frac{2 - \gamma }{1 - \gamma + \ln \left( \frac{\gamma }{2 - \gamma } \right) } ) \le d$. The parenthetical term is 0 at $\gamma = 1$, approaches $-\infty$ as $\gamma \rightarrow 0$, and strictly increasing in between. Thus, for any parameters $b > 0 > d$, the late equilibrium occurs for lower values of $\gamma$, while the full equilibrium occurs for higher $\gamma$ (less ability to recall). Alternatively, for a given $\gamma$, the late equilibrium emerges if grace-period utility is smaller or deadline penalties are less onerous. This dividing line between the two forms of equilibria is illustrated in Fig. 1.

Fig. 1

Form of equilibrium, as a function of recall ability $\gamma$ and the penalty-to-benefits ratio, $d/b$

To this point, we have assumed that only the best price may be deferred each period (single deferral). Alternatively, we can consider an environment in which buyers can defer any number of offers, where each offer independently may be lost with probability $\gamma$ (unlimited deferrals). This could provide a hedge against losing the best offer. In practice, however, it remains unexercised, as demonstrated in the following proposition.

Proposition 3

The equilibrium in a single-deferral model is also the unique equilibrium in an unlimited-deferrals model.

Despite the potential benefits of accumulating additional quotes, they come at a search cost of $d$. In the equilibrium solution, delayed buyers are indifferent about seeking a third draw if their current best offer is $R_0$, and they strictly prefer ending the search if they have a better price available. Given the tenuous benefit of the third draw, it is not surprising that the marginal value of additional draws is even lower.

Thus, even given the opportunity to retain more than one quote, this never occurs in equilibrium. We note that this result is related to the number of iterations before the search deadline. If buyers could draw $k$ quotes (rather than just one) before reaching search state 0, buyers with the least attractive quotes would defer all their offers until the deadline.¹⁰ A subset of these will retain and compare all $k$ offers once search state 0 is reached, resulting in stronger price competition. Even so, the same logic of Proposition 3 would apply so that after buyers reach the deadline, they are not willing to postpone purchase in hopes of accumulating more quotes. Therefore, buyers never retain more quotes than there are iterations before the deadline.

3.2 Recall and prices

In a full equilibrium, uncertain recall ($\gamma \in (0,1)$) has a surprising effect. As $\gamma$ increases, buyers are less likely to retain a deferred offer. Standard intuition suggests that this should allow sellers to extract more rent from the purchase. Indeed, in the late equilibrium, this is exactly what happens. Sellers are less likely to be undercut, so they are able to offer higher prices (both the maximum and the average offer) and earn greater profits.

In the full equilibrium, however, an increase in $\gamma$ causes a secondary effect of decreasing deadline concentration. The lower probability of retaining deferred offers would, all else equal, encourage early buyers to accept higher offers; this makes $R_1$ more profitable, drawing more sellers to offer that price. But the ironic consequence of making more $R_1$ offers is that fewer buyers reach search state 0, and they have better chances of still getting $R_1$. Thus, this smaller pool of desperate buyers is less desperate than before.

Surprisingly, this secondary effect dominates the first; $R_1^*$ and $R_0^*$ both fall as quotes are less likely to be retained. Thus, buyers are better off after a reduction in ability to recall past offers.

As noted in the previous section, the late equilibrium exists for lower $\gamma$, while the full equilibrium exists for higher $\gamma$. Since $\frac{\partial \varPi ^*}{\partial \gamma }$ is positive in the late equilibrium and negative in the full equilibrium, industry profits are greatest exactly at the threshold between a late and a full equilibrium, which we label $\hat{\gamma }$. At that point, no one offers $R_1^*$, but doing so would produce the same expected profit as $R_0^*$. Since $0 < \hat{\gamma } < 1$, it is not in the sellers’ collective best interest to ban the recall of past offers or guarantee perfect recall.

This might find useful application where a single manufacturer has a network of independent dealers. The manufacturer may not be able to monitor the pricing decisions of each dealer to forestall competition, but it could directly control whether a dealer is restocked in a given period. If the manufacturer’s goal is to maximize the profit of the group, it can restock fraction $1 - \hat{\gamma }$ of the dealers (randomly selected) each period. This policy would prevent “ruinous competition” from strong recall (wherein dealers would frequently undercut each other), but also keeps recall strong enough so that all buyers wait until just before their deadline, thereby allowing the dealers to extract the most rent from them.

The effect of grace-period utility $b$ is also illustrative of deadline concentration. As these benefits increase, early buyers are less inclined to make a purchase, preferring to receive the added benefits of one more search. Thus, fewer $R_1$ offers are made, and more buyers end up in search state 0. This allows sellers to offer higher prices, effectively capturing some of the increased benefits by taking advantage of buyer desperation.

In a similar vein, an increase in the postdeadline utility (e.g., a smaller penalty for exceeding the deadline) also reduces the haste of buyers to make early purchases. While this piles more buyers into search state 0, these buyers are less desperate than before, which is reflected in lower reservation prices. However, because $a^*$ decreases, more sellers are concentrated on the higher prices. Thus, even though the average offered price is lower, sellers earn more profit as a group.

All comparative statics in Table 1 are analytically derived, but require significant algebraic manipulation. The response to $\gamma$ is both the most surprising and the most difficult to sign; thus, the proof of the following claim appears in Appendix 6.

Table 1 Comparative statics

Proposition 4

In a full equilibrium, $R_1^*,\, E[p],\, \text{ and} \ R_0^*$ are decreasing in $\gamma$.

The full details for all comparative static proofs are provided in Sects. 4 and 5 of the supplementary Technical Appendix to this article, available from the authors.

3.3 Numerical illustration

To demonstrate the properties of the model, we present a numerical example with its equilibrium price distribution and comparative statics, letting $x = 1{,}300,\, c = 1{,}000,\, b = 50,\, d = -200,\, \text{ and} \gamma = 1/2$. This computation is presented in Section 8 of the Technical Appendix. Under these parameters, $a^* = 0.209$. The resulting full equilibrium is representative of the many parameterizations we have computed.¹¹

First, consider the equilibrium price distribution, depicted in Fig. 2. Note the atom at $R_1^* = 1{,}085$; just over a fifth of sellers offer this price. The remaining four-fifths are distributed between $\underline{p}^* = 1{,}128$ and $R_0^* = 1{,}385$, with slightly higher density on lower prices ($F^{\prime \prime }(p) < 0$). Sellers offering $\underline{p}^*$ make the sale roughly 50 % more often than those offering $R_0^*$, since the latter are almost surely undercut whenever a second quote is obtained, while the former are only undercut if the second quote is $R_1^*$. The gap between $R_1^*$ and $\underline{p}^*$ is also noteworthy. Sellers offering the former will secure a sale on all offers, rather than risking a positive probability of being undercut.

Fig. 2

Cumulative distribution of prices offered in equilibrium, with $R_1^* = 1{,}085$, $\underline{p}^* = 1{,}128$, and $R_0^* = 1{,}385$

In this example, the support of $F$ includes some prices greater than $x$. This is determined by the magnitude of penalty $d$; buyers pay more than $x$ whenever penalties loom large. The steady state distribution of buyers is $h_1 = \delta$, $h_0 = 0.4 \delta$, and $g_1(p) = 0.5 \delta F^{\prime }(p)$. Note that $\delta$ only increases the total population, but not the relative distribution and thus has no effect on seller incentives.

4 Special cases

We now briefly present several special cases of the model. These have particular interest as they highlight the separate roles played by recall or the deadline in generating price dispersion. Unless otherwise specified, we maintain the assumption that $b > 0 > d$.

4.1 Special case: no recall

In one extreme, suppose that $\gamma = 1$, meaning that deferred offers are certainly lost. In this case, only the full equilibrium exists, though with a notable difference compared to the general case: as $\gamma$ approaches 1, $\underline{p}$ approaches $R_0$. Thus, the continuous portion of the distribution collapses to an atom on $R_0$.

The distribution collapses because no one reaches state 0 with a retained offer, and everyone who does reach state 0 has the same reservation price $R_0$. Thus, if a seller offered slightly less than $R_0$, he will (still) sell to delayed buyers without picking up additional sales from early buyers.

Again, we let $a^*$ denote the atom on $R_1^*$; and hence, $R_0^*$ is offered with probability $1 - a^*$. Equilibrium prices become

$$\begin{aligned} R_1^*&= b + c\end{aligned}$$

(21)

$$\begin{aligned} R_0^*&= 2 b - d + c, \end{aligned}$$

(22)

with the atom $a^* = \frac{d}{d - b}$.

The steady state population has the same solution as in Eqs. 7 through 10, setting $\gamma = 1$. The expected profit per customer from offering $R_1$ is

$$\begin{aligned} \varPi _1(a^*) = (2 - a^*) \delta b \end{aligned}$$

(23)

while offering $R_0$ yields

$$\begin{aligned} \varPi _0(a^*) = (1 - a^*) \delta (2 b - d). \end{aligned}$$

(24)

Returning to the general case in Sect. 3, recall that only the full equilibrium exists for larger $\gamma$. Notably, the solution presented here is the limit of that equilibrium as $\gamma \rightarrow 1$. Also, recall from Table 1 that $\frac{\partial a^*}{\partial \gamma } > 0$; thus, in the general case where $\gamma < 1$, $a^*$ is bounded above by $\frac{d}{d - b}$.

At $\gamma = 1$, a continuum of late equilibria can also occur that were not possible for $\gamma < 1$. In these, all firms offer the same price $R_0 \in [c,c + 2b]$, and only delayed buyers accept this price. Buyers are willing to accept the price since further search will produce no better offers yet incur the penalty $d$. Sellers have no reason to undercut one another because no buyer retains early quotes. However, $R_0$ cannot exceed $c + 2b$; otherwise, a seller would find it profitable to deviate, offering $R_1 = R_0 - b$ and gaining twice as many sales.

This degenerate equilibrium cannot be sustained when $\gamma < 1$ because any small amount of recall will induce price competition among firms targeting delayed buyers, which generates the continuous portion of the price distribution.

4.2 Special case: full recall

Next, we consider the opposite extreme of perfect recall ($\gamma = 0$). In Sect. 3, we noted that as $\gamma$ decreases, eventually the late equilibrium must occur. This remains true at $\gamma = 0$. Indeed, the only possible equilibrium is for all sellers to charge $R_0 = c$.

Regardless of the price distribution they face, buyers will always defer their first offer received. They face no risk of losing the offer, nor do they discount future consumption; yet, they do earn additional utility $b$ by staying in the market one more iteration.¹² Since all buyers receive two quotes, competition among sellers drives prices to marginal cost.

4.3 Special case: weakened deadlines

The full recall case suggests a particular importance of the interim utility $b$, and the no recall case is strongly affected by the penalty $d$ even though no one incurs it in equilibrium. Here, we further investigate the effects of the drop in utility from search state 1 to 0, essentially weakening the deadline effect in the model. Indeed, one could go as far as to set $b = d$ to eliminate the deadline entirely, but one need not go that far. Just with $d \ge 0$ or $b \le 0$, price dispersion will be eliminated.

First, consider $b \ge d > 0$. In this case, buyers receive $d$ for the infinite future if they avoid making a purchase. Since there is no discounting, this infinite sum will always be preferred over the finite utility of purchasing $x$ at any price. Thus, no purchases (or meaningful search) ever occur.

Next, consider $b \ge d = 0$. Then, the unique equilibrium consists of all firms offering $R_0 = c$, which is only accepted by delayed buyers.¹³ Effectively, there is no cost of additional search, so if there was a non-degenerate price distribution, buyers would continue search until they found the lowest price in the support. Thus, other prices could not be sustained in equilibrium.

These two cases demonstrate that the threat of future penalties is crucial to sustaining equilibrium price dispersion—even though the penalty phase is not reached in equilibrium. This penalty $d$ essentially plays the same role as the marginal cost of search in stationary sequential search and largely determines the continuation value of reaching expiration.

Utility $b$, on the other hand, is reached in equilibrium. When $b > 0$, this almost seems like negative search costs, but a more natural interpretation is that the buyer is searching in order to replace a good that will provide one more period of utility $b$. We now examine what happens if $b \le 0$—a cost rather than a benefit. This is the one case in which an early equilibrium can emerge, where sellers only target early buyers.

If $b = 0 > d$, there exists a continuum¹⁴ of early equilibria, with all sellers charging the same price $R_1 \in [c,x]$. Early buyers will accept $R_1$ so as to avoid future penalties. Sellers cannot charge more, since buyers would defer and obtain $R_1$ from another seller in the next iteration.

For $b < 0$, the unique equilibrium is to charge $R_1 = x - b$. The equilibrium price cannot be lower; otherwise, a seller could deviate, offering $R_1 + \epsilon$. So long as $\epsilon < -b$, buyers would still accept it, rather than defer the offer to obtain $R_1$ in the next iteration and incur cost $b$.

Thus, we conclude that the positive interim utility is also critical to obtaining price dispersion in equilibrium. Buyers must have some reason to delay purchase to induce enough comparison shopping. When $b \le 0$, a full equilibrium cannot be sustained because there are too many people who accept $R_1$ relative to those who would accept the slightly larger $R_0$.

5 Expanding the model

5.1 Discounting and uncertain sampling

These special cases must be qualified somewhat, for they are highly dependent on the assumption that buyers do not discount future payoffs. One might expect that making buyers impatient would only strengthen degenerate equilibria just presented (as buyers are more eager to purchase early), but it has the opposite effect. Discounting creates greater variation in willingness to pay across states and thus makes it easier to maintain dispersion.

For instance, in Sect. 4.1, we noted that only a full equilibrium can occur when no recall is possible. With a discount factor $\beta < 1$, it is possible to reach a late equilibrium, depending on the other parameters. In Sect. 4.2, full recall resulted in a degenerate late equilibrium; with discounting, a full equilibrium can also be sustained.

In addition, discounting weakens the need for a strong deadline. For example, if $\beta < 1$, a full equilibrium can exist even when $b \le 0$. That said, even with heavy discounting, it is still the case that only an early equilibrium exists when $b$ is within some neighborhood of $d < 0$. It should not be surprising that deadlines are needed in some form. Without it, search would be stationary and the Diamond Paradox occurs—any symmetric equilibrium would lead all buyers to hold the same reservation price, with or without recall.

Yet, we have also seen that the degree of recall has important interaction with the deadlines. This affects which buyer types are targeted and how heavily, and influences the degree of dispersion. Indeed, our finding that less recall can lead to lower prices indicates how subtle this interplay can be.

In a further expansion of the model, we have considered what would happen if buyers are not guaranteed to find a seller each period; that is, they are matched with probability $\lambda < 1$. This adds further richness to the model, as buyers can then reach the penalty phase in equilibrium: either they received no quotes in their first two draws or they deferred and lost them.

This uncertain sampling would seem to make buyers more anxious to secure an early purchase; yet in equilibrium, it leads to greater price dispersion as it creates more distinction among types. It also eliminates most of the degenerate early equilibria from the special cases, as there always exist some unlucky buyers who were unable to get a quote when they first entered the market, and since they are at or past their deadline, these buyers will be tempting targets for sellers.

We provide the solution of this extended model with discounting and uncertain sampling in Sect. 6 of the Technical Appendix. The solution technique mimics that employed in the original model, though the analog to Eq. 20 is far more complex. Although uniqueness can no longer be shown analytically, we have not found parameter values for which there are multiple equilibria.

5.2 Shoppers versus searchers

Our work has important parallels with Stahl (1989). There, buyers are ex ante heterogeneous in their search costs. Fraction $\mu$ of buyers are shoppers who have zero search cost; the remaining buyers are searchers who share the same positive search cost. Both types have access to $N$ firms, from which they can sequentially receive quotes with perfect recall.

One can think of early buyers in our environment as temporary shoppers; they get enjoyment $b$ from seeking their second quote. However, this enthusiasm for shopping quickly fades, and they transform into searchers on any subsequent iterations. Of course, our model assumes all buyers are ex ante identical, beginning their market experience as shoppers and only differentiating themselves as some of them defer purchase of their first quote.

It is noteworthy that in the Stahl model, searchers always accept their first draw. Only shoppers compare more than one offer, and thus, they entirely drive the equilibrium price distribution. This is also why costly second visits have no effect on prices in Janssen and Parakhonyak (2011), since they do not apply to shoppers and hence do not affect the likelihood that a firm is undercut. In contrast, our price distribution is sensitive to both the population of shoppers, $h_1$, and the population of searchers with retained offers, $g_0(p)$.

It is likely that real-world consumers are heterogeneous in a number of dimensions (such as valuation of the good or search costs), some of which would be distinct even ex ante; such differences are well-known sources of equilibrium price dispersion. Our purpose in assuming ex ante homogeneity is to demonstrate that deadlines and uncertain recall can generate rich price dispersion despite starting with a uniform population of buyers. Adding ex ante heterogeneity is unlikely to disrupt this result.

For instance, in the spirit of Stahl’s original motivation, it is possible that some buyers dislike shopping or have significant opportunity costs from the beginning of their search. We can easily incorporate this in our model by having fraction $1 - \mu$ of new buyers enter the market in search state 0 with no prior quotes. This would alter steady state Equations 7 and 8 to become $h_1 = \mu \delta$ and $h_0 = (1 - \mu ) \delta + \gamma (1-a) h_1$, respectively. The other equations in the equilibrium definition remain unchanged.

While the equilibrium solution (presented in Sect. 7 of the Technical Appendix) will now depend on $\mu$, it is qualitatively very similar to the original model. The biggest change is to $\kappa (a)$; the inclusion of $\mu$ in several places makes analytical comparative statics unwieldy, though numerical computation is straightforward.

Starting in a full equilibrium in the original model ($\mu = 1$), a decrease in $\mu$ will increase both reservation prices and shifts the continuous portion of the distribution toward higher prices. The $\mu$ shoppers, with their potential for multiple quotes, are the only source of competition in the market; thus, average markup ($E[p] - c$) roughly doubles each time the population of shoppers is cut in half. Surprisingly, even though early buyers constitute a smaller fraction of total buyers, the fraction of firms targeting them ($a^*$) increases. As a consequence, it is easier to sustain a full equilibrium as $\mu$ decreases—as visualized in Fig. 1, the boundary between the full and late equilibria retains the same intercept in the upper right-hand corner ($d/b = 0,\, \gamma = 1$) but falls elsewhere.

Fixing a given $\mu < 1$, numerically evaluated comparative statics consistently follow those derived in Table 1. The only exception is that in a full equilibrium, $R_1^*$ can initially increase for lower values of $\gamma$, though it eventually falls with higher values of $\gamma$. This occurs because the concentration effect is less responsive to $\gamma$ when $\mu < 1$, since some of the population enter the market directly at the deadline. Even so, $R_0^*$ and $E[p]$ are both decreasing in $\gamma$, as they were when $\mu = 1$.

Figure 3 illustrates these comparative statics, with $R_1^*$ rising through $\gamma = 2/3$ and $R_0^*$ and $E[p]$ falling under any full equilibrium. The average price falls throughout partly because $a^*$ is increasing in $\gamma$, and this moves weight from higher prices to the lowest price, $R_1^*$. In addition, the increase in $R_1^*$ is small relative to the decrease in $R_0^*$.

Fig. 3

Equilibrium prices ($R_1^*$, solid $E[p]$, dashed $R_0^*$, dotted) as a function of recall ability $\gamma$, with shoppers and searchers ($\mu =0.5$, $b = 50$, $d = -200$, $c = 1,000$)

It is noteworthy that the equilibrium distribution $F(p)$ in Stahl (1989) is continuous throughout, rather than having a positive measure of firms target shoppers. This is because all shoppers sample all $N$ firms, creating an incentive to undercut. In contrast, our shoppers stop immediately if they receive the best price, meaning that price will not be compared to other offers and thus will never be undercut.

6 Conclusion

We analyze price formation in a market where buyers face a deadline to complete their transaction and have limited ability to recall their best prior offer. In this incomplete information environment, we solve for the endogenous price distribution that prevails in the steady state. When buyers’ recall ability is stronger, they typically only purchase just before the deadline (a late equilibrium); but with weaker recall ability, some prices are low enough to entice an early purchase (a full equilibrium). In our expanded model with discounting, the latter is possible even with perfect recall.

In the full equilibrium, we find that consumers benefit from reduced recall ability, in contrast to common wisdom. This occurs because less recall encourages buyers to purchase early, and this reduces the concentration of buyers near their deadline. With fewer desperate buyers, sellers cannot charge as much, even though price comparisons happen less frequently.

The equilibrium price distribution of our sequential model mimics the behavior of simultaneous search models where individuals get multiple quotes in a single period and choose the lowest price. The distinction is in the full equilibrium, where a mass of firms offer the lowest price, while others will be continuously dispersed at higher prices. This seems consistent with the typical results of a Google Shopping search: for a given item, there is often a heavy cluster of sites offering the lowest price as well as a spectrum of higher prices.

More broadly, our model is relevant in explaining why retailers offer sales. For instance, in Varian (1980) or Stahl (1989), sellers who offer a lower price than competitors do so to target buyers with superior information or lower search costs. In our model, such sellers are targeting new entrants who have time to spare or those who have retained offers, while higher prices only snare those who are closest to their deadline or who are unlucky with no retained offers.

Furthermore, our model could potentially be adapted to study other interesting environments. For instance, an important biological deadline occurs in marriage markets, as female fertility declines with age. In contrast, male fertility remains roughly constant. Both face uncertainty about future prospects and how long current suitors will wait for a decision. Thus, the marriage search process could be characterized by a reservation quality (of spouse), which would decline as the deadline approaches. In Akin et al. (2013), we show that a dynamic search model with deadlines can explain interesting facts found in the U.S. census regarding variations in spouse quality by a woman’s age at first marriage.

Appendix A: Proofs

1.1 A.1 Proof of Lemma 1

Proof

Let $\gamma \in (0,1)$ and let $p$ satisfy $0 < F(p) < 1$.

Let $M(p,q) \equiv \max \left\{ x - \min \{p,q\} , \; d + (1 - \gamma ) W_0( \min \{p,q\}) + \gamma V_0 \right\}$, which is the integrand of Eq. 3. Thus $W_0(p) = \int _{-\infty }^{+\infty } M(p,q) dF(q)$.

If $q < p$, then $\frac{\partial M}{\partial p} = 0$, since the inferior quote $p$ is discarded.

Suppose instead that $q \ge p$. For a given $p$, the choice to accept or defer is the same for any $q \ge p$, as $q$ is discarded. If the buyer would accept $p$, then $\frac{\partial M}{\partial p} = -1$. Integrated over all $q$, this yields

$$\begin{aligned} W_0^{\prime }(p) = \int _{-\infty }^{+\infty } \frac{\partial M(p,q)}{\partial p} dF(q) = - (1 - F(p)) > -1. \end{aligned}$$

If instead the buyer would defer $p$, then $\frac{\partial M}{\partial p} = (1-\gamma ) W_0^{\prime }(p)$. Integrated over all $q$, this yields

$$\begin{aligned} W_0^{\prime }(p) = \int _{-\infty }^{+\infty } \frac{\partial M(p,q)}{\partial p} dF(q) = (1 - F(p)) (1-\gamma ) W_0^{\prime }(p). \end{aligned}$$

The first two terms on the r.h.s. are strictly between 0 and 1, so this only holds if $W_0^{\prime }(p) = 0$. Thus, in either case, $W_0^{\prime }(p) > -1$.

In light of this, consider the choice to accept versus defer an offer. The utility from accepting, $x - p$, has a derivative w.r.t. $p$ of $-1$. The utility from deferral, $d + (1 - \gamma ) W_0(p) + \gamma V_0$, has a derivative $(1 - \gamma ) W_0^{\prime }(p) > -1$. Therefore, if $p > R_0$ then $x - p < d + (1 - \gamma ) W_0(p) + \gamma V_0$ , and vice versa.

1.2 A.2 Proof of Lemma 2

Proof

Let $I(z,u) = x - z - u - (1 - \gamma ) W_0(z) - \gamma V_0$. Note that $\frac{\partial I}{\partial u} = -1$ and $\frac{\partial I}{\partial z} = -1 - (1 - \gamma ) W_0^{\prime }(z) < 0$. By implicit differentiation, $\frac{\partial z}{\partial u} = -\frac{-1}{-1 - (1 - \gamma ) W_0^{\prime }(z)} < 0$. Since $R_0$ is defined by $I(R_0,d) = 0$, $R_1$ by $I(R_1,b) = 0$, and $b > d$, this implies that $R_1 < R_0$.

1.3 A.3 Proof of Lemma 3

Proof

(of Claim 3) Suppose an atom of weight $a > 0$ existed at price $p \in (R_1,R_0]$. A seller offering $p$ would find that a positive measure of their offers is tied with another offer of $p$. In particular, this occurs with probability $(1 - \gamma ) a > 0$, since $a$ is the probability that another offer is made at price $p$, and $1 - \gamma$ is the probability that the buyer retains the first offer made.

If this happens, the buyer randomizes with equal weight between the two offers. If the seller had offered $p - \epsilon$, where $\epsilon > 0$ is arbitrarily small, he would have garnered $\frac{(1 - \gamma ) a}{2}$ more sales among early buyers who defer, without losing any of the other $S(p)$ sales from offering $p$. This discrete jump in expected sales (with a negligible reduction in profit per sale) means offering $p$ is strictly dominated. Thus, no firm would offer $p$ and hence it cannot be part of the support.

While we have assumed equal probability in randomizing over the two offers, other tiebreaking rules have similar effect, as in Bertrand competition.

Proof

(of Claim 4) Suppose $\hat{p} = \sup P$ and $R_1 < \hat{p} < R_0$. We will show that any $\tilde{p} \in (\hat{p},R_0]$ will yield strictly greater profits.

First, consider buyers in search state 0 with no other offer; from Lemma 1, they will accept not only $\hat{p}$ but also any $\tilde{p} \in (\hat{p},R_0]$.

Next, consider buyers in search state 0 who have retained some prior offer. Since $\hat{p} = \sup P$ and there is no atom at $\hat{p}$, their prior offer is almost surely strictly better than $\hat{p}$ or $\tilde{p}$. Thus, either new offer is almost surely rejected.

Finally, note that those who are offered $\hat{p}$ in search state 1 will always defer it and almost surely obtain a better offer in search state 0. The same would occur if had $\tilde{p}$ been offered initially.

Thus, both offers generate sales from the same fraction of the population, namely those in state 0 with no offers. But $\tilde{p}$ has a larger markup than $\hat{p}$, so offering the former generates strictly greater expected profit. Since $\tilde{p} \notin P$, this contradicts $F(p)$ as being an equilibrium price distribution.

1.4 A.4 Proof of Proposition 1

Proof

Using the properties of $F$ in Lemma 3 and the reservation price properties of $R_0$ and $R_1$, we can restate the buyer’s Bellman equations as follows. Delayed buyers with no retained offers will accept any price at or below $R_0$, which includes the full support of $F$. Therefore, his expected utility is

$$\begin{aligned} V_0 = a (x - R_1) + \int _{\underline{p}}^{R_0} (x - q) F^{\prime }(q) \mathrm{d}q. \end{aligned}$$

(25)

A delayed buyer who has retained an offer $p$ will also make a purchase in the current iteration, accepting the lower price of either $p$ or his new offer $q$:

$$\begin{aligned} W_0(p) = (1 - F(p)) (x - p) + a (x - R_1) + \int _{\underline{p}}^{p} (x - q) F^{\prime }(q) \mathrm{d}q. \end{aligned}$$

(26)

An early buyer, however, will only accept $R_1$ if it is drawn; all other offers are deferred

$$\begin{aligned} V_1 = a (x - R_1) + \int _{\underline{p}}^{R_0} \left( b + (1 - \gamma ) W_0(q) + \gamma V_0 \right) dF(q). \end{aligned}$$

(27)

Next, note that $W_0(R_0) = V_0$. By substituting this into Eq. 2, we get

$$\begin{aligned} R_0 = x - d - V_0. \end{aligned}$$

(28)

Similarly, $W_0(R_1) = x - R_1$. Substituting this into Eq. 5, we obtain

$$\begin{aligned} R_1 = x - \frac{b}{\gamma } + V_0. \end{aligned}$$

(29)

Regarding the steady state population, note that Eqs. 7 through 10 are linear in terms of $H,\,h_1,\, h_0,\, \text{ and} \ g_0(p)$, and are easily solved.

To obtain the price distribution, we turn to the equal profit conditions. Offering $R_1$ results in profit $\frac{(2-a)\delta }{1- \gamma } (R_1 - c)$. After substituting for the steady state populations, for prices between $\underline{p}$ and $R_0$, Eq. 12 profit becomes

$$\begin{aligned} \pi (p) = \left( 2(1 - F(p)) + \frac{ (1 - a) \gamma }{1 - \gamma } \right)\delta (p-c). \end{aligned}$$

(30)

We then solve for $F(p)$ in this price range by equating $\pi (p) = \pi (R_0)$. Note that because this portion of the distribution is atomless and $R_0$ is the highest offered price, $F(R_0) = 1$. This yields

$$\begin{aligned} F(p) = 1 - \frac{ (1 -a) (R_0 - p) \gamma }{2 (p-c)(1 - \gamma )}, \end{aligned}$$

(31)

and taking the first derivative w.r.t. $p$ provides

$$\begin{aligned} F^{\prime }(p) = \frac{(1 - a)(R_0 - c)\gamma }{2 (p-c)^2(1 - \gamma )}. \end{aligned}$$

(32)

In addition, we must determine the value of $\underline{p}$. This is pinned down by the fact that $F(\underline{p}) = a$, since no prices between $R_1$ and $\underline{p}$ are offered. This provides the solution:

$$\begin{aligned} \underline{p} = \frac{(1- \gamma ) 2 c + \gamma R_0}{2 - \gamma }. \end{aligned}$$

(33)

With the price distribution pinned down, we can now compute expected prices in Eq. 25 to express $V_0$ in terms of $a$, $R_0$, and $R_1$. After evaluating the integral, we obtain

$$\begin{aligned} V_0 = x - c - (R_1 - c ) a - (R_0 - c) \frac{(1 - a) \gamma \ln \left( \frac{2-\gamma }{\gamma }\right)}{2(1 - \gamma )}. \end{aligned}$$

(34)

Notice that Eqs. 28, 29, and 34 provide three linear equations in terms of $R_0$, $R_1$, and $V_0$; of course, only the former two are of explicit interest. These jointly solve to obtain the proposed $R_0^*$ and $R_1^*$. After these are found, they can be written in terms of the function $\kappa (a)$, which is defined as the expected price in distribution $F(p)$, or equivalently, $\kappa (a) = x - V_0$.

Note that we obtain the proposed profit functions and price distribution by substituting $R_0^*$ and $R_1^*$ into Eqs. 30, 31, and 33. We note here that $\underline{p}^* < R_0^*$ as required:

$$\begin{aligned} c + \frac{\gamma }{2 - \gamma } (\kappa (a^*) - c - d) < \kappa (a^*) -d \quad \Longleftrightarrow \quad \frac{1 - \gamma }{2 - \gamma } (c + d - \kappa (a^*)) < 0. \end{aligned}$$

The fraction is clearly positive. If $\kappa (a^*) < c + d$, firms would earn negative profit, which violates the equilibrium conditions since charging $p = c$ earns 0 profit.

To compare $R_1^* < \underline{p}^*$, one must substitute for $\kappa (a^*)$, and the calculation depends on whether a late or a full equilibrium has occurred. If $a^* = 0$, this comparison yields

$$\begin{aligned} d \left( 1+\frac{4 (1-\gamma )^2}{(2-\gamma ) \left(2(1- \gamma ) +\gamma \ln \left(\frac{\gamma }{2-\gamma }\right)\right)} \right)< \frac{b}{\gamma }. \end{aligned}$$

The parenthetical term on the l.h.s. is always positive and is multiplied by $d < 0$, while the r.h.s. is always positive. Thus, the inequality must hold.

The comparison in the case of a full equilibrium requires more algebraic manipulation, but it always holds as well. These details are provided in Section 2.4.2 of the Technical Appendix.

If the respective profit condition holds, this solution is an equilibrium by construction. Existence is assured because $\varPi _1(a) - \varPi _0(a)$ is continuous in $a$. This falls to $-\infty$ as $a \rightarrow 1$ (which precludes $a = 1$ as an equilibrium outcome). Thus, if $\varPi _1(0) - \varPi _0(0) > 0$, there must exist an $a^* \in (0,1)$ such that $\varPi _1(a^*) = \varPi _0(a^*)$. Of course, if $\varPi _1(0) - \varPi _0(0) \le 0$, then a late equilibrium exists.

Finally, this proof by construction also demonstrates that no other equilibrium (beyond these two) can exist, as only the constructed solution will satisfy all equilibrium requirements.

1.5 A.5 Proof of Proposition 2

Proof

Suppose $\varPi _1(a^*) = \varPi _0(a^*)$ for some $a^* \in (0,1)$. Thus, Eq. 20 holds with equality.

We take the first derivative of $\varDelta (a) \equiv \varPi _1(a) - \varPi _0(a)$ w.r.t. $a$, evaluated at $a^*$. This later fact allows us to substitute for $d$ using Eq. 20. The details of this algebraic manipulation are included in Sect. 3 of the Technical Appendix; it results in

$$\begin{aligned}&\varDelta ^{\prime }(a^*) = \frac{2 \delta b}{\gamma (1 - a^*)^2} \\&\quad \cdot \left(2 (1-\gamma )(1-a^*) (3-a^* (1-\gamma )-\gamma )-\left( \gamma \left(1-a^* \right)^2 - (2-a^*)^2 \right) \ln \left( \frac{\gamma }{2-\gamma }\right) \right) \Bigg / \\&\quad \left( \left(2(1-\gamma )+\gamma \ln \left( \frac{\gamma }{2-\gamma }\right) \right) \left(-2 (1-\gamma )(1-a^*) - (2-a^*) \ln \left( \frac{\gamma }{2-\gamma }\right) \right)\right). \end{aligned}$$

The first line $\frac{2 \delta b}{\gamma (1 - a^*)^2}$ is always positive. The next term in the numerator is strictly increasing in $\gamma$. Its derivative w.r.t. $\gamma$ is

$$\begin{aligned}&- (1 - a^*)^2 \ln \left( \frac{\gamma }{2-\gamma }\right)\\&\quad +\frac{1}{\gamma (2 - \gamma )} \left(2 {a^*}^2 +2 \gamma a^* (1-a^*)(5-4 \gamma ) +4 \gamma ^2 (1-\gamma )^2 (1-a^*)^2 \right.\\&\quad +\left.4 \gamma ^3 (1-\gamma ) \left(1-2a^*+{a^*}^2\right) +(1-a^*) \left(8-18 \gamma +12 \gamma ^2\right) \right). \end{aligned}$$

Note that the logarithm will be negative since $\frac{\gamma }{2-\gamma } < 1$, so the first term is positive, as is the fractional term. Within the parentheses, one can immediately see that the first four terms are strictly positive for $\gamma \in (0,1)$. The last term is also strictly positive, since it reaches a minimum of 1 at $\gamma = 3/4$. Thus, this derivative is strictly positive for $\gamma \in (0,1)$. Thus, the numerator reaches its maximum value when $\gamma = 1$, where it evaluates to 0. Thus, the numerator is negative for any $\gamma < 1$ or $a^* \in (0,1)$.

In the denominator, the first term has a derivative w.r.t. $\gamma$ of $-\frac{2(1-\gamma )}{2 - \gamma } + \ln ( \frac{\gamma }{2-\gamma })$. The first term is obviously negative for $\gamma \in (0,1)$, as is the logarithmic term since $\frac{\gamma }{2-\gamma } < 1$. Thus, the first denominator term is strictly decreasing in $\gamma$, reaching its smallest value of 0 at $\gamma = 1$; hence, it is always positive.

The same applies to the second term in the denominator. Its derivative w.r.t. $\gamma$ is $- \frac{2-a (1-\gamma )^2-(2-\gamma ) \gamma }{(2-\gamma ) \gamma } < 0$. Note that the inequality holds even at $a = 1$ and is easier to satisfy for lower $a$. Thus, the second denominator term is decreasing in $\gamma$ and reaches its smallest value of 0 at $\gamma =1$. Thus, the term is always positive.

Thus, with a negative numerator and positive denominator, $\varDelta ^{\prime }(a^*) < 0$ for all $\gamma < 1$. $\varDelta (a)$ is a continuous function. Since it is decreasing in $a$ wherever it crosses $\varDelta (a) = 0$, it can cross at most once in $a \in [0,1]$.

Next, suppose there is an $a^* \in (0,1)$ such that $\varDelta (a^*) = 0$. Since this solution is unique and $\varDelta ^{\prime }(a^*) < 0$, then $\varDelta (0) > 0$. This precludes the existence of a late equilibrium. The reverse is also true: if $\varDelta (0) \le 0$, there could not exist another $a^* \in (0,1)$ such that $\varDelta (a^*) = 0$ without contradicting $\varDelta ^{\prime }(a^*) < 0$.

1.6 A.6 Proof of Proposition 3

Proof

We examine the buyer’s decisions in the unlimited-deferrals model, which can be described as a decision tree. Each iteration begins with a draw of a new quote, followed by the buyer deciding to either accept the current best offer or defer all offers. Stationarity requires that this decision depend only on the search state (0 or 1) and the set of $n \in \mathbb N _{++}$ available offers $\{ p_i \}_{i = 1}^n$ (which includes all retained offers and his latest draw). Deferral results in incurring the utility $b$ or $d$ and realizing which of the offers are retained for the next iteration.

We define the reservation prices $R_0$ and $R_1$ as in the single-deferral model and consider the same price distribution $F$. Thus, any offers must be at or below $R_0$. Buyers in state 1 still have no prior offers, so their strategy remains as before: accept $R_1$ and defer otherwise. We will show it is a best response for a buyer in search state 0 to accept their best available offer, regardless of the number or set of available offers. If this is the case, no buyer will ever defer a second quote; thus, the steady state distribution is unchanged, as are the expected profits from offering $R_1$ or $p \in [\underline{p}, R_0]$. Thus, the same equilibrium will exist.

Consider a buyer who has a set of offers $\{ p_i \}_{i = 1}^n$ at any iteration in the decision tree. Our proposed equilibrium directs him to accept the lowest offer among these prices; we ask if he would ever strictly prefer to make a one-shot deviation by deferring for one iteration and then accepting the best available offer.

Suppose that $p_i = R_0$ for all $i$. Immediate purchase provides utility $x - R_0$. If he defers, he draws and accepts price $q$ tomorrow, since $q \le R_0$. This holds even if all $n$ deferred offers are lost. This buyer is no better off than if he had only retained one offer $R_0$ or even none at all, which is to say, $W_0\left( \{ p_i \}_{i = 1}^n \right) = W_0\left(R_0 \right) = V_0$. The definition of $R_0$ in Eq. 2 is $x - R_0 = d + (1 - \gamma ) W_0\left(R_0 \right) + \gamma V_0$. Note that since $W_0\left(R_0 \right) = V_0$, the r.h.s. can be rewritten as:

$$\begin{aligned} d + (1 - \gamma ) W_0\left(R_0 \right) + \gamma V_0&= d + V_0 \\&= d + (1 - \gamma ^n) V_0 + \gamma ^n V_0 \\&= d + (1 - \gamma ^n) W_0\left(R_0 \right) + \gamma ^n V_0. \end{aligned}$$

Thus, $x - R_0 = d + (1 - \gamma ^n) W_0\left(R_0 \right) + \gamma ^n V_0$; the buyer with $n$ retained offers of $R_0$ is indifferent between acceptance and deferral. In particular, he cannot strictly prefer to defer his $n$ offers.

Suppose instead that $p_i = p < R_0$ for all $i$. Immediate purchase provides utility $x - p$. If he defers, with probability $\gamma ^n$, he will lose all $n$ of the deferred offers and will purchase using his new offer $q$; this gives expected utility $V_0$. With probability $1 -\gamma ^n$, he will retain one of the deferred offers. With probability $1 - F(p)$, the new draw is more expensive than $p$ and so he accepts a retained offer for utility $x - p$. Otherwise, he accepts $q$. In sum, his expected utility from deferral is

$$\begin{aligned}&d + \gamma ^n V_0 + (1 -\gamma ^n) \left( (1 - F(p)) (x - p) + a (x - R_1) + \int _{\underline{p}}^{p} (x - q) F^{\prime }(q) \mathrm{d}q \right) \\&\quad = d + \gamma ^n V_0 + (1 -\gamma ^n) W_0(p). \end{aligned}$$

Recall that $x - p = d + (1 - \gamma ^n) W_0(p) + \gamma ^n V_0$ when $p = R_0$. If we take the derivative of each side for any $p$, we get $-1$ on the l.h.s. and $(1 - \gamma ^n) W_0^{\prime }(p) > -1$ on the r.h.s., where the inequality holds due to Lemma 1. These derivatives indicate that as $p$ decreases from $R_0$, the immediate purchase utility on the left increases at a strictly faster rate than the deferral utility on the right, making the former strictly preferred. Indeed, since $(1 - \gamma ^n) W_0^{\prime }(p) > -1$ for all $p$ in the support of $F$, the difference between the two options only strengthens in favor of acceptance as $p$ continues to fall.

Finally, suppose that $\tilde{p}_1 = p < R_0$ and $\tilde{p}_i \in [p,R_0]$ for all other $n-1$ offers and compare this to the situation above where $p_i = p$ for all $i$. Note that either set of offers produces the same utility from immediate acceptance, since $\min p_i = \min \tilde{p}_i = p$. But the utility from deferral must be weakly worse under $\{ \tilde{p}_i \}_{i = 1}^n$ and strictly so if $\tilde{p}_i > p$ for some $i$. This is because with positive probability, the offer $p$ will be lost and the new offer $q$ will be worse than the other retained offers. Thus, purchase at price $p$ is still strictly preferred to deferral.

This demonstrates that buyers will never strictly prefer to make a one-shot deviation from the proposed strategy. Indeed, buyers are only indifferent if all available offers equal $R_0$, which occurs with measure zero and thus has no impact on the steady state distribution or firm pricing. For any other set of available prices, buyers cannot optimally defer one period and accept the next.

We next consider $k$-shot deviations. Our proposed strategy tells a buyer in search state 0 to always accept the best available offer. Thus, any finite-length deviation must take the form of deferring (perhaps contingent on available prices) for $k-1$ periods and then accepting the best price in the $k\text{ th}$ iteration. However, note that such a strategy includes a one-shot deviation of deferring in the $k-1\text{ th}$ iteration, which is not optimal. Thus, any finite deviation is not optimal as well.

Finally, the only infinite-length path occurs by repeatedly deferring; doing this would produce utility $-\infty$ since it involves repeatedly incurring the penalty $d$ without discounting. This strategy (or any of its subpaths) is clearly dominated by immediate acceptance of any price in $F$ and cannot be part of an optimal strategy. Therefore, the overall strategy is optimal, and the single-deferral equilibrium exists in the unlimited-deferral environment.

For the uniqueness of this equilibrium, consider the role of $F(p)$ in the preceding argument. Its functional form was completely absent from the argument, and in fact, it only relied on the fact that $R_0$ is the maximum of the support of $F$, as required under Claim 1 of Lemma 3. Thus, if an alternative distribution $\hat{F}$ was used, it would still be the case that buyers would strictly prefer to immediately accept any offer $p < R_0$.

It is true that buyers are indifferent between acceptance and deferral of an offer $R_0$. Yet Claim 3 of Lemma 3 still applies in this environment, so there are no atoms except at $R_1$. In particular, buyers almost never receive an offer of $R_0$. Thus, even if a strategy directed buyers to defer $R_0$, it would have no impact on the steady state distribution since such buyers would constitute measure zero of the population.

Therefore, the steady state distribution of buyers would be the same under any distribution $\hat{F}$ that is consistent with profit maximization. Yet, only the equilibrium $F^*$ is consistent with that steady state distribution, as shown in the proof of Proposition 1.

1.7 A.7 Proof of Proposition 4

Proof

We show that $\frac{\partial R_1}{\partial \gamma }<0$ here, but this also establishes that $\frac{\partial R_0}{\partial \gamma }<0$ and $\frac{\partial E[p]}{\partial \gamma }<0$. To see this, consider that $R_1$, $E[p]$, and $R_0$ are each expressed in terms of $\kappa (a)$. Furthermore, the equilibrium $a$ which satisfies $\phi (a) = 0$ will implicitly depend on $\gamma$, so when derivatives are taken with respect to $\gamma$, we obtain

$$\begin{aligned} \frac{\partial R_1}{\partial \gamma } \!=\! \frac{b}{\gamma ^2}+a^{\prime }(\gamma ) \kappa ^{\prime } \left(a(\gamma )\right), \; \frac{\partial E[p]}{\partial \gamma } \!=\! a^{\prime }(\gamma ) \kappa ^{\prime } \left(a(\gamma ) \right), \text{ and} \frac{\partial R_0}{\partial \gamma } \!=\! a^{\prime }(\gamma ) \kappa ^{\prime } \left(a(\gamma ) \right). \end{aligned}$$

Hence, if $\frac{b}{\gamma ^2}+a^{\prime }(\gamma ) \kappa ^{\prime }(a(\gamma ))<0$, then each of the derivatives will be negative.

Thus, we consider the derivative of $R_1$. To compute this, we use the implicit derivative for $a^{\prime }(\gamma )$, obtaining:

$$\begin{aligned} \frac{\partial R_1}{\partial \gamma } = \frac{N}{D}, \end{aligned}$$

where

$$\begin{aligned} N&\equiv b \left(4 (1-\gamma ) \left(\gamma (a^2 (3-2 a) - 1) - (3-2 a) a - \gamma ^2 (2-3 a) (1-a)^2 + \gamma ^3 (1-a)^3 \right) \right.\\&+ 2 (2 - \gamma ) \left(\gamma - a (2-a) - a (5-2 a (3-a)) \gamma -\gamma ^2 (1- a)^2 (3-2 a) \right) \ln \left(\frac{\gamma }{2-\gamma }\right) \\&\left.+\gamma (2 - \gamma ) (2 - a) (1- a)^2 \ln \left(\frac{\gamma }{2-\gamma }\right)^2\right), \end{aligned}$$

and

$$\begin{aligned} D&\equiv \gamma ^2 (2 - \gamma ) \left(- 2 (1 - \gamma ) (1- a) - (2-a) \ln \left(\frac{\gamma }{2-\gamma }\right)\right) \\&\times \left(2 (1 \!-\! \gamma ) (1\!-\! a) (3\!-\!a (1\!-\!\gamma )\!-\!\gamma )\!-\! \left(\gamma (1 - a)^2 - (2-a)^2 \right) \ln \left(\frac{\gamma }{2 - \gamma }\right) \right). \end{aligned}$$

We verify that $\frac{N}{D} < 0$ for any $0 < \gamma < 1$ and $0 < a < 1$, which necessarily includes the equilibrium $a^*$. Regarding the elements of $D$, it is obvious that $\gamma ^2 (2 - \gamma ) > 0$. The other two elements each appeared in $\varDelta ^{\prime }(a)$ in the proof of Proposition 2. There, we showed that the last element on the first line is positive, while the term on the second line is negative. Thus, we find that $D < 0$.

We will now show that $N > 0$. To do so, we will show that $N$ is increasing in $a$ and that $N$ is positive at its minimum. Consider the first derivative $N^{\prime }$ w.r.t. $a$

$$\begin{aligned} N^{\prime }&= 4 (1 - \gamma ) \left(4 a- 3 + 6 \gamma a (1- a) + \gamma ^2 (1- a) (7- 9 a)- 3 \gamma ^3 (1-a)^2\right) \\&-(2-\gamma ) \ln \left(\frac{\gamma }{2-\gamma }\right) \left(4(1-a)+2 \gamma (5 - 6 a (2-a)) -4 \gamma ^2 (1-a) (4-3 a) \right.\\&+\left.\gamma (1-a) (5-3 a) \ln \left(\frac{\gamma }{2-\gamma }\right)\right). \end{aligned}$$

We need to show that $N^{\prime } > 0$, but this is a complicated expression. Hence, we will show that $N^{\prime }$ is decreasing in $a$ and that its minimum value is positive. The derivative of $N^{\prime }$ w.r.t. $a$ is

$$\begin{aligned} N^{\prime \prime } =2 (2 - \gamma ) \left(2(1 - \gamma ) + \ln \left(\frac{\gamma }{2-\gamma }\right) \right) T(a), \end{aligned}$$

where

$$\begin{aligned} T(a) \equiv 2 (1-\gamma ) (1+ 3 \gamma (1- a) )+ \gamma (4-3 a) \ln \left(\frac{\gamma }{2-\gamma }\right). \end{aligned}$$

For all $\gamma \in (0,1)$, the first two terms in $N^{\prime \prime }$ are clearly positive. The third appeared in $\varDelta ^{\prime }(a)$ and was shown to be negative. To show that the last term $T$ is positive, we take its derivative w.r.t. $a$

$$\begin{aligned} T^{\prime }(a) = - 3 \gamma \left(2(1 - \gamma ) + \ln \left(\frac{\gamma }{2-\gamma }\right) \right). \end{aligned}$$

Again, the last term is negative, so $T^{\prime }(a) > 0$ for any $\gamma \in (0,1)$. Thus, $T$ is increasing in $a$ and has its minimum at $a = 0$. There, it takes a value of $T(0) = 2+4 \gamma -6 \gamma ^2+4 \gamma \ln \left(\frac{\gamma }{2-\gamma }\right)$. If we take the second derivative of $T(0)$ w.r.t. $\gamma$, we obtain

$$\begin{aligned} T_{\gamma \gamma } (0) = \frac{16}{\gamma (2 - \gamma )^2} - 12, \end{aligned}$$

which is strictly positive since $\gamma (2 - \gamma )^2$ is largest at $\gamma = 2/3$; there, $T_{\gamma \gamma } (0) = 3/2$, with all other values being strictly greater. Since $T_{\gamma \gamma } (0) > 0$, then $T_{\gamma } (0)$ must take its largest value at $\gamma = 1$, where it is equal to 0. In other words, $T_{\gamma } (0) < 0$, and hence, $T(0)$ takes its smallest value at $\gamma = 1$, where $T(0) = 0$. Thus, we conclude that $T(a) > 0$ for all $a \in (0,1)$ and all $\gamma \in (0,1)$, and hence $N^{\prime \prime } < 0$ on the same domain.

Since $N^{\prime \prime }$ is negative, $N^{\prime }$ must be decreasing in $a$ and, hence, reaches its smallest value at $a=1$. This minimum value computes to $N^{\prime }(1) = 4 (1-\gamma ) + 2 \gamma (2- \gamma ) \ln (\frac{\gamma }{2-\gamma })$. Note that $N^{\prime }_\gamma (1) = 4 (1 - \gamma ) \ln (\frac{\gamma }{2-\gamma }) < 0$. Thus, $N^{\prime }(1)$ takes its smallest value at $\gamma = 1$, where $N^{\prime }(1) = 0$. Therefore, $N^{\prime }(1) > 0$ for all $\gamma \in (0,1)$, and by extension, $N^{\prime } > 0$ for all $\gamma \in (0,1)$ and $a \in (0,1)$.

This means that $N$ is increasing in $a$ and reaches its minimum at $a=0$, which computes to

$$\begin{aligned} N(0)&= 2 \gamma \left(-2 \left(1+\gamma -3 \gamma ^2+\gamma ^3\right)\right.\\&\left.+(2-\gamma ) \left(1-3 \gamma +\ln \left(\frac{\gamma }{2-\gamma }\right)\right) \ln \left(\frac{\gamma }{2-\gamma }\right) \right). \end{aligned}$$

Note that $-2 \left(1+\gamma -3 \gamma ^2+\gamma ^3\right) > - 4(1 - \gamma )$, because this is equivalent to $2(1 - \gamma )^3 > 0$, which holds for all $\gamma < 1$. Also, we have previously noted that $2( \gamma - 1) > \ln (\frac{\gamma }{2-\gamma })$, which rearranges to $1-3 \gamma +\ln (\frac{\gamma }{2-\gamma }) < -1 - \gamma$. Therefore, we can use all three substitutions to obtain

$$\begin{aligned} N(0) > 2 \gamma \left(- 4(1 - \gamma ) + (2-\gamma ) (-1 - \gamma ) 2( \gamma - 1) \right). \end{aligned}$$

Note that $N_\gamma (0) = 0$ at $\gamma = 0,\,\frac{1}{2},\, \text{ and} \ 1$, taking values of $0,\, \frac{1}{4},\, \text{ and} \ 0$, respectively. Therefore, $N_\gamma (0) > 0$ for all $\gamma \in (0,1)$, and by extension, $N > 0$ and $\frac{\partial R_1}{\partial \gamma } < 0$ for all $\gamma \in (0,1)$ and $a \in (0,1)$.