Abstract
Broadband shock-associated noise (BBSAN) is a particular high-frequency noise that is generated in imperfectly expanded jets. BBSAN results from the interaction of turbulent structures and the series of expansion and compression waves which appears downstream of the convergent nozzle exit of moderately under-expanded jets. This paper focuses on the impact of the pressure waves generated by BBSAN from a large eddy simulation of a non-screeching supersonic round jet in the near-field. The flow is under-expanded and is characterized by a high Reynolds number \(\mathrm{Re}_\mathrm{j} = 1.25\times 10^6\) and a transonic Mach number \(M_\mathrm{j}=1.15\). It is shown that BBSAN propagates upstream outside the jet and enters the supersonic region leaving a characteristic pattern in the physical plane. This pattern, also called signature, travels upstream through the shock-cell system with a group velocity between the acoustic speed \(U_{\mathrm{c}}-a_\infty \) and the sound speed \(a_\infty \) in the frequency–wavenumber domain \((U_\mathrm{c}\) is the convective jet velocity). To investigate these characteristic patterns, the pressure signals in the jet and the near-field are decomposed into waves traveling downstream (\(p^+\)) and waves traveling upstream (\(p^-\)). A novel study based on a wavelet technique is finally applied on such signals in order to extract the BBSAN signatures generated by the most energetic events of the supersonic jet.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Supersonic jet noise has been studied since the discovery of screech phenomenon by Powell [1] in the 1950s. Utilizing Schlieren-based flow visualization, he identified sound waves that were propagating upstream. This noise, called screech, was explained as a feedback loop between the vortical structures convected downstream from the nozzle lip and the noise generated from the interaction with the shock cells that appear due to the mismatch in pressure at the exit of the nozzle. Supersonic jet noise is mainly composed of three components: screech tonal noise, broadband shock-associated noise (BBSAN), and turbulent mixing noise. The BBSAN was studied theoretically by Harper-Bourne and Fisher [2]. Their model was able to predict the pressure spectrum for different pressure ratios and angles of observation modeling shock cells by single-point acoustic sources. Tam and Tanna [3] investigated the BBSAN experimentally, concluding that it was generated by the same process as the screech tones, i.e., the weak but coherent interaction between large-scale turbulent structures convected downstream and the quasi-periodic shock-cell system. The origin of BBSAN was located by Norum and Seiner [4] in the downstream weaker shock cells as opposed to the screech phenomenon that is generated where the shock cells have a higher intensity and oscillation, usually located between the second and fourth shock-cell positions [5]. The shock-cell noise generation mechanism was extensively studied by Tam in the 1980s when he developed the stochastic model theory [6]. The model is based on the assumption that the large vortical structures can be modeled by a superposition of several intrinsic instability waves of the mean jet flow and that the nearly periodic shock-cell system can be decomposed into time-independent waveguide modes. The broadband shock-cell noise is therefore the superposition of the spectra generated by the unsteady disturbances that appear from the interaction between the instability waves and each of the waveguide modes. Finally, turbulent mixing noise of axisymmetric jets was analyzed by Tam et al. [7] who evidenced the existence of two universal similarity spectra, one for the noise generated by large turbulent structures and the other for fine-scale turbulence. Exhaustive reviews on supersonic jet noise were done by Raman [8] and Tam [9].
A new approach to the physical phenomenon of supersonic jet noise was introduced by Manning and Lele [10] with the increase in computing power at the end of the twentieth century. In performing a direct Navier–Stokes simulation (DNS), a two-dimensional weak shock impinging upon a shear layer was presented as the simplification of the shock-cell system of an imperfectly expanded jet. The shock is subjected to large fluctuations produced by the passage of the instability wave vortices. These fluctuations are coupled with the generation of a sharp compression of the acoustic wave that occurs when the shock travels upstream after the passage of the vortex, i.e., in the saddle-point of its oscillation cycle where the local vorticity becomes the weakest. At this point, the shock leaks through the shear layer as shock-cell noise. The shock-leakage phenomenon was further investigated by Suzuki and Lele [11] using the geometrical acoustic theory. The mechanism was numerically demonstrated by solving the time-dependent Eikonal equation on DNS data. Shock-leakage theory was further confirmed in the large eddy simulation (LES) of a planar jet by Berland et al. [12] who observed the shock waves responsible for the leak of the screech tonal noise through the saddle-points.
Several authors investigated the noise generated by supersonic jets using LES. In particular, Schulze and Sesterhenn [13], Schulze et al. [14], and Berland et al. [12] simulated a three-dimensional supersonic under-expanded planar jet. Mendez et al. [15] studied supersonic perfectly expanded axisymmetric jets at \(M_\mathrm{j}=1.4\) and Bodony et al. [16] examined supersonic under-expanded and perfectly expanded jets at \(M_\mathrm{j}=1.95\). The same jet was considered by Lo et al. [17], obtaining good agreement with numerical results from Bodony et al. [16]. The noise emitted from supersonic under-expanded rectangular nozzles at \(M_\mathrm{j}=1.4\) and the effect of chevrons were studied by Nichols et al. [18, 19] on the same configuration. Furthermore, temperature effects have been correctly captured by Brès et al. [20] for an over-expanded supersonic jet at \(M_\mathrm{j}=1.35\).
Many numerical studies of imperfectly expanded jets focus mostly on aerodynamic statistics and far-field noise spectra. The use of a wavelet decomposition represents an efficient alternative to a Fourier transform in order to perform a deep analysis of both hydrodynamic and acoustic near-field components. The wavelet transform originated in the 1980s with Morlet [21] and is nowadays one of the most popular time–frequency transforms, originating from the seminal work done by Farge in the 1990s [22]. The regular wavelet transform decomposes a one-dimensional signal into a two-dimensional representation of the signal. For a temporal signal, the wavelet transform represents the signal in time and scale. Wavelet-based techniques are able to detect intermittent events that are not periodic in time. The use of wavelet transforms in jet aerodynamics and acoustics is quite limited, and it has been centered on experimental long time signals. Camussi and Guj [23, 24] and Grassucci et al. [25] used wavelet techniques in order to identify the intermittent, but coherent, structures that are convected through the shear layer of subsonic experimental jets and airfoils responsible for subsonic mixing noise. Similarly, Camussi et al. [26] used a wavelet-based conditional analysis of unsteady flow and sound signals to highlight the role of intermittent perturbations both in the sound generation and the unsteady field of an aerofoil tip leakage flow experiment. Grizzi and Camussi [27] used a wavelet approach to study the near-field pressure fluctuations of a subsonic jet. Moreover, the filtering capabilities of the wavelet transform have been exploited by Crawley and Samimy [28] and Mancinelli et al. [29] to filter the hydrodynamic and acoustic components in the near-field of a subsonic jet. In addition, Cavalieri et al. [30] used a continuous wavelet transform in the temporal direction to identify intermittent acoustic events in the far-field radiated by a subsonic jet from an LES. Finally, Walker et al. [31] demonstrated with a wavelet study that multiple acoustic modes produced by the jet coexist for a screeching supersonic jet.
The present work investigates the near-field BBSAN source mechanisms in a supersonic under-expanded jet at \(M_\mathrm{j}=1.15\). The main analysis of the LES results is performed with a wavelet-based procedure and focuses on shock-cell noise. This post-processing technique gives a conditional-averaged time signature representing the most probable shape of the most energetic events in the jet flow responsible for BBSAN. The paper is structured as follows: First, the wavelet-based technique is introduced in Sect. 2. Section 3 presents the configuration for both jet parameters and numerical approach. The identification of temporal and spatial signatures of the BBSAN of the simulated jet is detailed in Sect. 4. The analysis is carried out first by identifying particular patterns in the frequency–wavenumber domain. Then, a wavelet-based procedure is used in order to study the signatures in time and space of the events responsible for the detected patterns. Additionally, validation results are presented in the Appendix to demonstrate the ability of the present LES to reproduce experimental data of an under-expanded turbulent jet.
2 Wavelet-based signature identification procedure
The wavelet-based technique applied in this work follows the works of Camussi et al. [26]. It was also implemented by Gefen et al. [32] in order to extract the signature through a conditional average of the most characteristic events of the flow. The continuous wavelet transform \(w (s, \tau )\) of the signal of interest q(t) can be expressed as
where \(\tau \) is the translation parameter, s is the dilatation or scale parameter, and \({\psi ^*}\left( \frac{t - \tau }{s}\right) \) is the complex conjugate of the daughter wavelet \(\psi \left( \frac{t - \tau }{s}\right) \) obtained by the translation and dilatation of the so-called mother wavelet \(\psi _0 (t)\). Mathematically, the wavelet transform is a convolution of a temporal signal with a dilated function with different scales of dilatation. Each scale represents a different window size in the windowed Fourier transform. In this work, the non-orthogonal continuous wavelet transform was carried out using the first derivative of a Gaussian function (DOG) as mother wavelet. The DOG function is also known as Marr or Mexican Hat function and it is defined as
where \(m=2\). The reference scale s (with units of time for a temporal signal) can be expressed in terms of frequency f(s) or Strouhal number \(\mathrm{St}(s)\). To avoid confusion, the equivalent frequency is denoted as a function of s which implies that the frequency (and similarly, the Strouhal number) is a function of the scale s. For the DOG mother wavelet, they are related as
The mother wavelet DOG was chosen among others (such as Paul and Morlet) as it allows for a better temporal discretization of peaks or discontinuities. This temporal accuracy is necessary due to the short-time signal obtained in general from simulations. Moreover, the low discretization in scale that offers the DOG mother wavelet implies that the signatures obtained are an average of different events from similar scales. This allows to study broadband phenomena and to increase the convergence of the signature because more events are being detected.
Example of conditional averaging (auto-conditioning) from the example shown in Fig. 1.
 signature.
signature.
 windows \(\xi _i\) before averaging
windows \(\xi _i\) before averaging
Figure 1 shows an example of the wavelet transform of a pressure signal with the mother wavelet DOG. This initial pressure signal (Fig. 1, top) is recorded at \(120^\circ \) from the jet axis in the far-field of the supersonic jet introduced in Sect. 3.1 (see also Appendix). In Fig. 1 bottom, the event detection method compares the local wavelet power \(\left| w (s, \tau )\right| ^2\) (Fig. 1, center) with a defined background spectrum energy at all scales as
where \(\sigma \) is the variance of the signal \(q(t), P_k\) is the normalized Fourier power spectrum of the background noise and \(\chi _2^2\) is the value of the Chi-squared distribution at a defined percentile value. In this work, a white noise and the value of the Chi-squared distribution at 95% are chosen. The reader is referred to the work of Torrence and Compo [33] for further details. Once the events have been selected and well localized in the time domain (\(t_i\) in Fig. 1, bottom), a conditional average can be performed at scales of interest. It is called auto-conditioning if the original signal q(t) is used or cross-conditioning if a different variable or signal is employed. At each instant \(t_i\) corresponding to a peak of energy (event), it is possible to extract a window of fixed time-length \(t_\mathrm{W}\) from the target signal g(t). The conditional average \(\{q;g\}\) can be calculated from the average of this set of windows as
where \(\xi _{i}\) is the interval surrounding each peak (Fig. 1, top). \(\xi _{i} \in \left[ \tilde{t}_{i} - \frac{t_\mathrm{W}}{2}, \tilde{t}_{i} + \frac{t_\mathrm{W}}{2} \right] \) and N is the number of events used for the conditional average. N can be lower than the total number of events detected. Indeed, a filtering window \(\phi _i\) centered at \(t_i\) can be used to discard events based on characteristic lengths of the problem as illustrated in Fig. 1 (bottom). The averaged signal is known as the signature representing the most probable shape of the most energetic events. An example of the averaged signature is shown in Fig. 2.
As the signature obtained is a function of time, its spectrum can be computed as shown in Fig. 3. The spectrum of the signature recovers the energy of the original signal at the Strouhal number where the events were detected. Moreover, the cross-conditioning can be applied to a full two- or three-dimensional field in order to obtain the influence of the event on the complete flow.
One of the limitations of this procedure is the fact that two different types of events that have the same or a similar scale cannot be easily identified. The event detection procedure of this study is based on the energy of the signal for different scales. In acoustics, if two independent events radiate noise at similar scales and with a similar energy content, the event detection procedure will not be able to discriminate between them. Having the knowledge of the physics and the case that is being studied can be used to pre-process the signal before applying the wavelet-based procedure.
3 Configuration
3.1 Jet definition
The case of study is an under-expanded single jet at Mach number \(M_\mathrm{j}\) of 1.15 with a nozzle to pressure ratio (NPR) of 2.27. The jet is established from a round convergent nozzle with an exit diameter \(D=38\) mm [34]. The lip of the nozzle at the exit has a thickness of 0.5 mm. The Reynolds number based on the exit diameter and perfectly expanded conditions noted with the subscript \((\bullet )_\mathrm{j}\) is
where the density is \(\rho _\mathrm{j}=1.42\) kg/m\(^3\), the axial velocity is \(U_\mathrm{j}=356.96\) m/s and the dynamic viscosity is \(\mu _\mathrm{j}=1.54\times 10^{-5}\) kg/m/s. The ambient conditions used for this case are \(P_\mathrm{ref} = 9.8 \times 10^4\) Pa and \(T_\mathrm{ref} = 288.15\) K. The total pressure is \(P_\mathrm{t}=2.225\times 10^5\) Pa, and the total temperature is \(T_\mathrm{t}=303.15\) K. The main conditions are summarized in Table 1.
3.2 Numerical formulation
The full compressible three-dimensional Navier–Stokes equations are solved using the finite volume multi-block structured solver elsA (Onera’s software [35]). The spatial scheme is based on the implicit compact finite difference scheme of sixth order of Lele [36], extended to finite volumes by Fosso-Pouangué et al. [37]. The above scheme is stabilized by the compact filter of Visbal and Gaitonde [38] of sixth order that is also used as an implicit subgrid-scale model for the present LES. This scheme is able to capture perturbation waves when they are discretized by at least six points per wavelength. Time integration is performed by a six-step second-order Runge–Kutta dispersion–relation-preserving scheme of Bogey and Bailly [39].
3.3 Simulation parameters and procedure
In order to obtain inflow conditions as close as possible to the experiment at the nozzle exit, a coupled nozzle/jet-plume three-dimensional Reynolds average Navier–Stokes (RANS) computation is first performed using the Spalart–Allmaras turbulence model [40]. The LES is then initialized from the RANS solution, as in [41, 42], keeping the conservative variables at the exit plane of the nozzle (the internal part of the nozzle is not included in the simulation). In the LES, the flow field is initialized over 120 dimensionless convective times (\(T_\mathrm{c}=t a_\infty /D\)), with the sound velocity at ambient conditions being \(a_\infty =340.29\) m/s. The flow statistics are then collected over \(T_\mathrm{c}=140\) convective times, with a non-dimensional time step \((\Delta t a_\infty )/D = 4 \times 10^{-4}\).
The computational domain is depicted in Fig. 4. Non-reflective boundary conditions of Tam and Dong [43] extended to three dimensions by Bogey and Bailly [44] are used at the lateral boundaries. Downstream, the outflow boundary condition is based on the characteristic formulation of Poinsot and Lele [45]. Additionally, sponge layers are set around the physical domain (marked out by the red line in Fig. 4) to attenuate exiting vorticity waves. No inflow forcing is applied as the interior of the nozzle is not modeled, but as it is shown in the Appendix, the turbulence levels reach experimental values [46] within the first diameter. Last, no-slip adiabatic wall conditions are defined at all external wall boundaries of the nozzle. Moreover, a small external co-flow of 0.5 m/s is added to help with the convergence of the simulation. The propagation of pressure fluctuations into the far-field is done by means of a Ffowcs Williams and Hawkings [47] (FW–H) acoustic analogy with the formulation 1A of Farassat [48]. The solution is saved at the sampling frequency \(f_\mathrm{s}\) of 112 kHz on the FW–H surface (identified by the green line in Fig. 4) located at \(r/\!D\!\!=\!3.5\) at the nozzle exit and following a topological grid expanding radially with the jet.
This simulation was run without any shock-capturing methodology. Indeed, as the jet is moderately under-expanded, the NPR is relatively low. In addition, since the interior of the nozzle was not included in the LES, no strong shock occurs at the nozzle exit [49]. As a consequence, the formed shock cells are weak and diffused (reflection from a Prandtl–Meyer expansion fan [50]) with Mach numbers lower than 1.4 (see Appendix).
3.4 Mesh definition
The LES mesh contains \(75\times 10^6\) cells with about \((1052 \times 270 \times 256)\) cells in axial, radial, and azimuthal directions respectively. In order to avoid the singularity at the jet axis, the mesh combines Cartesian and polar grid blocks, also known as butterfly (or O–H) topology [42, 51]. The lip of the nozzle and initial momentum thickness at the nozzle exit are discretized using 8 and 15 cells respectively. In the physical region of the domain (Fig. 4), the maximum expansion ratio between adjacent cells in the mesh is not greater than 4%. At the nozzle exit (\(x/D=0\)), the mesh has an aspect ratio of 2.5. This ensures an appropriate definition of the first expansion fan of the shock-cell system. The axial mesh size along the axis line is shown in Fig. 5a. The axial mesh size at the nozzle exit is \(\Delta x/D=0.003\) and stretches at a rate of 3% up to one jet diameter (point A) where it reaches a value of \(\Delta x/D=0.017\). Then, the mesh consists in a uniform discretization up to five diameters (point B) and slowly varies up to a mesh size \(\Delta x/D=0.063\) able to capture a maximum Strouhal number \(\mathrm{St}=\textit{fD}/U_\mathrm{j}\) about 2 at the end of the physical domain (point C). In the sponge layer, the mesh has a stretching ratio of 10%. The radial mesh size at different axial sections is shown in Fig. 5b. On the axis (\(r/D=0\)), the radial mesh size is mainly constant, reaching a value of \(\Delta r/D=0.007\) at the nozzle exit. Then, it is refined with a constant rate of 2.5% for all axial positions. At the nozzle exit, the mesh achieves its minimum size at the lip-line with a value of \(\Delta r/D=0.001\). The mesh is then coarsened up to the sponge layer at a rate between 3.5 and 4% assuring a Strouhal number of about 2 on the FW–H surface.
4 Characterization of BBSAN
The jet flow field represented by the vorticity modulus and the acoustic radiated (pressure fluctuation) are shown in Fig. 4. The two main jet noise components, i.e., the mixing noise traveling downstream and the BBSAN traveling upstream, are clearly visible. In order to have a better description of the jet flow field, an instantaneous view of the train of shock cells interacting with turbulence is shown in Fig. 6 using numerical Schlieren and vorticity magnitude. The periodic structure of the shock cells originating from the imposed overpressure at the nozzle exit is well observed.
The sound pressure level (SPL) directivity of the jet noise predicted in the far-field using FW–H analogy is shown in Fig. 7 for different angles at a radial distance \(r/D=53\) from the nozzle exit with respect to the jet direction. The reference pressure used to compute the SPL is \(2\times 10^{-5}\) Pa. The mixing noise can be clearly found dominant at angles lower than \(60^\circ \) and Strouhal numbers in the range \(0<\mathrm{St}<0.5\). Shock-cell noise is well captured for high angles \(\theta \ge 90^\circ \) and high frequencies \(\mathrm{St}>0.6\). Moreover, the noise spectrum exhibits a Doppler shift [52] with an increase in the central frequency of BBSAN when moving toward lower angles. This explains why BBSAN is mostly dissipated in the downstream direction in higher frequencies due to a lower mesh discretization.
In order to characterize the BBSAN in the current LES, three sets of lines and azimuthal arrays of numerical probes with an equi-distribution every \(\Delta x/D=0.01\) are analyzed (see Fig. 4). The first data set is located on the jet centerline (noted as AXIS). The second data set is located at the jet lip-line (noted as LIPLINE), and the third data set is located in the near-field (noted as NEARFIELD). The latter line has a radial position relative to the exit plane of the nozzle \(x/D=0\) of \(r/D=1\), with an expansion angle of \(5^\circ \) with respect to the jet axis. Both LIPLINE and NEARFIELD data sets are arranged in an equally distributed azimuthal array of four probes (\(\Delta \theta = 90^{\circ }\)) that lay on the xy-plane and xz-plane. All data were collected at the same sampling rate as the FW–H surface of 112 kHz.
4.1 Shock-cell noise pattern
The shock-cell pressure pattern is first studied in the Fourier domain in order to obtain some general insights about the under-expanded jet dynamics and about shock-cell noise. The two-dimensional spectral characteristics are first analyzed on the xy-plane in Fig. 8 for \(\mathrm{St} = 0.3,0.6\), and 0.9. The power spectral density (PSD) of pressure is performed on each point of the plane and azimuthally averaged. Results show that at \(\mathrm{St}=0.3\), a maximum is reached near the jet axis at \(6<x/D<8\) (end of the potential core). Moreover, the PSD map follows the jet expansion downstream (identified by the dashed line). This is expected at this low Strouhal number as it is characteristic of the mixing noise from turbulent structures that propagate downstream in correlation with Fig. 7. At \(\mathrm{St}=0.6\), the contour at 140 dB/St shows that the spectral energy extends more in the upstream angles with respect to the jet axis. Similarly, at \(\mathrm{St}=0.9\), the PSD of pressure in the near-field is stretched out above the last shock cells near the jet potential core with a lower angle (highlighted by the dashed line). These two frequencies (\(\mathrm{St} = 0.6,0.9\)) are related to shock-cell noise in the far-field in Fig. 7 and seem to come from different regions in the jet. The different origin centers of shock-cell noise can be explained noting that the central frequency of BBSAN is inversely proportional to the spacing of the shock cells [9] and that the shock-cell spacing decreases as the jet develops.
Furthermore, the PSD of pressure for the data sets AXIS and NEARFIELD can be used to represent the PSD along the x-coordinate. The PSD on AXIS is displayed in Fig. 9a. It illustrates the distribution of energy over the shock-cell system. The vertical patterns correspond to each axial position where the maximum compression of the shock cells is achieved. Horizontal patterns are detected at about \(\mathrm{St} = 0.3,0.6\), and 0.9. The maximum of energy spectrum is found at the location \(x/D=5\) that is used as a reference point in the next section. In order to highlight the acoustic pattern of the shock cell in the near-field, the pressure data NEARFIELD is filtered using an acoustic–hydrodynamic filtering procedure [53, 54]. Figure 9b shows the PSD in NEARFIELD of the acoustic component of pressure, which has the banana-shaped pattern of shock-cell noise as found in the literature [55] which resembles the BBSAN pattern obtained in the far-field (Fig. 7). This pattern appears due to the Doppler effect of shock-cell noise shown in Fig. 8. However, the tonal peaks shown in Fig. 9a are mostly dissipated and hidden by the BBSAN peak (the peak at \(\mathrm{St}=0.6\) can be seen for \(x/D<3\)).
Moreover, additional details can be obtained from the spectral results if the signal in the region within the shock cells (\(0<x/D<10\), see Fig. 6) is transformed into the frequency–wavenumber domain. The transformation on AXIS is shown in Fig. 10a and on the LIPLINE in Fig. 10b. Both locations illustrate that the excited waves previously found at \(\mathrm{St} = 0.3,0.6\), and 0.9 are in fact mainly in the negative part of the axial wavenumber and travel at a group velocity between \(U_\mathrm{c}-a_\infty \) and \(a_\infty \) where \(U_\mathrm{c}\) is equal to \(U_\mathrm{j}\) at the axis and \(U_\mathrm{c}=0.67U_\mathrm{j}\) at the lip-line. This indicates that both the axis and the lip-line are capturing a pressure wave traveling upstream even when the flow is fully supersonic on the axis. This can be explained taking into account the upstream directivity of shock-cell noise and it is further developed in the following.
Frequency–wavenumber pressure energy distribution maps along the axial direction for the data set a AXIS and b LIPLINE. The dotted line depicts the mean convective velocity \(U_\mathrm{c}\). The thin red lines represent the acoustic speeds \(+\,a_\infty \) (solid) and \(-\,a_\infty \) (dashed). The thick lines represent \(U_\mathrm{c}+a_\infty \) (solid) and \(U_\mathrm{c}-a_\infty \) (dashed)
The shock-cell noise generated from the interaction between the vortices of the shear layer and the shock cells is not only convected outside the jet at the ambient speed of sound but also convected inside the supersonic region of the jet at a mean axial velocity of \(U_\mathrm{j}-a_\infty \) as sketched in Fig. 11. The wave is deformed in the axial direction due to the supersonic velocity of the jet displacing it downstream locally. However, due to the fact that the origin of the wave in the shear layer is moving upstream at the speed of sound \(a_\infty \), it creates an oblique front wave that is recorded by an axial array of probes to travel upstream at the same speed \(a_\infty \). This phenomenon is clearly illustrated by the interaction of a spatially developing supersonic mixing-layer with a compression wave separating a supersonic stream as in [56].
4.2 Shock-cell noise signature
The decomposition in frequency–wavenumber domain (Sect. 4.1) allows the signal to be filtered into waves that travel upstream and waves that travel downstream (\(p^{-}\) and \(p^{+}\) signals respectively). The pressure signal of the different arrays is reconstructed using only the second and fourth quadrants (\(p^{-}\) signal) and the first and third quadrants (\(p^{+}\) signal) from Fig. 10.
The decomposition into two signals \(p^{-}\) and \(p^{+}\) is performed for each of the data sets. Due to the fact that shock-cell noise is mainly radiated upstream, the event identification procedure provides similar results on the near-field line array when it is applied to a hydrodynamic–acoustic filtered pressure signal (as in Fig. 9b) or to the above-mentioned \(p^{-}\) and \(p^{+}\) reconstructed signals [57]. For conciseness, in the NEARFIELD, only the results from the signals \(p^{-}\) and \(p^{+}\) are shown. Moreover, the event identification procedure is also performed on the axial velocity u (reference signal) on both AXIS and LIPLINE. For all data sets, the signatures are obtained using the axial velocity fluctuations u and the initial pressure fluctuations p without any filtering as target signals of the conditional average. Additionally, the spectra computed from the signatures are compared against the spectra from the full target signals at four locations of interest noted as: P0 on AXIS (\(x/D=5\)), P1 on LIPLINE (\(x/D=5\) and \(r/D=0.5\)), P2 in NEARFIELD (\(x/D=4.5\) and \(r/D=1.4\)), and P3 in NEARFIELD (\(x/D=0\) and \(r/D=1\)). P0 represents the position with the highest PSD in the shock cells (see Fig. 10a). P1 is a point in the shear layer where the interaction between vortical structures and the shock cells is the highest. P2 illustrates a point in the near-field where both low frequency mixing noise and shock-cell noise are present and P3 depicts a point where the acoustic component is mainly constituted by shock-cell noise and the hydrodynamic perturbations are low.
4.2.1 Signature of the front wave traveling upstream
Shock-cell noise is generated from the interaction between shock cells and the vortical structures convected through the shear layer. For this reason, the signature of the front wave traveling upstream depicted in Fig. 11 is first studied at P0 where the shock cells have maximum amplitude, at a reference scale of \(\mathrm{St}(s)=0.6\), which is the Strouhal number for which the higher energy content is identified on the axis as shown in Fig. 9a for the pressure PSD. In order to investigate pressure–velocity correlations responsible for the PSD peaks, cross-conditionings with a combination of axial velocity and pressure signals are computed. Following the notation from Sect. 2, the auto- and cross-conditionings between \(u, p^{+}\), and \(p^{-}\) signals (as reference signal) and u and p signals (as target, or plotting signals) are shown in Fig. 12. All signatures presented in this section and in the following sections are obtained through the averaging of several temporal windows of size \(10D/U_\mathrm{j}\) centered in time at the most energetic events of the reference scale with a filtering window of size \(2.5D/U_\mathrm{j}\). At this location, a total of 50, 21, and 91 events were used for the conditional averaging for \(u, p^{+}\), and \(p^{-}\) signals, respectively.
On the one hand, Fig. 12a shows that the signature \(\{u;u\}\) is centered at \(\tau =0\) with a maximum. Moreover, both \(p^{+}\) and \(p^{-}\) events detect a signature with origin (\(\tau =0\)) on a minimum (absolute for \(p^{+}\) and local for \(p^{-}\) signals) and its wavepacket shape is shifted into positive times. As u is the plotted variable, the pressure events detected at \(\tau =0\) perceive a velocity fluctuation delayed in time which means that pressure events are followed in time by velocity events. On the other hand, Fig. 12b shows how the signature \(\{u;p\}\) is, first, centered on the minimum of the signature and second, shifted into negative times. In this case, because the variable that is plotted is p, the signature computed with u events is advanced in time with respect to \(\tau =0\) where the events are centered. This confirms that the signature \(\{u;p\}\) is preceding in time the events related to u. Moreover, the maximum values of the signatures \(\{p^+;p\}\) and \(\{p^-;p\}\) are mostly centered at \(\tau =0\) and do not show any significant bias in time.
Cross-conditioning at AXIS \((x/D=5)\) of axial velocity and pressure variables using different localization variables. The dashed black line represents the envelope of the signature for all axial positions. The vertical dashed blue lines represent the peak of the expansion region of each shock cell
The signatures shown in Fig. 12 represent the most probable shape of the characteristic events detected at P0 (\(x/D=5\)) plotted at the same location P0. In order to study the evolution of the signatures (and thus of the events) along the axis of the jet and through the shock cells, a different axial location for the target signal can be used maintaining in time the same averaging windows used at P0. This cross-conditioning along the axis is shown in Fig. 13. As the signatures at the different axial positions are a function of time, only the central values of the signatures at time \(\tau =0\) are plotted. In addition, as it is depicted in Fig. 12, the maximum and minimum of the signature may not lay at \(\tau =0\). For this reason, the extrema are searched over the averaging temporal window at each axial position and outlined as the envelopes of the temporal signature in dashed lines in Fig. 13.
The signature \(\{u;u\}\) of the event detected in Fig. 13a grows axially. Most of the envelope peaks are localized on the compression peaks of the shock cells (vertical dashed line). The compression peaks are computed from the average flow and are illustrated in Fig. 6 by the vertical lines inside the diamond cells. The maximum peak of the signature is observed at \(x/D=5\), where shock cells start breaking down. Some other peaks are found farther downstream possibly due to a poor averaging because of a low number of events detected. Moreover, the signature obtained for the target signal p (Fig. 13b) shows that the pressure related to these events is contained in the potential core and decays after \(x/D=6\) to a small value at \(x/D=10\), even when the envelope for u is maximum. As it can be seen from these figures, the values of u and p are shifted in phase by 180\(^\circ \) meaning that a positive amplitude in u correlates with a negative amplitude in p. Similarly, the signatures \(\{p^{-};p\}\) are illustrated in Fig. 13c. The cross-conditioning presents as well a maximum around \(x/D=5\) (as in Fig. 13b) and the amplitudes of the signatures exhibit a bias for positive values as opposed to the signature \(\{u;p\}\) shown in Fig. 13b.
Furthermore, signatures are illustrated at \(\tau \in \{-\,0.42D/U_\mathrm{j}, 0, +\,0.42D/U_\mathrm{j}\}\) for all axial locations in Fig. 14 in order to give some insights into the axial direction to which the events are traveling. Figure 14a shows that the signature \(\{u;u\}\) moves downstream with an average speed close to the jet exit velocity \(U_\mathrm{j}\). The average speed of the signature is computed simply by measuring the spatial displacement of the main peak over the time shift. In a similar fashion, the signature \(\{p^{-};p\}\) moves upstream as shown in Fig. 14b with an average speed comparable to the ambient acoustic speed. This signature corresponds to the shock-cell noise that enters the jet as explained in Sect. 4.1 as it is the only signal that travels upstream.
Cross-conditioning at AXIS (\(x/D=5)\) of a axial velocity u and b pressure p at different times. The left blue triangles (
 ) represent the signature at \(\tau =-\,0.42D/U_\mathrm{j}\), the solid red line (
) represent the signature at \(\tau =-\,0.42D/U_\mathrm{j}\), the solid red line (
 ) at \(\tau =0\) and the right green triangles (
) at \(\tau =0\) and the right green triangles (
 ) at \(\tau =+\,0.42D/U_\mathrm{j}\). The dashed line represents the envelope of the signature for all shifted times
) at \(\tau =+\,0.42D/U_\mathrm{j}\). The dashed line represents the envelope of the signature for all shifted times
In order to have a better physical description of the evolution of these events in the jet flow, a spatial cross-conditioning can be applied as well over a two-dimensional field [26]. Because the amplitude of the hydrodynamic pressure inside the jet differs by several orders of magnitude with respect to the acoustic component propagating outside, the results are made dimensionless by the local standard deviation \(\sigma \) in order to discriminate the event influence. A signature is considered here to be relevant and converged if the modulus normalized by the standard deviation is greater than 1 and if there are enough windows to average out other turbulence scales. This means that the normalized amplitudes are close to zero outside of the region of influence of the signature. Figure 15a shows the signature \(\{u;u\}\) of the cross-conditioning obtained in the xy-plane where the reference events are detected at P0. The two-dimensional signature \(\{u;u\}\) illustrates localized events inside the potential core. The two-dimensional signature \(\{p^{-};p\}\) is depicted in Fig. 15b, c. This signature presents a pattern inside the potential core and another outside with opposite amplitudes that extend up to \(r/D=1\). As it was presented in Fig. 11, the pressure waves are convected upstream inside the potential core. Because they are being convected diagonally, the positive region of the external pressure wave lies on top of the negative pressure wave which gives this distinctive checkerboard pattern. The diagonal pattern is emphasized with dashed lines in Fig. 15c close to the nozzle exit.
Normalized two-dimensional cross-conditioning maps of a\(\{u;u\}\) and b\(\{p^{-};p\}\). The results are normalized by the local standard deviation and are plotted between \(+\) 1 (red contours) and − 1 (blue contours). The dashed contours depict the negative regions. The black solid lines represent the Mach number contours \(M > 1\). Figure (c) is a detail of (b) at the nozzle exit where the waves that enter the potential core are depicted by dashed lines
4.2.2 Signature of the shock/shear layer interaction
Turbulent vortical structures are generated and convected at the convection speed \(U_\mathrm{c}\) downstream in the shear layer. These structures interact with the shock cells not only generating shock-cell noise at the tips of the shocks but also distorting the shock cells due to pressure variations [58]. The shock/shear layer interaction responsible for the generation of BBSAN is studied in this section by analyzing the signatures of the characteristic events in the shear layer at P1 (LIPLINE). The events at P1 are detected at the same reference scale of \(\mathrm{St}(s)=0.6\) as performed at AXIS. At this location, a total of 81, 99, and 250 events were used for the conditional averaging of \(u, p^{+},\) and \(p^{-}\) events, respectively. For this data set, the two-dimensional cross-conditioning is averaged over the xy-plane and xz-plane. Moreover, as the events detected at \(r/D=0.5\) and \(x/D=5\) lay on four different azimuthal positions, each of them is treated independently before doing the average. This means that the times at which the events are detected may differ for the four azimuthal positions. Because of the averaging of the signatures over the four planes, information related to azimuthal modes is lost in the process [59, 60]. Nonetheless, using the same scale implies that the identified events correspond to the same characteristic frequency \(\mathrm{St}(s)\). For the same reason, events related to an axisymmetric mode should have similar detection times.
The signatures computed with events from \(u, p^{+}\), and \(p^{-}\) signals are shown in Fig. 16a, b for u and p variables. Figure 16a displays the signatures computed for u centered at \(\tau =0\) with a positive peak from events detected with u (in phase) and a negative peak from events related to \(p^{-}\) (opposite phase). Otherwise, the signature \(\{p^+;u\}\) lies in between a minimum and a maximum. This is characteristic of turbulent structures convected downstream in the shear layer. Moreover, no major time bias is discerned from these results. As P1 is located in the shear layer, the signature \(\{u;u\}\) shows an order of magnitude higher than the signatures \(\{p^+;u\}\) and \(\{p^-;u\}\) signals computed from pressure events. The signatures of pressure depicted in Fig. 16b shows that both events detected with \(p^{+}\) and \(p^{-}\) produce a signature with a maximum at \(\tau =0\) and a minimum for u with a slight negative time bias as in Fig. 12b.
Normalized two-dimensional cross-conditioning maps of a\(\{u;u\}\), b\(\{u;p\}\), c\(\{p^{+};p\}\), and d\(\{p^{-};p\}\), where the reference signal is located at P1. The results are normalized by the local standard deviation and are plotted between \(+\) 1 (red contours) and − 1 (blue contours). The dashed contours depict the negative regions. The black solid lines represent the Mach number contours \(M > 1\)
The two-dimensional signatures \(\{u;u\}\) and \(\{u;p\}\), are displayed in Fig. 17a, b. Similarly to the results on the axis illustrated in Fig. 15a at P0, the signature \(\{u;u\}\) shows a structure centered at point P1 where the events are detected. This pattern is contained in a small region which extends about 1.8 D axially and D / 2 radially. It is in fact contained in the shear layer and does not enter the potential core (nor the supersonic region). On the other hand, the signature obtained for the variable p shown in Fig. 17b presents structures that are extended radially through the shear layer and continue in the near-field region (\(r/D>1.5\) at \(x/D=5\)). Moreover, similarly to what was shown in Fig. 16a for the \(p^+\) events, the pressure p at P1 (computed from u events) lies in between a maximum and a minimum in the axial direction. These results suggest that \(p^+\) and u events give similar information but shifted in time as it was found on the axis. Furthermore, both signatures do not show any relevant patterns with values above \(\pm \,1\) inside the potential core. This could indicate that the events that are captured by u do not influence the shock-cell region (depicted by the solid black contours).
The two-dimensional signature \(\{p^{+};p\}\) is shown in Fig. 17c. The pressure signature exhibits vertical patterns that extend from the axis to up \(y/D=2\) in the near-field region. This signature identifies the influence of the pressure in the near-field of the vortical structures convected downstream through the shear layer. Lastly, the two-dimensional signature \(\{p^{-};p\}\) shown in Fig. 17d presents the same checkerboard pattern as shown in Fig. 15b for the events detected at P0. This implies that both locations detect the same event. Nevertheless, contrary to the results on AXIS, the maximum of the pattern is not located at the position where the events are detected (P0 on AXIS and P1 on LIPLINE), but they are located near the sonic line (noted with the black solid line) which suggests that the pressure perturbation is generated at this location as it is expected from shock-leakage phenomena [11].
4.2.3 Near-field signature of BBSAN
Once shock-cell noise is generated by the interaction of vortical structures and the shock cells, it travels through the shear layer and reaches the near-field region. In the following, the signatures are studied at P2 computed only from pressure events (\(p^{+}\) and \(p^{-}\) signals) as velocity fluctuations give the same information. The signature is computed at two different Strouhal numbers \(\mathrm{St}(s)=0.2\) and \(\mathrm{St}(s)=1.03\) for \(p^{+}\) and \(p^{-}\) events, respectively, which symbolizes the hydrodynamic and acoustic (BBSAN) fluctuations. At this location, a total of 104 and 257 events have been detected and used for \(p^{+}\) and \(p^{-}\), respectively, for the conditional averaging.
The one-dimensional temporal signals are shown in Fig. 18a, b plotting, respectively, u and p variables. The signatures \(\{p^+;u\}\) and \(\{p^+;p\}\) are centered at \(\tau =0\) with a positive peak, even though they are plotting with different variables. At this location, hydrodynamic fluctuations are equivalent in terms of velocity and pressure fluctuations, with similar amplitudes and shapes. On the other hand, the signatures \(\{p^-;u\}\) and \(\{p^-;p\}\) are in opposite phase presenting a positive peak at \(\tau =0\) for \(\{p^-;p\}\) and a negative one for \(\{p^-;u\}\). Moreover, due to the fact that two scales are used to identify the events \(p^{+}\) and \(p^{-}\), their signatures exhibit a different temporal period. Nonetheless, the signature of pressure highlights how the central peaks of the signature for the \(p^{-}\) events are modulated by the signature of the \(p^{+}\) events (Fig. 18b). This illustrates again how shock-cell noise (\(p^{-}\)) is generated from the interaction of the large-scale vortical structures (\(p^{+}\)) and shock cells.
The two-dimensional cross-conditioning shown in Fig. 19 allows to highlight clearly the two components of noise radiated in the near-field by a supersonic under-expanded jet. Indeed, the signature obtained outside the jet shear layer, for u in Fig. 19a and p in Fig. 19b, is characteristic of downstream propagating pressure waves, i.e., mixing noise. It presents a spatial length-scale \(\lambda \approx 3D\) greater than the one found at P1 (LIPLINE). In fact, if a convection speed \(U_\mathrm{c}\approx 0.67 U_\mathrm{j}\) is taken, the characteristic frequency computed \(f=U_\mathrm{c}/\lambda \) is in the order of the characteristic scale \(\mathrm{St}(s)=0.2\). A reason is that the scale s (with units of time and equivalent to \(\mathrm{St}(s)=0.6\)) used to detect events at P1 is a smaller one, which corresponds to a higher \(\mathrm{St}(s)\) [see (3)]. Nonetheless, the signature of shock-cell noise is detected as well over the nozzle at P3. Furthermore, in the jet shear layer, the signature disappears when plotting u. Due to the fact that the two-dimensional signature is made dimensionless by the local standard deviation, the patterns that are visible outside the shear layer for u are an artifact that comes from the velocity variations linked to the pressure variable. Indeed, as it was shown in Fig. 16a, the signature \(\{u;u\}\) in the shear layer computed is an order of magnitude higher than the signature \(\{p^+;u\}\). This indicates that the actual signature is masked under these more energetic events, which, in this case, are not correlated in time in the shear layer.
Last, the two-dimensional cross-conditioning \(\{p^{-};p\}\) (Fig. 19c) clearly identifies the signature of pressure perturbations coming from the shock cell/jet shear layer interaction region (near \(x/D=8\)) and propagating upstream at an average angle of \(140^\circ \).
Normalized two-dimensional cross-conditioning maps of a\(\{p^{+};u\}\), b\(\{p^{+};p\}\), and c\(\{p^{-};p\}\), where the reference signal is located at P2. The results are normalized by the local standard deviation and are plotted between \(+\) 1 (red contours) and − 1 (blue contours). The dashed contours depict the negative regions. The black solid lines represent the Mach number contours \(M > 1\)
4.3 Frequency response of the signatures
The two-dimensional signatures shown in Sect. 4.2 represent a filtered field regarding the turbulence, the mixing noise, or the shock-cell noise. They give an instantaneous qualitative idea of the spatial distribution of the signatures for events detected at \(\tau = 0\). As the signatures are defined between \(-12D/U_\mathrm{j}<\tau <12D/U_\mathrm{j}\), it allows a spectral analysis to be performed (as in Fig. 3). Figure 20 shows the PSD spectra of the signatures \(\{p^-;p\}\) and \(\{p^+;p\}\) at locations P0, P1, P2, and P3.
PSD spectra of the cross-conditioning of pressure at a P0, b P1, c P2, and d P3 computed with events detected at P1 (b and d) and P2 (a and c).
 corresponds to the PSD of the actual pressure p signal at the corresponding location,
corresponds to the PSD of the actual pressure p signal at the corresponding location,
 is the PSD of \(\{p^-;p\}\),
is the PSD of \(\{p^-;p\}\),
 is the PSD of \(\{p^+;p\}\) and the vertical lines depict the reference scales at \(\mathrm{St}=0.2, 0.6, 1.03\) used in Sect. 4.2 to detect the events
is the PSD of \(\{p^+;p\}\) and the vertical lines depict the reference scales at \(\mathrm{St}=0.2, 0.6, 1.03\) used in Sect. 4.2 to detect the events
At P0 on the jet axis (Fig. 20a), P1 in the jet shear layer (Fig. 20b), and P3 in the near-field (Fig. 20d), the peak at \(\mathrm{St}=0.6\) in Fig. 9 is well retrieved by \(\{p^-;p\}\). This clearly identifies a shock-cell noise component. However, this is not the case for signature \(\{p^+;p\}\) computed from the pressure propagating downstream which instead shows a broadband peak at \(\mathrm{St}=0.44\) at locations P1 (Fig. 20a). In fact, for \(\mathrm{St}<0.6\), the contribution of the \(\{p^+;p\}\) spectra is higher than the ones for \(\{p^-;p\}\). This shows that this region is dominated by events propagating downstream with a range of frequencies typical of mixing noise. At P3, both \(\{p^+;p\}\) and \(\{p^-;p\}\) capture similar spectra with peaks at \(\mathrm{St}=0.6\) and \(\mathrm{St}=0.8\). These results demonstrate that the events detected at P1 are able to reproduce a part of the spectra at P3, which mainly comes from shock-cell noise. This confirms that the wavelet-based procedure is able to detect this phenomenon even in a highly turbulent flow region such as the shear layer at the P1 location.
This result is clearly highlighted in Fig. 20c. At P2, the main difference between the signatures from \(p^{+}\) and \(p^{-}\) events is found. The vortical structures traveling downstream detected by \(p^{+}\) perfectly capture the low frequency peak amplitude at \(\mathrm{St}=0.2\) (Fig. 19b), which corresponds to the hydrodynamic component of the pressure. Moreover, the acoustic component (represented by pressure waves traveling upstream, see also Fig. 19c) is fully recovered by \(p^{-}\) events matching the shock-cell noise signature with the BBSAN peak in the vicinity of \(\mathrm{St}=1.03\), which is in agreement with the spectra of the unfiltered pressure p, and the acoustic component shown in Fig. 9b.
5 Conclusion
This paper is dedicated to the near-field analysis of a non-screeching supersonic under-expanded jet. The study focuses on the impact of the pressure waves generated by Broadband shock-associated noise (BBSAN). The analysis is performed on a numerical database generated using large eddy simulation (LES).
The power spectral density of pressure on the jet axis depicts several tones at \(\mathrm{St} = 0.3,0.6\), and 0.9 that present peaks at the compression regions of the shock cells and the absolute maximum at \(x/D=5\). If the PSD is represented in the frequency–wavenumber domain, the different waves are seen to travel at a group velocity that lies between the acoustic speed \(U_\mathrm{c}-a_\infty \) and the sound speed \(a_\infty \) in the negative region of the axial wavenumber. This region represents the part of the signal that is traveling upstream. A characteristic pattern is identified from the PSD on the axis (supersonic with shock cells) and on the jet lip-line (mainly subsonic). This wave that seems to travel upstream is an artifact of shock-cell noise that actually travels upstream through the subsonic shear layer and enters the supersonic region leaving this distinct pattern. This shows that shock-cell noise acts as a moving source that travels upstream and enters the potential core. As a result, an oblique front wave traveling upstream is generated and identified using an axial array of probes. In order to study the influence of this wave traveling upstream, the pressure signal was decomposed into waves traveling upstream and downstream (\(p^{-}\) and \(p^{+}\) signals respectively) and used as reference signals.
A wavelet-based post-processing technique was then performed on these reference signals and the axial velocity u on the axis, the lip-line, and the near-field. The wavelet analysis is used in this work to extract a temporal signature representative of the most energetic events generated from the BBSAN at the scales of interest. The results in the shock-cell region show that the pressure events precede the events in u which travel at the speed \(U_\mathrm{j}\). Moreover, the signatures of u grow in amplitude with the axial direction. On the other hand, the pressure signatures are caught in the potential core showing a global maximum at \(x/D=5\) and peaks at the compression regions of the shock cells. The two-dimensional cross-conditioning shows that both \(p^{-}\) events from the axis and from the shear layer (lip-line) highlight a checkerboard pattern in the range \(3<x/D<7\) and \(r/D<1\) that travels upstream. This pattern appears because the BBSAN enters the potential core as a diagonal front wave as illustrated close to the nozzle exit. Moreover, the two-dimensional signature obtained from \(p^{+}\) in the near-field is not well defined in the shear layer when plotting the axial velocity u but shows a continuous pattern for the pressure p because the shear layer contains u events an order of magnitude higher than in the rest.
The influence of the vortical structures (represented by \(p^{+}\)) responsible for the generation of shock-cell noise is depicted by the PSD of the pressure signatures at four locations of interest: the shock-cell region (P0), the shear layer (P1), and the near-field (P2 and P3). The PSD shows that the lower frequencies \(\mathrm{St}<0.6\) are dominated by the vortical structures at all locations. Moreover, events detected in the highly noisy region of the shear layer are able to reproduce part of the spectra over the nozzle, which mainly comes from shock-cell noise. When the events are detected in the near-field with different reference scales, the procedure described in the paper is able to easily separate the hydrodynamic from the acoustic fluctuations and recover the broadband shock-cell noise.
To conclude, the wavelet-based methodology developed to analyze temporal signatures in subsonic jets has been applied to supersonic jets. Two-dimensional field analysis from LES was performed. This analysis allowed the influence of different events on the field to be identified. Characteristic patterns that travel upstream were identified and analyzed. The extension of this methodology to a three-dimensional field can be easily foreseen. This should allow for the decomposition of the signal into azimuthal modes that will be used to perform the wavelet-based procedure in order to obtain a three-dimensional signature of the different modes.
References
Powell, A.: On the mechanism of choked jet noise. Proc. Phys. Soc. Lond. Sect. B 66(12), 1039 (1953). https://doi.org/10.1088/0370-1301/66/12/306
Harper-Bourne, M., Fisher, M.J.: The noise from shock waves in supersonic jets. In: Advisory Group for Aerospace Research and Development. AGARD-CP-131 (1973)
Tam, C.K.W., Tanna, H.K.: Shock associated noise of supersonic jets from convergent–divergent nozzles. J. Sound Vib. 81(3), 337–358 (1982). https://doi.org/10.1016/0022-460X(82)90244-9
Norum, T.D., Seiner, J.M.: Broadband shock noise from supersonic jets. AIAA J. 20(1), 68–73 (1982). https://doi.org/10.2514/3.51048
Krothapalli, A., Hsia, Y., Baganoff, D., Karamcheti, K.: The role of screech tones in mixing of an underexpanded rectangular jet. J. Sound Vib. 106(1), 119–143 (1986). https://doi.org/10.1016/S0022-460X(86)80177-8
Tam, C.K.W.: Stochastic model theory of broadband shock associated noise from supersonic jets. J. Sound Vib. 116(2), 265–302 (1987). https://doi.org/10.1016/S0022-460X(87)81303-2
Tam, C.K.W., Golebiowski, M., Seiner, J.M.: On the two components of turbulent mixing noise from supersonic jets. In: 2nd AIAA/CEAS Aeroacoustics Conference, 6–8 May, State College, Pennsylvania, AIAA Paper 1996-1716 (1996). https://doi.org/10.2514/6.1996-1716
Raman, G.: Supersonic jet screech: half-century from Powell to the present. J. Sound Vib. 225(3), 543–571 (1999). https://doi.org/10.1006/jsvi.1999.2181
Tam, C.K.W.: Supersonic jet noise. Annu. Rev. Fluid Mech. 27(1), 17–43 (1995). https://doi.org/10.1146/annurev.fl.27.010195.000313
Manning, T.A., Lele, S.K.: A numerical investigation of sound generation in supersonic jet screech. DTIC document, Standford University (1999)
Suzuki, T., Lele, S.K.: Shock leakage through an unsteady vortex-laden mixing layer: application to jet screech. J. Fluid Mech. 490, 139–167 (2003). https://doi.org/10.1017/S0022112003005214
Berland, J., Bogey, C., Bailly, C.: Large eddy simulation of screech tone generation in a planar underexpanded jet. In: 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), 8–10 May, Cambridge, Massachusetts, AIAA Paper 2006-2496 (2006). https://doi.org/10.2514/6.2006-2496
Schulze, J., Sesterhenn, J.: Numerical simulation of supersonic jet-noise. Proc. Appl. Math. Mech. 8(1), 10703–10704 (2008). https://doi.org/10.1002/pamm.200810703
Schulze, J., Sesterhenn, J., Schmid, P., Bogey, C., de Cacqueray, N., Berland, J., Bailly, C.: Numerical simulation of supersonic jet noise. In: Brun, C., Juvé, D., Manhart, M., Munz, C.-D. (eds.) Numerical Simulation of Turbulent Flows and Noise Generation, pp. 29–46. Springer, Berlin (2009). https://doi.org/10.1007/978-3-540-89956-3_2
Mendez, S., Shoeybi, M., Sharma, A., Ham, F.E., Lele, S.K., Moin, P.: Large-eddy simulations of perfectly-expanded supersonic jets: quality assessment and validation. In: 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 4–7 January 2010, Orlando, Florida, AIAA Paper 2010-271 (2010). https://doi.org/10.2514/6.2010-271
Bodony, D.J., Ryu, J., Lele, S.K.: Investigating broadband shock-associated noise of axisymmetric jets using large-eddy simulation. In: 12th AIAA/CEAS Aeroacoustics Conference, 8–10 May, Cambridge, Massachusetts, AIAA Paper 2006-2495 (2006). https://doi.org/10.2514/6.2006-2495
Lo, S.C., Aikens, K., Blaisdell, G., Lyrintzis, A.: Numerical investigation of 3-D supersonic jet flows using large-eddy simulation. Int. J. Aeroacoust. 11(7–8), 783–812 (2012). https://doi.org/10.1260/1475-472X.11.7-8.783
Nichols, J.W., Ham, F.E., Lele, S.K., Moin, P.: Prediction of supersonic jet noise from complex nozzles. In: Annual Research Briefs 2011, pp. 3–14. Center for Turbulence Research (2011)
Nichols, J., Ham, F., Lele, S., Bridges, J.: Aeroacoustics of a supersonic rectangular jet: experiments and LES predictions. In: 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 9–12 January, Nashville, Tennessee, AIAA Paper 2012-0678 (2012). https://doi.org/10.2514/6.2012-678
Brès, G.A., Ham, F.E., Nichols, J.W., Lele, S.K.: Unstructured large-eddy simulations of supersonic jets. AIAA J. 55(4), 1164–1184 (2017). https://doi.org/10.2514/1.J055084
Morlet, J.: Sampling theory and wave-propagation. In: Chen, C.H. (ed.) Issues in Acoustic Signal–Image Processing and Recognition, pp. 233–261. Springer, Berlin (1983). https://doi.org/10.1007/978-3-642-82002-1_12
Farge, M.: Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24(1), 395–458 (1992). https://doi.org/10.1146/annurev.fl.24.010192.002143
Camussi, R., Guj, G.: Orthonormal wavelet decomposition of turbulent flows: intermittency and coherent structures. J. Fluid Mech. 348, 177–199 (1997)
Camussi, R., Guj, G.: Experimental analysis of intermittent coherent structures in the near field of a high Re turbulent jet flow. Phys. Fluids 11(2), 423–431 (1999). https://doi.org/10.1063/1.869859
Grassucci, D., Camussi, R., Jordan, P., Grizzi, S.: Intermittency of the near pressure field induced by a compressible coaxial jet. Exp. Fluids 56(2), 1–13 (2015). https://doi.org/10.1007/s00348-014-1883-5
Camussi, R., Grilliat, J., Caputi-Gennaro, G., Jacob, M.C.: Experimental study of a tip leakage flow: wavelet analysis of pressure fluctuations. J. Fluid Mech. 660, 87–113 (2010). https://doi.org/10.1017/S0022112010002570
Grizzi, S., Camussi, R.: Wavelet analysis of near-field pressure fluctuations generated by a subsonic jet. J. Fluid Mech. 698, 93–124 (2012). https://doi.org/10.1017/jfm.2012.64
Crawley, M., Samimy, M.: Decomposition of the near-field pressure in an excited subsonic jet. In: 20th AIAA/CEAS Aeroacoustics Conference, 16–20 June, Atlanta, Georgia, AIAA Paper 2014-2342 (2014). https://doi.org/10.2514/6.2014-2342
Mancinelli, M., Pagliaroli, T., Di Marco, A., Camussi, R., Castelain, T.: Wavelet decomposition of hydrodynamic and acoustic pressures in the near field of the jet. J. Fluid Mech. 813, 716–749 (2017). https://doi.org/10.1017/jfm.2016.869
Cavalieri, A., Daviller, G., Comte, P., Jordan, P., Tadmor, G., Gervais, Y.: Using large eddy simulation to explore sound-source mechanisms in jets. J. Sound Vib. 330(17), 4098–4113 (2011). https://doi.org/10.1016/j.jsv.2011.04.018
Walker, S.H., Gordeyev, S.V., Thomas, F.O.: A wavelet transform analysis applied to unsteady aspects of supersonic jet screech resonance. Exp. Fluids 22(3), 229–238 (1997). https://doi.org/10.1007/s003480050041
Gefen, L., Pérez Arroyo, C., Camussi, R., Puigt, G., Airiau, C.: Broadband shock-cell noise signature identification using a wavelet-based method. In: 22nd AIAA/CEAS Aeroacoustics Conference, 30 May–1 June, Lyon, AIAA Paper 2016-2732 (2016). https://doi.org/10.2514/6.2016-2732
Torrence, C., Compo, G.P.: A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79(1), 61–78 (1998). https://doi.org/10.1175/1520-0477(1998)079%3c0061:APGTWA%3e2.0.CO;2
André, B., Castelain, T., Bailly, C.: Broadband shock-associated noise in screeching and non-screeching underexpanded supersonic jets. AIAA J. 51(3), 665–673 (2013). https://doi.org/10.2514/1.J052058
Cambier, L., Heib, S., Plot, S.: The Onera \(elsA\) CFD software: input from research and feedback from industry. Mech. Ind. 14(03), 159–174 (2013). https://doi.org/10.1051/meca/2013056
Lele, S.K.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42 (1992). https://doi.org/10.1016/0021-9991(92)90324-R
Fosso-Pouangué, A., Deniau, H., Sicot, F., Sagaut, P.: Curvilinear finite volume schemes using high order compact interpolation. J. Comput. Phys. 229(13), 5090–5122 (2010). https://doi.org/10.1016/j.jcp.2010.03.027
Visbal, M.R., Gaitonde, D.V.: On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 181, 155–185 (2002). https://doi.org/10.1006/jcph.2002.7117
Bogey, C., Bailly, C.: A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194(1), 194–214 (2004). https://doi.org/10.1016/j.jcp.2003.09.003
Spalart, P.R., Allmaras, S.: A one-equation turbulence model for aerodynamic flows. In: 30th Aerospace Sciences Meeting and Exhibit, 6–9 January, Reno, Nevada, AIAA Paper 1992-0439 (1992). https://doi.org/10.2514/6.1992-439
Shur, M.L., Spalart, P.R., Strelets, M.K.: Noise prediction for increasingly complex jets. Part I: Methods and tests. Int. J. Aeroacoust. 4(3&4), 213–246 (2005). https://doi.org/10.1260/1475472054771376
Shur, M.L., Spalart, P.R., Strelets, M.K., Garbaruk, A.V.: Further steps in LES-based noise prediction for complex jets. In: 44th AIAA Aerospace Sciences Meeting and Exhibit, 9–12 January, Reno, Nevada, AIAA Paper 2006-485 (2006). https://doi.org/10.2514/6.2006-485
Tam, C.K.W., Dong, Z.: Radiation and outflow boundary conditions for direct computation of acoustic and flow disturbances in a nonuniform mean flow. J. Comput. Phys. 4(02), 175–201 (1996). https://doi.org/10.1142/S0218396X96000040
Bogey, C., Bailly, C.: Three-dimensional non-reflective boundary conditions for acoustic simulations: far field formulation and validation test cases. Acta Acoust. 88(4), 463–471 (2002)
Poinsot, T.J., Lele, S.K.: Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101, 104–129 (1992). https://doi.org/10.1016/0021-9991(92)90046-2
André, B.: Etude expérimentale de l’effet du vol sur le bruit de choc de jets supersoniques sous-détendus. PhD Thesis, L’École Centrale de Lyon (2012)
Ffowcs Williams, J.E., Hawkings, D.L.: Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. 264(1151), 321–342 (1969). https://doi.org/10.1098/rsta.1969.0031
Farassat, F.: Derivation of formulations 1 and 1A of Farassat. Technical Memorandum 2007-214853, NASA (2007)
Tam, C.K.W.: Broadband shock-associated noise of moderately imperfectly expanded supersonic jets. J. Sound Vib. 140(1), 55–71 (1990). https://doi.org/10.1016/0022-460X(90)90906-G
Lui, C.C.M.: A numerical investigation of shock-associated noise. PhD Thesis, Stanford University (2003)
Andersson, N., Eriksson, L.E., Davidson, L.: A study of Mach 0.75 jets and their radiated sound using large-eddy simulation. In: 10th AIAA/CEAS Aeroacoustics Conference, May 10–12, Manchester, AIAA Paper 2004-3024 (2004). https://doi.org/10.2514/6.2004-3024
Tam, C.K.W.: Broadband shock associated noise from supersonic jets measured by a ground observer. AIAA J. 30(10), 2395–2401 (1992). https://doi.org/10.2514/3.11239
Pérez Arroyo, C., Daviller, G., Puigt, G., Airiau, C.: Hydrodynamic–acoustic filtering of a supersonic under-expanded jet. In: Grigoriadis, D., Geurts, B., Kuerten, H., Fröhlich, J., Armenio, V. (eds.) Direct and Large-Eddy Simulation X, pp. 79–84. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-63212-4_9
Tinney, C.E., Jordan, P.: The near pressure field of co-axial subsonic jets. J. Fluid Mech. 611, 175–204 (2008). https://doi.org/10.1017/S0022112008001833
Savarese, A., Jordan, P., Girard, S., Royer, A., Fourment, C., Collin, E., Gervais, Y., Porta, M.: Experimental study of shock-cell noise in underexpanded supersonic jets. In: 19th AIAA/CEAS Aeroacoustics Conference, Aeroacoustics Conferences, 27–29 May, Berlin, AIAA Paper 2013-2080 (2013). https://doi.org/10.2514/6.2013-2080
Daviller, G., Lehnasch, G., Jordan, P.: Numerical investigation of the influence of upstream conditions on properties of shock noise in shock/mixing layer interaction. In: International Symposium of Turbulence and Shear Flow Phenomena, vol. 1 (2013)
Pérez Arroyo, C.: Large eddy simulations of a dual-stream jet with shockcells and noise emission analysis. PhD Thesis, CERFACS and Institut National Polytechnique de Toulouse (2016)
Suda, H., Manning, T.A., Kaji, S.: Transition of oscillation modes of rectangular supersonic jet in screech. In: 15th AIAA Aeroacoustics Conference, 25–27 October, Long Beach, California, AIAA Paper 1993-4323 (1993). https://doi.org/10.2514/6.1993-4323
André, B., Castelain, T., Bailly, C.: Experimental study of flight effects on screech in underexpanded jets. Phys. Fluids 23(12), 1–14 (2011). https://doi.org/10.1063/1.3671735
Ray, P.K., Lele, S.K.: Sound generated by instability wave/shock-cell interaction in supersonic jets. J. Fluid Mech. 587, 173–215 (2007). https://doi.org/10.1017/S0022112007007306
Guariglia, D.: Shock-cell noise investigation on a subsonic/supersonic coaxial jet. PhD Thesis, von Karman Institute for Fluid Dynamics and Università Degli Study di Roma, La Sapienza (2017)
Singh, A., Chatterjee, A.: Numerical prediction of supersonic jet screech frequency. Shock Waves 17(4), 263–272 (2007). https://doi.org/10.1007/s00193-007-0110-1
Shur, M.L., Spalart, P.R., Strelets, M.K.: Noise prediction for underexpanded jets in static and flight conditions. AIAA J. 49(9), 2000–2017 (2011). https://doi.org/10.2514/1.J050776
Acknowledgements
The authors are thankful to L. Gefen from Università Degli Study di Roma, UniRomaTre for his help with the wavelet post-processing. This work was granted access to the HPC resources of CINES under the allocation 2016-[x20162a6074] made by GENCI. Moreover, It was supported by the Marie Curie Initial Training Networks (ITN) AeroTraNet 2 of the European Community’s Seventh Framework Programme (FP7) under Contract No. PITN-GA-2012-317142.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by D. Zeidan and H. D. Ng.
Appendix: Validation of the simulation against experimental results
Appendix: Validation of the simulation against experimental results
This appendix presents a comparison between the numerical results obtained from the large eddy simulation of the non-screeching under-expanded supersonic single jet and the experimental results from LMFA [46] and VKI [61].
1.1 Jet aerodynamics
The averaged Mach number profile on the axis for the LES and the experimental results are shown in Fig. 21. The LES shows good agreement for shock-cell spacing in the first three shock cells. However, further downstream, there is a shift between the experimental and the numerical Mach number profiles. Nonetheless, the shock-cell spacing is only reduced by about 5%. Even though the amplitudes are higher than in the experimental results, they follow the same decay and they capture the end of the potential core at the same position.
Mach number profile at AXIS.
 LMFA experiment [46] (notched nozzle),
LMFA experiment [46] (notched nozzle),
 LES
LES
The turbulence levels of the velocity components on the lip-line are shown in Fig. 22. As no turbulence injection is used in the LES, the initial turbulence levels at \(x/D=0\) are equal to zero. However, they reach the same levels of rms as in the experiments after one radius. The overshoot observed within the first two diameters can be explained by a rapid transition to turbulence. Due to this, the amplitude decays about 20% relative to the experiments at \(x/D=10\). Nonetheless, the rms values are high enough to be considered as turbulent flow as it can be deduced by the vorticity contours in Fig. 6.
Turbulence levels of the axial (\(U_\mathrm{rms}\)) and radial (\(V_\mathrm{rms}\)) component of velocity at LIPLINE (\(r/D=0.5\)). \(U_\mathrm{rms}\) and \(V_\mathrm{rms}\)
and \(V_\mathrm{rms}\) from LMFA experiment [46]. \(U_\mathrm{rms}\)
from LMFA experiment [46]. \(U_\mathrm{rms}\) and \(V_\mathrm{rms}\)
and \(V_\mathrm{rms}\) from LES
from LES
The turbulence length-scale \(L_{uu}\) computed from the auto-correlations \(R_{uu}\) along the lip-line is illustrated in Fig. 23. The integration of \(R_{uu}\) is calculated up to the value 0.1. The length-scale obtained has the same growth rate, but shifted 1.5 diameters in the axial direction. This displacement is probably due to the inlet steady profiles at the exit of the nozzle, where the laminar vortex pairing triggering transition to turbulence occurs in a more abrupt fashion as seen in Fig. 22.
Axial turbulence length-scale at LIPLINE(\(r/D=0.5\)).
 LMFA experiment [46],
LMFA experiment [46],
 LES
LES
1.2 Far-field acoustics
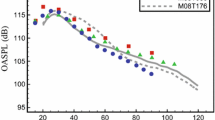
The sound pressure level (SPL) in the far-field at \(r/D=53\) from the nozzle exit plane is compared against experimental results from LMFA [46] (notched nozzle) and VKI [61]. The pressure fluctuations from the LES were propagated to the far-field using the Ffowcs Williams and Hawking’s analogy [48] and averaged over 20 azimuthal probes in order to artificially increase the convective time of the signal. The comparisons are shown in Fig. 24 for two different angles computed from the jet direction.
At \(60^\circ \) (Fig. 24a), the LES pressure spectra are dissipated by the cut-off Strouhal number of the mesh above \(\mathrm{St}\approx 2\). Good agreement is obtained with the experimental results between \(0.5<\mathrm{St}<2\). Below \(\mathrm{St}=0.5\), the amplitude differs because of the lack of convergence of the large structures and the differences in turbulence values and length-scales.
The BBSAN peak from the LES captured at \(120^\circ \) (Fig. 24b) has the correct amplitude (up to \(\mathrm{St}\approx 2\)), but it is shifted in frequency with respect to the experimental SPL due to the fact that the shock-cell length captured is 5% smaller than the experimental one. The screech is not captured in the numerical simulations. The initial conditions used for this LES and the fact that the interior of the nozzle is not modeled [12, 14, 62, 63] are probably the key reasons for not obtaining screech because the feedback loop cannot take place in the development of the boundary layer inside the nozzle.
Overall, the acoustic results show good agreement with experiments without screech, despite the slight differences in turbulence levels and turbulence length-scales. This shows that the phenomenon generating shock-cell noise is well represented in the simulation and can be studied without discussing the impact of screech on the flow. Moreover, from [46], it can be seen that the acoustic and aerodynamic results for the case at \(M_\mathrm{j}=1.15\) are the ones the least impacted by screech.
Rights and permissions
About this article
Cite this article
Pérez Arroyo, C., Daviller, G., Puigt, G. et al. Identification of temporal and spatial signatures of broadband shock-associated noise. Shock Waves 29, 117–134 (2019). https://doi.org/10.1007/s00193-018-0806-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-018-0806-4


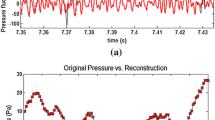




 from the original pressure signal shown in Fig.
from the original pressure signal shown in Fig.  from the signature shown in Fig.
from the signature shown in Fig. 




















 LMFA experiment [
LMFA experiment [ experiment VKI [
experiment VKI [ LES
LES