RR–MR transition of a Type V shock interaction in inviscid double-wedge flow with high-temperature gas effects

Abstract

The transition between regular reflection (RR) and Mach reflection (MR) of a Type V shock–shock interaction on a double-wedge geometry with non-equilibrium high-temperature gas effects is investigated theoretically and numerically. A modified shock polar method that involves thermochemical non-equilibrium processes is applied to calculate the theoretical critical angles of transition based on the detachment criterion and the von Neumann criterion. Two-dimensional inviscid numerical simulations are performed correspondingly to reveal the interactive wave patterns, the transition processes, and the critical transition angles. The theoretical and numerical results of the critical transition angles are compared, which shows evident disagreement, indicating that the transition mechanism between RR and MR of a Type V shock interaction is beyond the admissible scope of the classical theory. Numerical results show that the collisions of triple points of the Type V interaction cause the transition instead. Compared with the frozen counterpart, it is found that the high-temperature gas effects lead to a larger critical transition angle and a larger hysteresis interval.

1 Introduction

Shock–shock interaction is a common phenomenon in flows around flying objects at supersonic speed. Such interactions may cause a dramatic increase in local heat and pressure loads on the surface of the object as well as flow oscillations relevant to certain interaction modes, which consequently pose undesired challenges to the performance and reliability of the designed aerodynamic configurations. The problem has been widely investigated for a fairly long time. Yet it is not fully understood, especially when more complicated effects, such as molecular transport phenomena and thermochemical non-equilibrium, are taken into account.

The fundamental recognition on shock–shock interaction was established by Edney [1] in the 1960s, based on experimental observations and theoretical analysis of an oblique shock wave impinging on a blunt body in hypersonic flows. Six interaction patterns were identified depending on where the intersection of the oblique shock and the bow shock was. Olejniczak et al. [2] studied the hypersonic flow around a double-wedge geometry by inviscid numerical simulation. Only three of the six interactions of Edney and an unrecorded one referred to as Type IVr were revealed. Lind [3, 4] focused on the unsteady characteristics of Type IV shock interaction and the effect of geometry on the flow. Ben-Dor et al. [5] found the existence of self-induced oscillations of the shock wave flow pattern in a supersonic double-wedge flow in a narrow range of geometrical parameters. For hypersonic aircraft featured with double-wedge-like geometry, the possibility of self-induced oscillation should be carefully assessed and avoided. Hu et al. [6] analyzed the transition between regular reflection (RR) and Mach reflection (MR) of the Type V double-wedge shock–shock interaction in a calorically perfect gas. They proposed a geometric criterion for the $\hbox {RR} \leftrightarrow \hbox {MR}$ transition and indicated that it was the geometric criterion, instead of the detachment criterion or the von Neumann criterion, that governed the $\hbox {RR} \leftrightarrow \hbox {MR}$ transition in the hypersonic double-wedge flow.

Most theoretical and numerical research on the problems of shock–shock interaction in hypersonic double-wedge flow applied a calorically perfect gas model. This is obviously not a true representation of the flow physics for a hypersonic flight condition where the total temperature is generally over 1000 K. The effects of high temperature and non-equilibrium have been long noticed though. Olejniczak et al. [7] investigated the high-enthalpy double-wedge flow experimentally and numerically. Thermochemical non-equilibrium was considered in their numerical simulations, but the agreement between numerical and experimental results turned out to be poor. In an attempt to close the gap between experiments and simulations, Nompelis et al. [8] examined the effect of vibrational non-equilibrium on the heat transfer rate in hypersonic double-core flow and found that the vibrational non-equilibrium effects reduced the heat transfer to the model. Hu et al. [9] found that the critical angle for transition from a steady to an oscillation solution for a multi-species system with temperature-dependent thermodynamic properties was higher than the solution based on a perfect diatomic gas. Tchuen et al. [10] also reported that the double-wedge flow field was highly sensitive to the high-temperature gas effects, which may significantly change the shock shape, the thickness of the shock layer, and the pressure oscillations.

Fig. 1

Schematic diagrams of two submodes of Type V interaction over a double-wedge geometry. a Overall regular reflection (RR), b overall Mach reflection (MR)

Among all shock–shock interaction patterns in hypersonic double-wedge flow, the Type V interaction has drawn particular attention for its potential of causing high peak pressure and high-frequency vibrations. As mentioned previously, there are two submodes of Type V interaction, as illustrated in Fig. 1a, b corresponding, respectively, to an overall regular reflection (RR) and an overall Mach reflection (MR). For convenience of description, the relevant waves and intersections are labeled as follows: Sw1 is the impinging shock emanating from the first wedge, Sw2 is the impinging shock emanating from the second wedge, Bs is the bow shock generated by the second wedge. The so-called RR and MR are distinguished by the interaction structures between the transmitted shock Sw3 and the shock Sw2. UTP, MTP, and LTP denote the upper triple point, middle triple point, and lower triple point, respectively. (0)–(4) represent different regions in the Type V interaction.

We have concisely reported our study on the transition between RR and MR of a type V shock–shock interaction on a double-wedge geometry with high-temperature non-equilibrium effects [11], in which only a descriptive result was given. In this paper, we shall give a detailed analysis on the phenomena, and the emphasis will be placed on the high-temperature gas effects. Shock polar analysis considering the thermochemical non-equilibrium process will be performed to evaluate the critical angles of transition under classical criteria. Additionally, two-dimensional inviscid numerical simulations will be performed to reveal the interactive wave patterns as well as the transition processes.

2 Numerical and theoretical methods

2.1 Governing equations and numerical methods

The two-dimensional, compressible inviscid flow involving thermochemical non-equilibrium can be described by the following set of Euler equations combined with a multi-species chemical reaction model and a two-temperature vibrational relaxation model

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \begin{array}{l} {\rho _s}\\ \rho u\\ \rho v\\ E\\ {E_\mathrm{v}} \end{array} \right) +\frac{\partial }{\partial x}\left( \begin{array}{l} {\rho _s}u\\ \rho {u^2} + p\\ \rho uv\\ (E + p)u\\ {E_\mathrm{v}}u \end{array} \right) +\frac{\partial }{\partial y}\left( \begin{array}{l} {\rho _s}v\\ \rho uv\\ \rho {v^2} + p\\ (E + p)v\\ {E_\mathrm{v}}v \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{l} {\omega _s}\\ 0\\ 0\\ 0\\ {\omega _\mathrm{v}} \end{array} \right) \end{aligned}$$

(1)

in which p denotes the pressure, $\rho$ the total density, and $\rho _s$ the density of species s; u and v are the velocities in x and y directions, respectively; $\omega _s$ and $\omega _\mathrm{v}$ denote the rates of mass production of species and internal energy exchange, respectively; $E_\mathrm{v}$ is the vibrational energy of the mixture; and E is the total energy of the mixture

$$\begin{aligned} \begin{aligned} E&=\frac{\rho (u^2+v^2)}{2} +\sum \limits _{s=1}^{n_s} \rho _s \left( h_s^0+c^\mathrm{f}_{v,s} T_\mathrm{tr}\right) +E_\mathrm{v}. \end{aligned} \end{aligned}$$

(2)

We implement the two-temperature vibrational relaxation model and the chemical reaction model for air developed by Park [12, 13], in which five chemical species—$\hbox {O}_{2}$, $\hbox {N}_{2}$, NO, O, N—are involved. The vibrational energy of the diatomic molecules follows from

$$\begin{aligned} E_\mathrm{v}=\sum \limits _{s=m_s}\rho _{s} {e_{\mathrm{v},s}}=\sum \limits _{s=m_s} \rho _s \frac{R_s \varTheta _{\mathrm{v},s}}{e^{ \varTheta _{\mathrm{v},s} \big / T_{\mathrm{v}} }-1}. \end{aligned}$$

(3)

In the above equations, $n_s \,(n_s= 5)$ denotes the total number of chemical species; $m_s$ denotes the number of diatomic molecules; $h_s^0$, $R_s$, $c^\mathrm{f}_{v,s}$, and $\varTheta _{\mathrm{v},s}$ are the heat of formation, the gas constant, the transitional–rotational (frozen) heat capacity at constant volume, and the characteristic vibrational temperature of species s, respectively; $T_\mathrm{v}$ and $T_\mathrm{tr}$ are the vibrational and transitional–rotational temperatures, respectively.

The source term for vibrational energy follows from

$$\begin{aligned} \omega _\mathrm{v}=\sum \limits _{s=m_s} \left[ \rho _s\frac{e_{\mathrm{v},s}(T_\mathrm{tr})-e_{\mathrm{v},s}(T_\mathrm{v})}{\tau _s}+\omega _s\widehat{D_s}\right] \end{aligned}$$

(4)

in which $\widehat{D_{s}}$ represents the vibrational energy per unit mass (of diatomic molecules), which are created or destroyed at a rate of $\omega _s$, and the vibrational relaxation time $\tau _s$ utilizes the correlation developed by Millikan and White [14] with Park’s correction [13] for high temperature (over 8000 K).

The production rate of mass per unit volume for species s due to chemical reaction can be described by

$$\begin{aligned} \begin{aligned} \omega _s&=M_s\sum \limits _{r=1}^{n_r}(\beta _{s,r}-\alpha _{s,r})\\&\quad \cdot \left[ K_{\mathrm{f},r}\prod \limits _{s=1}^{n_s}\left( \frac{\rho _s}{M_s} \right) ^{\alpha _{s,r}}- K_{\mathrm{b},r}\prod \limits _{s=1}^{n_s}\left( \frac{\rho _s}{M_s} \right) ^{\beta _{s,r}}\right] \end{aligned} \end{aligned}$$

(5)

where $M_s$ is the molar weight of species s, $n_r$ is the number of reactions, $\alpha _{s,r}$ and $\beta _{s,r}$ are the stoichiometric coefficients for reactants and products in the rth reaction, respectively, $K_{\mathrm{f},r}$ and $K_{\mathrm{b},r}$ are the forward and backward rate coefficients. The forward rate of the rth reaction takes the form of

$$\begin{aligned} K_{\mathrm{f},r}(T)=T^{C_{2,r}}\exp \left( C_{0,r}-\frac{C_{1,r}}{T}\right) \end{aligned}$$

(6)

and the values of rate coefficients $C_{0,r}$, $C_{1,r}$ and $C_{2,r}$ are taken from [13]. The backward reaction rate can then be deduced from equation

$$\begin{aligned} K_{\mathrm{b},r}(T)=\frac{K_{\mathrm{f},r}(T)}{K_{\mathrm{eq},r}(T)} \end{aligned}$$

(7)

as long as the equilibrium constant $K_{\mathrm{eq},r}(T)$ is known. The equilibrium constant is essentially thermal state dependent. Again, we use Park’s fitting formula [13]

$$\begin{aligned} K_{\mathrm{eq},r}(T)=\exp \left( A_{1,r}+A_{2,r}z +A_{3,r}z^2 + A_{4,r}z^3+A_{5,r}z^4 \right) \nonumber \\ \end{aligned}$$

(8)

where $z=10{,}000\big /T$.

A two-dimensional finite volume numerical solver based on an unstructured mesh—VAS2D [15]—is employed to solve the flow. The solver applies a MUSCL–Hancock scheme to achieve a second-order accuracy in both time and space. Numerical fluxes through the mesh interface are computed with the artificially upstream flux vector splitting scheme [16]. The non-equilibrium source terms are solved with the second-order Runge–Kutta method. An adaptive mesh refinement technique is used to enhance the flow resolution in areas of sharp gradients (e.g., shock wave, contact discontinuity, and slip line) in an effective way. The above numerical methods have been well validated and applied in previous studies [17,18,19].

It should be noted that in this study we concentrate on the interaction of shock waves while viscous effects are not considered. The present numerical simulations, hence, do not precisely reflect the very complex reality and cannot be directly compared with experiments. The flows can be rather different if the viscous effects are involved. For instance, the boundary layers on the wedge walls will increase the deflection angles of the flows and thereby increase the angles of the impinging shock waves (i.e., Sw1 and Sw2 in Fig. 1); more importantly, the second impinging shock wave, Sw2, will interact with the boundary layer on the first wedge, by which flow separation may develop. The latter scenario may significantly complicate the wave system and bring much difficulty to the analysis.

2.2 Shock polar method

The method of the pressure–deflection angle ($p-\theta$) shock polar, first applied by Kawamura and Saito [20], is of great advantage in understanding the phenomenon of shock wave reflection and interaction. For a calorically perfect gas, the flow state behind an oblique shock wave can be represented by a single point on the shock polar diagram since the entire flow region behind the shock wave is uniform. The deflection angle of the flow, $\theta$, and the post-shock pressure, $p_2$, can be explicitly expressed as a function of the incoming flow Mach number, $M_\mathrm{a}$, and the pre-shock pressure, $p_1$

$$\begin{aligned} \frac{p_2}{p_1}= & {} 1 + \frac{2\gamma }{\gamma + 1}\left( {M_\mathrm{a}}^2\sin ^2\beta - 1\right) \end{aligned}$$

(9)

$$\begin{aligned} \theta= & {} \arctan \left[ \frac{2\cot \beta \left( {M_\mathrm{a}}^2\sin ^2\beta -1\right) }{{M_\mathrm{a}}^2\left( \gamma +\cos 2\beta \right) + 2} \right] \end{aligned}$$

(10)

where $\beta$ is the shock angle and $\gamma$ is the specific heat ratio of the gas.

In hypersonic flows, a massive amount of kinetic energy is converted to internal energy across a shock wave, which creates very high temperature behind the shock wave. The high temperature can cause significant excitation of multiple internal energy modes (e.g., the vibrational energy) and dissociation of polyatomic molecules. The influences of these effects on the flow are twofold. First, the internal energy at its equilibrium state will be distributed to other energy modes beyond the rotational and translational energies, which are the only physically possible ones in a calorically perfect gas. Consequently, the flow states across a shock will be different from that in frozen flow. Second, it takes time for the flow to approach the thermochemical equilibrium state. If the temporal scale or the spatial scale of this process is comparable to that of the gas dynamics, the flow is in thermochemical non-equilibrium and the time-dependent relaxation process must be considered. Either of the two aspects will make the calorically perfect shock polar analysis inappropriate in the case of high temperature.

Therefore, in this study, a modified shock polar method that considers the thermochemical relaxation process [17] is employed to analyze the shock interactions. The basic idea is to define an effective thickness, $\delta$, for each of the shock waves involved in the interaction. $0\le \delta \le \delta _{\mathrm{eq}}$, with $\delta _{\mathrm{eq}}$ representing the equilibrium thickness. The non-equilibrium relaxation flow structure after a shock wave is then numerically integrated over the distance from 0 to $\delta$ with the thermochemical models introduced above. The flow state at $\delta$ is taken as the post-shock flow state for the shock polar calculation. When $\delta \rightarrow 0$, the solution approaches that of a frozen flow; when $\delta \rightarrow \delta _{\mathrm{eq}}$, the solution approaches that of an equilibrium flow. The selection of the effective thicknesses is case dependent and is vitally important for the modified shock polar method. The method has been addressed in detail by Li et al. in previous research [17], and we shall not elaborate on it. We simply use the method to test the validity of classical transition criteria between shock reflection types.

Fig. 2

Schematic of the double-wedge geometry and the computational domain

2.3 Computational domain and conditions

The type of shock interaction that occurs in a supersonic double-wedge flow depends on a few test parameters. For inviscid flow, they are the flow Mach number, $M_\mathrm{a}$, the thermodynamic properties of the gas (e.g., $\gamma$), the wedge lengths, $L_1$ and $L_2$, and the angles of the two wedges, $\theta _1$ and $\theta _2$. In the present study, the incoming flow condition is fixed: The gas is composed of 79% nitrogen ($\hbox {N}_2$) and 21% oxygen ($\hbox {O}_2$) by mole fractions; the flow Mach number is $M_\mathrm{a} = 9$; and the temperatures and pressure are $T_\mathrm{v}=T_\infty = 500$ K and $p = 0.1$ atm, respectively. The two wedges are of the same length, $L_1=L_2=L = 100$ mm. A schematic of the wedge configuration as well as the computational domain is shown in Fig. 2. The wedge angles, $\theta _1$ and $\theta _2$, are the main test variables. $\theta _1$ varies from 10$^\circ$ to 30$^\circ$, and $\theta _2$ varies between $\theta _1$ and 75$^\circ$ monotonically to explore the critical transition angle.

The background computational grids without refinement are also shown in Fig. 2. For all simulations, the basic layout and the amount of the background grids are maintained, and the maximum size of the grids is always roughly $1.8\,\hbox {mm} \times 1.8\,\hbox {mm}$. The background grids are adaptively refined to resolve the flow. In this study, we implement a 6-level grid refinement, which ensures a numerical resolution of $1.8\big /2^6\,\hbox {mm} \approx 0.03$ mm in regions with large density gradient.

Fig. 3

Numerical Mach number contours of the typical inviscid hypersonic double-wedge flows showing the RR (upper) and MR (lower) modes of a Type V shock interaction

Fig. 4

Numerical results of inviscid hypersonic double-wedge flows obtained with different grid refinement levels. a Numerical flow fields (Mach number contours) for different grid refinement levels ($N_\mathrm{R}$ from 4 to 6). b Lengths of Mach stems versus the grid refinement level

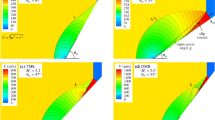
Figure 3 presents the typical flow fields (Mach number contours) of the RR and MR modes of a Type V shock interaction obtained by numerical simulation. The first wedge angles of the two cases are the same ($\theta _1=14^\circ$), and the second wedge angles differ by $1^\circ$ ($\theta _2=43.9^\circ$ for RR and $\theta _2=44.9^\circ$ for MR). The interaction phenomenon of interest is limited in a relatively small region, as marked by the rectangle in the figure, and is magnified for better observation.

Grid dependency of the numerical simulation is verified based on the above two wedge geometries. $\theta _2$ is shifted from $43.9^\circ$ to $44.9^\circ$ to cause a transition from RR to MR. Different refinement levels are implemented under the same test conditions, and the results are compared. Let $N_\mathrm{R}$ denote the refinement level. Figure 4a shows the wave patterns obtained with $N_\mathrm{R} = 4, 5$, and 6. Figures on the left are for $\theta _2=43.9^\circ$ and figures on the right for $\theta _2=44.9^\circ$. As expected, the shock waves and the slip lines turn sharper when the refinement level increases. The simulations with $N_\mathrm{R}=4$ are able to capture the general features of the flows as well as the transition of wave patterns, but it is only when $N_\mathrm{R}$ increases to 5 that the exact wave structures begin to converge. The trend is more clearly demonstrated in Fig. 4b: The lengths of two Mach stems that emerge, respectively, in the RR mode and the MR mode (marked in Fig. 4a) varying with the refinement level. It can be found that the coarse grids ($N_\mathrm{R}\le 3$) may fail to resolve the Mach stem, and that the lengths of Mach stems both approximately converge to stable values when $N_\mathrm{R}\ge 5$. The results indicate that the present numerical methods and the setup of computational grids, including the 6-level grid refinement, are qualified to properly resolve the phenomenon of interest.

Fig. 5

Pressure–deflection angle shock polar diagram for a Type V interaction

3 Results and discussion

3.1 Shock polar analysis

Shock polar analysis is first performed to reveal the theoretical critical transition conditions between the two submodes (RR and MR) of a Type V shock interaction. Figure 5 shows the typical $p-\theta$ shock polars for the interaction. According to the wave systems of a Type V interaction illustrated in Fig. 1, there are five shock waves as well as six flow regions involved in the $\hbox {RR} \leftrightarrow \hbox {MR}$ transition:

• Sw1: region (0) $\rightarrow$ region (1)

• Sw2: region (1) $\rightarrow$ region (2)

• Sw3: region (1) $\rightarrow$ region (3)

• Sw4: region (3) $\rightarrow$ region (4)

• Sw5: region (2) $\rightarrow$ region (4$^\prime$)

In Fig. 5, $R_0$–$R_4$ represent the shock polars established with the pre-shock flow conditions in region (0)–region (4), respectively. The polars drawn with solid lines are with high-temperature gas effects, and the ones drawn with dashed lines are with calorically perfect gas.

Figure 5 demonstrates two classical transition criteria, i.e., the von Neumann criterion, which is represented by polar $R_2^{\mathrm{von}}$, and the detachment criterion represented by polar $R^\mathrm{D}_2$. $\theta _\mathrm{von}$ and $\theta _\mathrm{D}$ are the corresponding critical deflection angles under the two criteria, respectively. The critical angle of detachment is generally larger than that of von Neumann, $\theta _\mathrm{D}>\theta _\mathrm{von}$. Theoretically, when the second wedge angle $\theta _2$ becomes larger than $\theta _\mathrm{D}$, the $\hbox {RR} \rightarrow \hbox {MR}$ transition of a Type V interaction occurs; when $\theta _2$ becomes smaller than $\theta _\mathrm{von}$, the $\hbox {MR} \rightarrow \hbox {RR}$ transition occurs. Between $\theta _\mathrm{von}$ and $\theta _\mathrm{D}$ is the double-solution domain.

Fig. 6

Pressure relaxation processes in different regions of a Type V interaction. a $\theta _1 = 10^\circ$, $\theta _2 = 25^\circ$, b $\theta _1 = 26^\circ$, $\theta _2 = 53^\circ$

The inclusion of non-equilibrium high-temperature gas effects requires the evaluation of the effective thicknesses of the five shock waves. Let $\delta _1$–$\delta _5$ denote the effective thicknesses for shock waves Sw1–Sw5, respectively. By integrating the steady conservation equations with the aforementioned thermochemical models after oblique shocks, the relaxation histories behind Sw1–Sw5 can be calculated. Figure 6 shows the relaxation curves of post-shock pressures (normalized by the pressures after frozen shocks of the same strength, $p_\mathrm{f}$) under two representative test conditions. One may find that the pressures generally increase as the relaxation proceeds and the relaxation curves and scales differ when the wedge angles are changed.

We need the flow states at certain positions ($\delta _1$–$\delta _5$) along the relaxation histories to conduct the non-equilibrium shock polar calculation. It is noticed that, in the mode of RR, four of the five shock waves (except Sw1) share a common intersection, LTP. The interaction phenomenon of interest as well as the transition of it takes place in the flow behind Sw1. Since the fluid element reaching point LTP has experienced a flow path of about one wedge length after Sw1, we simply let $\delta _1 = 100$ mm. In Fig. 6, we know that the flow induced by Sw1 at such a distance almost reaches equilibrium. The remaining effective thicknesses are relatively harder to determine because the interaction of Sw2 and Sw3 has no definite scale. They have upper limits, though, which are the streamwise sizes of the respective flow regions. Considering the latter four shock waves are parts of one interaction, we attempt to find a common effective thickness for all of them. And, because for most conditions the maximum length of the four shock waves is generally around 10 mm, we search the thickness value in the range of 0–10 mm. The pressures in regions (1), (2), and (3) near LTP from numerical simulations are used as a benchmark to evaluate the effective thickness. It appears that by setting $\delta _1 = 100$ mm and $\delta _2 = \delta _3 = \delta _4 = \delta _5 = 2$ mm the calculated pressure values agree well with those of numerical simulations and compromise among all tested conditions, as demonstrated by the selected cases in Table 1. (Note that pressure values in Table 1 are all normalized with the pressure of incoming flow.) The agreement also indicates that the present modified shock polar method is a valid tool for theoretical analysis of shock interaction with high-temperature gas effects.

Table 1 Pressure values in different flow regions of Type V interaction

Fig. 7

Critical angles for $\hbox {RR} \leftrightarrow \hbox {MR}$ transition obtained from shock polar analysis and numerical simulations

In Fig. 5, the polars of solid line are calculated with the high-temperature gas effects and the polars of dashed line are for a calorically perfect gas. Differences between them are observable. The former clearly leads to a larger critical transition angle. The calculated critical angles of the $\hbox {RR} \leftrightarrow \hbox {MR}$ transition over a wide range are summarized in Fig. 7, with solid lines representing the results involving high-temperature gas effects and dash-dot lines representing the ones with calorically perfect gas ($\gamma =1.4$, frozen flow). In either group, the upper line is the critical angle obtained by the detachment criterion ($\theta _\mathrm{D}^\mathrm{n}$), and the lower is the critical angle by the von Neumann criterion ($\theta _\mathrm{von}^\mathrm{n}$). The superscript “$\mathrm{n}$” denotes non-equilibrium as distinguished from “$\mathrm{f}$” denoting frozen.

The critical angles predicted with frozen and non-equilibrium flows share common features. First, they all increase with the leading wedge angle $\theta _1$. Second, the increasing slopes of von Neumann are steeper than those of detachment, which makes the predictions of the two criteria converge with the increase of $\theta _1$. For the von Neumann criterion, when the first wedge angle is smaller than 15$^\circ$, the difference caused by the high-temperature gas effects seems to be minuscule. The reason is that in such conditions both $\theta _1$ and $\theta _2$ are small, and hence, the high-temperature gas effects are insignificant. Besides that, it is clear that the critical angles of non-equilibrium flow are generally higher than those of frozen flow whichever criterion is applied.

Figure 7 also presents the critical angles of $\hbox {RR} \leftrightarrow \hbox {MR}$ transition obtained from numerical simulations (by symbols). Symbol “$\bullet$” represents the results of high-temperature non-equilibrium flows, and symbol “$\circ$” represents the results of frozen flows. The critical angles of $\hbox {RR} \rightarrow \hbox {MR}$ transition and $\hbox {MR} \rightarrow \hbox {RR}$ transition in frozen flows almost agree (not strictly agree though); therefore, the two sets of data points seem to overlap. But for non-equilibrium cases, an evident shift between $\hbox {RR} \rightarrow \hbox {MR}$ transition and $\hbox {MR} \rightarrow \hbox {RR}$ transition can be found, suggesting the existence of hysteresis. These phenomena, as well as the large deviation between numerical results and theoretical results, will be discussed in the following sections.

3.2 Numerical results

Numerical simulations are performed to examine the transition processes and mechanisms between RR and MR of the Type V interaction. With the first wedge angle ($\theta _1$) fixed at a certain value, the second wedge angle ($\theta _2$) is changed with a step of 0.2$^\circ$ in sequence until the $\hbox {RR} \rightarrow \hbox {MR}$ transition or $\hbox {RR}\leftarrow \hbox {MR}$ transition takes place. New meshes are created for different wedge angles. In the process of changing $\theta _2$, the solution of the previous case is mapped to the new mesh of the present case by interpolation and is used as the initial condition for the present case.

The numerical results and discussion are of two main parts, i.e., the $\hbox {RR} \rightarrow \hbox {MR}$ transition realized by increasing $\theta _2$ and the $\hbox {MR} \rightarrow \hbox {RR}$ transition realized by decreasing $\theta _2$. Attention is paid to the transition processes of wave patterns and the pressure loads on the wedge surface during the transition.

3.2.1 $\hbox {RR} \rightarrow \hbox {MR}$ transition

Figure 8 shows the Mach number contours for four different first wedge angles: (a) $\theta _1=10.0^\circ$, (b) $\theta _1=14.0^\circ$, (c) $\theta _1=18.0^\circ$, and (d) $\theta _1=22.5^\circ$. For each case, the second wedge angle, $\theta _2$, is increased gradually to reveal the transition boundary, and the wave patterns before, near, and after the transition are presented.

Fig. 8

Numerical Mach number contours showing the $\hbox {RR} \rightarrow \hbox {MR}$ transition of a Type V interaction in thermochemical non-equilibrium flows, $\varvec{\theta _1=10^\circ }{:}\,\mathbf{a1}\,\theta _2=43^\circ ,\,\mathbf{a2}\,\theta _2=43.5^\circ \rightarrow 43.7^\circ ,\,\mathbf{a3}\,\theta _2=43.7^\circ \rightarrow 44^\circ$; $\varvec{\theta _1=14^\circ }{:}\,\mathbf{b1}\,\theta _2=43.6^\circ ,\,\mathbf{b2}\,\theta _2=44.2^\circ \rightarrow 44.5^\circ ,\, \mathbf{b3}\,\theta _2=44.7^\circ \rightarrow 44.9^\circ$; $\varvec{\theta _1=18^\circ }{:}\,\mathbf{c1}\,\theta _2=44.1^\circ ,\,\mathbf{c2}\,\theta _2=45.2^\circ \rightarrow 45.5^\circ ,\mathbf{c3}\,\theta _2=45.8^\circ \rightarrow 46^\circ$; $\varvec{\theta _1=22.5^\circ }{:}\,\mathbf{d1}\,\theta _2=45^\circ ,\,\mathbf{d2}\,\theta _2=45.5^\circ \rightarrow 46^\circ ,\mathbf{d3}\,\theta _2=46.5^\circ \rightarrow 46.8^\circ$

For a given $\theta _1$, when $\theta _2$ is small, the transmitted shock (Sw3) emanating from the upper triple point and the second wedge shock (Sw2) undergo an overall regular reflection. As a result, two new transmitted shocks (Sw4 and Sw5) are formed. Sw5 reflects on the second wedge. In Fig. 8a1, b1, c1, d1, one may find the reflection of Sw5 is originally regular. With the increase of $\theta _2$, the interaction of shock waves Sw2 and Sw3 remains regular, while the reflection of Sw5 on the wedge transits from a regular one to a Mach one, as shown in Fig. 8a2, b2, c2, d2. The Mach stem of Sw5 grows and moves upstream with the further increase of $\theta _2$, and finally the triple point collides with the intersection of Sw2 and Sw3 (LTP), which suddenly breaks the old balance and leads to the occurrence of an overall Mach reflection between Sw2 and Sw3. The afterward MR configurations are presented in Fig. 8a3, b3, c3, d3. It should be noted that the $\hbox {RR} \rightarrow \hbox {MR}$ transition is rather abrupt, for the variation of $\theta _2$ from ($*2$) to ($*3$) ($*=a,b,c,d$) is no more than $0.3^\circ$, whereas the Mach stem appears immediately with a noticeable length and the wave pattern changes dramatically as well.

The critical $\theta _2$ for the $\hbox {RR} \rightarrow \hbox {MR}$ transition of a Type V interaction resulting from numerical simulation and previous shock polar calculation are compared in the $\theta _1-\theta _2$ plane of Fig. 7. Clearly, the critical $\theta _2$ from the numerical simulation is much smaller than that from the theoretical prediction based on the detachment criterion. As observed, the collision of the triple points coincides with the transition and is deemed to be the cause of the early occurrence of transition. A similar phenomenon and transition mechanism have been revealed and discussed by Hu et al. [6, 21] based on a perfect (frozen) gas model.

Fig. 9

Numerical Mach number contours showing the $\hbox {RR} \rightarrow \hbox {MR}$ transition of a Type V interaction in frozen flows, $\varvec{\theta _1=10^\circ }{:}\,\mathbf{a1}\,\theta _2=40^\circ ,\,\mathbf{a2}\,\theta _2=40^\circ \rightarrow 40.2^\circ ,\,\mathbf{a3}\,\theta _2=40.2^\circ \rightarrow 40.4^\circ$; $\varvec{\theta _1=22.5^\circ }{:}\,\mathbf{b1} \theta _2=43.4^\circ ,\,\mathbf{b2}\,\theta _2=43.4^\circ \rightarrow 43.6^\circ ,\,\mathbf{b3}\,\theta _2=43.6^\circ \rightarrow 43.8^\circ$

The present results with non-equilibrium high-temperature gas effects differ from those of frozen flow in a few respects. For comparison, two cases of the wave patterns with the same wedge lengths and the same incoming flow conditions while using a frozen diatomic gas model are illustrated in Fig. 9. As expected, for both cases the $\hbox {RR} \rightarrow \hbox {MR}$ transition occurs earlier than the prediction of the detachment criterion. When the first wedge angle is large ($\theta _1 = 22.5^\circ$), the transition is evidently triggered by the collision of two triple points. When the first wedge angle is small ($\theta _1 = 10^\circ$), however, unlike the case with high-temperature gas effects, here the shock Sw5 undergoes a regular reflection on the second wedge, and hence, the triple point collision scenario does not apply. The shock polar diagram, as shown in Fig. 10, can be used to analyze the phenomenon. It can be found that there is a difference between the polar $R_2 (\theta _2 = 40.4^\circ )$ with the critical polar $R_2^\prime (\theta _2 = 1.4^\circ )$ determined by the classical detachment criterion. A possible reason is that the shock waves (especially Bs and Sw3) in a Type V interaction are curving rather than straight, while the shock polar method is based on oblique shock theory that assumes straight uniform shocks. Thereby, in an actual situation, when $\theta _2 = 40.4^\circ$, the pressures and deflection angles of the flows behind shock waves Sw2 and Sw3 simply cannot be matched any more with the values of an overall regular reflection, and thus, the $\hbox {RR} \rightarrow \hbox {MR}$ transition happens. In accordance with the theoretical prediction, the critical transition angle with high-temperature gas effects is generally larger than that of the frozen flow. For example, when $\theta _1 = 10^\circ$, the transition angles in a flow with high-temperature gas effects and in frozen flow are $43.7^\circ$ and $40.2^\circ$, respectively, and when $\theta _1 = 22.5^\circ$, the angles are $46.5^\circ$ and $43.6^\circ$, respectively. The high-temperature gas effects cause excitation of the vibrational energy and dissociation of the gas molecules, which will decrease the normal flow velocity after the shock wave. The tangential velocity across the shock wave remains constant because it depends purely on the fluid dynamics and is not influenced by the high-temperature gas effects. Therefore, with the same oblique shock angle, the inclusion of high-temperature gas effects leads to a larger flow deflection angle. In this way, the maximum flow deflection angle (or the maximum wedge angle) that may sustain a regular interaction is extended.

Fig. 10

Shock polar diagram for a Type V interaction in frozen flows, $\theta _1=10^\circ$, $R_2$: $\theta _2=40.4^\circ$; $R_{2}^{'}$: $\theta _2=41.4^\circ$

Fig. 11

Pressure distributions on the second wedge during the $\hbox {RR} \rightarrow \hbox {MR}$ transition. a $\theta _1=10^\circ$, b $\theta _1=14^\circ$, c $\theta _1=18^\circ$, d $\theta _1=22.5^\circ$

Variation of the pressure distributions on the second wedge surface during the process of $\hbox {RR} \rightarrow \hbox {MR}$ transition is investigated. Figure 11 shows the pressure profiles corresponding to the four cases in Fig. 8. Note the pressures in the figures are all normalized by the free stream pressure, $p\big /p_\infty$, and the axis $x_0$ represents the horizontal distance to the joint of two wedges normalized by the wedge length. There is a sharp rise of pressure for all cases due to the reflection of shock Sw5 on the second wedge. The pressure in this region presents the maximum value along the whole wedge surface. For cases (a), (b), and (c), the peak pressure across the transition experiences a similar process. That is, the peak pressure is relatively low before the transition, rises up when the wedge angle approaches the critical point, and drops after the transition. For (a) $\theta _1 = 10^\circ$, the peak pressure after the transition almost reverts to the same level before the transition. But with the increase of $\theta _1$, the peak pressure after the transition tends to become higher and higher. For case (d) $\theta _1 = 22.5^\circ$, the peak pressure maintains a high level, which does not change much during the whole transition process. This is because the shock Sw5 in case (d) keeps a Mach reflection on the wedge before and after the transition, and the pressure behind the Mach stem stands for the maximum pressure a shock reflection may cause.

As a brief summary of the pressure variation during the $\hbox {RR} \rightarrow \hbox {MR}$ transition, the transition seems to cause a significant increase in peak pressure on the wedge surface when the first wedge angle is small. The maximum peak pressure is limited, though. When the first wedge angle becomes large, the increase in peak pressure due to transition will be overwhelmed by the high peak pressure beyond the transition.

3.2.2 $\hbox {MR} \rightarrow \hbox {RR}$ transition

The $\hbox {MR} \rightarrow \hbox {RR}$ transition takes place when the second wedge angle decreases from a large value that causes a MR-type interaction. Cases with the same first wedge angles as those in Fig. 8—$\theta _1=10.0^\circ$, $14.0^\circ$, $18.0^\circ$, and $22.5^\circ$—are selected to demonstrate the interaction mode transition process. Figure 12 shows the numerical Mach number contours.

Fig. 12

Numerical Mach number contours showing the $\hbox {MR} \rightarrow \hbox {RR}$ transition of a Type V interaction in thermochemical non-equilibrium flows, $\varvec{\theta _1=10^\circ }{:}\,\mathbf{a1}\,\theta _2=43.7^\circ ,\,\mathbf{a2}\,\theta _2=43.5^\circ \rightarrow 43.3^\circ ,\,\mathbf{a3}\,\theta _2=43.3^\circ \rightarrow 43^\circ$; $\varvec{\theta _1=14^\circ }{:}\,\mathbf{b1}\,\theta _2=44.5^\circ ,\,\mathbf{b2}\,\theta _2=44.5^\circ \rightarrow 44^\circ ,\mathbf{b3} \theta _2=44^\circ \rightarrow 43.8^\circ$; $\varvec{\theta _1=18^\circ }{:}\,\mathbf{c1}\,\theta _2=46^\circ ,\,\mathbf{c2}\,\theta _2=46^\circ \rightarrow 45.7^\circ ,\mathbf{c3}\,\theta _2=45.7^\circ \rightarrow 45.3^\circ$; $\varvec{\theta _1=22.5^\circ }{:}\,\mathbf{d1}\,\theta _2=47^\circ ,\,\mathbf{d2}\,\theta _2=47^\circ \rightarrow 46.8^\circ ,\,\mathbf{d3}\,\theta _2=46.8^\circ \rightarrow 46.5^\circ$

The cases in Fig. 12 seem to undergo the same transition process. The original MR-type interaction between Sw2 and Sw3 is featured by a Mach stem connecting two triple points, MTP and LTP. With the decrease in the second wedge angle $\theta _2$, the Mach stem is gradually shortened. When $\theta _2$ decreases to a certain value, the two triple points merge and the Mach stem disappears. In this manner, a transition from MR to RR takes place.

Similarly, the critical angle of the second wedge for the $\hbox {MR} \rightarrow \hbox {RR}$ transition is examined. Results from the numerical simulation are plotted in Fig. 7 to compare with the prediction based on the von Neumann criterion. The two are again found to differ from each other, but are not entirely incompatible. Instead, they intersect. When $\theta _1$ is less than $21^\circ$, the critical $\theta _2$ obtained by numerical simulation is larger than that of the von Neumann criterion, meaning an early transition. When $\theta _1$ is greater than $21^\circ$, the numerical result of $\theta _2$ is smaller than the von Neumann value, meaning a delayed transition. The early transition can be explained by the early meeting of the two triple points (MTP and LTP) as an adaptation to the overall flow structure, while the delayed transition will encounter the admissibility problem of stationary inverse Mach reflection (InMR). By numerical simulation with a perfect gas, Hu et al. [22] have confirmed the existence of double InMRs in double-wedge shock interactions. The diverging–converging–diverging stream tube downstream of the Mach stem is recognized as a necessary supportive boundary for the phenomenon. We identify the same InMR phenomenon in our numerical results with high-temperature gas effects in the cases of delayed transition. Given the rationality of existence of InMR, the delayed $\hbox {MR} \rightarrow \hbox {RR}$ transition can be explained with the same mechanism as that of the early transition.

Simulations with a calorically perfect gas (frozen flow) are also performed to investigate the influence of high-temperature gas effects on the phenomenon. As illustrated in Fig. 13, the basic feature of the $\hbox {MR} \rightarrow \hbox {RR}$ transition in frozen flow is consistent with that considering high-temperature gas effects, except that the critical values of $\theta _2$ in frozen flows are smaller.

Fig. 13

Numerical Mach number contours showing the $\hbox {MR} \rightarrow \hbox {RR}$ transition of a Type V interaction in frozen flows, $\varvec{\theta _1=10^\circ }{:}\,\mathbf{a1}\,\theta _2=41^\circ ,\,\mathbf{a2}\,\theta _2=41^\circ \rightarrow 40.6^\circ ,\,\mathbf{a3}\,\theta _2=40.6^\circ \rightarrow 40.3^\circ$; $\varvec{\theta _1=22.5^\circ }{:}\,\mathbf{b1}\,\theta _2=44.5^\circ ,\,\mathbf{b2}\,\theta _2=44.5^\circ \rightarrow 44^\circ ,\,\mathbf{b3}\,\theta _2=44^\circ \rightarrow 43.7^\circ$

The normalized pressure distributions along the wedge surface corresponding to the cases of Fig. 12 are presented in Fig. 14. For case (a) $\theta _1 = 10^\circ$, the peak pressure on the second wedge surface attenuates with the decrease of $\theta _2$. For case (b) $\theta _1 = 14^\circ$, there is a sharp rise of the peak pressure on the second wedge surface after the transition. For case (c) $\theta _1 = 18^\circ$ and case (d) $\theta _1 = 22.5^\circ$, the peak pressures remain high and change little during the transition. The relative angle of Sw5 to the second wedge wall and the reflection type of Sw5 on the second wedge largely determine the value of the peak pressure. As long as a Mach reflection is maintained during the transition process, the peak pressure reaches a maximum which stays relatively stable.

Fig. 14

Pressure distributions on the second wedge during the $\hbox {MR} \rightarrow \hbox {RR}$ transition. a $\theta _1=10^\circ$, b $\theta _1=14^\circ$, c $\theta _1=18^\circ$, d $\theta _1=22.5^\circ$

3.3 Transition hysteresis

Hysteresis of critical transition angles between the $\hbox {RR} \rightarrow \hbox {MR}$ transition and the $\hbox {RR} \rightarrow \hbox {MR}$ transition is a common phenomenon. Theoretically, the double-solution area between the detachment criterion and the von Neumann criterion represents the maximum hysteresis interval. For the present double-wedge shock interaction problem, although the transition of wave pattern follows neither the detachment criterion nor the von Neumann criterion, hysteresis of the critical transition angles still exists. As shown in Fig. 7, the hysteresis interval resulting from numerical simulation with high-temperature gas effects is about $1^\circ$ for all cases, while the one for frozen gas is only in the order of $0.1^\circ$ (which is numerically confirmed with a smaller change step of $\theta _2$). In other words, the high-temperature gas effects tend to widen the hysteresis between $\hbox {RR} \rightarrow \hbox {MR}$ and $\hbox {RR} \rightarrow \hbox {MR}$ transitions.

The reason behind the phenomenon is the intensity of high-temperature gas effects varying with wedge angles. A larger wedge angle results in more intensive high-temperature gas effects because of the higher degree of compression, which in turn causes a larger critical transition angle. This mutual influence essentially constitutes a positive feedback mechanism by which a slight increase of the critical angle in frozen flow will be amplified as long as the high-temperature gas effects are included. In brief, the transition hysteresis always exists regardless of the gas models (small though in frozen flows), and the hysteresis interval is simply amplified by the high-temperature gas effects.

4 Conclusion

The transition phenomenon between RR and MR of a Type V shock interaction in hypersonic double-wedge flow with the consideration of non-equilibrium high-temperature gas effects is investigated. A modified shock polar method that takes into account the non-equilibrium high-temperature gas effects is applied for theoretical analysis. Two-dimensional inviscid numerical simulations are performed to reveal the features of $\hbox {RR} \leftrightarrow \hbox {MR}$ transition as well as the critical transition conditions.

The results show that there is a significant difference between the critical wedge angles obtained by theoretical analysis and numerical simulation, indicating that the real transition mechanism between RR and MR in the Type V shock interaction is beyond the admissible scope of classical theory. The adaptation of local wave structure to the overall flow field, such as the migration and collision of triple points, seems to be the dominant cause of the transition. Hysteresis of the transition angles between $\hbox {RR} \rightarrow \hbox {MR}$ and $\hbox {MR} \rightarrow \hbox {RR}$ transitions is observed. By comparing with the frozen counterpart, it is found that the high-temperature gas effects lead to a larger critical wedge angle and a larger hysteresis interval. The pressure distribution on the wedge surface shows a peak value in the region where the lower transmitted shock reflects on the second wedge. The peak pressure generally varies during the overall $\hbox {RR} \leftrightarrow \hbox {MR}$ transition process. It may reach a maximum that corresponds to the pressure behind a normal shock in the flow behind the second impinging shock wave.