Implementation of a state-to-state analytical framework for the calculation of expansion tube flow properties

Abstract

Expansion tubes are an important type of test facility for the study of planetary entry flow-fields, being the only type of impulse facility capable of simulating the aerothermodynamics of superorbital planetary entry conditions from 10 to 20 km/s. However, the complex flow processes involved in expansion tube operation make it difficult to fully characterise flow conditions, with two-dimensional full facility computational fluid dynamics simulations often requiring tens or hundreds of thousands of computational hours to complete. In an attempt to simplify this problem and provide a rapid flow condition prediction tool, this paper presents a validated and comprehensive analytical framework for the simulation of an expansion tube facility. It identifies central flow processes and models them from state to state through the facility using established compressible and isentropic flow relations, and equilibrium and frozen chemistry. How the model simulates each section of an expansion tube is discussed, as well as how the model can be used to simulate situations where flow conditions diverge from ideal theory. The model is then validated against experimental data from the X2 expansion tube at the University of Queensland.

1 Introduction

Since spaceflight research began, shock tubes and shock tunnels have been widely used for the study of hypervelocity flows. However, they have generally been limited to the study of Earth orbit velocities up to around 8 km/s [1] because of a fundamental limitation: These facilities can only add energy to the flow through shock waves, and at sufficiently high shock speeds, there can be significant dissociation and potentially even ionisation of the test gas. This makes the conditions suitable for the study of plasmas behind planetary entry shock waves, and shock speeds up to 47.5 km/s have been generated in non-reflected shock tunnels [2], but unsuitable for aerodynamic testing [3]. Reflected shock tunnels have been used to study a wide variety of hypersonic phenomena, but also suffer from the same limitation: The twice shocked test gas feeding the nozzle may not recombine through the expansion, and this only gets worse for higher enthalpy conditions [4].

The expansion tube, a concept first proposed by Resler and Bloxsom in the 1950s [5], is a modified shock tube which uses a second downstream low pressure shock tube to circumvent the enthalpy limitation by adding only part of the required energy to the flow using a shock wave. After initial shock processing of the test gas in the shock tube, more energy is added to the final test flow by processing it with an unsteady expansion, where total enthalpy and total pressure are added to the shocked test gas as it unsteadily expands. At the expense of test time, this extra total enthalpy and total pressure are added to the flow without the dissociation which would occur in a shock tunnel, and therefore much higher enthalpy conditions can be reached [3]. The expansion tube is therefore particularly suitable for the study of planetary entry flow-fields. Due to the two modes of energy addition available, the final test flow can be controlled by balancing energy addition between these two modes, without the need for changes in physical hardware, such as nozzles, making the expansion tube a very versatile type of test facility.

The first detailed theoretical analysis was presented by Trimpi [6], who was the first to call the facility an expansion tube. Other theoretical work followed, such as Trimpi and Callis [7], Trimpi [8], and Norfleet and Loper [9]. Around this time, preliminary experimental expansion tube work was beginning, such as the work of Jones [10], Givens et al. [11], Norfleet et al. [12], and Spurk [13], all published in 1965. Over the next 20 years, expansion tube research was pioneered at NASA Langley on two different facilities. The first facility, which is discussed in Jones [10] and Jones and Moore [14], was a pilot cold hydrogen driven facility converted from an existing shock tube. The second facility, called the Langley 6-in. expansion tube [15], was a purpose-built expansion tube facility which could be run with either an arc heated driver [16], or a heated [17] or unheated [18] helium driver. While previous work had focused on trying to understand the expansion tube as a concept, the Langley 6-in. expansion tube was the first instance where one was used as a facility, and many studies were performed using blunt models, including Miller and Moore [19] and Shinn [20], where the pressure on the nose-cap of the space shuttle was analysed. Due to “financial and manpower constraints and to diminished programmatic needs”, the facility was decommissioned in 1983 [15]. A more comprehensive history and reference list of the work performed on the Langley 6-in. expansion tube can be found in [15], where it is also stated that “contrary to theory, only a single flow condition, in terms of Mach number and Reynolds number, acceptable for model testing was found with the expansion tube for a given test gas”, something which would have severely limited the usefulness of the facility. This facility was later recommissioned as HYPULSE at GASL [21]. Similar issues had also been seen for other facilities such as in Norfleet et al. [12], where it was stated that “the steadiness of the resulting flow leaves much to be desired and the definition of accurate flow conditions remains in serious doubt”.

In 1987, the first free piston driven expansion tube, later slightly modified and named X1, was built by converting the University of Queensland’s (UQ) existing TQ shock tube into an expansion tube using a grant from NASA Langley [22]. The facility had a driver section bore of 100 mm and a driven section bore of 38.6 mm [23]. It was postulated that a free piston driver would allow more test conditions to be created than had been possible in the Langley facility, and Paull et al. [23] found that additional operating conditions existed using an air test gas. However, test times were found to be shorter than what was predicted by theory. In 1992, Paull and Stalker [24] investigated expansion tube test flow disturbances by modelling disturbances which originated in the driver gas as first-order lateral acoustic waves. They found that in some situations these waves were transmitted into the test gas where they were able to prematurely end, or completely remove, the steady test time. These waves were transmitted to the test gas in the shock tube, from the driver/test gas interface, and then the waves were focussed down to particular frequencies by the unsteady expansion process in the acceleration tube. Paull and Stalker [24] also found that this transmission could be avoided by ensuring that there was a “sufficient increase” in sound speed from the unsteadily expanded driver gas to the shocked test gas at the driver/test gas interface, preventing the disturbances from being able to pollute the test gas. The size of the increase required depended on the frequency of the waves to be inhibited at the driver gas sound speed. Paull and Stalker [24] established a criterion for ensuring clean flow which led to a revival in the use of expansion tubes. This finding and others led to what is now 30 years of sustained expansion tube research at UQ, which is discussed in detail in Gildfind et al. [25]. Since 2000, there has been increased interest in expansion tubes, and new facilities of different sizes and purposes have been commissioned by several groups, such as those discussed by Sasoh et al. [26], Ben-Yakar and Hanson [27], Dufrene et al. [28, 29], Abul-Huda and Gamba [30], Jiang et al. [31], and McGilvray et al. [32].

If expansion tubes are to be useful for the study of planetary entry and other situations, it is important to be able to characterise the test flows which they create, and this is not a simple task. Expansion tube test flows are fundamentally transient, and depending on the size of the facility and the individual test condition, useful test times will be of the order of tens to thousands of microseconds. This useful test time precedes the arrival of the hot, high-pressure driver gas which is entrained with heavy particles from the diaphragms which were separating the different gas sections before the experiment was performed. It presents an extremely harsh flow environment, meaning that while expansion tubes require sensitive instrumentation which responds quickly to the transient flow, the instrumentation must also survive the harsh environment which follows it, limiting the types which can be used. Basic expansion tube instrumentation consists of pressure sensors mounted on the walls of the facility to measure shock speeds and wall static pressures, and test section mounted impact pressure probes to measure pitot pressure. These diagnostics are used as input and validation data for analytical or numerical simulations which are used to infer extra information about the flow condition which cannot be measured directly. Shock speeds are often used to verify simulations of expansion tube flow conditions because they can be measured non-intrusively in the facility. If shock speeds match between experiment and simulation, it generally indicates that overall wave processes are being simulated with reasonable accuracy.

Different types of phenomena occur during an expansion tube experiment, such as diaphragm rupture, unsteady wave processes, viscous effects, and high-temperature gas effects. This makes full numerical characterisation a costly computational process, and traditional techniques, such as the model presented in Neely and Morgan [33], used a semi-empirical approach, where measured shock speeds and wall and pitot pressure measurements were used to calculate “mean” or representative flow conditions. Current state of the art requires compressible, high-temperature, transient, two-dimensional axisymmetric computational fluid dynamics (CFD) calculations. These simulations generally cost tens or hundreds of thousands of hours of CPU time and are not suitable for the iterative design of new test conditions. Instead, two-dimensional CFD is used for accurate characterisation of established operating conditions.

UQ’s one-dimensional CFD code, L1d3 [34, 35], can simulate phenomena such as free piston driver compression, equilibrium chemistry, various diaphragm rupture phenomena, and longitudinal wave processes. Depending on the fidelity of the simulation, L1d3 can perform a full facility simulation in the order of hours, making it more suitable for condition design. However, generally expansion tube acceleration tubes are affected by low-density shock tube (or “Mirels”) effects [36,37,38], which cause over-expansion of the shocked test gas due to boundary layer growth in the acceleration tube. Due to its one-dimensional nature, L1d3 has no mechanism to simulate this phenomenon, making it unsuitable for the simulation of complete expansion tube test flows. Instead, L1d3 is generally used to provide the in-flow to higher fidelity simulations of the acceleration tube or to somewhat qualitatively verify overall wave processes.

By identifying important flow processes which occur during an expansion tube experiment and then modelling them from state to state using predominately analytical techniques, lower fidelity estimates can be made with orders of magnitude less computational expense. Coupling this with an understanding of where ideal processes may start to break down and what can be done to accommodate this analytically, reasonable predictions can still be made. This allows experimenters to perform preliminary design of new expansion tube test conditions in close to real time. If a reasonable starting point can be found theoretically, the condition can then be further tuned, if necessary, after initial experiments have been carried out and any discrepancies between theory and experiment have been identified.

In this paper, a new code, PITOT, is described. PITOT was written in the Python programming language and makes use of the Python libraries written by Jacobs et al. [39] for use with the ESTCj program. An early version of the code was first presented by James et al. [40]. PITOT is UQ’s in-house expansion tube and shock tunnel simulation code based on isentropic and compressible flow state-to-state gas processes. The code takes its name from a perfect gas expansion tube simulation code written by one of the authors in the early 1990s. PITOT uses NASA’s Chemical Equilibrium with Applications (CEA) equilibrium gas code [41, 42] to account for high-temperature gas effects, which are often important in the facility’s acceleration tube, where shock speeds normally range from 6 to above 20 km/s. PITOT also incorporates a perfect gas solver. It is capable of performing an equilibrium expansion tube simulation on a single processor in several minutes and a perfect gas simulation in seconds.

PITOT was written to be a virtual impulse facility, and simulations are therefore configured like an experimenter would configure a real experiment. It uses facility fill condition as inputs, and then the code runs through the flow processes in a state-to-state manner, analogous to how the different sections of the facility would operate in the real experiment. The code was written this way to create a simple and intuitive tool for trying to understand a facility and how different parameters affect flow conditions. PITOT can also be easily scripted to perform parametric studies and sensitivity analyses, and tools are provided with the code to do this. PITOT is open source and forms part of the Compressible Flow Computational Fluid Dynamics (CFCFD) code collection at UQ’s Centre for Hypersonics [43]. Instructions for obtaining the code can be found in Appendix 1.

While this paper is based around the X2 expansion tube at UQ, the discussion is generally applicable to any such facility. The following section, Sect. 2, provides a brief introduction to the X2 facility and explains what occurs during an X2 experiment. Section 3 provides a summary of how each section of the facility is simulated in PITOT. The final section, Sect. 4, discusses how this analysis can then be calibrated to allow it to be used to quantify experimental data, similar to a traditional semi-empirical expansion tube model such as the one presented by Neely and Morgan [33].

Fig. 1

Schematic and position–time (x–t) diagram of the X2 expansion tube (not to scale). The exact locations of sensors at6, at7, and at8 are slightly obscured due to their tight spacing just before the nozzle entrance

2 The X2 expansion tube

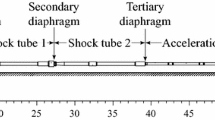
The free piston driven X2 Expansion Tube at UQ is a 23-m-long, medium-sized facility with a driven tube bore of 85 mm and a nozzle exit diameter of 201.8 mm. Measured in terms of driver gas sound speed (${a}_{4}$), X2 has the highest performance driver of any operational expansion tube facility and is capable of producing scaled test conditions for entry into most of the planets in our solar system. X2 is generally used to perform studies of blunt-body planetary entry radiation, and it has been used extensively to generate and measure radiating test flows for many planetary bodies, including Earth, Mars, Titan, Venus, and Uranus from 3 to 20 km/s [44,45,46,47,48,49,50,51,52,53]. X2 has also been used to develop and refine a new technique for the study of ablation phenomena in impulse facilities by using heated models [54,55,56,57]. Figure 1 shows the current dimensions of the X2 expansion tube when it is used in the most common configuration, with the nozzle, but without a secondary driver section. It also shows the notation employed for the different gas states, and the names and locations of the tube wall pressure sensors. A more detailed overview of X2 can be found in Gildfind et al. [25].

In its simplest configuration, an expansion tube has two driven sections: a shock tube, and a lower pressure downstream “acceleration tube” which is used to accelerate the shocked test flow through an unsteady expansion (see Fig. 1). An expansion tube can also be configured with an extra driven section called a “secondary driver”, which is added between the primary diaphragm and the shock tube. This section is filled with a light gas (generally helium) and is used to increase the performance of the driver condition, allowing the facility to drive a more powerful shock through the test gas than it could have done otherwise [45].

Before an experiment, all sections of the facility are evacuated and then filled with the required gases, at the required pressures. The experiment begins when the piston is released. The reservoir pressure (usually of the order of several MPa) causes the piston to rapidly accelerate, compressing the primary driver gas in front of it from its initial fill pressure to the primary diaphragm rupture pressure. At this rupture point, due to the compression of the driver gas, its pressure and temperature are both very high (tens of MPa, thousands of K). This hot, high-pressure driver gas (state 4) is used to drive a shock wave through the driven sections of the facility, processing the test gas to the required condition before it flows into the test section.

Figure 1 includes a facility schematic and position–time (x–t) diagram of the facility, showing the longitudinal wave processes which occur during an experiment. After primary diaphragm rupture, if the free piston driver is tuned [58,59,60,61], the high-speed piston maintains approximately constant gas properties in the driver (${T}_{4} \approx \hbox {constant}, {p}_{4} \approx \hbox {constant}$) by matching mass loss from driver gas venting into the driven tube with further piston displacement. Due to the area change at the primary diaphragm, the driver rupture condition (state 4) undergoes a steady expansion to the throat Mach number (${M}_\mathrm{throat}$) of 1 before it unsteadily expands into the shock tube (becoming state 3), driving a shock wave (${V}_{\mathrm{s},1}$) through the shock tube gas (state 1) and processing it to state 2. When this shock wave reaches the secondary diaphragm separating the shock and acceleration tubes, the diaphragm ruptures and the shocked test gas (state 2) starts to unsteadily expand into the acceleration tube (becoming state 7). The state 7 gas drives a shock wave (${V}_{\mathrm{s},2}$) through the accelerator gas (state 5) and processes it to state 6. Generally, X2 is operated with a contoured nozzle at the end of the acceleration tube which steadily expands the state 7 gas to the nozzle exit condition (state 8). The test time begins when the state 8 gas arrives at the test model, and it generally ends either with the arrival of the downstream edge of the test gas unsteady expansion or the leading u+a wave reflected off the driver/test gas contact surface [24].

3 Simulating an expansion tube with PITOT

This section details how PITOT simulates the complete operation of an expansion tube using state-to-state processes. Readers interested in a fully analytical solution procedure for expansion tube flow processes are directed to Appendix A of Gildfind et al. [45] where the equations are explained in detail.

The facility configuration for an example high-enthalpy expansion tube condition from the work of Fahy et al. [46] is shown in Table 1. The condition is a binary scaled air condition designed to match the 13:52:20UTC trajectory point of the Hayabusa entry at 1/5 scale. This flow condition is used in this section to illustrate how the selection of certain parameters in the code can affect the test flow estimates which it provides.

Table 1 Details of the 1/5 scale Hayabusa 13:52:20UTC trajectory point condition designed by Fahy et al. [46]

Table 2 State 4 values for X2-LWP-2 mm-0 from Gildfind et al. [64]

3.1 Driver simulation

Before an experiment is run, the primary driver section is filled to the required fill condition, consisting of a set driver pressure and gas composition, which is assumed to be at nominally atmospheric temperature. Next, the reservoir is filled to the required pressure with compressed air. The current X2 free piston driver conditions were designed by Gildfind et al. [62, 63] using a 10.5 kg piston and an 80%He/20%Ar (by volume) driver gas. Details of the conditions can be found in that work.

When the piston is released, it compresses the driver gas to the rupture condition of the primary diaphragm (state 4). This can be simulated in PITOT in two different ways. The first method assumes an isentropic compression of the driver gas from its initial fill condition to its rupture condition. If either the volumetric compression ratio of the driver condition ($\lambda$) or the primary diaphragm rupture pressure (${p}_{4}$) is known, then the temperature at primary diaphragm rupture (${T}_{4}$) and with it the gas state (state 4) can be found:

$$\begin{aligned} \left( \frac{T_{4}}{T_{\mathrm{fill}}}\right) = \left( \frac{p_{4}}{p_{\mathrm{fill}}}\right) ^{1 - \frac{1}{\gamma }} = \left( \frac{1}{\lambda }\right) ^{\gamma - 1}. \end{aligned}$$

(1)

This method does not take into account heat and total pressure losses in the compression process, and as such, tuned empirical estimates of the driver rupture condition can be used instead, which are hard-coded into PITOT as reference driver conditions. As an example of this, “effective” driver gas properties from Gildfind et al. [64] in 2015 were calculated for X2-LWP-2 mm-0 from experimental shock speeds through a helium test gas and are summarised in Table 2.

It is assumed that the driver rupture condition is approximately stagnated (${M}_{4} \approx 0$), and after the diaphragm has ruptured (see Fig. 2a), due to the tube area change, state 4 undergoes a steady expansion to a choked throat condition (${M}_\mathrm{throat} = 1$) at state $4^{\prime \prime }$, before undergoing an unsteady expansion into the driven sections downstream.

Orifice plates are often used in X2 to introduce an additional contraction at the tunnel area change to allow existing driver conditions to be used with larger percentages of helium in the driver gas than they were originally designed for. By sizing the orifice plate to maintain the choked volumetric flow rate out of the driver (i.e., preserving the $u \cdot A$, or in this case, $a \cdot A^{*}$, product), the piston dynamics can be preserved, while allowing the use of a higher sound speed driver gas. Generally, a choked throat is the most efficient driver configuration to use as the steady part of the expansion, which conserves total enthalpy and total pressure, is performed subsonically and the unsteady part of it, which reduces total enthalpy and total pressure in subsonic flow, but increases them in supersonic flow, is performed supersonically [3]. However, even though a higher sound speed driver gas used with an orifice plate undergoes a supersonic expansion into the driven tube, and therefore some of the available driver total pressure is lost, it will normally still drive a stronger shock than a choked throat condition with a lower sound speed. A further discussion of this, and a procedure for sizing the orifice plates, can be found in Gildfind et al. [64].

Fig. 2

Driver after rupture representation (not to scale). a Without orifice plate, b with orifice plate

Table 3 Driver rupture conditions for two cold driver conditions designed by Gu [50]. The rupture values (${p}_{4}$ and ${T}_{4}$) were found by the authors

In PITOT, the orifice plate is simulated by performing a second steady expansion from the throat condition (${M}_\mathrm{throat} = 1$) to a supersonic Mach number at state $4^{\prime \prime }$ (${M}_{4^{\prime \prime }} > 1$), similar to how a de Laval nozzle would be modelled. (This is shown in Fig. 2b.) ${M}_{4^{\prime \prime }}$ is found iteratively using the well-known Mach-area relation and the area ratio between the orifice plate ($A_{*}$) and the driven tube ($A_\mathrm{driven}$):

$$\begin{aligned} \left( \frac{A_\mathrm{driven}}{A_{*}} \right) ^{2} = \frac{1}{M^{2}_{4^{\prime \prime }}}\left[ \frac{2}{\gamma _\mathrm{D} + 1} \left( 1 + \frac{\gamma _\mathrm{D} - 1}{2}M^{2}_{4^{\prime \prime }}\right) \right] ^\frac{\gamma _\mathrm{D} + 1}{\gamma _\mathrm{D} - 1}. \end{aligned}$$

(2)

Starting from 2015, some X2 experiments have been performed without the free piston driver, instead using a small reservoir of room temperature helium as a “cold” driver [50]. This can be simulated by manually setting state 4 (${p}_{4}$ and ${T}_{4}$) to the cold driver rupture conditions. The authors used the methodology described in Gildfind et al. [64] to produce effective driver values for the cold driver, which are shown in Table 3. It should be noted that the sub-atmospheric rupture temperature (${T}_{4}$) values are not intended to be physical.

While it is not relevant for X2, PITOT is also able to simulate a basic shock tube driver (i.e., no area change) by setting the throat Mach number to 0.

3.2 Secondary driver simulation

The unsteadily expanding driver gas (starting at state $4^{\prime \prime }$ and unsteadily expanding to state sd3) drives a shock wave through the (typically) helium secondary driver gas (state sd1) processing it to state sd2. The speed of this shock (${V}_{\mathrm{s,sd}}$) is dependent on both the fill condition in the secondary driver (state sd1) and the driver throat condition (state $4^{\prime \prime }$), because it is the shock speed at which velocity and pressure are matched across the state sd3/sd2 interface. This is shown in Fig. 3, where a partial facility schematic and position–time (x–t) diagram centred around the secondary driver section can be seen.

Fig. 3

Secondary driver representation (not to scale)

Generally, the secondary driver fill condition (state sd1) is set and PITOT uses an iterative secant solver to find the point at which ${V}_\mathrm{sd3} = {V}_\mathrm{sd2}$ and ${p}_\mathrm{sd3} = {p}_\mathrm{sd2}$ and with it the correct shock speed (${V}_{\mathrm{s,sd}}$). This is done by guessing a ${V}_{\mathrm{s,sd}}$ value, finding the condition behind the shock wave (state sd2), and then expanding from the driver condition (state $4^{\prime \prime }$) to the pressure behind the shock wave (i.e., making ${p}_\mathrm{sd3} = {p}_\mathrm{sd2}$). If the correct shock speed has been guessed, ${V}_\mathrm{sd3}$ and ${V}_\mathrm{sd2}$ will be equal, and the secant solver set to find the zero of the function ${V}_\mathrm{sd3}$–${V}_\mathrm{sd2}$ will be satisfied, if not, a new guess for ${V}_{\mathrm{s,sd}}$ will be made, and the process is repeated until it converges.

A comprehensive study of expansion tube operation with a secondary driver can be found in Gildfind et al. [45].

Fig. 4

Shock tube representation (not to scale)

3.3 Shock tube simulation

Either the unsteadily expanding driver gas (state $4^{\prime \prime }$ unsteadily expanding to state 3) or the unsteadily expanding shock-processed secondary driver gas (state sd2 unsteadily expanding to state 3) drives a shock wave through the test gas in the shock tube, processing it from state 1 to state 2. The speed of this shock (${V}_{\mathrm{s},1}$) is dependent on both the fill condition in the shock tube (state 1) and the condition of the driving gas (either state $4^{\prime \prime }$ or state sd2). This is shown in Fig. 4, where two partial facility schematics (one with and one without a secondary driver section) and a position–time (x–t) diagram centred around the shock tube can be seen. ${V}_{\mathrm{s},1}$ is found in the same manner as ${V}_{\mathrm{s,sd}}$ was found in Sect. 3, except here the solution requires that ${V}_{3} = {V}_{2}$ and ${p}_{3} = {p}_{2}$.

As was discussed in the introduction, it should be noted that Paull and Stalker [24] found that if the sound speed of the shocked test gas ($a_{2}$) was not sufficiently larger than the sound speed of the expanded driver gas ($a_{3}$), then flow disturbances originating in the driver were able to be transmitted into the test gas in the shock tube, potentially shortening or completely removing the steady test time. They did not provide a single recommendation for the increase required, instead stating that it grew with the frequency of the waves to be inhibited and decreased with increasing $a_{3}$. However, inspection of Fig. 6 in their paper shows that an increase of at most 120% would be required to stop noise being transmitted in most situations. Users should keep this criterion in mind when designing test conditions. PITOT provides a summary of all gas states at the end of the calculation which can be used to check these values.

When very low-density shock tube fill pressures are used, after the post-shock conditions have been found, a flag in the code can be used to artificially set the velocity of the shocked test gas (${V}_{2}$) to the shock speed in the shock tube (${V}_{\mathrm{s},1}$). This is done to help PITOT account for low-density shock tube (or Mirels) effects [36,37,38] which are discussed further in Sect. 3.5.

3.4 Secondary/tertiary diaphragm modelling

Thin diaphragm modelling is an ever-present problem for the simulation of expansion tubes. While a fully ideal expansion tube model assumes that the diaphragm effectively does not exist, in certain cases the diaphragm’s inertia and its opening or “hold” time have a non-trivial effect on the overall flow condition, and it cannot be ignored. Issues with diaphragm rupture and hold times are known contributors to situations where expansion tube flow conditions can differ from simple shock tube theory [65,66,67], and for this reason it is important to be able to simulate them.

The inertial diaphragm model [65, 68] shown in Fig. 5 treats the diaphragm as an obstacle that the shocked test gas (state 2) must accelerate, and it models the time-dependent behaviour of the gas during this process. The inertial diaphragm model assumes that the diaphragm shears along its periphery as soon as the flow hits it and then it stays together as an obstacle in the flow field. The model also assumes that the front of the gas slug which hits the diaphragm is fully stagnated by it and that this twice shocked test gas (state 2r) then unsteadily expands from this state. The diaphragm then starts to accelerate into the tube in front of it, driving a shock in front of itself and acting as a “piston” between the shocked gas in front of it (state 6) and the gas behind it which is unsteadily expanding after being processed by the reflected shock (state 7). As the diaphragm accelerates, the reflected shock behind the diaphragm gradually loses strength until it decays to a Mach wave (${M}_{2\mathrm{r}} = 1$) and the effect of the diaphragm on the flow reaches a final steady state.

Fig. 5

Adapted from a theory and figure presented in Morgan and Stalker [65]

Partial shock and acceleration tube representation showing how an inertial diaphragm model simulates secondary or tertiary diaphragm rupture (not to scale).

A study by Kendall et al. [66] in the X1 expansion tube compared experimental shock speed data around the secondary diaphragm to both Morgan and Stalker’s [65] original inertial diaphragm model and a more sophisticated numerical inertial diaphragm model developed by Petrie-Repar [69]. Kendall et al. [66] found that Petrie-Repar’s [69] model simulated the diaphragm rupture better than Morgan and Stalker’s [65], but that good agreement between Petrie-Repar’s [69] model and the experiment only lasted for ${30}\,\upmu \hbox {s}$. After this point, the two reflected shock trajectories started to diverge, and the experimental transmitted shock was faster than what was predicted by the inertial diaphragm model. Kendall et al. [66] stated that this meant that the inertial diaphragm model “in its current form, is not complete”. It was suggested that the effect of the diaphragm on the test flow was lessened due to the diaphragm eventually vaporising. Petrie-Repar [69] investigated this numerically by simulating an initially curved diaphragm which then broke into a 7 or 14 pieces upon shock arrival at the diaphragm. Petrie-Repar’s [69] 14 piece model gave “good” agreement with downstream experimentally measured pressure traces using what was called a “heavy diaphragm” (${127}\,\upmu \hbox {m}$ thick), but shock arrival at that point occurred ${65}\,\upmu \hbox {s}$ earlier than the experiment because the model did not include viscous effects or a diaphragm hold time.

Wegener et al. [70] used holographic interferometry in X1 to optically investigate light diaphragm rupture. This was done by placing a light cellophane diaphragm at the end of the final driven section, turning X1 into a facility with a long shock tube, and then using the test section as an effective acceleration tube. It was found that upon rupture the initially curved diaphragm flattened, and after propagating a quarter of a tube diameter downstream, it began to fragment in the centre, gradually losing fragments as it travelled further downstream. Wegener et al. [70] found that the trajectory of the diaphragm and the gas interface were well approximated by the inertial diaphragm model for a short period of time after diaphragm rupture but that it gradually lost accuracy after the diaphragm had travelled half a tube diameter downstream from the rupture location. After this point, like Kendall et al. [66] had also observed, the interface began to accelerate more than the inertial diaphragm model predicted. Wegener et al. [70] stated that this was caused by the diaphragm losing mass as it fragmented. More recently, in 2007, Furakawa et al. [71] used the JX-1 expansion tube [26], which has a 50 mm driven section bore, to study thin secondary diaphragm rupture using both framing shadowgraph imaging of the diaphragm rupture process using a high-speed camera and wall pressure measurements. The use of a section of acrylic tube which functioned as a set of aspherical lenses allowed the experiments to be performed in situ in the facility. Three materials were tested: ${23}{\hbox {-}}\upmu \hbox {m}$-thick cellophane, and 3- and ${25}{\hbox {-}}\upmu \hbox {m}$-thick Mylar. Like what was found by Wegener et al. [70], the diaphragms could be seen travelling downstream after rupture and evidence of radiation from stagnated gas behind the diaphragm was seen for all but the ${3}{\hbox {-}}\upmu \hbox {m}$-thick Mylar. They concluded that the transmitted shock wave motion was influenced primarily by the diaphragm mass and that only the ${3}{\hbox {-}}\upmu \hbox {m}$-thick Mylar diaphragm was shown to have almost negligible effect on the test flow.

Currently, an inertial diaphragm model is not implemented in PITOT, but some kind of inertial diaphragm model is planned as an upgrade to the code in the future to help model conditions which cannot be simulated well otherwise.

Another way to simulate thin diaphragm rupture is to use a hold time model, where it is assumed that when the shocked test gas (state 2) hits the diaphragm, the diaphragm remains closed for a set period of time, causing some of the gas to be processed by a reflected shock, before it opens fully and its effect is removed from the flow. While it was not called a “hold time” model, this is the type of diaphragm model discussed by Haggard [72] in 1973, who stated that the effect of the mass of the secondary diaphragm could be modelled by a reflected shock at the diaphragm location. The hold time model has been used in several computational studies investigating the flow in an expansion tube [68, 73, 74] and comparing experimental results and the hold time model, Wilson [73] stated that “Even with the very simple model for the opening time used in this work, the qualitative features of the disturbance compare well with the experiments”.

This type of diaphragm model (and the related hold time) can be easily implemented in the in-house one-dimensional facility simulation CFD code L1d3 [34, 35] with a simple flag in the input script. An example where different secondary diaphragm hold times (“dt_hold” in the code) have been used is shown in Fig. 6, using simulations of the scaled Hayabusa entry condition detailed in Table 1. The shock speeds in the shock and acceleration tubes are compared for hold times between 0 and ${1000}\,\upmu \hbox {s}$ to see the effect on the test flow. The nominal equilibrium solution from PITOT without a hold time model is also shown.

Fig. 6

L1d3 [34, 35] one-dimensional CFD results showing how different diaphragm hold times (dt_hold) affect the shock speed of the test condition

Firstly, looking at Fig. 6 it can be seen that without a hold time, PITOT simulates the expected shock speeds very well, both in the shock and acceleration tubes. It can also be seen that when the diaphragm hold time is below ${1}\,\upmu \hbox {s}$, no change in acceleration tube shock speed (${V}_{\mathrm{s},2}$) and no slowdown of the shock speed at the secondary diaphragm are seen. With a hold time of ${10}\,\upmu \hbox {s}$, a sustained increase in ${V}_{\mathrm{s},2}$ is seen, as well as a small but noticeable slowdown of the shock speed just before the secondary diaphragm. This increase in performance likely comes from the weak reflected shock off the diaphragm which was not able to fully stagnate the test gas and remove all of its kinetic energy. For the final two simulated hold times (100 and ${1000}\,\upmu \hbox {s}$), a fully reflected shock is seen at the secondary diaphragm, with the shock speed dropping to 0 m/s. With a hold time of ${100}\,\upmu \hbox {s}$, a temporary increase in ${V}_{\mathrm{s},2}$ is seen after diaphragm rupture, which decays to the nominal value by the time it reaches the end of the tube. With a hold time of ${1000}\,\upmu \hbox {s}$, directly after diaphragm rupture ${V}_{\mathrm{s},2}$ is slower than the condition with no hold time, and it only continues slowing down.

For the simulation of conditions where it is believed that the diaphragm has a non-negligible effect on the flow, PITOT uses a time-independent hold time model where the effect of a diaphragm stopping the flow is modelled by a reflected shock. Like a normal hold time model, it cannot simulate the inertia of the diaphragm and it is only useful for simulating conditions where the diaphragm produces a measurable reflected shock in the test gas, but otherwise has a low inertial effect. What is shown in Fig. 8 below is similar to the condition with a hold time of ${10}\,\upmu \hbox {s}$ in Fig. 6 where a sustained increase in acceleration tube shock speed (${V}_{\mathrm{s},2}$) is seen due to the shock reflection at the diaphragm. An experimental example discussed in Sect. 4.4.1 uses this diaphragm model to explain experimental results seen in the acceleration tube which would not otherwise be predicted.

This time-independent hold time model predicts and models the hold time as a reflected shock of specified strength. Using the shock tube as an example, state 2 is first found using the standard procedure outlined in Sect. 3.3 before it is processed by a reflected shock of specified Mach number (${M}_\mathrm{r,st}$). The user can either choose to use the maximum Mach number, which will fully stagnate the state 2 gas, or a shock of user-specified Mach number which will leave the gas with some residual velocity. This new reflected condition (labelled state 2r in the code) is then the gas which unsteadily expands downstream into the acceleration tube. This is shown in Fig. 7.

Fig. 7

Shock tube representation with a reflected shock at the secondary or tertiary diaphragm (not to scale)

Figure 8a shows the effect that ${M}_\mathrm{r,st}$ has on the shocked test gas (state 2), using the nominal equilibrium solution for the Hayabusa condition detailed in Table 1, and the 100% helium driver condition values shown in Table 2. All of the values in the figure have been normalised by the value of each variable when the reflected shock Mach number (${M}_\mathrm{r,st}$) is equal to 1 (i.e., a reflected shock with no strength).

Fig. 8

Effect of reflected shock Mach number (${M}_\mathrm{r,st}$) on flow variables in the shock tube and test section for the nominal equilibrium solution for the Hayabusa condition detailed in Table 1. Values have been normalised by the value of each variable when ${M}_\mathrm{r,st} = 1$. a Effect on the post-reflected shock gas flow (state 2r), b effect on the test section flow (state 8)

It can be seen in Fig. 8b that the flow variables most affected by the reflected shock are the pressure (${p}_{2\mathrm{r}}$) and density ($\rho _{2\mathrm{r}}$), with maximum increases of around 1200 and 600%, respectively, and the velocity (${V}_{2\mathrm{r}}$) and Mach number (${M}_{2\mathrm{r}}$), that both go to 0. The other flow variables show little variation. The stagnation enthalpy (${H}_{\mathrm{t,2r}}$) shows an increase of 18% for a fully reflected shock, and the temperature (${T}_{2\mathrm{r}}$) shows an increase of 61%.

The questions which arise from the discussion of this diaphragm model are: (1) What reflected shock Mach number should be chosen, and (2) how sensitive the resulting flow condition is to that choice. This is investigated in Fig. 8b by using the results from Fig. 8a as inputs to examine results further downstream. Test section conditions were found by expanding the shocked test gas (state 2r) results from Fig. 8a to the acceleration tube shock speed (${V}_{\mathrm{s},2}$) and then steadily expanding them using the nozzle’s geometric area ratio of 5.64 [75]. Each variable has been normalised by the value when ${M}_\mathrm{r,st} = 1$.

Examining Fig. 8b, the effect that the reflected shock Mach number has on various flow variables in the test section can be seen. The test section Mach number (${M}_{8}$), density ($\rho _{8}$), and velocity (${V}_{8}$) are only affected slightly by the increasing reflected shock Mach number (${M}_\mathrm{r,st}$) with maximum changes of $-$8, $-$9, and 5%, respectively. The test section stagnation enthalpy (${H}_\mathrm{t}$) is affected more with a maximum change of 14%, but the main changes are seen in the test section pressure (${p}_{8}$) and temperature (${T}_{8}$) with increases of 31 and 38% seen, respectively.

To help predict if there is a hold time, PITOT is able to use facility length information and experimentally measured shock speeds to create ideal experimental x–t diagrams of facility test conditions. These ideal situations can then be compared to experimentally measured shock arrival times in the acceleration tube to roughly estimate experimental secondary diaphragm hold times. For the two experimental examples presented in Sect. 4.4, both used the same aluminium secondary diaphragm, but they showed different behaviour in relation to the diaphragm. The first example, discussed in Sect. 4.4.1, was a low enthalpy test condition and was estimated to have an experimental hold time of around ${150}\,\upmu \hbox {s}$. It required a fully reflected shock to recreate the experimentally measured acceleration tube shock speeds. The second example, discussed in Sect. 4.4.2, was a much faster test condition which was found to have an experimental hold time of around ${30}\,\upmu \hbox {s}$. A reflected shock at the secondary diaphragm was not required for that condition.

3.5 Acceleration tube simulation

Initially, the acceleration tube conditions are found using the same process as the secondary driver and shock tube conditions discussed in Sects. 3.2 and 3.3. The unsteadily expanding test gas (starting at state 2 and unsteadily expanding to state 7) drives a shock wave through the acceleration tube gas (state 5, generally laboratory air) processing it to state 6. The speed of the shock (${V}_{\mathrm{s},2}$) is dependent on both the fill condition in the acceleration tube (state 5) and the condition of the shocked test gas (state 2), such that ${V}_{7} = {V}_{6}$, and ${p}_{7} = {p}_{6}$. This is shown in Fig. 9. ${V}_{\mathrm{s},2}$ is found in the same manner as ${V}_{\mathrm{s,sd}}$ was found in Sect. 3, except here the solution requires that ${V}_{7} = {V}_{6}$ and ${p}_{7} = {p}_{6}$.

Fig. 9

Acceleration tube representation without over-expansion (not to scale)

Fig. 10

Acceleration tube representation with over-expansion (not to scale)

However, due to the low density of the acceleration tube gas, generally low-density shock tube boundary layer (or Mirels) effects [36,37,38] must be accounted for. Mirels proposed that these effects become significant below a 1 Torr (133 Pa) fill pressure, and X2’s acceleration tube fill pressure (${p}_{5}$) is generally between 0.5 and 100 Pa. Mirels effects cause a further expansion of the test gas than would be expected from basic shock tube theory because as mass in the post-shock state (state 6) is lost to the boundary layer, the post-shock pressure (${p}_{6}$) drops, causing further expansion of the test gas (state 7) to re-equalise the pressure across the interface between the two gases. In the limiting case, the test gas expands to the shock speed (${V}_{\mathrm{s},2}$ in this case), and the interface between states 6 and 7 becomes stationary relative to the shock. This limiting case is shown in Fig. 10. It can be seen that Fig. 10 is very similar to the ideal case shown in Fig. 9, but that in Fig. 10 the contact surface is travelling at the same velocity as the shock wave. It should be noted that in both the ideal case (Fig. 9) and the limiting Mirels case (Fig. 10), pressure and velocity are both matched across the interface between state 7 and state 6, but each figure represents a different interface in terms of matched pressure and velocity, due to the over-expansion. In the limiting Mirels case shown in Fig. 10, the matched velocity would be faster than the ideal velocity shown in Fig. 9 and equal to the shock speed. Correspondingly, the matched pressure in Fig. 10 would be lower than the ideal matched pressure shown in Fig. 9.

PITOT currently does not directly apply the analytical methodology derived by Mirels [36,37,38] to account for this, but can instead practically account for the effect. It is common practice when estimating test gas conditions to assume Mirels’ limiting case and to expand the test gas to ${V}_{\mathrm{s},2}$ instead of ${V}_{6}$. The real solution should theoretically lie between these two limits and can be tuned against experimental results. PITOT offers the choice between these two theoretical limits (${V}_{7} = {V}_{6}$ and ${V}_{7} = {V}_{\mathrm{s},2}$) and when ${V}_{\mathrm{s},2}$ is chosen, the ideal case is still solved using ${V}_{7} = {V}_{6}$ to find ${V}_{\mathrm{s},2}$, and then afterwards, the state 2 gas is unsteadily expanded to ${V}_{\mathrm{s},2}$ instead of ${V}_{6}$.

Table 4 Comparison between expansion of the shocked test gas (state 2 which expands to state 7) to the gas velocity behind the shock (${V}_{6}$) or the acceleration tube shock speed (${V}_{\mathrm{s},2}$) for the nominal equilibrium solution for the Hayabusa condition detailed in Table 1 (while it is noted that the column selected as the reference for the percentage change calculations is arbitrary, it has been chosen to use “State 2 expanded to ${V}_{6}$” as the reference)

It should be noted that these two limits can have a large effect on the related flow properties. Using the Hayabusa condition detailed in Table 1, the nominal theoretical solution predicts a shock tube shock speed (${V}_{\mathrm{s},1}$) of 4597 m/s, and an acceleration tube shock speed (${V}_{\mathrm{s},2}$) of 10,011 m/s. Table 4 shows a comparison of the various flow properties at both the nozzle entrance (state 7) and exit (state 8, using the nozzle geometric area ratio of 5.64) when the shocked test gas (state 2) is expanded to ${V}_{6}$ or ${V}_{\mathrm{s},2}$. The reference case was chosen to be the ideal condition (State 2 expanded to ${V}_{6}$).

It can be seen in Table 4 that there are large differences in variables between the two limits and that in general, roughly the same level of percentage difference between the two conditions is carried from the nozzle inlet to the nozzle exit. Two very important quantities for performing scaled expansion tube experiments are the stagnation enthalpy (${H}_\mathrm{t}$), a measure of the static and kinetic enthalpy of the test gas, and the density at the nozzle exit ($\rho _{8}$). In Table 4, a $+11.4\%$ difference in stagnation enthalpy (${H}_\mathrm{t}$) can be seen between the two limits, and a $-$47.4% change in nozzle exit density ($\rho _{8}$). These are not trivial changes, and for the theoretical model’s results to be most useful, it is important to calibrate PITOT against experimental measurements to ascertain how much the gas has expanded in the acceleration tube.

Sometimes chemical freezing is an issue in acceleration tubes due to how fast the gas expands and cools in the tube versus the time scales which may be required for the gas to chemically recombine [68]. For this reason, if necessary, PITOT also has the ability to freeze the chemistry of the shocked test gas (state 2) as it unsteadily expands to state 7 in the acceleration tube.

3.6 Nozzle simulation

Generally, a contoured nozzle is used at the end of X2’s acceleration tube to increase the model sizes which can be tested in the facility, increase the flow Mach number, and increase the available test time. When a nozzle is used, it is simulated in PITOT by performing a steady expansion through a known area ratio to process the test gas from its state at the nozzle entrance (state 7, shown in Fig. 11a) to its state at the nozzle exit (state 8, shown in Fig. 11b). Generally, the geometric exit-to-inlet area ratio of 5.64 of X2’s contoured Mach 10 nozzle¹ [75] is used for PITOT calculations, but it does not always represent the true state of expansion of the core flow. Unlike a reflected shock tunnel where the test gas is stagnated before being expanded through a de Laval nozzle, an expansion tube nozzle is fully supersonic, and the gas flowing through the nozzle has an associated boundary layer which has developed through the acceleration tube, and which continues to grow through the nozzle. This is shown in Fig. 12. This boundary layer growth is something which is very hard to accurately measure in an operational expansion tube facility.

Fig. 11

X2 nozzle representation, with the shock wave entering and exiting the nozzle (not to scale). a Nozzle entrance representation, b nozzle exit representation

As shown in Fig. 12, this changing boundary layer can be modelled with an “effective” area ratio which accounts for the effect of the boundary layer profile on the steady expansion. Generally, a comparison between wall pressure traces before the nozzle entrance and impact pressure probe traces at the nozzle exit are used to establish the effective area ratio of the nozzle for a given operating condition. To aid this analysis, and to help understand the effect that changes in effective area ratio can have on the resultant flow in the test section, PITOT has an “area ratio check” mode which lets the user specify a list of area ratios which are then analysed at the end of the analysis for a set nozzle inlet (state 7) condition.

Fig. 12

Nozzle exit representation showing an example of the boundary layer (not to scale)

In Fig. 13, a sample result using the Hayabusa condition from Table 1 for the nominal equilibrium condition can be seen. The test gas has been unsteadily expanded to the shock speed in the acceleration tube (${V}_{\mathrm{s},2} = {10{,}011\,\hbox {m/s}}$, see Sect. 3.5) and then steadily expanded using area ratios from 2.0 to 9.0, in increments of 0.1, covering a range on either side of the nozzle’s geometric area ratio of 5.64 [75]. The results have then been normalised by the results for the nozzle geometric area ratio of 5.64.

Fig. 13

Effect of changing nozzle area ratio on flow variables at the nozzle exit (state 8) for the nominal solution for the Hayabusa condition detailed in Table 1

Examining Fig. 13, and considering what occurs when the area ratio increases above the geometric area ratio, there are only small changes in nozzle exit velocity (${V}_{8}$, a 0.4% maximum increase), nozzle exit Mach number (${M}_{8}$, a 4% maximum increase), and nozzle exit temperature (${T}_{8}$, a 10% maximum decrease) over the full range shown. However, the other two state variables, the nozzle exit density ($\rho _{8}$) and pressure (${p}_{8}$), show much larger changes, with the variables decreasing by 38 and 44%, respectively.

Now examining Fig. 13, and considering what occurs when the area ratio drops below the geometric area ratio, there are only small changes in nozzle exit velocity (${V}_{8}$, a maximum 1% decrease), nozzle exit Mach number (${M}_{8}$, a maximum 8% decrease), and nozzle exit temperature (${T}_{8}$, a 19% increase) over the full range shown. However, once again the other two state variables, the nozzle exit density ($\rho _{8}$) and pressure (${p}_{8}$), show much larger changes, with increases of 284 and 345%.

Overall, Fig. 13 shows that the nozzle exit velocity (${V}_{8}$), Mach number (${M}_{8}$), and temperature (${T}_{8}$) are not sensitive to changes in the nozzle area ratio. However, the nozzle exit density ($\rho _{8}$) and pressure (${p}_{8}$) are very sensitive to it for area ratios below the geometric one.

In addition to its effect in the acceleration tube (see Sect. 3.5), in some situations chemical freezing can also occur in expansion tube nozzles due to how fast the gas expands and cools in relation to the time scales required for chemical recombination. For this reason, if necessary, PITOT has the ability to freeze the chemistry of the steady expansion from state 7 to state 8.

3.7 Simulation of various basic test models

Many different types of test models are used in the X2 expansion tube, and PITOT has a series of modes which allow it to estimate the flow properties over these models. For the simulation of the stagnation streamline of blunt-body models (see Fig. 14) or pitot pressure probes in the test section, PITOT has the functionality to allow it to calculate conditions behind a normal shock in the test section for both frozen and equilibrium flows.

Fig. 14

Representation of flow over a blunt-body test model (not to scale)

To protect the pressure transducers used in the test section from the high-pressure driver gas and debris which follows the test gas down the tube, ${15}^{\circ }$ half-angle conical pressure probes are often used instead of blunt pitot pressure probes in UQ’s expansion tubes, and PITOT has the functionality to solve the Taylor–Maccoll conical flow equations [76, 77] to find the conical shock angle ($\beta$) and surface gas state for a specified cone half-angle ($\theta$) in the test section.

Both symmetric and asymmetric wedge models are common test models in UQ’s expansion tubes, and PITOT has the functionality to find the shock angle ($\beta$) and the post-shock gas state for a wedge model of specified wedge angle ($\theta$) in the test section.

While Fig. 14 includes the contoured nozzle generally used at the end of the X2 expansion tube, PITOT can also simulate the same test models without a nozzle (state 8 in Fig. 14 would become state 7).

4 Quantifying experimental data using PITOT

For the purpose of analysing experimental data, PITOT has several experimental test modes which make use of experimentally measured shock speeds to perform parts of the analysis, effectively “calibrating” the analysis by removing potential errors in the theoretical modelling of different sections of the facility. PITOT can be run in a fully experimental mode where all shock speeds are taken directly from experimental data, or a partially experimental mode where either the shock tube or acceleration tube shock speeds (${V}_{\mathrm{s},1}$ and ${V}_{\mathrm{s},2}$) are taken from experimental data, and the remaining calculations are performed theoretically. How these modes function is discussed in this section.

4.1 Experimental calibration of the shock tube

In Sect. 3.3, the shock tube shock speed (${V}_{\mathrm{s},1}$) was computed based on the shock tube fill condition (state 1) and the driver condition which is unsteadily expanding into the shock tube (either state $4^{\prime \prime }$ or state sd2, both of which will unsteadily expand to state 3), by finding the point where ${p}_{3} = {p}_{2}$ and ${V}_{3} = {V}_{2}$. While state 1 is experimentally well defined, the condition of the unsteadily expanding driver gas depends on the estimated driver rupture condition (state 4). While the state 4 estimate may be sufficient to perform reasonably accurate parametric studies of the facility, it may not be accurate enough for the rebuilding of an experiment. By shocking the state 1 gas with an experimentally measured ${V}_{\mathrm{s},1}$ value instead of a value computed from state 4, driver modelling errors are largely removed from the flow calculation. Experimental uncertainty associated with the shock speed measurement and the shock tube fill condition are introduced to the calculation, but are usually much smaller and can be easily taken into account.

4.2 Experimental calibration of the acceleration tube

In Sect. 3.5, the acceleration tube shock speed (${V}_{\mathrm{s},2}$) was computed based on the acceleration tube fill condition (state 5) and the condition of the shocked test gas which is unsteadily expanding into the acceleration tube (state 2 which will unsteadily expand to state 7), by finding the point where ${p}_{6} = {p}_{7}$ and ${V}_{6} = {V}_{7}$. In most situations, after ${V}_{\mathrm{s},2}$ has been found, the shocked test gas (state 2) is then “over-expanded” to ${V}_{\mathrm{s},2}$ to find state 7, simulating the limiting case of the Mirels effect for a low-density shock tube [36,37,38]. Practically, there are some issues with this.

Firstly, by its nature the acceleration tube is a low-density shock tube, and for some conditions with low acceleration fill pressures (${p}_{5}$), ${V}_{\mathrm{s},2}$ can be very sensitive to small changes in ${p}_{5}$, and even small errors in state 5 can have a significant effect on the unsteadily expanded test gas (state 7). If ${V}_{\mathrm{s},2}$ or the unsteadily expanded test gas pressure (${p}_{7}$) is known experimentally, state 2 can be expanded to either of these values, removing ${p}_{5}$ from the calculation. Additional experimental uncertainty is added to the calculation, but by simulating the bounds of these inputs, the correct solution can be bounded, in a way which is independent of state 5. If the gas has in fact reached the limiting Mirels case where the unsteadily expanded test gas (state 7) has expanded to the shock speed, measurements of ${V}_{\mathrm{s},2}$ and ${p}_{7}$ can be used to verify this. If the pressure is greater than the limiting Mirels case, this can be used to ascertain the degree of expansion which has occurred.

Secondly, there is the issue of modelling the weak secondary or tertiary diaphragm separating the shock and acceleration tubes (see Sect. 3.4). While PITOT is able to simulate a reflected shock wave of user-specified strength at the end of the shock tube as a type of diaphragm hold time model, it is a limited model, and the effect of the diaphragm is generally assumed to be small. This may not be true, and must be kept in mind when assessing simulation results.

4.3 Experimental calibration of the nozzle

As was discussed in Sect. 3.6, due to the fact that an expansion tube flow is never stagnated, significant boundary layers can build up in the acceleration tube and nozzle. The boundary layer profile through the nozzle is a large source of experimental uncertainty, and it can cause the nozzle to behave as if it has a different area ratio than its geometric value (see Figs. 11, 13). As was shown in Fig. 13, different nozzle area ratios can have a large effect on the nozzle exit density and pressure ($\rho _{8}$ and ${p}_{8}$).

During the testing of new flow conditions in X2, a pitot rake model is installed at the nozzle exit, where nine impact pressure probes (either pitot or ${15}^{\circ }$ half-angle conical probes) are spaced 17.5 mm apart radially relative to the nozzle exit plane, covering a total centre-to-centre height of 140 mm. The middle probe (pt5) is generally oriented with the centre line of the nozzle. These pitot rake tests are used to measure the size of the core flow of test conditions, estimate steady test time, and provide additional diagnostics to ascertain the gas state in the test section (state 8).

While it would be very useful to have measurements of the other state variables, by their nature, high-enthalpy shock tunnel facilities are powered by driver gas which follows the test gas down the tube and whose high pressure and temperature can damage sensitive instrumentation. This makes it difficult to measure state variables other than pressure, and often other state variables must be inferred from changes in the flow pressure. If the condition of the unsteadily expanded test gas entering the nozzle (state 7) is known with a reasonable amount of accuracy from experimental measurements of ${V}_{\mathrm{s},2}$ and the unsteadily expanded test gas pressure (${p}_{7}$), and if the impact pressure at the nozzle exit has been experimentally measured, PITOT’s “area ratio check” mode can be used to find the “effective” nozzle area ratio which is consistent with both of these results. Once this effective area ratio is known, the related nozzle exit state (state 8) can then be found. Once again, this is affected by any uncertainties in the measured quantities, but the bounds of the real solution can be found.

4.4 Examples

Now that experimental calibration has been discussed, two different examples will be presented.

The first example is a cold driver air example from the work of Gu [50], using two experiments performed by the authors and Gu. The example was chosen since its low velocity nature should remove some of the high-temperature effects normally present in an expansion tube facility, making it a condition which should be well suited to simulation using PITOT.

The second example is a regular X2 free piston driven air test condition that was originally designed by Zander et al. [54] and has since been used by Lewis et al. [55,56,57]. It was chosen because it is a condition which has been used for several years now, and because new pitot rake data were available for the condition from August 2016, which incorporated some upgraded diagnostics. Upgrades included replacing the static pressure mounts along the length of X2’s acceleration tube with new vibrationally isolated ones. Two extra sensors (at7 and at8) were also added to the end of the acceleration tube to give two pressure measurements just before the entrance to the nozzle. All of the “at”-labelled pressure sensors except “at1” are now recorded both in the main data acquisition system at 2.5  MHz and in a separate system at 60  MHz. This lowers the sampling rate error on the shock speed calculations by an order of magnitude. The effect of the upgrades can be seen when comparing Table 6 in Sect. 4.4.1, with experimental data taken before the upgrades, to Tables 9 and 10 in Sect. 4.4.2, whose experimental data were taken after the upgrades. Pressures and shock speeds down the whole length of X2’s acceleration tube are shown in Tables 9 and 10, whereas only values from the end of the acceleration tube are shown in Table 6.

The experimental shock speed naming convention for the two examples (i.e., sd1–sd3) is a reference to the two specific wall pressure sensor locations used to find that particular shock speed value, and where experimental shock speeds are shown in figures in this subsection (i.e., Figs. 15, 16, 20), the values are shown at the midpoint between the two sensor locations. Where experimental pressure measurements are shown in Tables 6 and 10, the names correspond to either wall pressure sensor locations or the locations of pressure sensors in the X2 pitot rake. (Approximate X2 wall pressure sensor locations are shown in Fig. 1, and exact values can be found in Gildfind et al. [78].)

The experimental shock speed uncertainties shown in Tables 6 and 9 were found using the standard shock speed uncertainty calculation procedure described in Appendix 2. The experimental pressure measurements shown in Tables 6 and 10 were found by filtering the data with a 6th-order low-pass filter with a cutoff frequency of 100 kHz, taking the mean of the steady pressure time for the relevant signal, and then removing the mean of the noise taken just before shock arrival. The uncertainties on the pressure measurements were found using a 95% confidence interval on the standard deviation of the experimental data. This implies that 95% of the distribution of the experimental data sits within the uncertainty of the mean value. Mean uncertainties shown in the tables were calculated using the root sum squared method. Where experimentally measured pressure signals are shown in figures (i.e., Figs. 17, 18, 19, 21,  22), they have been filtered using a 6th-order low-pass filter with a cutoff frequency of 100 kHz, with the unfiltered data shown behind it using a lower opacity.

4.4.1 Example 1: Cold driver condition

The fill details of the cold driver air example are shown in Table 5. The experimentally measured shock speeds, and wall transducer and pitot rake ${15}^{\circ }$ half-angle cone pressure measurements for two experiments, x2s2902 and x2s2903, are shown in Table 6.

Table 5 Facility configuration details for the cold driver air test condition used by the authors and Gu [79]

Table 6 Experimentally measured quantities from the two experiments performed by the authors and Gu [79]

In Fig. 15, the experimental shock tube shock speed (${V}_{\mathrm{s},1}$) values shown in Table 6 for the two experiments are compared to the theoretical equilibrium shock speed value from PITOT when effective cold driver values from Table 3 are used. It can be seen that the two experiments, x2s2902 and x2s2903, are statistically consistent with each other, with the first two shock speed measurements for each experiment having overlapping uncertainties, and the final measurement being almost the same. However, the theoretical result from PITOT underestimates the experimental shock speeds by around 5%. As was discussed in Sect. 4.1, this error can be removed by not using the driver model in the calculation and instead specifying an experimentally measured ${V}_{\mathrm{s},1}$ value. For the theoretical acceleration tube calculations shown in Figs. 16 and 17, an average ${V}_{\mathrm{s},1}$ value of 2050 m/s has been used instead of the driver model.

Fig. 15

Experimentally measured shock tube shock speeds (${V}_{\mathrm{s},1}$) from Table 6 compared to the theoretical equilibrium result from PITOT

In Fig. 16, the experimental acceleration tube shock speed (${V}_{\mathrm{s},2}$) values shown in Table 6 are compared to various theoretical equilibrium shock speed estimates from PITOT when the experimental shock tube fill condition (state 1) has been shocked by a specified average ${V}_{\mathrm{s},1}$ value of 2050 m/s. On the legend in Fig. 16, it can be seen that for some of the simulations, the velocity of the shocked test gas (${V}_{2}$) has been set to the shock tube shock speed (${V}_{\mathrm{s},1}$), and a reflected shock has been used at the end of the shock tube (${M}_\mathrm{r,st} > 1$). These settings have been used to simulate the use of a low-density shock tube and a secondary diaphragm which produces a measurable reflected shock in the already shocked test gas (state 2), but otherwise has a low inertial effect. These modes are discussed in Sects. 3.3 and 3.4.

Fig. 16

Experimentally measured acceleration tube shock speeds (${V}_{\mathrm{s},2}$) from Table 6 compared to various semi-experimental equilibrium PITOT simulations

Fig. 17

Measured acceleration tube wall pressure traces for two experiments performed using the test condition described in Table 5 compared to the unsteadily expanded test gas (state 7) pressures for the semi-experimental equilibrium PITOT simulations shown in Fig. 16

In Fig. 16, for the simulation where the shocked test gas velocity (${V}_{2}$) has not been changed and the reflected shock has not been used (${M}_\mathrm{r,st} = 1$), ${V}_{\mathrm{s},2}$ is underestimated by around 10%. This shows that it is not possible to simulate this condition closely with PITOT without using some kind of non-ideal model for either the low-density shock tube or the secondary diaphragm (or both). By using the non-ideal shock tube model and making ${V}_{2} = {V}_{\mathrm{s},1}$ the discrepancy can be reduced to around 4%. By using only a fully reflected shock at the end of the shock tube (${M}_\mathrm{r,st} = \hbox {maximum} = 2.9$), the discrepancy can be reduced to around 7%. This shows that the discrepancy can only be reduced further by making ${V}_{2} = {V}_{\mathrm{s},1}$ and using a reflected shock at the end of the shock tube (${M}_\mathrm{r,st} > 1$). The final three lines on the figure show the theoretical shock speeds with both non-ideal models and differing reflected shock Mach numbers (${M}_\mathrm{r,st}$). It can be seen that each reflected shock Mach number value (${M}_\mathrm{r,st} = 2.0$, 2.4, and the maximum of 2.9) falls inside the range of some of the experimental measurements, but it is not obvious which value is the most correct. To resolve this, the pressure of the unsteadily expanded test gas (state 7) can be analysed. This is shown in Fig. 17.

Figure 17 shows the tube wall static pressure traces at the end of the acceleration tube for the two experiments compared to the expected theoretical unsteadily expanded test gas (state 7) pressures for the various simulations shown in Fig. 16. Figure 17 shows theoretical data where the test gas has both been expanded to the acceleration tube shock speed (${V}_{7} = {V}_{\mathrm{s},2}$) and the theoretical ideal gas velocity in the acceleration tube (${V}_{7} = {V}_{6}$). Firstly, in general it can be seen that the theoretical ${p}_{7}$ values where ${V}_{7} = {V}_{6}$ are all too large when compared to the experimental data. Therefore, the remaining discussion about Fig. 17 will focus on the theoretical data where ${V}_{7} = {V}_{\mathrm{s},2}$.

Comparing the experimental and theoretical data shown in Fig. 17, it is difficult to ascertain exactly where to compare the experimental data to the theoretical equivalent. To estimate which part of each pressure trace is the accelerator gas and which is the test gas, a theoretical calculation of the accelerator gas slug length was performed from Mirels [36] using the measured ${V}_{\mathrm{s},2}$ value. Equations 2 and 20 from Mirels [36] were used to find the slug length. It was assumed that the boundary layer was laminar and that the $\beta$ value required for Equation 2 could be found from Equation 17 in the same paper. From this, the passage time of the accelerator gas slug was found to be around ${40}\,\upmu \hbox {s}$ for each signal shown here, and this is shown in Fig. 17 for signal at4 as the “accelerator gas slug”. At the end of that gas slug, there is a section of steadily dropping pressure which is likely to be test gas, but without a stable pressure reading. This has been labelled the “start of test gas”. The next section is labelled “steady test gas estimate”, and it has been used to calculate the experimental state 7 pressure values shown in Table 6 for signals at4, at5, and at6. The section after this labelled “end of steady test gas” appears to have a similar pressure to the “steady” section before it, but with more noise. Potentially, it is the section where the test and driver gases start to mix, and it has not been used to calculate the steady pressure values.

Considering the experimental ${p}_{7}$ values shown in Table 6, the mean values for x2s2902 and x2s2903 are $3.3 \pm 0.2\,\hbox {kPa}$ and $3.2 \pm 0.2\,\hbox {kPa}$, respectively. In Fig. 16, it was shown that only the conditions with a shocked test gas velocity equal to the shock tube shock speed (${V}_{2} = {V}_{\mathrm{s},1}$) and a reflected shock exiting the shock tube (${M}_\mathrm{r,st} > 1$) were able to match the experimental shock speed data. Here, it is similar, with only the simulations with reflected shock Mach number (${M}_\mathrm{r,st}$) values of 2.4 and 2.9 falling within the uncertainties of the experimental data with theoretical unsteadily expanded test gas pressure (${p}_{7}$) values of 3.1 and 3.4 kPa, respectively. For this reason, it has been decided to use a shocked test gas velocity equal to the shock tube shock speed (${V}_{2} = {V}_{\mathrm{s},1}$) and a fully reflected shock at the end of the shock tube (${M}_\mathrm{r,st} = \hbox {maximum} = 2.9$) for all of the experimental data analysed in Figs. 18 and 19.

Figure 18 is similar to Fig. 17 above; however, in Fig. 18 the experimental wall pressure traces for the two experiments are compared to PITOT simulations based on experimental shock speeds only. While examining shock speed and wall pressure data in the acceleration tube in Figs. 16 and 17, it was found that setting the shocked test gas velocity in the shock tube to the shock tube shock speed (${V}_{2} = {V}_{\mathrm{s},1}$) and using a fully reflected shock at the end of the shock tube (${M}_\mathrm{r,st} = \hbox {maximum} = 2.9$) gave the best comparison between PITOT and the experimental data. For this reason, this has again been done for the PITOT simulations shown in Figs. 18 and 19.

Fig. 18

Measured acceleration tube wall pressure traces for two experiments performed using the test condition described in Table 5 compared to equilibrium PITOT simulations performed using experimentally measured shock speeds from experiment x2s2902

The goal of Fig. 18 is to ascertain the effect that the uncertainty on the experimental shock speed data has on how well the overall flow condition can be known. If uncertainties on the shock tube and acceleration tube fill conditions (state 1 and state 5) are assumed to be sufficiently small, the main sources of uncertainty are the shock speed uncertainties in each section of the facility and the uncertainties about the effective nozzle area ratio (see Sect. 3.6). Using the extremities of the measured shock speed data, a sensitivity analysis can be performed to ascertain realistic bounds on the resulting flow condition parameters in the acceleration tube and, following that, the test section. This will be done here using the data from x2s2902 and a tool that the authors wrote to use PITOT to examine this. While the experimental data for both experiments are very similar, to simplify the discussion, it has been decided to focus on only x2s2902.

Considering the shock speed data for x2s2902 shown in Table 6, the absolute minimum shock tube shock speed (${V}_{\mathrm{s},1}$) possible is $2010\,\hbox {m/s}$ and the absolute maximum is $2100\,\hbox {m/s}$. If it is assumed that ${V}_{\mathrm{s},1}$ is not changing across the locations where it is measured, the values can be averaged, giving a mean value of $2050 \pm 10\,\hbox {m/s}$ and a much smaller shock speed range of 2040–2070 m/s. Similarly, for the acceleration tube shock speed (${V}_{\mathrm{s},2}$), the absolute maximum range possible is 3570–3750 m/s. Once again, if it is assumed that ${V}_{\mathrm{s},2}$ is not changing across the locations where it is measured, the values can be averaged, giving a mean value of $3660 \pm 20\,\hbox {m/s}$ and a much smaller shock speed range of 3630–3680 m/s. Every possible combination of these shock speeds for both the “absolute minimum and maximum” and “mean minimum and maximum” cases was simulated in PITOT to find a realistic range of unsteadily expanded test gas pressure (${p}_{7}$) values, and these values are shown in Fig. 18 with the experimental acceleration tube wall pressure data.

Results where the test gas has both been expanded to the acceleration tube shock speed (${V}_{7} = {V}_{\mathrm{s},2}$) and the theoretical ideal gas velocity in the acceleration tube (${V}_{7} = {V}_{6}$) are shown in Fig. 18. Once again, the same as when Fig. 17 was discussed, the PITOT simulations shown in Fig. 18 where ${V}_{7} = {V}_{6}$ have an unrealistically high unsteadily expanded test gas pressure (${p}_{7}$) for every case. Therefore, the following analysis will only focus on the pressure values where ${V}_{7} = {V}_{\mathrm{s},2}$.

From Table 6, it can be seen that the mean wall pressure trace (${p}_{7}$) values for x2s2902 and x2s2903 are $3.3 \pm 0.2\,\hbox {kPa}$ and $3.2 \pm 0.2\,\hbox {kPa}$, respectively. From the sensitivity analysis, the absolute maximum ${p}_{7}$ range shown in Fig. 18 is 2.7–5.0 kPa. Using the less conservative mean uncertainty values, the ${p}_{7}$ range is a more realistic 3.4–4.0 kPa, with a nominal value of 3.7 kPa. The simulated mean values from the sensitivity analysis and the experimental ${p}_{7}$ measurements have overlapping uncertainties, indicating that the analysis so far has been adequate, with the pressure potentially around 3.4 kPa, where the two overlap.

Fig. 19

Measured ${15}^{\circ }$ half-angle cone pressure traces in the test section (${p}_{10\mathrm{c}}$) for two experiments performed using the test condition described in Table 5 compared to theoretical values from equilibrium PITOT simulations using the nozzle’s geometric area ratio of 5.64 and measured experimental shock speeds from experiment x2s2902

Now that the bounds on the unsteadily expanded test gas (state 7) values have been considered, the last step is to find realistic bounds on the test section state (state 8). This is not necessarily a simple task. Firstly, there is uncertainty about the unsteadily expanded test gas state (state 7) entering the nozzle. Secondly, there is uncertainty about the effective area ratio of the nozzle, and finally, it is only possible to infer the nozzle exit state (state 8) from pressures measured over pressure probes in the test section (state 10), which in this case are ${15}^{\circ }$ half-angle conical pressure probes. Figure 19 shows the experimental cone pressure data for the two experiments from’s X2 pitot rake. The pitot rake is generally instrumented with nine pressure probes mounted vertically along the nozzle exit plane, with the middle probe (pt5) oriented with the centre line of the nozzle. However, in this case, the centre-line probe was replaced with a small cylinder model to perform infrared radiation measurements, and the wake flow of this cylinder was interacting with probes pt4 and pt6 on either side of the model, so only data from probes 1 to 3 and 6 to 9 are shown in Fig. 19.

Flow arrival in the test section is generally seen as a spike in the measured impact pressure traces due to the different post nozzle expansion properties of the accelerator gas compared to the test gas. This is then followed by a short period of relatively steady test time, seen for around ${300}\,\upmu \hbox {s}$ for this condition, where measurements would be taken for a more complicated experiment. In most cases, the steady test time is terminated by a gradual pressure rise as less expanded test gas starts to flow over the probes.

Due to the fact that the PITOT results where the test gas was unsteadily expanded to the ideal gas velocity in the acceleration tube (${V}_{7} = {V}_{6}$) shown in Figs. 17 and 18 were found to be too large to be a correct assumption, it was decided to only show PITOT results where the test gas has been unsteadily expanded to the acceleration tube shock speed (${V}_{7} = {V}_{\mathrm{s},2}$) in Fig. 19. These unsteadily expanded test gas values (state 7) were then steadily expanded through the nozzle using the nozzle’s geometric area ratio of 5.64 to find the values shown in Fig. 19.

The experimental ${15}^{\circ }$ half-angle cone pressure (${p}_{10\mathrm{c}}$) measurements shown in Table 6 were found using the “steady test time” shown in Fig. 19. Looking at Table 6, it can be seen that the mean experimental ${p}_{10\mathrm{c}}$ values for x2s2902 and x2s2903 are $1.4 \pm 0.4\,\hbox {kPa}$ and $1.5 \pm 0.4\,\hbox {kPa}$, respectively. These results are imprecise as they have quite large percentage uncertainties (around 25%), and for some of the individual signals (pt3 and pt9) the percentage uncertainties are quite large (around 100%). If the mean range from the sensitivity analysis is again considered, it can be seen in Fig. 19 that this mean data compares quite well to the experimental data, with a ${p}_{10\mathrm{c}}$ range of 1.7–1.9 kPa, with a nominal value of 1.8 kPa. This compares well with the experimental data. The range of the more conservative absolute minimum and maximum uncertainty simulations is 1.5–2.2 kPa, the bottom end of which also compares well with the experimental data.

Due to the large uncertainties on the cone pressure (${p}_{10\mathrm{c}}$) data, it would be hard to perform an “area ratio check” for different nozzle area ratios (see Sect. 3.6) and have confidence in the result. For this reason, the test section state (state 8) range found using the nozzle’s geometric area ratio of 5.64 and the mean uncertainties on the shock speed measurements have been used to estimate the flow condition parameters. This is shown in Table 7 where the final condition details at both nozzle entry (state 7) and nozzle exit (state 8) for experiment x2s2902 are shown. Both a nominal solution found using only the mean shock speeds and a solution bound for every variable found using the range of the uncertainties on those shock speeds are presented. This is already considered by the authors to be a conservative analysis, but it should be noted that more conservative estimates of the flow condition bounds could be found by using the absolute minimum and maximum shock speed ranges instead, or by performing an area ratio check to ascertain what variation in area ratio would still fall inside the uncertainties on the experimentally measured ${p}_{10\mathrm{c}}$ data shown in Table 6.

Table 7 Final result of the condition analysis of the cold driver air test condition from Table 5

4.4.2 Example 2: Free piston driven condition

The fill details of the example free piston driven air condition can be found in Table 8. The experimentally measured shock speeds, and filtered wall transducer and pitot rake ${15}^{\circ }$ half-angle cone pressure measurements for experiment x2s3232 are shown in Tables 9 and 10, respectively.

Table 8 Facility configuration details for the free piston driven air test condition designed by Zander et al. [54]

Table 9 Experimentally measured shock speeds for the free piston driven air test condition detailed in Table 8 from experiment x2s3232

To simplify this second example, some lessons learnt while analysing the first example in Sect. 4.4.1 will be used. Considering Figs. 18 and 19 where the pressure values from the sensitivity analysis based on the shock speed uncertainties for experiment x2s2902 are compared to experimental data, it can be seen that the pressure values found from the bounds of the absolute minimum and maximum possible shock speeds (“abs. minimum exp.” and “abs. maximum exp.”) are much less representative of the real spread in the data than the pressure values found using the bounds of the mean uncertainties of the shock speeds (“mean minimum exp.” and “mean maximum exp.”), and in Table 7 the mean uncertainty values were used to find the expected range of the final flow condition data. For this reason, only the bounds of the mean uncertainties will be used for the sensitivity analysis for this example.

In Fig. 20a, the experimental shock tube shock speed (${V}_{\mathrm{s},1}$) values shown in Table 9 for experiment x2s3232 are compared to the theoretical equilibrium shock speed value from PITOT when the effective driver values from Table 2 are used. It can be seen that the theoretical result from PITOT overestimates the experimental shock speeds by around 5%. As was discussed in Sect. 4.1, this error can be removed by not using the driver model in the calculation and instead specifying an experimental ${V}_{\mathrm{s},1}$ value. For the theoretical acceleration tube calculations shown in Fig. 20b, an average experimental ${V}_{\mathrm{s},1}$ value of $4020\,\hbox {m/s}$ has been used instead of the driver model.

Fig. 20

Experimentally measured shock speeds from Table 9 compared to results from PITOT. a Shock tube shock speeds (${V}_{\mathrm{s},1}$), b acceleration tube shock speeds (${V}_{\mathrm{s},2}$)

In Fig. 20b, the experimental acceleration tube shock speed (${V}_{\mathrm{s},2}$) values shown in Table 9 for experiment x2s3232 are compared to both the fully theoretical equilibrium value from PITOT when the effective driver values from Table 2 were used, as well as a result from PITOT where the shock tube fill condition (state 1) was shocked by the specified experimental ${V}_{\mathrm{s},1}$ value of 4020 m/s. The driver model in PITOT overestimated ${V}_{\mathrm{s},1}$ in Fig. 20a by around 5%, so it was expected that it would also overestimate ${V}_{\mathrm{s},2}$ here, and that is what is seen, with the fully theoretical value being around 6% higher than the mean experimental ${V}_{\mathrm{s},2}$ value from Table 9. Large variations are seen in the first seven experimental ${V}_{\mathrm{s},2}$ measurement locations. However, the shock speed becomes fairly consistent for the last three downstream measurements. The authors believe that this could be caused by a few different phenomena, such as diaphragm effects, changing shock shape, or errors in the measured transducer locations for some of the sensors. It is also interesting to note in Fig. 20b that even using the experimentally measured mean ${V}_{\mathrm{s},1}$ value of 4020 m/s, PITOT still overestimates the acceleration tube shock speed by 2% compared to the measured at4–at6 value of $7990 \pm 50\,\hbox {m/s}$, showing that either the shock has attenuated slightly and slowed down from the expected value or that the acceleration tube fill pressure (${p}_{5}$) may have been slightly higher than expected.

Table 10 Filtered experimentally measured pressure data for the free piston driven air test condition detailed in Table 8 from experiment x2s3232

Fig. 21

Measured acceleration tube wall pressure traces for the test condition described in Table 8 compared to equilibrium PITOT simulations performed using experimentally measured shock speeds from experiment x2s3232

If the uncertainties on the shock and acceleration tube fill conditions (state 1 and state 5) are assumed to be small, the main sources of uncertainty for the experiment are from the shock speed measurements in each section of the tube and the effective nozzle area ratio (see Sect. 3.6). By performing a sensitivity analysis using the uncertainties on the measured shock speed data, realistic bounds on the resulting flow condition parameters in the acceleration tube can be ascertained, and following that, the test section.

Considering the shock speed data for x2s3232 shown in Table 9, the mean shock tube shock speed ($V_{\mathrm{s},1}$) is $4020 \pm 30\,\hbox {m/s}$, giving a mean shock speed range of 3990–4050 m/s. The mean acceleration tube shock speed ($V_{\mathrm{s},2}$) considering just the “at”-labelled shock speeds in Table 9 is $7950 \pm 50\,\hbox {m/s}$, giving a mean shock speed range of 7900–8000 m/s. The sensitivity analysis simulated every possible combination of these mean shock speeds in PITOT to find the full potential range of unsteadily expanded test gas pressure (${p}_{7}$) values. These values are shown in Fig. 21 with the experimental acceleration tube wall pressure trace data from experiment x2s3232 for wall sensors at1 to at8. Figure 21 shows data where the test gas has both been expanded to the acceleration tube shock speed (${V}_{7} = {V}_{\mathrm{s},2}$) and the theoretical ideal gas velocity in the acceleration tube (${V}_{7} = {V}_{6}$).

Firstly, it can be seen that for all of the PITOT results shown in Fig. 21 where ${V}_{7} = {V}_{6}$ the unsteadily expanded test gas pressure (${p}_{7}$) is too large for it to have been a correct assumption. Therefore, the following analysis will focus only on the pressure values where ${V}_{7} = {V}_{\mathrm{s},2}$.

From Table 10, it can be seen that the mean wall pressure (${p}_{7}$) value for x2s3232 is $4.8 \pm 0.3\,\hbox {kPa}$. Where $V_7 = V_{\mathrm{s},2}$, the p7 range shown in Fig. 21 from the sensitivity analysis is 4.5–5.9 kPa, with a nominal value of 5.2 kPa. These values are consistent within the bounds of their associated uncertainties, and there is a -8.4% difference between the experimentally measured mean ${p}_{7}$ value, and the nominal value from the sensitivity analysis using PITOT and the measured shock speeds.

Now that the bounds on the unsteadily expanded test gas state (state 7) values have been considered, the final step is to assign realistic bounds to the nozzle exit state (state 8). This is not necessarily a simple task, because there are uncertainties about the gas state entering the nozzle (state 7) and about the effective area ratio of the nozzle, and it is only possible to infer the nozzle exit state (state 8) from measurements over pressure probes in the test section (state 10). Figure 22 shows the experimental ${15}^{\circ }$ half-angle cone pressure data for the experiment from the X2 pitot rake. To provide a starting point for the analysis, the state 7 values have been steadily expanded using the nozzle’s geometric area ratio of 5.64 to find the values shown in Fig. 22. It can be seen in Fig. 22 that the condition appears to have a steady test time of around ${60}\,\upmu \hbox {s}$.

Fig. 22

Measured ${15}^{\circ }$ half-angle cone pressure traces in the test section (${p}_{10\mathrm{c}}$) for the test condition described in Table 8 compared to equilibrium PITOT simulations performed using the nozzle’s geometric area ratio of 5.64 and measured experimental shock speeds from experiment x2s3232

Once again, the same as when Fig. 21 was discussed, for all of the PITOT results shown in Fig. 22 where ${V}_{7} = {V}_{6}$, the ${15}^{\circ }$ half-angle cone pressure (${p}_{10\mathrm{c}}$) is too large for it to have been a correct assumption. Therefore, the following analysis will only focus on the pressure values where ${V}_{7} = {V}_{\mathrm{s},2}$.

The experimental ${15}^{\circ }$ half-angle cone pressure (${p}_{10\mathrm{c}}$) measurements shown in Table 10 were found using the “steady test time” shown in Fig. 22. Looking at Table 10, it can be seen that the pressures for sensors pt1 and pt9 have similar values ($4.8 \pm 0.7\,\hbox {kPa}$ and $4.9 \pm 0.4\,\hbox {kPa}$, respectively) which are lower than the other sensors by at least a kilopascal, indicating that they are probably out of the core flow of the test condition. Considering the geometry of the pitot rake, this gives a core flow of around 120 mm. For this reason, the mean ${p}_{10\mathrm{c}}$ value for experiment x2s3232, $6.2 \pm 0.6\,\hbox {kPa}$, has been calculated without sensors pt1 and pt9. With ${V}_{7} = {V}_{\mathrm{s},2}$, the ${p}_{10\mathrm{c}}$ range found from the mean experimental shock speed values is 5.6–6.9 kPa, with a nominal value of 6.2 kPa, which is the same as the experimentally measured mean value. This difference of 0% between the experimentally measured mean ${p}_{10\mathrm{c}}$ value and the nominal value from the sensitivity analysis using PITOT and the measured shock speeds indicates that the choice to use the geometric area ratio of 5.64 was reasonable.

Table 11 presents the final condition details at nozzle entry and exit (states 7 and 8) and also post-normal shock in the test section at equilibrium (state 10e) for experiment x2s3232 using the nozzle’s geometric area ratio of 5.64. Both a nominal solution found using only the mean experimentally measured shock speeds and a solution bound for every variable found using the uncertainties on those mean values are presented. While the solution bounds show the potential variation which may exist for the flow condition, the analysis showed that the nozzle entry pressure (${p}_{7}$) from the sensitivity analysis was consistent with the experimentally measured values (with an 8.3% difference between the nominal theoretical value and the mean experimental one) and the nominal ${15}^{\circ }$ half-angle cone pressure (${p}_{10\mathrm{c}}$) was the same as the mean experimental value, showing that potentially it is reasonable to describe experiment x2s3232 in a less conservative manner using just the nominal solution.

Table 11 Final result of the condition analysis of the free piston driven air test condition from Table 8

4.4.3 Concluding remarks about the examples

Overall, it has been shown that it is possible for both cold and free piston driven conditions to use an appropriately experimentally calibrated version of PITOT to recreate results obtained from experiments. It has also been shown that the experimentally measured shock speeds can be used to provide realistic solution bounds for the experimental data.

The main discrepancy was seen in the modelling of the driver, with driver rupture conditions (${p}_{4}$ and ${T}_{4}$) inferred from experimental shock speeds through a helium test gas [64] under-predicting the shock tube shock speed (${V}_{\mathrm{s},1}$) by 5% for the first example, and over-predicting it by 5% for the other. Especially for the free piston driven example, there may be several reasons for this. Firstly, a free piston driver is complicated, and the variations may be real. The diaphragm scoring is performed by many different personnel and could have been performed slightly differently for each experiment; the wear rings on the piston may have had a different amount of wear for each experiment; the driver temperature could have been different for each experiment; or the back pressure of the high-pressure bottle bank which is used to fill the reservoir could have been different, causing the temperature of the expanded reservoir gas to be different for each experiment. All of these small changes can affect the performance of the driver. Secondly, all of X2’s shock tube wall pressure sensors are located in the last quarter of the tube’s length (see Fig. 1) because the physical geometry of the facility leaves only a small straight section at the end where sensors can easily be placed. This is not ideal for monitoring driver performance and complicates using measured shock speeds to try to understand the driver, because the shock may have slightly attenuated or even been sped up by compression waves sent down the tube from the driver before it reaches the sensors. While the inferred driver conditions used for the free piston driven condition were an average of ten different experiments performed at three different shock tube fill pressures, 50, 150, and 500 kPa [64], their ability to be universally applicable could still have been affected by the measurement locations. Colleagues of the authors have had success using initial experimental data to create more targeted effective driver rupture values that could then be used to accurately predict the shock speeds of new but similar conditions performed at a similar time, but existing data is not always available.

Before continuing, it is worth considering what effect that the inferred solution bounds would have on a real X2 experiment. As a simple way to simulate the relatively blunt models usually used on X2, conditions behind an equilibrium normal shock in the test section (state 10e) were added to the sensitivity analysis result shown in Table 11. Generally, for expansion tube flow conditions, whether they are being used for scaled experiments or not, the stagnation enthalpy (${H}_\mathrm{t}$) and the post-shock density are the most important flow variables. The first because it is a measure of the energy in the free-stream gas which will be mainly converted to thermal energy behind the shock wave, and the second because it controls the chemical length scales behind the shock, which are important for scaling and more generally, for generating conditions focussed on studying either equilibrium or non-equilibrium behaviour. Looking at Table 11 and considering the nozzle exit (state 8) ${H}_\mathrm{t}$ value, the uncertainty on the nominal value caused by the solution bounds is ±1.3%. The flight equivalent velocity ($U_\mathrm{e}$), which is a function of ${H}_\mathrm{t}$, shows an even smaller uncertainty of ±0.7%. If the post-shock (state 10e) values are now considered, it can be seen that the post-shock temperature (${T}_{10\mathrm{e}}$), which is also a function of ${H}_\mathrm{t}$, shows an uncertainty of ±0.6%. This is a positive result for the accurate simulation of stagnation enthalpy, as its uncertainty was found to be of the same order as the shock speed uncertainties (around 1%, see Table 9). However, it also shows that even with shock speed uncertainties around 1%, the post-shock density is still very sensitive to that and has an uncertainty of around ±10%. In a more general sense, this is something which would be expected for most test conditions, as it was discussed in Sects. 3.5 and 3.6 that the pressure and density were the most sensitive variables to changes in how the gas expanded through the acceleration tube and nozzle. This is still a small uncertainty for an impulse facility, but it shows that blunt-body experiments which cannot tolerate post-shock density uncertainties of around ±10% may not be suitable for expansion tube simulation, even with very small shock speed uncertainties.

5 Conclusions

This paper has presented a framework for the rapid simulation of an expansion tube facility by identifying central flow processes involved in facility operation, and simulating them from state to state through the facility by using isentropic and compressible flow relations, and equilibrium and frozen chemistry. Potential issues with modelling the light secondary and tertiary diaphragms, acceleration tube, and nozzle of an expansion tube facility were discussed, along with the solutions available in the model to deal with these issues. The theoretical effect of these solutions on the overall flow condition was also presented for an example expansion tube flow condition.

A method for using this framework to quantify experimental data using several different techniques was then presented. A technique for using the model with experimentally measured shock speeds in the shock tube to remove potential issues with driver modelling uncertainty was presented. A technique for using experimentally measured wall pressures and shock speeds in the acceleration tube to quantify the degree of over-expansion in the acceleration tube was also presented, as well as a technique to use experimentally measured pressures in the acceleration tube and test section to quantify the effective area ratio of a facility’s nozzle.

Finally, two different experimental examples using data from the X2 expansion tube were presented to validate the model for quantifying experimental expansion tube flow conditions. One example was a cold driver condition and the other was a free piston driven test condition regularly used in the laboratory. Both examples were able to be quantified using the model presented in this paper, by configuring the theoretical model to correctly recreate experimentally measured pressures and shock speeds. An inferred nominal solution for the test section state (state 8) of each example was presented, as well as a solution bound for each inferred quantity to take into account the uncertainty in the measured shock speed values used with the model. The authors believe that this is the current best practice to calculate an inferred expansion tube test section condition without using CFD simulation, as it provides an insight into the potential variation of the different test flow quantities.

Further work aims to improve the model where required by adding more complex models for different phenomena. This includes implementing an inertial diaphragm model [65, 68] to better model the thin secondary and tertiary diaphragm rupture, and directly implementing Mirels methodology for modelling the expected attenuation of the shock wave and over-expansion of the unsteadily expanding gas in a low-density shock tube [36,37,38] to allow better prediction of acceleration tube behaviour. A larger goal is a more comprehensive validation of this model against both experimental and two-dimensional facility CFD simulation data, so that the model can be compared to the full suite of data collected from these CFD simulations, instead of just the few experimental measurements which can be taken.

Another direction for further work is to implement an improved driver model into the code, because for both examples presented in Sect. 4.4 there was a 5% difference between the measured experimental shock tube shock speeds and the theoretical values predicted by the driver models used to simulate the experiments. This is not a large difference, and the driver model can be removed when simulating experimental data if necessary, but it limits the utility of fully theoretical simulations. This work could be taken in several different directions. The first direction would be to add estimated heat losses during the piston compression process and total pressure losses at the area change to the current fully theoretical driver model to make it more realistic. The second would be to perform a more comprehensive study of using shock speeds in the shock tube to infer effective driver rupture conditions than the one performed by Gildfind et al. [64]. Potentially taking data over a large range of shock tube fill pressures and test gases and providing a small database rather than a single value would provide results which are applicable to more situations. This could possibly also be done without performing any new experiments by mining old analysed experiments for this information. A more physical part of this proposed work would be to increase quality control for everything related to the driver, such as the diaphragm scoring depth, the accuracy of the driver and reservoir fill pressures, and estimating driver and reservoir gas temperatures at the time of firing to try to ensure that they remain inside specified limits.

Appendices

Appendix 1: Setting up and running PITOT

PITOT forms part of the CFCFD code collection at UQ’s Centre for Hypersonics [43], and as such, PITOT relies on installation of the accompanying Compressible Flow Python Library (cfpylib) to run. The latest version of the CFCFD code collection, instructions on how to obtain it, and the dependencies required to use it, can be found at the website found in the accompanying CFCFD reference [43] principally on the page titled “Getting the codes and preparing to run them”. A page with separate specific instructions for PITOT also exists [80]. The authors have written an accompanying Makefile which can be used to install PITOT on a compatible Linux system with the correct dependencies installed. The authors use Ubuntu and are aware that PITOT has been used on other Linux distributions as well. It is surely possible to manually install PITOT on a Macintosh or Windows system, but the authors cannot confirm this. The main obstacle would be getting PITOT to find and use CEA [41, 42] on the other operating systems.

PITOT is written in the Python programming language, and after it is installed, the most common way to run the program is to write a configuration file which conforms to Python syntax and then parse it to the overarching program by entering the line below into the terminal:

$$\begin{aligned} \$ \,\,\texttt {pitot.py} --\texttt {config}\_\texttt {file=filename.cfg} \end{aligned}$$

Example annotated configuration files for various scenarios can be found in the examples folder of the CFCFD code collection covering both simple simulations and more complex ones using custom facilities, custom test gases, and other “advanced” features. PITOT has been built to be modular and easy to script, and the configuration info can also be parsed to the program inside a Python script using a Python dictionary. Several different tools which make use of this have been created by the authors to perform tasks such as analysing air contamination or performing parametric studies of different fill pressures in the facility. These tools are included with the basic PITOT installation. The overall PITOT source code is open source and users can browse the code and make changes themselves if it is required.

Appendix 2: Calculating experimental shock speed uncertainty

This appendix details the current procedure used for the calculation of expansion tube shock speed uncertainty in the Centre for Hypersonics at UQ. It is the procedure used by the shot analysis codes in the laboratory for the calculation of shock speed uncertainty, and it includes uncertainty and error from three different sources:

• 1. Distance uncertainty from the measured sensor locations and the physical size of each sensor.

• 2. Time uncertainty in ascertaining shock arrival on the sensors.

• 3. Sampling rate error from the clocking speed of the data acquisition system.

In a shock tube or expansion tube, a shock travels through the tube at shock speed ${V}_\mathrm{s}$. Over the full length of the tube, depending on the strength of the facility driver and the severity of non-ideal effects such as low-density shock tube (or Mirels) effects [36,37,38], wall friction, or heat losses, there may be attenuation of the shock and it will slow down as a function of distance (${V}_\mathrm{s} (x)$), but as this analysis is interested in the local shock speed between two wall pressure sensors, this will not be considered here, and it will be assumed that ${V}_\mathrm{s}$ remains constant between the two sensors.

Consider a shock moving through the acceleration tube of an expansion tube at shock speed ${V}_\mathrm{s}$. Just in front of the shock are two wall pressure sensors, at1 and at2, mounted at locations ${x}_{1}$ and ${x}_{2}$, measured from a single datum point. This is shown in Fig. 23 and constitutes time ${t}_{0}$.

At a certain time after ${t}_{0}$ called ${t}_{1}$, the shock will pass pressure sensor at1. When this occurs, there will be a step increase in pressure at location ${x}_{1}$, which will be recorded by the sensor and later used to ascertain ${t}_{1}$. Similarly, at a certain time after ${t}_{1}$ called ${t}_{2}$, the shock will pass pressure sensor at2, and the step increase in pressure seen at the location ${x}_{2}$ will be recorded by sensor at2 and later used to ascertain ${t}_{2}$.

Fig. 23

Representation of a moving shock wave about to pass wall pressure sensors at1 and at2 in the X2 expansion tube (not to scale)

Knowing the distance between the two sensors (${x}_{2} - {x}_{1}$), and the time at which the shock passes both locations (${t}_{1}$ and ${t}_{2}$), the nominal shock speed can be found as simply distance ($\Delta x$) divided by time ($\Delta t$):

$$\begin{aligned} V_\mathrm{s} = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{\Delta x}{\Delta t}. \end{aligned}$$

(3)

It can be seen that (3) is a function of two distances (${x}_{1}$ and ${x}_{2}$), and two times (${t}_{1}$ and ${t}_{2}$). Therefore, to quantify the uncertainty, the uncertainties on both the distance and the time must be considered.

Three different types of distance uncertainty are considered:

• 1. Uncertainty in the measurement of the sensor locations (${x}_{1}$ and ${x}_{2}$).

• 2. Uncertainty in the response of the pressure sensor due to the physical size of the sensor. (The pressure sensors used on X2 in the acceleration tube are 112A22 50 PSI pressure transducers from PCB Piezotronics with a sensor diameter of 5.54 mm [81].)

• 3. Uncertainty due to the shape of the shock not being planar like it is assumed.

These three uncertainties are encapsulated by a single distance uncertainty ($\delta {x}_{i}$) of $\pm 2.0\times 10^{-3}$ m (2 mm) for each sensor location.

Therefore, because the distance uncertainties are independent measurements, the total distance uncertainty ($\delta \Delta x$) for the shock speed calculation is:

$$\begin{aligned} \delta \Delta x = \sqrt{\delta x_{1}^{2} + \delta x_{2}^{2}}. \end{aligned}$$

(4)

One source of time uncertainty and one source of error are considered:

• 1. Time uncertainty in ascertaining shock arrival on the sensors.

• 2. Sampling rate error from the clocking speed of the data acquisition system.

Pressure transducers have a finite rise time to full signal (${\le }{2.0}\,\upmu \hbox {s}$ for the 112A22 pressure transducers used in X2’s acceleration tube [81]), and the facility’s data acquisition system is recording at a set clock speed (2.5 MHz for all sensors on X2, with most acceleration tube sensors also teed off into a 60 MHz card to reduce sampling rate error), meaning it can be difficult to ascertain exactly when the shock has passed each location. Two separate uncertainties are used to quantify this.

Firstly to remove any large uncertainties created by an automated process on what can sometimes be a relatively noisy signal, shock arrival times are found manually by a graphical interface which experimenters use to select shock arrival times for each signal. Instead of selecting a single time for shock arrival, experimenters are instructed to select the data point just before and just after when they believe the shock has arrived, giving a time range for shock arrival. The analysis code then finds both of the data points, calculates the midpoint, and adds a shock arrival uncertainty ($\delta {t}_{i}$) to the data which is half of the distance between the original two points.

Secondly, to take into account the sampling rate error, an extra time uncertainty is added based on the size of a single sample ($\delta {t}_\mathrm{sr}$) to take into account the fact that the shock could arrive at any point in the sample. The size of a full sample instead of only half of a sample has been used as a conservative measure to take into account the fact that multiple samples are actually involved in the calculation process. Recently, acceleration tube pressure data (where shock speeds are often of the order of 10 km/s) have also been recorded on a high-speed National Instruments PXI-5105 card clocking at 60 MHz to reduce the sampling rate error on the acceleration tube shock speeds after it was found that the largest source of experimental uncertainty on these measurements was caused by the normal data acquisition system clocking at 2.5 MHz.

Therefore, because the time uncertainties are independent measurements, the total time uncertainty ($\delta \Delta t$) for the shock speed calculation is:

$$\begin{aligned} \delta \Delta t = \sqrt{\delta t_{1}^{2} + \delta t_{2}^{2} + \delta t_\mathrm{sr}^{2}}. \end{aligned}$$

(5)

Now that total distance and time uncertainties ($\delta \Delta x$ and $\delta \Delta t$) are known, the total shock speed uncertainty ($\delta {V}_\mathrm{s}$) can be found using the uncertainty formula for the division of independent variables, which is shown below in the form appropriate for calculating the shock speed uncertainty:

$$\begin{aligned} \delta V_\mathrm{s} = V_\mathrm{s} \cdot \sqrt{ \left( \frac{\delta \Delta x}{\Delta x} \right) ^{2} + \left( \frac{\delta \Delta t}{\Delta t} \right) ^{2}}. \end{aligned}$$

(6)