A conventional value for the geoid reference potential $W_{0}$

Abstract

$W_{0}$ is defined as the potential value of a particular level surface of the Earth’s gravity field called the geoid. Since the most accepted definition of the geoid is understood to be the equipotential surface that coincides with the worldwide mean ocean surface, a usual approximation of $W_{0}$ is the averaged potential value $W_{\mathrm{S}}$ at the mean sea surface. In this way, the value of $W_{0}$ depends not only on the Earth’s gravity field modelling, but also on the conventions defining the mean sea surface. $W_{0}$ computations performed since 2005 demonstrate that current published estimations differ by up to $-2.6~\hbox {m}^{2}~\hbox {s}^{-2}$ (corresponding to a level difference of about 27 cm), which could be caused by the differences in the treatment of the input data. The main objective of this study is to perform a new $W_{0}$ estimation relying on the newest gravity field and sea surface models and applying standardised data and procedures. This also includes a detailed description of the processing procedure to ensure the reproducibility of the results. The following aspects are analysed in this paper: (1) sensitivity of the $W_{0}$ estimation to the Earth’s gravity field model (especially omission and commission errors and time-dependent Earth’s gravity field changes); (2) sensitivity of the $W_{0}$ estimation to the mean sea surface model (e.g., geographical coverage, time-dependent sea surface variations, accuracy of the mean sea surface heights); (3) dependence of the $W_{0}$ empirical estimation on the tide system; and (4) weighted computation of the $W_{0}$ value based on the input data quality. Main conclusions indicate that the satellite-only component $(n = 200)$ of a static (quasi-stationary) global gravity model is sufficient for the computation of $W_{0}$. This model should, however, be based on a combination of, at least, satellite laser ranging (SLR), GRACE and GOCE data. The mean sea surface modelling should be based on mean sea surface heights referring to a certain epoch and derived from a standardised multi-mission cross-calibration of several satellite altimeters. We suggest that the uncertainties caused by geographically correlated errors, including shallow waters in coastal areas and sea water ice content at polar regions should be considered in the computation of $W_{0}$ by means of a weighed adjustment using the inverse of the input data variances as a weighting factor. This weighting factor should also include the improvement provided by SLR, GRACE and GOCE to the gravity field modelling. As a reference parameter, $W_{0}$ should be time-independent (i.e., quasi-stationary) and it should remain fixed for a long-term period (e.g., 20 years). However, it should have a clear relationship with the mean sea surface level (as this is the convention for the realisation of the geoid). According to this, a suitable recommendation is to adopt a potential value obtained for a certain epoch as the reference value $W_{0}$ and to monitor the changes of the mean potential value at the sea surface $W_{\mathrm{S}}$. When large differences appear between $W_{0}$ and $W_{\mathrm{S}}$ (e.g., ${>}\pm 2$ m$^{2}$ s$^{-2})$, the adopted $W_{0}$ may be replaced by an updated (best estimate) value. In this paper, the potential value obtained for the epoch 2010.0 (62,636,853.4 m$^{2}$ s$^{-2})$ is recommended as the present best estimate for the $W_{0}$ value. It differs $-2.6~\hbox {m}^{2}~\hbox {s}^{-2}$ from the so-called IERS $W_{0}$ value (62,636,856.0 m$^{2}$ s$^{-2})$, which corresponds to the best estimate available in 1998.

1 Introduction

Per definition, $W_{0}$ is understood as the value of the gravity potential of the real Earth on a particular equipotential surface called the geoid. Since the Earth’s gravity potential field contains an infinite number of equipotential surfaces, the geoid is to be defined arbitrarily by convention. The usual convention follows the definition given by Gauss (1876) and Listing (1873): the geoid is the equipotential surface that best fits (in a least square sense) the undisturbed mean sea level. As this condition cannot be satisfied exactly due to different causes (like existence of the continents, oceanic currents, atmospheric pressure effects, external gravity forces, etc.) an additional convention about the mean sea level is required. This convention should consider not only the reductions applied to remove disturbing effects, but also the time span and the location where the sea surface level should satisfy the Gauss–Listing definition. It can be realised over different time spans at a local tide gauge, or as average from several tide gauges, or over the ocean areas sampled globally (e.g., Mather 1978; Heck and Rummel 1990; Ekman 1995; Heck 2004).

The concepts of the geoid and $W_{0}$ are intrinsically tied: from one side, the potential value $W_{0}$ defines which of the infinite equipotential surfaces of the Earth’s gravity field is appointed as the geoid. From the other side, the geoid is the realisation (geometric description) of the level surface with the potential value $W_{0}$. To get consistency between the definition ($W_{0})$ and the realisation (geoid model), it is expected that the $W_{0}$ value is estimated from the same observations applied for the geoid modelling.

As a reference level for the determination of vertical coordinates, $W_{0}$ defines the scale (size) of the reference (zero-height) surface with respect to the Earth’s body; i.e., it defines the vertical datum of a height system. As a parameter of the gravity field, $W_{0}$ is required for the transformation between the time scales Geocentric Coordinate Time and the Terrestrial Time; and it can be introduced as a primary parameter for the definition of a reference mean Earth ellipsoid; i.e., a level ellipsoid that best fits the geoid. In the first case, local realisations of $W_{0}$ (i.e., $W_0^{(i)})$ are sufficient for the determination of vertical coordinates referring to a local height system i. In the other two cases and in the case of a worldwide unified vertical reference system, a global estimation of $W_{0}$ is required. This global estimation is possible thanks to the satellite altimetry and the Earth’s gravity field modelling based on space techniques, in particular low Earth orbiting satellites like GRACE,¹ GOCE,² and the satellites for laser ranging observations like LAGEOS, ETALON, etc. However, the estimation of $W_{0}$ should be founded on clear outlined conventions that guarantee its uniqueness, reliability, and reproducibility; otherwise, there would be as many $W_{0}$ reference values as computations.

In this context, the International Association of Geodesy (IAG) decided to instal the working group Vertical Datum Standardisation to provide the basis for a formal IAG convention on $W_{0}$. This working group was established for a period of 4 years (2011–2015) as a common initiative of the Focus Area 1 (Unified Height System) of the Global Geodetic Observing System (GGOS), IAG Commissions 1 (Reference Frames) and 2 (Gravity Field), and the International Gravity Field Service (IGFS). According to the IAG nomenclature (Drewes et al. 2012), it is called Joint Working Group JWG 0.1.1. The first activities faced by JWG 0.1.1 concentrated on (1) making an inventory about the published $W_{0}$ computations to identify methodologies, conventions, standards, and models presently applied (cf. Sánchez 2012) and (2) bringing together the different groups working on the determination of a global $W_{0}$ in order to perform a unified computation (cf. Sánchez et al. 2014). This paper presents the concluding results of the JWG 0.1.1 activities. It provides especially a detailed description of the computation methods, the applied models, and the uncertainty of the estimations according to the accuracy of the input data.

At first, the computation of the $W_{0}$ value included in the IERS³ Conventions is described. Afterwards, the methodology and the input data applied in this study are presented. In the following sections, the sensitivity of the $W_{0}$ estimation to the Earth’s gravity field model (including omission and commission errors as well as time-dependent changes), to the mean sea surface model, to the time-dependent sea surface changes, to the mean dynamic topography, to the tide system, and to the accuracy of the input data is analysed. To conclude the paper, the results are discussed and the conventions required for the reproducibility of a global reference $W_{0}$ value are outlined.

Table 1 Values of the constant $L_{G}$ according to new best estimates of $W_{0}$

2 The IERS conventions and $W_{0}$

The International Astronomical Union (IAU) introduced in 1991 different time scales for the relativistic definition of the celestial space-time reference frame (IAU 1991). The timescales are (cf. Fukushima 1995): the Geocentric Coordinate Time (TCG), the Barycentric Coordinate Time (TCB), and the Terrestrial Time (TT). The first two scales are defined as coordinate times in coordinate systems having their spatial origins at the centre of mass of the Earth and at the solar system barycentre, respectively (italic text textually copied from IAU 1991, Recommendation III, numeral 3). TT is the time reference for apparent geocentric ephemeris and its main realisation is provided by the International Atomic Time (TAI) (i.e., TT − TAI $=$ 32.184 s at 1997-01-01 0h, cf. IAU 1991 Resolution A4, note 4). TAI is a coordinate time standard defined in a geocentric reference frame with the SI second as realised on the rotating geoid as the scale unit.⁴ TT is defined to differ from TCG by the scale factor (cf. IAU 1991, Recommendation IV and IAU 2000, Resolution B1.9):

$$\begin{aligned} \frac{\mathrm{d} \mathrm{TT}}{\mathrm{d} \mathrm{TCG}}=1-L_G, \end{aligned}$$

(1)

where

$$\begin{aligned} L_G=\frac{W_0}{c^2}, \end{aligned}$$

(2)

c is the speed of light. The computation of the constant $L_{G}$ explains why a $W_{0}$ value was included in the IAU Standards and in the IERS Conventions.

Since the introduction of the new timescales in 1991, $L_{G}$ (cf. Eq. (2)) was recomputed every time when a new best estimate for $W_{0}$ was available (see Table 1). In the IAU General Assembly of 2000, it was decided to declare $L_{G}$ as a defining constant (IAU 2000, Resolution B1.9); i.e., it should not change with new estimations of $W_{0}$. However, a $W_{0}$ value was maintained as an IERS standard (see Petit and Luzum 2010, Table 1.1), although it is no longer needed by the IERS. The $L_{G}$ value applied at present by the IAU and the IERS is based on the $W_{0}$ value recommended by Groten (1999) and further mentioned by Groten (2004). The primary reference for the computation of that $W_{0}$ value is dated in 1998 (Burša et al. 1998); i.e., it corresponds to the best estimate available in 1998. This value (62,636,856.0 ± 0.5 m$^{2}$ s$^{-2})$ is usually called the IERS W $_{0}$ value; in this paper, it is named the 1998 $W_{0}$ value because the IERS did not participate in its determination.

Fig. 1

Approximation applied for the estimation of the 1998 $W_{0}$ value (adapted from Burša et al. 1997, Fig. 4; Burša et al. 1998, Fig. 1)

Figure 1 describes the basic concept applied for the computation of the 1998 $W_{0}$ value (cf. Burša et al. 1997, Fig. 4; Burša et al. 1998, Fig. 1). Satellite altimetry provides the coordinates $\varphi$ (geodetic latitude), $\lambda$ (geodetic longitude) and h (ellipsoidal height) of points M describing the sea surface. If the ellipsoidal heights of these points are reduced by the sea surface topography $\Xi$ (in the following also called mean dynamic topography MDT), it is assumed that these points now describe the geoid ($M_{0})$; i.e., the equipotential surface with the value $W_{0}$. Using these coordinates ($\varphi$, $\lambda$, $h-\Xi$) and a global gravity model (GGM), the potential value at any point $M_{0}$ on the geoid (i.e., $W_{0})$ can be computed. By definition, the potential values at all points $M_{0}$ on the geoid are the same. However, since points on the geoid cannot be materialised in practice, $W_{0}$ is estimated by satisfying the condition (cf. Burša et al. 1998, Eq. [5]):

$$\begin{aligned} \int \limits _{S} {\Xi ^2~\mathrm{d}S}=\min , \end{aligned}$$

(3)

where S stands for the ocean areas. For the estimation of the potential values, Burša et al. (1998) used the gravity model EGM96⁵ (Lemoine et al. 1998) in combination with their own mean sea surface model. The h values were derived from TOPEX/Poseidon measurements covering the period 1993–1996, while the $\Xi$ values were obtained from the model POCM4b⁶ (Stammer et al. 1996). Based on Mather (1978), the condition (3) in later Burša’s computations is replaced by (cf. Burša et al. 2002):

$$\begin{aligned} \int \limits _{S} {( {W-W_0 })^2~\mathrm{d}S}=\min . \end{aligned}$$

(4)

Burša et al. (1997) mention that omitting the values $\Xi$ causes a difference of about $-0.8~\hbox {m}^{2}~\hbox {s}^{-2}$ in the estimated $W_{0}$ value (cf. Burša et al. 1997, Eq. [12] and [15]). Recent computations following the Burša et al. (1998) methodology but applying newer models for the mean sea surface, the mean dynamic topography, and the Earth’s gravity field obtain $W_{0}$ estimates that differ by more than $-2~\hbox {m}^{2}~\hbox {s}^{-2}$ from the 1998 $W_{0}$ value (Čunderlík and Mikula 2009; Čunderlík et al. 2014; Dayoub et al. 2012; Sánchez 2007, 2008; Sánchez et al. 2014). These new computations show that the 1998 $W_{0}$ value corresponds to a reference level (i.e., geoid) located more than 20 cm below the level derived from up-to-date (physical and geometric) Earth models. Accordingly, a further objective of the JWG 0.1.1 is to evaluate if it is suitable to introduce the 1998 $W_{0}$ value as a formal IAG convention or, if it is necessary to adopt a new (updated) estimate of $W_{0}$.

3 Approach for the estimation of $W_{0}$

As $W_{0}$ defines the geoid, its estimation should be based on the same observables used for the geoid modelling. The estimation of absolute potential values (like $W_{0})$ from observational data is only possible after introducing adequate constraints. The main constraint is that the gravitational potential V must vanish at infinity; i.e., $V_{\infty }=0$. Fulfilling this condition is only possible in the frame of the geodetic boundary value problem (GBVP).

The determination of $W_{0}$ using the scalar-free GBVP (e.g., Sacerdote and Sansò 1986; Heck 1989) is possible when the so-called vertical datum parameter $\Delta W_{0}$ is included as unknown together with the vertical position of the boundary surface S and the gravity potential W. $\Delta W_{0}$ represents the difference between the real Earth’s gravity potential $W_{0}$ and the normal potential $U_{0}$ introduced for the linearisation of the observation equations (cf. $\delta W$ in Sacerdote and Sansò 2004, $\Delta {\hat{w}}$ in Heck and Rummel 1990):

$$\begin{aligned} \Delta W_0=W_0-U_0. \end{aligned}$$

(5)

$W_{0}$ is unknown, but it is implicitly included in the observables building the boundary conditions, especially in the geopotential numbers and physical heights used for the estimation of gravity anomalies. Since these observables do not refer to a single vertical datum, there shall be as many $\Delta W_{0}$ parameters as existing i datums $W_0^{(i)}$:

$$\begin{aligned} \Delta W_0^{(i)}=W_0^{(i)}-U_0. \end{aligned}$$

(6)

This can be understood as splitting the boundary surface S into i unconnected regions (Sacerdote and Sansò 2004). If they were connected (for instance by means of spirit or oceanic levelling), $\Delta W_0^{(i)}$ becomes a constant (i.e., $\Delta W_0^{(i)}=\Delta W_0)$ and the new unknown parameter $\delta W_0^{(i)}$ emerges:

$$\begin{aligned} \delta W_0^{(i)}=W_0-W_0^{(i)}, \end{aligned}$$

(7)

$\delta W_0^{(i)}$ represents the level difference between the local vertical datums $W_0^{(i)}$ and that one selected as the reference level $W_{0}$ (cf. $C_{Q_{i0}}$ in Rummel and Teunissen 1988). Since this approach allows the determination of level differences between the regions i, it is widely applied for the vertical datum unification (see e.g., Gruber et al. 2012; Gerlach and Rummel 2013; Rülke et al. 2014; Sideris et al. 2014).

In the frame of the fixed GBVP, the only unknown is the potential W, because the geometry of the boundary surface S is considered to be known (e.g., Sacerdote and Sansò 2004; Heck 2011). At present, the precise representation of the Earth’s surface by means of GNSS (Global Navigation Satellite Systems) and SAR (Synthetic Aperture Radar) techniques in continental areas, as well as by means of satellite altimetry in ocean areas allows a reliable solution of the fixed GBVP introducing the Earth surface as the boundary surface S. The main limitation is, however, the reduced availability of global distributed gravity disturbances. The existing gravity databases contain gravity anomaly values mainly, which could be easily transformed into gravity disturbances if the ellipsoidal height of the gravimetric points were known. As this is not the case, this transformation depends on the (in general unknown) level differences between the vertical datums underlying the physical heights used for the computation of the gravity anomalies (Grombein et al. 2015).

To reduce the multiple vertical datum dependence in the determination of $W_{0}$, we can make two basic assumptions: (1) all the ocean areas conform to one vertical datum region $(i=1)$ and (2) the estimated potential in this region can be conventionally declared as the global $W_{0}$ value. Afterwards, the local potential reference values $W_0^{(i)}$ of the other regions $(i=2,\ldots ,n)$ can be estimated by means of the scalar-free or fixed GBVP, according to the observables available. This convention has three main advantages: (1) the sea surface scanned by satellite altimetry does not depend on any local vertical datum; (2) the availability of gravity functionals can be easily increased by interpolation methods with less accuracy loss than in continental areas (where the rough topography must be taken into account); and (3) it conforms to the Gauss–Listing definition.

In the first computation tests implemented by the JWG 0.1.1, gravity anomalies derived from satellite altimetry and shipborne gravimetry (provided by BGI⁷) were considered as boundary conditions to solve the fixed GBVP in ocean areas. However, due to lack of information about the metadata underlying some shipborne gravity data (like the gravity reference system, accuracy of the gravity anomalies, reference frame of the gravity anomaly positions, etc.), it was decided not to include these data in the computations. Thus, instead of solving the fixed GBVP using proper boundary conditions, we applied global gravity models (GGMs) to determine the potential value at the sea surface. This does not pose any problem, since the GGMs provide analytical solutions in spherical harmonics of the Laplace equation outside the Earth and it can be assumed that potential values based on these GGMs satisfy the regularity at infinity.

According to Sacerdote and Sansò (2001), the difference between the potential at the mean sea surface $W_{\mathrm{S}}$ and the potential of the geoid $W_{0}$ divided by the mean normal gravity $\bar{\gamma }$ can be understood as an approximation of the sea surface topography $\Xi$ (cf. Sacerdote and Sansò 2001, Eq. [3]):

$$\begin{aligned} \Xi \cong \frac{W_{\mathrm{S}} -W_0 }{\bar{\gamma }_{\mathrm{S}}}, \end{aligned}$$

(8)

and $W_{0}$ can be chosen such that the square integral of the sea surface topography over oceans is minimised (italic text and Eq. (9) taken from Sacerdote and Sansò 2001, p. 53, Eq. [4]):

$$\begin{aligned} \frac{\partial }{\partial W_0 }\int \limits _{S} {\Xi ^2\,\mathrm{d}\sigma } =-2\int \limits _{S} {\frac{1}{\bar{\gamma }_{\mathrm{S}}^2 }( {W_{\mathrm{S}} -W_0 })~\mathrm{d}\sigma } =0. \end{aligned}$$

(9)

$W_{0}$ is then given by (cf. Sacerdote and Sansò 2001, Eq. [5]):

$$\begin{aligned} W_0=\frac{\int _{S}{\frac{W_{\mathrm{S}}}{\bar{\gamma }_{\mathrm{S}}^2}~\mathrm{d}\sigma }}{\int _{S}{\frac{1}{\bar{\gamma }_{\mathrm{S}}^2}~\mathrm{d}\sigma }}. \end{aligned}$$

(10)

If the sea surface S would coincide with an equipotential surface, it would be sufficient to determine the potential W at any point at S to know the potential value $W_{\mathrm{S}}$. Since this is not the case, Eq. (10) has to be evaluated in a discrete form based on those points k describing a quasi-stationary representation of the sea surface.

The potential value at each point k can be estimated by (cf. Hofmann-Wellenhof and Moritz 2005, Eq. [2-234]):

$$\begin{aligned} W_k =U_0-h_k \bar{\gamma }_k +T_k , \end{aligned}$$

(11)

where $h_{k}$ is the ellipsoidal height, ${\bar{\gamma }}_k$ is the mean normal gravity value (cf. Hofmann-Wellenhof and Moritz 2005, Eq. [4-60]), $U_{0}$ is the ellipsoid’s normal potential, and $T_{k}$ is the anomalous potential obtained from a GGM. $T_{k}$ includes the zero degree-term due to the difference between the values of GM utilised in the GGM and in the reference level ellipsoid. Replacing the integral in Eq. (10) by an area-weighted summation over discrete points k and introducing the potential value W given by Eq. (11), $W_{0}$ corresponds to:

$$\begin{aligned} W_0 =U_0 +\frac{\sum _1^k {\left[ {\frac{T_k -h_k \bar{\gamma }_k }{\bar{\gamma }_k^2 }} \right] } \,\delta S_k }{\sum _1^k {\left[ {\frac{1}{\bar{\gamma }_k^2 }} \right] \delta S_k } }, \end{aligned}$$

(12)

with $\delta S_k =\cos \varphi \;{}\delta \varphi {}\;\delta \lambda$.

One possibility to get S closer to an equipotential surface (i.e., the geoid) is to subtract the mean dynamic topography $\Xi$ from the sea surface heights h (as Burša et al. 1998; Dayoub et al. 2012 or Sánchez et al. 2014 already proposed). In this case, $\Xi$ is to be represented as a quasi-stationary parameter exactly as the sea surface heights h are also represented. This means, all time dependent effects acting on the instantaneous sea surface should be removed. Some examples of such effects are the ocean and solid Earth tides, centrifugal deformation due to variations of the Earth’s rotation velocity and pole motion, solid tide loading, atmospheric and oceanic loading (i.e., inverse barometer and barotropic effects), and changes in ocean currents caused by winds, temperature variability, salinity, etc. More details in e.g., Wunsch and Stammer (1997), Chelton et al. (2001), Fu and Le Traon (2006), Ablain et al. (2009). If $\Xi$ is taken into account, the condition (9) is no longer required and Eq. (11) becomes:

$$\begin{aligned} W_{k0}=U_0-({h_k-\Xi _k}){\bar{\gamma }}_{k0}+T_{k0}. \end{aligned}$$

(13)

In this case, the potential value $W_{0}$ best fitting the individual values $W_{S_0 }$ given on the surface $S_{0}$ (i.e., $[h_{\mathrm{S}} -\Xi _{\mathrm{S}}])$ corresponds to

$$\begin{aligned} W_0= & {} \frac{1}{S_0}\int \limits _{S_0}{W_{S_0}~\mathrm{d}S_0}\nonumber \\= & {} U_0+\frac{1}{S_0}\int \limits _{S_0}{\left[ {T_{S_0}- ({h_{\mathrm{S}}-\Xi _{\mathrm{S}}}){\bar{\gamma }}_{S_0}}\right] }\,\mathrm{d}S_0, \end{aligned}$$

(14)

or, in discrete representation to:

$$\begin{aligned} W_0=U_0+\frac{\sum _1^k {\left[ {T_{k0} -({h_k -\Xi _k })\;{\bar{\gamma }}_{k0}}\right] }\,\delta S_{k0}}{\sum _1^k {\delta S_{k0}}}. \end{aligned}$$

(15)

4 Input data for the empirical estimation of $W_{0}$

An empirical estimation of $W_{0}$ is possible by solving Eq. (12) or Eq. (15). To assess the sensitivity of this estimation to the different input data, our first computations are based on Eq. (12). Afterwards, we undertake a refined computation using Eq. (15). The input data are:

• (a) Ellipsoidal heights of the sea surface $h_{k}$ provided by a mean sea surface model (MSS). As already mentioned, it is expected that time dependent effects acting on the sea surface scanned by satellite altimetry are removed before any MSS model is computed. Additionally, since the MSS models contain sea surface heights averaged over a certain time period, it is assumed that those heights are quasi-stationary (at least for the period considered for averaging).

• (b) Mean dynamic topography (MDT) models providing the values $\Xi _{k}$. It would be ideal if the time period applied to compute the MSS and the MDT models is the same.

• (c) The normal gravity field ($U_{0}$, ${\bar{\gamma }}_k)$ corresponds to the reference ellipsoid GRS80 (Moritz 2000).

• (d) The anomalous potential $T_{k}$ is derived from a quasi-stationary (static) global gravity model (GGM). The surface S is represented in the first computations (Eq. (12)) by the sea surface heights $h_{k}$, and afterwards, in the refined computation (Eq. (15)), by [$h_{k}-\Xi _{k}$].

Our computations are based on the zero-tide system following the IAG recommendation No. 16 adopted at the XVIII General Assembly of the International Union of Geodesy and Geophysics (IUGG) held in Hamburg in 1983 (Tscherning 1984). It should be noted that the zero-tide system and the mean-tide system are identical for the ellipsoidal heights of the sea surface; i.e., the MSS models.

5 Sensitivity of the $W_{0}$ estimation to the model of the Earth’s gravity field

At present, there is a huge variety of global gravity models available. Besides the processing strategy applied to estimate the harmonic coefficients, we can classify them according to the input data taken into account for their computation. There are GGMs previous to the gravity missions CHAMP,⁸ GRACE and GOCE, model EGM96 (Lemoine et al. 1998) being the most well-known of them. Then, there are GGMs including

• (a) CHAMP data only; e.g., EIGEN⁹-1S, EIGEN-2 (Reigber et al. 2002, 2003) and ITG¹⁰-CHAMP (Ilk et al. 2003); or

• (b) GRACE data only; e.g., UTEX-CSR¹¹ (Tapley et al. 2003, 2007, 2013a) and ITG-GRACE (Mayer-Gürr et al. 2006, Mayer-Gürr et al. 2007, 2010); or

• (c) GOCE data only; e.g., the series GO_CONS_GCF (R1, R2) (Migliaccio et al. 2011; Pail et al. 2010; Bruinsma et al. 2010); or

• (d) a combination of GRACE, GOCE and SLR observations; e.g., the series EIGEN-6S (Förste et al. 2011, 2012) and the extended version of the models GO_CONS_GCF (R3, R4, R5) (Bruinsma et al. 2013) or,

• (e) a combination of CHAMP, GRACE, GOCE and SLR data; e.g., the models GOCO (Pail et al. 2010; Goiginger et al. 2011; Mayer-Gürr et al. 2012), and

• (f) a combination of satellite data with terrestrial gravity data, like the models EGM2008¹² (Pavlis et al. 2012, 2013) and the series EIGEN-6C (Förste et al. 2012).

The IAG Service International Centre for Global Earth Models ¹³ (ICGEM) provides at present more than 150 static GGMs and several series of monthly GGMs derived from GRACE. The evaluation of all these models for the purpose of this study is not possible and therefore, the GGMs used in this work were selected according to the following criteria:

• (a) GGMs expanded to the maximum possible degree n and order m, to assess the dependence of the $W_{0}$ estimation on the spectral resolution of the GGM;

• (b) GGMs based on the latest releases (available in 2014) of GRACE and GOCE data, because they guarantee a larger number of observations and a higher accuracy;

• (c) GGMs including SLR data, because the higher accuracy of the lower degree harmonics (see e.g., Bloßfeld 2015; Haberkorn et al. 2015);

• (d) The model EGM96, because it was used to compute the 1998 $W_{0}$ value (see Burša et al. 1998);

• (e) The model EGM2008, because it is recommended as the conventional GGM in the IERS Conventions 2010 (Petit and Luzum 2010) and because it is the first model including degree harmonics above 360.

Table 2 summarises the main characteristics of the selected GGMs. Those GGMs given in the tide-free system were transformed to the zero-tide system following the convention outlined in the GOCE standards (cf. Gruber et al. 2010, Eq. [80]):

$$\begin{aligned} {\bar{C}}_{20}^{\mathrm{ZT}} -{\bar{C}}_{20}^{\mathrm{TF}}=k_{20} \cdot \left\langle {\Delta {\bar{C}}_{20}}\right\rangle , \end{aligned}$$

(16)

$k_{20}=0.30190$ and $\langle {\Delta {\bar{C}}_{20}}\rangle =-1.391412\cdot 10^{-8}$ are the loading Love number and the averaged value of the tidal correction for Sun and Moon for the coefficient $C_{20}$, respectively.

Table 2 Global gravity models used for the empirical estimation of $W_{0}$

To assess the sensitivity of the $W_{0}$ estimation to the Earth’s gravity field model, these computations are initially implemented using only one MSS model, in this case MSS_CNES_CLS11 (Schaeffer et al. 2012).

5.1 Dependence of $W_{0}$ on the omission error of the GGM

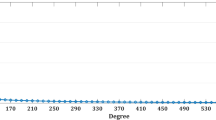
The first aspect to be considered in this analysis is the so-called omission error. The anomalous potential T is computed while varying the maximum degree of the spherical harmonics expansion $(n_{\max }= 10, 20,\ldots , 2190).$ The resulting $W_0^{({n=n_{\max }})}$ values are compared with that value gained using all available harmonics, i.e., $W_0^{( {n=2190})}$. This test is performed with the EGM2008 (Pavlis et al. 2012, 2013). All the input data are assumed free of error in such a way that the differences $[{W_0^{({n=2190})}-W_0^{({n=n_{\max }})}}]$ only reflect the changes caused by truncating the GGM series expansion at $n_{\mathrm{max}}$.

The values $[{W_0^{( {n=2190})}-W_0^{({n=n_{\max }})}}]$ are in general negative (Fig. 2). This means the fewer harmonic coefficients included in the computation of T the larger is $W_{0}$; i.e., the geocentric radius of the corresponding equipotential surface is smaller. The omission error from $n_{\max } =10$ to $n_{\max }=100$ varies between $-4.778$ and $-0.100~\hbox {m}^{2}~\hbox {s}^{-2}$. This represents an outwards displacement (away from the geocentre) of the corresponding equipotential surface of approximately +490 and +11 mm, respectively. From $n_{\max }=150,$ the omission error decreases significantly $(-0.013~\hbox {m}^{2}~\hbox {s}^{-2}\rightarrow \sim +1.4~\hbox {mm})$ and from $n_{\max }=360,$ it is practically negligible $(-0.0004~\hbox {m}^{2}~\hbox {s}^{-2}\rightarrow \sim +0.04~\hbox {mm}).$ The immediate conclusion is that the $W_{0}$ value can be estimated using the satellite-only component $(n_{\max }\approx 200)$ of the GGM. This conclusion is in agreement with results presented previously in similar studies such as Sánchez (2007), Burša et al. (2007), Dayoub et al. (2012), and Sánchez et al. (2014). These authors recommend to include harmonics up to degree $n=120$ in the computation of $W_{0}$. However, it should be mentioned that the results obtained by Burša et al. (2007) present two maxima in the omission error: one of more than $2~\hbox {m}^{2}~\hbox {s}^{-2}$ at $n,m=30,$ and the other one of about $0.8~\hbox {m}^{2}~\hbox {s}^{-2}$ at $n,m=60$ (cf. Burša et al. 2007, Fig. 3). These maxima could not be identified or confirmed in this study and therefore, it is not possible to explain them. On the contrary, the omission error effects shown in Fig. 2 agree quite well with those published by Sánchez (2007), Dayoub et al. (2012), and Sánchez et al. (2014).

Fig. 2

Effects of the omission error in the estimation of W $_{0}$ after truncating the series expansion of the model EGM2008 at degree $n = n_{\max }$ (MSS: MSS_CNES_CLS11)

5.2 Dependence of $W_{0}$ on the selected GGM

A further aspect to be considered is a comparison of the $W_{0}$ values obtained after applying the different GGMs listed in Table 2. To facilitate this comparison, all models are truncated at $n=180$ (maximum degree of the model GGM05S). These results allow concluding that all the models, except EGM96, produce practically the same $W_{0}$ value (Fig. 3). GGMs including long time series of SLR data (e.g., EIGEN-6C3stat, EIGEN-6C2, and GO_CONS_GCF_2_DIR_R4) produce a slightly larger $W_{0}$ value (0.006 m$^{2}$ s$^{-2}\rightarrow \sim -1~\hbox {mm})$ in comparison with those models that do not include SLR data. Nevertheless, these discrepancies are much smaller than the formal error of the computations (Table 3). In contrast, the $W_{0}$ value obtained from the model EGM96 presents a larger difference $(0.06~\hbox {m}^{2}~\hbox {s}^{-2}\rightarrow \sim -7~\hbox {mm}).$

Table 3 presents the dispersion and standard deviation of the $W_{0}$ values obtained using the aforementioned GGMs. These two statistical indicators are quite large for the model GGM05S; this confirms the necessity of regularising the coefficients of this model (from $n=150$) as Tapley et al. (2013b) suggest. Figure 4 shows as example the geographical distribution of the residuals $[{W_k-W_0^{({n=180})}}]$ gained from the models EIGEN-6C3stat, EGM2008, EGM96, and GGM05S. The largest residuals are obtained at high latitudes (outside $\varphi =60^{\circ }$ N/S) using the EGM96 model and along the striations caused by the non-regularised gravity solution from GRACE in the model GGM05S. To reduce this effect, it would be necessary to smooth the model to a 100-km resolution. However, this would increase the omission error effects in the estimation of $W_{0}$ (see Sect. 5.1).

The main conclusion of this analysis is that the estimation of $W_{0}$ should be based on the satellite-only component $(n \le 200)$ of a GGM relying at least on the combination of GRACE, GOCE, and SLR data.

Fig. 3

$W_{0}$ values derived from the GGMs listed in Table 2 (the value 62,636,853.00 should be added)

Table 3 Dispersion of the $W_{k}$ values and standard deviation of the $W_{0}$ value obtained after applying the GGMs listed in Table 2

Fig. 4

Geographical distribution of the residuals $[{W_k-W_0^{({n=180})}}]$

5.3 Influence of the time-dependent Earth’s gravity field changes in $W_{0}$

The computations described so far are based on quasi-stationary GGMs. In this section, we want to analyse the effect of secular and seasonal variations of the gravity field in the estimation of $W_{0}$. This evaluation is performed by applying the same procedure described in the two previous sections, but using (1) the monthly GRACE-based GGM series published as GFZ Release 05 (Dahle et al. 2012) and (2) the time-dependent coefficients $( {{\bar{C}}_{nm} ( t),\;\bar{S}_{nm} ( t)})$ up to n, m = 50 of the model EIGEN-6C2 (Förste et al. 2012). As before, the geometry of the surface S is represented by the model MSS_CNES_CLS11 (Schaeffer et al. 2012) and all input data are assumed free of errors. This allows to assess the sensitivity of $W_{0}$ to the time-dependent variations of the GGM.

The time series of the $W_{0}$ values obtained with the time-dependent model EIGEN-6C2 present smaller amplitudes that the series of the $W_{0}$ values computed using the monthly GFZ Release 05 models (Fig. 5). The amplitude of the $W_{0}$ estimations based on the GFZ Release 05 varies from $-0.0108~\hbox {m}^{2}~\hbox {s}^{-2}$ to $+0.0201~\hbox {m}^{2}~\hbox {s}^{-2}$, its linear trend being $-6.617\times 10^{-4}~\hbox {m}^{2}~\hbox {s}^{-2}~\hbox {a}^{-1}$ (i.e., an outwards displacement of the corresponding level surface of about +1.3 mm in 20 years). The linear trend for the $W_{0}$ values based on the EIGEN-6C2 model is $-2.647\times 10^{-4}~\hbox {m}^{2}~\hbox {s}^{-2}~\hbox {a}^{-1}$ (i.e., an outwards displacement of +0.5 mm in 20 years). These magnitudes are much smaller than the formal error in the estimation of $W_{0}$ (see Table 3) and therefore, they can be assumed as insignificant. These results are confirmed by (Dayoub 2010, Section 3.2). The immediate conclusion of this analysis is that the estimation and practical realisation of $W_{0}$ may be based on a static (quasi-stationary) GGM; i.e., the Earth’s gravity field time variations can be neglected without decreasing the reliability of the estimated $W_{0}$ value.

Based on the analysis presented in Sects. 5.1, 5.2, and 5.3, we can conclude that:

• (a) $W_{0}$ can be estimated using the satellite-only component of a GGM $(n = 200);$

• (b) This satellite-only component should be based (at least) on the combination of GRACE, GOCE and SLR data;

• (c) $W_{0}$ can be estimated with a static (quasi-stationary) GGM.

From the GGMs used in this study, these requirements are satisfied by EIGEN-6C2, GO_CONS_GCF_2_ DIR_R4, and EIGEN-6C3stat; as a matter of fact, all of them produce similar $W_{0}$ estimates (Fig. 3); i.e., the discrepancies are much smaller than the computation formal errors (Table 3). It is also expected that new GGMs including these three characteristics (like the models EIGEN-6C4, Shako et al. 2014 or GOCO05S, Mayer-Gürr et al. 2015) reproduce these results within the same uncertainty level presented in Table 3. In the following, we analyse the dependence of the $W_{0}$ estimation on the geometrical representation of the surface S. To better identify this dependence, we keep the GGM unchanged through the different computations using the model EIGEN-6C3stat. The influence of the commission error of the GGM in the estimation on $W_{0}$ is analysed in Sect. 7.

Fig. 5

Changes in the $W_{0}$ estimates after applying the monthly GRACE-based models GFZ Release 05 and the time-dependent harmonics of the model EIGEN-6C2. The linear trend of $W_{0}$ using the GFZ Release 05 is $-6.617\times 10^{-4}$ m$^{2}$ s$^{-2}$ a$^{-1}$ (a displacement of about $+$1.3 mm in 20 years), while the linear trend using EIGEN-6C2 is $-2.647\times 10^{-4}$ m$^{2}$ s$^{-2}$ a$^{-1}$ (a displacement of about $+$0.5 mm in 20 years)

Table 4 Global mean sea surface models used for the empirical estimation of $W_{0}$

6 Sensitivity of the $W_{0}$ estimation to the mean sea surface model

For the empirical estimation of $W_{0}$ using Eq. (12), it is assumed that the geometrical representation of the surface S is given by the sea surface heights $h_{k}$ included in a mean sea surface model (MSS). In this case, the models MSS_CNES_CLS11 (Schaeffer et al. 2012) and DTU10 (Andersen and Knudsen 2009, Andersen 2010) are applied. Their main characteristics are listed in Table 4. As the ellipsoidal coordinates of these models are given with respect to the so-called TOPEX/Poseidon ellipsoid $(a = 6{,}378{,}136.3~\hbox {m}, 1/f=298.257),$ the first step is to convert these coordinates to the GRS80 ellipsoid. Afterwards, mean sea surface heights at a resolution of $0.5^{\circ }\times 0.5^{\circ }$ ¹⁴ are built for each model, to guarantee that the values $W_{k}$ are estimated exactly at the same ($\varphi$, $\lambda$) positions. In addition, since these models have a different latitudinal coverage, the computation of $W_{0}$ is performed by truncating this coverage at different latitudes. This facilitates the comparison of the results gained from each model.

Fig. 6

$W_{0}$ estimates after applying the models MSS_CNES_CLS11 and DTU10 varying their latitudinal coverage from $\varphi =50^{\circ }$ N/S to $\varphi =82^{\circ }$ N/S. The value 62,636,800 m$^{2}$ s$^{-2}$ must be added (GGM: EIGEN-6C3stat)

The $W_{0}$ estimates using the model MSS_CNES_CLS11 are on average $0.3~\hbox {m}^{2}~\hbox {s}^{-2}$ larger than those values obtained from the model DTU10 (Fig. 6), cf. Čunderlík et al. (2014), Sánchez et al. (2014). This level difference (about $-3~\hbox {cm}$) mirrors the mean discrepancy already identified by Schaeffer et al. (2012) between both models (Fig. 7). According to their conclusions, this discrepancy is mainly caused by (1) differences in the modelling of the inter-annual oceanic variability (different reference time periods); (2) different approaches for the data processing at high latitudes; (3) the smoothing of the so-called sea mounts in the MSS_CNES_CLS11 model, and (4) the extrapolation of the satellite altimetry data in coastal and insular areas.

Fig. 7

Level differences between the potential values computed after using the models MSS_CNES_CLS11 and DTU10 in combination with the GGM EIGEN-6C3stat. The potential differences are scaled by the normal gravity value to be represented in units of length; i.e., ${\lfloor {W_k^{( {{\mathrm{CLS11}}})} -W_k^{( {\mathrm{DTU10}})} }\rfloor }/{\gamma _k}$

Fig. 8

Dispersion (above) and standard deviation (below) of the $W_{0}$ estimation based on the models MSS_CNES_CLS11 and DTU10 after varying their latitudinal coverage from $\varphi = 50^{\circ }$N/S to $\varphi =82^{\circ }$N/S (GGM: EIGEN-6C3stat)

Figure 8 shows the dispersion of the values $W_k$ and the standard deviation of the $W_{0}$ estimates as a function of the latitudinal coverage of the MSS models: the lower the latitudinal coverage the better the dispersion and the standard deviation values. Based on similar results, Sánchez (2007) recommends to compute $W_{0}$ excluding those areas outside $\varphi =60^{\circ }$N/S. However, decreasing the latitudinal coverage produces a smaller $W_{0}$ value (cf. Fig. 6); i.e., the corresponding surface level moves outwards. This effect is caused by the sea surface topography: it presents extreme negative values at high latitudes (e.g., ca. $-2$ m in the area of influence of the Antarctic circumpolar current and ca. −1 m around Greenland) and extreme positive values in the tropical regions (e.g., more than +1.5 m in the regions were the currents Kuroshima and Aguhlas are active). In this way, if the latitudinal coverage is reduced, the condition (9) is not satisfied over all ocean areas, but only in the selected area limited by $\varphi = 60^{\circ }$ N/S. It means, the $W_{0}$ value fits the mean sea level at that area and it is no longer global, but only local (cf. Dayoub et al. 2012). The immediate conclusion of this analysis is that the empirical estimation of $W_{0}$ should be based on the total area covered by the mean sea surface model.

Fig. 9

Estimates for the value of $W_{0}$ based on yearly mean sea surface models. The value 62,636,800 m$^{2}$ s$^{-2}$ must be added (GGM: EIGEN-6C3stat). Please note that there are very few satellite altimetry data in 1992 (see Fig. 1 in Bosch et al. 2014)

6.1 Influence of time-dependent sea surface changes in $W_{0}$

According to the reference period used for the computation of the models MSS_CNES_CLS11 and DTU10 (see Table 4), it can be assumed that they refer to the mean epochs 1996 and 2001, respectively. Therefore, their direct comparison (Fig. 7) may be understood as meaningless because the time-dependent variations of the sea surface are not homogeneously handled. Since the mean sea surface modelling depends, among others, on the time span considered for the average of the sea surface heights, in the following we concentrate on analysing the $W_{0}$ estimation after applying a series of yearly mean sea surface models. These yearly MSS models are based on the sea surface heights available at the OpenADB ¹⁵ Version 4 database (Schwatke et al. 2010). These data are utilised as they are computed after the crossover calibration method (Dettmering and Bosch 2010; Bosch et al. 2014) and include a data standardisation of most of the satellite altimetry missions available since 1992. Main characteristics are: all input data refer to the ITRF2008 (Altamimi et al. 2011); the satellite orbit analysis is based on only one GGM (EIGEN-6S2, Förste et al. 2012); the ocean tide reductions are derived from the model EOT11a (Savcenko and Bosch 2012); the effects caused by the atmospheric pressure on the sea surface are modelled according to the dynamic atmospheric correction derived from the model Mog2D¹⁶ (Lynch and Gray 1979; Carrère and Lyard 2003) and published by the Space Oceanography Division of the CLS (Collecte Localisation Satellites). In this work, we derive mean values from the OpenADB sea surface heights available along the ground tracks of the following altimeter satellites: TOPEX/Poseidon, TOPEX-EM, ERS-1 ERM+GM, ESR-2 ERM, Jason-1, Jason-1 EM, Jason-2 and GFO. The main objective of this procedure is to guarantee that the yearly mean sea surface models are homogeneously computed; i.e., following unified standards and methods. In this way, variations in the estimated $W_{0}$ values reflect changes of the sea surface instead of inconsistencies in the satellite altimetry data analysis (like those presented by e.g., Rio and Andersen 2009; Schaeffer et al. 2012).

The computation of yearly mean sea surface models within this study is based on the strategy Remove-Estimate-Restore: As mentioned, input data are the OpenADB sea surface heights along the satellite ground tracks referring to the observation epoch t; i.e., $h_k(t)$. From these heights, an a priori (or reference) mean sea surface model $({h_{0,k}})$ is subtracted to obtain sea level anomalies $s_k (t)=h_k(t)-h_{0,k}$. In this case, we use the MSS_CNES_CLS11 as the reference model. Based on the sea level anomalies $s_k (t)$, mean values ${\hat{s}}_i$ at each nodal point i of a $0.5^{\circ }\times 0.5^{\circ }$ grid are computed/interpolated. For this purpose, a cap of radius $\psi _{\max }$ is defined around each nodal point, and all sea level anomalies $s_k (t)$ contained in this cap along one year are averaged using the weight function:

$$\begin{aligned} P_{\psi } =\mathrm{e}^{-\sigma \psi ^2};\quad \sigma =\ln (2)\,\tau ^{-2}, \end{aligned}$$

(17)

$\tau$ is an empirical factor that allows to control the decay slope of the exponential function $P_{\psi }$. ${\psi }$ is the spherical distance to the node. In this study, we apply the same parameters defined for the model EOT11a (i.e., ${\psi }_{\max }=1.5^{\circ }$ and $\psi =0.3{\psi }_{\max }$, Savcenko and Bosch 2012) to be in agreement with the standards applied in the OpenADB database. Once mean sea level anomalies are available at the grid nodal points, the reference model heights $h_{0,k}$ (also averaged on the $0.5^{\circ }\times 0.5^{\circ }$ grid) are restored; i.e., $h_i ={\hat{s}}_i+h_{0,i}$.

In the computation of the mean values ${\hat{s}}_i$, the input sea level heights $h_k(t)$ are weighted additionally with the inverse of the covariance matrix obtained in the crossover calibration procedure for each satellite altimetry mission (cf. Bosch et al. 2014, Eqs. [19], [20], [21]). These covariance matrixes are also available at OpenADB. In this way, after an error propagation analysis, the uncertainties $\sigma _{{\hat{s}}_i}$ of the mean sea surface anomalies ${\hat{s}}_i$ are known and the uncertainties of the mean sea surface heights $\sigma _{h_i}$ at the nodal points can be estimated using:

$$\begin{aligned} \sigma _{hi}=\sqrt{\sigma _{{\hat{s}}_i}^2+\sigma _{\mathrm{CLS11}}^2} \end{aligned}$$

(18)

$\sigma _{\mathrm{CLS11}}$ corresponds to the dispersion after computing $0.5^{\circ }\times 0.5^{\circ }$ grid mean sea surface heights values from the original $2'\times 2'$ grid provided by Schaeffer et al. (2012). Those nodal points with $\sigma _{hi}\ge 10~\hbox {cm}$ are again interpolated but using as input data the mean values ${\hat{s}}_i$ instead of $s_k(t)$.

To minimise the uncertainties caused in the satellite altimetry measurements by shallow waters in coastal areas and the sea water ice content in the polar regions, a strip of 10 km along continental and islands areas, as well as the polar ice covered zones are excluded from the interpolation. In the first case, we use the continental mask included in the GMT¹⁷ (Wessel et al. 2013). In the second case, we use the boundaries of the mean annual ice coverage published by NSIDC¹⁸ (Fetterer et al. 2002). Once the interpolation is performed, the mean sea surface heights corresponding to the polar ice covered areas are restored by means of the reference model MSS_CNES_CLS11. Remaining uncertainties in the shallow waters are down-weighted using Eq. (19) (see Sect. 7).

According to this procedure, yearly mean sea surface models were computed from 1992 to 2013. These models are then used to determine $W_{0}$ (Eq. (12)). Figure 9 shows the estimated $W_{0}$ value for each year. As expected, differences between these $W_{0}$ estimations mirror with opposite sign the changes of the yearly mean sea level scanned by satellite altimetry. The equipotential surface coinciding with the mean sea level in 1993 corresponds to a potential value $0.4117~\hbox {m}^{2}~\hbox {s}^{-2}$ larger than the potential value of that equipotential surface coinciding with the mean sea level in 2010. This corresponds to a sea level rise of about $+$2.4 mm a$^{-1}$ (cf. e.g., $+2.4\pm 1.1~\hbox {mm}~\hbox {a}^{-1}$ from Jason-1 and $+2.7\pm 1.5~\hbox {mm}~\hbox {a}^{-1}$ from Envisat, see Leuliette and Miller 2009). These results are in agreement with previous studies based on TOPEX/Poseidon and Jason-1, where the mean yearly change of the potential value $W_{\mathrm{S}}$ at the sea surface was estimated to be $-0.022~\hbox {m}^{2}~\hbox {s}^{-2}~\hbox {a}^{-1}$ for the period 1993–2001 (Sánchez 2007) and $-0.027~\hbox {m}^{2}~\hbox {s}^{-2}~\hbox {a}^{-1}$ for the period 1992.9–2009.0 (Dayoub et al. 2012).

It is clear that the empirical estimation of the $W_{0}$ value primarily depends on the Earth’s gravity field and on the definition of the mean sea level. The geoid, as any equipotential surface, changes due to mass redistributions. Some of these changes can be modelled (cf. Fig. 5) some others must be monitored (determined by repeated observations). However, as far as the volume enclosed by the perturbed/deformed geoid does not change, the potential value $W_{0}$ remains the same (see Sect. 8). Regarding the mean sea level, it could be assumed that the Gauss–Listing definition must be satisfied at any time and the geoid would have to grow or to decrease accordingly with the changes of the mean sea level; i.e., an estimate for $\mathrm{d}W_{0}/\mathrm{d}t$ in m$^{2}$ s$^{-2}$ a$^{-1}$ would be necessary. However, understanding that $W_{0}$ can be introduced as a defining parameter of the mean Earth ellipsoid, the semi-major axis (a) of the level ellipsoid would be a derived parameter and it would change if $W_{0}$ changes. To provide a reference ellipsoid that remains unchanged with time, it is necessary to decouple $W_{0}$ from the sea surface variations. The same is required, if $W_{0}$ is introduced as the reference level for the vertical coordinate determination. Practical and scientific applications modelling time-dependent changes in vertical coordinates demand quasi-stationary reference surfaces. If those references surfaces were time-dependent, it would not be possible to separate position variations from the reference surface variations; i.e., eventual changes of the reference level (i.e., $\mathrm{d}W_{0}/\mathrm{d}t)$ could not be distinguished from variations of the geopotential number at a given point (i.e., $\mathrm{d}C_{P}/\mathrm{d}t).$ In addition, although the vertical points do not move, their geopotential numbers (or physical heights) would have to be permanently changed in accordance with the reference level variations. This poses a huge disadvantage from the practical point of view. To avoid this problem, $W_{0}$ as fundamental parameter is to be defined as time-independent; i.e., its realisation could be given by the potential value valid at a certain epoch and then it remains fixed, unchanged for a long term (Ihde et al. 2015). It is, however, recommended to monitor the changes of the potential value at the sea surface and to compare it with the adopted $W_{0}$ value. When large differences appear (e.g., ${>}{\pm } 2~\hbox {m}^{2}~\hbox {s}^{-2})$, the adopted $W_{0}$ may be replaced by an updated (best estimate) value.

The main remarks regarding the dependence of the $W_{0}$ estimation on the sea surface model are:

• (a) The geoid is understood as the equipotential surface of the Earth’s gravity field that best fits (in a least square sense) the undisturbed mean sea level. Since satisfying this condition is impossible in addition to the sea level changes, a convention is needed to define the mean sea level;

• (b) As a basic convention it is stated that the computation of $W_{0}$ should be based on a quasi-stationary representation (model) of the sea surface, including the maximum latitudinal coverage available in the satellite altimetry data;

• (c) Although time-dependent sea level changes have an impact on the estimation of $W_{0}$, $W_{0}$ should be defined as time-independent in order to be introduced as a reference parameter for the determination of vertical coordinates or for the computation of a level ellipsoid;

• (d) Accordingly, it is suggested to estimate $W_{0}$ at a certain epoch and then to fix this value through a long-time period (e.g., >20 years).

Fig. 10

Comparison of the $W_{0}$ values estimated using (h) and $(h-\Xi )$ to describe the vertical position of the surface S. The value 62,636,800 m$^{2}$ s$^{-2}$ shall be added (GGM: EIGEN-6C3stat)

6.2 Effects of the mean dynamic topography on the estimation of $W_{0}$

Computations implemented until now are based on Eq. (12), which minimises the MDT assuming that $\Xi =[W_k-W_0]/{\bar{\gamma }}_k$. If the MDT is explicitly taking into account in the representation of S (to get a closer approximation to an equipotential surface), $W_{0}$ can be estimated using Eq. (15). The values $\Xi _{k}$ to be subtracted from the sea surface heights can be provided by a geodetic or an oceanographic MDT model. In the first case, the input data are sea surface heights (h) derived from satellite altimetry and geoid undulations (N) obtained from a pre-given geoid model; i.e., $\Xi =h-N$. In this way, the numerator in Eq. (15) becomes $[T_k-N_k{\bar{\gamma }}_k]$. If T and N are estimated consistently (applying the same geodetic measurements and models), the residuals in Eq. (15) are zero and $W_0=U_0$. If there is no consistency in the determination of T and N, the residuals would reflect the discrepancies between the computation procedures. For example, T is computed using EIGEN-6C2 and MSS_CNES_CLS11, while N is estimated from DTU12MDT. Since DTU12MDT is derived from the MSS model DTU10 minus the geoid model derived from EIGEN-6C2, the residuals in Eq. (15) would mirror the inconsistencies existing between both mean sea surface models; i.e., the MSS_CNES_CLS11 and the DTU10. An additional problem in using such a geodetic MDT model in the estimation of $W_{0}$ is that the geoid utilised in its determination may be already assigned with a geopotential value (see Rapp 1997, Eq. [3]; Lemoine et al. 1998, Eq. [5.2.1-4]). In this way, the estimation will result in a geopotential value that is already known and this makes the calculation trivial. Consequently, it is not sensible to use a geodetic MDT model for the estimation of $W_{0}$.

The oceanographic MDT models are based on the solution of equations of motion of the water masses (hydrodynamics). Here it is assumed that the water is in hydrostatic and geostrophic equilibrium above some identifiable, isobaric (reference) surface of no-motion, which coincides with an equipotential surface. The selection of this reference surface depends on (1) the availability of the hydrographic observables (e.g., temperature, salinity, pressure, water velocity along ocean currents, etc.); (2) the assumptions about the hydrostatic and geostrophic equilibriums; and (3) the certainty with the water friction forces are known. Therefore, the selected reference surface is not always the same and it usually does not coincide with the geoid (i.e., the reference surface for the geodetic models). Due to these uncertainties, the MDT models derived from oceanographic measurements are compared and improved using the MDT values derived from satellite altimetry and a geoid model (see e.g., Le Traon and Morrow 2001). At present, the most accepted oceanographic MDT model is the ECCO-2¹⁹ (Menemenlis et al. 2008). Although this model assimilates oceanographic observables, the estimation of the MDT is constrained to pre-given values derived from satellite altimetry and a GRACE-based geoid model. Nevertheless, we use these MDT values as $\Xi _{k}$ to compute $W_{0}$ by means of Eq. (15). The ECCO-2 model contains the quasi-stationary MDT for the time period 1992–2010 and we use a latitudinal coverage of $\varphi =70^{\circ }$N/S with a spatial resolution of $1^{\circ }\times 1^{\circ }$. To describe the vertical position vector of the surface $S_{0}$ (i.e., $[\varphi ,\lambda , h_{k}-\Xi _{k}]),$ mean sea surface heights $h_{k}$ for the same time span and at the same resolution are determined using the OpenADB data (cf. Sect. 6.1). Figure 10 compares the $W_{0}$ estimates obtained with Eq. (15) (i.e., using $(h-\Xi )),$ with those $W_{0}$ values derived from Eq. (12) (i.e., using h only). If the maximum latitudinal coverage ($\varphi =70^{\circ }$N/S) is included, the potential value $W_0^{({h-\Xi })}$ is practically identical with $W_0^{(h)}$. If the latitudinal coverage decreases, $W_0^{({h-\Xi })}$ remains almost unchanged, while $W_0^{(h)}$ shows the behaviour already discussed about neglecting sea surface topography features (cf. Fig. 6).

The main conclusion of this analysis is that Eqs. (12) and (15) produce the same results when all the ocean areas covered by the satellite altimetry are included in the estimation of $W_{0}$; i.e., a MDT model is not indispensable to estimate $W_{0}$ (cf. Dayoub et al. 2012; Sjöberg 2011).

7 Impact of the input data accuracy on the $W_{0}$ estimation

The numerical evaluations presented so far assume that all the input data are free of error. The uncertainty estimates contained in Table 3 only show the dispersion of the potential values $W_{k}$ at the grid nodal points k with respect to the $W_{0}$ value computed according to Eqs. (10) and (12). In the following, we analyse the dependence of the $W_{0}$ estimation on the accuracy of the input data. The basic observation equation is Eq. (12). It is a function of the normal potential $U_{0}$, the normal gravity ${\bar{\gamma }}$, the ellipsoidal coordinates $(\varphi ,\lambda ,h)$ of the points k describing the sea surface, and the anomalous potential T. The main contributors to the uncertainty of $W_{0}$ are h and T, since $U_{0}$ and ${\bar{\gamma }}$ are considered free of error. The standard deviation $\sigma _{h_k}$ of the mean sea surface heights $h_{k}$ is assumed to be equivalent to Eq. (18). It includes the uncertainty estimated from the cross-calibration procedure and the dispersion derived after computing the mean sea level heights at the $0.5^{\circ }\times 0.5^{\circ }$ grid. The standard deviation $\sigma _{T_k}$ of the anomalous potential values $T_{k}$ is obtained from the variance–covariance matrix of the GGM utilised for the computation of $W_{0}$, in this case the model EIGEN-6C3stat at $n = 200$ (Förste et al. 2012). It shall be pointed out here that only the main diagonal of the GGM variance-covariance matrix is taking into account for the estimation of $\sigma _{T_k}$. This means, correlations between harmonic coefficients of different degree and order are neglected.²⁰ According to the error propagation theory, the variance $\sigma _{W_k}^2$ of the values $W_k$ at the points k is given by:

$$\begin{aligned} \sigma _{W_k}^2=\sigma _{T_k}^2+{\bar{\gamma }}_k^2\sigma _{h_k}^2, \end{aligned}$$

(19)

and the inverse of this variance can be introduced as the weight function for a weighed estimation of $W_{0}$. In this way, Eq. (12) becomes (cf. Sjöberg 2011, Eq. [10a]):

$$\begin{aligned} W_0=U_0 +\frac{\sum _1^k {\left[ {\frac{T_k -h_k \bar{\gamma }_k }{\bar{\gamma }_k^2 }\,\cdot \;\frac{1}{\sigma _{T_k }^2 +\bar{\gamma }_k^2 \sigma _{h_k }^2 }} \right] } \,\delta S_k }{\sum _1^k {\left[ {\frac{1}{\bar{\gamma }_k^2 }\cdot \;\frac{1}{\sigma _{T_k }^2 +\bar{\gamma }_k^2 \sigma _{h_k }^2 }} \right] \delta S_k }}. \end{aligned}$$

(20)

Equation (20) is solved using the yearly mean sea surface models described in Sect. 6.1. $\sigma _{h_k}$ varies from ±0.002 to ±0.100 m, while $\sigma _{T_k}$ varies from ±0.1055 to ± 0.1535 m$^{2}$ s$^{-2}$. The accuracy of $T_{k}$ is in agreement with the expected accuracy of GOCE-based GGM (i.e., geoid accuracy of 1–2 cm at a spatial resolution of about 100 km, see Drinkwater et al. 2007). As an example, Fig. 11 shows the standard deviation $\sigma _{W_k}$ of the potential values $W_{k}$ for the year 2005. The difference between a non-weighted and a weighted estimation of $W_{0}$ is significant. It not only changes the $W_{0}$ value by about $-0.34~\hbox {m}^{2}~\hbox {s}^{-2}$, but also improves the dispersion of the $W_{k}$ values $(\sigma =\pm 8.5168~\hbox {m}^{2}~\hbox {s}^{-2})$ and the standard deviation of $W_{0}$ $(\sigma _{W_0}=\pm 0.0219~\hbox {m}^{2}~\hbox {s}^{-2})$; cf. Table 3. The weighted estimation of $W_{0}$ allows to reduce the effects of the so-called geographically correlated errors in the satellite altimetry data. According to Bosch et al. (2014), these errors are important for mapping and monitoring the sea surface, as they cancel in single-satellite crossover differences, but map directly in the sea surface height. The geographically correlated errors mainly reflect errors coming from the orbit determination process, but they may also include effects like errors in the time tagging of the observations or errors in the corrections applied to the data (e.g., tropospheric reductions, sea state bias, etc.). Therefore, we stress the importance of computing $W_{0}$ using standardised yearly mean sea surface models.

Fig. 11

Standard deviation $\sigma _{W_k}$ of the potential values $W_{k}$ (Eq. (19)) for the year 2005

8 Dependence of the $W_{0}$ empirical estimation on the tide system

According to Burša (1995b, (1995c), $W_{0}$ can be considered as a parameter non-dependent on the tide system. In that analysis, Burša (1995b, Eq. [29]) assumes that $W_{0}$ only depends on (1) the volume enclosed by the surface $W=W_{0}$; (2) the geocentric gravitational constant GM; and (3) the Earth’s angular velocity. If there are no changes in any of these parameters, $W_{0}$ remains constant. Direct and indirect effects of the tidal potential on $W_{0}$ are compensated by the deformation of the corresponding level surface, but the volume enclosed by this surface does not change. Burša (1995c, p. 60) explicitly says: At any fixed point the zero-frequency direct plus indirect distortion makes the actual geopotential different from the ideal tide-free potential. As the Bruns theorem suggests, the tidally distorted equipotential surface is shifted from that tide-free, however, the same geopotential value is appropriate to both surfaces. It means, geoidal potential $W_{0}$ should remain unchanged for both, tide-free geoid, as well as, tidally distorted one. Based on this and assuming that at least one point at the geoid surface is known, Burša (1995c, Section 3) shows that the change in $W_{0}$ due to tidal effects is zero. However, in practice no points on the geoid are available. On the contrary, the empirical estimation of $W_{0}$ assimilates observables determined at the Earth’s surface and those observables are influenced by the manner the tide effects are handled; i.e., they depend on the tide system. Therefore, in this section we want to assess how much $W_{0}$ changes if the input data are given in different tide systems.

Computations described in the previous sessions are based on GGMs given in the zero-tide system and sea surface heights given in mean-tide system (which in this case is equivalent to the zero-tide system). Now we want to estimate $W_{0}$ in the mean-tide system and in the tide-free system. For the estimation of $W_{0}$ in the tide-free system, the mean sea surface heights are converted into tide-free positions using the conventional tide-free reduction applied by the IERS for the determination of the ITRF positions (cf. Petit and Luzum 2010, Eqs. [7.14a] and [7.14b]). The IERS conventional tide-free reduction is applied in this case because the same hypotheses are used for the conversion of the harmonic coefficient $C_{20}$ from the free- to the zero-tide system (cf. Eq. (16)). As the mean sea surface heights $h_{k}$ used in this study refer to the GRS80 ellipsoid, the conversion from the zero-tide into the conventional tide-free positions is given by (cf. Ihde et al. 2008, Eq. [5]–[7]):

$$\begin{aligned} \Delta h_T =0.0602-0.1790\,\sin ^2\varphi -0.0018\,\sin ^4\varphi . \end{aligned}$$

(21)

The coefficient $C_{20}$ of the GGM is originally provided in tide-free system; in this way, no further transformations are necessary. Once sea surface heights and GGM are given in the tide-free system, $W_{0}$ (Eq. (12)) is computed again.

For the computation of $W_{0}$ in the mean-tide system, the direct permanent tidal effect ($W_{2})$ is added to the values $T_{k}$ before solving Eq. (12). This effect is computed according to Ihde et al. (2008, Section 5, Eq. [5-4]):

$$\begin{aligned} W_2 ( \varphi )=0.9722-2.8841\,\sin ^2\varphi -0.0195\,\sin ^4\varphi . \end{aligned}$$

(22)

Once this effect is restored to the values $T_{k}$, Eq. (12) is solved using the same mean sea surface models as before (cf. Sect. 6.1), because, as already mentioned, for the geometry of the Earth’s surface mean-tide and zero-tide system are identical.

The $W_{0}$ estimation in zero-tide $W_0^{\mathrm{ZT}}$ and tide-free $W_0^{\mathrm{TF}}$ produces practically the same value. The difference $[W_0^{\mathrm{TF}}-W_0^{\mathrm{ZT}}]$ is 0.0278 m$^{2}$ s$^{-2}$, which is in the same order as the formal error of the computations (see Table 3). Thus, it can be considered insignificant. The difference between the mean-tide estimation $W_0^{\mathrm{MT}}$ and the other ones is a little larger. $[{W_0^{\mathrm{MT}}-W_0^{\mathrm{ZT}}}]$ is 0.0943 m$^{2}$ s$^{-2}$ and $[{W_0^{\mathrm{MT}}-W_0^{\mathrm{TF}}}]$ is 0.0665 m$^{2}$ s$^{-2}$. This can be a consequence of omission errors by restoring only the second degree tidal effects (see Eq. (22)), or by not including the entire Earth’s surface (continents $+$ oceans) in the computations. In fact, if the latitudinal coverage of the MSS model diminishes, the discrepancy between the estimates based on different tide systems increases. Therefore, it is very important that the input data for the computation of $W_{0}$ (GGM and MSS models) are given in the same tide system. We recommend the zero-tide system. To reduce possible uncertainties between computations performed in different tide systems, it sounds reasonable to round the reference $W_{0}$ value to only one digit after the decimal marker.

Fig. 12

Yearly weighted $W_{0}$ estimations fitted by means of a lineal regression. The $W_{0}$ value for the year 2010.0 (62,636,853.353 m$^{2}$ s$^{-2})$ can be rounded to one decimal place (62,636,853.4 m$^{2}$ s$^{-2})$ and be adopted as the IAG conventional reference $W_{0}$ value

9 Discussion about the conventions needed for a conventional $W_{0}$ value

Computations implemented along this paper and in previous studies make evident that the value estimated for $W_{0}$ depends on the Earth’s gravity field modelling, the mean sea surface model, and the standards and conventions applied to process the data. Therefore, in addition to perform a standardised computation of $W_{0}$, a further objective of this study is to face some open questions formulated in previous analyses. For instance, based on the discussion presented by Dayoub et al. (2012, Section 4), in this study

• seven additional satellite altimetry missions to TOPEX/Poseidon and Jason 1 were included to extend the time-span of the mean sea surface level from 1992.9–2009.0 to 1992.9–2014.0;

• standardised and cross-calibrated satellite altimetry data were applied to reduce possible effects caused by altimeter biases or by different datums of the missions;

• time-dependence of GGM and MSS models was analysed within the $W_{0}$ computation.

Based on Burša et al. (2007), in this study:

• the effects produced by the atmospheric pressure on the sea surface were modelled according to the dynamic atmospheric correction to reduce the uncertainty associated to the inverse barometric effect.

Based on Čunderlík et al. (2014), in this study:

• mean yearly sea surface models based on the newest reduction models and analysis strategies were used to minimise possible effects associated with different modelling strategies of the inter-annual oceanic variability;

• newest global gravity models based on GRACE, GOCE and SLR data were used to ensure a high reliability in the long wavelength components of the Earth’s gravity field modelling;

• effects of the GGM omission and commission errors on the $W_{0}$ were analysed;

• MSS models and satellite-only GGM were reduced to the same reference epochs to ensure consistency in their combination.

Based on Sánchez et al. (2014), in this study:

• mean sea surface heights in the polar regions were included as far as the present coverage of the satellite altimetry data this allows;

• a weighted computation based on the accuracy of the input data was performed to reduce possible effects caused by geographically correlated errors and the poor quality of satellite altimetry measurements in the polar regions and along coastal and insular areas;

• the improved accuracy offered by GOCE in the long and mean wavelengths of the GGM was totally capitalised by increasing the weight of those areas where $T_{k}$ presents a higher accuracy;

• $W_{0}$ was computed in the different tide systems (i.e., zero-tide, tide-free and mean-tide systems).

According to the different analyses performed in this paper, we recommend the adoption of a $W_{0}$ value relying on the following conventions:

• (a) Gauss–Listing geoid’s definition: $W_{0}$ is the geopotential value of that level surface that best approximates (in the sense of the least squares) the global mean sea surface when totally calm (i.e., if not external forces would act on the oceans).

• (b) Since a global sampling of the sea surface is not truly possible (due to the continents and limited latitudinal coverage of the satellite altimetry), the concept global is here understood as the maximal coverage of the satellite altimetry (see Sect. 6).

• (c) Since a totally calm condition of the sea surface is not achievable, a quasi-stationary representation of the sea surface is needed; i.e., time-dependent effects affecting the instantaneous sea surface should be reduced previously (see Sect. 6.1).

• (d) To reduce the mean dynamic topography effects, all the ocean areas scanned by satellite altimetry should be included in the estimation of $W_{0}$ (see Sect. 6.2).

• (e) The Earth’s gravity field model should be based on the combination of, at least, SLR, GRACE and GOCE data (see Sect. 5.2). It is proof from empirical estimations that the satellite-only component $(n=200)$ of a static (quasi-stationary) global gravity model is sufficient for this computation. In other words, omission errors caused by truncating the global gravity model at $n=200$ (see Sect. 5.1) as well as time-dependent variations of the Earth’s gravity field (see Sect. 5.3) can be assumed negligible in the estimation of a global $W_{0}$.

• (f) The uncertainties caused in the satellite altimetry data by geographically correlated errors, including shallow waters in coastal areas and sea water ice content at polar regions, should be considered in the computation of $W_{0}$; i.e., a weighed adjustment including the inverse of the input data variances as a weighting factor is recommendable. This weighting factor should also reflect the improvement provided by SLR, GRACE and GOCE to the gravity field modelling (see Sect. 7).

• (g) Theoretically, $W_{0}$ does not depend on the tide system; however, it is recommended to perform the computations in the zero-tide system (see Sect. 8).

• (h) As a reference parameter, $W_{0}$ should be time-independent (i.e., quasi-stationary) and it should remain fixed for a long-term period (e.g., 20 years). However, it is recommended to monitor the changes of the potential value at the sea surface $W_{\mathrm{S}}$ and to compare it with the adopted $W_{0}$ value (see Sect. 6.1). When large differences appear (e.g., more than ±2 m$^{2}$ s$^{-2})$, the adopted $W_{0}$ may be replaced by an updated (best estimate) value.

• (i) Due to the time-dependent variations of the sea surface, the realisation of the Gauss–Listing definition necessarily has to be associated to a certain epoch (see Sect. 6.1). In this context, there are many possibilities; for instance,

  • we can agree to use the mean value for the lunar period of 18.6 years (as usual in the definition of the local vertical datums). If this period starts in 1992.9 (when the first satellite altimetry data were available), the Gauss–Listing definition would be satisfied at the mean epoch 2003.2. If the 18.6-year period ends in 2014.0 (latest altimetry data included in this study), the mean epoch would be 2004.7;

  • we can consider the availability of satellite altimetry data from 1992.9 up to 2014.0 as time span, and the reference epoch would be 2003.45;

  • we can also say that, given that in 1992 a very few altimetry data are available, the time span is defined from 1993.0 up to 2014.0. In this case, the reference epoch would be 2003.5;

  • another possibility is to consider the period covered by GRACE and GOCE; i.e., from 2002.0 until 2013.8, and the reference epoch would be 2007.9.

  Each of these options is based on a time-span to build a mean value and they handled the inter-annual oceanic variability in a different way. Thus, the immediate question is how much $W_{0}$ would change, if the time-span is moved to earlier or later years. To avoid this problem, and following the results presented by Dayoub et al. (2012) and Sánchez et al. (2014), it is valid to assume that the potential at the mean sea surface changes linearly and this change can be represented by means of a constant rate. According to this, a suitable possibility is to determine the linear trend of the potential value estimated at the sea surface based in yearly mean sea surface models (Fig. 12) and to adopt the value corresponding to a certain year. Noting that the potential value at the sea surface changes about −0.027 m$^{2}$ s$^{-2}$ a$^{-1}$ (see Sect. 6.1); it would be convenient to select a recent year (e.g., 2010.0) to provide a reference value valid for a longer period in the future (e.g., until 2030; see convention (h) above).

• (j) Based on this discussion, we recommend to adopt the $W_{0}$ value obtained for the epoch 2010.0 after fitting the yearly $W_{0}$ weighted-estimations for the period 1993.0–2014.0 by means of a lineal regression:

  $$\begin{aligned}&W_{0} = 62{,}636{,}853.4~\hbox {m}^{2}~\hbox {s}^{-2} \end{aligned}$$

  (23)

Since (23) is to be adopted as a convention, an accuracy indicator can be omitted. However, it can be mentioned that the formal error of (23) is ±0.02 m$^{2}$ s$^{-2}$ (cf. Table 3).

10 Conclusions

The empirical estimation of a $W_{0}$ value depends on the Earth’s gravity field, the mean sea surface model, and the standards and conventions applied to process the data. Consequently, like any reference parameter, $W_{0}$ should be based on adopted conventions that guarantee its uniqueness, reliability, and reproducibility; otherwise, there would be as many $W_{0}$ reference values as computations. Along this paper, different methodologies, different GGMs, different MSS models, different reference epochs, different weights for the input data, and different tide systems were evaluated for the $W_{0}$ computation. Based on these results, detailed conventions to ensure the reproducibility of a reference $W_{0}$ value were outlined. As the usual approximation of $W_{0}$ is the averaged potential value $W_{\mathrm{S}}$ at the mean sea surface; it is expected that $W_{0}$ changes in the same way like $W_{\mathrm{S}}$ changes. However, $W_{0}$ as a reference parameter should be defined as time-independent, and it would be necessary to decouple it from the Earth’s gravity field and sea surface variations. Thus, it is proposed to adopt the potential value valid at a certain epoch and to keep it fixed for a long-term period (e.g., 20 years). However, it is recommended to monitor the changes of the potential value $W_{\mathrm{S}}$ at the sea surface and to compare it with the adopted $W_{0}$ value. When large differences appear (e.g., ${>}{\pm }2~\hbox {m}^{2}~\hbox {s}^{-2})$, the adopted $W_{0}$ may be replaced by an updated (best estimate) value. At present, the most accepted value is the so-called IERS $W_{0}$ value (62,636,856.0 m$^{2}$ s$^{-2})$, which corresponds to the best estimate available in 1998. This 1998 $W_{0}$ value presents a discrepancy larger than −2 m$^{2}$ s$^{-2}$ with respect to recent $W_{0}$ estimations and, in accordance with the conventions outlined in this paper; a better estimate for $W_{0}$ should be adopted as a formal IAG convention. To provide a reference $W_{0}$ value valid for a longer period in the future (e.g., until 2030), a suitable recommendation is to adopt as a formal IAG convention the potential value obtained in this study for the epoch 2010.0; i.e., $W_{0}=62{,}636{,}853.4~\hbox {m}^{2}~\hbox {s}^{-2}$.

The main implication of a new $W_{0}$ value for the IAU timescales is related to the accuracy of the realisation of the TAI. At present, the best possible clock accuracy (i.e., timescale accuracy) is about $2\times 10^{-16}$, which corresponds to a potential difference of about $20~\hbox {m}^{2}~\hbox {s}^{-2}$. From this point of view, a change of $2.6~\hbox {m}^{2}~\hbox {s}^{-2}$ in $W_{0}$ (as proposed in this paper) is practically negligible for the IAU and the IERS.