Information sharing in democratic mechanisms

Abstract

We examine how democratic mechanisms can yield socially desirable outcomes in the presence of uncertainty about an underlying state of nature. We depart from a conventional mechanism design approach because we aim for democratic mechanisms to reflect some basic properties of decision-making in democracies. In particular, actual decisions are made by majority voting. The proposals to be voted upon are made by a selfish agenda-setter. Moreover, communication is limited to a binary message space (that is, voting Yes or No). We show how suitable democratic mechanisms can resolve uncertainty, reveal the state of nature, and implement the Condorcet winner. We demonstrate that this implementation result requires (at most) two voting stages regardless of the number of states or the number of alternatives. We also show that implementation requires a conditional privilege for a small representative subset of the population.

1 Introduction

1.1 Motivation and approach

The ability of democratic decision-making procedures to achieve socially optimal outcomes is at the core of a long-standing and complex debate with many unresolved issues. One challenging question, in particular, is how democratic mechanisms in the sense of Gersbach (2009) can help reveal information about underlying state variables.

There is a stream of literature that deals with information aggregation in a common value setting. That is, voters agree that there is a “best” alternative that should be selected. However, they are uncertain about which alternative is the best one. More specifically, each voter receives only a noisy signal of how good the alternatives are. For instance, members of a jury agree that a defendant should be convicted if they committed the crime, and acquitted otherwise. However, the different jurors may perceive the available evidence differently. Likewise, members of a recruiting committee may all agree that they wish to hire the most suitable candidate for a job, but have different subjective impressions of the candidates. In such settings, voting procedures can be a viable tool to aggregate the information dispersed among the voters. Ideally, this information aggregation fades out the noise in individual signals and thus reveals the underlying state variable. A seminal result in this area is the Condorcet Jury Theorem.

Our paper differs from the information aggregation literature: In our model, citizens have private information about their type. Hence, they are perfectly aware of their own preferences over the alternatives. Moreover, their type is also a noisy signal of the underlying state of nature. In order to distinguish our work from the aforementioned literature on information aggregation, we use the term information sharing throughout. By sharing private information about their types, citizens can learn the state of nature and thus the type distribution. In the class of democratic mechanisms which we consider, knowledge about the type distribution is important to enable implementation of the Condorcet winner. We will see that some citizens may find it in their interest to hide or misrepresent information about the state.

We study situations in which individual benefits from public policies are privately observed realizations from a probability distribution which itself depends on an unknown state variable. In particular, citizens are uncertain not only of other citizens’ types, but also of the underlying distribution of types in the population. To give one example, many societies face trade-offs between protecting citizens from terrorism and privacy concerns. Citizens differ in their preferences over these considerations. Each citizen may be uncertain about the extent to which other individual citizens weigh privacy vs. counter-terrorism. Moreover, a citizen is also uncertain about the distribution of such preferences in the population.

In this paper, we consider a continuum society which faces the following collective choice problem: There is a finite number of feasible public good levels. An individual citizen’s preferences over these public good levels depend on his privately observed type. An underlying state of nature determines the probability distribution from which each citizen’s type is independently drawn. Each state of nature is associated with a Condorcet winner. That is, one feasible public good level is preferred by the majority to any other feasible public good level. Citizens have a common prior belief about the state of nature. They can learn the actual state, and thus the Condorcet winner, by aggregating their private information.

We are interested in a class of collective choice procedures called “democratic mechanisms” (Gersbach 2009). They bear some resemblance to mechanisms with restricted message spaces as well as to voting games. More specifically, democratic mechanisms share information in a similar way as studied in the mechanism design literature. However, decisions in democratic mechanisms are made by majority voting and proposals are made by selfish agenda-setters. We intend democratic mechanisms to reflect some important principles and features of real democratic processes:

• Voters are typically not able to communicate their preferences in full detail. Instead, they may only be able to vote in favor or against a proposal, or choose between, say, a Republican and a Democrat. The notion of a democratic mechanism reflects this by allowing only a binary message space.

• Arguably, the most basic principle of democratic decision-making is that the implementation of an alternative requires approval by a majority. Indeed, our model of democratic mechanisms assumes that a status quo can only be replaced by a new policy if the majority of citizens agree. This is in contrast to a standard mechanism design approach, where citizens only reveal information, but do not explicitly make the actual decision.

• Actual democratic processes are often shaped by elites (politicians, lobbyists, activists) who are selfish and use their power over the political process for their own benefit. Our notion of a democratic mechanism reflects this by letting a selfish “agenda-setter” choose the feasible alternative which is then voted upon.

Binary messages, majority voting, and a selfish agenda-setter are the three features that define our notion of a democratic mechanism. We aim for democratic mechanisms which involve as few voting stages as possible, and are therefore “procedurally efficient.” The rationale is that, in practice, it is costly to organize an election or a referendum.

In the present paper, we ask which democratic mechanisms reliably reveal the state of nature and implement the Condorcet winner in the aforementioned collective choice problem. In order to accomplish implementation, a democratic mechanism must overcome two obstacles, which we refer to as manipulation and exploitation. We discuss these two obstacles in turn:

First, in order to discover the Condorcet winner, citizens need to share their private information using binary messages. A standard problem in mechanism design is the presence of incentives to strategically misrepresent one’s private information, thus manipulating the mechanism. Not surprisingly, this obstacle to information sharing is also present in democratic mechanisms. In addition, due to the agenda-setter’s active role, there is a second obstacle to the desired implementation result: Once the state of nature has been revealed, the agenda-setter may want to use this knowledge for his own benefit, rather than work “in good faith” towards the implementation of the Condorcet winner. Such strategic behavior by the agenda-setter is called exploitation throughout this paper.

1.2 Main results

We show an impossibility result and an existence result: first, we focus on the simplest possible (“baseline”) democratic mechanisms, which rely on a single voting stage preceded by binary communication. We show that a baseline democratic mechanism fails to generally implement the Condorcet winner. We distinguish between the case where implementation fails because citizens manipulate information sharing, and the case where implementation fails because the agenda-setter exploits information sharing. Second, we derive an existence result, that is, we construct a democratic mechanism which is immune to both the voters’ and the agenda-setter’s attempts to manipulate or exploit information sharing, and which therefore implements the Condorcet winner. This democratic mechanism relies on two features: It grants a conditional privilege to a small random sample of the population, and requires a two-stage voting procedure. These two features are essential for implementation.

At a more detailed level, the mechanism we develop can be described as follows: a small representative sample of the population is drawn. Members of the sample group coordinate their binary messages so as to communicate information about the state. An agenda-setter observes the sample group’s messages and proposes a public good level. This proposal is decided upon in two voting stages: first, the entire population makes a choice between the proposal and the highest feasible alternative which is lower than the proposal. Second, the winner of this vote is pitted against the status quo. Sample group members as well as the agenda-setter are exempted from taxation if and only if the proposal made by the agenda-setter prevails in both voting stages.

We show that this democratic mechanism guarantees the implementation of the Condorcet winner by eliminating all bad incentives for both exploitation and manipulation. Our democratic mechanism yields truthful information sharing, optimal public good provision, and consequently the implementation of the Condorcet winner in two voting stages, regardless of the number of states or alternatives. Our democratic mechanism requires granting a conditional privilege to a small subset of citizens. This privilege involves a tax-exemption as well as, possibly, a transfer. Due to this conditional privilege, the democratic mechanism we propose leads to an allocation of utilities that is close, but not exactly equal, to utilities that are stable to majority voting. In a nutshell, in order to find and implement the Condorcet winning policy alternative, our democratic mechanism must allow for a small distortion away from the Condorcet winning allocation. This distortion, however, is arbitrarily small.

1.3 Contribution and literature

Our contribution lies at the interface of mechanism design, social choice, and constitutional choice. As in mechanism design theory, we consider an environment with privately informed agents, and our aim is to find game forms which accomplish a socially desirable collective choice through truthful revelation of private information. Moreover, our focus on democratic mechanisms is related to social choice theory in two ways: first, it makes decisions by voting. Second, our approach pays attention to both the voters’ and the agenda-setter’s incentives. Finally, we evaluate the democratic mechanism devised in our paper against the requirement that citizens be treated equally, which is central to constitutional choice.

A closely related recent contribution is Bierbrauer and Hellwig (2016) . Their work is a starting point for our research in two respects: first, we follow Bierbrauer and Hellwig in considering decision-making on public good levels through voting procedures. Second, we allow groups of citizens to coordinate their signals, and establish an implementation result which is robust to such coordinated behavior. This uses one of Bierbrauer and Hellwig’s main insights, namely that “coalition-proofness” is a desirable property of an incentive mechanism for public good provision. However, we focus on different issues than Bierbrauer and Hellwig. In particular, we examine whether and how the Condorcet winner can be implemented by voting procedures in the presence of two complications: first, in contrast to the mechanism design approach, proposals are made by a selfish agenda-setter and there is no mechanism designer. Second, our model includes uncertainty about the type distribution. This uncertainty has to be resolved in order to proceed with implementation.

Our objective is to implement the Condorcet winner, which need not coincide with the social welfare optimum. The rationale is that we are interested in what can be accomplished by a class of democratic procedures. It seems innocuous that a democratic system should select an alternative that the majority prefers to any other alternative. Nevertheless, this requirement is non-trivial: Many electoral systems do not satisfy it. For example, in elections with a run-off round, the Condorcet winner may fail to be selected. Therefore, it seems interesting to study democratic mechanisms which do reliably select the Condorcet winner.

One could have in mind richer mechanisms in which the required (super-) majority depends on the alternative that is voted upon, as in the recent work of Bierbrauer and Hellwig (2016). With such more complex rules, one could aim for democratic mechanisms which find the social welfare optimum rather than the Condorcet winner. Moreover, we could distinguish between critical and day-to-day decisions by either introducing fixed costs for any positive level of public good provision or allowing for different types of public good provision. Critical decisions would then be about whether to provide the public good at all or which type of public good to provide. For such cases, Aidt and Giovannoni (2011) have outlined a theory how different collective decision rules can be used for different types of decisions. This theory could be applied in our context as well.

In this paper, we are interested in the implementation of the Condorcet winner through a special class of collective decision procedures called democratic mechanisms. Of course, there are alternative ways how one could accomplish this goal. For instance, a social planner could identify the Condorcet winner by eliciting citizens’ pairwise preferences over all the alternatives. The procedure we propose has two advantages over the elicitation of all pairwise preferences: first, it is much more efficient than elicitation of all the pairwise preferences. Second, we want to let go of the idea that there is a benevolent social planner who designs a scheme to elicit citizens’ preferences. Instead, we allow for a selfish agenda-setter. Our contribution is therefore not that we show how one can arrive at the Condorcet winner. Rather, we have studied how the Condorcet winner can be implemented using a special class of collective decision procedures that is efficient and allows for the agenda to be shaped by selfish members of society. Setting the right incentives for the selfish agenda-setter and curbing his power to exploit the mechanism for his own self-interest is a crucial challenge in our paper.

Our work fits into the context of a vast body of literature on optimal constitutions which has developed after the classic work of Buchanan and Tullock (1962). Aghion and Bolton (2003) have introduced incomplete social contracts and have explored how simple or qualified majority rules balance the need to overcome vested interests and respect majority preferences. Gersbach (2009) has shown how increasingly sophisticated combinations of agenda rules, treatment rules, and decision rules can yield first-best allocations when each citizen faces only two possible realizations: being either a winner or a loser of a public project. The present paper allows for uncertainty about the distribution of valuations. Neither individual valuations nor the underlying distribution are common knowledge. In particular, we explore the scope of democratic mechanisms with minimal message spaces but with rich type spaces and uncertainty about type distribution.

There is a literature on polling in which candidates for political office learn about the location of the median voter through surveys, and then decide where to position themselves on the political spectrum.¹ Our approach differs from the polling literature in that the sampling group is given incentives to report truthfully.

The paper is organized as follows. In Sect. 2, we formally introduce the collective choice problem faced by our model society. In Sect. 3, we formalize the notion of a democratic mechanism. In Sect. 4, we consider the simplest possible (“baseline”) democratic mechanism, and demonstrate how it is prone to exploitation and manipulation. Then, we proceed to introduce a democratic mechanism which reliably accomplishes information sharing and guarantees the implementation of the Condorcet winner. We discuss the main implementation result in Sect. 5. In Sect. 6, we discuss a simplified implementation result which holds on a subclass of public good problems. Section 7 concludes.

2 The collective choice problem

We consider a collective choice problem in a society which consists of a continuum of risk-neutral citizens of unit mass. Citizens can choose how much of a public good should be provided. This is similar to the approach in Bierbrauer and Hellwig (2016). However, our main results and conclusions would translate into a more general setting with feasible alternatives that are discrete and can be ordered along a single dimension, and with single-peaked preferences.²

Each citizen is privately informed about his type z. The type space Z is a closed, non-empty, and non-degenerate interval in ${\mathbb {R}}_{++}.$³ We refer to a citizen of type z as citizenz. We denote the interior of the type space by int(Z). The provision of a public good level $q \in {\mathbb {R}}_{+}$ comes at a cost c(q) to each citizen. The cost function c(q) is strictly increasing and strictly convex, and $c(0)=0.$ A citizen’s benefit from a unit of public good provision is given by his type. More specifically, we can write citizen z’s utility from public good provision as $u(z,q) = zq-c(q).$

The model features both individual and aggregate uncertainty. We assume that there are finitely many states of nature; the state space is $N=\{1,\ldots , n\}.$ We will often use i or k to index the elements of N. If the state of nature is k,  then citizens’ types are independent draws from a probability distribution on Z with density $f_{k}$ and cumulative distribution function $F_{k}.$ Citizens share a common prior belief p about the state of nature, where $p_{k} > 0$ for every $k\in N.$ Due to Bayesian updating, citizen z believes in state k with probability $\beta _{k}(z)=\frac{f_{k}(z) p_k}{\sum _{j=1}^{n} f_{j}(z) p_j }>0.$

We make the following assumptions:

Assumption 1

• 1. For any $z\in int(Z),$ we have $F_{1}(z)> \cdots > F_{n} (z).$

• 2. For every $k\in N,$ there is a Condorcet winner, that is, there is $q_{k} > 0$ such that a majority of citizens prefers $q_{k}$ to any $q\in {\mathbb {R}}_{+} \setminus \{q_{k}\}.$

  Moreover, it holds that $0<q_{1}<\cdots <q_{n}.$

• 3. For every $k\in N$ there is some ${\widetilde{q}}_{k} > 0$ such that a majority of citizens strictly prefers a public good level $q>0$ to zero public good if and only if $q<{\widetilde{q}}_{k},$ and a majority strictly prefers zero public good to $q>0$ if and only if $q>{\widetilde{q}}_{k}.$

• 4. For every $k\in N$ and every $z\in Z,$ it holds that $\beta _{k} (z) >0$ and Bayesian updating is monotone.⁴

In Appendix A, we explain how Assumption 1 can be deduced from a set of deeper model assumptions on the cost function, type space, and probability distributions.

In the remainder of the paper, we restrict attention to a discrete and finite set Q of feasible public good levels. We assume that $\{ 0 \} \cup \{q_{1}, \ldots , q_{n}\} \subset Q.$ We consider zero public good provision as a status quo, and we require the Condorcet winners to be feasible. Moreover, it is convenient to assume $(0, q_{1}) \cap Q = \emptyset .$

For any $q^{\prime } \in (0,q_{n}),$ let

$$\begin{aligned} \psi _{-}(q^{\prime })= & {} \max \{ q \in Q \vert q<q^{\prime } \},\\ \psi _{+}(q^{\prime })= & {} \min \{ q \in Q \vert q>q^{\prime } \}. \end{aligned}$$

To sum up, the state space N,  the type space Z,  the family of cumulative distribution functions F,  the feasible set Q,  the cost function c,  and the common prior p constitute a choice problem, which we denote by P. The set of all such problems is denoted by ${\mathcal {P}}.$ For each problem $P\in {\mathcal {P}},$ it is commonly known that a Condorcet winner exists. However, no individual citizen knows which alternative is the Condorcet winner. In what follows, we will be interested in decision-making procedures which reliably implement the Condorcet winner for the whole class ${\mathcal {P}}.$

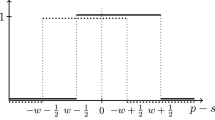
It is important to note that suitably coordinated binary messages suffice to aggregate information and reveal the Condorcet winner. To be more specific, we can interpret $F_{k}(z)$ as the cross-sectional distribution of z in the population when the state is k. It is well-known that this interpretation requires the application of a suitable version of the law of large numbers for a continuum of random variables. More specifically, for any public good problem $P\in {\mathcal {P}}$ with type space Z,  state space N,  cumulative distribution functions F,  and set of feasible alternatives Q,  fix some $z^{P} \in int(Z),$ and assume that all citizens $z\ge z^{P}$ send one message (say “Yes”) and all citizens of type $z< z^{P}$ send another message (say “No”). Denote by $\delta$ the observed measure of citizens sending message “Yes.” Then, define $\varphi ^{P} : [0,1] \rightarrow Q$ as follows:

$$\begin{aligned} \varphi ^{P}(\delta ) = {\left\{ \begin{array}{ll} q_{1} \ &{}\quad \text {if} \ 0 \le \delta< 1-F_{2}(z^{P}),\\ q_{k} \ &{}\quad \text {if} \ 1-F_{k}(z^{P}) \le \delta < 1-F_{k+1} (z^{P}), \ \text {for} \ k=2,\ldots , n-1, \\ q_{n} \ &{}\quad \text {if} \ 1-F_{n}(z^{P}) \le \delta \le 1. \end{array}\right. } \end{aligned}$$

Recall that we have assumed that $F_{1}(z)>\cdots >F_{n}(z)$ for any $z\in int(Z).$ Thus, learning the share of citizens whose type is higher than some critical (interior) type suffices to learn the state. More precisely, if all citizens $z\ge z^{P}$ send one message, and all citizens $z<z^{P}$ send the other message, then the map $\varphi ^{P}$ reveals the Condorcet winner. The critical type $z^{P}$ can be chosen arbitrarily for each public good problem.

The question arises how one could accomplish coordination on a particular value of $z^{P}.$ In the sequel of the paper, we will discuss democratic mechanisms in which an agenda-setter has a rich message space, while other citizens can only communicate by sending binary messages. It is therefore possible for the agenda-setter to establish coordination by simply asking, “Is your type higher or lower than $z^{P}$?” for some $z^{P}$ of his choice.

3 Democratic mechanisms

In the literature, a mechanism is commonly defined as a map from messages to outcomes. The decision-making process is as follows: first, a designer announces the mechanism. Then, citizens report their types. Finally, the outcome associated to the reported type profile by the mechanism is implemented. This mechanism design approach hinges on several tacit assumptions: first, it requires the message space to be as rich as the type space. Second, it assumes that the designer is benevolent with regard to some social objective, and that he is committed to the mechanism he has designed. In particular, after observing the messages, the designer cannot “change his mind” and choose an alternative different from the one prescribed by the mechanism. Third, the mechanism design approach assumes a kind of coercive power of the designer: The outcome of the mechanism can be implemented without the citizens’ explicit consent.

Our argument is that there is a discrepancy between these tacit assumptions in the mechanism design approach and observed features of the democratic process. It is our aim to bridge this gap. In particular, we modify the standard notion of a mechanism in three ways:

• First, we allow only binary messages. This reflects the idea that, in a democratic decision-making process, citizens are often unable to express their preferences in full detail.

• Second, we allow a selfish agenda-setter to intervene in the decision-making process. In democratic systems, the process is shaped by politicians, activists, lobbyists, or civil servants who have preferences of their own.

• Third, we require the explicit consent of a majority of citizens before the status quo can be replaced by any alternative outcome. This is arguably the most basic condition one would want to impose on a democratic process.

There is a natural tension between the agenda-setter’s selfishness and the requirement of majority voting. In particular, the need for approval by the majority could be seen as balancing the power of the selfish agenda-setter.

We are now going to give a more formal description of the kind of decision-making process that we refer to as a democratic mechanism. It can be decomposed into two parts: first, private information is communicated and shared through binary messages. Second, a decision is taken through voting. More specifically, decision-making in a democratic mechanism proceeds as follows:

Citizens simultaneously send binary messages. We denote the binary message space by $\{Yes,No\}.$ We will often refer to the message “Yes” as the positive signal, and to the message “No” as the negative signal. We denote the observed share of citizens who have sent the positive signal by $\delta \in [0,1].$ For every public good problem $P\in {\mathcal {P}},$ an information mapping$\varphi ^{P}$ designates a feasible public good level given the observed share of positive signals. In mapping reports to outcomes, the information mapping bears a resemblance to a “mechanism” in the conventional sense (albeit with a restricted message space). The crucial difference is that the communication entering the information mapping is mere cheap talk. The alternative designated by $\varphi ^{P}$ is not “automatically” implemented. Instead, after messages have been sent and $\delta$ has been observed, there is a voting procedure V in which a selfish agenda-setter makes a proposal that may or may not coincide with $\varphi ^{P}(\delta ).$ The status quo can only be replaced by an alternative if the majority explicitly approves it.⁵ However, the voting procedure V may specify any number of additional voting stages before this final decision is made. Let $\varphi = (\varphi ^{P})_{P\in {\mathcal {P}}}.$ Then, the pair $(\varphi , V)$ constitutes a democratic mechanism.⁶

Like a “mechanism” as conventionally understood, a democratic mechanism involves a mapping from messages to outcomes. In addition, however, it involves voting on the suggested outcome as well as agenda-setting by a selfish agent.

Given a democratic mechanism $(\varphi , V)$ and a public good problem $P\in {\mathcal {P}}$ (with type space Z,  feasible set $Q, \ldots$ ), let a communication strategy$\sigma ^{P}: Z \rightarrow \{ Yes, No\}$ assign a message to each type. Similarly, let a proposal strategy$\rho ^{P}: Z \times [0,1] \rightarrow Q$ assign a proposal to the agenda-setter’s type and to the observed share of positive signals.

We say that citizens can manipulate information sharing in the democratic mechanism $(\varphi , V)$ if there is $P\in {\mathcal {P}}$ such that the following holds: For every pair⁷$(\rho ^{P}, \sigma ^{P})$ such that

$$\begin{aligned} \varphi ^{P}(\delta _{i} (\sigma ^{P})) = \rho ^{P} (z,\delta _{i} (\sigma ^{P})) = q_{i}, \quad \forall i\in N, \ \forall z\in Z, \end{aligned}$$

there is a subset ${\widehat{Z}} \subset Z$ and a communication strategy ${\widehat{\sigma }}^{P}$ such that (i) ${\widehat{\sigma }}^{P} (z) = \sigma ^{P} (z)$ for all $z\in Z \setminus {\widehat{Z}},$ while ${\widehat{\sigma }}^{P} (z) \ne \sigma ^{P} (z)$ for some $z\in {\widehat{Z}}$; and (ii) the strategy profile $(\rho ^{P}, {\widehat{\sigma }}^{P})$ makes all members of ${\widehat{Z}}$ weakly better off⁸, and makes some members of ${\widehat{Z}}$ strictly better off than the strategy profile $(\rho ^{P}, \sigma ^{P}).$ The problem of manipulation is familiar from mechanism design theory. We note that the above definition of manipulation allows citizens to participate in a coordinated deviation even if they have no strict incentive to do so. This definition of manipulation makes it harder to discover the state and implement the Condorcet winner, and thus makes our existence result stronger. A narrower definition of manipulation (that is, requiring that citizens only participate if they become strictly better off), however, would not undo the impossibility result stated in Proposition 1. In order to derive the impossibility result, we have to consider the case where a group of citizens sharing the same preference ranking over alternatives coordinate their actions in order to manipulate information sharing. We note that the above definition of manipulation would even allow coordination within larger groups of citizens.

We say that the agenda-setter can exploit information sharing in the democratic mechanism $(\varphi , V)$ if there is $P\in {\mathcal {P}}$ such that the following holds: For every pair $(\rho ^{P}, \sigma ^{P})$ of a proposal and a communication strategy such that

$$\begin{aligned} \varphi ^{P}(\delta _{i} (\sigma ^{P})) = \rho ^{P} (z,\delta _{i} (\sigma ^{P})) = q_{i}, \quad \forall i\in N, \ \forall z\in Z,\end{aligned}$$

there are a state $i\in N$ and a type $z\in Z$ such that, upon observing $\varphi ^{P}(\delta _{i} (\sigma ^{P})),$ citizen z is better off proposing some ${\widehat{q}} \in Q \setminus \{q_{i}\}$ rather than proposing $q_{i}.$ The problem of exploitation is not present in standard mechanism design theory.

We say that a democratic mechanism $(\varphi , V)$implements the Condorcet winner if the following holds: For every public good problem $P\in {\mathcal {P}},$ there are strategies $(\rho ^{P}, \sigma ^{P})$ such that (i) $\varphi ^{P}(\delta _{i} (\sigma ^{P})) = \rho ^{P} (z,\delta _{i} (\sigma ^{P})) = q_{i}$ for every $i\in N$ and every $z\in Z,$ (ii) citizens cannot manipulate information sharing, and (iii) the agenda-setter cannot exploit information sharing.⁹

4 Baseline democratic mechanism

The simplest possible voting procedure is the following: After observing the messages sent by citizens, a selfish agenda-setter makes a proposal. Citizens decide by simple majority voting whether to implement this proposal or stick to the status quo. A democratic mechanism which involves this voting procedure (and some information mapping) is called a baseline democratic mechanism. In a baseline democratic mechanism, the decision to vote in favor of the proposal or the status quo is binary and final. Hence, there is no room for strategic behavior during the voting procedure. Indeed, sincere voting is optimal in a baseline democratic mechanism. That is, if the agenda-setter has made the proposal $q\in Q,$ then citizen z votes in favor of q if and only if he prefers it to zero public good provision, which is the status quo. More formally, citizen z votes in favor of q if and only if $z\ge c(q)/q.$

We want to show that baseline democratic mechanisms do not generally implement the Condorcet winner. In the previous section, we have already hinted at the two conditions for implementation of the Condorcet winner: The citizens should have no incentive to manipulate information sharing, and the agenda-setter should have no incentive to exploit information sharing, whatever his type is. For baseline democratic mechanisms, we establish impossibility in two ways: first, Proposition 1 below shows that whenever information sharing is not manipulated, it can be exploited. Then, we take the opposite perspective: Suppose that the agenda-setter does not exploit information sharing. Proposition 2 claims that, under an additional condition on the public good problem, a subset of citizens can successfully manipulate information sharing if the agenda-setter does not exploit it.

Proposition 1

In a baseline democratic mechanism, if citizens do not manipulate information sharing, then the agenda-setter can exploit it. In particular, exploitation is possible for every $P\in {\mathcal {P}}.$

The proof of Proposition 1 can be found in Appendix B.

Our definition of implementation requires that exploitation is impossible for every $P\in {\mathcal {P}}.$ Proposition 1 not only says that there is $P\in {\mathcal {P}}$ for which exploitation is possible. Actually, we have shown that, even in the absence of manipulation, exploitation can prevent implementation in every public good problem $P\in {\mathcal {P}}.$

Now we turn to manipulation of information sharing by citizens. We allow groups of citizens with the same preference ranking to coordinate their signals. We allow manipulations that depend on cooperation of citizens who only weakly benefit. This is a conservative assumption that biases our results against implementation.

Given that we work with a continuum society, it is not meaningful to consider “unilateral deviations” by individual citizens. Instead, we have assumed that citizens who have the same preference ranking over the feasible alternatives can coordinate their actions. For the implementation of the Condorcet winner, we require that it is robust to deviations by such a group of citizens. This approach is in line with one of the main insights of a recent paper by Bierbrauer and Hellwig (2016) , who argue that such “coalition-proofness” is a desirable property of an incentive mechanism. The assumption that groups of citizens with the same preference ranking can coordinate their moves is clearly more conservative than allowing only deviations by a smaller group or by individuals. One might wonder whether groups of citizens who do not all have the same preference ranking could also coordinate their actions.

In particular, we will consider a subset of citizens denoted by $Z_{-}.$ This set $Z_{-} \subset Z$ contains all types lower than $c(q_{1})/q_{1}.$ Those are the citizens who consistently prefer lower public good levels to higher ones. Continue to suppose that information is shared by having citizen z send the positive signal if and only if $z\ge z^{P},$ for some $z^{P} > c(q_{1}) / q_{1}.$ Citizens in $Z_{-}$ may be able to manipulate this information sharing in the following way: Some share of members of $Z_{-}$ could send positive instead of negative signals. In this way, they could mimic the vote share associated with a higher state than the actual state. Thereby, they would prompt the agenda-setter to make a proposal which is “too high.” This proposal would then lose against the status quo, resulting in zero public good provision.

To be more precise, let us consider public good problems with the following properties:

Definition 1

• 1. The public good problem $P\in {\mathcal {P}}$ has the distance property if ${\widetilde{q}}_{i} < q_{i+1}$ for every $i=1,\ldots , n-1.$

• 2. Suppose that the public good problem $P\in {\mathcal {P}}$ has the distance property. Then, a state $i\in N$ is concealable if $F_{i}(z)-F_{i+1}(z)$ is a quasi-concave function of z,  and attains its unique maximum at a point in $Z_{-}.$

The intuition behind the distance property is as follows: due to the single-peaked preferences, if the true state is i,  and the agenda-setter “overshoots” by proposing a quantity somewhat greater than $q_{i},$ then a majority would prefer that greater quantity to the status quo. If the scope for “overshooting” is so great that even $q_{i+1}$ would be preferred by the majority over the status quo, then the distance property is violated.

Let us briefly discuss possible economic interpretations of the “distance property.” For instance, consider the example of a school district that decides on the number of teachers it hires. This problem would not have the distance property: The increments between feasible alternatives are (nearly) arbitrarily small. After all, there is no constraint which says that teachers must be hired in units of, say, a hundred teachers. As a counter-example, consider the case of building a new bypass road around a city. In such a case, the available options could be (i) building no new road at all, (ii) building the road as a single carriageway, or (iii) building the road as a dual carriageway. This problem would have the distance property: The costs and benefits differ a lot between the different options, and there is no easy way to introduce additional options which differ only incrementally from the available alternatives. After all, building only a short piece of a bypass road is not useful, nor are arbitrarily small stretches of dual carriageways.

The next proposition claims that, in a baseline democratic mechanism, even if the agenda-setter does not exploit information sharing, implementation fails due to manipulation when the distance property holds and a state is concealable.

Proposition 2

In a baseline democratic mechanism, if the agenda-setter does not exploit information sharing, then citizens can manipulate it. In particular, manipulation is possible for every public good problem $P\in {\mathcal {P}}$ which satisfies the distance property, and in which at least one state is concealable.

The proof of Proposition 2 can be found in Appendix B. We now provide a numerical example which illustrates the distance property and the concealable state.

Example 1

Fix some $\varepsilon >0.$ Let the type space be $Z=[\varepsilon , \varepsilon +1 ],$ and the cumulative distribution functions

$$\begin{aligned} F_{1}(z)= & {} z-\varepsilon ,\\ F_{2}(z)= & {} (z-\varepsilon )^{1.2}. \end{aligned}$$

Moreover, let the cost function be $c(q) = q^{1.1} + \varepsilon q.$ This implies that marginal cost is $c^{\prime }(q) = 1.1 ( q^{0.1}) + \varepsilon$ and average cost $c(q)/q = q^{0.1}+\varepsilon .$

Using the equality $F_{k}(c^{\prime }(q_{k})) = 1/2,$ we can compute the Condorcet winners

$$\begin{aligned} q_{1}= & {} \left( \frac{0.5}{1.1} \right) ^{10} \approx 0.000377,\\q_{2}= & {} \left( \frac{0.5^{(1/1.2)}}{1.1}\right) ^{10} \approx 0.0012. \end{aligned}$$

Moreover, we can use the equality $F_{1} (c(\widetilde{q}_{1})/{\widetilde{q}}_{1} ) =1/2$ to compute

$$\begin{aligned} {\widetilde{q}}_{1} = (0.5)^{10} \approx 0.000977. \end{aligned}$$

Indeed, we observe that $q_{1}< {\widetilde{q}}_{1} < q_{2},$ that is, the distance property holds in this example.

It is easy to check that the vertical distance $F_{1}(z)-F_{2}(z)$ is maximized at the point

$$\begin{aligned} z^{*} = \left( \frac{1}{1.2} \right) ^5 +\varepsilon \approx 0.402 + \varepsilon .\end{aligned}$$

The set $Z_{-}$ contains all types lower than

$$\begin{aligned} c(q_{1})/q_{1} = (q_{1})^{0.1}+\varepsilon = \frac{0.5}{1.1} + \varepsilon \approx 0.4545 + \varepsilon . \end{aligned}$$

We observe that the inequality $z^{*} < c(q_{1})/q_{1}$ holds, that is, state 1 is concealable in this example.

The analysis and propositions in this section amount to an impossibility result: The baseline democratic mechanism does not generally implement the Condorcet winner. We note that either Proposition 1 or Proposition 2 alone imply this impossibility. Hence, it is not the interaction of exploitation and manipulation which leads to the failure of implementation. Even if either exploitation or manipulation could be eliminated, implementation of the Condorcet winner would remain impossible with a baseline democratic mechanism.

In the next section, we extend democratic mechanisms beyond the “baseline” in such a way that implementation of the Condorcet winner is accomplished.

5 Implementation result

In this section, we show how the baseline democratic mechanism can be modified in order to obtain the desired implementation of the Condorcet winner. In particular, two modifications of the baseline democratic mechanism are needed: first, voting proceeds in two stages rather than just one stage. Second, a small representative sample of the population (as well as the agenda-setter) is granted a conditional privilege.

The subsequent derivations also reveal that both modifications are necessary to obtain the general implementation result on our theorem. Privileges for the sample group and the agenda-setter are needed to ensure that they can only exploit or manipulate information sharing by aiming for a public good level higher than the Condorcet winner. The two-stage voting procedure is a corrective by which citizens outside the sample group can prevent excessive public good provision. Therefore, the combination of the (conditional) privileges and the two-stage voting procedure is essential for the implementation result. Neither a scheme of privileges nor a voting procedure with several stages alone can overturn the impossibility result described in the previous section.

5.1 Description of the mechanism

We now give the formal description of the democratic mechanism with sampling and two-stage voting.

5.1.1 Information mapping

A sample group of size $\lambda \in (0,1)$ is randomly drawn from the population. Sample group members simultaneously send binary messages. The share $\delta$ of sample group members who have sent the positive signal is observed. When the public good problem is $P\in {\mathcal {P}},$ one feasible alternative is designated by the map $\varphi ^{P}.$

5.1.2 Voting procedure

An agenda-setter determines the proposal $q\in Q.$ The voting procedure has two stages: first, there is a selection stage in which citizens choose either the proposal q or the amendment $\psi _{-}(q).$ If the share of citizens who choose q is at least $(1+\lambda )/2,$ then q is selected. Otherwise, $\psi _{-}(q)$ is selected. Second, there is a voting stage in which citizens choose either the selected alternative from the previous stage, or the status quo. In order to win, the selected alternative requires a super-majority of $(1+\lambda )/2$ if the selected alternative is q,  or a simple majority if the selected alternative is $\psi _{-}(q).$¹⁰

5.1.3 Conditional privilege

If and only if the proposal q is finally implemented, then the agenda-setter and the sample group members are tax-exempt and, in addition, receive a transfer of $\tau .$

The intuition behind this democratic mechanism is as follows: On the one hand, the privileges granted to the agenda-setter and sample group members give them an incentive to aim for a high public good level, regardless of their type. On the other hand, the two-stage voting procedure and the conditional character of the privilege allows citizens to rebuke any attempt by the “privileged few” to implement an excessive public good level.

The following theorem is the main implementation result of this paper.

Theorem 1

With $\lambda$ close to zero, the democratic mechanism with sampling and two-stage voting implements the Condorcet winner if $\tau$ is sufficiently large.

The proof of Theorem 1 is relegated to Appendix C.

Since the sample contains the same information as the entire population, this eliminates any incentives by members of the sample to manipulate information sharing. However, it does give rise to an incentive for the agenda-setter to exploit information sharing. In order to counteract this problem, the tax-exemption is conditioned on the outcome of the selection stage. At that stage, the entire population is given an opportunity to make a minimal downward correction of the proposal. Given that $\tau$ is sufficiently high, this eliminates the incentive to exploit information sharing.

For a better understanding of Theorem 1 and its proof, let us briefly discuss what it means for the transfer $\tau$ to be “sufficiently large.” In the proof of Theorem 1, we have had to check whether it can be profitable for the agenda-setter or sample group members to prevent the implementation of the Condorcet winner, say $q_{i}.$ If they had such a profitable deviation, it would result in some quantity ${\widehat{q}}_{i} \ne q_{i}$ being implemented instead. In the proof, we have shown that this is only possible if ${\widehat{q}}_{i}$ has been an amendment at the selection stage. Hence, the agenda-setter and sample group would not receive any privileges under their deviation, and so an agenda-setter or sample group member of type z would receive a payoff of $z\widehat{q}_{i} -c({\widehat{q}}_{i}).$ Without the deviation, the Condorcet winner would be implemented, and agenda-setter as well as sample group members would not pay tax but rather receive the transfer. Hence, an agenda-setter or sample group member of type z would receive a payoff of $zq_{i} + \tau .$ Hence, $\tau$ is “sufficiently large” if it satisfies

$$\begin{aligned} \tau \ge z({\widehat{q}}_{i}-q_{i}) -c({\widehat{q}}_{i}). \end{aligned}$$

In a subclass of public good problems, transfers are not needed; that is, even $\tau = 0$ may satisfy the above inequality and be “sufficiently large.” We discuss this issue in Sect. 5.3 and Corollary 1 below.

5.2 Discussion of the mechanism

We have shown that the PCSS mechanism implements the alternative that is the Condorcet winner. One may object, however, that the resulting allocation under our implementation result is not stable to majority voting: After all, the vast majority would prefer that the Condorcet-winning alternative be implemented without any tax-exemption of transfer to the agenda-setter and to sample group members. Since the sample group can be small, however, we can say that the PCSS mechanism implements the Condorcet winning alternative, while getting close to the Condorcet winning allocation. The small wedge between the implemented allocation and the Condorcet winning allocation is the price that one pays for accomplishing implementation of the Condorcet winning alternative. We emphasize that the mechanism only grants privileges conditional on the approval of the proposal by a super-majority of size $(1+\lambda )/2.$ This is the same as saying that sample group members become privileged only if the majority of citizens outside the sample group give explicit approval to the proposal, and implicit approval to the privileges. This argument clarifies the motivation for the super-majority rule: whenever a decision on a feasible alternative implies granting privileges to the sample group, this decision requires a majority of citizens outside the sample group. However, when citizens vote on a feasible alternative which is an amendment (rather than a proposal), no privileges are involved, and so a simple majority among the entire population suffices.

Compared to the baseline democratic mechanism, the mechanism discussed in the present section requires voting in two stages: first, there is a selection between the proposal, say q,  and its “predecessor” $\psi _{-}(q).$ Second, the winner of that selection stage is pitted against the status quo. We stress that these two stages suffice for the implementation result, regardless of the number of states and alternatives. As an alternative decision-making procedure, one might have in mind to elicit preferences over all the pair of feasible alternatives. Clearly, this would require a number of voting stages increasing with $n^{2}-n.$ Thus, the democratic mechanism with sampling and two-stage voting is attractive from the point of view of procedural efficiency. In reality, it may often be costly to organize many voting stages, that is, many stages of referendum on the same issue. Therefore, procedural efficiency is an important concern, especially in large societies.

We note that the existence theorem does not depend on the prior belief of citizens about the probability distribution p on the states. All citizens are assumed to share a common prior belief about the probability of the different states. Our results do not depend on what exactly these prior probabilities are. This is an important and desirable robustness property of the mechanism.¹¹

In all, we have seen that well-designed and conditional privileges for a small representative sample group may help societies overcome uncertainty about the underlying type distribution, share dispersed information, make more informed decisions, and choose policy options preferred by a majority.

We have argued that, in order to achieve implementation, it is vital to grant a privilege to some members of the society. This privilege consists of a tax-exemption and a transfer. Taxes are typically not raised for one purpose at a time, nor to finance specifically one public good project. Therefore, when a citizen is granted a tax-exemption, this gives him a benefit which goes beyond not participating in the cost of the public good which we consider. In our model, such extra benefits would correspond to a cash transfer granted along with a tax-exemption. Therefore, a privilege which encompasses both a tax-exemption and a transfer seems well-motivated. Nevertheless, in the next subsection, we will show that implementation can be accomplished even if $\tau =0$ under an extra restriction on the collective choice problem. Moreover, we will show that even without this restriction, implementation with $\tau =0$ is possible if one is willing to add more selection stages. As a general remark on concerns about equal treatment and non-discrimination, we would like to stress that the privileges for sample group members could easily be thought of as a subsidization. In actual constitutions, equal treatment clauses do not apply to subsidies, and thus defining privileges as subsidies would avoid violating equal treatment principles (see e.g. Gersbach et al. 2013).

5.3 Extensions

Theorem 1 states an implementation result provided that the transfer $\tau$ is sufficiently large. We have pointed out that this transfer can be suitably interpreted as the benefit of an exemption from all taxes other than the ones needed to finance the public good provision under consideration here. We are now going to derive a condition under which the implementation result holds even for $\tau = 0.$

In the proof of Theorem 1, it turns out that a strictly positive transfer $\tau >0$ is necessary for implementation only if there are a state $i\in N,$ a type $z \in Z ,$ and a quantity ${\widehat{q}}_{i} \in Q$ which satisfy the inequalities

$$\begin{aligned} {\widetilde{q}}_{i} \> \ {\widehat{q}}_{i}> & {} q_{i},\end{aligned}$$

(1)

$$\begin{aligned} z{\widehat{q}}_{i} -c({\widehat{q}}_{i} )> & {} zq_{i}, \end{aligned}$$

(2)

If such $i\in N$ and ${\widehat{q}}_{i} \in Q$ do not exist, then the implementation result of Theorem 1 holds even for $\tau =0.$ Thus, from the proof of Theorem 1, we obtain the following corollary:

Corollary 1

Consider a subset of public good problems with the property that the type space Z,  the cost function c,  and the cumulative distribution functions $(F_{i})_{i\in N}$ are such that for all $i\in N$ and for all $z\in Z,$ it holds that

$$\begin{aligned} z\le \frac{c[\psi _{-}({\widetilde{q}}_{i})]}{ \psi _{-}({\widetilde{q}}_{i}) - q_{i } }. \end{aligned}$$

On this subset of public good problems, the democratic mechanism with sampling and two-stage voting implements the Condorcet winner with $\tau =0.$

In the description of the democratic mechanism with sampling and two-stage voting, we have imposed that any proposal $q\in Q$ be pitted against its “predecessor” $\psi _{-}(q)$ at the selection stage. This is equivalent to requiring the agenda-setter to propose a pair of two “successive” alternatives. Another way to accomplish implementation is to randomly appoint a second, “rival” agenda-setter who chooses the amendment and receives a reward (tax-exemption and transfer) if and only if the amendment is selected and becomes the final outcome of the mechanism. In such a model, one can show that there is a Bayesian equilibrium in which the rival agenda-setter always believes with probability one that his proposal is the Condorcet winner and always suggests the predecessor of the proposal as an amendment. The existence of such an equilibrium follows from the same logic as the proof of Theorem 1.

One extension is to modify the democratic mechanism with sampling and selection by adding more selection stages. For this purpose, we define $\psi _{-}^{t} = \psi _{-}^{t-1} (\psi _{-}(q))$ for $t=1,2,\ldots$. Hence, in particular, $\psi ^{2}_{-} (q) \equiv \max \{q\in Q \vert q < \psi _{-}(q)\}.$ If the proposal is q,  then the first selection stage would be between q and $\psi _{-}(q),$ the second stage between $\psi _{-}(q)$ and $\psi ^{2}_{-}(q),$ and, in general, selection stage t between $\psi _{-}^{t-1}$ and $\psi _{-}^{t},$ as long as an amendment defeats the current proposal. For such a more general mechanism with T selection stages, it can be shown that implementation of the Condorcet winner with $\tau =0$ is possible if the type space Z,  the cost function c,  and the cumulative distribution functions $(F_{i})_{i\in N}$ are such that for all $i\in N$ and for all $z\in Z,$ it holds that

$$\begin{aligned} z\le \frac{c[\psi _{-}^{T}({\widetilde{q}}_{i})]}{ \psi ^{T}_{-}({\widetilde{q}}_{i}) - q_{i } }. \end{aligned}$$

Thus, there is a trade-off between the mechanism’s procedural efficiency and its ability to ensure equal treatment and, in particular, a limitation of the sample group’s privileges.

One important extension of our model is to ask whether the implementation of the Condorcet winner can be accomplished if the status quo is not zero public good provision, but some other public good level ${\bar{q}}\in Q\setminus \{0\}.$ If this is the case, then the implementation result of Theorem 1 satisfies a kind of “dynamic robustness” property: If the state of nature changes over time, then the democratic mechanism with sampling and two-stage voting can be applied again in order to move from the “old” Condorcet winner to the “new” Condorcet winner. We conjecture that, indeed, the democratic mechanism with sampling and two-stage voting can be suitably modified to implement the Condorcet winner for any given status quo. In particular, the democratic mechanism needs two features to ensure implementation:

• First, sample group members as well as the agenda-setter must be given a conditional privilege that is greater the more the agenda-setter’s proposal differs from the status quo.

• Second, there must be a selection stage in which citizens choose between the proposal and an amendment which is slightly closer to the status quo than the proposal. As before, the sample group members’ and agenda-setter’s privilege must be conditional on the acceptance of the proposal.

To be more specific, one could define an $(\gamma , \theta )$-tax treatment specifying that a citizen receives a lump sum transfer of $\theta$ and needs to pay a tax $\gamma c(q)$ when the public good level is $q\in Q.$ If $\gamma >1$ is chosen sufficiently high, then a citizen of any type $z\in Z$ who is subjected to an $(\gamma , \theta )$-tax treatment strictly prefers zero public good provision over $q_{1},$ and strictly prefers $q_{i}$ over $q_{i+1}$ for any $i=1,\ldots , n-1.$ In addition, if $\theta >0$ is chosen sufficiently high, then a citizen of any type $z\in Z$ prefers to be subjected to the $(\gamma , \theta )$-tax treatment than to be a “regular” citizen who pays c(q) and receives no transfer.

Consider the following modifications to the democratic mechanism with sampling and two-stage voting: at the selection stage, the proposal q is pitted against $\psi _{-}(q)$ (as before) if $q>\bar{q},$ but is pitted against $\psi _{+}(q)$ if $q<{\bar{q}}.$ If $q=\bar{q},$ then ${\bar{q}}$ remains in effect. The agenda-setter and the sample group are granted a tax-exemption and receive the transfer of $\tau$ (as before) if the agenda-setter proposes some $q\in Q$ with $q>{\bar{q}},$ and subsequently q “wins” both at the selection and voting stages. The agenda-setter and the sample group are subjected to the $(\gamma , \theta )$-tax treatment if the agenda-setter proposes some $q\in Q$ with $q<{\bar{q}},$ and subsequently q “wins” at both the selection stage and voting stage. As before, the special treatment of the sample group imposes a cost on each citizen outside the sample group but this cost vanishes in the limit when the mass of the sample group tends to zero.

6 Simplified implementation

So far in this paper, we have aimed at implementation for the entire set ${\mathcal {P}}$ of public good problems. In this section, we are going to restrict attention to the subset of public good problems which have the distance property. On that subset of public good problems, the agenda-setter’s opportunities to exploit information sharing are restricted. This allows us to accomplish implementation of the Condorcet winner with a simpler mechanism.

We have previously defined the distance property. Intuitively, it means that feasible alternatives are drastically different from each other. When the distance property holds, any alternative higher than the Condorcet winner will lose against the status quo, and can therefore not be implemented. Thus, an agenda-setter who wants to exploit information sharing can only do so “in one direction,” namely, by aiming at an alternative lower than the Condorcet winner. This allows for the Condorcet winner to be implemented using a simpler democratic mechanism. In particular, it requires only an unconditional privilege for a representative sample group. Moreover, a single voting stage suffices. More specifically, consider the following democratic mechanism with sampling and one-stage voting. A randomly drawn sample group of size $\lambda \in (0,1)$ sends binary messages, and the information mapping $\varphi$ as defined in the previous section is used to designate an alternative. Then, an agenda-setter chooses a proposal $q\in Q,$ and citizens vote between q and the status quo. The agenda-setter and the sample group are tax-exempt.

Theorem 2

For public good problems with the distance property, the Condorcet winner can be implemented by a democratic mechanism with sampling and one-stage voting, with $\lambda >0$ sufficiently small.

The proof can be found in Appendix D.

If the democratic mechanism with sampling and one-stage voting was applied to a public good problem without the distance property, it would lead to over-provision of public good. The reason is that the mechanism gives sample group members incentives to exaggerate the benefits from public good provision.

One might wonder which practical interpretation can be given to the distance property. Suppose that the issue at hand is to decide on a large infrastructure project, such as building a tunnel either with a single tube or with two tubes. This problem could be interpreted as having the distance property: There are few feasible alternatives, and their costs and benefits drastically differ from each other. As a counter-example, consider the problem of choosing the number of police officers in a city. This choice problem features many different alternatives among which one can choose “almost continuously.” Such situations should be interpreted as not having the distance property.

7 Discussion, applications, and conclusion

The main insight of this paper is that democratic decision-making procedures can be used to identify and implement policies desired by the majority even in the presence of uncertainty about the type distribution. The resolution of such uncertainty and the associated implementation result hinge crucially on the use of a conditional privilege for a small sample group and the agenda-setter. The privilege itself and its conditional character motivate members of the sample not to exploit nor manipulate the resolution of uncertainty in any way.

Absent any such conditional privilege, however, democratic mechanisms based solely on communication prior to voting are prone to strategic behavior. In particular, there are two incentive problems: The agenda-setter’s selfishness creates an incentive to exploit information sharing. Even in the absence of exploitation, information sharing is prone to manipulation.

We stress that the introduced democratic mechanisms do not depend on the citizens’ ex ante beliefs about the states of nature. This is a particularly desirable robustness property of democratic mechanisms, since these mechanisms should be applicable to a variety of situations and since their rules should not depend on citizens’ current beliefs.

We ask under what conditions citizens have incentives to share their private information and thereby resolve uncertainty about the underlying type distribution. The paper does, however, also allow for some conclusions about settings without such uncertainty about the underlying type distribution. To see this, suppose that citizens were informed about the underlying distribution of preferences in the population. In that case, the communication stage of our democratic mechanism would be redundant. However, the selection stage of the democratic mechanism would still be useful as a safeguard against the selfishness of an agenda-setter. For instance, think of the agenda-setter as a bureaucrat who wishes to maximize the size of public projects. It is a well-known theme in the political economy literature that sometimes privileged groups, such as members of the government bureaucracy, would like to maximize public good provision in order to secure their own perks or ego rents. One could explore to what extent the corrective present in the selection stage of our democratic mechanism with sampling and two-stage voting and the related conditional character of the privileges could be applied to that problem. Giving the citizens a vote between the proposed alternative and a “smaller” alternative could protect the public from this kind of behavior in some circumstances (depending how different the alternatives are from each other).

In the present paper, we assume that the message space of all citizens accept the agenda-setter is binary. This restriction applies both at the communication and voting stages. In the latter case, the motivation is that a referendum typically reduces complex decisions to a matter of simple Yes-or-No approval. At the communication stage, the restriction to binary messages is a mere simplification. Our results would persist if we allowed for a richer message space at the communication stage. This is straightforward with regard to our existence result: Implementation is possible with binary messages, and citizens with richer message spaces can replicate binary messages, so the existence result holds for richer message spaces. For the impossibility result, what we need is that a particular group of citizens can emulate in one state the messages that would be sent in another state. As long as all citizens have the same message space, this is independent of the assumption that the message space is binary.

In terms of practical implementation, it would be possible to subsume the selection and voting stages on one ballot paper. On that ballot, citizens could express their preferences over the proposal, the amendment, and the status quo at once. Such “three-way” ballots are possible in reality and have been applied in the Swiss system of direct democracy.

There is a variety of extensions and further applications which can be considered in future research. For instance, one could examine to what extent our results carry over to choices from different sets of possible policies, such as continuous policy spaces, or multi-dimensional collective choice problems in which several public goods can be combined in a bundle of public goods. Moreover, one might consider an electorate with different income levels and the possibility to differentiate the tax burden as a function of income. In such a model, one could investigate the effect of a policy chosen by a democratic mechanism on the degree of inequality among citizens.

Another relevant question is how the mechanisms discussed in the present paper could be applied in parliamentary settings. Procedural efficiency is an issue in parliamentary democracy as well, since excessively long deliberations on a single issue have opportunity costs, and distract attention from other topics. Procedurally efficient parliamentary decisions might be achieved by a democratic mechanism with sampling and two-stage voting with a randomly chosen sample group from the population and a subsequent decision by a majority in parliament.

While such extensions will considerably expand the scope of democratic mechanisms in a polity, it is likely that optimal democratic mechanisms with procedural efficiency will involve conditional tax privileges for small groups. In the presence of uncertainty about the type distribution, we expect such conditional privileges to be an essential ingredient of democratic mechanisms.

Appendices

Appendix A

In Appendix A, we provide a detailed account of assumptions on the cost function, the probability distributions, the type space, and the Condorcet winners which generate the properties imposed in Sect. 2 and, in particular, in Assumption 1.

1.1 Cost function

Although we will eventually consider a discrete set of possible quantities, it is convenient to start by defining continuous cost and utility functions on ${\mathbb {R}}_{+}.$ In particular, we assume that the per capita cost of providing a quantity $q\in {\mathbb {R}}_+$ of the public good is given by a twice continuously differentiable, strictly increasing, and strictly convex function $c: {\mathbb {R}}_{+} \rightarrow {\mathbb {R}}_{+}$ with $c(0)=0.$ This implies in particular that average cost c(q)/q is strictly increasing. One typical interpretation of such a cost function is that each citizen is initially endowed with $w \ (w>0)$ units of a private consumption good which can either be consumed or transformed into the public good. The per capita costs c(q) then represent the utility losses due to foregone private consumption.

1.2 Probability distributions

We assume that the family of probability distributions from which the types are drawn in each state can be represented by continuously differentiable probability density functions which satisfy a property known as the monotonicity of likelihood ratios. More formally, let the first derivative of $f_{k}$ be $(f_{k}^{\prime })_{k=1,\ldots ,n}.$ Then, we assume that $f_k (z)>0$ for all $k\in N$ and all $z\in Z$ and, moreover, that

$$\begin{aligned} \frac{f'_{k+1} (z)}{f_{k+1} (z)}>\frac{f'_{k} (z)}{f_{k} (z)}, \quad \forall z\in Z, \ \forall k\in N\setminus \{n\}. \end{aligned}$$

(3)

The monotonicity of likelihood ratios property has three key implications. First, the probability distribution associated with $F_{k+1}$ (strictly) first-order stochastically dominates the one associated with $F_{k}$ for every $k\in N\setminus \{n\},$ that is, $F_{k+1}(z) < F_{k}(z)$ for every $z\in int(Z).$ In that sense, the benefits from the public good are higher in state $k+1$ than in state k. Second, the monotonicity of likelihood ratios implies a single-crossing property of the probability density functions, which will be crucial for our analysis. Finally, the monotonicity of likelihood ratios imposes monotone Bayesian updating (Milgrom 1981). More specifically, citizen z believes in state $k=1,\ldots ,n$ with probability

$$\begin{aligned} \beta _{k}(z)=\frac{f_{k}(z) p_k}{\sum _{j=1}^{n} f_{j}(z) p_j}, \end{aligned}$$

(4)

and the associated probability distributions for citizen $z_{2}$ stochastically dominates the one for citizen $z_{1}$ if $z_{1}< z_{2}.$

We note that the monotonicity of likelihood ratios implies, loosely speaking, that a higher type tends to believe in higher states of nature with higher probability.

1.3 Type space

We assume that, for every $z\in Z,$ the most desired public good level of citizen z belongs to Q. Formally, since the most preferred public good level of citizen z is given by $z=c^{\prime }(q),$ we assume $c^{\prime }(0) \le inf(Z)$ and $c^{\prime }(q^{max}) \ge sup (Z)$ where inf(Z) and sup(Z) are the infimum and supremum of the type space Z and $q^{max}$ the highest possible public good level in Q.¹²

Together with the strict convexity of the cost function, this property implies that the preferences of each type $z\in Z$ are single-peaked, and the most preferred quantity of citizen z is that q which solves $c^{\prime }(q)=z.$

Moreover, we assume $c(q_{1})/q_{1} \in int(Z).$

1.4 Condorcet winner

Citizen z is the median voter in state k if $F_{k} (z) = 1/2.$ We define for each state $k\in N$ a quantity $q_{k} \in {\mathbb {R}}_{+}$ as the unique solution to

$$\begin{aligned} F_{k} \left( c'(q_{k}) \right) = {1}/{2}, \end{aligned}$$

so that $q_{k}$ is the most preferred quantity of the median voter in state k. The definition and the assumptions regarding the cost function and the monotonicity of likelihood ratios imply that $0<q_{1}<\cdots <q_{n}.$ Due to the strict convexity of the cost function, we have

$$\begin{aligned} \frac{c(q_{k})-c(q)}{q_{k}-q}< & {} c^{\prime } (q_{k}), \quad \forall q < q_{k}, \ \forall k\in N,\\ \frac{c(q_{k})-c(q)}{q_{k}-q}> & {} c^{\prime } (q_{k}), \quad \forall q > q_{k}, \ \forall k\in N.\\ \end{aligned}$$

Due to the single-peaked preferences, these statements can be expressed in terms of the distribution functions as Inequalities (5) and (6) below. These expressions are well-defined since $c(q_{1})/q_{1} \in int(Z).$

$$\begin{aligned} F_{k} \left( \frac{c(q_{k}) - c(q) }{q_{k} - q} \right)< 1/2, \quad \forall q<q_{k}, \ \forall k\in N, \end{aligned}$$

(5)

$$\begin{aligned} F_{k} \left( \frac{c(q_{k}) - c(q) }{q_{k} - q} \right)> 1/2, \quad \forall q>q_{k}, \ \forall k\in N. \end{aligned}$$

(6)

Verbally, in state k,  a simple majority of citizens prefers $q_k$ over any other quantity $q\in {\mathbb {R}}_{+} \setminus \{q_{k} \}.$ Thus, $q_{k}$ is the Condorcet winner in state k.

1.5 Point of indifference

Moreover, for every $k\in N,$ we define the quantity $\widetilde{q}_{k} \in {\mathbb {R}}_{+}$ as the unique¹³ solution to

$$\begin{aligned} F_{k}\left( c({\widetilde{q}}_{k}) / {\widetilde{q}}_{k} \right) = 1/2. \end{aligned}$$

(7)

In state k,  a majority of citizens prefers any quantity $q<{\widetilde{q}}_k$ to zero public good, but prefers zero public good to any quantity $q>{\widetilde{q}}_k.$ Given that average cost c(q)/q is strictly increasing and that $c(q)/q < c^{\prime }(q),$ we have ${\widetilde{q}}_{k} > q_{k}$ for every $k\in N.$

Appendix B

1.1 Proof of Proposition 1

Take any $P\in {\mathcal {P}},$ and suppose that citizens do not manipulate information sharing. That is, they use a communication strategy $\sigma ^{P}$ such that $\varphi (\delta _{i}(\sigma ^{P})) = q_{i}$ for every $i\in N.$ Due to sincere voting, if the true state is i,  the agenda-setter anticipates that any proposal $q\in Q$ such that $q < \widetilde{q}_{i}$ is going to win against the status quo. Suppose that the agenda-setter’s type z is such that $z=c^{\prime }(q)$ for some $q\in Q$ such that $q < {\widetilde{q}}_{i}$ and $q\ne q_{i}.$ In this case, it is in the agenda-setter’s interest to choose $\rho ^{P} (z, \delta _{i}(\sigma ^{P})) = q$ rather than $\rho ^{P} (z, \delta _{i}(\sigma ^{P})) = q_{i}.$ Indeed, he can exploit information sharing. $\square$

1.2 Proof of Proposition 2

Suppose by way of contradiction that a baseline democratic mechanism implements the Condorcet winner. Take some public good problem $P\in {\mathcal {P}}$ which has the distance property, and in which a state $i\in N\setminus \{n\}$ is concealable. Let $\sigma ^{P}$ be a communication strategy and $\rho ^{P}$ a proposal strategy such that

$$\begin{aligned} \varphi ^{P}(\delta _{k}(\sigma ^{P})) = \rho ^{P}(z,\delta _{k}(\sigma ^{P})) = q_{k} \end{aligned}$$

for every $k\in N$ and every $z\in Z.$ By construction of $\varphi ^{P},$ the communication strategy $\sigma ^{P}$ is such that citizen z votes Yes if and only if $z\ge z^{P}.$ We show that $\sigma ^{P}$ cannot be optimal.

Due to the premise that state $i\in N\setminus \{n\}$ is concealable, the function $F_{i}(z)-F_{i+1}(z)$ has a unique maximizer $z^{*}_{i}$ which belongs to $Z_{-}.$

Let ${\widetilde{z}} = \min \{z^{P}, z^{*}_{i}\}.$ We have

$$\begin{aligned} \delta _{i+1} (\sigma ^{P}) - \delta _{i} (\sigma ^{P}) \le F_{i} ({\widetilde{z}}) - F_{i+1}({\widetilde{z}}). \end{aligned}$$

In particular, this inequality implies

$$\begin{aligned} \delta _{i} (\sigma ^{P}) + F_{i}({\widetilde{z}}) \ge \delta _{i+1}(\sigma ^{P}). \end{aligned}$$

Due to continuity of the cumulative distribution function, there is a $\zeta$ such that $\zeta \le {\widetilde{z}} \le z^{*}_{i} \le {\widehat{z}}$ and

$$\begin{aligned} \delta _{i}(\sigma ^{P}) + F_{i}(\zeta ) = \delta _{i+1}(\sigma ^{P}). \end{aligned}$$

Consider a joint deviation from $\sigma ^{P},$ under which citizens $z\le \zeta$ vote Yes, and citizens $z> \zeta$ vote according to $\sigma ^{P}.$ Since $\zeta \le {\widehat{z}},$ this is a deviation by members of $Z_{-}$ only. If the true state is i,  then the resulting share of Yes-votes is $\delta _{i}(\sigma ^{P}) + F_{i}(\zeta ) = \delta _{i+1}(\sigma ^{P}).$ Thus, under this deviation, the proposal $q_{i+1}$ will be made at the voting stage with probability one if the true state is i. Since citizens vote sincerely, this proposal will be rejected since $q_{i+1} > {\widetilde{q}}_{i},$ and the resulting public good level will be zero. By construction, members of $Z_{-}$ prefer zero over $q_i.$ Now we have shown that the deviation by $Z_{-}$ is (strictly) profitable if the true state is i. Suppose next that the true state is some $j\in N\setminus \{i\}.$ Due to the distance property, no quantity $q\in Q$ with $q>q_{j}$ would be accepted at the voting stage in state j. Thus, under the deviation, the outcome must be some $q^{\prime }_{j}\le q_{j}$ if the state is j. All members of $Z_{-}$ weakly prefer $q^{\prime }_{j}$ to $q_{j}.$ Since $p_{i} > 0$ and thus $\beta _{i}(z)> 0$ for all $z\in Z,$ the deviation is (strictly) profitable in expectation. $\square$

Appendix C

1.1 Proof of Theorem 1

Now we turn to the proof of the implementation result. First, we are going to consider the final voting stage. The criterion for sincere voting differs depending on whether the final vote is between the proposal and the status quo or between the amendment and the status quo. We state the appropriate definition of sincere voting. Second, we are going to establish conditions under which decisions at the selection stage are also sincere, in a sense to be made precise. Third, we state a profile of strategies and beliefs which is a Bayesian equilibrium, involves sincere selection, and leads to the implementation of the Condorcet winner.

1.2 Sincere voting

The voting stage of the democratic mechanism with sampling and two-stage voting is a final and binary choice which leaves no room for profitable strategic behavior. As a result, citizens vote sincerely at the voting stage. However, the sample group receives a privilege conditional on final acceptance of the proposal. This conditional privilege must be taken into account in order to determine the appropriate meaning of “sincere voting” in the present context. Suppose that at the voting stage, the alternative $q\in Q$ is pitted against the status quo, which is zero public good provision. Consider first the case where q is not the original proposal, but the amendment. In that case, neither tax-exemptions nor transfers will be granted, so that sincere voting simply means that citizen z votes for q if and only if $z\ge c(q)/q.$

Now suppose instead that q is the original proposal made by the agenda-setter. Since $zq>0$ for all $q\in Q \setminus \{0\}$ and all $z\in Z,$ it is sincere for every sample group member to vote in favor of q. Citizen z,  who is not a sample group member, votes sincerely in favor of q if

$$\begin{aligned} z> \frac{ c(q) + \lambda \tau }{(1-\lambda )q}. \end{aligned}$$

The conditional privilege distorts sincere voting behavior for citizens outside the sample group. We argue that this distortion is negligible, however, when $\lambda >0$ is small enough.

For any given values of $\lambda$ and $\tau ,$ and for every state $i\in N,$ define ${\widetilde{q}}^{(\lambda , \tau )}_{i}$ as the solution to the equality

$$\begin{aligned} F_{i} \left( \frac{ c(\widetilde{q}^{(\lambda , \tau )}_{i} ) +\lambda \tau }{(1-\lambda ) \widetilde{q}^{(\lambda , \tau )}_{i} } \right) = 1/2. \end{aligned}$$

We note that ${\widetilde{q}}^{(\lambda , \tau )}_{i}<{\widetilde{q}}_{i}$ for $\lambda >0$ and $\tau \ge 0.$ Moreover, for any value of $\tau \ge 0,$ we find that ${\widetilde{q}}^{(\lambda , \tau )}_{i}$ converges to ${\widetilde{q}}_{i}$ as $\lambda \downarrow 0.$ Verbally, considering the limit as the sample group becomes arbitrarily small, the distortion of sincere voting behavior due to the conditional privilege vanishes.

1.3 Sincere selection

We turn to the selection stage which precedes the voting stage. In this selection stage, voters select either a proposal q or an amendment $\psi _{-}(q).$ In principle, a “selection strategy” should specify whether a citizen of a given type with a given belief about the state of nature selects any given proposal or the associated amendment. For the purpose of our argument, however, it will be enough to specify the optimal selection by citizens who believe with probability one that any alternative selected at the selection stage will win against the status quo at the voting stage. In that case, the decision to select the proposal or the amendment is a final and binary choice of the alternative to be implemented. Consequently, it is optimal to select sincerely, and we only have to spell out what sincere selection means: A citizen z outside the sample group prefers proposal q over amendment $\psi _{-}(q)$ if $zq - \frac{c(q) + \lambda \tau }{(1-\lambda )} > z\psi _{-}(q) -c(\psi _{-}(q)).$ A sample group member always prefers q over $\psi _{-}(q)$ because $\tau + zq > z\psi _{-}(q) -c(\psi _{-}(q)),$ that is, a sample group member sincerely selects the proposal.

1.4 Strategies and beliefs

We now proceed with the construction of a communication strategy, a proposal strategy, and some consistent beliefs. The communication strategy is as follows:

$$\begin{aligned} \sigma ^{P} (z) = {\left\{ \begin{array}{ll} Yes &{}\quad \text {if } \ z\ge z^{P},\\ No &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

The proposal strategy is such that the agenda-setter does not exploit information sharing, that is, for every $z\in Z,$ we have $\rho ^{P}(z,\delta ) = \varphi ^{P}(\delta ),$ thus:

$$\begin{aligned} \rho ^{P}(z,\delta ) = {\left\{ \begin{array}{ll} q_{1} \ &{}\quad \text {if} \ 0\le \delta< 1-F_{2} (z^{P}),\\ q_{k} \ &{}\quad \text {if} \ 1-F_{k}(z^{P}) \le \delta < 1-F_{k+1}(z^{P}), \ k=2,\ldots , n-1,\\ q_{n} \ &{}\quad \text {if} \ 1-F_{n} (z^{P}) \le \delta \le 1. \end{array}\right. } \end{aligned}$$

The agenda-setter (regardless of his type) believes with probability one that information sharing has been “successful” so that the alternative identified by the information mapping is the Condorcet winner. Thus, using $e_{i}$ to denote the n-vector with component i equal to one and all other components equal to zero, we can write his beliefs as follows:

$$\begin{aligned} \pi ^{P}_{AS} (\delta ) = {\left\{ \begin{array}{ll} e_{1} \ &{}\quad \text {if} \ 0\le \delta< 1-F_{2} (z^{P}),\\ e_{k} \ &{}\quad \text {if} \ 1-F_{k}(z^{P}) \le \delta < 1-F_{k+1}(z^{P}), \ k=2,\ldots , n-1, \\ e_{n} \ &{}\quad \text {if} \ 1-F_{n} (z^{P})\le \delta \le 1. \end{array}\right. }\end{aligned}$$

Citizens other than the agenda-setter, regardless of their type, believe with probability one that the proposal $q\in Q$ made by the agenda-setter is the Condorcet winner, thus:

$$\begin{aligned} \pi ^{P} (q) = {\left\{ \begin{array}{ll} e_{1} \ &{}\quad \text {if} \ q<q_{2},\\ e_{k} \ &{}\quad \text {if} \ q_{k}\le q < q_{k+1}, \ k=2,\ldots , n-1,\\ e_{n} \ &{}\quad \text {if} \ q \ge q_{n}. \end{array}\right. } \end{aligned}$$

We note that citizens other than the agenda-setter base their beliefs only on the proposal q made by the agenda-setter, while the observed share $\delta$ of positive signals determines the agenda-setter’s beliefs. This construction of beliefs has allowed us to specify optimal selection only for the case where citizens believe that whichever alternative they select at the selection stage is going to become the final outcome of the mechanism.

In order to establish the theorem, we need to show two things: first, the communication strategy $\sigma ^{P}$ and the proposal strategy $\rho ^{P}$ as defined above actually lead to the implementation of the Condorcet winner in every state. Second, these strategies are optimal given the beliefs $\pi ^{P}_{AS} (\delta )$ and $\pi ^{P}(q).$

1.4.1 Implementation

We see that $\rho ^{P} (z, \delta _{k}(\sigma ^{P})) = \varphi ^{P} (\delta _{k} (\sigma ^{P})) = q_{k}$ for every $k\in N.$ Thus, if the communication strategy $\sigma ^{P}$ and the proposal strategy $\rho ^{P}$ are played, then the agenda-setter believes with probability one in the true state, and he proposes the Condorcet winner. The beliefs $\pi ^{P}_{AS}$ and $\pi ^{P}$ are such that citizens believe with probability one that the quantity proposed by the agenda-setter is the Condorcet winner. Hence, all citizens believe that both the proposal made by the agenda-setter and the amendment would prevail against the status quo at the voting stage. Citizens select sincerely at the selection stage. In particular, all sample group members select the proposal. Since the proposal is the Condorcet winner, also at least half of the citizens outside the sample group select it. Hence, in the entire population, a share of at least $(1+\lambda )/2$ select the proposal. Because of sincere voting at the voting stage and the fact that the proposal is the Condorcet winner on the path of play, the Condorcet winner does become the final outcome of the mechanism, as desired.

1.4.2 Optimal signaling and agenda-setting

Now we show that no deviation by the agenda-setter or by sample group members can be profitable. Notice that sample group members and agenda-setter receive the payoff $zq_{k}+\tau \ge zq_{k}$ on the path induced by the profile under consideration when the state is k. Suppose by way of contradiction that there is a profitable deviation for the agenda-setter or (some coalition within) the sample group. For every $k\in N,$ let ${\widehat{q}}_{k}$ be the outcome which follows after a profitable deviation. Due to the premise that the deviation is profitable, there must be a state $i\in N$ such that ${\widehat{q}}_{i}>q_{i}.$ This is only possible if the agenda-setter proposed either ${\widehat{q}}_{i}$ or $\psi _{+}({\widehat{q}}_{i}).$ Either way, by construction of $\pi ^{P},$ citizens believe with probability one that both the proposal and the amendment would win against the status quo at the voting stage. Hence, citizens outside the sample group select sincerely, while sample group members select the proposal. However, the majority of citizens outside the sample group prefer $q_{i}$ over ${\widehat{q}}_{i}$ simply because $q_{i}$ is the Condorcet winner in state i. Hence, ${\widehat{q}}_{i}>q_{i}$ can only be the outcome of the mechanism if it has been an amendment at the selection stage, and has then prevailed against the status quo $q=0$ at the voting stage. Hence, under the deviation, there is no tax exemption and no transfer. Since the deviation is profitable for an agenda-setter or sample group member of type z,  it must hold that $z{\widehat{q}}_{i} -c({\widehat{q}}_{i}) > zq_{i} + \tau .$ However, for any $z\in Z,$ this inequality is violated for sufficiently large $\tau .$ Indeed, we obtain a contradiction for large enough $\tau .$$\square$

Appendix D

In Appendix D, we show that the democratic mechanism with sampling and one-stage voting implements the Condorcet winner in those public good problems which satisfy the distance property.

1.1 Sincere voting

From the point of view of citizens outside the sample group, the provision of a public good quantity $q\in Q$ is no longer associated with a tax burden of c(q),  but of $\left( \frac{1}{1-\lambda }\right) c(q).$ Consequently, the utility of citizen z outside the sample group from the public good level $q\in Q$ is given by

$$\begin{aligned} {\widehat{u}} (z,q) = zq -\left( \frac{1}{1-\lambda }\right) c(q). \end{aligned}$$

The popular vote in the democratic mechanism with sampling is a binary and final choice and thus strategic voting can never be beneficial. The citizens vote sincerely in the democratic mechanism with sampling and one-stage voting. We now formally spell out the sincere voting rule in the democratic mechanism with sampling and one-stage voting. Of course, this rule is different for sample group members and for regular citizens. Indeed, suppose that at the voting stage of the democratic mechanism with sampling and one-stage voting the alternative $q\in Q$ is pitted against the status quo, which is zero public good provision. Since $Z\subset {\mathbb {R}}_{++},$ we have that $zq>0$ for every $q\in Q\setminus \{0\},$ and thus all sample group members vote sincerely in favor of the proposal. Citizen z,  who is not a sample group member, prefers q to zero public good provision if

$$\begin{aligned} z > \frac{c(q)}{(1-\lambda )q }.\end{aligned}$$

Analogously to the argument in Appendix C, the privileges for the sample group distort sincere voting behavior of citizens outside the sample group. Again, we argue that this distortion is negligible when $\lambda$ is small.

For every state $i\in N,$ define ${\widetilde{q}}^{\lambda }_{i}$ as the solution to the equality

$$\begin{aligned} F_{i} \left( \frac{c(\widetilde{q}^{\lambda }_{i})}{(1-\lambda ){\widetilde{q}}^{\lambda }_{i}} \right) = 1/2.\end{aligned}$$

In words, if the true state is i,  then a majority of citizens outside the sample group prefers any quantity $q\in Q$ with $q<{\widetilde{q}}^{\lambda }_{i}$ over zero public good provision, and prefers zero public good provision to any quantity $q\in Q$ such that $q>{\widetilde{q}}^{\lambda }_{i}.$ The assumptions introduced on the cumulative distribution functions $(F_{i})_{i\in N}$ guarantee that ${\widetilde{q}}^{\lambda }_{i}$ exists.

For every $\lambda > 0,$ we have ${\widetilde{q}}^{\lambda }_{i} < {\widetilde{q}}_{i},$ and we find that ${\widetilde{q}}^{\lambda }_{i}$ converges to ${\widetilde{q}}_{i}$ as $\lambda \downarrow 0.$ Suppose that $q\in Q$ is a proposal which is preferred by the majority to zero public good provision under uniform taxation. Then, q is also preferred to zero public good provision by the majority under the tax-exemption, provided that $\lambda >0$ is small enough.

1.2 Strategies and beliefs

Define the following communication strategy $\sigma ^{P}$:

$$\begin{aligned} \sigma ^{P} (z) = {\left\{ \begin{array}{ll} \text {Yes} \ &{}\quad \text {if } \quad z\ge z^{P},\\ \text {No} \ &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

Moreover, consider the proposal strategy:

$$\begin{aligned} \rho ^{P}(z,\delta ) = {\left\{ \begin{array}{ll} q_{1} \ &{}\quad \text {if} \ 0\le \delta< 1-F_{2} (z^{P}),\\ q_{k} \ &{}\quad \text {if} \ 1-F_{k} (z^{P}) \le \delta < 1-F_{k+1} (z^{P}), \ k=2,\ldots , n-1,\\ q_{n} \ &{}\quad \text {if} \ 1-F_{n} (z^{P}) \le \delta \le 1 . \end{array}\right. } \end{aligned}$$

Define a belief for the agenda-setter as:

$$\begin{aligned} \pi ^{P}_{AS} (\delta ) = {\left\{ \begin{array}{ll} e_{1} \ &{}\quad \text {if} \ 0\le \delta< 1-F_{2} (z^{P}),\\ e_{k} \ &{}\quad \text {if} \ 1-F_{k} (z^{P}) \le \delta < 1-F_{k+1} (z^{P}), \ k=2,\ldots , n-1,\\ e_{n} \ &{}\quad \text {if} \ 1-F_{n} (z^{P}) \le \delta \le 1 . \end{array}\right. } \end{aligned}$$

It is straightforward that the belief $\pi ^{P}_{AS}$ is consistent with the strategies $\sigma ^{P}$ and $\rho ^{P}.$ Moreover, if these strategies are played, then the outcome is the Condorcet winner. In order to establish the implementation result, we need to show that $\sigma ^{P}$ and $\rho ^{P}$ are optimal given the beliefs $\pi ^{P}_{AS}.$ We show first that the proposal strategy $\rho ^{P}$ is optimal. Indeed, let i be the true state, so that $q_{i}$ is the Condorcet winner. Due to the distance property and sincere voting, any proposal $q\in Q$ such that $q>q_{i}$ will be rejected, and any proposal $q\in Q$ such that $q \le q_{i}$ will be accepted in the popular vote. Since the agenda-setter is tax-exempt, it follows immediately that it is optimal for him to propose the quantity $q_{i}$ whenever his belief is $e_{i}.$ Otherwise, if the agenda-setter makes any proposal $q\in Q\setminus \{q_{i}\},$ the outcome of the mechanism is some $q^{\prime }\in \{q, 0\},$ and $q^{\prime } < q_{i}.$ Next we show that the communication strategy is optimal. All members of the sample group as well as the agenda-setter are tax-exempt. A joint deviation by a subset of the sample group (or a deviation by the agenda-setter) could only be profitable if it led to some public good level $q > q_{i}.$ Due to sincere voting, however, such a public good level will not be implemented.

$\square$