Modeling emission-generating technologies: reconciliation of axiomatic and by-production approaches

Abstract

We study the link between two recent approaches to modeling emission-generating technologies: the by-production approach and the axiomatic approach. The by-production approach models these technologies as intersections of two independent sub-technologies reflecting (1) the relations between goods in intended-output production designed by human engineers and (2) the emission-generating mechanism of nature governed by material-balance considerations. The axiomatic approach proposes a set of axioms that a pollution-generating technology should satisfy. We show that the by-production technology satisfies these axioms and that, conversely, any technology satisfying the axioms can be decomposed into two sub-technologies satisfying the by-production properties. In either approach, the technology can be functionally represented by two radial distance functions with well-defined properties. These distance functions can also serve as measures of technological and environmental efficiency. We exploit the link between the by-production and axiomatic approaches to offer preliminary suggestions about suitable functional forms for the empirical estimation of the two distance functions.

1 Introduction

Murty et al. (2012) (MRL), building on ideas of Frisch (1965), Murty and Russell (2002) and Førsund (2009), argued analytically that pollution-generating technologies are best modeled as the intersection of two sub-technologies: an intended-production sub-technology and a residual-generation sub-technology. They referred to this structure as a “by-production technology.”

At a more basic level, Murty (2015a) proposed a formal axiomatic structure designed to capture the salient aspects of an emission-generating technology. She also formulated a binary functional representation for such structures, employing radial distance functions.

In this paper, we show that Murty’s axiomatic restrictions hold if and only if the technology is a by-production technology. We also suggest an alternative functional representation of the emissions-generating technology, one that dispenses with Murty’s assumption of convexity that is needed in her paper for representing the technology with the functional relations she proposes. This relaxation is important not only because it allows analysis of non-convexities in standard (intended) production technologies, owing to, e.g., regions of increasing returns to scale or free-disposal-hull input-requirement or output-possibility sets, but also because it takes into account the fundamental non-convexity that arises when a firm’s own emissions have detrimental effects on the production of its desired outputs. Starrett (1972) demonstrated that the technologies of firms that are victims of pollution externalities are non-convex.¹

After describing the salient features of an emission-generating technology in Sects. 2–4, we lay out a modified version of Murty’s axiomatic structure in Sect. 5. Section 6 proposes a functional representation of an emission-generating technology using radial distance functions. For given input and abatement quantities, one function identifies the lower boundary of the technology set with respect to emissions, while the other identifies the upper boundary with respect to intended output. The union of these boundaries constitutes the (weakly) efficient set in output-emission space.

The basic underlying properties of MRL by-production technologies are described in Sect. 7, and Sect. 8 establishes the equivalence of these technologies and those satisfying the axioms in Sect. 5. Section 9 explores some possible avenues of empirical implementation that exploit the representation theorems in Sects. 6 and 7 and the relation, discussed in Sect. 8, between by-production technologies of MRL and the emission-generating technologies satisfying the axiomatic restrictions of Murty. Section 10 concludes.

2 Emission-generating technologies

In this section, we lay out the characteristics of a technology with two types of outputs: intended production and unintended emissions. We focus on technologies for which the emissions can be fully accounted for by the quantities employed of emission-generating inputs.² We refer to such a technology as an emission-generating technology.

The components of an emission-generating technology are as follows:

• m intended outputs indexed by j. A quantity vector of intended outputs is denoted by $y\in \mathbf{R}^m_+$.

• n inputs of which $1,\ldots , n_z$ (with $1\le n_z\le n$) are emission causing and the remaining $n_o= n-n_z$ are non-emission causing. A quantity vector of inputs is denoted by $x=\langle x_z, x_o\rangle \in \mathbf{R}^n_+$, where $x_z\in \mathbf{R}^{n_z}_+$ is the quantity vector of emission-causing inputs and $x_o\in \mathbf{R}^{n_o}_+$ is the quantity vector of non-emission causing inputs. Emission-causing inputs are indexed by i; e.g., $x_{z_i}$ is the quantity of the ith emission-causing input.

• $m'$ types of emissions. A quantity vector of emissions is denoted by $z\in \mathbf{R}^{m'}_+$. Emissions are indexed by k.

• s types of abatement outputs indexed by l. A quantity vector of cleaning-up outputs is denoted by $a\in \mathbf{R}^s_+$.

A production vector is of the form $\langle x, a, y, z\rangle =\langle x_z, x_o, a, y, z\rangle \in \mathbf{R}^{n+s+m+m'}_+=:\mathbf{R}_+^t$.³ An emission-generating technology is a set of technologically feasible production vectors and is denoted by $\mathfrak {I}\subset \mathbf{R}^{t}_+$.

3 The costly disposal hull of an emission-generating technology

Obviously, the amounts of intended and cleaning-up outputs that can be produced by any finite vector of inputs $x\in \mathbf{R}_+^n$ are limited; i.e., there exist upper bounds on $\mathfrak {I}$ in the direction of intended and cleaning-up outputs, given an input vector x. If the inputs are not used efficiently in the production process, they produce less than their full potential of the intended and cleaning-up outputs. Similarly, if $x_z\in \mathbf{R}^{n_z}_+$ amounts of emission-generating inputs are used in the production process and $a\in \mathbf{R}^s_+$ amounts of cleaning-up operations are performed, material-balance conditions imply that certain minimal amounts of emissions have to be generated.⁴ If cleaning-up operations are not performed efficiently or if the physical conditions in which material-balance conditions operate are not favorable, then more than these minimal amounts of emissions could be generated.⁵ Thus, oxygen supply and temperature are two physical factors that determine the extent of emissions generated during combustion of fossil fuels. Existence of inefficiencies in cleaning-up activities is illustrated by the drop in efficiency of catalytic converters in cars through use. These are special devices installed in cars and other automobiles that use catalyst substances to convert harmful gases produced when the engines burn petrol or diesel into less harmful gases. Over time, their efficiency in doing so can fall from 99 to 95 %. (See http://www.drivingtesttips.biz/catalytic-converter.html.) Motor vehicles have to undergo pollution testing periodically in most countries to see whether pollution control devices in place are performing efficiently.

There must also be upper bounds on emission generation for given amounts of emission-generating inputs. For example, the sulfur content of a unit of a particular type of coal is fixed. Combusting a unit of this type of coal under favorable conditions and with scrubbing being performed efficiently minimizes the amount of $\hbox {SO}_2$ produced. However, there is also a maximal amount of $\hbox {SO}_2$, determined by the sulfur content, that potentially can be produced by a unit of this type of coal. The realized emission level can be higher than the minimal amount possible when coal is burned under unfavorable conditions or when scrubbing is not performed efficiently.

The existence of an upper as well as a lower boundary for emissions complicates the modeling of an emission-generating technology, particularly in the study of its disposability and the implied monotonicity properties.⁶ Incorporating the upper boundary for emissions into our axiomatic structure, however, would require explicit (and messy) modeling stipulations, keeping track of economically irrelevant boundary properties without adding any substantive content. Fortunately, there is a (harmless) way around this complication. As we treat emissions as undesirable by-products, technological (hence economic) efficiency requires minimization of the production of emissions, conditional on input quantities. Our attention, therefore, can be restricted to the study of the properties of the lower bounds on emission generation.

To this end, define the costly disposal hull (cdh) of $\mathfrak {I}$ as

$$\begin{aligned} T:=\left\{ \langle x, a, y, z+\zeta \rangle \in \mathbf{R}^{t}_+\ \big |\ \langle x,a,y,z\rangle \in \mathfrak {I}\ \ \hbox {and}\ \ \zeta \in \mathbf{R}^{m'}_+\right\} . \end{aligned}$$

The cdh of an emission-generating technology includes all production vectors in the emission-generating technology. Further, given any production vector in the primitive emission-generating technology $\mathfrak {I}$, any production vector with the same amounts of inputs and intended and cleaning-up outputs but with arbitrarily higher amounts of emissions is also included in the cdh of the emission-generating technology. The following remark summarizes these points.

Remark 1

The definition of T implies that⁷

• (i) $\mathfrak {I}\subseteq T$,

• (ii) if $\langle x,a, y, z\rangle \in \mathfrak {I}$ and $z'\ge z$ then $\langle x,a, y, z'\rangle \in T$, and

• (iii) if $\langle x,a, y, z\rangle \in T$ and $z'\ge z$ then $\langle x,a, y, z'\rangle \in T$.

Thus, the salient feature of the two technologies is that the (weakly and strictly) efficient points of the “pseudo-technology” T and the true (primitive) technology $\mathfrak {I}$ coincide.

We make use of restrictions of T to subspaces of $\mathbf{R}^t_+$. Salient examples are the intended-output possibility set,

$$\begin{aligned} T^y(x,a,z)=\{y\in \mathbf{R}^{m}_+\ |\ \langle x,a,y,z\rangle \in T\}, \end{aligned}$$

(3.1)

the pollution-generation set,

$$\begin{aligned} T^z(x,a,y)=\{z\in \mathbf{R}^{m'}_+\ |\ \langle x,a,y,z\rangle \in T\}, \end{aligned}$$

(3.2)

and the set of vectors of intended outputs and emissions that are feasible under T,

$$\begin{aligned} T^{y,z}(x,a)=\{\langle y,z\rangle \in \mathbf{R}^{m+m'}_+\ |\ \langle x,a,y,z\rangle \in T\}. \end{aligned}$$

(3.3)

Fig. 1

Feasible set with one intended output and one type of emission

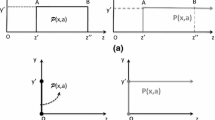
We illustrate these concepts in Fig. 1 for the simple case of a technology with a single intended output and one type of emission ($m=m'=1$). The costly disposal hull of the set of intended output and emission levels that are feasible under T with input vector $x=\langle x_z, x_o\rangle$ and a amount of cleaning-up, denoted by $T^{y,z}(x,a)$, is the rectangular area $[z^o, \infty ]\times [0,y^{*}]$. Thus, the maximal intended output that can be produced with input quantities x when a amount of cleaning-up is produced is $y^*$. The minimal amount of emission possible when $x_z$ amount of emission-causing inputs is used under favorable conditions and a amount of cleaning-up is performed efficiently is $z^o$. However, the figure shows that inefficiency in cleaning-up or unfavorable conditions may imply as much as $z^{*}$ level of emission. Thus, the set of intended output and emission combinations that are feasible under the basic technology $\mathfrak {I}$ with input quantities x and a amount of cleaning-up is given by the rectangular area $[z^o,z^*]\times [0,y^*]$. The point $\langle z',y'\rangle$ is in $T^{y,z}(x,a)$. The sets $T^z(x,a,y^{*})$ and $T^y(x,a,z^{*})$ of emissions and intended outputs, respectively, corresponding to cdh T, are given by the line segments, $[z^o,\infty ]$ and $[0,y^*]$, respectively.

A production vector $\langle x,a, y, z\rangle$ in $\mathfrak {I}$ (respectively, T) is a strictly efficient point of $\mathfrak {I}$ (respectively, T) if $\langle -\bar{x}, \bar{a},\bar{y},-\bar{z}\rangle > \langle -x,a,y,-z\rangle$ implies that $\langle \bar{x}, \bar{a},\bar{y},\bar{z}\rangle$ is not contained in $\mathfrak {I}$ (respectively, T)—i.e., if there does not exist any other production vector in $\mathfrak {I}$ (respectively, T) with no larger amounts of inputs or emissions and no smaller amounts of intended and cleaning-up outputs.

A production vector $\langle x,a, y, z\rangle$ in $\mathfrak {I}$ (respectively, T) is a frontier point of $\mathfrak {I}$ (respectively, T) if $\langle -\bar{x}, \bar{a},\bar{y},-\bar{z}\rangle \gg \langle -x,a,y,-z\rangle$ implies that $\langle \bar{x}, \bar{a},\bar{y},\bar{z}\rangle$ is not contained in $\mathfrak {I}$ (respectively, T)—i.e., if there does not exist any other production vector in $\mathfrak {I}$ (respectively, T) with smaller amounts of all inputs and all emissions and larger amounts of all intended and cleaning-up outputs.

Note that, in Fig. 1, the production vector $\langle x, a, y^*, z^o\rangle$ is a frontier point of both $\mathfrak {I}$ and its cdh T. The following remark—an implication of the definition of the cdh of an emission-generating technology—facilitates theoretical and empirical analysis of an emission-generating technology:

Remark 2

The strictly efficient points and the frontier points of the sets $\mathfrak {I}$ and T coincide.

Hence, in order to study the functional (possibly parametric) representation of the strictly efficient frontier of the set $\mathfrak {I}$ and the trade-offs among various goods along this frontier, we can work with its cdh—i.e., the set T—which is analytically more tractable than the set $\mathfrak {I}$. Moreover, this is the frontier that is relevant for the purpose of economic analysis and policy prescription: The upper boundary for pollution is no more relevant for these purposes than is the lower boundary of a standard (non-polluting) production set. For these reasons, unless required, we will ignore the distinction between the set $\mathfrak {I}$ and its cdh T and will refer to the set T as the emission-generating technology itself in what follows. The set of frontier points of T (and hence, $\mathfrak {I}$) is called the frontier of T (respectively, $\mathfrak {I}$) and is denoted by $\mathcal{F}(T)$.

4 A few remarks based on our intuitive understanding of the structure of an emission-generating technology

4.1 An emission-generating technology is a conjunction of intended-output production and material-balance conditions

Our basic intuition about an emission-generating technology is that it is a conjunction of an intended-output production process designed by human engineers and an emission-generating mechanism of nature governed by conditions like material balance. An emission-generating technology involves a simultaneous production of both the intended output and the (unintended) emission; i.e., while all inputs are used to produce intended and abatement outputs, the use of emission-causing inputs, in particular, generates emissions and the abatement activities mitigate them.

Remark 3

A production vector $\langle x_z, x_o, a, y, z\rangle$ is feasible with respect to an emission-generating technology T, if and only if the intended-output technology implies that the vector y of intended outputs is feasible with input and cleaning-up quantities $\langle x_z, x_o, a\rangle$ and the material-balance conditions imply that $\langle x_z, a\rangle$ can generate the emission vector z.

Fig. 2

Feasible sets with one input, one intended output, and one type of emission

Figure 2 illustrates this conjunction for very simple cases. Figure 2a shows an illustrative set $T^{x,y}(a,z)$ for fixed abatement and emission vectors $\langle a,z\rangle$ when $n=n_z=m=1$, and Fig. 2b shows a set $T^{x,z}(a,y)$ for fixed abatement and intended-output vector $\langle a,y\rangle$ when $n=n_z=m'=1$. Thus, part (a) is an illustration of a standard neo-classical technology showing the feasible set of intended output and input levels when abatement output is held fixed. Part (b) captures the relation in nature between the (emission-causing) input and the emission. It shows the cdh of the nature’s emission-generating mechanism. The minimal level of emission that can be produced increases with increase in the input. It is clear from Fig. 2a that the vector $\langle x^*,a,y^*\rangle$ is feasible under the intended production technology, while Fig. 2b shows that the vector $\langle x^*,a,z^*\rangle$ is permitted by nature’s emission mechanism. Hence, the production vector $\langle x^*, a, y^*,z^*\rangle$ is feasible under the overall emission-generating technology, which is a conjunction of the two technologies.

4.2 Explaining infeasibility of some combinations of inputs, intended and cleaning-up outputs, and emission levels

To understand the basic structure of an emission-generating technology, it is important to highlight some situations when the set $T^{y,z}(x,a), T^z(x,a,y)$, or $T^y(x,a,z)$ could be empty.

Remark 4

• (i) Given $\langle x,a\rangle \in \mathbf{R}^{n+m'}_+$, the set $T^{y,z}(x,a)$ is empty if it is not possible for input vector x to produce abatement-output vector a.

• (ii) Given $\langle x_z, x_o ,a,y\rangle \in \mathbf{R}^{n+m+m'}_+$, the set $T^{z}(x_z, x_o,a,y)$ is empty if it is not possible for input vector $x=\langle x_z, x_o\rangle$ to produce intended-output vector y and abatement output a.

• (iii) Given $\langle x_z, x_o ,a,z\rangle \in \mathbf{R}^{n+m'+s}_+$, the set $T^y(x_z, x_o,a,z)$ is empty if it is not possible for emission-causing input vector $x_z$ and abatement output vector a to generate emission vector z.

The first and second parts of Remark 4 say that it is possible that a given input vector may not have the potential to produce some (high) levels of intended and cleaning-up outputs. Thus, part (i) of the remark says that $T^{y,z}(x,a)$ will be empty if cleaning-up levels in vector a are too high to be produced by input vector x.

Similarly, part (ii) of the remark says that the set of emission levels $T^{z}(x_z, x_o,a,y)$ will be empty if the input quantities in vector $x=\langle x_z, x_o\rangle$ are insufficient to produce vector y of the intended outputs and vector a of abatement outputs. Note that this may be true even when material-balance conditions imply that vector $x_z$ of emission-causing inputs along with vector a of abatement outputs has the potential to generate positive levels of the emissions. Thus, in this case, the production vector $\langle x_z, x_o, a,y,z\rangle$ is not in T because $\langle x_z, x_o, a\rangle$ cannot produce vector y of intended outputs, even though material-balance conditions could imply that emissions vector z can be generated by $\langle x_z, a\rangle$. In Fig. 2 (where $n=n_z=1$), $T^z(x^*,a,y')=\emptyset$ because Fig. 2a shows that $\langle x^*, a\rangle$ cannot produce $y'$ amount of the intended output, even though material-balance conditions seen in Fig. 2b imply that there exists an emission level compatible with input and cleaning-up quantities $\langle x^*, a\rangle$; e.g., emission level $z^*$ can be generated by $\langle x^*, a\rangle$.

The situation in part (iii) of Remark 4 is one where the set of intended output levels $T^y(x_z, x_o,a,z)$ is empty. This will be true if the minimal amounts of emissions that $\langle x_z, a\rangle$ can generate under the material-balance conditions are higher than levels of emissions in vector z. For example, the firm could be using too much fossil fuels and doing too little cleaning-up than that required to generate vector z of emissions of $\hbox {CO}_2$ and $\hbox {SO}_2$. Note, this can be true even when intended production technology can produce vector y of intended outputs given inputs and abatement levels $\langle x_z, x_o, a\rangle$. Thus, it is possible that $\langle x_z, x_o, a,y,z\rangle \notin T$ because material balance implies that the vector $\langle x_z, a\rangle$ produces far more emission than the vector z, even though vector y of intended outputs can be produced by the vector $\langle x_z, x_o, a\rangle$.

In Fig, 2, $T^y(x^*,a, z')=\emptyset$ because Fig. 2b shows that the minimal amount of emission that input and cleaning-up level $\langle x^*, a\rangle$ can generate under nature’s emission generating mechanism is $z^*$, which is greater than $z'$, even though the intended production technology in Fig. 2a shows that there exists an intended output level that is compatible with input and cleaning-up quantities $\langle x^*, a\rangle$. For example, $y^*$ amount of intended output can be produced by $\langle x^*, a\rangle$.

5 Axiomatisation of an emission-generating technology

Murty (2015a) proposed a formal set of axioms defining an emission-generating technology. The axioms seek to characterize properties of an emission-generating technology that simultaneously produce intended outputs and emissions. Most important are the disposability properties of various goods—emission-causing and non-emission causing—that are involved in both the material-balance condition and intended-output production. As most of these axioms are discussed in detail in Murty (2015a), the following presentation is somewhat consolidated and abbreviated.

We make use of the following subspace slices of the technology:

$$\begin{aligned} \varOmega =\big \{\langle x,a,z\rangle \in \mathbf{R}^{n+s+m'}_+\ |\ T^y(x,a, z)\ne \emptyset \big \} \end{aligned}$$

(5.1)

and

$$\begin{aligned} {\varGamma }=\big \{\langle x,a,y\rangle \in \mathbf{R}^{n+s+m'}_+\ |\ T^z(x,y,a)\ne \emptyset \big \}. \end{aligned}$$

(5.2)

Consider the following set of axioms for an emission-generating technology:

• (EG0) T is closed and contains the origin $\underline{0}^t$.

• (EG1) $T^y(x,a,z)$ is bounded and satisfies free disposability of inputs and outputs and independence from emissions:

  $$\begin{aligned} y \in T^y(x,a,z),\ \bar{x}_o\ge x_o,\ \hbox {and}\ \bar{y}\le y\ \Longrightarrow \ \bar{y}\in T^y(x_z,\bar{x}_o,a,z) \end{aligned}$$

  (5.3)

  and

  $$\begin{aligned}&y \in T^y(x,a,z),\ \bar{x}_z\ge x_z,\ \bar{y}\le y,\ \bar{a}\le a,\ \hbox {and}\ \langle \bar{x}_z, x_o, \bar{a}, \bar{z}\rangle \in \varOmega \nonumber \\&\qquad \Longrightarrow \ \bar{y}\in T^y(\bar{x}_z, x_o,\bar{a},\bar{z}). \end{aligned}$$

  (5.4)

• (EG2) $T^z(x,a,y)$ satisfies joint essentiality of emission-causing inputs for emission generation

  $$\begin{aligned} x_z={\underline{0}}^{(n_z)}\ \Longrightarrow {\underline{0}}^{(m')}\in T^z(x,a,y) \end{aligned}$$

  (5.5)

  and costly disposability and independence from non-emission causing inputs and intended outputs:

  $$\begin{aligned}&z\in T^z(x,a,y),\ \bar{x}_z\le x_z,\ \bar{a}\ge a,\ \bar{z}\ge z,\ \hbox {and}\ \langle \bar{x}_z, \bar{x}_o,\bar{a},\bar{y}\rangle \in \varGamma \nonumber \\&\qquad \Longrightarrow \ \bar{z}\in T^z(\bar{x}_z,\bar{x}_o,\bar{a},\bar{y}). \end{aligned}$$

  (5.6)

Non-emptiness and closedness of T are standard production-technology restrictions, as is the shutdown condition $\underline{0}^t\in T$.

In addition to the standard assumption of boundedness of the intended-production possibility set for given input quantities and abatement output, (EG1) contains two free disposability conditions. The first, applicable to intended outputs and inputs that do not generate pollution, is standard in production theory: It says that arbitrary decreases in outputs and increases in non-pollution generating inputs are technologically feasible.

The second disposability condition in (EG1) is more complicated, entailing changes in pollution-generating inputs and abatement outputs (that affect both intended-output production and nature’s emission-generating potential). It is based on our intuition about emission-generating technologies in part (iii) of Remark 4. It implies free disposability of pollution-generating inputs and abatement outputs in the restricted set $\varOmega$. It says that, if a vector $\langle x,y,a,z\rangle$ is technologically feasible, then so is an alternative vector with no less of any emission-causing input and no more of any intended output or abatement output, so long as the alternative vector remains technologically feasible when combined with the pollution vector z. This last caveat is important. When emission-causing inputs are increased or cleaning-up outputs are decreased, the existing levels of emissions may no longer remain the same (recall part (iii) of Remark 4). Hence, (5.4) says that decreases in intended outputs are feasible if and only if increases in emission-causing inputs or decreases in cleaning-up outputs permit generation of existing levels of emissions. Thus, condition (5.6) implies

$$\begin{aligned}&y \in T^y(x,a,z),\ \bar{x}_z\ge x_z,\ \bar{y}\le y,\ \bar{a}\le a,\ \hbox {and}\ \langle \bar{x}_z, x_o, \bar{a},z\rangle \in \varOmega \\&\qquad \Longrightarrow \ \bar{y}\in T^y(\bar{x}_z, x_o,\bar{a},z). \end{aligned}$$

Condition (5.4) in (EG1) also builds in the (convenient) assumption that emissions generated by a producing unit do not affect its own intended-output production possibilities, provided that the new pollution levels do not result in an empty production possibility set; i.e., it implies⁸

$$\begin{aligned} y \in T^y(x,a,z)\ \hbox {and}\ \langle x_z, x_o, a, \bar{z}\rangle \in \varOmega \ \Longrightarrow \ y\in T^y(x_z, x_o,a,\bar{z}). \end{aligned}$$

(5.7)

To understand this assumption, consider the set of intended-output vectors that are feasible under technology T with given quantities of inputs, cleaning-up outputs, and emission levels $\langle x_z, x_o, a, z\rangle \in \varOmega$; i.e., consider the set $T^y(x_z, x_o, a,z)$. Then a change in the emission vector to $\bar{z}$ has no effect on the set of feasible intended-output vectors if $T^y(x_z, x_o, a,z)=T^y(x_z, x_o, a,\bar{z})$. But this will be true only if the given vector of inputs, along with the given level of cleaning-up, can produce the changed level of emission—i.e., only if $T^y(x_z, x_o, a,\bar{z})\ne \emptyset$.⁹

(EG2) captures the fact that the material-balance conditions in nature imply that emission-causing inputs are jointly essential in producing the emission; i.e., if none of the emission-causing inputs are employed in production, no emissions will be generated. More precisely, in this situation, the minimal amount of emission generated is zero. In the context of the cdh of the emission-generating technology, this implies that if no emission-causing input is used in production, the feasible set of emission levels includes zero amounts of all emissions.

(EG2) also encapsulates our assumption that generation of emissions is independent of intended-output production and usage of non-emission-causing inputs, i.e., it implies

$$\begin{aligned} z\in T^z(x,a,y)\ \hbox {and}\ \langle x_z,\bar{x}_o,a,\bar{y}\rangle \in \varGamma \ \Longrightarrow \ z\in T^z(x_z,\bar{x}_o,a,\bar{y}). \end{aligned}$$

(5.8)

Thus, this assumption captures the idea that arbitrary changes in these goods, when technologically feasible, do not affect emission levels.¹⁰

The costly disposability conditions in (EG2), firstly, make T a cdh of itself:

$$\begin{aligned} z\in T^z(x,a,y)\ \ \hbox {and}\ \ \bar{z}\ge z\ \Longrightarrow \ \bar{z}\in T^z(\bar{x},\bar{a},\bar{y}). \end{aligned}$$

(5.9)

Secondly, they capture a feature of the cdh T based on our intuition about emission-generating technologies in part (ii) of Remark 4: Given a vector in the emission-generating technology, an alternative vector with less of any input and more of any abatement output is also in the cdh, so long as the lower input and greater abatement output in the alternative vector is technologically compatible with the given intended-output levels—i.e., so long as $T^z(\bar{x},y,\bar{a})\ne \emptyset$.¹¹

In the remainder of the paper, we adopt the following definition of an emission-generating technology.

Definition

A technology is an emission-generating technology (EGT) if it satisfies assumptions (EG0), (EG1), and (EG2).

6 Functional representation of an EGT

It has been a half century since Frisch (1965), critical of the highly restrictive use of single functions to represent complex relationships among inputs and outputs, proposed the use of multiple functional restrictions to model production processes realistically. His critique is especially compelling in the case of emission-generating technologies, as has been argued by Murty and Russell (2002), Førsund (2009) and MRL 2012. These studies demonstrate that the complex real-world trade-offs among inputs and outputs in these technologies cannot be captured by a single functional relation. For example, it is impossible for a single function to capture, simultaneously, the positive relations between emissions and emission-causing inputs and the positive relations between emissions and intended outputs.¹²

We employ two radial distance functions to represent an EGT.¹³ Define $D^{\mathrm{EG}}_1:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$ and $D^{\mathrm{EG}}_2:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$ by

$$\begin{aligned} D^{\mathrm{EG}}_1(x,a,y,z)=\Bigg \{ \begin{array}{ll} \inf \Big \{\lambda \in \mathbf{R}_{++}\ |\ y/\lambda \in T^y(x,a,z)\Big \}&{} \quad \hbox {if}\ T^y(x,a,z)\ne \emptyset \\ \infty &{} \quad \hbox {if}\ T^y(x,a,z)=\emptyset \end{array}\nonumber \\ \end{aligned}$$

(6.1)

and

$$\begin{aligned} D^{\mathrm{EG}}_2(x,a,y,z)=\Bigg \{\begin{array}{ll} \min \{\lambda \in \mathbf{R}_{+}\ | \lambda z \in T^z(x,a,y)\}\Big \} &{} \hbox {if}\ T^z(x,a,y)\ne \emptyset \\ \infty &{} \hbox {if} T^z(x,a,y)=\emptyset . \end{array}\qquad \end{aligned}$$

(6.2)

The $D_1^{\mathrm{EG}}$ distance function image evaluated at $\langle x,a, y',z'\rangle$ (a feasible point in the technology) in Fig. 1 is $|y' |/|y^* |<1$. Note that this value of the distance function is independent of z and increasing in y, e.g., $D_1^{\mathrm{EG}}(x,a, y',z^o)=D_1^{\mathrm{EG}}(x,a, y',z')$ and $D_1^{\mathrm{EG}}(x,a, y^*,z')>D_1^{\mathrm{EG}}(x,a, y',z')$. Moreover, as the upper boundary of intended-output production shifts upward with an increase in x or a decrease in a, the distance function value decreases.

The $D_2^{\mathrm{EG}}$ distance function image evaluated at $\langle x,y',a,z'\rangle$ in Fig. 1 is $|z^o|/|z' |<1$. This value is independent of y; e.g., $D_2^{\mathrm{EG}}(x,a, y',z')=D_2^{\mathrm{EG}}(x,a, y^*,z')$. Moreover, as the left-side (lower) boundary of emission shifts to the right for increases in x and decreases in a, the value of $D_2^{\mathrm{EG}}$ increases.

The effects of changes in a single input on the upper and lower boundaries for a single output and a single emission are depicted in Fig. 2a, b.

Fig. 3

Construction of the distance function for two types of emissions and two types of sub-technologies

Figure 3a, b depict the construction of the distance function image for two types of sub-technologies for emissions. The level set $T^z(x,y,a)$ in Fig. 3a shows (piece-wise) substitutability between the two emission levels, while Fig. 3b evinces pure complementary (fixed proportions up to inefficiencies) between the two emissions.¹⁴ The distance function images evaluated at $\langle x,y,a,z^*\rangle$ are given by the ratios of norms, $||z' || / || z^* ||$.

Theorem 1

Suppose T is an EGT. $D^{\mathrm{EG}}_1$ is independent of z and homogeneous of degree 1 in y and $D^{\mathrm{EG}}_2$ is independent of y and homogeneous of degree −1 in z. On $\varOmega$, $D^{\mathrm{EG}}_1$ is non-increasing in x and non-decreasing in y. On $\varGamma , D^{\mathrm{EG}}_2$ is non-decreasing in x and non-increasing in z and a.¹⁵

Proof

The two independence conditions follow immediately from the two independence conditions in (EG1) and (EG2).

The homogeneity conditions are easily proved. Trivially, if $T^y(x,a,z)= \emptyset , D^{\mathrm{EG}}_1(x,a,\kappa y,z)=\infty =\kappa \infty =\kappa D^{\mathrm{EG}}_1(x,a,y,z)$, and if $T^z(x,y,a,z)= \emptyset , D^{\mathrm{EG}}_2(x,a,y,\kappa z)=\infty =\kappa ^{-1}\infty =\kappa ^{-1} D^{\mathrm{EG}}_2(x,a,y,z)$ for $k> 0$. Assuming $T^y(x,a,z)\ne \emptyset$ and $T^z(x,a,y)\ne \emptyset$,

$$\begin{aligned} D^{\mathrm{EG}}_1(x,a,\kappa y,z)= & {} \inf \Big \{\lambda \in \mathbf{R}_{++}\ |\ \kappa y/\lambda \in T^y(x,a,z)\Big \}\nonumber \\&\kappa \inf \Big \{\lambda /\kappa \in \mathbf{R}_{++}\ |\ y/(\lambda /\kappa ) \in T^y(x,a,z)\Big \}\nonumber \\= & {} \kappa D^{\mathrm{EG}}_1(x,a,y,z) \end{aligned}$$

(6.3)

and

$$\begin{aligned} D^{\mathrm{EG}}_2(x,a,y,\kappa z)= & {} \min \{\lambda \in \mathbf{R}_{+}\ |\ \lambda (\kappa z) \in T^z(x,a,y)\}\nonumber \\= & {} (1/\kappa )\min \{\lambda \kappa \in \mathbf{R}_{+}\ |\ (\lambda \kappa ) z \in T^z(x,a,y)\}\nonumber \\= & {} \kappa ^{-1}D^{\mathrm{EG}}_2(x,a,y,z). \end{aligned}$$

(6.4)

To establish the monotonicity conditions for $D^{\mathrm{EG}}_1$, consider two vectors in $\varOmega$ satisfying $\langle -x,a,z\rangle \ge \langle -\bar{x},\bar{a},z\rangle$ and suppose $y\ge \bar{y}$. Then the disposability conditions in (EG1) imply $T^y(x,a,z)\subseteq T^y(\bar{x},\bar{a},z)$, which, together with $y\ge \bar{y}$, implies

$$\begin{aligned} D^{\mathrm{EG}}_1(x,a,y,z)= & {} \inf \Big \{\lambda \in \mathbf{R}_+\ |\ y/\lambda \in T^y(x,a,z)\Big \}\nonumber \\\ge & {} \inf \Big \{\lambda \in \mathbf{R}_+\ |\ y/\lambda \in T^y(\bar{x},\bar{a},z)\Big \} \nonumber \\\ge & {} \inf \Big \{\lambda \in \mathbf{R}_+\ |\ \bar{y}/\lambda \in T^y(\bar{x},\bar{a},z)\Big \}=D^{\mathrm{EG}}_1(\bar{x},\bar{a},\bar{y},z).\qquad \end{aligned}$$

(6.5)

The monotonicity conditions for $D^{\mathrm{EG}}_2$ are similarly established by first noting that, for any pair of vectors in $\varGamma$ satisfying $\langle -\bar{x},\bar{a},y\rangle \ge \langle -x,a,y\rangle$, (EG2) implies that $T^z(x,a,y) \subseteq T^z(\bar{x},\bar{a},y)$. Conjoined with $\bar{z}\ge z$, this implies

$$\begin{aligned} D^{\mathrm{EG}}_2(x,a,y,z)= & {} \min \{\lambda \in \mathbf{R}_+\ |\ \lambda z \in T^z(x,a,y)\}\Big \}\nonumber \\\ge & {} \min \{\lambda \in \mathbf{R}_+\ |\ \lambda z \in T^z(\bar{x},\bar{a},y)\}\Big \} \nonumber \\\ge & {} \min \{\lambda \in \mathbf{R}_+\ |\ \lambda \bar{z}\in T^z(\bar{x},\bar{a},y)\}\Big \}=D^{\mathrm{EG}}_2(\bar{x},\bar{a},y,z).\qquad \end{aligned}$$

(6.6)

$\square$

We now show that the two distance functions, $D^{\mathrm{EG}}_1$ and $D^{\mathrm{EG}}_2$, provide a functional representation of an EGT.¹⁶

Theorem 2

Suppose T is an EGT. Then $\langle x,y,a,z\rangle \in T$ if and only if $D^{\mathrm{EG}}_1(x,a,y,z)\le 1$ and $D^{\mathrm{EG}}_2(x,a,y,z)\le 1.$ Moreover, $\langle x,a,y,z\rangle$ is contained in the frontier of T if and only if $D^{\mathrm{EG}}_1(x,a,y,z)= 1$ or $D^{\mathrm{EG}}_2(x,a,y,z)=1.$

Proof

Suppose $\langle x,a,y,z\rangle \in T$. Then $T^y(x,a,z)\ne \emptyset$ and $T^z(x,a,y)\ne \emptyset$, so that $D^{\mathrm{EG}}_1(x,a,y,z)$ and $D^{\mathrm{EG}}_2(x,a,y,z)$ must be finite. Suppose that $D^{\mathrm{EG}}_1(x,a,y,z)>1$; it follows that $y/D^{\mathrm{EG}}_1(x,a,y,z)\ll y\in T^y(x,a,z)$, contradicting the definition of $D^{\mathrm{EG}}_1$. Suppose that $D^{\mathrm{EG}}_2(x,a,y,z)>1$; it follows that $D^{\mathrm{EG}}_2(x,a,y,z)\ z\gg z\in T^z(x,a,y)$, contradicting the definition of $D^{\mathrm{EG}}_2$.

Suppose now that $D^{\mathrm{EG}}_1(x,a,y,z)\le 1$ and $D^{\mathrm{EG}}_2(x,a,y,z)\le 1$ but $\langle x,a,y,z\rangle \notin T_{\mathrm{EG}}$. Then either $y\notin T^y(x,a,z)$ or $z\notin T^z(x,a,y)$, in which case the disposability conditions imply that $y/D^{\mathrm{EG}}_1(x,a,y,z)\notin T^y(x,a,z)$ or $D^{\mathrm{EG}}_2(x,a,y,z)\ z\notin T^z(x,a,y)$. These conditions are inconsistent with, respectively, the definition of $D^{\mathrm{EG}}_1$ or the definition of $D^{\mathrm{EG}}_2$.

Suppose that $\langle x,a,y,z\rangle \in T$ is contained in the frontier of T, $\mathcal{F}(T)$. As T is closed, $\langle x,a,y,z\rangle \in T$, and $D^{\mathrm{EG}}_1(x,a,y,z)\le 1$ and $D^{\mathrm{EG}}_2(x,a,y,z)\le 1.$ Suppose that $D^{\mathrm{EG}}_1(x,a,y,z)< 1$ or $D^{\mathrm{EG}}_2(x,a,y,z)<1.$ Then, by definitions of $D^{\mathrm{EG}}_1$ and $D^{\mathrm{EG}}_2$, $y/D^{\mathrm{EG}}_1(x,a,y,z)\in T^y(x,a,z)$ or $D^{\mathrm{EG}}_2(x,a,y,z) z\in T^z(x,a,y)$. Thus, $\langle x,a,y/D^{\mathrm{EG}}_1,z\rangle \in T$ with $y\ll y/D^{\mathrm{EG}}_1(x,a,y,z)$ or $\langle x,a,y,D^{\mathrm{EG}}_2(x,a,y,z) z\rangle \in T$ with $z\gg D^{\mathrm{EG}}_2(x,a,y,z) z$. Recalling the definition of a frontier point, this violates $\langle x,a,y,z\rangle \in \mathcal{F}(T)$. $\square$

Note that the properties of $D_1^{\mathrm{EG}}$ and $D_2^{\mathrm{EG}}$ in Theorems 1 and 2 trivially hold in the simple case illustrated in Fig. 1, where $D^{\mathrm{EG}}_1(x,a,y',z)=|y' |/y^* |$ for all $z\ge z^o$ and $D^{\mathrm{EG}}_2(x,a,y,z')=|z^o|/|z' |$ for all $y\in (0,\bar{y})$.

7 The by-production technology (BPT) and its functional representation

MRL call the technology T a by-production technology if it is formed by the intersection of two sub-technologies, $T_1$ and $T_2$. Sub-technology $T_1$ is a standard technology: independent of emission levels, possessing the shut-down option, and satisfying standard free disposability with respect to all inputs and intended and abatement outputs. Thus, the sub-technology exhibits the standard trade-offs between inputs and intended and abatement outputs along its efficient frontier. In particular, along the efficient frontier, the trade-offs between inputs and intended and abatement outputs are nonnegative. Sub-technology $T_2$ is the costly disposal hull of nature’s emission-generating mechanism. MRL propose costly disposal assumptions with respect to emissions, emission-causing inputs, and cleaning-up activities. These proposed disposability assumptions imply that, along the efficient frontier of $T_2$ (where emission generation is minimized), the trade-offs between emissions and emission-generating inputs are nonnegative and the trade-offs between emissions and cleaning-up outputs are non-positive. It is intuitive that all emission-causing inputs are jointly essential in producing emissions in nature; i.e., if none of the emission-causing inputs is used, no emissions are generated.

Definition

A technology is a by-production technology (BPT) if it is the intersection of two sub-technologies $T_1$ and $T_2$ satisfying the following restrictions:

• (BP1) The set $T_1$ is closed, contains $\langle {\underline{0}}^n,{\underline{0}}^s,{\underline{0}}^{m},z\rangle$ for all $z\in \mathbf{R}^{m'}$, and satisfies the independence condition,

  $$\begin{aligned} \langle x,a,y,z\rangle \in T_1\ \Longrightarrow \langle x,a,y,\bar{z}\rangle \in T_1\ \ \forall \ \bar{z}\in \mathbf{R}^{m'}_+ \end{aligned}$$

  (7.1)

  and the disposability conditions,

  $$\begin{aligned} \langle x,a,y,z\rangle \in T_1,\ \bar{x}\ge x,\ \bar{a}\le a,\ \hbox {and}\ \bar{y}\le y\ \Longrightarrow \ \langle \bar{x},\bar{a},\bar{y},z\rangle \in T_1. \end{aligned}$$

  (7.2)

  Moreover, the set $\big \{y\ |\ \langle x,a,y,z\rangle \in T_1\big \}$ is bounded for all $z\ge 0$.

• (BP2) The set $T_2$ is closed, satisfies the independence condition,

  $$\begin{aligned} \langle x_z, x_o, a, y, z\rangle \in T_2,\ \Longrightarrow \ \langle x_z, \bar{x}_o, a, \bar{y}, z\rangle \in T_2\quad \forall \ \langle \bar{x}_o, \bar{y}\rangle \in \mathbf{R}^{n_z+m}_+,\nonumber \\ \end{aligned}$$

  (7.3)

  the costly disposability condition,

  $$\begin{aligned} \langle x, a, y, z\rangle \in T_2,\ \ \bar{z}\ge z,\ \bar{x}_z\le x_z, \ \hbox {and}\ \bar{a}\ge a \ \Longrightarrow \ \langle \bar{x}_z, x_o, \bar{a}, y, \bar{z}\rangle \in T_2,\nonumber \\ \end{aligned}$$

  (7.4)

  and the joint-essentiality condition,

  $$\begin{aligned} {\underline{0}}^{m'}\in \big \{z\ |\ \langle {\underline{0}}^{n_z},x_o,a,y,z\rangle \in T_2\big \}\ \forall \ \langle x_o, a, y\rangle \in \mathbf{R}^{n_o+s+m}_+. \end{aligned}$$

  (7.5)

  The two sub-technologies $T_1$ and $T_2$ underlying a BPT can be represented, respectively, by two distance functions, $D^{\mathrm{BP}}_1:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$ and $D^{\mathrm{BP}}_2:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$, defined by

  $$\begin{aligned} D^{\mathrm{BP}}_1(x,a,y,z)=\inf \Big \{\lambda \in \mathbf{R}_{++}\ |\ \langle x,a,y/\lambda ,z\rangle \in T_1\Big \} \end{aligned}$$

  (7.6)

  and

  $$\begin{aligned} D_2^{\mathrm{BP}}(x,a,y,z)=\min \{\lambda \in \mathbf{R}_{+}\ |\ \langle x,a,y,\lambda z\rangle \in T_2\}\Big \}. \end{aligned}$$

  (7.7)

Theorem 3

If $T_1$ satisfies (BP1) and $T_2$ satisfies (BP2), then $D_1^{\mathrm{BP}}$ is independent of z, homogeneous of degree 1 in y, non-increasing in x, and non-decreasing in y and a and $D_2^{\mathrm{BP}}$ is independent of y, homogeneous of degree -1 in z, non-decreasing in x, and non-increasing in z and a.

A comparison of Theorems 1 and 3 indicates that the properties of distance functions $D^{\mathrm{EG}}_1$ and $D^{\mathrm{EG}}_2$ are, respectively, identical to the properties of distance functions $D_1^{\mathrm{BP}}$ and $D_2^{\mathrm{BP}}$, and indeed the proof of Theorem 3, which we leave to the reader, parallels closely the proof of Theorem 1.

The following two theorems are also easy to prove:

Theorem 4

Suppose T is a BPT such that $T=T_1\cap T_2$, where $T_1$ satisfies (BP1) and $T_2$ satisfies (BP2). Then $\langle x, a, y, z\rangle \in T$ if and only if $D^{\mathrm{BP}}_1(x, a, y, z)\le 1$ and $D^{\mathrm{BP}}_2(x, a, y, z)\le 1$.

Theorem 5

Given two arbitrary distance functions satisfying the properties in Theorem 3, say $D_1:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$ and $D_2:\mathbf{R}_+^t\rightarrow \mathbf{R}_+$, the sub-technologies,

$$\begin{aligned} T_1:=\{\langle x,a,y,z\rangle \ |\ D_1(x,a,y,z)\le 1\} \end{aligned}$$

and

$$\begin{aligned} T_2:=\{\langle x,a,y,z\rangle \ |\ D_2(x,a,y,z)\le 1\}, \end{aligned}$$

satisfy (BP1) and (BP2); hence, $T:=T_1\cap T_2$ is a BPT.

Thus, Theorem 4 says that a BPT has a functional representation: Functions $D^{\mathrm{BP}}_1$ and $D^{\mathrm{BP}}_2$ that are derived from its sub-technologies in (7.6) and (7.7), respectively, can be used to represent it. On the other hand, Theorem 5 says that to construct a BPT along with its two sub-technologies that satisfy (BP1) and (BP2), respectively, it is enough to specify two arbitrary distance functions $D_1$ and $D_2$ having properties of functions $D^{\mathrm{BP}}_1$ and $D^{\mathrm{BP}}_2$, respectively, in Theorem 3.

8 Relation between EGTs and BPTs

Suppose T is an EGT. Theorem 2 shows that the two distance functions, $D^{\mathrm{EG}}_1$ and $D^{\mathrm{EG}}_2$, defined in (6.1) and (6.2), respectively, can be employed to extract the two relevant frontiers of T—the lower frontier of emission generation defined by nature’s emission-generating mechanism and the upper frontier of intended outputs defined by engineering relations of human design in intended production. The properties of $D^{\mathrm{EG}}_1$ and $D^{\mathrm{EG}}_2$ stated in Theorem 1 imply that, along these two frontiers, all intuitive trade-offs hold:¹⁷ Along the frontier defined by $D^{\mathrm{EG}}_1$, trade-offs between inputs and outputs (intended or cleaning-up) are nonnegative, while the relations between any two intended or cleaning-up outputs or between any two inputs are non-positive. Along the frontier defined by $D^\mathrm{EG}_2$, trade-offs between emission-causing inputs and emissions are nonnegative and between emissions and abatement outputs are non-positive. Employing $D^\mathrm{EG}_1$ and $D^\mathrm{EG}_2$, we can construct two sub-technologies,

$$\begin{aligned} \hat{T}_1=\big \{\langle x,a,y,z\rangle \in \mathbf{R}^t_+\ |\ D^\mathrm{EG}_1(x,a,y,z)\le 1\big \} \end{aligned}$$

(8.1)

and

$$\begin{aligned} \hat{T}_2=\big \{\langle x,a,y,z\rangle \in \mathbf{R}^t_+\ |\ D^\mathrm{EG}_2(x,a,y,z)\le 1\big \}. \end{aligned}$$

(8.2)

The remark below follows as an application of Theorem 2.

Remark 5

If T is an EGT, there exist two sub-technologies $\hat{T}_1$ and $\hat{T}_2$, defined as in (8.1) and (8.2), such that $T=\hat{T}_1\cap \hat{T}_2$. Thus, the axioms (EG0), (EG1), and (EG2) imply that T can be decomposed into two sub-technologies whose relevant frontiers reflect trade-offs in intended production and emission generation.

Conversely, we show below that, if we begin as in MRL with two independent sub-technologies—one capturing standard relations between inputs and outputs in intended production [i.e., satisfying (BP1)] and the other capturing the physical laws of nature that describe how emissions are generated from emission-causing substances (i.e., satisfying (BP2))—then the intersection of these technologies satisfies axioms (EG0), (EG1), and (EG2); i.e., the resulting composite technology is an EGT. In this sense, our proposed axioms (EG0), (EG1), and (EG2) are also necessary for decomposing a technology into an intended production technology and nature’s emission-generating mechanism.

Theorem 6

If a technology T is a BPT, then it is an EGT, i.e., if $T_1$ and $T_2$ satisfy (BP1) and (BP2), respectively, and $T=T_1\cap T_2$ then T satisfies (EG0), (EG1), and (EG2).

Proof

It is immediate that T, the intersection of closed sets, is itself closed. Similarly, $\langle {\underline{0}}^n,{\underline{0}}^m,{\underline{0}}^{s},z\rangle$ for all $z\in \mathbf{R}^{m'}$ and $\langle {\underline{0}}^{n_z},x_o,y,a,{\underline{0}}^{m'}\rangle$ for all $\langle x_o,y,a\rangle \in R_+^{n_o+m+s}$ immediately imply $0^t\in T$. Thus, (EG0) holds.

Next we show that (EG1) holds, starting with the independence condition (5.7). Suppose $T^y(x_z, x_o, a, z)\ne \emptyset$ and $T^y(x_z, x_o, a, \bar{z})\ne \emptyset$. We need to show that $T^y(x_z, x_o, a, z)=T^y(x_z, x_o, a, \bar{z})$. Suppose $y\in T^y(x_z, x_o, a, z)$. Then $\langle x_z, x_o, a, y,z\rangle \in T$. Hence, definition of T implies that $\langle x_z, x_o, a, y,z\rangle \in T_1$. Since $T_1$ satisfies (7.1), we have $\langle x_z, x_o, a, y,\bar{z}\rangle \in T_1$. Since $T^y(x_z, x_o, a, \bar{z})\ne \emptyset$, let $\bar{y}\in T^y(x_z, x_o, a, \bar{z})$. Hence, we have $\langle x_z, x_o, a, \bar{y}, \bar{z}\rangle \in T_2$. Since $T_2$ satisfies (7.3), we have $\langle x_z, x_o, a,y,\bar{z}\rangle \in T_2$. Hence, $\langle x_z, x_o, a, y,\bar{z}\rangle \in T=T_1\cap T_2$. Hence, $y\in T^y(x_z, x_o, a, \bar{z})$.

We next show that T satisfies (5.3). Let $\langle x_z, x_o, a, y, z\rangle \in T$. Hence, from the definition of T, $\langle x_z, x_o, a, y,z\rangle \in T_1$ and $\langle x_z, x_o, a, y, z\rangle \in T_2$. Suppose $\bar{y}\le y$ and $\bar{x}_o\ge x_o$. Since $T_1$ satisfies Assumption (7.2), we have $\langle x_z, \bar{x}_o, a, \bar{y}, z\rangle \in T_1$. Also, since $T_2$ satisfies Assumption (7.3), we have $\langle x_z, \bar{x}_o, a, \bar{y}, z\rangle \in T_2$. Hence, $\langle x_z, \bar{x}_o, a, \bar{y}, z\rangle \in T=T_1\cap T_2$.

Finally, we show that T satisfies (5.4). Let $T^y(x_z, x_o, a, z)\ne \emptyset , \bar{x}_z\ge x_z, \bar{a}\le a$, and $T^y(\bar{x}_z, x_o, \bar{a},z)\ne \emptyset$. We need to show that $T^y(x_z, x_o, a, z)\subseteq T^y(\bar{x}_z, x_o, \bar{a},z)$. Let $y\in T^y(x_z, x_o, a, z)$. Then $\langle x_z, x_o, a, y, z\rangle \in T$. Hence, from the definition of T, $\langle x_z, x_o, a, y,z\rangle \in T_1$ and $\langle x_z, x_o, a, y, z\rangle \in T_2$. Since $T_1$ satisfies Assumptions (7.2), we have $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T_1$. Since $T^y(\bar{x}_z, x_o, \bar{a},z)\ne \emptyset$, there exists $\bar{y}\ge 0$ such that $\bar{y}\in T^y(\bar{x}_z, x_o, \bar{a},z)$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, \bar{y}, z\rangle \in T$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, \bar{y}, z\rangle \in T_2$. Since $T_2$ satisfies Assumption (7.3), we have $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T_2$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T=T_1\cap T_2$.

To establish that (EG2) holds, we first show that $\underline{0}^{m'}\in T^z\left( 0^{n_z}, x_o, a, y\right)$ if $T^z\left( 0^{n_z}, x_o, a, y\right) \ne \emptyset$. Since $T:=T_1\cap T_2$, the independence assumption (7.1) implies that $\langle \underline{0}^{n_z}, x_o, a, y,\underline{0}^{m'}\rangle \in T_1$. By (BP2), $\langle \underline{0}^{n_z}, x_o, a, y,\underline{0}^{m'}\rangle \in T_2$, so that $\langle \underline{0}^{n_z}, x_o, a, y,\underline{0}^{m'}\rangle \in T$; i.e., $\underline{0}^{m'}\in T^z\left( \underline{0}^{n_z}, x_o, a, y\right)$.

To show that T satisfies the independence condition in (EG2), suppose $T^z(x_z, x_o, a, y)\ne \emptyset$ and $T^z(x_z, \bar{x}_o, a, \bar{y})\ne \emptyset$. We need to show that $T^z(x_z, x_o, a, y)=T^z(x_z, \bar{x}_o, a, \bar{y})$. Suppose $z\in T^z(x_z, x_o, a, y)$ and $\bar{z}\in T^z(x_z, \bar{x}_o, a, \bar{y})$. Then $\langle x_z, \bar{x}_o, a, \bar{y},\bar{z}\rangle \in T$. Hence, definition of T implies that $\langle x_z, \bar{x}_o, a, \bar{y},\bar{z}\rangle \in T_1$. Since $T_1$ satisfies (7.1), hence $\langle x_z, \bar{x}_o, a, \bar{y},z\rangle \in T_1$. Since $z\in T^z(x_z, x_o, a, y)$, we have $\langle x_z, x_o, a, y, z\rangle \in T$ and the definition of T implies that $\langle x_z, x_o, a, y, z\rangle \in T_2$. Since $T_2$ satisfies (7.3), we have $\langle x_z, \bar{x}_o, a, \bar{y},z\rangle \in T_2$. Hence, $\langle x_z, \bar{x}_o, a, \bar{y},z\rangle \in T=T_1\cap T_2$. Hence, $z\in T^z(x_z, \bar{x}_o, a, \bar{y})$.

Finally, we show that T satisfies (5.6). Let $T^z(x_z, x_o, a, y)\ne \emptyset , \bar{x}_z\le x_z$, $\bar{a}\ge a$, and $T^z(\bar{x}_z, x_o, \bar{a},y)\ne \emptyset$. We need to show that $T^z(x_z, x_o, a, y)\subseteq T^z(\bar{x}_z, x_o, \bar{a},y)$. Let $z\in T^z(x_z, x_o, a, y)$. Then $\langle x_z, x_o, a, y, z\rangle \in T$. Hence, from the definition of T, $\langle x_z, x_o, a, y, z\rangle \in T_2$. Since $T_2$ satisfies (7.4), $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T_2$. Since $T^z(\bar{x}_z, x_o, \bar{a},y)\ne \emptyset$, there exists $\bar{z}\ge 0$ such that $\bar{z}\in T^z(\bar{x}_z, x_o, \bar{a},y)$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, y, \bar{z}\rangle \in T$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, y, \bar{z}\rangle \in T_1$. Since, $T_1$ satisfies (7.1), $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T_1$. Hence, $\langle \bar{x}_z, x_o, \bar{a}, y, z\rangle \in T=T_1\cap T_2$ or $z\in T^z(\bar{x}_z, x_o, \bar{a},y)$. $\square$

9 Preliminary thoughts on empirical implementation

The study in the previous section of the relationship between BPTs formulated in MRL and EGTs analyzed in Murty (2015a) can be exploited in empirical work to construct (or estimate) EGTs. This point is clarified in the remark below:

Remark 6

Theorem 5, combined with Theorem 6, implies that the intersection of sub-technologies defined by two independent and arbitrary distance functions $D_1$ and $D_2$ satisfying, respectively, the monotonicity properties of functions $D^{\mathrm{BP}}_1$ and $D^{\mathrm{BP}}_2$ in Theorem 3 is an EGT.

The discussion in the previous section, along with Remark 6, implies that to estimate an EGT with a given data set it suffices to estimate a BPT. MRL have suggested empirical construction of a BPT, and concomitant calculation of overall and environmental efficiency indexes, employing DEA (mathematical programming) methods. Here we offer some informal, preliminary suggestions about specification of functional forms for distance functions $D_1$ and $D_2$ for the econometric estimation of an EGT.

9.1 Radial distance function representations

At the most general level, econometric application would require specification of functional forms for $D_1$ and $D_2$ satisfying the monotonicity and homogeneity properties in Theorem 5 and estimation of the frontiers defined by $D_1(x,y,a,z)-1=0$ and $D_2(x,y,a,z)-1=0$. Estimation of parametric specifications of these functions would amount, respectively, to identification of the upper boundary of the EGT with respect to y and the lower boundary with respect to z and the shifts in these frontiers as x and a change. In the simple case of a single output and a single emission, these frontiers are, respectively, the horizontal and vertical boundaries of $T^{yz}(x,a)$ in Fig. 1.

9.2 Specification of functional forms for $D_1$ and $D_2$

The function $D_1$, which is independent of z, is a standard distance function for production technologies. Most state-of-the-art studies employ flexible functional forms, which have the advantage of letting the data (and the estimation technique) determine the properties of the technology other than those deemed theoretically necessary (typically homogeneity and monotonicity conditions). A classic example is that of Atkinson and Primont (2002), who estimated a translog distance function using data for US electric utilities.

Flexible functional forms are ideal when little is known—or assumed—about the technology beyond standard regularity conditions. Of course, more specific information about the technology should ideally be incorporated into the specification and estimation of the functional representations of the technology. The same is of course true about the emissions-generation aspect of the technology, which is governed by nature’s material-balance conditions. The appropriate specification of functional form for $D_2$ is likely to be highly specialized—dependent on specific information about the physical properties of emission generation based on the material-balance conditions of nature. Let us consider two examples.

Example 1

When coal is burned, its carbon content is converted into $\hbox {CO}_2$ (carbon dioxide) and CO (carbon monoxide). The relative proportions of the two emissions depend upon the availability of oxygen in the production process.¹⁸ Since the carbon content of a given amount of coal is fixed, the more $\hbox {CO}_2$ generated the less is generated of CO and vice versa. In that sense, there is some substitutability in the production of these two types of emissions. The degree of this substitutability can be estimated using data.

Example 2

Consider a variety of coal used in electricity generation that has both sulfur ($\hbox {SO}_2$) and carbon ($\hbox {CO}_2$) contents. Combusting this coal leads to a by-production of both types of emissions. Given that sulfur and carbon contents of a unit of such coal are fixed, one could expect that there is a complementarity in the generation of $\hbox {SO}_2$ and $\hbox {CO}_2$ in nature when this type of coal is burned.¹⁹ When a fixed amount of this coal is combusted, certain minimal amounts of $\hbox {SO}_2$ and $\hbox {CO}_2$ are generated. It is intuitive that increases in the generation of $\hbox {CO}_2$ above the minimal amount possible owing to environmental inefficiencies have no effect on the minimal amount of $\hbox {SO}_2$ that can be generated, as this depends on the sulfur content of the coal. Analogously, increases in the generation of $\hbox {SO}_2$ above the minimal amount possible have no effect on the minimal amount of $\hbox {CO}_2$ that can be generated. Figure 3b captures this complementarily in the generation of the two types of emissions. The “iso-coal” curve in the emission space is L-shaped.

In the case of Example 1, a very simple specification allowing a range of degrees of substitutability between the two emissions generated by a single emission-causing input, is

$$\begin{aligned} D^{\sigma }_2(x_z, z_1,z_2)=\frac{\beta x_z}{\Big (\alpha _1z_1^{\rho }+\alpha _2z_2^{\rho }\Big )^{1/\rho }},\quad \alpha _1,\alpha _2>0,\quad \alpha _1+\alpha _2=1,\quad 0\ne \rho \le 1.\nonumber \\ \end{aligned}$$

(9.1)

The elasticity of substitution between the two emissions, $\sigma =1/(1-\rho )$, reflects the degree to which adjustments of oxygen availability change the relative amounts of the two emissions.²⁰ A simple incorporation of a single abatement activity is as follows:

$$\begin{aligned} D^{\sigma }_2(x_z, z_1,z_2,a)=\frac{\beta x_z-\gamma a}{\Big (\alpha _1z_1^{\rho }+\alpha _2z_2^{\rho }\Big )^{1/\rho }},\quad \gamma \ge 0. \end{aligned}$$

(9.2)

Figure 3a captures this substitutability in the generation of the two types of emissions. The iso-coal curve in the emission space is downward sloping.

Note that the distance function specifications in Examples (9.1) and (9.2) satisfy all the monotonicity and homogeneity properties specified in Theorem 3 for function $D^{\mathrm{BP}}_2$. Because of this, (it can easily be verified that) the trade-offs between emissions and the emission-causing input and between emissions and the abatement output along the efficient frontier defined by distance function $D^{\sigma }_2$ (i.e., along production vectors that satisfy $D^{\sigma }_2(x, a, y, z)=1$) are positive and negative, respectively. This is as required by the material-balance conditions. These trade-offs can be obtained, employing the implicit function theorem, as²¹

$$\begin{aligned} \frac{\partial z_k}{\partial x_z}=-\frac{\partial D^{\sigma }_2/\partial x_z}{\partial D^{\sigma }_2/\partial z_k}\quad \hbox {and}\quad \frac{\partial z_k}{\partial a}=-\frac{\partial D^{\sigma }_2/\partial a}{\partial D^{\sigma }_2/\partial z_k},\quad k=1,2. \end{aligned}$$

The following specification of $D_2$ considers the case with two emission-causing inputs (e.g., two different types of coal) generating a single emission.

$$\begin{aligned} D_2(x_{z_1}, x_{z_2}, z,a)=\frac{x_{z_1}^{\alpha }+x_{z_2}^{\beta }-\gamma a}{z},\quad \gamma \ge 0,\ \alpha>1,\ \beta >1. \end{aligned}$$

(9.3)

This specification also satisfies the requisite properties in Theorem 3. In addition to the trade-offs discussed above between emissions and emission-causing inputs and abatement outputs, note also that the trade-off between the two emission-causing inputs along an iso-emission curve (when the abatement level is also held fixed) is given by the implicit function theorem as

$$\begin{aligned} \frac{\partial x_{z_1}}{\partial x_{z_2}}=-\frac{\partial D^{\sigma }_2/\partial x_{z_1}}{\partial D^{\sigma }_2/\partial x_{z_2}}, \end{aligned}$$

which is negative. Lower iso-emission curves correspond to lower levels of emissions and the set of all input bundles $\langle x_{z_1}, x_{z_2}\rangle \in \mathbf{R}^2_+$ that can produce a given amount of emissions is downward sloping.

Generalization of the structures in (9.1) and (9.2) with multiple emissions and emission-causing inputs to accommodate more complicated emission-generating technologies is not straightforward. For example, the incorporation of multiple emission-generating inputs raises the possibility that the mix of such inputs affects the trade-offs among emissions, so that the elasticity of substitution must be a function of the vector of input quantities. This structure poses severe difficulties in constraining the function to satisfy the requisite monotonicity property in $x_z$. Thus, for complicated emission-generating mechanisms, it is likely to be advisable to employ flexible functional forms, constrained to satisfy the homogeneity and monotonicity conditions.

In the case of emission-generating technologies described in Example 2, the level sets in emission space are Leontief (fixed proportions) sets, depicted in Fig. 3b for the case of two types of emissions. The distance function for this sub-technology is given by²²

$$\begin{aligned} D_2^L(x_z, z_1,z_2)=\Bigg ( \min \bigg \{\frac{z_1}{\alpha _1x_z},\frac{z_2}{\alpha _2x_z}\bigg \}\Bigg )^{-1}. \end{aligned}$$

(9.4)

An abatement activity can be incorporated by, for example, expressing the (Leontief) coefficients as functions of abatement and input quantities:

$$\begin{aligned} D^L_2(x_z,a,z)=\Bigg (\min \Bigg \{\frac{z_1}{\alpha _1(x_z,a)},\frac{z_{2}}{\alpha _{2}(x_z,a)}\Bigg \}\Bigg )^{-1}, \end{aligned}$$

(9.5)

Empirical implementation of this structure requires specification and estimation of the functions, $\alpha _1$ and $\alpha _2$, which must be non-decreasing in $x_z$ and non-increasing in a.

10 Concluding remarks

The principal objective of the foregoing is to reconcile the abstract axiomatic characterization of an emission-generating technology in Murty (2015a) with the empirically oriented by-production technology formulated by Murty et al. (2012). It turns out that the by-production structure satisfies the Murty axioms.

We also propose representations of EGTs using radial distance functions. Because of the disposability properties of these technologies, two functions are required for a representation: one for the intended production sub-technology and one for the emissions-generation sub-technology (or sub-technologies).While we have not explored these possibilities here, it should be noted that the radial distance functions can also serve as measures of technological and environmental efficiency. That is, a production vector is technologically efficient only if $D_1(x,a,y,z)=1$ and environmentally efficient only if $D_2(x,a,y,z)=1$. Moreover,

$$\begin{aligned} E_1(x,a,y,z):=1/ D_1(x,a,y,z)\in (0,1] \end{aligned}$$

(10.1)

and

$$\begin{aligned} E_2(x,a,y,z):=1/ D_2(x,a,y,z)\in (0,1] \end{aligned}$$

(10.2)

are (radial) measures of technological and environmental efficiency.²³

The exact structure of an EGT is likely to be highly technology specific, requiring specialized modeling that employs scientific information supplied by engineers. Nevertheless, in our view there is significant potential value in the search for a generic structure that can accommodate a range of characteristics of emission-generating technologies. Fittingly, multiple ideas along this line are percolating in the literature. We view these efforts as parallel to our own. Especially noteworthy [in addition to the already cited Førsund (2009) paper] are contributions by Pethig (2006), Coelli et al. (2007), Serra et al. (2014), Rødseth (2015) and Kumbhakar and Tsionas (2016). We are confident that these various lines of investigation will converge to a common generic framework for modeling emission-generating technologies, an essential component of the design of environmental policies to mitigate the effects of pollution externalities.²⁴