1 Introduction

The advancement in industries such as aerospace, cars and rail transportations strongly rely on the development of multi-functional materials with particular combinations of physico-chemical properties. Similarly, the spectacular evolution of technology is directly dependent, from a fundamental perspective, on the availability of high-quality functional materials and the scientific progress in materials and nanomaterials engineering and design. Experimental and theoretical investigations of novel materials and their fabrication and conditioning processes play a key role in the development of many aspects of the current global society [1,2,3]. In this paper, we report on the investigation of the mechanical properties of a silicon carbide-based ceramic composite material, SiCf/SiC. This ceramic is formed by a matrix of fibre-reinforced SiC embedded in bulk SiC. SiCf/SiC is known for its particularly interesting combination of physico-mechanical properties, specifically its low thermal expansion coefficient, low density, high tensile modulus, and high specific strength. Owing to these properties, SiCf/SiC has shown a great potential for its integration in a wide spectrum of applications. Nevertheless, the elaboration process of high-quality SiCf/SiC implicates several challenges associated with its hardness, brittleness, and anisotropy [4]. More specifically, grinding is a machining technique commonly used for the processing of SiCf/SiC composites [5, 6]. Nonetheless, SiCf/SiC samples are prone to matrix cracking and fibres damage in a grinding process, which deteriorates their structural properties and hinders their efficient use and applicability [7, 8]. In the present work, we aim at developing a calculation-based understanding of the effects induced by the grinding process on the cracking and fracture removal mechanisms in SiCf/SiC composites. Our goal is to elucidate the roles of the various grinding process parameters that affect the mechanical properties of the material during sample preparations. This is to develop practical feedback that can help in improving preparation conditions and the efficiency of high-quality SiCf/SiC samples’ fabrication.

The literature is rich with an interesting body of theoretical and experimental works dealing with the problem of understanding the mechanism of grinding brittle materials. Hereafter, we present a non-exhaustive state of the art of interesting investigations reported in this direction. In fact, the cutting force is most often perceived as an essential contributing factor in the grinding process, influencing the cutting temperature, machining accuracy, and surface integrity [9]. Sun et al. [10] established a grinding force model for silicon, based on the scratching theory of single diamond grain. They showed that the material removal rate can be improved according to their model’s predictions. Huang et al. [11] proposed a cutting force prediction model of BK7 optical glass by analysing the micro kinematics between the individual diamond grains and the material. Their model could be used in selecting process parameters for realising high efficiency and precision. Xiao et al. [12] considered the ductile and brittle material removal mechanisms and proposed a cutting force model of side grinding for zirconia ceramics. The reported theoretical model was shown to be applicable for evaluating the cutting force, and it can provide a better understanding of the effects of ductile removal and brittle fracture removal on the grinding. According to the latest research, the removal mechanism of grinding brittle materials can be divided into the ductile, ductile-to-brittle transition, and brittle stages depending on the cutting force and the ground surface morphology [13]. Cheng et al. [14] designed a series of scratch tests and developed a cutting force model; the critical cutting depth and forces of the ductile-to-brittle transition have been determined to distinguish the three cutting stages. Rao et al. [15] established a modified model to predict the critical cutting depth by considering the changes in mechanical properties. The results revealed the material deformation and adhesive behaviour of RB-SiC ceramics during scratching. Zhang et al. [16] analysed the forming mechanism of the three cutting stages and presented a theoretical grinding force model; the model revealed the connection between the grinding force and the grinding parameters.

Unlike homogeneous hard and brittle materials, composite materials comprise multiphase materials, and anisotropy is its noticeable characteristic. Some researchers have focused on modelling the processing of composites in recent decades. Yin et al. [17] developed a dynamic cutting force model of SiCp/Al composites based on the analysis of the mechanical and heat generation mechanisms. The model can accurately present the dynamic fluctuation characteristics of the cutting process. For long fibre-reinforced composites, Zhang et al. [18] developed a series of particular surface grinding experiments and established a cutting force model of unidirectional Cf/SiC composites based on the multiple-exponential function method. Their results show that the grinding parameters have a significant impact on the grinding force. Ning et al. [19] and Wang et al. [20] homogenised the monolayer carbon fibre reinforced plastic (CFRP) composites through microscopic analysis and developed a cutting force model. Their predictions agree well with experimental results under different groups of input variables.

However, for laminated composites, the anisotropy between the layers has an important contribution to their mechanical properties and accordingly to their fracture mechanism. In this direction, Zhu et al. [21] conducted a statistical analysis of the yarn parameters of a plain-woven CFRP and proposed a numerical multiscale model to evaluate the effective elastic properties of the composites, which was found to be in good agreement with experimental data obtained from tensile, compressive, and shear tests. Zhu et al. [22] developed a three-dimensional analytical method to quantitatively determine the effective elastic constants of thick composite laminates. The Young’s modulus, shear modulus, and Poisson’s ratios of wavy fibre composite laminates were obtained and discussed. Their method provided a useful tool to evaluate the effective elastic properties of composite laminates. Macedo et al. [23] used an asymptotic homogenisation numerical model to obtain elastic properties of unidirectional fibre-reinforced composites. Discrepancies between experimental and numerical data were explained in terms of simplifications considered in the homogenisation model. Due to the complexity and instability of the preparation process of SiCf/SiC composites, the elastic properties of laminated composites contain large differences. Therefore, the effective elastic properties should be determined through theoretical analysis to establish a more accurate cutting force model.

Although numerous investigations have been reported on the modelling of brittle and homogeneous materials, the cutting force modelling of laminated composites, such as SiCf/SiC, has not been sufficiently developed. The goal of our study is to introduce a new approach to improve accuracy in modelling laminate composites by combining the anisotropy and fracture removal mechanism of the brittle materials in the development of a new cutting force model for the case of SiCf/SiC. The effective elastic properties of orthogonal laminated SiCf/SiC composites were discussed considering anisotropy using a macromechanical analysis. In addition, we classify the removal mechanisms into three cutting stages based on the critical conditions for the ductile–brittle transition. The final cutting force model was verified by experiment. The cutting force model reveals the relationship between the interaction force and material removal process and provides important theoretical guidance for side grinding of orthogonal laminated SiCf/SiC composites.

2 Material analysis

2.1 Material preparation

SiCf/SiC is composed of SiC fibres (SiCf) and an SiC matrix (SiCm). The composites were prepared using melt infiltration (MI). First, the interface was prepared on the fibre surface using a chemical vapour infiltration (CVI) process. Then, multiple bundles of fibres were converted into unidirectional bands, and the preforms were obtained by laminated hot pressing and high-temperature cracking. Finally, the preforms were siliconised to obtain the materials. The material parameters of SiCf/SiC composites are shown in Table 1.

Table 1 Material parameters of SiCf/SiC composites
Full size table

The orthogonal laminated SiCf/SiC composites present a two-dimensional (2D) structure as shown in Fig. 1a. The structure of the monolayer SiCf/SiC composites is shown in Fig. 1b. The direction along the fibres is longitudinal and represented by direction 1; the direction perpendicular to the fibres is transverse and represented by direction 2; the direction perpendicular to plane 1–2 is vertical and represented by direction 3. The dimension of the thickness direction (direction 3) can be considered much smaller than that of the other two directions.

Fig. 1
figure 1

a Structure of orthogonal laminated SiCf/SiC composites, b SiCf/SiC monolayer composite material

Full size image

In the overall analysis, the matrix can be considered an isotropic material, and the fibre as a transversely isotropic material. Then, the monolayer SiCf/SiC composites can be regarded as isotropic materials in the plane 1–2. The mechanical properties of SiCf/SiC composites are shown in Table 2.

Table 2 Mechanical properties of SiCf/SiC composites
Full size table

For the presentation, subscript f represents the silicon carbide fibre, and subscript m represents the silicon carbide matrix. For example, Ef1 represents the fibre elastic modulus in direction 1; υf12 represents the Poisson’s ratio in direction 1 of the SiCf in plane 1–2. The longitudinal effective elastic properties E1 and transverse effective elastic properties E2 of monolayer SiCf/SiC composites can be obtained by the following equation [24]:

$$\begin{array}{l}{E}_{1}={E}_{f1}{V}_{f}+{E}_{m}{V}_{m}\\ {E}_{2}=\frac{{E}_{m}}{\sqrt{{V}_{f}}\left(1-{E}_{m}/{E}_{f2}\right)}\end{array}$$
(1)

2.2 Analysis of the effective elastic properties of orthogonal laminated SiCf/SiC composites

When analysing the macroscopic properties of laminated composites, a monolayer composite is considered a macroscopic homogeneous material, whose elastic properties are expressed by Eq. (1). In addition, the interlaminar performance of monolayer composites should be considered. The following assumptions are made in the analysis of the effective elastic properties:

  1. (1)

    Each monolayer composite has the same thickness.

  2. (2)

    The connection between the layers does not contain gaps.

  3. (3)

    Stress and strain are evenly distributed in the laminated SiCf/SiC composites.

  4. (4)

    The material follows Hooke’s law (linear elasticity).

Assuming that the thickness of the laminated SiCf/SiC composite material is h, each layer has the same thickness of hi, and the total number of layers of the material is N. The geometric centre of the material is selected as the origin Om, and the relative coordinate system of the material (xm-ym-zm) is established to facilitate the analysis, as shown in Fig. 2a.

Fig. 2
figure 2

Laminated SiCf/SiC composites: a global view, b relationship between fibre orientation and material coordinate system, and c xm-zm cross-section

Full size image

Figure 2b shows the relationship between the fibre’s orientation and the material’s coordinate system. The materials studied in this work are monolayer SiCf/SiC composites with θi = 0°/90° orthogonal tiling without a braided structure. In Fig. 2c, the coordinates of the points in the thickness direction for the material are denoted by zm; the superscript k signifies quantities for the kth layer. The stress–strain constitutive relations in the composites can be expressed as follows:

$$\left\{\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\sigma }_{23}\\ {\sigma }_{31}\\ {\sigma }_{12}\end{array}\right\}=\left[\begin{array}{cccccc}{C}_{11}& {C}_{12}& {C}_{13}& {C}_{14}& {C}_{15}& {C}_{16}\\ {C}_{12}& {C}_{22}& {C}_{23}& {C}_{24}& {C}_{25}& {C}_{26}\\ {C}_{13}& {C}_{23}& {C}_{33}& {C}_{34}& {C}_{35}& {C}_{36}\\ {C}_{14}& {C}_{24}& {C}_{34}& {C}_{44}& {C}_{45}& {C}_{46}\\ {C}_{15}& {C}_{25}& {C}_{35}& {C}_{45}& {C}_{55}& {C}_{56}\\ {C}_{16}& {C}_{26}& {C}_{36}& {C}_{46}& {C}_{56}& {C}_{66}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{11}\\ {\varepsilon }_{22}\\ {\varepsilon }_{33}\\ 2{\varepsilon }_{23}\\ 2{\varepsilon }_{31}\\ 2{\varepsilon }_{12}\end{array}\right\}$$
(2)

where σ and ε are the stress components and strain components, respectively. C11, C12, …, C66 are the components of the stiffness matrix [C]. [C] = [S]−1, and [S] is the compliance matrix.

The effective constitutive relations can be written as follows:

$${\sigma }_{ij}^{*}=\left[{C}^{**}\right]{\varepsilon }_{kl}^{*}\text{,} \,\ {\varepsilon }_{ij}^{*}=\left[{S}^{**}\right]{\sigma }_{kl}^{*}$$
(3)

where [C**] are effective stiffness coefficients and [S**] are effective compliant coefficients. σ* ij and ε* ij are the average stress and strain, respectively, which are expressed as follows:

$$\begin{array}{c}{\sigma }_{ij}^{*}=\frac{1}{V}{\int }_{V}{\sigma }_{ij}dV\\ {\varepsilon }_{ij}^{*}=\frac{1}{V}{\int }_{V}{\varepsilon }_{ij}dV\end{array}$$
(4)

As a monolayer composite is transversely isotropic, the compliance matrix can be expressed as follows:

$$\left[S\right]={\left[C\right]}^{-1}=\left[\begin{array}{cccccc}\frac{1}{{E}_{1}}& -\frac{{\upsilon }_{12}}{{E}_{1}}& -\frac{{\upsilon }_{12}}{{E}_{1}}& 0& 0& 0\\ -\frac{{\upsilon }_{21}}{{E}_{2}}& \frac{1}{{E}_{2}}& -\frac{{\upsilon }_{23}}{{E}_{2}}& 0& 0& 0\\ -\frac{{\upsilon }_{21}}{{E}_{2}}& -\frac{{\upsilon }_{23}}{{E}_{2}}& \frac{1}{{E}_{2}}& 0& 0& 0\\ 0& 0& 0& \frac{1}{{G}_{23}}& 0& 0\\ 0& 0& 0& 0& \frac{1}{{G}_{12}}& 0\\ 0& 0& 0& 0& 0& \frac{1}{{G}_{12}}\end{array}\right]$$
(5)

where υ12 and υ23 are longitudinal and transverse Poisson’s ratios of monolayer composites, respectively, which can be expressed as follows:

$$\begin{array}{l}{\upsilon }_{12}={\upsilon }_{f12}{V}_{f}+{\upsilon }_{m}{V}_{m}\\ {\upsilon }_{23}={\upsilon }_{f23}{V}_{f}+{\upsilon }_{m}{V}_{m}\left[\frac{1+{\upsilon }_{m}-{\upsilon }_{12}\left({E}_{m}/{E}_{1}\right)}{1-{\upsilon }_{m}^{2}+{\upsilon }_{m}{\upsilon }_{12}\left({E}_{m}/{E}_{1}\right)}\right]\end{array}$$
(6)

υ21 is the ratio of the contraction strain to the tensile strain in direction 1 with unidirectional stretching along direction 2, υ21 / E2 = υ12 /E1. Furthermore, G23 and G12 are the shear modulus in planes 2–3 and 1–2, respectively, which can be expressed as follows:

$${G}_{23}=\frac{{E}_{2}}{2\left(1+{\upsilon }_{23}\right)}\text{,} \,\ {G}_{12}=\frac{{E}_{1}}{2\left(1+{\upsilon }_{12}\right)}$$
(7)

The constitutive relationship of a monolayer composite conforms to Eq. (2), which can be written as follows [25]:

$$\left\{\begin{array}{c}{\sigma }_{33}^{*}\\ {\sigma }_{23}^{*}\\ {\sigma }_{31}^{*}\\ {\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right\}=\left[\begin{array}{ll}\left[A\right]& \left[B\right]\\ {\left[B\right]}^{T}& \left[D\right]\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{33}\\ 2{\varepsilon }_{23}\\ 2{\varepsilon }_{31}\\ {\varepsilon }_{11}^{*}\\ {\varepsilon }_{22}^{*}\\ 2{\varepsilon }_{12}^{*}\end{array}\right\}$$
(8)

where [A], [B], and [D] can be expressed as follows:

$$\left[A\right]=\left[\begin{array}{ccc}{C}_{33}& {C}_{34}& {C}_{35}\\ {C}_{34}& {C}_{44}& {C}_{45}\\ {C}_{35}& {C}_{45}& {C}_{55}\end{array}\right]\;\;\left[B\right]=\left[\begin{array}{ccc}{C}_{13}& {C}_{23}& {C}_{36}\\ {C}_{14}& {C}_{24}& {C}_{46}\\ {C}_{15}& {C}_{25}& {C}_{56}\end{array}\right]\;\;\left[D\right]=\left[\begin{array}{ccc}{C}_{11}& {C}_{12}& {C}_{16}\\ {C}_{12}& {C}_{22}& {C}_{26}\\ {C}_{16}& {C}_{26}& {C}_{66}\end{array}\right]$$
(9)

The effective constitutive relation of a monolayer composite conforms to Eq. (3), which can be written as follows:

$$\left\{\begin{array}{c}{\sigma }_{33}^{*}\\ {\sigma }_{23}^{*}\\ {\sigma }_{31}^{*}\\ {\sigma }_{11}^{*}\\ {\sigma }_{22}^{*}\\ {\sigma }_{12}^{*}\end{array}\right\}=\left[\begin{array}{cc}{\left[a\right]}^{-1}& {\left[a\right]}^{-1}\left[b\right]\\ {\left[b\right]}^{T}{\left[a\right]}^{-1}& {\left[b\right]}^{T}{\left[a\right]}^{-1}\left[b\right]+\left[d\right]\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{33}^{*}\\ 2{\varepsilon }_{23}^{*}\\ 2{\varepsilon }_{31}^{*}\\ {\varepsilon }_{11}^{*}\\ {\varepsilon }_{22}^{*}\\ 2{\varepsilon }_{12}^{*}\end{array}\right\}$$
(10)

where [a], [b], and [d] are given by the following equations:

$$\begin{array}{l}\left[a\right]=\frac{1}{h}\sum\limits_{k=1}^{N}{\int }_{{z}_{m}^{k-1}}^{{z}_{m}^{k}}{\left[A\right]}^{-1}dz\\ \left[b\right]=\frac{1}{h}\sum\limits_{k=1}^{N}{\int }_{{z}_{m}^{k-1}}^{{z}_{m}^{k}}{\left[A\right]}^{-1}\left[B\right]dz\\ \left[d\right]=\frac{1}{h}\sum\limits_{k=1}^{N}{\int }_{{z}_{m}^{k-1}}^{{z}_{m}^{k}}\left(\left[D\right]-{\left[B\right]}^{T}{\left[A\right]}^{-1}\left[B\right]\right)dz\end{array}$$
(11)

Therefore, the effective compliance matrix of laminated SiCf/SiC composites can be expressed as follows [26]:

$$\left[{S}^{**}\right]={\left[{C}^{**}\right]}^{-1}=\left[\begin{array}{cccccc}{S}_{11}^{**}& {S}_{12}^{**}& {S}_{13}^{**}& {S}_{14}^{**}& {S}_{15}^{**}& {S}_{16}^{**}\\ {S}_{21}^{**}& {S}_{22}^{**}& {S}_{23}^{**}& {S}_{24}^{**}& {S}_{25}^{**}& {S}_{26}^{**}\\ {S}_{31}^{**}& {S}_{32}^{**}& {S}_{33}^{**}& {S}_{34}^{**}& {S}_{35}^{**}& {S}_{36}^{**}\\ {S}_{41}^{**}& {S}_{42}^{**}& {S}_{43}^{**}& {S}_{44}^{**}& {S}_{45}^{**}& {S}_{46}^{**}\\ {S}_{51}^{**}& {S}_{52}^{**}& {S}_{53}^{**}& {S}_{54}^{**}& {S}_{55}^{**}& {S}_{56}^{**}\\ {S}_{61}^{**}& {S}_{62}^{**}& {S}_{63}^{**}& {S}_{64}^{**}& {S}_{65}^{**}& {S}_{66}^{**}\end{array}\right]=\left[a\right]-\left[b\right]{\left[d\right]}^{-1}{\left[b\right]}^{T}$$
(12)

According to the relationship between the effective compliant coefficients and effective elastic properties, the effective elastic constants of laminated SiCf/SiC composites can be obtained by the following equations:

$${E}_{x}=\frac{1}{{S}_{11}^{**}}\quad{E}_{y}=\frac{1}{{S}_{22}^{**}}\quad{\upsilon}_{xy}=-\frac{{S}_{12}^{**}}{{S}_{11}^{**}}$$
(13)

Finally, the effective elastic constants of the laminated SiCf/SiC composites are obtained as Ee = Ex ≈ Ey = 134.24 Gpa, υe = υxy = 0.26. These constants are used for the modelling shown in Sect. 3.

3 Development of the cutting force model

3.1 Analysis of the cutting state of the grinding tool and workpiece

The grinding process in the tool-workpiece system involves the cutting of the whole diamond grains. A clear understanding of the interaction between the diamond grains and workpiece can be obtained by analysing the cutting state and dynamic trajectory of a single diamond.

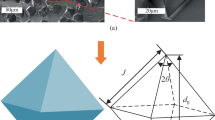
A schematic diagram of side grinding is shown in Fig. 3a. The directions of feeding, cutting, and the tool axis are set as the x, y, and z-axes, respectively. Fx and Fy are the average forces measured by the dynamometer in the x and y directions in the grinding process, respectively. Fm is the total force used to evaluate the cutting forces in the entire grinding process; vf is the feed rate of the tool, mm/s; ω is the angular velocity of the spindle, rad/s. ω = 2πn, and n is the spindle rotation speed, r/min. The thickness of the workpiece is denoted as hm, mm. The diamond grains are considered octahedrons to simplify the modelling, as shown in Fig. 3b. θ is the semi-angle between two opposite edges of the diamond grains, and Sa is the edge length of the diamond grains.

Fig. 3
figure 3

a Side grinding, b octahedral diamond grain

Full size image

However, the diamond grains on the tool are randomly distributed, and the protruding height is not uniform, as shown in Fig. 4a, where O represents the tool centre and Rt denotes the radius of the tool substrate. The random protrusion height of diamond grains is δgi. Figure 4b shows the plane expansion of the diamond grains on the tool surface. A probability density function is required to describe the characteristics of the random protruding height of the diamond grains and thereby better analyse the interaction between the diamond grains and workpiece. The cutting force model can be established accordingly. The protruding height of diamond grains on the tool surface conforms to the Rayleigh distribution [2]:

$$f\left({\delta }_{gi}\right)=\left\{\begin{array}{cc}\left({\delta }_{gi}/{\beta }^{2}\right){e}^{-\left({\delta }_{gi}^{2}/2{\beta }^{2}\right)}&,{\delta }_{gi}\ge 0\\ 0 & ,{\delta }_{gi}<0\end{array}\right.$$
(14)

where β is a parameter defined by the probability density function.

Fig. 4
figure 4

a Randomly protruding height of diamond grains, b the plane expansion of diamond grains, c average protrusion height of diamond grains, d the plane expansion of the average protrusion height of diamond grains

Full size image

The average protrusion height of diamond grains is δga, as shown in Fig. 4c. Ra is the average tool radius used to calculate the trajectory of the diamond grains. Ra = Rt + δga; δga can be determined by the expectation of the Rayleigh function. According to the probability statistics method, the expected and variance can be obtained by the following equations:

$$\begin{array}{l}E\left({\delta }_{gi}\right)=\beta \sqrt{\frac{\pi }{2}}\approx \text{1.253}\beta \\ Var\left({\delta }_{gi}\right)=\left(2-\frac{\pi }{2}\right){\beta }^{2}\approx 0.429{\beta }^{2}\\ E\left({\delta }_{gi}^{2}\right)={\int }_{0}^{\infty }{\delta }_{gi}^{2}f\left({\delta }_{gi}\right)d{\delta }_{gi}\end{array}$$
(15)

Substituting Eq. (14) into Eq. (15),

$$E\left({\delta }_{gi}^{2}\right)={\left[{e}^{-{\delta }_{gi}^{2}/2{\beta }^{2}}\left(-2{\beta }^{2}-{\delta }_{gi}^{2}\right)\right]}_{0}^{\infty }=2{\beta }^{2}$$
(16)

The total removal volume of all diamond grains should be equal to the removal volume of the grinding process, which can be expressed as follows:

$$E\left({\delta }_{gi}^{2}\right)=\frac{2{a}_{e}{v}_{f}}{\pi {C}_{e}{l}_{c}{v}_{s}}$$
(17)

where Ce is the number of active diamond grains per square millimetre (Ce = 5 in this paper); vs is the cutting speed of a single diamond grain, mm/s; ae is the cutting width, mm; and lc is the grinding tool/workpiece arc length of contact, which can be expressed as follows:

$${l}_{c}=\sqrt{2{R}_{a}\cdot {a}_{e}}$$
(18)

Therefore, δga can be obtained as:

$${\delta }_{ga}=E\left({\delta }_{gi}\right)=\sqrt{\frac{{a}_{e}{v}_{f}}{2{C}_{e}{l}_{c}{v}_{s}}}$$
(19)

As shown in Fig. 4d, after taking the average of the random protruding height, the randomly distributed diamond grains on the tool have a uniform height, consistent with the height of the average height plane, thus simplifying the grinding behaviour generated by the random protruding height, beneficial to the complete description of the processed surface.

The cutting mechanism of a single diamond grain is shown in Fig. 5a. 1Based on research on indentation and scratch experiments of hard and brittle materials, there are three cutting stages with a gradual increase of the normal cutting force Fn of a single diamond grain: ductile stage (stage I), ductile-to-brittle transition stage (stage II), and brittle stage (stage III). The normal and tangential cutting forces are represented by Fn and Ft, respectively. Fp, the theoretical cutting force, is the resultant of these two forces, as shown in Fig. 5a.

Fig. 5
figure 5

a Cutting mechanism of a single diamond grain, b three cutting stages

Full size image

2According to the definition of Vickers hardness, the normal cutting force can be obtained by the following equation [27]:

$${F}_{n}=\xi H{a}^{2}$$
(20)

where ξ is the geometrical factor of the indenter, ξ≈1.885; H denotes Vickers hardness, which is 20 GPa; a denotes the indentation size, a = hgtanθ, where hg is the cutting depth of a single diamond grain.

Therefore, the three cutting stages depend on hg, influencing the local contact deformation and material removal mechanism.

When 0 < hg1 < hgp, the cutting stage is the ductile stage (stage I), as shown in Fig. 5b. 1Here, the contact area between the diamond grain and workpiece is mainly the plastic deformation area caused by the pressure of the diamond grain, and no obvious cracks are present. Therefore, the materials are removed through plastic flow, and the tangential direction of the diamond grain is mainly affected by the rubbing force. The critical state of the ductile–brittle transition refers to the state in which the crack generated by the last diamond grain is immediately removed by the next grain. The critical depth can be expressed as follows [16]:

$${h}_{gp}=\tau {h}_{gc}$$
(21)

where hgp is the critical depth between stage I and stage II; hgc is the critical depth between stage II and stage III; τ is coefficients of the ductile stage, which is 0.25 in this paper.

When hgp < hg2 < hgc, the cutting stage is the ductile–brittle transition stage (stage II), as shown in Fig. 5b. 2At this stage, the plastic zone beneath the diamond gradually expands. The median crack begins to appear beneath the plastic zone, which is usually related to strength degradation. The median crack occurs in the loading and unloading process. Unloading and tool wear result in uneven local stress distribution along the grinding path, and lateral cracks occurred during unloading. The residual stress component is the main source of crack propagation, and the tangential direction of the diamond grain is mainly subjected to ploughing force. The critical depth between stage II and stage III is related to the material properties, which can be expressed as follows [15]:

$${h}_{gc}^{*}=\psi \left(T\right)\left(\frac{{E}_{e}}{H}\right){\left(\frac{{K}_{IC}}{H}\right)}^{2}$$
(22)

where KIC is the static fracture toughness of the material, which is 15.5 MPa/m1/2; ψ(T) is a function of temperature, which is given as follows:

$$\psi \left(T\right)=0.52+0.85\mathrm{exp}\left(-T/{T}_{0}\right){T}_{0}=251.1^\circ C$$
(23)

where T is ambient temperature, °C.

However, based on previous reports, using static fracture toughness in dynamic processing is not appropriate. The dynamic fracture toughness KID is approximately 30% of KIC [28]. Therefore, substituting KID for KIC can better conform to the actual grinding process and provide more accurate theoretical guidance for modelling, and the critical depth hgc can be written as follows:

$${h}_{gc}=\psi \left(T\right)\left(\frac{{E}_{e}}{H}\right){\left(\frac{{K}_{ID}}{H}\right)}^{2}$$
(24)

When hgc < hg3, the cutting stage is the brittle transition stage (stage III), as shown in Fig. 5b. 3At this stage, the plastic zone beneath the diamond grain expands further. Continuous crack branches occur beneath the plastic zone, and obvious transverse cracks occur in the workpiece and extend to the ground surface, resulting in material detritus and a large amount of removal. The diamond grains are subjected to tangential and normal loads. The tangential cutting force causes the expansion of transverse cracks, reducing the surface quality of the workpiece and improving the removal rate. The lengths of the median crack, lateral crack, and plastic zone, denoted as Cm, Cl, and Ch, respectively, can be expressed as follows [29]:

$$\begin{array}{l}{C}_{m}={\eta }_{1}^{2/3}{\left(\frac{{E}_{e}}{H}\right)}^{1/3}{\mathrm{cos}}^{4/9}\theta {\left[\frac{{\chi }_{e}}{{\chi }_{r}}\left(\frac{{F}_{t3}}{{K}_{ID}}\right)+\left(\frac{{F}_{n3}}{{K}_{ID}}\right)\right]}^{2/3}\\ {C}_{l}={\eta }_{2}{\mathrm{cot}}^{5/12}\theta {\left[\frac{{E}_{e}^{3/4}}{H{K}_{ID}{\left(1-{\upsilon }_{e}^{2}\right)}^{1/2}}\right]}^{1/2}{F}_{n3}^{5/8}\\ {C}_{h}={\eta }_{3}{\mathrm{cot}}^{1/3}\theta \frac{{E}_{e}^{1/2}}{H}{F}_{n3}^{1/2}\end{array}$$
(25)

where χe and χr are the indentation coefficients of the elastic stress field and residual stress field, respectively (χe = 0.032, χr = 0.026); η1, η2, and η3 are the dimensional constants (η1 = 0.0366, η2 = η3 = 0.226).

The cutting depth increases gradually from the time when a single diamond grain touches the workpiece to when it is removed. The maximum undeformed chip thickness hgm can be obtained by the following expression [30]:

$${h}_{gm}=2{\delta }_{ga}{\left(\frac{{a}_{e}}{2{R}_{a}}\right)}^{1/4}\sqrt{\frac{{v}_{f}}{{v}_{s}{\eta }_{c}f}{\left(\frac{4\pi }{3{V}_{d}}\right)}^{2/3}}$$
(26)

where ηc is the ratio of chip width to average undeformed chip thickness, ηc = 10; f is the fraction of diamond grains that are actively cut during grinding, f = 0.5; The grinding tool used in this study has a concentration of 100 or volume fraction of Vd = 0.25.

3.2 Modelling development assumptions

The tangential and normal forces of a single diamond, decided by the dynamic trajectory and average cutting depth of a single diamond in the grinding process, are analysed to establish the cutting force model with the following assumptions and simplifications:

  1. (1)

    The diamond grains are perfectly bonded to the tool and will not fall off during grinding.

  2. (2)

    The diamond grains are octahedrons of the same size and the semi-angle θ is 60°.

  3. (3)

    The experimental system keeps stable during the grinding process.

  4. (4)

    The material deformation during the grinding process conforms to Hooke's law.

3.3 Cutting force model of a single diamond grain under three cutting stages

3.3.1 Kinematical analysis of a single diamond grain

The dynamic trajectory of a single diamond grain was analysed dynamically to clarify the side grinding process, and its position can be expressed by machining parameters. The three cutting stages of the ground region from A to A’ is shown in Fig. 6. The position and velocity of a single diamond grain in the grinding process can be expressed as follows:

$$\left\{\begin{array}{l}x={R}_{a}sin(2\pi nt)+{v}_{f}t\\ y={R}_{a}cos(2\pi nt)\\ z=0\end{array}\right.\;\left\{\begin{array}{l}{v}_{x}=2\pi n{R}_{a}\cdot cos(2\pi nt)+{v}_{f}\\ {v}_{y}=-2\pi n{R}_{a}\cdot sin(2\pi nt)\\ {v}_{z}=0\end{array}\right.$$
(27)

where t is the cutting time, s.

Fig. 6
figure 6

Grinding process of a single diamond grain

Full size image

The moment when a single diamond grain touches the workpiece is t0 (t0 = 0 for convenience). At stage I, the tool centre moves from O to O1, and the corresponding cutting time is t0-t1. The corresponding cutting time is t1-t2 and t2-t3 when the tool centre moves from O1 to O2 at stage II and from O2 to O3 at stage III, respectively. The cutting lengths of a single diamond grain during the grinding process can be expressed as follows:

$$\begin{array}{c}{l}_{1}={\int }_{{t}_{0}}^{{t}_{1}}\sqrt{{v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}}dt\\ {l}_{2}={\int }_{{t}_{1}}^{{t}_{2}}\sqrt{{v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}}dt\\ {l}_{3}={\int }_{{t}_{2}}^{{t}_{3}}\sqrt{{v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}}dt\end{array}$$
(28)

where l1, l2, and l3 are the cutting lengths at stage I, stage II, and stage III, respectively.

The feeding distance and cutting time of a single diamond grain can be obtained by the following expression:

$$\begin{array}{ccc}{x}_{1}={v}_{f}{t}_{1}& {x}_{2}={v}_{f}{t}_{2}& {x}_{3}={v}_{f}{t}_{3}\\ {\gamma }_{1}=\omega {t}_{1}& {\gamma }_{2}=\omega {t}_{2}& {\gamma }_{3}=\omega {t}_{3}\\ {t}_{1}=\frac{{h}_{gp}}{{v}_{f}\ \mathrm{sin}\ {\gamma }_{1}}& {t}_{2}=\frac{{h}_{gc}}{{v}_{f}\ \mathrm{sin}\ {\gamma }_{2}}& {t}_{3}=\frac{{h}_{gm}}{{v}_{f}\ \mathrm{sin}\ {\gamma }_{3}}\end{array}$$
(29)

where x1, x2, and x3 are the feeding distance at stage I, stage II, and stage III, respectively. γ1, γ2, and γ3 are the rotation angle of the tool and the corresponding cutting time.

3.3.2 Cutting force model of a single diamond grain at the ductile stage

As the cutting depth hg1 of a single diamond grain is constantly changing with time at the ductile stage, the average cutting depth needs to be determined. The material removal volume of a single diamond grain at stage I, denoted as Vg1, can be considered a triangular pyramid volume with the following expression:

$${V}_{g1}=\frac{1}{3}{l}_{1}\times {h}_{gp}\times {h}_{gp}\mathrm{tan}\ \theta =\frac{1}{3}{l}_{1}{h}_{gp}^{2}\mathrm{tan}\ \theta$$
(30)

The equivalent removal volume of a single diamond grain at the ductile stage can be idealised as a triangular prism, denoted as Vga1 with the following expression:

$${V}_{ga1}={l}_{1}\times {h}_{ga1}\times {h}_{ga1}\mathrm{tan}\ \theta ={l}_{1}{h}_{ga1}^{2}\mathrm{tan}\ \theta$$
(31)

Then, Vg1 = Vga1, and the average cutting depth at stage I, denoted as hga1, can be expressed as follows:

$${h}_{ga1}=\frac{\sqrt{3}}{3}{h}_{gp}$$
(32)

The connection between the average normal cutting force Fn1 and average cutting depth hga1 at stage I can be expressed as follows [31]:

$${F}_{n1}=2H{h}_{ga1}^{2}\mathrm{tan}\ \theta {\left(2+{\mathrm{tan}}^{2}\ \theta \right)}^{1/2}$$
(33)

Substituting Eqs. (21) and (32) into Eq. (33), the average normal cutting force Fn1 can be expressed as follows:

$${F}_{n1}=\frac{H{h}_{gc}^{2}\mathrm{tan}\ \theta }{24}{\left(2+{\mathrm{tan}}^{2}\ \theta \right)}^{1/2}$$
(34)

At stage I, plastic deformation of the workpiece begins at yield criterion point with the increase of cutting depth, and the single diamond grain is mainly subjected to the rubbing force Ft1 in the tangential direction, which can be expressed as follows:

$${F}_{t1}=\mu {F}_{n1}$$
(35)

where μ is the friction coefficient.

The friction coefficient of the diamond grain can be approximated to the ratio of the projected areas in the cutting and tangential directions [32], which is given as follows:

$$\mu =\frac{{S}_{t1}}{{S}_{n1}}$$
(36)

where St1 and Sn1 are the tangential and normal projection areas of the diamond grain at stage I, respectively, and they can be expressed as follows:

$$\begin{array}{l}{S}_{t1}=\frac{1}{2}\times 2\times {h}_{g1}\mathrm{tan}\ \theta \times {h}_{g1}={h}_{g1}^{2}\mathrm{tan}\ \theta \\ {S}_{n1}={\left(\sqrt{2}\times {h}_{g1}\mathrm{tan}\ \theta \right)}^{2}=2{h}_{g1}^{2}{\mathrm{tan}}^{2}\ \theta \end{array}$$
(37)

Substituting Eqs. (35), (36), and (37) into Eq. (34), the average rubbing force Ft1 can be expressed as follows:

$${F}_{t1}=\frac{H{h}_{gc}^{2}\mathrm{tan}\ \theta }{48}{\left(2+{\mathrm{tan}}^{2}\ \theta \right)}^{1/2}$$
(38)

Finally, the total average cutting force at the ductile stage can be expressed as follows:

$${F}_{1}=\sqrt{{F}_{n1}^{2}+{F}_{t1}^{2}}\text{=}\frac{\sqrt{5}H{h}_{gc}^{2}\mathrm{tan}\ \theta }{48}{\left(2+{\mathrm{tan}}^{2}\ \theta \right)}^{1/2}$$
(39)

3.3.3 Cutting force model of a single diamond grain at the ductile–brittle transition stage

The material removal volume of the single diamond grain at stage II, denoted as Vg2, can be obtained by the following expression:

$${V}_{g2}=\frac{1}{3}\left({l}_{1}+{l}_{2}\right)\times {h}_{gc}\times {h}_{gc}\mathrm{tan}\ \theta -\frac{1}{3}{l}_{1}\times {h}_{gp}\times {h}_{gp}\mathrm{tan}\ \theta$$
(40)

The removed volume of this stage is equivalent to the volume of the triangular prism, denoted as Vga2, can be expressed as follows:

$${V}_{ga2}={l}_{2}\times {h}_{ga2}\times {h}_{ga2}\mathrm{tan}\ \theta ={l}_{2}{h}_{ga2}^{2}\mathrm{tan}\ \theta$$
(41)

Then, Vg2 = Vga2, and the average cutting depth at stage II, denoted as hga2, can be expressed as follows:

$${h}_{ga2}={h}_{gc}{\left(\frac{15{l}_{1}+16{l}_{2}}{48{l}_{2}}\right)}^{1/2}$$
(42)

Under the same normal load, the crack depth of multiple diamond grinding is approximately half of that of single diamond grinding. The connection between the average normal cutting force Fn2 and average cutting depth hga2 at stage II can be expressed as follows [12]:

$${F}_{n2}=\frac{1}{2}\xi H{h}_{ga2}^{2}{\mathrm{tan}}^{2}\ \theta$$
(43)

Substituting Eq. (42) into Eq. (43), the average normal cutting force Fn2 can be expressed as follows:

$${F}_{n2}=\frac{1}{2}\xi H{h}_{gc}^{2}\left(\frac{15{l}_{1}+16{l}_{2}}{48{l}_{2}}\right){\mathrm{tan}}^{2}\ \theta$$
(44)

The single diamond grain is mainly subjected to the ploughing force Ft2 in the tangential direction at this stage, which can be expressed as follows:

$${F}_{t2}={\sigma }_{s}{S}_{t2}$$
(45)

where σs is the compressive yield stress at the contact area, which is defined as follows:

$${\sigma }_{s}={\left(\frac{{H}^{4}}{{E}_{e}}\right)}^{1/3}$$
(46)

and St2 is the projected area of the tangential direction of the diamond grain, which is related to the cutting depth. The projected area can be calculated by the average cutting depth as follows:

$${S}_{t2}=\frac{1}{2}\times 2{h}_{ga2}\mathrm{tan}\ \theta \times {h}_{ga2}={h}_{ga2}^{2}\mathrm{tan}\ \theta$$
(47)

Substituting Eqs. (42), (46), and (47) into Eq. (45), the average ploughing force can be expressed as follows:

$${F}_{t2}=\frac{{h}_{gc}^{2}\left(15{l}_{1}+16{l}_{2}\right)\mathrm{tan}\ \theta }{48{l}_{2}}{\left(\frac{{H}^{4}}{{E}_{e}}\right)}^{1/3}$$
(48)

Finally, the total average cutting force at the ductile–brittle transition stage is given as follows:

$${F}_{2}=\sqrt{{F}_{n2}^{2}+{F}_{t2}^{2}}\text{=}\frac{{h}_{gc}^{2}H\mathrm{tan}\ \theta \left(15{l}_{1}+16{l}_{2}\right)\sqrt{4{H}^{2/3}+{\xi }^{2}{E}_{e}^{2/3}{\mathrm{tan}}^{2}\ \theta }}{96{l}_{2}{E}_{e}^{1/3}}$$
(49)

3.3.4 Cutting force model of a single diamond grain at the brittle stage

The material removal volume of the single diamond grain at stage III, denoted as Vg3, can be obtained by the following expression:

$${V}_{g3}=\frac{1}{3}{l}_{c}\times {h}_{gm}\times {h}_{gm}\mathrm{tan}\ \theta -\frac{1}{3}\left({l}_{1}+{l}_{2}\right)\times {h}_{gc}\times {h}_{gc}\mathrm{tan}\ \theta$$
(50)

The removed volume of this stage is equivalent to the volume of the triangular prism, denoted as Vga3, can be expressed as follows:

$${V}_{ga3}={l}_{3}\times {h}_{ga3}\times {h}_{ga3}\mathrm{tan}\ \theta ={l}_{3}{h}_{ga3}^{2}\mathrm{tan}\ \theta$$
(51)

Then, Vg3 = Vga3, and the average cutting depth at stage III, denoted as hga3, can be expressed as follows:

$${h}_{ga3}={\left(\frac{{h}_{gm}^{2}{l}_{c}-{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)}{3{l}_{3}}\right)}^{1/2}$$
(52)

The average normal cutting force Fn3 and tangential cutting force Ft3 of a single diamond grain at stage III can be obtained by the following expression [33]:

$$\begin{array}{l}{F}_{n3}=\frac{1}{{\eta }_{2}}{h}_{ga3}^{2}{H}^{2}{\mathrm{tan}}^{8/3}\theta \left[\frac{3\left(1-2{\upsilon }_{e}\right)}{{E}_{e}\left(5-4{\upsilon }_{e}\right)}+\frac{2\sqrt{3}\mathrm{cot}\theta }{\pi \left(5-4{\upsilon }_{e}\right){\sigma }_{s}}\right]\\ {F}_{t3}=\frac{{C}_{l}}{{\eta }_{2}{C}_{h}}{h}_{ga3}^{2}{H}^{2}{\mathrm{tan}}^{8/3}\theta \left[\frac{3\left(1-2{\upsilon }_{e}\right)}{{E}_{e}\left(5-4{\upsilon }_{e}\right)}+\frac{2\sqrt{3}\mathrm{cot}\theta }{\pi \left(5-4{\upsilon }_{e}\right){\sigma }_{s}}\right]\end{array}$$
(53)

The total average cutting force at the brittle stage can be expressed as follows:

$${F}_{3}=\sqrt{{F}_{n3}^{2}+{F}_{t3}^{2}}$$
(54)

Substituting Eqs. (52) and (53) into Eq. (54), the total average cutting force F3 is given as follows:

$$\begin{array}{l}{l}{F}_{3}=\frac{{H}^{2}{\mathrm{tan}}^{8/3}\ \theta \sqrt{{C}_{l}^{2}+{C}_{h}^{2}}}{3{\eta }_{2}{l}_{3}{C}_{h}}\left[{h}_{gm}^{2}{l}_{c}-{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)\right]\\\qquad\quad\left[\frac{3\left(1-2{\upsilon }_{e}\right)}{{E}_{e}\left(5-4{\upsilon }_{e}\right)}+\frac{2\sqrt{3}\mathrm{cot}\ \theta }{\pi \left(5-4{\upsilon }_{e}\right){\sigma }_{s}}\right]\end{array}$$
(55)

3.4 Final cutting force model of side grinding of orthogonal laminated SiCf/SiC composites

The final average cutting force Fs is a combination of the total average cutting force at the three cutting stages, which can be obtained by the following expression:

$${F}_{s}=\frac{{l}_{1}{F}_{1}+{l}_{2}{F}_{2}+{l}_{3}{F}_{3}}{{l}_{c}}$$
(56)

The total theoretical removal volume rate of a single diamond in the grinding process, denoted as Vs, depends on the amount of interference between the diamond and workpiece at stage I and stage II and the propagation of transverse cracks at stage III; Vs can be expressed as follows:

$${V}_{s}={l}_{1}{h}_{ga1}^{2}\mathrm{tan}\ \theta +{l}_{2}{h}_{ga2}^{2}\mathrm{tan}\ \theta +2{l}_{3}{C}_{h}{C}_{l}$$
(57)

The total material removal volume rate in a rotation period, denoted as Vm, can be expressed as follows:

$${V}_{m}={l}_{c}{h}_{m}{h}_{gm}$$
(58)

Therefore, the number of theoretical contact diamond grains between the tool and workpiece in the grinding process, denoted as Ca, can be expressed as follows:

$${C}_{a}=\frac{{V}_{m}}{{V}_{s}}=\frac{3{h}_{m}{h}_{gm}{l}_{c}}{{h}_{gc}^{2}\mathrm{tan}\ \theta \left({l}_{1}+{l}_{2}\right)+6{C}_{h}{C}_{l}{l}_{3}}$$
(59)

However, the random distribution of diamond grains and the overlap and interference of different diamond grains will affect the total material removal volume and cutting force. Therefore, the correction coefficient λ is introduced. The final theoretical cutting force in the grinding process is given as follows:

$${F}_{p}=\lambda {C}_{a}{F}_{s}=\frac{3\lambda {h}_{m}{h}_{gm}\left({l}_{1}{F}_{1}+{l}_{2}{F}_{2}+{l}_{3}{F}_{3}\right)}{{h}_{gc}^{2}\mathrm{tan}\ \theta \left({l}_{1}+{l}_{2}\right)+6{C}_{h}{C}_{l}{l}_{3}}$$
(60)

Substituting Eqs. (39), (49), (55), and (59) into Eq. (60), the final theoretical cutting force Fp is given as follows:

$${F}_{p}=\frac{\lambda {h}_{m}{h}_{gm}H\left[0.333{h}_{gc}^{2}{l}_{1}{C}_{h}+0.298{h}_{gc}^{2}{l}_{2}{C}_{h}+0.684\sqrt{{C}_{h}^{2}+{C}_{l}^{2}}\left[{h}_{gm}^{2}{l}_{c}-{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)\right]\right]}{{C}_{h}\left[\sqrt{3}{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)+6{C}_{h}{C}_{l}{l}_{3}\right]}$$
(61)

4 Experimental design and discussions

4.1 Experimental setup

The experimental system is shown in Fig. 7. The system consists of data acquisition, machining, and operating systems. The experiment was conducted on a machining centre (JDGR200_A10H, Jingdiao, China). The cutting analogue signals were measured using a dynamometer (9527B, Kistler, Switzerland) and amplified with a charge amplifier (5070A, Kistler). Then, these signals will be transformed into digital signals by an A/D converter (5697A, Kistler) and handled by DynoWare software. The SiCf/SiC composites specimen with dimension of 70 mm (length) × 25 mm (width) × 3 mm (height) was fixed using a custom fixture. The grinding tool was prepared by a vacuum brazing process. The tool diameter is 6 mm, and the mesh number is 80.

Fig. 7
figure 7

Experimental setup

Full size image

4.2 Calculation of correction coefficient λ

According to Eq. (61), the correction coefficient λ can be written as follows:

$$\lambda =\frac{{F}_{m}{C}_{h}\left[\sqrt{3}{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)+6{l}_{3}{C}_{h}{C}_{l}\right]}{{h}_{m}{h}_{gm}H\left[0.333{h}_{gc}^{2}{l}_{1}{C}_{h}+0.298{h}_{gc}^{2}{l}_{2}{C}_{h}+0.684\sqrt{{C}_{h}^{2}+{C}_{l}^{2}}\left[{h}_{gm}^{2}{l}_{c}-{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)\right]\right]}$$
(62)

The value of λ can be obtained by experimentation, and then, the final cutting force model can be expressed. The experiments involve three groups of input parameters (spindle speed n, feed rate vf, and cutting width ae). The cutting parameters for obtaining λ are listed in Table 3.

Table 3 Cutting parameters for obtaining λ
Full size table

Each group of parameters was tested three times to reduce the error. The experimental force at the stable stage was determined, and the resultant force Fm, Fm = (Fx + Fy)1/2 was obtained. The correction coefficient λ was calculated by substituting the resultant force into Eq. (62), and the final results are shown in Fig. 8.

Fig. 8
figure 8

Influences of input variables on the correction coefficient λ: (a) spindle speed, (b) feed rate, and (c) cutting width

Full size image

The value of the correction coefficient showed minimal change with the change of different input variables. Therefore, the three-stage average parameter is selected, and the final average value of the correction parameter λ is 0.186. Therefore, the final theoretical average cutting force Fp can be expressed as follows:

$${F}_{p}=\frac{0.186{h}_{m}{h}_{gm}H\left[0.333{h}_{gc}^{2}{l}_{1}{C}_{h}+0.298{h}_{gc}^{2}{l}_{2}{C}_{h}+0.684\sqrt{{C}_{h}^{2}+{C}_{l}^{2}}\left[{h}_{gm}^{2}{l}_{c}-{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)\right]\right]}{{C}_{h}\left[1.73{h}_{gc}^{2}\left({l}_{1}+{l}_{2}\right)+6{C}_{h}{C}_{l}{l}_{3}\right]}$$
(63)

4.3 Model verification and discussion

The cutting force Fp calculated by the model was compared with the cutting force Fm measured in the experiment to verify the accuracy of the cutting force model. The experimental parameters are listed in Table 4.

Table 4 Cutting parameters for milling experiments
Full size table

Five gradients were set for each parameter of the experiment. Each experiment was repeated three times to reduce error. A comparison between the cutting force measured in the experiment and the cutting force calculated by the model is shown in Fig. 9; as shown, their changing trend and value are in good agreement.

Fig. 9
figure 9

Comparison of experimental and theoretical cutting force values: (a) spindle speed, (b) feed rate, and (c) cutting width

Full size image

In addition, the cutting force model was used to predict the cutting force with different input variables to better understand the influencing factors of the cutting force of side grinding of orthogonal laminated SiCf/SiC composites. The predicted relationship between the cutting force and input variables is shown in Fig. 10.

Fig. 10
figure 10

Relationship between the predicted cutting force values and input variables: (a) spindle speed, (b) feed rate, and (c) cutting width

Full size image

Figure 10a shows the influence of the spindle speed on the cutting force. When the cutting width and feed rate are constant, the cutting force decreases with increasing spindle speed because when the material with a given volume is removed, more diamond grains will participate in the grinding process as the spindle speed increases. The cutting time will decrease, and the depth of engagement between the diamond grains and workpiece will become smaller. Moreover, the maximum undeformed chip thickness of a single diamond grain is reduced, resulting in a decrease in material removal in the brittle region, thus reducing the cutting force of each grain. Higher cutting speeds will reduce the probability of continuous cracking and fracture density, increase flow toughness, and reduce strength degradation. Therefore, the final cutting force will be reduced, consistent with the trend of the experimental results.

Figure 10b shows the influence of feed rate on the cutting force. When the spindle speed and cutting width are constant, the cutting force increases as the feed rate increases, consistent with the experimental result because more diamond grains are involved in the grinding process at lower feed rate, resulting in lower engagement depth between the diamond grains and workpiece. The cracks gradually form, based on the local stress concentration, and spread from stage II. After the crack has formed and propagated, the tensile stress concentration decreases, and the crack cannot nucleate until the next tensile stress concentration is established. Therefore, tensile stress in the workpiece will continue to accumulate at low feed rate, resulting in a high possibility of continuous cracking and crack interaction. The reduced removal rate leads to a reduction in the undeformed chip thickness, resulting in more plastic flow and less brittle fracture and reducing the cutting force.

Figure 10c shows the influence of cutting width on the cutting force. When the spindle speed and feed rate are constant, the cutting force increases with the increase of cutting width because when the cutting width increases, the contact area between the tool and workpiece expands, leading to more diamond grains participating in the grinding process. The tool may be partially deformed when subjected to greater cutting force, thus resulting in a longer actual contact length than the theoretical length. Moreover, the cutting proportion of the brittle region increases as the cutting width increases, which will increase the cutting force. The predicted result is consistent with the experimental result.

In this model, the effective elastic constants of orthogonal laminated SiCf/SiC composites are idealised and calculated, but some deviations may occur due to different processes and stability in actual production. Concurrently, some diamond grains wear may occur in the actual grinding process, possibly causing the actual cutting force to be greater than the predicted cutting force. The limitations may have some impact on the results.

Analytical modelling of side grinding of orthogonal laminated SiCf/SiC composites is a complex process because of the random size, shape, and arrangement of the diamond grains on the tool surface. In addition, the apparent anisotropy of SiCf/SiC creates a more complex structure than that of other isotropic homogeneous materials. In this study, the corresponding idealised analysis of laminated SiCf/SiC composites is performed, and the cutting force model of side grinding is established. The predicted data are in good agreement with the experiment. Results indicate that the macromechanical analysis is an effective method for studying the effective elastic properties of orthogonal laminated SiCf/SiC composites. The model indicated that the cutting force was lower at a high spindle speed, low feed rate, and small cutting width. Moreover, the cutting force value presents a non-linear decreasing trend with increasing spindle speed but increases linearly with increasing feed rate and cutting width. The spindle speed and cutting width have more influence on the cutting force than the feed rate. The model can adequately evaluate the effective elastic properties of orthogonal laminated SiCf/SiC composites and effectively improve the machining efficiency while ensuring machining quality in future applications.

5 Conclusions

In this study, the effective elastic properties of orthogonal laminated SiCf/SiC composites were analysed, and the cutting force model was established by considering three cutting stages. The accuracy of the model was verified by experimentation and the following conclusions were obtained:

  1. 1.

    For macroscopic mechanical property analyses of orthogonal laminated SiCf/SiC composites, the anisotropy between the layers should also be considered, and the effective elastic constants can be obtained through theoretical analysis.

  2. 2.

    The grinding process of SiCf/SiC composites can be divided into the ductile stage, ductile-to-brittle transition stage, and brittle stage for analysis. The tangential cutting force plays an important role in the grinding process. The interaction between the tool and workpiece is consistent with the microscopic contact between the diamond grains and material.

  3. 3.

    Increasing the spindle speed and decreasing the feed rate and cutting width can reduce the cutting force. The cutting force value presents a non-linear decreasing trend with increasing spindle speed but increases linearly with increasing feed rate and cutting width. The spindle speed and cutting width have more influence on the cutting force than the feed rate.

  4. 4.

    Under different combinations of input variables, the predicted value is in good agreement with the experimental value, and the average error is 7.43%. The modelling process can be applied to evaluate the effective elastic properties of orthogonal laminated SiCf/SiC composites and predict the cutting force.

  5. 5.

    Nevertheless, some deviations may occur due to different processes and stability in the actual production of SiCf/SiC composites. In addition, tool wear may occur in the actual grinding process. These limitations may account for an error. To improve the precision of the model and reduce the error, the fabrication technology of the composites could be improved, and topological modelling of diamond grains on the tool surface can be conducted in a future study.