Design optimization of ultrasonic vibration cutting tool to generate well-decoupled elliptical trajectory

Abstract

Ultrasonic elliptical vibration cutting (UEVC) is a superior machining method for difficult-to-cut materials. The shape of the elliptical tool trajectory crucially affects the integrity of the machined surface. However, the existing designs of UEVC tool typically suffer from difficult motion decoupling, resulting in the low controllability of elliptical trajectory. This study presents a new optimization design method of UEVC tool with dual longitudinal generators to create well-decoupled elliptical trajectory. A theoretical model which establishes the effects of key design variables on the tool resonant characteristics was adopted to optimize the configuration angle (the included angle of two longitudinal generators) as 90°. The structural parameters of the connection blocks of the two generators were also optimized to achieve resonance matching in both the normal (depth-of-cut) and tangential (cutting) directions. The optimized tool has a stable resonant frequency of 18 kHz, a working space of 5.1 μm × 5.3 μm, and a small trajectory error of less than 0.75 μm. The vibration measurement results showed that the optimized design can enable the high controllability of tool trajectory. Grooving experiments were conducted to verify the improved cutting performance of the designed tool due to the excellent control of tool trajectory.

1 Introduction

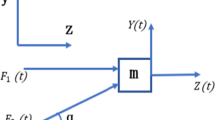
Ultrasonic elliptical vibration cutting (UEVC) is a special machining technology that applies ultrasonic elliptical vibration to the tool to enhance the machining performance, as shown in Fig. 1a [1, 2]. The elliptical trajectory is a crucial processing parameter in UEVC [3,4,5]. As shown in Fig. 1b, the orientation of the elliptical trajectory plays a critical role in generating a high-quality surface of brittle materials [6]. There exists an apparent correlation between the pose angle of elliptical vibration trajectory and machining quality. The cutting resistance can be reduced under a certain pose angle range [7]. The amplitude and phase difference of elliptical vibration trajectory have different effects on the surface microstructure and roughness of workpiece separately [8, 9]. Therefore, the adjustability of elliptical vibration trajectory has become one of the important indexes for the performance evaluation of ultrasonic elliptical vibration cutting device. The accuracy of trajectory adjustment is also conducive to predict and analyze the surface formation mechanism and surface integrity.

Fig. 1

Ultrasonic elliptical vibration cutting for (a) surface machining and (b) the influence of the elliptical trajectory on surface state after cutting [6]

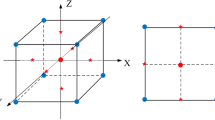
Early types of ultrasonic elliptical vibration generators have been developed for UEVC [10, 11]. However, they all have their own limitations in vibration trajectory adjustment. The novel vibration generators with single excitation are often used to generate elliptical vibration trajectory relying on special structures. When the structure is finalized, under the action of single excitation vibration, the shape of elliptical trajectory is determined finally, but its pose and inclination angle cannot be adjusted [12,13,14]. The UEVC advices in 3-DOF vibration state can produce elliptical vibration in three-dimensional space. But their adjustment ranges of vibration trajectory are small and their vibration decoupling processes are complex and trajectory adjustments are also difficult in multi degree of freedom state [15, 16]. In the classical types of UEVC tools, two ultrasonic power sources with a phase difference are used to excite ultrasonic vibrations for creating the elliptical vibration trajectory based on different vibration modes [17,18,19]. One of the most widely dual-excitation ultrasonic elliptical vibration cutting devices is developed by Guo et al. using a certain configuration angle of 60° (see in Fig. 2). Its ellipse shape can be adjusted in a certain range and has been widely used for various applications, including micro-groove turning and structural coloration of metallic surfaces [20,21,22,23]. However, it also does not have a function to accurately adjust the ellipse pose and inclination angle [24].

Fig. 2

Widely applied ultrasonic elliptical vibration cutting tool with (a) a configuration angle of 60° and (b) the ellipse shapes at different phase inputs [20]

The complex structures and dual-excitation modes complicate the design of the vibration system and increase the difficulty of vibration decoupling [25,26,27]. At present, the configuration angle θ of reliable UEVC tools with double longitudinal vibrations is less than or equal to 90° and lacks accurate decoupling analysis [28,29,30,31]. Some studies illustrate that the vibration decoupling and elliptical shapes of different vibration modes are affected by the configuration structure and vibration transmission paths of the tools [32, 33]. The equivalent stiffness and damping of the system in the connection transition region increase the difficulty of decoupling analysis [34, 35]. In addition, the resonant modes of the two vibration generators are coupled, and the overall resonant frequency of the coupled system is significantly affected. This phenomenon can result in a large discrepancy between the resonant frequencies of the two coupled vibration modes [36, 37]. These factors make it difficult to find suitable design variables for the optimization of a tool with two compound vibration modes and ensure an optimal elliptical vibration trajectory. Therefore, it is still challenging to achieve accurate vibration decoupling and realize target vibration performance in the design of the UEVC device.

In this study, a new decoupling method of elliptical vibration under dual-excitation vibration state is established. This decoupling process can characterize the mapping relationship between vibration coupling and configuration angle accurately. In addition, a new design principle for resonant frequency matching of dual excitation generators is also proposed. The appropriate design variables and configuration angle are optimized. Finally, cutting tests are conducted to verify the adjusting performance of elliptical vibration locus.

2 Vibration decoupling model of the dual-excitation elliptical vibration tool

2.1 Modeling the dynamic characteristics of the vibration tool

A vibration model of the tool with an arbitrary configuration angle is established for the universal coupling analysis. Two piezoelectric transducers are located on the outside of the fixed nodal plane, and the connection block and the connected column sections of the horns are installed on the inside of the fixed nodal plane. The angle between the two central axes of the two generators is θ. The composite normal vibration direction is the same as the cutting depth direction, and the composite tangential vibration direction is the same as the cutting direction in the workpiece coordinate system. X and Y are the axial and vertical directions of the physical coordinate system and are used for vibration coupling and motion decomposition analysis, respectively. X_C and Y_D are the cutting direction and cutting depth direction, respectively, in the workpiece coordinate system and are used for analyzing the motion trajectory, as shown in Fig. 3.

Fig. 3

Design of the ultrasonic elliptical vibration cutting tool with an arbitrary configuration angle

The vibration modeling can be performed by decomposing the vibration excitation of horn 2, whereas horn 1 represents the reference. The vibration modeling in the physical coordinate system only requires vibration decomposition and coupling analysis in the X- and Y-directions for the transmission of vibration input 2. The vibration input 1 does not have to be decomposed because it is equivalent to the longitudinal vibration in the X-direction. In the workpiece coordinate system, it is necessary to analyze the change in the elliptical vibration trajectory at the tooltip. According to the vibration theory of a 2-degree-of-freedom system in the physical coordinate system of the tool, the equivalent vibration system is shown in Fig. 4.

Fig. 4

Model of the vibration system with the arbitrary configuration angle θ

O is the starting position of the vibration in the fixed nodal plane; P_1/2 is the vibration output end of the connection block; and Q is the vibration output end of the end effector. k and c are the equivalent stiffness and damping of the connection column section, respectively; k₁ and c₁ are the equivalent stiffness and damping of the circular flexure hinge, respectively; k_X and c_X are the equivalent stiffness and damping of the interaction of horn 1 and horn 2 in the X-direction, respectively; and k_Y and c_Y are the equivalent stiffness and damping of the interaction of horn 1 and horn 2 in the Y-direction, respectively. Moreover, k_X/Y and c_X/Y change with the angle θ and are set as functions of angle θ. As shown in Fig. 4, the mass m is equivalent to the total mass of the insert and the end effector, and the equivalent mass M consists of the mass M₁ of the connection column section and the mass M₂ of the connection block.

The steady-state responses of the longitudinal vibration F₁(t) and F₂(t) at point P_1/2 can be derived as:

$$\left\{\begin{array}{l}{X}_{1}(t)={A}_{1}sin(\omega t+\varphi +\alpha )\\ {\theta }_{1}(t)={A}_{1}sin(\omega t+\alpha )\end{array}\right.$$

(1)

where

$${A}_{1}=\frac{A\text{[}\sqrt{{(k)}^{2}+{(c\omega )}^{2}}\text{]/}k}{\sqrt{{\left[1-{(\frac{\omega }{{\omega }_{n}})}^{2}\right]}^{2}+{\left[2\xi (\frac{\omega }{{\omega }_{n}})\right]}^{2}}}$$

and α =  − arctan(− cω/k) + arctan((− c₁ω)/(k − Mω²)), ω_n = $\sqrt{{\text{k}}/{\text{M}}}$, ξ = c/c_n, c_n = 2Mω_n.

When X₁(t) and θ₁(t) are transferred to the output end Q of the end effector, the two equivalent vibration excitations in the X- and Y-directions can be defined as [38]:

$$\left\{\begin{array}{l}{F}_{X}(t)={k}_{1}[{X}_{1}(t)-x]+{c}_{1}[{\dot{X}}_{1}(t)-\dot{x}]+{k}_{1}[{\theta }_{1}(t)cos{\theta }_{XY}-x]\\\qquad\quad+{c}_{1}[{\dot{\theta }}_{1}(t)cos{\theta }_{XY}-\dot{x}]\\ {F}_{Y}(t)={k}_{1}[{\theta }_{1}(t)sin{\theta }_{XY}-y]+{c}_{1}[{\dot{\theta }}_{1}(t)sin{\theta }_{XY}-\dot{y}]\end{array}\right.$$

(2)

where tanθ = y/x. In Eq. (2), the vibration excitation F_X(t) is defined as:

$$\begin{array}{c}{F}_{X}(t)={k}_{1}{A}_{1}sin(\omega t+\varphi +\alpha )+{c}_{1}{A}_{1}\omega cos(\omega t+\varphi +\alpha )\\ +{k}_{1}{A}_{1}sin(\omega t+\alpha )cos{\theta }_{XY}+{c}_{1}{A}_{1}\omega cos(\omega t+\alpha )cos{\theta }_{XY}\end{array}$$

(3)

where θ_XY is the vibration position of the output end of the end effector and is related to the phase difference φ and the angle θ. Equation (3) can be set as:

$${F}_{X}(t)={A}_{3}sin(\omega t+\frac{\varphi }{2}+\Delta \beta )$$

(4)

where

$$\left\{\begin{array}{l}{A}_{3}=\sqrt{[{({k}_{1}{A}_{1})}^{2}+{({k}_{1}{A}_{1}\omega )}^{2}][1+co{s}^{2}{\theta }_{XY}+2cos{\theta }_{XY}cos\varphi ]}\\ \Delta \beta =\alpha +arctan({c}_{1}\omega /{k}_{1})+arctan[({A}_{2}-{A}_{2}cos{\theta }_{XY})tan\frac{\varphi }{2}\\ \qquad\quad/({A}_{2}+{A}_{2}cos{\theta }_{XY})]\end{array}\right.$$

The steady-state responses of F_X(t) at the output end Q of the end effector are expressed as follows:

$$X(t)=C\cdot sin(\omega t+\varphi +\Delta \beta -\Delta {\varphi }_{1})$$

(5)

where

$$C=\frac{{A}_{3}\text{/}(2{k}_{1}+{k}_{X})}{\sqrt{{\left[1-{(\frac{\omega }{{\omega }_{nX}})}^{2}\right]}^{2}+{\left[2{\xi }_{X}(\frac{\omega }{{\omega }_{nX}})\right]}^{2}}}$$

and ω_nX = $\sqrt{{\text{k}}_{\text{X}}/{\text{m}}}$, ξ_X = (2c₁ + c_X)/c_nX, c_nX = 2mω_nX, and

$$\Delta {\varphi }_{1}=arctan[2{\xi }_{X}(\frac{\omega }{{\omega }_{nX}})/1-{(\frac{\omega }{{\omega }_{nX}})}^{2}]$$

Similarly, the steady-state responses of F_Y(t) at the output end Q of the end effector are expressed as follows:

$$Y(t)=D\cdot sin(\omega t+\Delta \alpha -\Delta {\varphi }_{2})$$

(6)

where

$$D=\frac{\sqrt{{({k}_{1}{A}_{1})}^{2}+{({k}_{1}{A}_{1}\omega )}^{2}}sin{\theta }_{XY}\text{/}(2{k}_{1}+{k}_{Y})}{\sqrt{{\left[1-{(\frac{\omega }{{\omega }_{nY}})}^{2}\right]}^{2}+{\left[2{\xi }_{Y}(\frac{\omega }{{\omega }_{nY}})\right]}^{2}}}$$

and ω_nY = $\sqrt{{k}_{\mathrm{Y}}/m}$, ξ_X = (c₁ + c_Y)/c_nY, c_nY = 2mω_nY, and

$$\Delta {\varphi }_{2}=arctan[2{\xi }_{Y}(\frac{\omega }{{\omega }_{nY}})/1-{(\frac{\omega }{{\omega }_{nY}})}^{2}]$$

According to the relationship between the workpiece coordinate system and the physical coordinate system of the tool in Fig. 3, the steady-state vibration response of the tool in the workpiece coordinate system can also be written as:

$$\left\{\begin{array}{c}{X}_{f}(t)=Y(t)\cdot cos\frac{\theta }{2}+X(t)\cdot sin\frac{\theta }{2}\\ {Y}_{c}(t)=Y(t)\cdot sin\frac{\theta }{2}+X(t)\cdot cos\frac{\theta }{2}\end{array}\right.$$

(7)

If the influences of the phase parameters Δα, Δβ, Δϕ₁, and Δϕ₂ on the vibration response and the phase delays are ignored, the elliptic equations can be obtained by eliminating the time variable t in Eqs. (5) and (6) and can be derived as:

$${(\frac{X}{C}-\frac{Y}{D}cos\varphi )}^{2}=[1-{(\frac{Y}{D})}^{2}]si{n}^{2}\varphi$$

(8)

In the workpiece coordinate system, Eq. (10) can also be written as:

$$\begin{aligned}&{(\frac{{X}_{C}cos\frac{\theta }{2}+{Y}_{D}sin\frac{\theta }{2}}{C}-\frac{{X}_{C}sin\frac{\theta }{2}+{Y}_{D}cos\frac{\theta }{2}}{D}cos\varphi )}^{2}\\&=[1-{(\frac{{X}_{C}sin\frac{\theta }{2}+{Y}_{D}cos\frac{\theta }{2}}{D})}^{2}]si{n}^{2}\varphi\end{aligned}$$

(9)

The elliptical vibration trajectory of the tool tip in the resonant state is directly affected by the angle θ and the phase difference φ. Furthermore, based on Fig. 4 and Eq. (2), M and m are combined to analyze the dynamics of the system in the X- and θ-directions. The vibration differential equations in the X-direction are as follows:

$$\left\{\begin{array}{l}M{\ddot{x}}_{1}=k[{F}_{1}(t)-{x}_{1}]+c[{\dot{F}}_{1}(t)-{\dot{x}}_{1}]-{k}_{1}({x}_{1}-x)-{c}_{1}({\dot{x}}_{1}-\dot{x})\\ m\ddot{x}={k}_{1}({x}_{1}-x)+{c}_{1}({\dot{x}}_{1}-\dot{x})-{k}_{X}x-{c}_{X}\dot{x}+[{k}_{1}({x}_{1\theta }-{x}_{\theta })\\\qquad \quad+{c}_{1}({\dot{x}}_{1\theta }-{\dot{x}}_{\theta })]cos{\theta }_{XY}\end{array}\right.$$

(10)

and the vibration differential equations in the θ-direction are as follows:

$$\left\{\begin{array}{l}M{\ddot{x}}_{1\theta }=k[{F}_{2}(t)-{x}_{1\theta }]+c[{\dot{F}}_{2}(t)-{\dot{x}}_{1\theta }]-{k}_{1}({x}_{1\theta }-{x}_{\theta })\\ \qquad\quad-{c}_{1}({\dot{x}}_{1\theta }-{\dot{x}}_{\theta })\\ m{\ddot{x}}_{\theta }={k}_{1}({x}_{1\theta }-{x}_{\theta })+{c}_{1}({\dot{x}}_{1\theta }-{\dot{x}}_{\theta })-[{k}_{X}{x}_{\theta }+{c}_{X}{\dot{x}}_{\theta }]sin{\theta }_{XY}\\ \qquad\quad-[{k}_{X}{x}_{\theta }+{c}_{X}{\dot{x}}_{\theta }]cos{\theta }_{XY}\end{array}\right.$$

(11)

The resonant frequencies of the integrated system, including M and m in the X- and θ-directions, can be determined by Eqs. (10) and (11), respectively. The phase difference φ determines the ellipticity of the elliptical vibration locus. When the phase difference φ = 0° or 180°, the vibration locus is approximately a straight line; when φ ∈ (0°, 180°), the vibration locus is approximately an ellipse. If the input amplitude and frequency are the same, the angle θ influences the amplitude of the vibration locus in the X_C- and Y_D-directions by affecting the equivalent output amplitudes of point P and Q and the related phases of the vibration responses.

2.2 Theoretical analysis of the effects of the configuration angle

The normal resonance frequency and the tangential resonance frequency should be the same. So their phase differences between the two longitudinal excitations in the two resonance modes should be 0° and 180° in a standard UEVC tool. Under the two resonance modes, the tool can generate the ultrasonic elliptical vibration locus in the resonance state, as shown in Fig. 5.

Fig. 5

The two ideal resonant modes and their elliptical vibration locus

According to the vibration response of vibration coupling described in “Sect. 2” the angle θ and phase difference φ are two initial factors affecting the elliptical vibration trajectory at the output of the end effector. When the phase delay error is not considered, the elliptical vibration trajectories of the tool tip for different phase differences φ and angles θ are shown in Fig. 6.

Fig. 6

The ideal elliptical vibration locus for different angles φ

The poses and ellipticity of elliptical vibration trajectories change with the phase difference φ. Besides, according to vibration coupling, the resonance frequencies are also affected by θ and φ. According to Eqs. (5), (6), and Fig. 6, we can obtain the functional relationship between the ratio of the X-direction amplitude to the Y-direction amplitude of the resonance and the angle θ for φ = 0° or 180°, as shown in Fig. 7.

When the input amplitudes of the two transducers are the same and the configuration angle is 90°, the amplitude ratio C/D between the X-direction and Y-direction is 1 theoretically (Fig. 7). The reason is that only single longitudinal vibration is transmitted in the X- and Y-directions, whereas only one bending vibration mode is transmitted in the vertical direction. In this state it does not interfere with the longitudinal vibration mode. Besides, the maximum amplitude ratio between two resonance states with different phase differences is equal when the angle θ = 90°. Similarly, we can also obtain the relative ratio of the resonance frequencies in the X- and Y-directions for any angle θ by using the natural frequencies in the X- and Y-directions with θ is 90° as the reference, as shown in Fig. 8.

Fig. 7

Maximum amplitude ratio in the X- and Y-directions for different angles θ

Fig. 8

Relative ratio of the resonance frequencies in the X- and Y-directions for different angles θ

When θ = 90°, there is a minimum natural frequency in the X-direction and a maximum natural frequency in the Y-direction. It is easy to obtain a relatively consistent resonant frequency with a minimum frequency difference between the two directions. At this time, the system reaches the optimal design layout of the UEVC tool with double excitations. Therefore, the layout state of θ = 90° and φ = 0°/180° facilitates the vibration coupling analysis and improves the system’s performance.

2.3 Configuration of a well-decoupled ultrasonic elliptical vibration cutting tool

When the angle θ is less than 90°, the computational complexity of calculating the vibration decoupling mode and response becomes very high. This design can decrease the accuracy of calculation and complicate the design process. The main reason is that when included angle θ is less than 90°, it can result in a bending vibration mode and another additional longitudinal vibration mode in the vibration direction. The complex vibration modes increase the difficulty of vibration decoupling and reduce the accuracy of the steady-state response and frequency calculation. When θ is 90°, the two longitudinal ultrasonic transducers and their horns are perpendicular to each other, pointing in the X- and Y-directions of the physical coordinate system of the tool. This layout facilitates the analysis of the steady-state response and resonant frequency and improves the accuracy of design and calculation. A vertical design of the UEVC with double longitudinal vibrations coupling is proposed to enable the adjustability of the elliptical vibration trajectory. This design is helpful for decoupling of the double longitudinal vibration, as shown in Fig. 9.

Fig. 9

UEVC tool with dual longitudinal vibration excitations

The two vibrations with phase difference produced by the two ultrasonic transducers are transmitted to tooltip and are combined into an elliptical vibration locus [39]. When the tool works normally, the shape and pose of the elliptical vibration locus can be adjusted by changing the phase difference between the two ultrasonic power signals.

3 Optimization of the structural parameters

A general model is established to clarify the relationship between the design parameters and the vibration response. We evaluate the influences of the parameters on the resonance performance of the UEVC, including the trajectory control, amplitude output, analytical model results, and frequency estimation. The configuration can be optimized by choosing appropriate design parameters and vibration input parameters.

3.1 Effects of the structural parameters of the horn and connection blocks

The prerequisite for achieving a stable elliptical vibration of the system is that the coupled generator produces an ultrasonic resonance in the X_C- and Y_D-directions, as shown in Fig. 10. The resonant frequencies of the system in both directions are same or similar.

Fig. 10

Normal and tangential resonance state of the integrated horn

The two horns have the same resonance load on each other and they are equivalent to two spring damping system with different phase differences. The equivalent vibration structure of the system is shown in Fig. 11.

Fig. 11

Equivalent structure of the normal and tangential longitudinal vibrations. (a) Normal resonance in the Y_D-direction. (b) Tangential resonance in the X_C-direction

k_XA = k_YA and c_XA = c_YA denote the normal equivalent stiffness and damping of the connecting section of the connection block and the end effector, respectively. In the tangential resonance, k_XT = k_YT and c_XT = c_YT are the equivalent stiffness and damping in the X_C- and Y_D-directions of the connecting section between the connection block and the end effector, respectively. If there are differences in the equivalent stiffness and damping in the X_C- and Y_D-direction, their resonant frequencies are different.

For the vibration transmission in the X-direction, the natural frequency ω_XA of the system with phase difference 0° can be calculated:

$$\begin{aligned}{c}{\omega }_{XA}^{2}&=\frac{\left[(k+{k}_{XA})M+({k}_{1}+{k}_{XA})m\right]}{2Mm}\\& \pm \frac{\sqrt{{\left[(k+{k}_{XA})M-({k}_{1}+{k}_{XA})m\right]}^{2}+4{k}_{1}^{2}Mm}}{2Mm}\end{aligned}$$

(12)

Similarly, the natural frequency ω_YA in Y-direction can be obtained and ω_A = ω_XA = ω_YA, while the natural frequency ω_XT in X-direction can also be obtained when φ = 180° and ω_T = ω_XT = ω_YT.

When the equivalent stiffnesses, damping, and pitch positions in each connection position are constant, the qualities of the system’s parts are the main factors affecting the resonance. The modal superposition method is used to solve the equation of motion. The steady-state vibration response of the tooltip has the largest unidirectional longitudinal vibration amplitude and it can be written as:

$$\begin{aligned}{x}_{2}(t)=&U{}_{12}\left|{H}_{1}(\omega )\right|Bsin(\omega t+\varphi -{\varphi }_{1})\\&+U{}_{22}\left|{H}_{2}(\omega )\right|Bsin(\omega t+\varphi -{\varphi }_{2})\end{aligned}$$

(13)

where U₁₂ and U₂₂ are the corresponding vectors in the regular mode matrix U; |H(ω)| is the magnification factor corresponding to the regular coordinates; φ₁ and φ₂ are the phase angles corresponding to the regular coordinates; and B is an amplitude function determined by stiffness k, damping c, and frequency ω.

According to Fig. 11a, the steady-state vibration response of the system consists of the steady-state vibration responses of the two horns. The synthetic steady-state vibration response of the integrated horn in the X_C-direction can be obtained as:

$${X}_{C}(t)=\sqrt{2}\cdot {x}_{2}(t)$$

(14)

According to Fig. 11b, when the frequency ω of the input external excitation vibrations F₁(t) and F₂(t) coincide with the natural frequency ω_i, the amplitude of the steady-state forced vibration of the horn in the ith order canonical coordinate is very large, i.e., the steady-state vibration response of the tool tip has the largest unidirectional longitudinal vibration amplitude and it can be written as:

$$\begin{aligned}{x^{''}}_{2}(t)=&{U^\prime}_{12}\left|{H^\prime}_{1}(\omega )\right|Bsin(\omega t+\varphi -{\varphi^\prime}_{1}+\pi )\\&+{U^\prime}_{22}\left|{H}_{2}(\omega )\right|Bsin(\omega t+\varphi -{\varphi^\prime}_{2}+\pi )\end{aligned}$$

(15)

The steady-state vibration response of the system consists of the steady-state vibration responses of the two horns. The synthetic steady-state vibration response of the integrated horn in the Y_D-direction can be obtained as:

$$Y_D(t)=\sqrt2\cdot{x^{''}}_2(t)$$

(16)

Similar to the composite normal longitudinal vibration mode, the longitudinal vibration mode has two natural frequencies. They are composite responses generated by the superposition of the two external excitation vibrations with the same frequency and different phases.

The integrated horn and the single horn should generate the same longitudinal resonance frequencies in the X_C- and Y_D-directions under ideal conditions, i.e., the two external excitation vibrations can create the elliptical trajectory with the same frequency. The same or similar longitudinal resonance frequency when the phase difference is 0° or 180° must be also produced. Thus, the elliptical trajectory can be formed when phase difference φ ∈ (0, π). Therefore, the resonant frequencies of the integrated horn in the ideal state in the normal and tangential directions should be equal, namely:

$${\omega }_{A}={\omega }_{T}$$

(17)

If the equivalent k and c of the two resonant modes are equal, the normal resonance frequency of the integrated horn is equal to the tangential resonance frequency.

The resonance frequency of the integrated horn is related to the mass M, the mass m of the end effector, and the equivalent stiffness and damping of each part. Therefore, the only approach to obtain optimal design and matched resonant frequency is to adjust the mass M. This adjustment can change the design parameters of the integrated horn for different vibration modes. For a specific design and material, the parameter relationships are:

$$\left\{\begin{array}{l}{k}_{1}=\alpha k\\ {k}_{XA}=\beta k\\ {k}_{XT}=\gamma k\\ m=\eta M\end{array}\right.$$

(18)

where α, β, and γ are the scale coefficients of the stiffness of each part, and η is mass ratio of m and M.

The normal and tangential resonance frequencies of the integrated horn are:

$$\left\{\begin{array}{c}{\omega }_{A}^{2}={A}_{1}\frac{k}{M}=\frac{k}{M}\{\frac{[(1+\beta )+(\alpha +\beta )\eta ]}{2\eta }\pm \frac{\sqrt{{[(1+\beta )-(\alpha +\beta )\eta ]}^{2}+4{\alpha }^{2}\eta }}{2\eta }\}\\ {\omega }_{T}^{2}={A}_{2}\frac{k}{M}=\frac{k}{M}\{\frac{[(1+\gamma )+(\alpha +\gamma )\eta ]}{2\eta }\pm \frac{\sqrt{{[(1+\gamma )-(\alpha +\gamma )\eta ]}^{2}+4{\alpha }^{2}\eta }}{2\eta }\}\end{array}\right.$$

(19)

We use the mass ratio of m and M as an independent variable. Then ω₀ = $\sqrt{k/M}$  = 1 and ω_A can be set as an example to illustrate the trend of difference in the natural frequencies of the composite longitudinal vibration of the integrated horn, as shown in Fig. 12.

Fig. 12

Natural frequency trend of a horn with mass M

The main mass M is composed of the column section M₁ of a single horn and the column section M₂ of the connection block, as shown in Fig. 13. The trend of the frequency of the tangential longitudinal vibration resonance with the main mass M is consistent with the normal longitudinal vibration. The main mass M has the most significant impact on the resonance frequency. When α and β remain constant, the resonant frequencies can be adjusted by optimizing the mass ratio m/M.

Fig. 13

Mass distribution and structure of a single horn

When α and β remain constant, Eq. (19) is redefined as:

$$\left\{\begin{array}{c}{\omega }_{A}^{2}=\frac{k}{({M}_{1}+{M}_{2})}{A}_{1}\\ {\omega }_{T}^{2}=\frac{k}{({M}_{1}+{M}_{2})}{A}_{2}\end{array}\right.$$

(20)

According to Fig. 5 and Eq. (19), a difference exists between the two resonance frequencies in the X_C- and Y_D-directions. The reason is that the equivalent stiffness and damping of the two vibration modes are different. Therefore, it is necessary to compare and analyze the normal and tangential resonance frequencies, namely:

$$\Delta f=min(\left|{\omega }_{A}-{\omega }_{T}\right|)$$

(21)

The two frequencies satisfying Eq. (21) can be selected to optimize the design parameters of the integrated horn for matching the two resonances. After m and M₂ have been determined, M₁ can be adjusted by changing l₁ and keeping M₂ unchanged. In addition, l₁ needs to be optimized to ensure mass symmetry at both sides of the nodal surface and obtain the same normal and tangential resonance frequencies.

3.2 Model verification using FEM simulation

The horn consists of stainless steel and the connection block and end effector are made of aluminum alloy whose vibration transmission state can be seen in Fig. 14. The diameter of the rear column section of the horn is d = 40 mm, and the column section length of the connection block is l = 20 mm. The insert is a TPGH110302 PCD CNC turning tool, and the material parameters are shown in Table 1.

Fig. 14

Vibration transmission state of the integrated horn

Table 1 Main material parameters of the horns and tool

Since integrating horns can be equivalent to mechanical impedance, it can lead to great reduction of the resonant frequency of the UEVC. So the initial design frequency can be set to 20 kHz, greater than the target resonance frequency of 18 kHz. Using the calculation principle of longitudinal vibration 1/4 wavelength, it can be concluded that the size of the column sections in front and rear nodal surfaces of the cylindrical horn is 72 mm. Then the data of initial size and material is induced into Eqs. (19) and (20) for calculation and the range of mass ratio of m to M is 0.01 ~ 0.02. According to Fig. 12, the range of ratio of ω_A to ω₀ of the system with frequency reduction is 0.5 ~ 0.6 and the range of ω_A is 10 ~ 12 kHz. Therefore, the size design frequency of 20 kHz is not suitable and the sizes of column sections on both sides of the nodal surface need to be adjusted again.

According to the range of ratio of ω_A to ω₀ and the target resonance frequency, it is estimated that the range of size design frequency based on longitudinal vibration can set to be 30 ~ 45 kHz. Taking the sizes of end effector and connection column section into calculation, the size parameters of the horns with design frequency of 30 kHz are shown in Table 2.

Table 2 Main structural parameters of the horns and tool

In the simulation of ABAQUS, it should be noted that threaded connection is equivalent to the binding state between the two contact surfaces of end effector and horn. When the position of vibration nodal plane is determined, the thickness of the fixed flange on nodal plane and circle flexure hinge (as shown in Fig. 9) also affect resonant state of system. Therefore, the thickness can be uniformly set to 1 mm and the minimum thickness of circle flexure hinge can be set to 3 mm. In addition, all DOFs of the two fixed nodal surfaces of the fixed flanges towards the end effector are set as the constrained state and the grid cell type of model is C3D10. The external excitation vibration is simulated at the input end to replace piezoelectric transducer under different resonant frequencies. This omission does not affect the vibration simulation results of the resonant frequencies and relative amplitudes. The external excitation vibration is input on the contact surface of the horn. The end face of the front cover of the transducer is used for the modal and harmonic response vibration analysis in FEM. The normal and tangential resonance modes of the integrated horn are shown in Fig. 15.

Fig. 15

Simulated resonance modes of the integrated horn: (a) normal; (b) tangential

The integrated horn produces two composite resonance modes at 16,874 Hz and 17,360 Hz, respectively, and the frequency difference Δf between the two is 486 Hz. It indicates that the normal and tangential resonant frequencies cannot match. Therefore, the parameters of the integrated horn need to be optimized to reduce the difference again. The relationships between the resonance frequencies and l₁ and l₂ for the two resonance modes of the integrated horn are shown in Fig. 16.

Fig. 16

The relationship between the resonance frequencies and the column sizes l₁ and l₂

For the same column size l₁, the resonant frequencies decrease with an increase in l₂; for the same l₂, the resonance frequencies decrease with an increase in l₁. Increasing l₂ is equivalent to increasing the overall size of the integrated horn, causing a reduction in the resonance frequency. The relationship between the resonance frequency difference, l₁ and l₂ are shown in Fig. 17. For the same l₁, the difference between the two resonance frequencies decreases with an increase in l₂; for the same l₂, the resonance frequency of the integrated horn increases with an increase in l₁.

Fig. 17

The relationship between the differences between normal and tangential resonance frequencies and the column sizes of the integrated horn

3.3 Results of design optimization

When a range of the difference between the normal and tangential resonance frequencies is set as 0–300 Hz, the optimum ranges of l₁ and l₂ are 12–14 mm and 41–46 mm, respectively. The ideal operating frequency of a standard ultrasonic transducer is 18000 ± 200 Hz. So the optimum ranges of l₁ and l₂ can be set as 12–14 mm and 42–45 mm, respectively. The main dimensional parameters of the integrated horn with target frequency of 18 kHz after design optimization are shown in Table 3.

Table 3 Main structural parameters of the horns and tool in the optimal design

The remaining dimensional parameters are consistent with the preset design. The optimized design model is simulated to verify the final design, as shown in Fig. 18.

Fig. 18

Simulated normal and tangential resonance modes of the integrated horn after optimization: (a) normal; (b) tangential

The normal resonant frequency is 17926 Hz and the tangential resonant frequency is 18194 Hz in simulation. The difference Δf between the two resonant frequencies is 268 Hz. Relative to the target preset frequency of 18 kHz, their frequency deviation error rates are 0.41% and 1.07%, respectively. The simulation result demonstrates the accuracy of the optimization method.

4 Experimental verification of the vibration performance

4.1 Experimental setup

A prototype of the optimized UEVC tool is developed for experimental verification, as shown in Fig. 19. The experimental setup consists of the UEVC tool, the ultrasonic power supply, and the measurement devices. The schematic diagram of experimental setup is shown in Fig. 20. The power supply with dual power outputs can be used to adjust the phase difference from 0 to 180°. The measurement devices consist of a signal collector, a computer and two laser displacement sensors (KEYENCE LK-H008) with measurement accuracy of 0.005 µm and sampling period of 2.55 µs.

Fig. 19

Prototype of the ultrasonic elliptical vibration cutting tool

Fig. 20

Experimental setup of the ultrasonic elliptical vibration system

The vibration experiments are conducted with varying excitation frequencies in a range of 16 ~ 20 kHz and phase differences between the two input electrical signals are set as 0° and 180°, respectively.

4.2 Measurement results of the resonance frequency

The resonant frequency is mainly measured by the impedance analyzer and it is compared with the simulation. In impedance analysis, the positive poles of the two transducers are connected together and the negative poles are connected together. Then the wire with two positive poles is connected with the positive pole of the impedance analyzer, and the wire with two negative poles is connected with the negative pole of the impedance analyzer. At this time, the phase difference of measured resonant frequency is 0°, that is, the input signals of the two transducers have the same phase. The impedance analyzer PV70A directly measures the resonant frequencies in the normal direction (phase difference is 0). The comparison of resonance frequencies of the ultrasonic system is obtained by the impedance analyzer, the simulation, and vibration experiments, as shown in Table 4.

Table 4 Results of the normal and tangential resonance frequencies (Hz)

The simulation results of the normal and tangential resonance frequencies after the optimization are consistent with the impedance analysis and experimental measurement. The frequency differences meet the requirements of the design, and the system achieves optimal frequency matching.

4.3 Measurement results of the elliptical vibration trajectory

The measurement of elliptical vibration trajectory under different phase differences is conducted to verify the proposed design principle. Resonant test frequencies of system with different phase differences can be first set as the resonant frequency of system with phase difference 0°. Then the phase difference between the two output electrical signals is adjusted, and two displacement sensors are set at the output of end effector. When the phase difference state is selected and the vibration output of end effector can obtain approximate theoretical trajectory, the system realizes resonance under this phase difference. Therefore, the consistency of the resonant frequency under different phase differences and the effectiveness of design can be confirmed by measuring elliptical vibration trajectory directly.

The elliptical trajectory can be flexibly changed in a working space of 5.1 μm × 5.3 μm by adjusting the phase difference after filtering. The elliptical trajectories for phase differences of 0°, 45°, 90°, 135°, and 180° are shown in Fig. 21. The peak-to-peak voltage of output 1 is 320 V, that of output 2 is 280 V, and the current is 0.75 A. The designed UEVC tool reaches ultrasonic elliptical vibration states, indicating that the optimization design is feasible.

Fig. 21

Vibration trajectory of the tool output end for different phase differences (μm): (a) 0° ± 3°; (b) 45° ± 3°; (c) 90° ± 3°; (d) 135° ± 3°; (e) 180° ± 3°

4.4 Cutting experiments with different elliptical vibration trajectories

Cutting experiments are carried out with different elliptical vibration trajectories by adjusting different phase differences to further verify the performance of designed UEVC tool. The process parameters for the plane machining are shown in Table 5. The poses of ellipse are characterized by the included angle Ф between the long diameter of ellipse and the cutting direction. The elliptical cutting paths and their shape feature in the cutting coordinate system are shown in Fig. 22.

Table 5 Parameters of elliptical vibration cutting

Fig. 22

Position and orientation in cutting coordinate system of elliptical cutting trajectories corresponding to different phase differences: (a) 30°; (b) 45°; c 90°; (d) 135°; (e) 150°

Surface fluctuation and residual height are adopted as indices to characterize the quality of machined surface. The surface topography of these groove bottom in cutting direction is measured by white light interferometer (see Fig. 23). The measurement content consists of data of two parameters: H_F and H_A. H_F is the surface fluctuation in the range of 100 μm and H_A is the elliptical cutting residual height in the range of 10 μm (see Fig. 24a). The theoretical residual height H_T can be calculated from the kinematic trajectory of tool (see Fig. 24b), where the blunt circle radius of the tool is not considered.

Fig. 23

Machined surfaces of different elliptical vibration trajectories for different phase differences: (a) 30° ± 3°; (b) 45° ± 3°; (c) 90° ± 3°; (d) 135° ± 3°; (e) 150° ± 3°

Fig. 24

Measurement method of surface topography. (a) Measurement of actual residual height. (b) Calculation of theoretical residual height. (c) Measurement results of surface topography

The measured and predicted results of surface fluctuation and residual height are shown in Fig. 24c. The results demonstrate that the shape and pose of elliptical vibration trajectory significantly affect surface quality. When cutting included angle Ф = 0°, the minimum residual height of elliptical cutting on the surface in the range of 10 μm is 67 nm and the minimum surface fluctuation on the surface in the range of 100 μm is 97 nm. When the cutting included angle Ф is 75°, the maximum difference between residual height of elliptical cutting and the surface fluctuation appears on the surface.

The experimental and predicted theoretical results of residual height have a same variation tendency with the increase of phase difference φ. There are two main reasons for the difference between the actual residual height H_A and the theoretical residual height H_T. (1) In the calculation, H_A is characterized by the arithmetic mean of the difference between the surface height line and the contour bottom envelope in 10 μm cutting path. H_F can amplify H_A to some certain extent. (2) Only a few of the larger and smaller values of the contour coincide with the envelope. So, the actual residual height H_A on the actual contour line is greater than H_T. In addition, the influence of nose radius of tool tip cannot be ignored, which can reduce the surface residual height to a certain extent [40].

In summary, the results of cutting experiments verify that the designed tool has the capacity to optimize the UEVC process by flexibly adjusting the tool vibration trajectory.

5 Conclusions

This study proposed an optimized design of an ultrasonic elliptical vibration cutting (UEVC) tool with dual longitudinal vibration excitations to achieve high adjustability of vibration trajectory. The key design parameters of the integrated horn were identified and optimized. Vibration experiments and cutting tests were conducted to verify performance of the optimized UEVC tool. The following conclusions can be drawn.

• (1) The vibration decoupling of the UEVC system with a configuration angle θ of 90° (the included angle of two longitudinal generators) is better than that with an acute angle due to the conciseness of kinematic equation. This layout state cannot introduce additional interference vibration modes in decoupling.

• (2) The main mass M of a single horn is the primary parameter affecting the normal and tangential resonance frequencies of the integrated horn. The frequency deviation of the integrated horn between the normal and tangential directions can be reduced by adjusting the structural parameters of the horn beam.

• (3) The designed UEVC tool can generate standard elliptical vibration trajectories with adjustable shapes in a working space of 5.1 μm × 5.3 μm when the phase difference of two input voltages changes from 0 to 180°.

• (4) The orientation of elliptical vibration trajectories critically affects the morphology of machined surface. When the included angle between the long axis of the ellipse and the cutting direction is 0°, the minimum surface roughness and surface fluctuation were obtained.