1 Introduction

Precision milling process has been widely applied in the manufacturing of Al-based structural parts for aerospace applications, such as manned space stations, deep space explorers, and high-performance satellites. However, the dimension accuracy and surface performance of the parts cannot be precisely controlled in many cases, and thus, the stable operation of aerospace equipment cannot be guaranteed in the space. One of the most critical problems limiting the performance of precision milling parts is the coupled vibration caused by the dynamic load interaction of the manufacturing process and the machine tool. The complex dynamic characteristics in the milling process results in an in-depth understanding of the synthetically interaction of the vibrations induced by the manufacturing process and the machine tool. Previous studies in the literature have generally focused on the experimental-theoretical investigation of machine tool vibration and milling process dynamics without engaging in a thorough analysis of the process and machine interaction (PMI) [1, 2].

In some cases, most of the research works focus on the spindle and tool vibration. The vibration in precision milling would result in the periodic variation of the relative displacement between tool and workpiece and affect the surface generation in process [3]. Filiz [4] developed analytical models for the dynamics of micro-scale cutting-tools and experimental models for an ultra-high-speed spindle. Zhang and To [5, 6] developed a specialized model for an aerostatic bearing spindle under impulsive excitation from intermittent cutting forces of ultra-precision raster milling to analyze the effects of the particular spindle vibration on surface generation. They found that the phase shift is a key factor influencing the surface patterns. Jiang et al. [7] built a three-dimensional model of machined surface topography in simulation to analyze the influence of tool wear and vibration on the spatial trajectory of the knife tip. They concluded that axis amplitude is a key factor affecting surface residual height. These works show that the vibration load of machine tools has a significant impact on precision machining, but the research mainly focuses on the vibration of the machine tool.

In the milling process, the vibrations mainly include three parts: free vibration, forced vibration, and self-excited vibration (chatter). Generally, chatter occurs when the excitation frequency in cutting is equal or close to one of the natural frequencies of the machine tool, referred to as instable cutting [8, 9]. Chatter behavior depends upon a number of different aspects including spindle speeds, material properties, tool geometry, and even the location of tool respect to the rest of machine [10]. However, when the depth of the cut is small in precision milling, the influence of chatter vibration can possibly be disregarded [11]. Therefore, the forced vibration of the cutting process is the main factor in stable precision milling. In some studies, the cutting force is limited in the static field to investigate deformation mechanism, surface integrity, and microstructure [12,13,14,15,16]. A new basis for modeling dynamic forces from the static component and harmonic contributions is presented, as modeling the dynamic high speed milling force signal accounts for secondary harmonics [17]. Moradi and Vossoughi developed an extended dynamic model of a peripheral milling process including process damping and structural and cutting force nonlinearities using experimental coefficients [18].

Furthermore, with combining the dynamic force and vibration response, Jalili et al. [19] studied the influences of the axial depth of cut, cutting tool diameter, cutting tool length, and number of cutter teeth on the frequency response of the tool tip vibrations using a 3-D nonlinear dynamic model of the milling process. Jiang et al. [20] found a larger tool radius and a smaller cutting depth can control the vibration of curved thin-walled part. Wang et al. [21] proposed a cutting force prediction algorithm considering the influence of cutter vibrations and cutter run-out. Grossi et al. [22, 23] found that dynamic cutting force coefficients change appreciably with spindle speed as mechanics of cutting change, and then carried out a deep investigation of cutting force coefficients to estimate the cutting force and tool-tip vibrational behavior.

The process vibration is the result of the coupling of machine-process vibration. However, few study in the field focuses on the interaction effect of the machine tool dynamic load and the process dynamic force. In the common interaction analysis, the cutting force will cause related vibration of machine, and the vibration also reacts on the cutting force due to the cutting parameters fluctuation by vibration. In this study, the interaction effect of milling vibration and the dynamic force is explored during the milling of Al 7075-T651. First, the dynamic milling process is simplified to theoretically study the vibration interaction model in the precision milling process. Then, the dynamic process force in milling is measured and preprocessed based on wavelet packet transform. The coupled force reflects the cutting mechanism, as well as the process vibration; the machine tool non-cutting vibration is regarded as another dynamic load, while the frequency response function (FRF) of dynamic performance is used to build the interaction link between the dynamic force and the vibration response. Finally, the interaction vibration is calculated applying interaction effect model based on forced vibration and linear system assumption to verify the interaction effect model.

2 Theoretical analysis

2.1 Interaction effect analysis approach

Based on PMI analysis as shown in Fig. 1, the process and the machine tool loads result in the unpredictable effects of interaction. The interaction of vibration to the dynamic forces of milling can include dynamic instabilities in the system, such as chatter vibrations or dynamic deflections. However, while the cutting depth is very small in precision stable cutting process, the vibrations with a force–displacement interaction between the machine tool and the cutting process is the main phenomenon.

Fig. 1
figure 1

Analysis of process and machine interaction

Full size image

In the process vibration-force interaction, the machine free-run vibration would bring the initial change of cutting parameters as △\({v}_{0}\), △\({f}_{0}\), and △\({\alpha }_{p0}\). Then, the material removal process produces dynamic cutting force and reacts on the process, and finally results in the stable dynamic change of cutting parameters and appears the continuous vibration and dynamic force in machining.

In the interaction effect calculation, the dynamic behavior is determined by impacting the machine tool with a dynamic force and measuring the response in the form of vibration. The measured FRF is applied as a relation function between cutting force load and vibration. Furthermore, the dynamic milling force in stable process is applied as the interaction source, and wavelet packet transform is applied in signal preprocessing to extract the periodic component. Finally, the milling-forced vibration response is calculated according to the proposed conversion method, and the predicted interaction vibration is obtained in consideration of both free-run machine tool vibration and process forced vibration based on the linear superposition method. In the verification, the coupled vibration is tested and compared with the predicted vibration.

2.2 Theoretical modeling

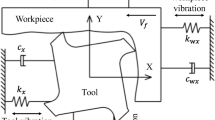
The dynamic milling process considering the dynamic milling force is simplified in the vibration interaction theoretical modeling. As shown in Fig. 2, the dynamic milling process is simplified as a three-degrees-of-freedom system [24, 25], which is expressed in three directions (X-feed direction, Y-perpendicular to feed direction, and Z-axial direction). The milling forces produced during the material removal will cause corresponding forced vibrations of workpiece and tool in X, Y, and Z directions. The workpiece vibrations will enhance the tool vibrations, while the tool vibration will deteriorate the stability of the whole process system. The governing equation can be described as follows:

Fig. 2
figure 2

Schematic diagram of milling dynamics

Full size image
$$\left[M\right]\ddot{S}(t)+\left[C\right]\dot{S}(t)+\left[K\right]S(t)=F(t)$$
(1)

where

$$F\left(t\right)={[{F}_{x}\left(t\right), {F}_{y}\left(t\right),{F}_{z}\left(t\right)]}^{T}$$
(2)

\(F\left(t\right)\) is the milling forces vector; M, C, and K are the modal mass, damping, and stiffness of tool and workpiece, respectively; and S is the vibration displacement vector. With the subscript “m” and “w,” \({M}_{m}, {C}_{m}, {K}_{m},{\mathrm{and }S}_{m}\) stand for the milling tool and \({M}_{w}, {C}_{w}, {K}_{w},\mathrm{ and }{S}_{w}\) stand for the workpiece.

$${S}_{m}\left(t\right)={[{x}_{m}\left(t\right), {y}_{m}\left(t\right),{z}_{m}\left(t\right)]}^{T}$$
(3)
$${S}_{w}\left(t\right)={[{x}_{w}\left(t\right), {y}_{w}\left(t\right),{z}_{w}\left(t\right)]}^{T}$$
(4)

The vibration leads to dynamic change of cutting depth. Figure 3 demonstrates the dynamic changes of cutting thickness produced by the single cutter tooth, which can be summarized as

Fig. 3
figure 3

Dynamic changes of cutting thickness

Full size image
$${\phi }_{j}=\left(j-1\right){\phi }_{p}+\phi$$
(5)
$${\phi }_{p}=2\pi /N$$
(6)

In which \({\phi }_{j}\) is the instantaneous radial contact angle of the jth cutter tooth, \({\phi }_{p}\) is the average circumferential angle of each cutter tooth. The total cutting thickness can be expressed by the sum of static cutting thickness and dynamic cutting thickness:

$$h\left({\phi }_{j}\right)={\{f}_{t}sin{\phi }_{j}+\Delta {f}_{v}\}\mathrm{g}\left({\phi }_{j}\right)$$
(7)

where \({f}_{t}\mathrm{sin}{\phi }_{j}\) is static cutting thickness, \({f}_{t}\) is the feed rate per tooth, \(\Delta {f}_{v}\) is dynamic change of cutting depth, and \(g\left({\phi }_{j}\right)\) is milling cutter teeth participation parameter.

In the study of dynamic force, only its dynamic change is considered,

$$h\left({\phi }_{j}\right)=\Delta xsin{\phi }_{j}+\Delta ycos{\phi }_{j}$$
(8)

where \(\Delta x=\Delta {x}_{m}-\Delta {x}_{w}, \Delta y=\Delta {y}_{m}-\Delta {y}_{w}, \Delta z=\Delta {z}_{m}-\Delta {z}_{w}\) are the dynamic changes in three directions.

The tangential, the radial dynamic cutting forces, and the axial cutting force can be expressed as

$${F}_{tj}={K}_{tc}{a}_{p}h\left({\phi }_{j}\right)$$
(9)
$${F}_{rj}={K}_{r}{F}_{tj}$$
(10)
$${{F}_{zj}=F}_{aj}={K}_{ac}\Delta {a}_{pj}{f}_{t}$$
(11)

\({a}_{p}\) is the axial cutting depth; \({K}_{r}=\frac{{K}_{rc}}{{K}_{tc}}\), \({K}_{rc}\) is the coefficient of radial force, and \({K}_{tc}\) is the tangential force coefficient. Then

$${F}_{xj}=-{F}_{tj}\mathrm{cos}{\phi }_{j}-{F}_{rj}\mathrm{sin}{\phi }_{j}$$
(12)
$${F}_{yj}=+{F}_{tj}\mathrm{sin}{\phi }_{j}-{F}_{rj}\mathrm{cos}{\phi }_{j}$$
(13)

The total cutting force is

$${F}_{x}={\sum}_{j=0}^{N-1}{F}_{xj}\left({\phi }_{j}\right)$$
(14)
$${F}_{y}={\sum}_{j=0}^{N-1}{F}_{yj}\left({\phi }_{j}\right)$$
(15)
$${F}_{z}={\sum}_{j=0}^{N-1}{F}_{aj}$$
(16)

Therefore, the cutting force can be expressed as

$$\left(\genfrac{}{}{0pt}{}{{F}_{x}}{\begin{array}{c}{F}_{y}\\ {F}_{z}\end{array}}\right)=\frac{1}{2}{a}_{p}{K}_{tc}\left[\begin{array}{ccc}\begin{array}{c}{\alpha }_{xx}\end{array}& {\alpha }_{xy}& 0\\ {\alpha }_{yx}& {\alpha }_{yy}& 0\\ 0& 0& \frac{2{K}_{ac}\Delta {a}_{pj}}{{a}_{p}{K}_{tc}}\end{array}\right]\left(\genfrac{}{}{0pt}{}{{\Delta }_{x}}{\begin{array}{c}{\Delta }_{y}\\ {\Delta }_{z}\end{array}}\right)$$
(17)
$${\alpha }_{xx}={\sum}_{j=0}^{N-1}-{g}_{j}\left[\mathrm{sin}2{\phi }_{j}+{K}_{r}\left(1-\mathrm{cos}2{\phi }_{j}\right)\right]$$
(18)
$${\alpha }_{xy}={\sum}_{j=0}^{N-1}-{g}_{j}\left[\left(1+\mathrm{cos}2{\phi }_{j}\right)+{K}_{r}\mathrm{sin}2{\phi }_{j}\right]$$
(19)
$${\alpha }_{yx}={\sum}_{j=0}^{N-1}{g}_{j}\left[\left(1-\mathrm{cos}2{\phi }_{j}\right)+{K}_{r}\mathrm{sin}2{\phi }_{j}\right]$$
(20)
$${\alpha }_{yy}={\sum}_{j=0}^{N-1}{g}_{j}\left[\mathrm{sin}2{\phi }_{j}-{K}_{r}\left(1+\mathrm{cos}2{\phi }_{j}\right)\right]$$
(21)

By means of discretization, Eq. (17) can be expressed in matrix form in time domain:

$$\left[F\left(\tau \right)\right]=\frac{1}{2}{a}_{p}{K}_{tc}\left[A\left(\tau \right)\right]\left[\Delta \left(\tau \right)\right]$$
(22)

where \(A\left(\tau \right)\) is the periodic function with angular frequency \(\omega\) and \(\left[\Delta \left(\tau \right)\right]\) is the dynamic displacement vector.

In frequency domain, the periodic function in milling force can be expanded as follows:

$$\left[A\left(\tau \right)\right]={\sum}_{r=-\infty }^{\infty }\left[{A}_{r}\right]{e}^{ir\omega t}$$
(23)
$$\left[{A}_{r}\right]=\frac{1}{T}{\int }_{0}^{T}\left[A\left(\tau \right)\right]{e}^{-ir\omega \tau }d\tau$$
(24)

For both the milling machine tool and the workpiece, the dynamic milling force would excite the continuously vibration. Taking one direction as an example, the response of milling force excitation can be calculated through the Duhamel integral as follows [26]:

$$x\left(t\right)=\frac{1}{m{\omega }_{d}}{\int }_{0}^{t}F\left(\tau \right){e}^{-\varepsilon {\omega }_{n}\left(t-\tau \right)}\mathrm{sin}{\omega }_{d}\left(t-\tau \right)d\tau +{e}^{-\varepsilon {\omega }_{n}t}({x}_{0}\mathrm{cos}{\omega }_{d}t+\frac{{\dot{x}}_{0}+\varepsilon {\omega }_{n}{x}_{0}}{{\omega }_{d}}\mathrm{sin}{\omega }_{d})$$
(25)

When the initial displacement \({x}_{0}\) and the initial velocity \({\dot{x}}_{0}\) is zero, Eq. (25) can be omitted:

$$x\left(t\right)=\frac{1}{m{\omega }_{d}}{\int }_{0}^{t}F\left(\tau \right){e}^{-\varepsilon {\omega }_{n}\left(t-\tau \right)}\mathrm{sin}{\omega }_{d}\left(t-\tau \right)d\tau ={\int }_{0}^{t}{h}_{xx}\left(t-\tau \right)F\left(\tau \right)d\tau$$
(26)

Therefore, the response can be calculated under the linear system assumption as follows:

$$\left[\begin{array}{c}x(t)\\ y(t)\\ z(t)\end{array}\right]=\left[\begin{array}{c}{\int }_{0}^{t}{h}_{xx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{xy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{xz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{yx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{yy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{yz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{zx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{zy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{zz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \end{array}\right]$$
(27)

The vibration analysis above is based on the cutting force excited vibration in milling under non-chatter condition. Furthermore, the machine tool vibration in the system should also be considered; thus, Eq. (27) can be extended to the study of milling vibration with the mechanical vibration superposition principle.

$$\left[\begin{array}{c}{x}_{m}\left(t\right)\\ {y}_{m}\left(t\right)\\ {z}_{m}\left(t\right)\end{array}\right]=\left[\begin{array}{c}{\int }_{0}^{t}{h}_{mxx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{mxy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{mxz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{myx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{myy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{myz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{mzx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{mzy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{mzz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \end{array}\right]+\left[\begin{array}{c}{x}_{m0}(t)\\ {y}_{m0}(t)\\ {z}_{m0}(t)\end{array}\right]$$
(28)

For workpiece vibration,

$$\left[\begin{array}{c}{x}_{w}\left(t\right)\\ {y}_{w}\left(t\right)\\ {z}_{w}\left(t\right)\end{array}\right]=\left[\begin{array}{c}{\int }_{0}^{t}{h}_{wxx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wxy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wxz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{wyx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wyy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wyz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \\ {\int }_{0}^{t}{h}_{wzx}\left(t-\tau \right){F}_{x}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wzy}\left(t-\tau \right){F}_{y}\left(\tau \right)d\tau +{\int }_{0}^{t}{h}_{wzz}\left(t-\tau \right){F}_{z}\left(\tau \right)d\tau \end{array}\right]$$
(29)

3 Experimental setup

To verify the theoretical model based on interaction effect analysis, the milling experiments are conducted on the milling machine (Model XR1000), as shown in Fig. 4. The milling forces are measured by a Kistler force dynamometer (Type 9139AA) mounted at the machine bed, and the vibration accelerations of the machine tool and workpiece in X and Y directions are obtained by two Kistler annular ceramic shear tri-axial accelerometers (Type 8763B). In the experiment, the Z direction is non-cutting direction and the cutting vibration along the Z direction is regarded having little effect on this direction due to the rigidity of the system. Therefore, this study only considers the vibration from the spindle and workpiece along the X and Y directions. The signals of forces and vibrations are recorded before (free-run), during and after steady-state milling with a Kistler Instrument (types 5165 and 5167). The impact testing is conducted with a PCB hammer (model 086C04) to analysis the frequency response functions.

Fig. 4
figure 4

Experimental setup

Full size image

In the experiments, the aluminum alloy (7075-T651) workpieces with a size of 125 × 75 × 10 mm are applied. This kind of material is widely used in the aerospace industry and has the following chemical composition: Al 89.655%, Cu 1.533%, Cr 0.199%, Fe 0.397%, Mg 2.333%, Mn 0.083%, Si 0.114%, Ti 0.037%, and Zn 5.649%. The side and face milling cutter tool in the test has a tooth number of 3, a diameter of 8.0 mm, a rake angle of 15°, a clearance angle of 6°, and a helix angle of 55°. As shown in Table 1, an L9(33) orthogonal experiment is designed based on Taguchi method, in which spindle speed, feed rate, and axial cutting depth are from 8000 to 12,000 r/min, 0.4 to 0.8 m/min and 0.3 to 0.5 mm, respectively. A straight groove is machined for each milling process, and the Y direction of the machine tool is selected as the feed direction.

Table 1 Milling experiments parameters
Full size table

4 Results and discussions

4.1 Frequency response functions of the spindle and workpiece

Prior to the cutting experiments, the FRFs of the spindle and workpiece in X, Y, and Z directions are obtained by impacting the tool point and the workpiece cutting position, respectively. The analysis bandwidth is 1250 Hz, and the frequency resolution is 1 Hz during experiments. The results are shown in Fig. 5, which illustrate the vibration resistance ability in the cutting process. The FRFs are regarded as the interaction relation function between cutting excitation force and response vibration based on linear system assumption, and the dynamic exciting forces are the main resources of forced vibration while there is also a little self-excited vibration during the milling process.

Fig. 5
figure 5

The FRFs of the spindle and the workpiece in the impact tests. (a) impact tool from X direction; (b) impact tool from Y direction; (c) impact tool from Z direction; (d) impact workpiece from X direction; (e) impact workpiece from Y direction; (f) impact workpiece from Z direction

Full size image

It can be found that the first-order natural frequencies of the tool in X, Y, and Z directions are about 910 Hz, 900 Hz, and 490 Hz, respectively, with the corresponding amplitude-frequency characteristic values 1.06 g/N, 0.36 g/N, and 0.06 g/N. The first-order natural frequencies in X, Y, and Z directions of the workpiece are 253 Hz, 487 Hz, and 476 Hz, respectively, with the corresponding amplitude-frequency characteristic values 0.03 g/N, 0.07 g/N, and 0.1 g/N. It is confirmed that the cutting parameters in Table 1 avoid the chatter during machining.

4.2 Dynamic milling force and vibration

4.2.1 Force and vibration signals in the milling process

By taking the ninth experiment as an example, the original force and vibration signals produced during the milling process are demonstrated in Fig. 6, which show the components of the cutting forces and vibrations in different directions. The forces in three directions range from − 30 to 30 N due to the alternative cutter teeth. The vibrations of spindle are larger than those of the workpiece, which indicates the workpiece receives smaller impacts under good clamping stiffness.

Fig. 6
figure 6

The forces and vibrations produced in the milling process in different directions. (a) cutting forces; (b) vibrations of spindle; (c) vibrations of workpiece

Full size image

Based on the aforementioned analysis, the original signals contain not only the forces and vibrations produced by the milling process, but also affected by the spindle and the machine tool. Therefore, these milling signals require preprocessing to distinguish the forces and vibrations generated by the different causes.

4.2.2 Preprocessing of the milling force signal

The frequency spectrums of the milling force signals are shown in Fig. 7, dynamic forces generated during the milling process consist of two parts: one is the periodic component produced by the periodic rotary motion of the spindle, which has extremely high energy and will cause the periodic interaction vibration of machine tool; the other is the random fluctuating component of cutting force. Therefore, in order to extract the periodic components and get accurate interaction effect analysis [27], wavelet packet transform is applied to preprocess the force signals.

Fig. 7
figure 7

The spectrums of the actual milling force signal in different directions. (a) force signal in X direction; (b) force signal in Y direction; (c) force signal in Z direction

Full size image

The milling force signal is decomposed into four layers using the dmey wavelet. The optimal wavelet packet decomposition tree is shown in Fig. 8. The decomposition result of the wavelet packet is called the wavelet coefficient and designated as \({S}_{4}^{0}\), \({S}_{4}^{1}, {S}_{4}^{1}, \cdots\). The wavelet coefficients of each node in the fourth layer are reconstructed using the wavelet packet reconstruction algorithm, so that the original force signal is represented as follows:

Fig. 8
figure 8

Four-level decomposition structure of wavelet packet

Full size image
$$S={S}_{4}^{0}+{S}_{4}^{1}+, \cdots , +{S}_{4}^{15}$$
(30)

The entropy of each band is acquired as E(4, 0), E(4, 1), \(\cdots\), E(4, 15), and these entropies are normalized using Eq. (31). The energy distributions of each frequency band of the milling force signal in the X, Y, and Z directions are shown in Fig. 9.

Fig. 9
figure 9

The energy distribution in each band of the wavelet packet reconstructed signal

Full size image
$${H}_{(4,j)}=\frac{{E}_{(4,j)}}{\sqrt{{\sum}_{j=0}^{15}{E}_{(4,j)}^{2}}}$$
(31)

In order to analyze the differences in working state in different frequency bands and identify the corresponding relationship between energy distribution and working state, the reconstructed signals of all nodes in the fourth layer are analyzed by fast Fourier transform in the frequency domain. By taking the milling force signal in the Y direction (the feed direction) as an example, spectrums of each node in the fourth layer are shown in Fig. 10.

Fig. 10
figure 10

The spectrums of the force signal in the Y direction applying wavelet packet decomposition. (a) spectrum in subband (4,0); (b) spectrum in subband (4,1); (c) spectrum in subband (4,2); (d) spectrum in subband (4,3); (e) spectrum in subband (4,4); (f) spectrum in subband (4,5); (g) spectrum in subband (4,6); (h) spectrum in subband (4,7); (i) spectrum in subband (4,8); (j) spectrum in subband (4,9); (k) spectrum in subband (4,10); (l) spectrum in subband (4,11); (m) spectrum in subband (4,12); (n) spectrum in subband (4,13); (o) spectrum in subband (4,14); (p) spectrum in subband (4,15)

Full size image

With the help of fast Fourier transformation, frequency bands with larger energy distribution can be selected to construct the milling force equation. According to the principle of the wavelet packet energy spectrum, several frequency bands of the force in Y direction with energy ratios greater than 1% (the reference line in Fig. 9) are selected, while those with energy ratios close to 0 are abandoned. The sum of the cosine signals of these selected frequency bands is applied to express the milling force equation \(F\left(\tau \right)\), and the required main frequency, amplitude, and phase information of the milling force signal in the Y direction are shown in Table 2.

Table 2 The wavelet packet decomposition information of the milling force signal in the Y direction
Full size table

Therefore, the milling force equation calculated in the Y direction according to the original force signal is as follows:

$$\begin{aligned}{F}_{y}&=14.27\mathrm{cos}\left(2\mathrm{pi }\times 200\mathrm{t}-3.05\right)\\&+0.79\mathrm{cos}\left(2\mathrm{pi}*298\mathrm{t}+3.08\right)\\&+1.94\mathrm{cos}\left(2\mathrm{pi}*381\mathrm{t}+1.07\right) \\&+ 10.29\mathrm{cos}\left(2\mathrm{pi }\times 400\mathrm{t}+2.80\right)\\&+1.99\mathrm{cos}\left(2\mathrm{pi}*600\mathrm{t}+2.25\right)\\&+1.29\mathrm{cos}\left(2\mathrm{pi}*650\mathrm{t}+0.91\right) \\ &+ 2.49\mathrm{cos}\left(2\mathrm{pi }\times 1202\mathrm{t}+2.48\right) \end{aligned}$$
(32)

Similarly, the milling force equation in the X direction can be obtained as follows by using the same processing method:

$$\begin{aligned}{F}_{x}&=0.17\mathrm{cos}\left(2\mathrm{pi }\times 79\mathrm{t}-1.80\right)\\&+0.97\mathrm{cos}\left(2\mathrm{pi}*101\mathrm{t}+1.89\right)\\&+19.16\mathrm{cos}\left(2\mathrm{pi}*200\mathrm{t}+1.89\right) \\ &+ 0.68\mathrm{cos}\left(2\mathrm{pi }\times 301\mathrm{t}+0.84\right)\\&+1.68\mathrm{cos}\left(2\mathrm{pi}*381\mathrm{t}+3.00\right)\\&+9.21\mathrm{cos}\left(2\mathrm{pi}*400\mathrm{t}+1.01\right) \\ &+ 1.45\mathrm{cos}\left(2\mathrm{pi }\times 600\mathrm{t}+1.06\right)\\&+1.34\mathrm{cos}\left(2\mathrm{pi}*800\mathrm{t}+1.79\right) \end{aligned}$$
(33)

Then the milling force equation in the Z direction can be obtained as follows:

$$\begin{aligned}{F}_{z}&=0.18\mathrm{cos}\left(2\mathrm{pi }\times 70\mathrm{t}-0.72\right)+0.63\mathrm{cos}\left(2\mathrm{pi}*99\mathrm{t}-0.54\right)\\&+8.84\mathrm{cos}\left(2\mathrm{pi}*200\mathrm{t}-0.76\right) + 0.58\mathrm{cos}\left(2\mathrm{pi }\times 301\mathrm{t}-3.12\right)\\&+0.35\mathrm{cos}\left(2\mathrm{pi}*326\mathrm{t}+0.94\right)+1.44\mathrm{cos}\left(2\mathrm{pi}*400\mathrm{t}-1.68\right) \\ &+ 1.07\mathrm{cos}\left(2\mathrm{pi }\times 498\mathrm{t}+1.68\right)+0.85\mathrm{cos}\left(2\mathrm{pi}*600\mathrm{t}+0.76\right)\\&+0.56\mathrm{cos}\left(2\mathrm{pi}*650\mathrm{t}+0.36\right) + 0.74\mathrm{cos}\left(2\mathrm{pi }\times 999\mathrm{t}-0.81\right) \end{aligned}$$
(34)

The force equations can be applied in predicting the milling force signal. The predicted signal not only eliminates noise while retaining feature information, but also avoids the influence of aperiodic truncation on the signal. The predicted force signals based on the Eqs. (32)–(34) are shown in Fig. 11 which contain characteristic components in milling and match well with the dynamic force model.

Fig. 11
figure 11

The comparison of predicted and meaured milling force signal in different directions. (a) force in X direction; (b) force in Y direction; (c) force in Z direction

Full size image

4.2.3 Preprocessing of the spindle free-run signal

As shown in Eq. (28) in the modeling, the spindle free-run signal is superposed on the forced vibration signal. The measured spindle free-run vibration signal and its spectrum are shown in Fig. 12.

Fig. 12
figure 12

The spindle free-run vibration signal and its frequency spectrum in the X and Y directions. (a) spindle free-run vibration signal; (b) frequency spectrum of vibraion in X direction; (c) frequency spectrum of vibraion in Y direction

Full size image

The previous preprocessing method is also applied to extract the characteristic frequency information of the measured spindle free-run signal. After being decomposed into four layers by dmey wavelet, the energy distribution of each frequency band of the spindle free-run signal in the X and Y directions are shown in Fig. 13.

Fig. 13
figure 13

The energy distribution in each band of the wavelet packet reconstructed signal

Full size image

Taking the spindle free-run vibration signal in the X direction as an example, spectrums of each node in the fourth layer are shown in Fig. 14.

Fig. 14
figure 14

The spectrums of spindle free-run vibration signal in the X direction applying wavelet packet decomposition. (a) spectrum in subband (4,0); (b) spectrum in subband (4,1); (c) spectrum in subband (4,2); (d) spectrum in subband (4,3); (e) spectrum in subband (4,4); (f) spectrum in subband (4,5); (g) spectrum in subband (4,6); (h) spectrum in subband (4,7); (i) spectrum in subband (4,8); (j) spectrum in subband (4,9); (k) spectrum in subband (4,10); (l) spectrum in subband (4,11); (m) spectrum in subband (4,12); (n) spectrum in subband (4,13); (o) spectrum in subband (4,14); (p) spectrum in subband (4,15)

Full size image

According to the principle of wavelet packet energy detection, main frequency bands (energy ratio greater than 1%, evaluated by the reference line in Fig. 13) are selected to construct the free-run vibration equation \(a\left(\tau \right)\) of the spindle. The required main frequency, amplitude, and phase information of the spindle free-run vibration signal in the X direction are shown in Table 3.

Table 3 The wavelet packet decomposition of the spindle free-run vibration signal in the X direction
Full size table

The spindle free-run vibration equations can be expressed as the sum of multiple cosine signals:

$$\begin{aligned}{a}_{x}&=0.004\mathrm{cos}\left(2\mathrm{pi }\times 86\mathrm{t}+1.46\right)+0.130\mathrm{cos}\left(2\mathrm{pi}*200\mathrm{t}-1.90\right)\\&+0.007\mathrm{cos}\left(2\mathrm{pi}*234\mathrm{t}+0.56\right) + 0.020\mathrm{cos}\left(2\mathrm{pi }\times 400\mathrm{t}-1.84\right)\\&+0.022\mathrm{cos}\left(2\mathrm{pi}*762\mathrm{t}-0.08\right)+0.132\mathrm{cos}\left(2\mathrm{pi}*800\mathrm{t}+0.88\right) \end{aligned}$$
(35)
$$\begin{aligned}{a}_{y}&=0.006\mathrm{cos}\left(2\mathrm{pi }\times 127\mathrm{t}+2.68\right)+0.117\mathrm{cos}\left(2\mathrm{pi}*200\mathrm{t}+0.92\right)\\&+0.016\mathrm{cos}\left(2\mathrm{pi}*234\mathrm{t}+0.56\right) + 0.013\mathrm{cos}\left(2\mathrm{pi }\times 400\mathrm{t}+0.70\right)\\&+0.020\mathrm{cos}\left(2\mathrm{pi}*566\mathrm{t}+1.10\right)+0.009\mathrm{cos}\left(2\mathrm{pi}*634\mathrm{t}+1.20\right) \\ &+ 0.019\mathrm{cos}\left(2\mathrm{pi }\times 800\mathrm{t}-2.35\right)+0.013\mathrm{cos}\left(2\mathrm{pi}*1034\mathrm{t}-1.86\right) \end{aligned}$$
(36)

For the same time series t, the preprocessed milling force signal and the preprocessed spindle free-run vibration signal can be ensured to be synchronized in the time domain. The predicted spindle free-run vibration signals based on the Eqs. (35) and (36) are shown in Fig. 15.

Fig. 15
figure 15

The predicted spindle free-run vibration signals in different directions. (a) predicted spindle free-run vibration of X direction; (b) predicted spindle free-run vibration of Y direction

Full size image

4.3 Comparison of interaction analysis result

During the milling process, the cutting forces are periodic due to the rotating multi-tooth milling cutter entering the workpiece. Therefore, these forces can be periodic at tooth- or spindle-passing frequencies, which may have strong harmonics up to four to five times the tooth- or spindle passing frequencies. If any of the force harmonics coincide with one of the natural frequencies of the machine or workpiece structure, the processing system will exhibit forced vibrations. The interaction effect based on forced vibration theory in equations investigates applying the frequency-domain dynamic force and frequency response function. In interaction analysis, the predicted vibration is calculated in the proposition of process interaction by applying Eqs. (28) and (29). The time-domain signals of the predicted vibration and the actual measured vibration are shown in Fig. 16. It can be seen that the predicated results obtained in interaction effect approach match with the vibration signals that directly tested, whether they come from the measurement point of the spindle or the workpiece.

Fig. 16
figure 16

Comparison between the predicted vibration and the measured vibration (Exp. no. 9). (a) spindle vibrations in X direction; (b) spindle vibrations in Y direction; (c) workpiece vibrations in X direction; (d)  workpiece vibrations in Y direction

Full size image

In order to compare the amplitude of the calculated vibration and the actual measured vibration in the frequency domain, the spectrums of two vibration signals are shown in Fig. 17. It shows that the main frequencies of the vibration signal spectrograms in the X and Y directions of the spindle are close at 200 Hz, 400 Hz, and 600 Hz, where 200 Hz is the rotational frequency of the spindle, 400 Hz is the double frequency of the rotational frequency, and 600 Hz (the tooth-passing frequency) is the three-times frequency of the rotational frequency. Therefore, the amplitudes of the characteristic frequency at the low frequency match well. However, at the high frequency, there is some differences due to the extraction method of the signal and some other unpredictable effects.

Fig. 17
figure 17

Spectrum of the predicted vibration and the measured vibration (Exp. no. 9). (a) spindle vibrations in X direction; (b)  spindle vibrations in Y direction; (c) workpiece vibrations in X direction; (d)  workpiece vibrations in Y direction

Full size image

In order to determine the magnitude error of the predicted vibration, the root mean square (RMS) of the vibration signal is calculated using Eq. (37) in which measured vibration signal and the calculated vibration are \({\mu }_{a}\) and \({\mu }_{\widehat{a}}\), respectively, and the relative error of the RMS between the two can be expressed as:

$${\mathrm{Vibration}}_{\mathrm{rms}}=\sqrt{\frac{1}{N}{\sum }_{i=1}^{N}{a\left(i\right)}^{2}}$$
(37)
$${\varepsilon }_{\mathrm{rms}}=\frac{\left|{\mu }_{\widehat{a}}-{\mu }_{a}\right|}{{\mu }_{a}}\times 100\%$$
(38)

Table 4 lists the RMS errors of the predicted vibrations of the spindle and the workpiece under all precision milling parameter combinations. After statistical calculation, the overall percentage of the errors of vibrations from the spindle and the workpiece in X and Y directions are around 20.8%, 21.8%, 17.4% and 17.6%, respectively. The prediction error of the spindle vibration is larger than that of the workpiece vibration, which can be attributed to the complex structure of the spindle. The vibration of the spindle consists of the vibrations from various components, such as bearings and sleeves, and is prone to producing vibrations in different dominant frequencies. On the other hand, the vibration of the workpiece is mainly composed by the self-excited vibrations from workpiece and the tool. The spindle speed and the number of cutter tooth influence the dominant frequencies significantly, which is easier to be identified through spectral analysis and can be predicted better.

Table 4 The relative RMS error of the vibrations
Full size table

5 Conclusions

This study investigated the interaction effect between the dynamic force and the vibration response in the precision milling of 7075-T651 based on forced-vibration transformation approach. By both theoretical modeling and experimental verification, the following conclusions can be drawn from the above investigation:

  • In order to study the interaction of vibration and force during milling process and to calculate their dynamic responses, the machine tool is considered as a multi-degree-of-freedom linear structure and the distribution of different vibration components is analyzed. The interaction effect between machine tool spindle vibration and cutting force excitation caused by spindle rotation in the milling process is considered, and the calculated expressions for milling tool and workpiece vibration are summarized based on the principle of linear superposition of mechanical vibration.

  • The milling force generated during machining consists of two parts, one is the periodic component produced by the periodic rotation of the spindle, which is the main cause of the periodic vibration and interaction of the machine tool; the other is the fluctuating component of the cutting force, which is the higher harmonic frequency of the tool teeth pass. The force and vibration signals are decomposed and reconstructed using the wavelet packet transform, and the force signals are reconstructed using the wavelet packet components of the 2nd, 3rd, 4th, 5th, 6th, 7th, and 15th nodes, while the vibration signals are reconstructed using the wavelet packet components of the 1st, 2nd, 3rd, 5th, 9th, and 10th nodes.

  • The root mean square is used to evaluate the effectiveness of the proposed vibration calculation method. The overall percentage of RMS errors of predicted vibrations from the spindle and the workpiece in X and Y directions are controlled at around 20.8%, 21.8%, 17.4%, and 17.6% respectively. The frequency spectrums of vibrations can be well predicted, while the errors are mainly caused by the vibration amplitude. The comparison of predicted spindle and workpiece vibrations indicates that the self-excited vibrations generated by the workpiece and the tool can be better identified than spindle vibrations.

  • The milling vibrations commonly occur in the machining of structural parts of aerospace equipment due to the large and thin-walled characteristics of these parts. The goal of this study is to provide an explicit analysis and prediction method of milling vibrations for these parts, so that the chatter can be suppressed, and machining quality can be improved. The future research will focus on solving the aliasing problem of vibration signals in nonlinear coupled systems, the dynamics analysis of weakly rigid machine tools, and the improvement of vibration prediction results.