1 Introduction

Superplasticity represents the ability of polycrystalline solids to exhibit very large tensile elongations under certain conditions of temperature and strain rate. The forming conditions required to achieve a superplastic behavior are a high forming temperature (T ≥ 0.5Tm where Tm is the melting temperature of the material in Kelvin degrees) and a very low strain rate (generally between 10–3 to 10–5 s−1). Moreover, superplasticity requires the material to have a fine particle size, typically 10 μm, that is stable during the forming process. These forming conditions are associated with low values of the flow stress and a value of the strain rate sensitivity index, m, greater than 0.3 [1]. In [2], it was stated that a value of the strain rate sensitivity index, m, greater than 0.3 and a value of the tensile elongation greater than 200% indicate a superplastic behavior, although different materials can achieve values of the tensile elongation greater than 1000%. Superplasticity may produce parts with complex geometric shapes through only a single forming step; these parts could not be easily or economically produced with not very ductile materials [3].

Superplastic forming (SPF) is the manufacturing process that exploits the superplastic behavior of some materials [4]. The metal sheet is subjected to a stretching process through the action of a pressurized gas instead of the traditional punch; the process is known as blow forming. It requires the sheet to be fixed between a die and a blank holder to prevent it from sliding inside the die cavity. Once the die has warmed up to bring the sheet to the required process temperature, the pressurized gas will force the sheet to copy the internal geometry of the forming die.

In recent decades, superplastic forming has drawn growing interest from both automotive and aeronautical fields. SPF allows to decrease the weight of the product by eliminating fasteners because it can be used to form components with complex shapes that are very close to that of the final product; it can be considered a near-net-shape forming process. The major disadvantage of SPF is the slowness of the production process (forming times involve tens of minutes). Therefore, SPF is suitable for the production of a low volume of products [3]. Recently, some researchers have turned their attention to faster blow forming processes by giving up the high ductility of the material [5].

The finite element method (FEM) is widely used to successfully simulate superplastic forming processes. FEM allows predicting detailed information on the forming process, such as the stress, the strain, and the thickness distributions. The design stage also requires determining the pressure–time load curve able to stretch the material with an optimal value of the strain rate [6]. The optimization of the pressure–time loading cycle does not exclude adopting a gas with a constant pressure during the forming process.

In [7], an SPF process to manufacture a hemispherical product was studied and it was showed that the obtained hemisphere has an uneven final distribution of thicknesses. The thickness reduces from the edge to the pole of the sheet. This non-uniformity of the thickness decreases as the strain rate sensitivity index m increases, as demonstrated in [8].

To make more uniform the final distribution of the product thicknesses, a multiphase forming process was proposed in [9,10,11] which requires the use of a pre-shape from which the forming process is carried out. Although the non-uniformity of the thickness distribution was reduced, the multiphase forming processes have, however, long forming times. In [12,13,14], it was proposed to modify the constant initial blank thickness profile to affect the thickness distribution of the final product. In these studies, optimizing the initial profile of the blank thickness leads to profiles that follow parabolic laws or with discontinuous variations that are difficult to manufacture in practice. On the contrary, in [8], a product with an almost hemispherical shape was obtained by a blank with a variable thickness obtained by machining an aluminum alloy sheet with a constant initial thickness. The blank was created without considering any optimization criteria.

This work aims to present the optimal design of the thickness of a blank of AZ31 superplastic magnesium alloy to manufacture a product with geometry more complex than the simple hemisphere. The adopted approach is of type trial and test and it is related only to axisymmetric geometries of the finished part. In this work, the use of a FEM model that parametrically generates the thickness of the semi-finished product is not required, because it has been used in the literature by leading to discontinuous variations in the final thickness of the semi-finished product which are difficult to realize in practice [12,13,14]. The optimization is carried out in terms of forming time and product weight. Through FEM, it was possible to verify that, once the geometry of the die was fixed, starting from a circular sheet of constant thickness, the distribution of the thicknesses of the final product is obtained. This thickness distribution can be modified (making more uniform the thickness, reducing the forming times and the weight of the product) by appropriately changing the thickness profile of the starting sheet (through machining). The initial blank thickness profile was obtained after setting restrictive conditions: this profile can vary only linearly and continuously. Therefore, it is possible to achieve the set goal by modifying only two geometric parameters of the circular blank: they are the thickness at the edge x and the width of the constant thickness profile, y. The approach adopted to optimize the geometry of the semi-finished product does not determine the more uniform distribution of the thicknesses but only a distribution more uniform than that due to a sheet with a constant initial thickness.

2 Blow forming test

2.1 Material

Due to their low ductility at room temperature, magnesium-based alloys are poorly suited for cold forming. In [15], industrially used magnesium alloys with superplastic behavior at high temperatures are analyzed.

This work has studied the magnesium alloy AZ31 with an average particle size of 10 μm. The chemical composition of the alloy by weight is Mg-3% Al1% Zn. The semi-finished product consists of a circular disc with a thickness of 1.0 mm and a diameter of 80 mm. The material has a superplastic behavior at a temperature of 440° C. The hardening law of the material that correlates the equivalent stress \(\tilde{\sigma }\) to the equivalent strain \(\overline{\varepsilon }\) and the equivalent strain rate \(\dot{\overline{\varepsilon }}\) is:

$$\tilde{\sigma }=C{\overline{\varepsilon }}^{n}{\dot{\overline{\varepsilon }}}^{m}$$
(1)

where m, n, and C are the strain rate sensitivity index, the hardening index, and the strength coefficient respectively.

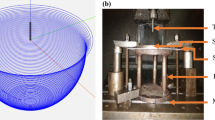
In general, the material constants are obtained from the tensile test, although it is known that the uniaxial stress of the material during the tensile test is different from the biaxial stretching due to the forming process. It has been shown in [16, 17] that free-forming tests allow deriving the material constant values of Eq. (1). The free forming process consists to shape a hemisphere without the sheet coming into contact with a die. Figure 1 shows the scheme of the free-forming process. Therefore, to determine the values of the material constants, m, n, and C, an inverse analysis technique was used to minimize the differences between data from an experimental free-forming activity and from a numerical simulation of the related free-forming process that was carried out through finite element analysis.

Fig. 1
figure 1

Superplastic free-forming scheme

Full size image

2.2 Material mechanical characterization

The experimental tests on free-forming were carried out through two different pressure values (p1 = 0.275 MPa and p2 = 0.4 MPa) to determine the forming times needed to achieve the geometries characterized by H = 0.5 and H = 1, where the H parameter is the dimensionless displacement measured at the apex of the hemispheric sheet as the ratio between h and a in Fig. 1.

At the same time, several numerical simulations of the free-forming process were realized with different values of m, n, and C parameters.

The procedure to characterize mechanically the material required three stages:

Stage 1—Evaluation of m parameter value according to the membrane theory [17, 18]:

$$m=\mathit{ln}\left({p}_{1}/{p}_{2}\right)/\mathit{ln}\left({t}_{2}/{t}_{1}\right)$$
(2)

where t1 and t2 represent the values of the forming time needed to achieve the geometry characterized by H = 1 by using constant values of pressure, p1, and p2 respectively.

Stage 2—Estimation of Q(n) function through both numerical and experimental data according to the following expression:

$$Q\left(n\right)={\left(\frac{{\left(ln\tau \right)}^{FEM}-{\left(ln\tau \right)}^{EXP}}{{\left(ln\tau \right)}^{EXP}}\right)}_{{p}_{1}}^{2}+{\left(\frac{{\left(\mathit{ln}\tau \right)}^{FEM}-{\left(\mathit{ln}\tau \right)}^{EXP}}{{\left(ln\tau \right)}^{EXP}}\right)}_{{p}_{2}}^{2}+{\left(\frac{{\left(l\overline{n }\varepsilon \right)}^{FEM}-{\left(l\overline{n }\varepsilon \right)}^{EXP}}{{\left(l\overline{n }\varepsilon \right)}^{EXP}}\right)}_{{p}_{1}}^{2}+{\left(\frac{{\left(l\overline{n }\varepsilon \right)}^{FEM}-{\left(l\overline{n }\varepsilon \right)}^{EXP}}{{\left(l\overline{n }\varepsilon \right)}^{EXP}}\right)}_{{p}_{2}}^{2}$$
(3)

where τ parameter, that is the normalized time, is defined as:

$$\tau ={t}_{H=1}/{t}_{H=0.5}$$
(4)

where \({t}_{H=1}\) and \({t}_{H=0.5}\) are the values of the forming time needed to achieve the geometries characterized by H = 1 and H = 0.5 through a constant pressure-free-forming process. The \(\overline{\varepsilon }\) parameter is the equivalent strain. The quotes FEM and EXP refer to the numerical and experimental values respectively.

In [18], it was shown that the normalized time τ depends only on the n and m material constants. Therefore, once evaluated the value of the m parameter through Eq. (2), many numerical simulations were performed with different values of the n parameter inside a suitable range; in this way, it was possible to estimate the values of the Q(n) function. The final value of the n parameter was that minimizing the Q(n) function.

Stage 3—Evaluation of F(C) function according to the expression:

$$\mathrm{F}\left(C\right)={\left(\frac{{\left({t}_{H=1}\right)}^{FEM}-{\left({t}_{H=1}\right)}^{EXP}}{{\left({t}_{H=1}\right)}^{EXP}}\right)}_{{p}_{1}}^{2}+{\left(\frac{{\left({t}_{H=1}\right)}^{FEM}-{\left({t}_{H=1}\right)}^{EXP}}{{\left({t}_{H=1}\right)}^{EXP}}\right)}_{{p}_{2}}^{2}$$
(5)

where \({\left({t}_{H=1}\right)}^{FEM}\) and \({\left({t}_{H=1}\right)}^{EXP}\) are the values of the forming time required to achieve a geometry characterize by H = 1 by a constant pressure-free-forming process through finite element modeling (FEM) and experimental tests (EXP). The numerical values were obtained by varying the C strength coefficient within a suitable range. The value of the C strength coefficient was that minimizing the F(C) function.

2.3 Experimental equipment

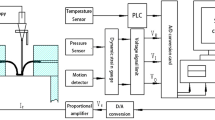
The experimental tests were carried out through specific equipment designed at the Technology and Manufacturing Systems Laboratory of the University of Cassino (see Fig. 2). It has an interface, to acquire data, made up of a pc, a multimeter KEITHLEY 2700 and a power supply ATTEN TPR3003T (1 in Fig. 2), an interface to manage the test parameters and to translate the punch (2 in Fig. 2), a mold-creeper (3 in Fig. 2), a punch and a load cell LUNITEK FT (4 in Fig. 2), a crossbar (5 in Fig. 2) actuated by a rotating screw jack (6 in Fig. 2) and an electric motor (7 in Fig. 2). Further details are reported in [19]. The sheet was placed between two half-dies. A half-die, which acts as a blank holder and contains the forming chamber, is inside an external half-die which is heated by an electric resistance able to keep the equipment and the workpiece at a constant and uniform temperature. Figure 3 shows the die in two parts during the closing process.

Fig. 2
figure 2

Blow forming equipment

Full size image
Fig. 3
figure 3

Die (in two parts) enveloped by an electric heating band and used for the superplastic forming process: a open; b during closing; c closed

Full size image

The two half-dies were locked by steel bolts in such a way as to avoid the sheet from sliding into the forming chamber.

The temperature of the sheet is kept constant at 440° C during the test. The temperature of both the die and the sheet was controlled using thermocouples whose location was specifically designed.

Pressurized air was conveyed through a hole of the outer half-die to act on the bottom surface of the disc. A proportional valve controlled the gas pressure.

A measurement laser monitored the displacement of the sheet at the apex of the hemisphere as a function of the forming time. It passed through a loophole on the internal half-die.

The signals from the thermocouples and the measurement laser were collected by the LabVIEW® software on a PC. A scheme of the equipment and further details of the adopted experimental procedure can be found in [19].

Once the forming process was completed, the thickness along the manufactured part was measured by a Prismo Vast MPS coordinate measuring machine of Zeiss®. Standardized fixturing elements were used to orient and lock each formed sheet on the coordinate measuring machine. The part reference system was defined by measuring both the plane of the fixturing equipment on which the sheet is supported and the cylindrical surface of the sheet that is in contact with the blank holder. Five measurement profiles at a distance of 1.5 mm were measured along with two orthogonal directions on the inner and outer surfaces of the formed sheet by a probe with a tip radius of 3 mm, while a stylus length of 48 mm and 40 mm was used for the inner and the outer surfaces respectively (see Fig. 4). One hundred fifty points were measured on each profile of 150 mm for a total of 1500 points on both the inner and the outer surface of each sheet. The geometric algorithm presented in [20] was used to calculate the distance between each couple of points.

Fig. 4
figure 4

Measurement of formed sheets

Full size image

3 Numerical model

Finite element simulations were performed through the non-linear finite element software package MSC.MARC by using an axisymmetric model with full integration iso-parametric quadrangular elements. The element size was adapted to have two elements along with the thickness for a total number of elements equal to 128. Superplastic forming problems require the use of rigid-plastic flow formulation. The hardening law of the sheet in superplastic AZ31 magnesium alloy follows the classic power law, whose constants have been obtained as reported in paragraph 2.2. The die was modeled as a rigid body. In addition to the axisymmetric condition, the boundary conditions were implemented by locking the nodes into contact with the blank holder; moreover, the forming pressure was applied to the top edge of the sheet. The hardening law of the AZ31 superplastic magnesium alloy that made up the sheet follows the power law of Eq. (1). The contact between the die surface, which was considered rigid, and the surface of the sheet, which was considered deformable, was defined through the Coulomb friction model. Figure 5 shows the geometry of the die used for the blow forming process to optimize the uniformity of the product thicknesses and the forming time. The geometry of the die has a horizontal surface that is 8 mm long from the axis of symmetry. It is connected to the bottom surface of the die using two curved surfaces with a radius of 2 and 5 mm respectively. The surface with a 2 mm radius of curvature involves the greatest deformation on the sheet. The bottom surface of the die is connected to the support surface of the sheet by two curved surfaces with a radius of 8 and 2 mm respectively. The design of the blow forming process requires that the thickness profile of the initial blank be modified in such a way to involve the lowest values of the forming time and the product weight. The adopted optimization procedure responds to the constraint to obtain a blank easy to manufacture actually (thus, the thickness profile of the initial blank can vary only linearly). Two parameters, x, and y respectively in Fig. 6, were chosen to carry out the optimization. The x parameter is the thickness at the edge of the initial circular sheet. The y parameter is the length of the blank part with a 1 mm thickness. The y = 0 and x = 1 mm conditions represent the circular disc with a constant thickness (see Fig. 6). At first, some values inside the range 0.9–0.7 mm were assigned to the x parameter and the obtained thickness at the edge was linearly connected to the thickness at the symmetry axis that was considered always equal to 1 mm (see Fig. 7). Once the value of the x parameter was chosen, the y parameter was made to vary to complete the optimization.

Fig. 5
figure 5

Geometry of the die used to form the AZ31 superplastic magnesium-based alloy and the formed part

Full size image
Fig. 6
figure 6

Blank with a variable thickness used to form the AZ31 superplastic magnesium-based alloy

Full size image
Fig. 7
figure 7

Flowchart of the adopted optimization method

Full size image

4 Results and discussion

4.1 Friction coefficient estimation

To carry out the simulations through a finite element model, the value of the friction coefficient in the Coulomb friction model needed to be evaluated. Therefore, the forming process of the blank with a constant initial thickness using the die shown in Fig. 5 was simulated with three values of the μ friction coefficient, 0, 0.1, and 0.2 respectively. The obtained results were compared with the experimental data. Figure 8 shows the comparison of the results. It is possible to note that the greatest deviations occur on the flat surface between the axis of symmetry and the minimum radius of curvature (r = 2 mm). The value of the μ friction coefficient that minimizes the difference between numerical and experimental results was 0.1. It was used μ = 0.1 in all the subsequent simulations.

Fig. 8
figure 8

Distribution of thicknesses obtained through FEM in a product formed with different values of the friction coefficient from a blank with a constant thickness. Comparison between numerical and experimental results

Full size image

4.2 Forming process optimization

Figure 9 shows the distribution of the thicknesses of the product obtained by forming a blank with a constant thickness of 1.0 mm. It was achieved by FEM and it represents the reference situation. It is possible to note that, starting from the axis of symmetry, the thickness decreases up to reach the minimum radius of curvature (r = 2 mm), where it undergoes the greatest reduction (which could lead to the breaking of the component) and then, it goes back towards the edge of the sheet. Table 1 shows the forming time and the R parameter that is calculated as the ratio between the minimum and the maximum thicknesses obtained by FEM. This R parameter is an index of the reached uniformity of thicknesses (R tends to be 1 for an ideal product with a constant thickness). The forming process, which involves a blank with a constant thickness, highlights that the part region at the minimum radius of curvature is fed little by the material between the minimum radius of curvature and the edge of the sheet. This zone contributes little to the uniformity of the thicknesses of the formed component.

Fig. 9
figure 9

Distribution of thicknesses obtained through FEM in a product formed from a blank with a constant thickness

Full size image
Table 1 FEM results used to design the profile of the thicknesses in the initial blank
Full size table

The optimization of the forming process was performed through the variation of only the geometry of the blank. The design of the optimal blank was carried out in two stages. In the first one, the forming process was simulated using a blank whose initial profile of thicknesses was varied linearly from the axis of symmetry (s = 1.0 mm, y = 0 mm) to the edge of the sheet (s = x). The x parameter assumed the values of 0.90 mm, 0.80 mm, and 0.70 mm respectively. Figure 9 shows the comparison between the final distributions of the thicknesses obtained using the three different blanks with a variable thickness together with that due to a blank with a constant thickness. It can be seen that the thickness value at the minimum radius of curvature of the die tends to increase as the value of the x parameter decreases. The maximum increase is about 9% from a blank with a constant thickness to a blank with a variable thickness that is characterized by x = 0.70 mm. Table 1 shows that the forming time decreases as the x parameter increases; it reaches a reduction of 41% for a blank with a variable thickness that is characterized by x = 0.70 mm. Table 1 shows the weight reduction connected with a blank with a variable thickness too; it achieves a reduction of 20% for a blank with x = 0.7 mm. However, Fig. 10 shows that the blank characterized by x = 0.70 mm presents a really low value of thickness at the edge of the sheet. To avoid a break at the edge of the formed product, x = 70 mm was considered a limit condition and, therefore, to be discarded. Therefore, it was considered optimal the condition represented by the blank with x = 0.80 mm. In this way, the R parameter increases passing from R = 0.581 (of a blank with a constant thickness) to R = 0.717 (of a blank with a variable thickness that is characterized by x = 0.80 mm) and the weight reduction is equal to 13.3%.

Fig. 10
figure 10

Distribution of thicknesses obtained through FEM in a product formed from blanks with a variable thickness

Full size image

The second stage of the optimal blank design involved the y parameter. Figure 10 shows that all blanks with a variable thickness have, in the area between the symmetry axis and the minimum radius of curvature (the distance is 8 mm), decreasing thicknesses. Since the material of this area affects the thickness of the most critical area (that with the minimum value of curvature radius), the thickness of the area between the symmetry axis and the minimum radius of curvature was brought to the maximum possible value (1 mm). This means that the thickness of the initial blank was set equal to 1.0 mm for a distance from the symmetry axis equal to 8 mm (y = 8 mm). Figure 11 highlights the obtained positive results in terms of final thickness distribution. The minimum value of thickness increases by about 14% in comparison to that due to a blank with an initial constant thickness. From Table 1, it can be seen that the R value further increases to 0.750, while the forming time and the product weight are reduced by about 22% and 5% in comparison with that due to a blank with an initial constant thickness.

Fig. 11
figure 11

Comparison among the distributions of the thicknesses due to the optimization carried through FEM

Full size image

4.3 Comparison between numerical and experimental results

Experimental tests were carried out by forming both blanks with an initial constant thickness (s = 1 mm and volume V = 5026 mm3) and blanks with an initial variable thickness (y = 8 mm, x = 0.8 mm, and volume V = 4303 mm3). Figure 5 shows a formed part.

The blank with a variable thickness was obtained by a machining process from a disc with a constant thickness of 1 mm. The forming process involved a time similar to that numerically estimated and reported in Table 1. In detail, the forming times were 3390 s and 2640 s for the blanks with constant and variable thicknesses respectively. The tests were carried out at a constant forming pressure of 0.4 MPa.

Figure 12 shows the comparison between numerical and experimental results in terms of final thickness distribution. The comparison confirms the results highlighted through the numerical modeling. In particular, it can be seen that the experimental results differ by a maximum of 4% from the numerical ones.

Fig. 12
figure 12

Comparison between numerical and experimental results in terms of thickness distributions in the considered product formed from a blank with constant and variable thicknesses

Full size image

5 Conclusions

This work presents the design of the thickness of a blank in AZ31 superplastic alloy to form, without changing the geometry of the die, parts without defects of lesser weight in less process time. Starting from a blank with a constant thickness, it was possible, through finite element analysis, to identify a blank characterized by a variable thickness that involves the distribution of the thicknesses in the manufactured product more uniform than that due to a blank with a constant thickness. This blank with a variable thickness allows to form parts lighter than those due to a blank with a constant thickness; it was observed a weight reduction from 5 to 13%. It involves a forming time shorter than that due to a blank with a constant thickness too; it was observed a time reduction of about 22%. Finally, it was noted a good agreement between numerical and experimental results (the maximum difference was about 4%) that testifies the reliability of obtained results.

In this work, the adopted approach may be applied only to axisymmetric sheet blanks, such as circular sheet blanks. It starts from a sheet with a constant initial thickness. Then, the blank is modified according to the criterion of continuously reducing the thickness corresponding to those areas of the sheet which are less deformed in a process with a constant initial thickness. The adopted criterion is general and, therefore, may be applied to more complex parts. However, the feasibility of this issue needs to be demonstrated in the following work.