1 Introduction

Thin-walled workpieces are widely used in various fields such as automobile, aerospace, and energy industries [1,2,3].

However, due to the weak rigidity of thin-walled workpieces, it is prone to encounter regenerative chatter or large-amplitude vibrations during machining, which seriously affect the machining quality [4]. Therefore, how to improve the machining performance of thin-walled workpieces has become a major concern in both academia and industry.

Proper selection of cutting parameters via SLDs is an important way to avoid regenerative chatter [5]. Many methods have been proposed to draw SLDs in the cutting parameter space, such as the frequency domain methods [6, 7] and the time domain methods [8, 9]. Nevertheless, the prediction accuracy of SLDs for thin-walled parts is challenged by various factors. For example, the feeding movement of cutting tool and the continuous removing of material changes the dynamic properties of thin-walled workpiece. Bravo et al. [10] presented three-dimensional SLDs to incorporate the influence of tool position. Budak et al. [11] and Song et al. [12] proposed structural modification methods to simulate the effect of material removal. Eksioglu et al. [13] and Sun and Jiang [14] considered the variance of tool/workpiece dynamics along tool axis for peripheral milling of thin-walled parts. Finite element method (FEM) is widely used in the abovementioned literature to facilitate efficient simulation of time-varying and position-varying dynamics of thin-walled workpiece. But FEM cannot completely replace the experimental modal analysis (EMA) [15,16,17]. On the one hand, the damping ratio cannot be simulated with FEM. On the other hand, the simplification of boundary conditions may result in non-negligible prediction error of workpiece dynamics. In addition, the existence of runout [18], mode coupling [19], multiple structural modes [20], and nonlinear feedback of vibrations [21] also affect the stability prediction accuracy. Therefore, it is not a best choice to mitigate thin-walled part milling chatter by only depending on selecting parameters from SLDs.

Low stiffness is the main reason that thin-walled workpiece suffers from regenerative chatter and large-amplitude forced vibrations. Using fixture support to enhance the dynamic stiffness of thin-walled workpiece could essentially improve the cutting performance of thin-walled workpieces. Kolluru et al. [22] reported that the utilization of ancillary fixture could reduce the milling vibrations to one-eighth of the original level during the milling process of thin-walled casing. Ma et al. [23] found that magnetorheological fluid flexible fixture could significantly improve the stability limit of thin-walled workpiece. Fei et al. [24] discovered that the milling deformation could be effectively suppressed by placing a moving fixture element on the uncut surface of thin-walled workpiece.

In order to investigate the mechanism of vibration suppression and stability improvement of fixture on thin-walled workpiece, analytical methods and finite element methods are successively used to model the dynamics of fixture-workpiece system. Based on Rayleigh-Ritz method, Meshreki et al. [25] proposed an analytical formulation to represent the dynamic responses of multipocket thin-walled structures under fixture constraints, and further built multispan beam models to account for the effect of material removing [26]. Finite element simulation verified that the predicted error is less than 5%. Wan et al. [27, 28] regarded the fixture-workpiece system as an equivalent thin-multi-span plate with intermediate line and point supports, and set up the dynamic equation using the Lagrangian method. The aforementioned methods and simulation results provide reference for fixture design and tunning.

It is worth noting that simple utilization of fixture cannot always improve machining performance. The workpiece position error, fixture-induced deformation error, and datum error may damage the machining precision [29,28,31]. It is a prerequisite to figure out the influences of fixture design parameters and tunning schemes. Liu et al. [32] optimized the number and positions of locators on the secondary locating surface, which guaranteed the machining precision with minimum locators. Raghu and Melkote [33] analyzed the influence of clamping sequence on workpiece position and orientation. Siebenaler and Melkote [34] studied the role of compliance of the fixture body on workpiece deformation using finite element method. Wan et al. [28] investigated the influence of fixture layout on dynamic response of thin-walled multi-framed workpiece. On this basis, the layout was further optimized by Wan and Zhang [27] to improve the machining stability. Matsubara et al. [35] reported that fixture support with surface contact performed better than point contact at suppressing machining vibrations. Zhong and Hu [36] proposed N-2-1 fixturing scheme to mitigate machining deformation for large-scale thin-walled workpiece. Hao et al. proposed 6+X locating principle [37] and machining sequence adaptive tunning scheme [38] to control milling deformation.

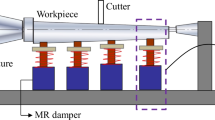
Nevertheless, to the best of the authors’ knowledge, few studies concentrate on the quantitative influences of support force on milling dynamics of thin-walled workpiece, partially due to the lack of controllable actuators. This paper proposes an effective method to model the tool-workpiece-fixture system dynamics and studies the influences of different support forces, where the precise control of support force is realized through an innovative design of pheumatic fixture, as shown in Fig. 1. The remainder of this paper is organized as follows. Section 2 establishes the dynamic model of the system. Section 3 calculates the stability of the system. Section 4 carries out the experimental verification. Section 5 concludes the paper.

Fig. 1
figure 1

Workpiece-fixture system with precise control of support force

Full size image

2 Dynamic model of the system

2.1 Dynamic equation of the tool-workpiece-fixture system

The schematic diagram of tool-workpiece-fixture system is shown in Fig. 1, where the pneumatic fixture support locates at the uncut side of the thin-walled workpiece and the support force can be precisely controlled via the pneumatic cylinder. The dynamic equation of the system can be expressed in physical space as:

$$ {M}_{wf}\ddot{q}(t)+{C}_{wf}\dot{q}(t)+{K}_{wf}q(t)=F(t) $$
(1)

where Mwf, Cwf, Kwf are the mass, damping, and stiffness matrices, respectively; \( \ddot{\mathbf{q}}(t) \), \( \dot{\mathbf{q}}(t) \), and q(t) are the acceleration, velocity, and displacement, respectively; F(t) is the cutting force vector.

The dynamic equation can be transformed from physical space to modal space by [39]:

$$ \mathbf{q}(t)=\mathbf{P}\boldsymbol{\Gamma } (t) $$
(2)

where P is the mode shape matrix, and Γ(t) is the modal displacement vector.

$$ P=\left[{P}_T\kern0.5em -{P}_{Wf}\right]={\left[\begin{array}{cccccc}{p}_{1x,1;T}& \cdots & {p}_{1x,{m}_T;T}& -{p}_{1x,1; Wf}& \cdots & -{p}_{1x,{m}_{Wf}; Wf}\\ {}{p}_{1y,1;T}& \cdots & {p}_{1y,{m}_T;T}& -{p}_{1y,1; Wf}& \cdots & -{p}_{1y,{m}_{Wf}; Wf}\\ {}\vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ {}{p}_{nx,1;T}& \cdots & {p}_{nx,{m}_T;T}& -{p}_{nx,1; Wf}& \cdots & -{p}_{nx,{m}_{Wf}; Wf}\\ {}{p}_{ny,1;T}& \cdots & {p}_{ny,{m}_T;T}& -{p}_{ny,1; Wf}& \cdots & -{p}_{ny,{m}_{Wf}; Wf}\end{array}\right]}_{2n\times \left({m}_T+{m}_{Wf}\right)},\varGamma (t)={\left[\begin{array}{c}{\varGamma}_{1;T}\\ {}\vdots \\ {}{\varGamma}_{m_T;T}\\ {}{\varGamma}_{1; Wf}\\ {}\begin{array}{c}\vdots \\ {}{\varGamma}_{m_{Wf}; Wf}\end{array}\end{array}\right]}_{\left({m}_T+{m}_{Wf}\right)\times 1} $$
(3)

where n is the number of contact points between tool and workpiece; mT and mWf represent the number of modes for the tool and the workpiece-fixture subsystem, respectively; PT and PWf are the mode shape submatrices with regard to the tool and the workpiece-fixture, respectively; the element \( {p}_{\boxed{A}\boxed{B},\boxed{C};\boxed{D}} \) in matrix P denotes the mode shape value, where the subscripts mean \( \boxed{A}=1\cdots n \) is the serial number of discrete contact node between tool and workpiece, \( \boxed{B}=x\kern0.5em \mathrm{or}\kern0.5em y \) is the direction of vibrations, \( \boxed{C}=1\cdots {m}_T\kern0.5em \mathrm{or}\kern0.5em 1\cdots {m}_{Wf} \) is the serial number of mode for the tool or the workpiece-fixture, and \( \boxed{D}={m}_T\kern0.5em \mathrm{or}\kern0.5em {m}_{Wf} \) represents the tool or the workpiece-fixture; The element \( {\Gamma}_{\boxed{E};\boxed{F}} \) in matrix Γ(t) denotes the modal displacement, where the subscripts mean \( \boxed{E}=1\cdots {m}_T\kern0.5em \mathrm{or}\kern0.5em 1\cdots {m}_{Wf} \) is the serial number of mode for the tool or the workpiece-fixture, and \( \boxed{F}={m}_T\kern0.5em \mathrm{or}\kern0.5em {m}_{Wf} \) represents the tool or the workpiece-fixture.

Substituting Eq. (2) into Eq. (1), the dynamics equation in modal space can be written as:

$$ {M}_{\varGamma}\ddot{\varGamma}(t)+{C}_{\varGamma}\dot{\varGamma}(t)+{K}_{\varGamma}\varGamma (t)={P}^TF(t) $$
(4)

where MΓ, CΓ, KΓ are the modal mass, modal damping, and modal stiffness matrices, respectively:

$$ {\displaystyle \begin{array}{c}{M}_{\varGamma }=\operatorname{diag}\left({m}_{1;T},\cdots, {m}_{m_T;T},{m}_{1; Wf},\cdots, {m}_{m_{Wf}; Wf}\right),\\ {}{C}_{\varGamma }=\operatorname{diag}\left({c}_{1;T},\cdots, {c}_{m_T;T},{c}_{1; Wf},\cdots, {c}_{m_{Wf}; Wf}\right),\\ {}{K}_{\varGamma }=\operatorname{diag}\left({k}_{1;T},\cdots, {k}_{m_T;T},{k}_{1; Wf},\cdots, {k}_{m_{Wf}; Wf}\right),\end{array}} $$
(5)

where ma; T, ca; T, ka; T(a = 1, 2, ⋯, mT) are the modal mass, modal damping, and modal stiffness with regard to the a ‐ th mode of the tool, respectively; mb; Wf, cb; Wf, kb; Wf(b = 1, 2, ⋯, mWf) are the modal mass, modal damping, and modal stiffness with regard to the b ‐ th mode of the workpiece-fixture subsystem, respectively. The modal parameters in Eq. (5) are obtained by combining EMA and FEM in this paper, which will be detailed in Section 2.3.

2.2 Cutting force modeling considering runout

As shown in Fig. 2, the inevitable tool runout phenomenon changes the equivalent cutting radius, causes multiple regeneration, affects the stability limits, and thus should be taken into account in dynamics modeling [40]. Based on the mechanistic force model [5], the elemental cutting forces in tangential and radial directions can be expressed as:

$$ \left[\begin{array}{c}d{F}_t\left(t,j,k\right)\\ {}d{F}_n\left(t,j,k\right)\end{array}\right]=g\left(\varphi \left(t,j,k\right)\right)\left\{\left[\begin{array}{c}{k}_{tc}\\ {}{k}_{nc}\end{array}\right]h\left(t,j,k\right) dz+\left[\begin{array}{c}{k}_{te}\\ {}{k}_{ne}\end{array}\right] ds\right\} $$
(6)

where ktc and knc are the shear force coefficients in tangential and radial directions, respectively; kte and kne are the edge force coefficients in tangential and radial directions, respectively; dz and ds are the axial height and edge length with regard to each discrete slice, respectively; φ(t, j, k) and h(t, j, k) are the instantaneous rotation angle and the instantaneous uncut chip thickness with regard to cutting element (j, k) at time t, respectively; and g(φ(t, j, k)) is an unit step function to determine whether the element is cutting or not:

Fig. 2
figure 2

Schematic diagram of the milling process. a 2-DOF milling considering runout. b Discretization of the helix tool. c Dynamic chip thickness

Full size image
$$ g\left(\varphi \left(t,j,k\right)\right)=\Big\{{\displaystyle \begin{array}{c}1,{\varphi}_{st}\left(j,k\right)\le \operatorname{mod}\left(\varphi \left(t,j,k\right),2\pi \right)\le {\varphi}_{ex}\left(j,k\right)\\ {}0,\mathrm{otherwise}\end{array}} $$
(7)

where φst(j, k) and φex(j, k) are the start and exit angles, respectively.

The instantaneous rotation angle φ(t, j, k) is:

$$ \varphi \left(t,j,k\right)=\frac{2\pi \varOmega}{60}t-\frac{z_j\tan \left({\beta}_k\right)}{R}+{\varphi}_{ref} $$
(8)

where Ω is the spindle speed in revolution per minute, zj is the axial height of the j ‐ th slice, βk is the helix angle of Tooth k, R is the radius of the tool, and φref is the angular distance between Tooth k and negative y axis at the tool tip at t = 0.

Due to the effects of chip regeneration, the instantaneous uncut chip thickness in Eq. (6) contains two parts: the quasi-static part hs(t, j, k, p) and the dynamic part hd(t, j, k, p).

$$ h\left(t,j,k,p\right)={h}_s\left(t,j,k,p\right)+{h}_d\left(t,j,k,p\right) $$
(9)

where

$$ {h}_s\left(t,j,k,p\right)={f}_{\mathrm{t}}\left(t,j,k:k-p\right)\sin \varphi \left(t,j,k\right)+R\left(j,k\right)-R\left(j,k-p\right) $$
(10)

and

$$ {h}_d\left(t,j,k,p\right)=\left[x(t)-x\left(t-\tau \left(j,k,p\right)\right)\right]\sin \varphi \left(t,j,k\right)-\left[y(t)-y\left(t-\tau \left(j,k,p\right)\right)\right]\cos \varphi \left(t,j,k\right) $$
(11)

where p denotes the runout induced multi-regenerative index; ft(t, j, k : k − p) is the feed between Tooth k and Tooth k − p at the j ‐ th axial slice; τ(j, k, p) denotes the multi-regenerative time delay; R(j, k) and R(j, k − p) are the actual rotating radius of Tooth k and Tooth k − p, respectively.

$$ R\left(j,k\right)=\sqrt{R^2+{\rho}^2-2 R\rho \cos \left({\theta}_t\right)} $$
(12)

where

$$ {\theta}_t=\min \left\{\lambda -\psi \left(j,k:1\right)-{z}_j\frac{\tan \left({\beta}_k\right)}{R}\right\} $$
(13)

where ρ is the runout offset and λ is the runout orientation; ψ(j, k : 1) is the pitch angle between Tooth k and Tooth 1 on axial height zj.

The multi-regenerative instantaneous uncut chip thickness h(t, j, k, p) can be calculated efficiently by:

$$ h\left(t,j,k,p\right)=\max \left\{\min \left[h\left(t,j,k,p\right),p=1,\cdots, N\right],0\right\} $$
(14)

where N denotes the number of teeth.

Once the instantaneous uncut chip thickness and cutting force coefficients are obtained, the cutting forces for each element can be expressed in Cartesian coordinate system as:

$$ \left[\begin{array}{c}d{F}_x\left(t,j,k\right)\\ {}d{F}_y\left(t,j,k\right)\end{array}\right]=\left[\begin{array}{cc}-\cos \varphi \left(t,j,k\right)& -\sin \varphi \left(t,j,k\right)\\ {}-\sin \varphi \left(t,j,k\right)& \cos \varphi \left(t,j,k\right)\end{array}\right]\left[\begin{array}{c}d{F}_t\left(t,j,k\right)\\ {}d{F}_n\left(t,j,k\right)\end{array}\right] $$
(15)

Finally, the total instantaneous cutting forces are:

$$ \left[\begin{array}{c}{F}_x(t)\\ {}{F}_y(t)\end{array}\right]=\sum \limits_{j=1}^{N_a}\sum \limits_{k=1}^N\left[\begin{array}{c}d{F}_x\left(t,j,k\right)\\ {}d{F}_y\left(t,j,k\right)\end{array}\right] $$
(16)

where Na is the number of discrete axial slices.

2.3 Identification of dynamic parameters

The dynamic parameters of thin-walled workpiece change with the movement of cutting point. Fixture support further complicates the identification of position-dependent frequency response function (FRF). In this subsection, FRF of the workpiece-fixture subsystem is identified by combining EMA and FEM, i.e., the modal parameters are identified using EMA and the mode shapes are simulated using FEM.

Step 1: Modal parameter identification using EMA

Modal parameters including natural frequencies and damping ratios are identified using experimental modal tests, as shown in Fig. 3. An impact hammer (PCB 086C01) is used to excite the thin-walled plate (aluminum alloy 7075, 100mm × 9mm × 85mm) and a miniature accelerometer (352C23) is used to measure the dynamic responses at each discrete node. Since it is very prone to encounter double-hit during the hammer test of thin-walled workpiece, the driving point (i.e., point where hammer excitation and response reception locate at the same position) is chosen far away from the plate corner (i.e., position with the lowest stiffness), as shown in Fig. 3 b. By moving the accelerometer from Point 1 to Point 27, the mode shapes are also experimentally identified, which will be used to validate the simulation results of FEM in the next section.

Fig. 3
figure 3

Experimental modal test. a Setup. b Thin-walled workpiece

Full size image

The end of fixture support is a cylindrical rod (aluminum alloy 7075) with 5mm diameter. Since the workpiece in Fig. 3 b has multiple modes, the mode coupling effect will consequently make the analysis very complicated. In order to better understand the influence of fixture support, the support position is placed at the middle of the workpiece, i.e., the node of the torsional mode shape, as shown in Fig. 3 b.

Modal tests are performed for different supporting conditions. For the case without support, the cylindrical rod is out of contact with the plate surface. For the case with support, the cylindrical rod is in contact with the uncut surface of the plate, and the support force is tuned with the air pressure regulating valve and measured with the force sensor (Fig. 1). In this paper, 0N, 40N, 60N, 80N, 100N, and 120N are chosen for comparison study. 0N means that the cylindrical rod is in contact with the plate but the support force is 0N (the air pressure is 0Pa).

Take 80N as an example. The FRFs with and without fixture support are compared in Fig. 4. It reveals that the fixture support exerts considerable influence on the dynamic properties of thin-walled workpiece, in terms of natural frequency and FRF amplitude. The first mode shifts to higher frequency band and splits into two modes. Meanwhile, the FRF amplitude reduces from 3.84×10−3mm/N to 2.00×10−4mm/N and 1.85×10−4mm/N, as shown in Fig. 4 b. For the second mode, since the support rod locates at the node of mode shape, the natural frequency does not change and the amplitude is slightly reduced.

Fig. 4
figure 4

Comparisons of measured FRFs for cases with and without fixture support. a Comparisons at different tool position. b Comparisons at Point 1

Full size image

The influence of support force on FRF of thin-walled workpiece is illustrated in Fig. 5. Generally speaking, the change of support force has almost no effect on the natural frequency of each mode, while the FRF amplitude slightly decreases as the growth of support force. Nevertheless, when the support force reaches to a certain value, the variance of FRF amplitude becomes negligible. For example, the FRF curves with regard to 80N, 100N, and 120N are almost the same, as shown in Fig. 5 b. This may attribute to the reason that when support force is small, the contact status between workpiece and support is not stable. Enough preload (the critical values is around 80N in this case) is necessary for the workpiece-fixture subsystem to exert stable FRF.

Fig. 5
figure 5

Comparisons of FRFs under different support forces. a FRFs at Point 3. b FRFs at Point 4

Full size image

Based on the above analysis, FRFs when the contact status between workpiece and fixture is stable are used for modal parameter identification with the least squares complex frequency (LSCF) method embedded in LMS Test Lab software. The measured and fitted FRF curves are shown in Fig. 6 and the identified modal parameters are listed in Table 1 for workpiece with and without fixture support, respectively. The support force is 80N in this case.

Fig. 6
figure 6

Measured and fitted FRFs of the workpiece. a Without support. b With support

Full size image
Table 1 Identified modal parameters for workpiece with and without support
Full size table

Step 2: Mode shape extraction using FEM

The utilization of FEM can significantly reduce the burden of experimental modal test, especially for mode shape identification of thin-walled workpiece. In this paper, the commercial software ABAQUS is used to predict the natural frequencies and mode shapes of the thin-walled plate with fixture support. The material properties are set to density ρd = 2800kg/m3, elastic modulus E = 71Gpa, and Poisson’s ratio υ = 0.33 for aluminum alloy 7075. In the simulation, the bottom of the workpiece is fixed. The fixture support is simulated by using preloading condition with the following contact options: friction in the tangential direction is set to rough, and hard contact is used in the normal direction and set to allow separation after contact. For the interaction options, the finite slip formula and the surface-surface discretization method are used. For the support boundary options, the tangential direction is restricted and the normal direction is free. The FEM outputs for workpieces with and without fixture support are shown in Fig. 7.

Fig. 7
figure 7

Comparisons of FEM and EMA in terms of natural frequency and mode shape

Full size image

According to Fig. 7, the simulation results of FEM are in good agreement with the experimental results of EMA for the case without fixture support, in terms of both natural frequencies and mode shapes. It indicates that the boundary conditions and material inputs of FEM are acceptable. For the case with fixture support, the natural frequency and mode shape of the second mode still match well. However, the FEM only output one bending mode at 1213.6Hz, while the EMA shows two bending modes at 1225.3Hz and 1379.3Hz, respectively. This discrepancy may attribute to the very complicated nonlinear interaction at the contact position after the fixture support is added, and specific in-depth analysis needs to be further explored. In this paper, the advantages of FEM and EMA are combined, i.e., the modal parameters including natural frequencies, damping ratios, and normalized mode shape values at driving point are identified using EMA, and the mode shapes are extracted using FEM. Two bending modes and one torsional mode for cases with support are used to predict the 3D SLDs in Section 3.

Step 3: Identification of dynamic parameters at each point on the cutting path

Natural frequencies and mode shapes are inherent properties of structure, and thus do not change with cutting position. The change of dynamics along tool path is represented by the mode shape values. In Step 1, the mode shape value is normalized at driving point, i.e., the mode shape value at driving point is 1. Take the same normalization rule on the extracted mode shapes in Step 2, i.e., all values are divided by the shape value at the same driving point, which produces the resultant mode shape values for all discrete points on the cutting path.

3 Stability calculation

According to Section 2, the governing dynamic equation can be re-organized as:

$$ {M}_{\varGamma}\ddot{\varGamma}(t)+{C}_{\varGamma}\dot{\varGamma}(t)+{K}_{\varGamma}\varGamma (t)=\sum \limits_{k=1}^N\sum \limits_{j=1}^{N_a}\left\{{P}^T{K}_c\left(t,j,k\right)P\left[\varGamma (t)-\varGamma \left(t-\tau \left(j,k\right)\right)\right]\right\}+\sum \limits_{k=1}^N\sum \limits_{j=1}^{N_a}{P}^T{F}_0\left(t,j,k\right) $$
(17)

where

$$ {\displaystyle \begin{array}{c}{K}_c\left(t,j,k\right)=\operatorname{diag}\left({0}_{4\times 4}\kern0.5em \cdots \kern0.5em {0}_{4\times 4}\kern0.5em {K}_{c, ele}\left(t,j,k\right)\kern0.5em {0}_{4\times 4}\kern0.5em \cdots \kern0.5em {0}_{4\times 4}\right),\\ {}{F}_0\left(t,j,k\right)=\operatorname{diag}\left(\begin{array}{ccccccc}{0}_{2\times 1}& \cdots & {0}_{2\times 1}& {F}_{0, ele}\left(t,j,k\right)& {0}_{2\times 1}& \cdots & {0}_{2\times 1}\end{array}\right)\end{array}} $$
(18)

where Kc, ele(t, j, k) is the directional coefficient matrix, and F0, ele(t, j, k) is the cutting force matrix.

$$ {\displaystyle \begin{array}{c}{K}_{c, ele}\left(t,j,k\right)=g\left(\varphi \left(t,j,k\right)\right)\left[\begin{array}{cc}-\cos \varphi \left(t,j,k\right)& -\sin \varphi \left(t,j,k\right)\\ {}-\sin \varphi \left(t,j,k\right)& \cos \varphi \left(t,j,k\right)\end{array}\right]\left[\begin{array}{c}{k}_{tc}\\ {}{k}_{nc}\end{array}\right]\left[\sin \varphi \left(t,j,k\right)\kern0.5em -\cos \varphi \left(t,j,k\right)\right] dz\\ {}{F}_{0, ele}\left(t,j,k\right)=g\left(\varphi \left(t,j,k\right)\right)\left[\begin{array}{cc}\cos \varphi \left(t,j,k\right)& \sin \varphi \left(t,j,k\right)\\ {}-\sin \varphi \left(t,j,k\right)& \cos \varphi \left(t,j,k\right)\end{array}\right]\left(\left[\begin{array}{c}{k}_{tc}\\ {}{k}_{nc}\end{array}\right]{h}_s\left(t,j,k\right) dz+\left[\begin{array}{c}{k}_{te}\\ {}{k}_{ne}\end{array}\right] ds\right)\end{array}} $$
(19)

To predict the stability of the system, Eq. (17) can be transformed from modal space into state space:

$$ \dot{x}(t)= Ax(t)+\sum \limits_{\mathrm{k}=1}^N\sum \limits_{j=1}^{N_a}\left\{B\left(t,j,k\right)\left[x(t)-x\left(t-\tau \left(j,k\right)\right)\right]+D\left(t,j,k\right)\right\} $$
(20)

where

$$ {\displaystyle \begin{array}{c}x(t)=\left[\begin{array}{c}\varGamma (t)\\ {}\dot{\varGamma}(t)\end{array}\right],A=\left[\begin{array}{cc}0& I\\ {}-{M}_{\varGamma}^{-1}{K}_{\varGamma }& -{M}_{\varGamma}^{-1}{C}_{\varGamma}\end{array}\right],\\ {}B\left(t,j,k\right)=\left[\begin{array}{cc}0& 0\\ {}{M}_{\varGamma}^{-1}{P}^T{K}_c\left(t,j,k\right)P& 0\end{array}\right],D\left(t,j,k\right)=\left[\begin{array}{c}0\\ {}{M}_{\varGamma}^{-1}{P}^T{F}_0\left(t,j,k\right)\end{array}\right]\end{array}} $$
(21)

On the basis of Eq. (20), the multi-regenerative stability can be analyzed by using the Floquet theory. In this paper, the proposed method in Ref. [41] is expanded to predict the stability of thin-walled workpiece with tool runout under fixture support constraints.

4 Experimental verification

In this section, the 3D SLDs of the thin-walled plate with and without support are predicted and verified through experiments. In addition, a series of comparisons and analyses are carried out on the cutting process under different support forces.

4.1 Cutting tests of workpiece with and without support

Prior to stability analysis, the cutting force coefficients and runout values are obtained based on the methods proposed in Ref. [42]. In this paper, a three-flute solid carbide end mills with diameter 20 mm and helix angle 45° is used to perform all the cutting tests. The identified parameters are listed in Table 2.

Table 2 Identified cutting force coefficients and runout parameters.
Full size table

Considering the position dependency of system dynamics, the stability limits are drawn in a three-dimensional parameter space composed of spindle speed, tool position, and axial depth of cut. Both the cases with and without fixture support are demonstrated, as shown in Fig. 8 a and b. Figure 8 reveals that there is indeed an improvement in the stability limit after adding fixture support.

Fig. 8
figure 8

Three-dimensional stability lobe diagrams. a Without support. b With support

Full size image

The experimental setup is shown in Fig. 9. The thin-walled workpiece (aluminum alloy 7075) is fixed to Kistler dynamometer (9257B) by using six bolts. During the milling process, two miniature accelerometers (PCB 352C23 with sensitivity 5.33mV/g and 5.53 mV/g, respectively) are fixed on the uncut side of the workpiece to record acceleration signals in the direction of thickness, and a microphone (GRAS 46AE with sensitivity 50 mV/Pa) is also used to collect sound pressure.

Fig. 9
figure 9

Experimental setup

Full size image

Since this paper mainly studies the influence of support force on the dynamics of thin-walled workpiece, how to accurately control the support force is very important. Here, a pneumatic cylinder is introduced into the experimental design to ensure constant support force, which is controlled by the air pressure regulating valve as marked by the red circle in Fig. 9. In addition, to read the magnitude of support force, a force sensor is installed between the fixture support and the output end of the pneumatic cylinder.

To further verify the prediction results, a series of experiments are carried out. The axial depth of cut is kept constant along the whole tool path (ap = 3mm). Therefore, the predicted 3D SLDs in Fig. 8 can be interpreted by a sectional view, as shown in Fig. 10 a for case without support and Fig. 10 e for case with support, where the colored area represents chatter zone and the uncolored area represents stable zone. The radial depth of cut is ar = 0.2mm and the feed rate is ft = 0.05mm/tooth. Three spindle speeds are selected to validate the prediction results: Ω = 5300rpm, 6000rpm, and 6700rpm. The cutting status is judged by means of short-time Fourier transform (STFT) on acceleration signals. Chatter, marginal, and stable conditions are labeled using pentagram, square, and circle markers, respectively.

Fig. 10
figure 10

SLDs and time-frequency diagrams. a–d Without support. e–h With support

Full size image

STFT diagrams for cases without fixture support are shown in Fig. 10 b–d. When the spindle speed is 5300rpm, the chatter energy is obvious around 2000Hz at the beginning and end of tool path while negligible at the middle. When the spindle speed is 6000rpm, the frequency spectra are similar to those of 5300rpm, but the chatter energy is more obvious around 2000Hz. In addition, chatter frequencies also appear near 1000Hz. When the speed is 6700rpm, there is no obvious chatter energy on the whole path. It validates that the theoretical stability prediction results are in good agreement with the cutting tests for cases without fixture support.

STFT diagrams for cases with fixture support are shown in Fig. 10 f–h. Similarly, experimental results reveal that chatter happens at the beginning and end of tool path for 5300rpm and 6000rpm. It is stable on the whole path for 6700rpm. It indicates that the proposed method can successfully predict the stability for thin-walled workpieces with fixture support. The slight discrepancies may attribute to the reason that the introduction of support makes the theoretical model more complicated, which deserves further exploration.

In addition, STFT diagrams also reveal that fixture support can remarkably mitigate the chatter energy, even if it cannot completely prevent the occurrence of chatter, as shown in Fig. 10 b versus f and c versus g. Take 6000rpm as an example. The cutting acceleration signals are compared in detail from the viewpoint of time-history evolution and frequency spectra.

As shown in Fig. 11 a and e, in general, the amplitude of acceleration for case with fixture support is smaller than that for case without fixture support, especially at the middle of tool path. Besides, the envelope of time domain signals for case with fixture support also appears smoother. Through dividing the cutting signals into three parts, the frequency spectra are obtained by performing fast Fourier transform (FFT), as shown in Fig. 11 b–d and f–h, where the symbol “SF” stands for “spindle rotation frequency” and “CF” stands for “Chatter frequency”. FFT diagrams validate the stability prediction results again: chatter happens at the beginning and end of tool path, while stable cutting locates at the middle. In addition, the length of stable cutting signals labeled B in Fig. 11 e is larger than the counterpart in Fig. 11 a. It reveals that the utilization of fixture support expands the stable zone of thin-walled workpiece.

Fig. 11
figure 11

Acceleration signals and frequency spectra for 6000rpm. a–d Without support. e–h With support

Full size image

To further validate the effect of fixture support on stability improvement, the measured cutting force signals in thickness direction are also compared in time domain, as shown in Fig. 12. The amplitude of cutting forces after utilization of fixture support decreases by about 60%.

Fig. 12
figure 12

Cutting force signals of workpiece. a Without support. b With support

Full size image

4.2 Cutting tests under different support forces

In this section, the influence of support forces on milling dynamics of thin-walled workpiece is further explored. Five supporting conditions are selected: without support, 0N, 40N, 80N, and 120N. It is worth noting that there is essential distinction between the case without support and the case with 0N support force. “Without support” means the fixture is out of contact with the thin-walled workpiece. “0N” means the fixture is in contact with the workpiece but the support force is 0N. For 0N conditions, there exist complicated interactions when the workpiece vibrates under cutting excitation.

Cutting tests under different supporting conditions are carried out for the spindle speed 6000rpm and 5300rpm, respectively. Similarly, acceleration signals are selected for STFT analysis, as shown in Fig. 13. Since the cases without support and 80N have been analyzed in Section 4.1, only the rest supporting conditions are displayed.

Fig. 13
figure 13

Time-frequency diagrams of acceleration signals under different supporting conditions: a–c 6000rpm. d–f 5300rpm

Full size image

The results show that fixture support can effectively mitigate the chatter energy in milling process of thin-walled workpiece. Even for 0N case, the chatter energy in Fig. 13 a also decreases a lot in comparison with the case without support in Fig. 10 c. Generally speaking, the chatter mitigation performance of fixture improves with the increase of support force. But when the support force reaches certain value, the performance improvement becomes minimal and negligible. For example, the time-frequency diagram for 80N is similar with that for 120N, as shown in Fig. 10 g versus Fig. 13 c for 6000rpm and Fig. 10 f versus Fig. 13 f for 5300rpm.

The above phenomenon is consistent with the influence of support forces on FRF in Fig. 5. It is attributed to the complicated contact status between fixture and workpiece. Prior to stable contact, the vibration mitigation performance of fixture increases with the growth of support forces. But when a stable contact is established with enough preloading, the effectiveness of support force becomes saturated.

5 Conclusion and discussion

In this paper, the influence of fixture support force on milling dynamics of thin-walled workpiece is systematically investigated on the basis of designed force-tunable pneumatic fixture. Cutting experiments validate the built dynamic model of tool-workpiece-fixture system and the predicted 3D stability lobe diagrams. Detailed analyses on FRF change, stability improvement, and cutting signals under different fixture supporting conditions draw some important conclusions:

(1) Fixture can significantly shift the natural frequency of thin-walled workpiece and reduce the FRF amplitude of target mode.

(2) In general, fixture expands the chatter-free zone of thin-walled workpiece. Even for chatter conditions, fixture can significantly mitigate the chatter frequency energy.

(3) The influence of fixture supporting force on stability limits and cutting signals is closely related to the contact status between fixture and workpiece. The cutting performance can be enhanced by increasing the supporting force, but there exists a critical value, beyond which the improvement will become saturated.

The basic rules of fixture supporting forces on milling dynamics of thin-walled workpieces are explored in this paper. Nevertheless, the interaction mechanism between fixture and workpiece during machining process remains to be investigated further in the future.