1 Introduction

Mechanical scratching technology is widely used to manufacture microstructure and microarray because of its advantages of simple machining method, low cost, and high machining accuracy [1,2,3]. Meanwhile, the scratching tests are also used to investigate the wear and tribology properties of the bulk materials, coatings, thin films, and MEMS [4]. The scratching tool adopts different geometrics and positions for different machining requirements. In this paper, a diamond-tip scratching tool (irregular triangular pyramid tool) is used to mechanical scratching the metal materials, and the final product is mainly used as the grating microstructure. According to the research results of Tseng [5] and metal cutting theory, it can be known that the mechanical scratching is equivalent to the three-dimensional oblique cutting and plowing when the diamond wedge scratching tool scratching with the edge forward and a certain elevation angle. The material plastic flow characteristics of the contact surface is determined on the important parameters of the negative rake angle, the material deformation amount, the scratching force, the groove quality, and the tool wear. However, the chip flow angle and the material plastic flow direction are often derived from the approximate solution according to the metal cutting theory and assumptions. There is no theoretical model of the material plastic flow characteristics suitable for the diamond wedge scratching tool. Therefore, studying the plastic flow characteristics of metal material in mechanical scratching with a diamond wedge scratching tool is essential for enriching the mechanical scratching theory, developing the scratching technology, and improving the scratching quality.

The research on the material plastic flow characteristics of the tool-workpiece contact surface can be divided into two categories. The one is to investigate the chip flow angle (CFA) in the oblique cutting with multi-edges tool. The CFA is defined as the angle between the flow out direction of the chip and the normal direction of the main cutting edge. And the other is assuming that there is a constant angle between the material plastic flow line and the scratching direction, the characteristic axis, or characteristic plane by considering the whole scratching tool.

Scholars have systematically investigated the CFA in oblique cutting with multi-edge tool. Stabler [6] pointed out that the CFA is equal to the inclination angle in oblique cutting. And its modified model [7] obtained that the CFA is equal to the inclination angle multiplied by the scale factor (the scale factor ranges from 0.9 to 1, which is mainly related to material properties and cutting conditions). Cowell [8] proposed a simplified model of multi-edges tool with rounded corners. The model assumed that the material flow out direction is perpendicular to the equivalent cutting edge. And the model could only apply to the situation where the rake angle and inclination angle are all equal to 0°. Russell and Brown [9] also pointed out that the CFA is related to the inclination angle and rake angle. Based on the CFA model of Cowell and Stabler, Hu et al. [10] predicted a CFA model when the rake angle and inclination angle are not equal to 0°. Young et al. [11] further extended Hu’s CFA model for the cutting tool with rounded corners. Okushima and Minato [12] divided the main cutting edge into sub-cutting edges with countless small width. Therefore, the CFA is composed of the CFAs of these sub-cutting edges. Based on the geometric characteristics of the cutting tool, Morcos [13] pointed out that the CFA is not only related to the inclination angle and the rake angle but also the friction coefficient of the tool-workpiece contact surface. Luk [14] and Shaw [15] also concluded that the CFA is related to the friction coefficient of the tool-workpiece contact surface and the material properties. Brown [16] and Rubenstein [17] assumed that the material flow out direction is consistent with the direction of friction force. Armarego and Brown [18] studied the CFA based on the shear surface model, assuming that the direction of the shear force is consistent with the shear velocity and the direction of friction force is consistent with the friction velocity. Considering a temperature-dependent friction law of the tool-workpiece contact surface, Moufki et al. [19, 20] calculated the CFA by assuming the direction of the friction force is collinear to the chip flow direction. Usui et al. [21, 22] solved the CFA through the minimum energy theory. In this model, the tool sharp angle is 90° and the cutting layer is set as rectangle. The relationship among the rake angle, the shear angle, the friction angle, and the maximum shear flow stress is obtained through the orthogonal cutting experiments under the same cutting condition. Based on the CFA model of Usui, Wang et al. [23] established a CFA model by the minimum shear area with double-edged cutting tool, and the CFA under the influence of ratios of two edge lengths has been studied. Wan [24] and Xia [25] separately investigated the CFA of general double-edge tool and trapezoid three-edge tool in oblique cutting.

Considering the whole scratching tool, scholars have also investigated the material plastic flow line. Goddard and Wilman [26] assumed that the projection of material plastic flow line of the pyramid indenter surface in the horizontal plane is parallel to the scratching direction when studying the friction characteristics of the pyramid indenter. Van et al. [27] assumed that there is a minimum angle deviation of the material plastic flow vector and velocity vector in scratching with a pyramid indenter; namely, the projection of the material plastic flow vector in the scratching direction is the largest. Tayebi et al. [28] extended the model of Goddard and Wilman [26] for spherical asperities and assumed an inclined angle of the material plastic flow line along the contact surface. Komvopoulos et al. [29] proposed a material plastic flow line model for a conical tip having a spherical extremity and a frontal contact area. Briscoe et al. [30] divided the contact area of the scratching conical-workpiece into two regions when studying the friction characteristics of a perfectly conical tip with low apex angle. The one is the adhesive friction region where the material flows from the top of the conical indenter into the bottom, and the other is the sliding friction region where the material flows backwards around the circumference of the conical surface. Subhash and Zhang [31] assumed that the material plastic flow line of the conical surface goes around the conical tip and has a constant angle with the vertical axis when investigating the friction characteristics of the conical tip. Lafaye et al. [32] pointed out that the material plastic flow line would be divided into three kinds depending on the cone angle of the conical indenter, namely, the horizontal line for very low cone angle, the vertical line for very large cone angle, and the secant line for the intermediate cone angle. Jardret et al. [33] assumed that there is a constant angle between the material plastic flow line and the scratching direction when a Berkovich indenter scratching with the edge forward. Hamid et al. [4] established a friction model of the Berkovich indenter and pointed out that there are two parts of the material plastic flow line on the indenter surface. One part of the material plastic flow line is concentrically arranged near the main scratching edge, and the other part of the material plastic flow line is parallelly arranged far away from the main scratching edge. Meanwhile, the parallel part accounted for most of the tool-workpiece contact area.

In summary, the CFA of the cutting tool with multi-edges and round-edge and the material plastic flow line of the contact surface of the pyramidal, spherical, conical, and Berkovich indenters (triangular pyramid) have been investigated systematically by scholars. The research shows that the CFA and the direction of the material plastic flow line are often derived from the approximate solution in the metal cutting theory and the assumption of the material plastic flow line direction of the contact surface with the regular-shaped scratching tool. The research also shows that the CFA is affected by multi-cutting factors. However, there is no relevant research on the material plastic flow characteristics of the mechanical scratching with diamond wedge scratching tool (irregular triangular pyramids). Therefore, based on the three-dimensional force balance equation and the vector method, the unit plastic flow vector (PFV), the working negative rake angle, and the CFA theoretical model are established firstly in this paper. And then, the evolution law of the material PFV and the CFA under the influence of the multi-scratching factors is studied according to the theoretical model and the scratching experiments. The deviation of the unit PFV characterization parameter is analyzed for verifying the theoretical model, as well. Finally, the applicability of unit PFV and CFA is explored.

2 Theoretical model

2.1 The plastic flow vector theoretical model

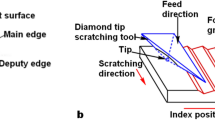
As shown in Fig. 1, the diamond wedge scratching tool will be used for mechanical scratching the metal materials in this paper. During the mechanical scratching, the main edge is forward; namely, the direction of the main edge is the same as scratching direction; the scratching tool is raised with a certain elevation angle; then, the main edge blade splits the metal material or coating; the two negative rake angle contact surfaces act on the material with cutting and extruding; and the deformed material are extruded into V-groove by the two deputy edges. As shown in Fig. 1b, the micro-groove structure will be created by cycling this mechanical scratching process when the workpiece moves along the index position direction.

Fig. 1
figure 1

Schematic diagram of mechanical scratching: a diamond wedge scratching tool, b formed groove

Full size image

2.1.1 Basic assumption

According to the research results of Goddard et al. [26,27,28,29,30,31,32,33], and without considering the crossover and sudden change of the material plastic flow direction [34], the unit PFV theory will be established. Before the theory model, the basic assumptions were made as follows:

  1. (1)

    When scratching at a constant speed, the stiffness of the scratching tool’s cantilever is greater; the scratching depth is approximately a fixed value; and the edge radius is approximately zero because of the scratching depth is greater than the edge radius.

  2. (2)

    On the contact surface of the scratching tool-workpiece, the material undergoes plastic deformation along the plastic flow line direction, and the deformation of the material in the third principal stress direction perpendicular to the plastic flow plane is ignored.

  3. (3)

    The plastic flow line of the material is approximately parallel to each other, and the angle between the projection in the base plane (perpendicular to the scratching direction) and the normal axis is approximately a constant value.

2.1.2 Theoretical model construction

Base on Figs. 1 and 2a is the projections of the scratching tool with elevation angles of 0° on the plane of the XOY, XOZ, and YOZ, and Fig. 2b is the projections of the contact surface of the scratching tool-workpieces with elevation angles of θe on the plane of the XOY, XOZ, and YOZ. Based on Fig. 2c, it can be seen that the red line on the contact surface of the scratching tool with an elevation angle of θe is the plastic flow line, and the vector characterizing the direction of the plastic flow line is defined as the unit PFV. According to the basic assumptions, there is much unit PFV on the two contact surfaces OAB and OAC, and the unit PFV of the single contact surface is parallel to each other. Then, the plastic flow plane connected by unit PFV is parallel to each other (the unit PFV corresponds to the plastic flow plane D0E0A0AF). In addition, the working negative rake angle of the scratching tool and the relationship between the tool-workpiece of the plastic flow plane is consistent. Namely, the shear angle, friction angle, and shear flow stress of the plastic deformation material are all equal. According to the above basic assumptions and the relationship of the space vector, the unit PFV can be solved by establishing the three-dimensional force balance equation and the vector method in the scratching coordinate system.

Fig. 2
figure 2

The three-dimensional projection and the unit PFV of the diamond wedge scratching tool: a the three-dimensional projection of the scratching tool with the elevation angle of 0° and b the three-dimensional projection of the scratching tool with the elevation angle of θe, and c the unit PFV of the contact surface of the scratching tool

Full size image

θw, θB, θr, and θe repesent the wedge angle, beside angle, relief angle, and elevation angle of the scratching tool, respectively, as shown in Fig. 2a and b. According to Fig. 2c, it is clear that the contact vertices of the tool-workpiece are the points O, A, B and C, respectively. Point B0 and C0 are the projections of point B and C in the base plane XOZ, respectively. B0C0 and the normal axis Z intersect at point G0. Then the coordinates of each contact vertex can be expressed as:

$$ O\left(x,y,z\right)=\left(0,0,0\right) $$
(1)
$$ A\left({x}_A,{y}_A,{z}_A\right)=\left(0,{h}_0\tan \left(\frac{\pi }{2}-{\theta}_e\right),{h}_0\right) $$
(2)
$$ B\left({x}_B,{y}_B,{z}_B\right)=\left(\frac{h_B\tan \left(\frac{\pi }{2}-{\theta}_B\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{-{h}_B\left(\tan \left(\frac{\pi }{2}-{\theta}_r\right)\cos {\theta}_e+\sin {\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_{\mathrm{r}}\right)\sin {\theta}_e},{h}_B\right) $$
(3)
$$ C\left({x}_C,{y}_C,{z}_C\right)=\left(\frac{-{h}_C\tan \left({\theta}_w+{\theta}_B-\frac{\pi }{2}\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{-{h}_C\left(\tan \left(\frac{\pi }{2}-{\theta}_r\right)\cos {\theta}_e+\sin {\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},{h}_C\right) $$
(4)

where h0, hB, and hC are the scratching depth (do not consider the accumulation of the material in front of the main edge, and the height of point A is approximately equal to the scratching depth), the contact height of the contact surface OAB, and OAC, respectively. Then, the normal vector and of the contact surface OAB and OAC can be given:

$$ {\displaystyle \begin{array}{c}\overrightarrow{n_{OA B}}=\left({n}_{BX},{n}_{BY},{n}_{BZ}\right)\\ {}=\left({y}_{OA}{z}_{OB}-{y}_{OB}{z}_{OA},{z}_{OA}{x}_{OB}-{z}_{OB}{x}_{OA},{x}_{OA}{y}_{OB}-{x}_{OB}{y}_{OA}\right)\\ {}=\left(\frac{h_B{h}_0\left(\tan \left(\frac{\pi }{2}-{\theta}_e\right)+\tan \left(\frac{\pi }{2}-{\theta}_r\right)\cos {\theta}_e+\sin {\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{h_B{h}_0\tan \left(\frac{\pi }{2}-{\theta}_B\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},-\frac{h_B{h}_0\tan \left(\frac{\pi }{2}-{\theta}_B\right)\tan \left(\frac{\pi }{2}-{\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e}\right)\end{array}} $$
(5)
$$ {\displaystyle \begin{array}{c}\overrightarrow{n_{OA C}}=\left({n}_{CX},{n}_{CY},{n}_{CZ}\right)\\ {}=\left({y}_{OA}{z}_{OC}-{y}_{OC}{z}_{OA},{z}_{OA}{x}_{OC}-{z}_{OC}{x}_{OA},{x}_{OA}{y}_{OC}-{x}_{OC}{y}_{OA}\right)\\ {}=\left(\frac{h_C{h}_0\left(\tan \left(\frac{\pi }{2}-{\theta}_e\right)+\tan \left(\frac{\pi }{2}-{\theta}_r\right)\cos {\theta}_e+\sin {\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{-{h}_C{h}_0\tan \left({\theta}_w+{\theta}_B-\frac{\pi }{2}\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{h_C{h}_0\tan \left({\theta}_w+{\theta}_B-\frac{\pi }{2}\right)\tan \left(\frac{\pi }{2}-{\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e}\right)\end{array}} $$
(6)

where (xOA, yOA, zOA),(xOB, yOB, zOB), and (xOC, yOC, zOC) are the spatial coordinates of \( \overrightarrow{OA} \),\( \overrightarrow{OB} \),and\( \overrightarrow{OC} \), respectively. Therefore the unit normal vector \( \overrightarrow{n_B} \) and \( \overrightarrow{n_C} \) of the contact surface OAB and OAC can be represented as:

$$ \overrightarrow{n_B}=\left({n}_{Bx},{n}_{By},{n}_{Bz}\right)=\left(\begin{array}{c}\frac{n_{BX}}{\sqrt{{n_{BX}}^2+{n_{BY}}^2+{n_{BZ}}^2}},\frac{n_{BY}}{\sqrt{{n_{BX}}^2+{n_{BY}}^2+{n_{BZ}}^2}},\\ {}\frac{n_{BZ}}{\sqrt{{n_{BX}}^2+{n_{BY}}^2+{n_{BZ}}^2}}\end{array}\right) $$
(7)
$$ \overrightarrow{n_C}=\left({n}_{Cx},{n}_{Cy},{n}_{Cz}\right)=\left(\begin{array}{c}\frac{n_{CX}}{\sqrt{{n_{CX}}^2+{n_{CY}}^2+{n_{CZ}}^2}},\frac{n_{CY}}{\sqrt{{n_{CX}}^2+{n_{CY}}^2+{n_{CZ}}^2}},\\ {}\frac{n_{CZ}}{\sqrt{{n_{CX}}^2+{n_{CY}}^2+{n_{CZ}}^2}}\end{array}\right) $$
(8)

As shown in Fig. 2c, \( \overrightarrow{A{D}_0} \) is the plastic flow line through point A and intersects with the base plane XOZ at point D0 (the intersection line of plane OAB and base plane XOZ is OD0G0). \( \overrightarrow{E{D}_0} \) is the unit PFV of AD0 parallel to other plastic flow line and is represented by \( \overrightarrow{L_B} \). Points A0 and E0 are the projections of point A and E in the base plane XOZ, respectively. \( \overrightarrow{D_0F} \) is parallel to \( \overrightarrow{A{A}_0} \) and Y axis. Therefore, \( \overrightarrow{L_B} \) and \( \overrightarrow{D_0F} \) together constitute the plastic flow plane D0E0A0AF passing through the point A. According to the spatial geometric relationship of the above vectors, the expressions related to the unit PFV can be obtained as follows:

$$ \overrightarrow{E{D}_0}=\overrightarrow{L_B}=\left({L}_{Bx},{L}_{By},{L}_{Bz}\right) $$
(9)
$$ \overrightarrow{n_B}\cdot \overrightarrow{L_B}=0 $$
(10)
$$ {L_{Bx}}^2+{L_{By}}^2+{L_{Bz}}^2=1 $$
(11)

\( \overrightarrow{L_{B0}} \) (\( \overrightarrow{O{G}_0} \)) is the projection of \( \overrightarrow{L_B} \) in the base plane XOZ. Based on the assumption that the material plastic flow line of the contact surface is parallel to each other and having constant angle between the projection of the PFV in the base plane XOZ and the normal Z axis, and according from Eq. (9) to Eq. (11), the unit plastic flow vector \( \overrightarrow{L_B} \) and \( \overrightarrow{L_C} \) of the contact surface OAB and OAC can be expressed as:

$$ \overrightarrow{L_B}=\left({m}_B\sin {\varphi}_B,-\frac{n_{Bx}{L}_{Bx}+{n}_{Bz}{L}_{Bz}}{n_{By}},-{m}_B\cos {\varphi}_B\right) $$
(12)
$$ \overrightarrow{L_C}=\left(-{m}_C\sin {\varphi}_C,-\frac{n_{Cx}{L}_{Cx}+{n}_{Cz}{L}_{Cz}}{n_{Cy}},-{m}_C\cos {\varphi}_C\right) $$
(13)

where

$$ {\displaystyle \begin{array}{c}{m}_B=\sqrt{\frac{1}{1+{\left(\frac{n_{Bx}\sin {\varphi}_B-{n}_{Bz}\cos {\varphi}_B}{n_{By}}\right)}^2}}\\ {}{m}_C=\sqrt{\frac{1}{1+{\left(\frac{n_{Cx}\sin {\varphi}_C-{n}_{Cz}\cos {\varphi}_C}{n_{Cy}}\right)}^2}}\end{array}} $$

φB and φC are the angle between the projection of the unit PFV \( \overrightarrow{L_B} \) and \( \overrightarrow{L_C} \) and the normal Z axis in the base plane XOZ, respectively.

It can be seen the three-dimensional force \( \overrightarrow{F_{Bx}} \), \( \overrightarrow{F_{By}} \), and \( \overrightarrow{F_{Bz}} \) in the mechanical scratching condition in Fig. 3. Based on the assumption that the direction of the material plastic flow line is consistent with the friction force, the material will shear flow along the same direction in the plastic flow plane. At this moment, the rake angle of the scratching tool, the shear angle, the friction angle, and the shear flow stress of the material will be a constant value. Therefore, the three-dimensional force vectors \( \overrightarrow{F_{Bx}} \), \( \overrightarrow{F_{By}} \), and \( \overrightarrow{F_{Bz}} \) in the scratching coordinates XYZ can be converted into the two-directional force vectors \( \overrightarrow{F_{Bx1}} \) and \( \overrightarrow{F_{By1}} \) in the plastic flow coordinates X1Y1. Namely, the resultant force can be expressed by the following equation:

$$ {F}_B=\sqrt{{\left|\overrightarrow{F_{Bx}}\right|}^2+{\left|\overrightarrow{F_{By}}\right|}^2+{\left|\overrightarrow{F_{Bz}}\right|}^2}=\sqrt{{\left|\overrightarrow{F_{Bx1}}\right|}^2+{\left|\overrightarrow{F_{By1}}\right|}^2} $$
(14)
$$ {F}_C=\sqrt{{\left|\overrightarrow{F_{Cx}}\right|}^2+{\left|\overrightarrow{F_{Cy}}\right|}^2+{\left|\overrightarrow{F_{Cz}}\right|}^2}=\sqrt{{\left|\overrightarrow{F_{Cx1}}\right|}^2+{\left|\overrightarrow{F_{Cy1}}\right|}^2} $$
(15)
Fig. 3
figure 3

Distribution of scratching force

Full size image

It can be seen from Fig. 3 that the directions of \( \overrightarrow{F_{Bx}} \)is the same as \( \overrightarrow{F_{Bx1}} \). Namely, \( \overrightarrow{F_{By1}} \) is the resultant force of \( \overrightarrow{F_{Bx}} \) and \( \overrightarrow{F_{Bz}} \) in the base plane. In addition, the direction of \( \overrightarrow{F_{By1}} \) is the same as \( \overrightarrow{L_{B0}} \) in the base plane. Therefore, the angles φB and φc can be expressed as:

$$ \tan {\varphi}_B=\frac{\mid \overrightarrow{F_{Bx}}\mid }{\mid \overrightarrow{F_{Bz}}\mid } $$
(16)
$$ \tan {\varphi}_C=\frac{\mid \overrightarrow{F_{Cx}}\mid }{\mid \overrightarrow{F_{Cz}}\mid } $$
(17)

Then, the three-dimensional force balance equation of the scratching tool can be expressed as follows:

$$ \left\{\begin{array}{c}\sum {F}_X=0\Rightarrow \int {p}_{OAB}d{A}_{OAB}\overrightarrow{n_B}\cdotp \overrightarrow{x}+\int {\tau}_{OAB}d{A}_{OAB}\overrightarrow{L_B}\cdotp \overrightarrow{x}+\int {p}_{OAC}d{A}_{OAC}\overrightarrow{n_C}\cdotp \overrightarrow{x}+\int {\tau}_{OAC}d{A}_{OAC}\overrightarrow{L_C}\cdotp \overrightarrow{x}-{F}_x=0\\ {}\sum {F}_Y=0\Rightarrow \int {\mathrm{p}}_{OAB}d{A}_{OAB}\overrightarrow{n_B}\cdotp \overrightarrow{y}+\int {\tau}_{OAB}d{A}_{OAB}\overrightarrow{L_B}\cdotp \overrightarrow{y}+\int {p}_{OAC}d{A}_{OAC}\overrightarrow{n_C}\cdotp \overrightarrow{y}+\int {\tau}_{OAC}d{A}_{OAC}\overrightarrow{L_C}\cdotp \overrightarrow{y}-{F}_y=0\\ {}\sum {F}_Z=0\Rightarrow \int {p}_{OAB}d{A}_{OAB}\overrightarrow{n_B}\cdotp \overrightarrow{z}+\int {\tau}_{OAB}d{A}_{OAB}\overrightarrow{L_B}\cdotp \overrightarrow{z}+\int {p}_{OAC}d{A}_{OAC}\overrightarrow{n_C}\cdotp \overrightarrow{z}+\int {\tau}_{OAC}d{A}_{OAC}\overrightarrow{L_C}\cdotp \overrightarrow{z}-{F}_z=0\end{array}\right. $$
(18)

where \( \overrightarrow{x} \), \( \overrightarrow{y} \), and \( \overrightarrow{z} \) are the unit vectors along the X, Y, and Z axes, respectively. AOAB and AOAC are the contact surfaces OAB and OAC, respectively. AOAB and AOAC can be expressed as:

$$ \left\{\begin{array}{c}{A}_{OAB}=\sqrt{A_1\left({A}_1-| OA|\right)\left({A}_1-| OB|\right)\left({A}_1-| AB|\right)}\\ {}{A}_{OAC}=\sqrt{A_2\left({A}_2-| OA|\right)\left({A}_2-| OC|\right)\left({A}_2-| AC|\right)}\end{array}\right. $$
(19)

where

$$ {\displaystyle \begin{array}{c}{S}_1=\frac{1}{2}\Big(\mid OA\mid +\mid OB\mid +\mid AB\mid \\ {}{S}_2=\frac{1}{2}\left(| OA|+| OC|+| AC|\right)\end{array}}\Big) $$

In this paper, the normal contact pressure and the average friction coefficient is assumed to be uniform on the contact surface. Then, Eq. (18) can be simplified as:

$$ \left\{\begin{array}{c}{F}_{Bx}={F}_{Bz}\tan {\varphi}_B=-{p}_B{A}_{OAB}{n}_{Bx}-{p}_B{\mu}_B\int {L}_{B,x}d{A}_{OAB}\\ {}{F}_{By}=-{p}_B{A}_{OAB}{n}_{By}+{p}_B{\mu}_B\int {L}_{B,y}d{A}_{OAB}\\ {}{F}_{Bz}={p}_B{A}_{OAB}{n}_{Bz}+{p}_B{\mu}_B\int {L}_{B,z}d{A}_{OAB}\end{array}\right. $$
(20)
$$ \left\{\begin{array}{c}{F}_{Cx}={F}_{Cz}\tan {\varphi}_C={p}_C{A}_{OAC}{n}_{Cx}+{p}_C{\mu}_C\int {L}_{C,x}d{A}_{OAC}\\ {}{F}_{Cy}=-{p}_C{A}_{OAC}{n}_{Cy}+{p}_C{\mu}_C\int {L}_{C,y}d{A}_{OAC}\\ {}{F}_{Cz}={p}_C{A}_{OAC}{n}_{Cz}+{p}_C{\mu}_C\int {L}_{C,z}d{A}_{OAC}\end{array}\right. $$
(21)

where \( \overrightarrow{F_{Bx}} \), \( \overrightarrow{F_{By}} \), \( \overrightarrow{F_{Bz}} \), \( \overrightarrow{F_{Cx}} \), \( \overrightarrow{F_{Cx}} \), and \( \overrightarrow{F_{Cx}} \) are the force components of the contact surface OAB and OAC, respectively. pB, pC, μB, and μC are the normal contact pressure and the average friction coefficient of the contact surface OAB and OAC, respectively.

By simplifying Eq. (20) and Eq. (21), φB and φC can be expressed as:

$$ {\displaystyle \begin{array}{c}\tan {\varphi}_B=\frac{-{p}_B{A}_{OAB}{n}_{bx}-{p}_B{\mu}_B\int {L}_{B,x}d{A}_{OAB}}{p_B{A}_{OAB}{\mathrm{n}}_{bz}+{p}_B{\mu}_B\int {L}_{B,z}d{A}_{OAB}}=\frac{-{n}_{Bx}-{\mu}_s{m}_B\sin {\varphi}_B}{n_{Bz}-{\mu}_s{m}_B\cos {\varphi}_B}\\ {}\Rightarrow {\varphi}_B= arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\end{array}} $$
(22)
$$ {\displaystyle \begin{array}{c}\tan {\varphi}_C=\frac{p_C{A}_{OAC}{n}_{cx}+{p}_C{\mu}_C\int {L}_{C,x}d{A}_{OAC}}{p_C{A}_{OAC}{n}_{cz}+{p}_C{\mu}_C\int {L}_{C,z}d{A}_{OAC}}=\frac{n_{Cx}-{\mu}_C{m}_C\sin {\varphi}_C}{n_{Cz}-{\mu}_C{m}_C\cos {\varphi}_{\mathrm{C}}}\\ {}\Rightarrow {\varphi}_C= arc\tan \left(\frac{n_{Cx}}{n_{Cz}}\right)\end{array}} $$
(23)

Therefore, the unit PFV \( \overrightarrow{L_B} \) and \( \overrightarrow{L_C} \) can be calculated as Eq. (24) and Eq. (25).

$$ {\displaystyle \begin{array}{c}\overrightarrow{L_B}=\left({L}_{Bx},{L}_{By},{L}_{Bz}\right)\\ {}=\left({m}_B\sin \left( arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\right),\frac{-{n}_{Bx}{m}_B\sin {\varphi}_B+{n}_{Bz}{m}_B\cos {\varphi}_B}{n_{By}},-{m}_B\cos \left( arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\right)\right)\end{array}} $$
(24)
$$ {\displaystyle \begin{array}{c}\overrightarrow{L_C}=\left({L}_{Cx},{L}_{Cy},{L}_{Cz}\right)\\ {}=\left(-{m}_C\sin \left( arc\tan \left(\frac{n_{Cx}}{n_{Cz}}\right)\right),\frac{n_{Cx}{m}_C\sin {\varphi}_B+{n}_{Cz}m\cos {\varphi}_C}{n_{Cy}},-{m}_C\cos \left( arc\tan \left(\frac{n_{Cx}}{n_{Cz}}\right)\right)\right)\end{array}} $$
(25)

2.2 The working negative rake angle of scratching tool

Based on the theoretical model of the unit PFV of the contact surface, the working negative rake angle of the scratching tool can be further solved in the plastic flow plane. According to the definition of the rake angle of cutting tool, the complementary angle of the angle between the unit PFV and the scratching direction in the plastic flow plane equal to the working negative rake angle of the scratching tool. Then, the absolute value γB0 and γC0 of the working negative rake angle corresponding to the contact surface OAB and OAC of the scratching tool can be expressed as:

$$ {\gamma}_{B0}=\frac{\pi }{2}- arc\cos \left(\frac{\overrightarrow{L_B}\cdotp \overrightarrow{y}}{\mid \overrightarrow{L_B}\mid \cdotp \mid \overrightarrow{y}\mid}\right)=\frac{\pi }{2}- arc\cos \left(\frac{-{n}_{Bx}{m}_B\sin {\varphi}_B+{n}_{Bz}{m}_B\cos {\varphi}_B}{n_{By}}\right) $$
(26)
$$ {\gamma}_{C0}=\frac{\pi }{2}- arc\cos \left(\frac{\overrightarrow{L_C}\cdotp \overrightarrow{y}}{\mid \overrightarrow{L_C}\mid \cdotp \mid \overrightarrow{y}\mid}\right)=\frac{\pi }{2}- arc\cos \left(\frac{n_{Cx}{m}_C\sin {\varphi}_B+{n}_{Cz}m\cos {\varphi}_C}{n_{Cy}}\right) $$
(27)

2.3 The chip flow angle of scratching tool

$$ \overrightarrow{AB}=\left(\begin{array}{c}\frac{h_B\tan \left(\frac{\pi }{2}-{\theta}_B\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e},\frac{-{h}_B\left(\tan \left(\frac{\pi }{2}-{\theta}_r\right)\cos {\theta}_e+\sin {\theta}_e\right)}{\cos {\theta}_e-\tan \left(\frac{\pi }{2}-{\theta}_r\right)\sin {\theta}_e}\\ {}-{h}_0\tan \left(\frac{\pi }{2}-{\theta}_e\right),{h}_B-{h}_0\end{array}\right) $$
(28)

Traditionally, the CFA is defined as the angle between the flow out direction of the chip and the normal direction of the main cutting edge. The main cutting edge of the contact surface OAB is the equivalent cutting edge \( \overrightarrow{AB} \) in mechanical scratching, and the \( \overrightarrow{AB} \) corresponding to the two edges OA and OB. As shown in Fig. 2c, regardless of the material accumulation before the main scratching edge OA, the equivalent cutting edge \( \overrightarrow{AB} \) can be solved by Eq. (26). Then, the CFA ∠AD0M of the contact surface OAB is equal to the complementary angle of \( \overrightarrow{L_B} \) and \( \overrightarrow{AB} \). The CFA ∠AD0M can be represented by θCFA and expressed as Eq. (27).

$$ {\theta}_{CFA}=\frac{\pi }{2}- arc\cos \left(\frac{\overrightarrow{L_B}\cdotp \overrightarrow{AB}}{\mid \overrightarrow{L_B}\mid \cdotp \mid \overrightarrow{AB}\mid}\right) $$
(29)

Similarly, the CFA of the contact surface OAC can be solved based on the vector \( \overrightarrow{L_C} \) and \( \overrightarrow{AC} \).

Based on the theoretical model above, it is clear that the unit PFV is determined by the normal vector of the contact surface, the working negative rake angle of scratching tool is determined by the unit PFV. Therefore, the unit PFV and the working negative rake angle are both determined by the normal vector of the contact surface. However, the CFA is not only related to the normal vector of the contact surface, but also the equivalent cutting edge of the scratching tool.

3 Mechanical scratching experiment

3.1 Experimental setup

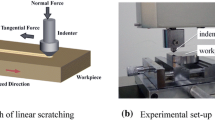
In order to verify the theoretical model of the unit PFV and the working negative rake angle of the scratching tool, the mechanical scratching experiments were carried out. As shown in Fig. 4a, an ultra-precision, vertical, computerized numerical control (CNC), scratching machine (GP100) was utilized for the experiments. The accurate precision tool setting of laser diffraction could be achieved by using HE-NE laser diffractometer and RZ-H200 area array CCD camera [35]. The SIGMA KOKI angle fine-tuning rotary turret made in Japan was used to clamp and rotate tools. The tool rotation angle deviation could be controlled at ± 5′ to ensure the accuracy of the tool rotation angle. The diamond wedge scratching tool (scratching tool) was used in the scratching experiments as shown in Fig. 4b. The geometric parameters of the scratching tool are the wedge angle = 85°, B side angle = 47.5°, relief angle = 35°, edge radius = 215.6nm, and the length of main edge = 2.65mm. And the mechanical parameters of the scratching tool are shown in Table 1.

Fig. 4
figure 4

Experimental setup: a scratching machine, GP100, and b diamond wedge scratching tool

Full size image
Table 1 Mechanical parameters of the scratching tool
Full size table

3.2 Experimental program

According to the theoretical model of the unit PFV and the working negative rake angle, it can be seen that the working negative rake angle is determined by the unit PFV. Therefore, the working negative rake angle theoretical model can be verified by proving the theoretical model of the unit PFV. The elevation angle of the scratching tool, speed, and material is used as experimental variables base on the theoretical model of unit PFV. In order to clearly observe the material plastic flow line of the formed groove surface, the large scratching is used in the scratching experiment. The scratching materials are pure copper-T2, pure aluminum-AL1060, and pure zinc-Zn, and the material properties are shown in Table 2. And the initial scratching experiment parameters are set as follows: the elevation angle of the scratching tool is 10°, the speed is 1mm/s, and the material is T2. The mechanical scratching condition for verifying the theoretical model of unit PFV is shown in Table 3.

Table 2 Material parameters of T2 and AL1060
Full size table
Table 3 Mechanical scratching condition
Full size table

3.3 Plastic flow angle in the XOY plane—φ xy

The material plastic flow line will leave on the machined V-groove surface when the scratching tool scratching along the metal material. Because of the unit PFV on the V-groove surface is a space vector, it cannot be directly obtained by the experiments. However, the projection of the unit PFV in the XOY plane (vertical view plan) can be obtained by the experiments. Figure 5 shows the plane decomposition of \( \overrightarrow{L_{Bxy}} \), which is the projection of the unit PFV \( \overrightarrow{L_B} \) in the XOY plane. And the angle between \( \overrightarrow{L_{Bxy}} \) and \( \overrightarrow{L_{By}} \) is defined as the plastic flow angle in the XOY plane—φxy (PFA). Based on Eq. (24), the theoretical expression of the PFA φxy can be calculated according to Eq. (30). Since the projection of the material plastic flow line can be obtained by the SEM detection experiments, and the PFA φxy can further be obtained. Therefore, the PFA φxy will be used to verify the theoretical model.

$$ {\varphi}_{xy}=a\tan \left(\frac{\mid {L}_{Bx}\mid }{\mid {L}_{By}\mid}\right)=a\tan \left(\frac{\mid {n}_{By}\sin \left( arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\right)\mid }{\mid -{n}_{Bx}{m}_B\sin \left( arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\right)+{n}_{Bz}{m}_B\cos \left( arc\tan \left(-\frac{n_{Bx}}{n_{Bz}}\right)\right)\mid}\right) $$
(30)
Fig. 5
figure 5

Decomposition of the unit plastic flow vector \( \overrightarrow{L_B} \) of XOY plane

Full size image

Figure 6a is the vertical view of the machined groove inspected by the EVO MA 25/LS scanning electron microscope SEM. Figure 6b is the vertical view of the single-sided machined groove extracted by magnification. It can be seen that the surface of the machined groove has a stagnant region and a plastic flow region, and there is a clear boundary phenomenon between the two regions [36,37,38]. Figure 6c is the further enlargement of the material plastic flow region near the boundary line between the two regions. It can be seen that the material is almost stagnant and there is no obvious material plastic flow line in the stagnant region, while obvious material plastic flow line can be observed in the plastic flow region. It is observed that the change law of the material plastic flow line is that the material plastic flow line near the boundary line of the two regions is slightly curved, but the material plastic flow line extending into the plastic flow region is approximately straight and parallel to each other. The experimental phenomenon is feasible to the basic assumption in mechanical scratching. In order to obtain accurate experimental value of the PFA, 50 material plastic flow lines are randomly selected in the plastic flow region on the machined groove to measure the direction angle, and the average value is taken as the PFA experimental value.

Fig. 6
figure 6

Vertical view of machined groove and material plastic flow line: a vertical view of machined groove, b vertical view of single-sided machined groove, c local enlargement of material plastic flow line

Full size image

4 Results and discussion

4.1 The influence of multi-scratching factors on the plastic flow angle

Based on the mechanical scratching experiments and the unit PFV theoretical model, the PFA are investigated under the influence of the elevation angle of the scratching tool, speed, and material. Based on the vertical view of machined V-groove, the material plastic flow line and the experimental values of the PFA corresponding to the multi-scratching factors were observed by the SEM in Fig. 7. The theoretical PFA and its deviation corresponding to the multi-scratching factors are shown in Table 4. And the change curves of the theoretical PFA and the experimental PFA are shown in Fig. 8.

Fig. 7
figure 7

Plastic flow angle under the influence of multi-scratching factors: a–e elevation angle of the scratching tool is 5°, 10°, 15°, 20°, and 25°, respectively; f–h speed is 1 mm/s, 10 mm/s, and 100 mm/s, respectively; and i–k material is T2, Al1060, and Zn, respectively

Full size image
Table 4 The PFA and its deviation in the influence of multi-scratching factors
Full size table
Fig. 8
figure 8

Change curves of the theoretical PFA and experimental PFA corresponding to the multi-scratching factors: a elevation angle of the scratching tool, b speed, and c material

Full size image

As shown in Fig. 7, the material plastic flow line on the machined V-groove surface are all approximately straight line and parallel to each other because of the multi-scratching factors. According to Fig. 7a–d, it can be seen that the experimental PFA increases from 33.032 to 47.203° when the elevation angle of the scratching tool increases from 5 to 25°. Base on Fig. 7f–h, it can be seen that when the speed increases from 1 to 100 mm/s, the experimental PFA are 41.335°, 41.029° and 42.505°, respectively. Namely, the experimental PFA is approximately equal and no significant change occurs. According to Fig. 7i–k, it is clear that the experimental PFA of T2 and AL1060 material are 41.335° and 41.772°, respectively. But the experimental PFA of the pure Zn material is 66.633°, which is much larger than the experimental PFA of the T2 and AL1060 material. The experimental results show that the experimental PFA is related to elevation angle of the scratching tool and independent on the scratching speed and material. In addition, it also shows that the unit PFV theoretical model is only applicable to the plastic metal material with well ductility and the stronger adhesion characteristics (such as AL1060 and T2) but not suitable for the brittle metallic material (pure Zn is brittle at room temperature).

Through Table 4 and Fig. 9, it is found that the evolution law of the experimental PFA is consistent with the theoretical PFA because of the multi-scratching factors. Namely, the evolution law of the PFA is that the larger the elevation angle is, the larger the PFA will be; and the speed and material have little effect on the PFA. In addition, the maximum deviation of PFA is 6.687°, which validates the unit PFV theoretical model.

Fig. 9
figure 9

Three-dimensional topography and section profile of the machined V-groove: a map of machined V-groove, b three-dimensional topography of the machined V-groove, and c section profile of the machined V-groove

Full size image

According to the investigating of the PFA deviation, it can be seen that the deviation considered from two aspects. The one is the macro aspect. The deviation may be caused by the position error of the scratching tool and the measurement error from the SEM experiments. The other is the micro aspect. A stagnant region and a plastic flow region are generated on the machined V-groove surface in mechanical scratching. And there is an obvious mutual traction effect between the material of the stagnant region and the plastic flow region. Namely, the material plastic flow line of the plastic flow region near the boundary is constricted by the material of the stagnant region, and the material flow rate lags behind the overall material flow rate. Therefore, the material plastic flow line of the plastic flow region near the boundary will be deflected and slightly, which leads to the experimental PFA being generally smaller than the theoretical value. Meanwhile, according to the PFA deviation because of the multi-scratching factors, it is clear that the experimental values of the PFA are all smaller than the theoretical value. Therefore, it can be considered that the reason for the PFA deviation mainly comes from the material stagnant phenomenon in mechanical scratching.

4.2 The influence of multi-scratching factors on the chip flow angle

In order to further study the influence of multi-scratching factors on the chip flow angle (CFA) of the contact surface OAB, the lateral ridge heights hB corresponding to multi-scratching factors are measured by 3D laser confocal microscope LEXT OLS4000 as shown in Table 5. Based on Eq. (28), Eq. (29), and the hB, the CFAs corresponding to the multi-scratching factors can be obtained in Table 5. And the change curves of the CFA are shown in Fig. 10.

Table 5 The chip flow angle corresponding to the multi-scratching factors
Full size table
Fig. 10
figure 10

Change curves of the chip flow angle under the influence of multi-scratching factors: a elevation angle of the scratching tool, b speed, and c material

Full size image

By comparing the lateral ridge heights hB and the CFA corresponding to the different elevation angles of the scratching tool, it can be seen that when the elevation angle θe increasing from 5 to 25°, the contact length between the tool-workpiece and hB both become larger; namely, the spatial position of the equivalent cutting edge change, which will finally cause the CFA to rapidly decrease from 85.315 to 71.597°. Comparing the hB and the CFA corresponding to the different speed, it can be seen that as the scratching speed decreases from 100 to 1 mm/s, the contact length between the tool-workpiece and hB become larger; namely, the spatial position of the equivalent cutting edge change, which will finally induce the CFA to decrease from 80.367 to 79.345°. Comparing the hB and the CFA corresponding to T2 and AL1060 material, it can be seen that compared with the T2 material, the plastic adhesion of AL1060 material is better, which causes of the stronger adhesion and friction characteristics between the contact surface, then the contact length between the tool-workpiece and hB becomes larger, and the spatial position of the equivalent cutting edge changes, which finally induces the CFA to become smaller. The above research results indicate that the elevation angle, speed, and material have direct impact on the CFA. This result is basically consistent with the conclusion obtained by Stabler and Morcos et al. [7, 13,14,15]. Comparing the degree of influence of the above multi-scratching factors on the CFA, it can be seen that the elevation angle has the greatest influence on the CFA, followed by the speed and material.

According to the research on the relationship among the multi-scratching factors, the unit PFV and the CFA, it can be seen that compared with the CFA, the PFV can reflect the material plastic flow characteristics of the contact surface more directly in the same mechanical scratching condition. Namely, the PFV can reflect the plastic flow direction of the chip on the contact surface. On the basis of the unit PFV, the CFA pays more attention to reflecting the relationship between the multi-scratching factors and the equivalent cutting edge. The change of multi-scratching factors will cause the change of the V-groove shape and lateral contact height hB, which will indirectly cause a change of the equivalent cutting edge. Therefore, it becomes complicated to characterize the material plastic flow direction by using the CFA in mechanical scratching.

5 Conclusion

In order to investigate the material plastic flow characteristics of metal in mechanical scratching, the unit plastic flow vector (PFV), the working negative rake angle of the scratching tool, and the chip flow angle (CFA) theoretical model are established. And the evolution law of chip flow angle (PFA) and CFA under the influence of the multi-scratching factors is also studied through a combination of theory and experiment. The relevant results are summarized as follows:

  1. 1)

    Based on the three-dimensional force balance equation and the vector method, the unit PFV, the working negative rake angle, and the CFA theoretical model are established in this paper. The theoretical models show that the unit PFV and the working negative rake angle are both determined by the normal vector of the contact surface. However, the CFA is not only related to the normal vector of the contact surface but also to the equivalent cutting edge of the scratching tool.

  2. 2)

    Under the influence of the multi-scratching factors, the evolution law of the unit PFV was investigated by the theoretical model and the mechanical scratching experiments. The results show that the evolution law of the experimental PFA is consistent with the theoretical value under the influence of the multi-scratching factors. Namely, the evolution law of the PFA is that the larger the elevation angle is, the larger the PFA will be; the speed and material have little effect on the PFA. In addition, the maximum deviation of the PFA is 6.687°, which validates the unit PFV theoretical model.

  3. 3)

    Under the influence of the multi-scratching factors, the evolution law of the CFA was investigated by the theoretical model and the mechanical scratching experiments. The results show that the larger the elevation angle is, the lower the speed is, and the better the plastic adhesion of the material is, and the CFA will become smaller. What’s more, the elevation angle has the greatest influence on the CFA, following by the speed and material. By comparing the unit PFV and CFA corresponding to the multi-scratching factors, it is found that the PFV can directly reflect the material plastic flow direction on the contact surface. However, the CFA pays more attention to reflecting the relationship between the multi-scratching factors and the equivalent cutting edge.

The research content of this paper lays a theoretical and experimental basis for solving the material plastic flow characteristics of the contact surface of the regular triangular pyramid scratching tool (such as the Berkovich indenter), the irregular triangular pyramid cutting tool (the diamond wedge scratching tool), and the double-edged cutting tool in metal cutting and mechanical scratching.