1 Introduction

Nowadays, particular characteristics of advanced high-strength steel (AHSS) alloys due to their high strength and low weight have motivated engineering to apply them in different apparatuses. In the past decade, these interests have been rapidly grown up in such a way that a large number of researchers have investigated different mechanical aspects of these alloys. Recently, Martínez-Palmeth et al. [1] presented an experimental and numerical analysis of the formability of high-strength H240LA steel sheets. Also, Zhang et al. [2] introduced an inverse identification of the post-necking work hardening behavior of thick HSS through full-field strain measurements during diffuse necking. Experimental response of high-strength steels to localized blast loading is given in [3]. He et al. [4] expressed a rate and temperature-dependent unified creep-plasticity model. They reported the temperature function, drag stress evolution function, and the adjustment equations to be determined. On contrary, one of the disadvantages of these alloys is its high springback which is arisen from the Bauschinger effect of hardening mechanisms during forward loading and reverse unloading processes [5]. Some general-related considerations around the Bauschinger effect can be found in the work done by [6] as well as the references inside it. Today, the warm or hot forming processes are used to reduce the springback phenomenon in these alloys. The hot forming process is used for molds with different shapes [7]. In the following, we will have a look at the hot forming processes for U-shaped deep draw bending and hot stamping. In the field of the U-shaped deep drawing process, a lot of researches have been done in recent years [8]. On the other hand, Mori et al. [9] developed a warm and hot stamping process of ultra-high tensile strength steel sheets by using a resistance heating to improve springback and formability. Also, the effects of the heating temperature on the springback and formability of ultra-high tensile strength steel sheets were examined. The results showed that the springback of the high tensile strength steel sheets eliminate by heating the sheet.

Yanagimoto et al. [10] investigated the springback of high-strength steel after hot and warm sheet forming to evaluate the effect of forming temperature on the amount of springback and showed that the springback is markedly reduced when the forming temperature is higher than 750 K. Moreover, Naderi et al. [11] studied the hot stamping of 22MnB5 boron steel sheets by using a water or nitrogen cooling media. Also, the evolution of the temperature and force were simulated during the hot stamping process by using a coupled thermomechanical FEM program. They concluded that die cooling media has a significant effect on the material properties after hot stamping. Xing et al. [12] proposed a material model based on experimental data of mechanics and thermal physical properties, and used it for hot stamping condition of quenchable steel and performed the numerical simulation of hot forming, quenching, and springback with the ABAQUS software. The obtained results showed that the springback of hot stamping parts increases when the blank holder force decreases; it increases when the clearance between the punch and dies increases and when the die radius increases. Liu et al. [13] investigated the flow behavior of the 22MnB5 AHSS through hot tensile tests. They build a finite element model of the hot stamping process for the shaped part by the ABAQUS/Explicit to investigate the influence of blank holder force and die gap on the hot forming process. Obtained results showed that large blank holder force reduces the amount of springback, and die gap has a considerable influence on the distribution of temperature on the side wall. Worswick et al. [14] carried out both experimental and numerical considerations for hot stamped axial crush members with a non-tailored and three-tailored configurations as one-half of the rail was quenched while the other formed half was heated during several temperatures. Liu et al. [15] performed several tensile tests to examine the flow stress of the material HSS 22MnB5 at different strains, strain rates, and temperatures. They carried out material modeling and FE numerical simulations to investigate the effect of the processing parameters on the hot forming process and they concluded that springback is mainly caused by different cooling rates, and the nonhomogeneous shrink of material during the hot forming process and the creep strain is the main factor influencing the amount of the springback. Lee et al. [16] performed the U-draw/bending experiments of DP and TRIP steel sheets and presented particular simulations to investigate the characteristics of springback in sheet metals and used the finite element method for the simulation of springback. The obtained results showed that the springback predictions were greatly influenced by the choice of the hardening model but slightly affected by the choice of the yield criterion.

In the case of the semi-analytical model to predict springback of metallic parts, several studies have been done in recent years [17]. In addition, Heller and Kleiner [18] developed a mathematical model to make a fast semi-analytical simulation of the air bending process of thin and thick sheets. The mathematical description of the shift of individual fibers and the changes of thickness has been considered. This novel model can be used in practical cases and where the numerical method cannot be used. Lee et al. [19] introduced a simplified hybrid technique to anticipate springback in a 2D draw bend test considering the bending effects of membrane. The model can accommodate general anisotropic yield functions along with nonlinear isotropic-kinematic hardening under the plane strain condition. Also, for validation purposes, the results were compared with experiments. Panthi and Ramakrishnan [20] proposed a phenomenological model to explore an arc bending process by means of the deformation energy approach and compared with experimental and FE results. Le Quilliec et al. [21] presented a semi-analytical model for large strain analysis of sheet metal forming under plane strain bending and tension. In that work, the loading is assumed to be distributed homogeneously in the length direction. The semi-analytical model is applied to standard test cases and then compared with full-scale simulations. Also, the springback behavior of 3D tubes was proposed by [22] by approximating its deformation through a theoretical discretization for stress distributions and residual deformations. Then, a new method was applied for springback prediction in a typical 3D tube by demonstrating a remarkable agreement between theoretical and experimental results.

In previous articles, the authors investigated analytically the effect of hardening parameters, mechanical condition, pre-strain, and variable unloading modulus on springback in U-draw bending process of DP780 steel [23,24,25].

In this paper, a novel finite element model is presented to predict springback behavior of DP780 steel sheets during and after the hot stamping process based on a temperature-dependent Chaboche hardening model and Yld2000-2d yield function. The ABAQUS software is used to simulate the forming process stages via the forward Euler explicit integration scheme and plane strain condition. Furthermore, UMAT and VUMAT user subroutines are used in order to define the material behavior. Finally, the hot stamping process of DP780 steel is simulated based on these models and algorithms.

2 Theory

2.1 Temperature-dependent Chaboche hardening model

In the case of a combined isotropic-kinematic hardening model, the yield function can be expressed with:

$$ F=\overline{\sigma}\left(\boldsymbol{\sigma} -\boldsymbol{X}\right)-R-{\sigma}_y=0 $$
(1)

where σ is the Cauchy stress tensor, σy is the initial yield stress, and X is the back stress tensor which indicates the yield surface transition. Also, R is the size of yield surface which develops through isotropic hardening and \( \overline{\sigma} \) is the equivalent stress.

Back stress vector can be composed of n components, which each part changes with its own law as follows [26]:

$$ \boldsymbol{X}={\sum}_{i=1}^n{\boldsymbol{X}}_i $$
(2)

In the Chaboche hardening model, each part of back stress tensor develops according to the Armstrong and Frederick law [27] as follow:

$$ d{\boldsymbol{X}}_i={c}_id{\boldsymbol{\varepsilon}}^p-{\gamma}_i{\boldsymbol{X}}_id{\overline{\upvarepsilon}}^{\mathrm{p}} $$
(3)

where dεp is the plastic strain increment, \( d{\overline{\varepsilon}}^p \) is the equivalent plastic strain increment, and the parameters ci and γi are the material constants. The first part in Eq. (3) is suggested by Prager [28], which represents linear kinematic hardening. The second phrase in Eq. (3) represents a nonlinear revolution which develops through isotropic hardening for a non-proportional strain. With these statements, the Chaboche hardening model is able to capture the Bauschinger effect and transient behavior during yield process in large strains. Since this model is not able to model permanent softening, the second phrase in one part of back stress tensor should be eliminated. Several isotropic-kinematic hardening rules are compared with the Armstrong-Frederick and Chaboche hardening criteria by Karvan and Farahani [29]. The framework of hardening rules was constructed on the basis of viscoplasticity constitutive equation to account for the effects of stress rate and time dependency.

The Chaboche hardening model uses a saturated function for isotropic hardening as follows:

$$ dR=b\left({R}_s-R\right)d{\overline{\varepsilon}}^p $$
(4)

where R and Rs are the current and final size of the yield surface and b is the material constant. The size of the yield surface increases with equivalent plastic strain and saturates to Rs value.

The constants of the Chaboche model can be obtained with tension-compression tests. In order to obtain the constants during uniaxial loading, the following equations obtained from Eq. (3) integrating will be used in one direction:

$$ X=\frac{3}{2}\upsilon \frac{c}{\gamma }+\left({X}_0-\frac{3}{2}\upsilon \frac{c}{\gamma}\right){e}^{-\gamma \left({\overline{\varepsilon}}^p-{\overline{\varepsilon}}_0^p\right)} $$
(5)

where υ =  ± 1 represents the flow direction, \( {\overline{\varepsilon}}_0^p \) and X0 represent the amount of pre-strain and initial reverse flow stress, respectively.

Also, the isotropic hardening can be represented by the following equation:

$$ R={R}_o+{R}_s\left(1-{e}^{-b{\overline{\varepsilon}}^p}\right) $$
(6)

where Ro is the yield stress and Ro + Rs is the saturated stress value at large strains.

The temperature affects the Chaboche model in two cases, on the size of yield surface (isotropic hardening) and back stress change (non-isotropic hardening). The evolution of size and location of yield surface with respect to temperature (T) can be expressed as [30]:

$$ d{\mathbf{X}}_i={c}_i(T)d{\varepsilon}^p-{\gamma}_i(T){X}_id{\overline{\varepsilon}}^p+\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{X}_i dT $$
(7)
$$ dR=b(T)\left({R}_s(T)-R\right)d{\overline{\varepsilon}}^p $$
(8)

In comparison with Eq. (3), there is a temperature-dependent back stress in Eq. (7) in order to obtain an independent temperature micro-structure hardening model. Also, the parameters Rs, Ro, C1, C2, and γ1 can be described based on a linear function of temperature as follows:

$$ {\xi}_i={k}_{\xi_i}+{m}_{\xi_i}\left(T-{T}_R\right)\kern1.75em i=1.2.\dots .6 $$
(9)

where ξi(i = 1.2. ….6) is the coefficients Rs, Ro, C1, C2, γ1, b, and TR is the room temperature. The temperature coefficients \( {k}_{\xi_i} \) and \( {m}_{\xi_i} \) for each Chaboche coefficient are listed in Table 1.

Table 1 Material parameters of the temperature-dependent Chaboche model [30]
Full size table

The differences between experimental data and the Chaboche model are shown in Fig. 1.

Fig. 1
figure 1

Comparisons of the experimental data and Chaboche model for tensile and CT tests at each tested temperature for DP780. a 25 °C. b 50 °C. c 75 °C. d 100 °C (adapted from [30])

Full size image

2.2 Barlat’s Yld2000-2d yield function

The non-quadratic anisotropic yield function Yld2000-2d has the following form [31]:

$$ \Phi \left(\sigma, X\right)={\phi}^{\prime }+{\phi}^{{\prime\prime} }-2{\overline{\sigma}}^m=0 $$
(10)

where :

$$ {\phi}^{\prime }={\left|{S}_1^{\prime }-{S}_2^{\prime}\right|}^m\kern0.5em \mathrm{and}\kern0.5em {\phi}^{{\prime\prime} }={\left|2{S}_2^{{\prime\prime} }+{S}_1^{{\prime\prime}}\right|}^m+{\left|2{S}_1^{{\prime\prime} }+{S}_2^{{\prime\prime}}\right|}^m $$
(11)

where S′ and S″ are the linearly transformed stress tensors and the subscripts 1 and 2 are their principal values. The transformations of the Cauchy stress σ into S′ and S″ involve two linear transformations:

$$ {\mathbf{S}}^{\prime }={\mathbf{C}}^{\prime}\mathbf{s}={\mathbf{C}}^{\prime}\mathbf{T}\boldsymbol{\upsigma } ={\mathbf{L}}^{\prime}\boldsymbol{\upsigma} $$
(12a)
$$ {\mathbf{S}}^{{\prime\prime} }={\mathbf{C}}^{{\prime\prime}}\mathbf{s}={\mathbf{C}}^{{\prime\prime} }T\boldsymbol{\upsigma} ={\mathbf{L}}^{{\prime\prime}}\boldsymbol{\upsigma} $$
(12b)

The transformation T calculates the deviatoric stress s and other transformations C′ and C″ induce anisotropy. The products of the two transformations are represented as L′ and L″ which can be expressed in matrix form as below:

$$ \left[\begin{array}{c}{S}_{xx}^{\prime}\\ {}{S}_{yy}^{\prime}\\ {}{S}_{xy}^{\prime}\end{array}\right]=\left[\begin{array}{ccc}{L}_{11}^{\prime }& {L}_{12}^{\prime }& 0\\ {}{L}_{21}^{\prime }& {L}_{22}^{\prime }& 0\\ {}0& 0& {L}_{66}^{\prime}\end{array}\right]\left[\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\sigma}_{xy}\end{array}\right] $$
(13a)
$$ \left[\begin{array}{c}{S}_{xx}^{{\prime\prime}}\\ {}{S}_{yy}^{{\prime\prime}}\\ {}{S}_{xy}^{{\prime\prime}}\end{array}\right]=\left[\begin{array}{ccc}{L}_{11}^{{\prime\prime} }& {L}_{12}^{{\prime\prime} }& 0\\ {}{L}_{21}^{{\prime\prime} }& {L}_{22}^{{\prime\prime} }& 0\\ {}0& 0& {L}_{66}^{{\prime\prime}}\end{array}\right]\left[\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\sigma}_{xy}\end{array}\right] $$
(13b)
$$ \left[\begin{array}{c}{L}_{11}^{\prime}\\ {}{L}_{12}^{\prime}\\ {}{L}_{21}^{\prime}\\ {}{L}_{22}^{\prime}\\ {}{L}_{66}^{\prime}\end{array}\right]=\left[\begin{array}{ccc}2/3& 0& 0\\ {}-1/3& 0& 0\\ {}0& -1/3& 0\\ {}0& 2/3& 0\\ {}0& 0& 1\end{array}\right]\left[\begin{array}{c}{a}_1\\ {}{a}_2\\ {}{a}_7\end{array}\right] $$
(14a)
$$ \left[\begin{array}{c}{L}_{11}^{{\prime\prime}}\\ {}{L}_{12}^{{\prime\prime}}\\ {}{L}_{21}^{{\prime\prime}}\\ {}{L}_{22}^{{\prime\prime}}\\ {}{L}_{66}^{{\prime\prime}}\end{array}\right]=\frac{1}{9}\left[\begin{array}{ccccc}-2& 2& 8& -2& 0\\ {}1& -4& -4& 4& 0\\ {}4& -4& -4& 1& 0\\ {}-2& 8& 2& -2& 0\\ {}0& 0& 0& 0& 9\end{array}\right]\left[\begin{array}{c}{a}_3\\ {}{a}_4\\ {}{a}_5\\ {}{a}_6\\ {}{a}_8\end{array}\right] $$
(14b)

The value of anisotropy coefficients a1–a8 are given in Table 2. For the yield function exponent, m = 6 is recommended for BCC and m = 8 for FCC materials.

Table 2 Parameters of the Yld2000-2d yield criterion
Full size table

2.3 Variable elastic modulus

Elastic modulus can be considered as a function of equivalent plastic strain using the experimental data of Numisheet 2011 with a function proposed by [32] as follows:

$$ E\left({\overline{\varepsilon}}^p\right)={E}_0-\left({E}_0-{E}_a\right)\left(1-{e}^{-\xi {\overline{\varepsilon}}^p}\right) $$
(15)

where Ea, E0, and ξ in the above equation are respectively the saturated Young’s modulus, initial young modulus, and the material parameter as shown in Fig. 2. It can be seen that by increasing the plastic strain, the elastic modulus decreases to reach the finally saturated value (Ea). The parameters E0, Ea, and ξ in Eq. (15) are respectively equal to 198.8 GPa, 167.15 GPa, and 99.55 [33]. Here, we assumed that material elastic modulus is constant and has no change with temperature.

Fig. 2
figure 2

The relation between Young’s modulus and plastic strain during the uniaxial loading

Full size image

3 Forward Euler explicit integration scheme

According to the associated flow rule, we have:

$$ d{\boldsymbol{\upvarepsilon}}^p= d\lambda \frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}} $$
(16)

where dλ is the plastic multiplier. According to the plastic work formulation:

$$ d{w}^p=\left(\boldsymbol{\upsigma} -\mathbf{X}\right):d{\boldsymbol{\upvarepsilon}}^p=\overline{\sigma}d{\overline{\varepsilon}}^p $$
(17)

where \( d{\overline{\varepsilon}}^p \) is the increment of the equivalent plastic strain.

Using the Euler theorem for the homogeneous, the yield function Φ is a homogeneous function of degree m as follows:

$$ \frac{\mathrm{\partial \Phi }}{\partial \sigma }:\left(\boldsymbol{\upsigma} -\mathbf{X}\right)=2m{\overline{\sigma}}^m $$
(18)

The strain increment can be decomposed to the elastic component and plastic component as follows:

$$ d\boldsymbol{\upvarepsilon} ={\mathbf{d}\boldsymbol{\upvarepsilon}}^e+{\mathbf{d}\boldsymbol{\upvarepsilon}}^p $$
(19)

According to the plastic work formulation and the Euler’s theory for the homogenous functions, the equivalent plastic strain increment can be achieved as follows:

$$ d{\overline{\varepsilon}}^p=2m{\overline{\sigma}}^{m-1} d\lambda $$
(20)

According to the Hooke’s law, the Cauchy stress is a proportional elastic strain as follows:

$$ d\boldsymbol{\upsigma} ={\mathbf{C}}^e:d{\boldsymbol{\upvarepsilon}}^e={\mathbf{C}}^e:\left(d\boldsymbol{\upvarepsilon} -d{\boldsymbol{\upvarepsilon}}^p\right) $$
(21)

where Ce is the second-order elasticity tensor. According to the consistency condition during the plastic deformation, the Cauchy stress should stay on the yield surface which leads to the following relation:

$$ d\boldsymbol{\Phi} =\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}:\left(d\boldsymbol{\upsigma} -d\mathbf{X}\right)+\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial {\overline{\varepsilon}}^p}d{\overline{\varepsilon}}^p=0 $$
(22)

Substituting Eqs. (7), (20), and (21) into Eq. (22) and after some manipulation, it can be written as:

$$ \frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:\left({\mathbf{C}}^e:\left(d\boldsymbol{\upvarepsilon} -d{\boldsymbol{\upvarepsilon}}^p\right)-{\sum}_{i=1}^2\left({c}_i(T)d{\boldsymbol{\upvarepsilon}}^p-{\gamma}_i(T){\mathbf{X}}_id{\overline{\varepsilon}}^p+\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{\mathbf{X}}_i dT\right)\right)-2m{\overline{\sigma}}^{m-1}b(T)\left({R}_s(T)-R\right)d{\overline{\varepsilon}}^p=0 $$
(23)

Substituting Eq. (20) in the above equation, it can be re-arranged as follows:

$$ \frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\sigma}}:\left({\mathbf{C}}^e:\left(d\boldsymbol{\upvarepsilon} - d\lambda \frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}\right)-{\sum}_{i=1}^2\left({c}_i(T) d\lambda \frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}-2m{\gamma}_i(T){\mathbf{X}}_i{\overline{\sigma}}^{m-1} d\lambda +\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{\mathbf{X}}_i dT\right)\right)-4{m}^2b(T)\left({R}_s(T)-R\right){\overline{\sigma}}^{2\left(m-1\right)} d\lambda =0 $$
(24)

Therefore, according to the above equation, the plastic multiplier can be defined as follows:

$$ d\lambda =\frac{\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}:\left({\mathbf{C}}^e:d\boldsymbol{\upvarepsilon} -{\sum}_{i=1}^2\left(\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{\mathbf{X}}_i dT\right)\right)}{\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}:\left({\mathbf{C}}^e:\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}+{\sum}_{i=1}^2\left({c}_i(T)\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}-2m{\gamma}_i(T){\mathbf{X}}_i{\overline{\sigma}}^{m-1}\right)\right)+4{m}^2b(T)\left({R}_s(T)-R\right){\overline{\sigma}}^{2\left(m-1\right)}} $$
(25)

Substituting the above equation into Eq. (21) leads to obtain the following equation:

$$ d\boldsymbol{\upsigma} ={\mathbf{C}}^e:\left(d\boldsymbol{\upvarepsilon} -\frac{\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}\left(\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:{\mathbf{C}}^e\right):d\boldsymbol{\upvarepsilon} -\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}\left(\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:{\sum}_{i=1}^2\left(\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{\mathbf{X}}_i dT\right)\right)}{\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:\left({\mathbf{C}}^e:\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}+{\sum}_{i=1}^2\left({c}_i(T)\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}-2m{\gamma}_i(T){\mathbf{X}}_i{\overline{\sigma}}^{m-1}\right)\right)+4{m}^2b(T)\left({R}_s(T)-R\right){\overline{\sigma}}^{2\left(m-1\right)}}\right) $$
(26)

The stress increment can be defined as follows:

$$ d\boldsymbol{\upsigma} ={\mathbf{C}}^{ep}d\boldsymbol{\upvarepsilon} +\frac{\left({\mathbf{C}}^e:\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}\right)\bigotimes \left(\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:{\sum}_{i=1}^2\left(\frac{1}{c_i(T)}\frac{\partial {c}_i(T)}{\partial T}{\mathbf{X}}_i dT\right)\right)}{\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}:\left({\mathbf{C}}^e:\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}+{\sum}_{i=1}^2\left({c}_i(T)\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}-2m{\gamma}_i(T){\mathbf{X}}_i{\overline{\sigma}}^{m-1}\right)\right)+4{m}^2b(T)\left({R}_s(T)-R\right){\overline{\sigma}}^{2\left(m-1\right)}} $$
(27)

where the tangential elastoplastic stiffness matrix can be written as:

$$ {\mathbf{C}}^{ep}={\mathbf{C}}^e-\frac{\left({\mathbf{C}}^e:\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}\right)\bigotimes \left({\mathbf{C}}^e:\frac{\mathbf{\partial \boldsymbol{\Phi}}}{\partial \boldsymbol{\upsigma}}\right)}{\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:{\mathbf{C}}^e:\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}+\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}:{\sum}_{i=1}^2\left({c}_i(T)\frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}}-2m{\gamma}_i(T){\mathbf{X}}_i{\overline{\sigma}}^{m-1}\right)+4{m}^2b(T)\left({R}_s(T)-R\right){\overline{\sigma}}^{2\left(m-1\right)}} $$
(28)

In the case of the plane strain condition, the elastic stiffness matrix can be defined as:

$$ \left[\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\tau}_{xy}\end{array}\right]=\frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\left[\begin{array}{ccc}1-\nu & \nu & 0\\ {}\nu & 1-\nu & 0\\ {}0& 0& \frac{1-2\nu }{2}\end{array}\right]\left[\begin{array}{c}{\varepsilon}_{xx}\\ {}{\varepsilon}_{yy}\\ {}{\gamma}_{xy}\end{array}\right] $$
(29)

Here, a forward Euler explicit integration scheme is applied to calculate the stress and strain increment. The plastic strain and back stress can be updated with:

$$ {\boldsymbol{\upvarepsilon}}^{t+\Delta t}={\boldsymbol{\upvarepsilon}}^t+ d\lambda \frac{\mathrm{\partial \Phi }}{\partial \boldsymbol{\upsigma}} $$
(30)
$$ {{\mathbf{X}}_i}^{t+\Delta t}={{\mathbf{X}}_i}^t+\Delta {\mathbf{X}}_i $$
(31)
$$ {\mathbf{X}}^{t+\Delta t}={\mathbf{X}}^t+\Delta \mathbf{X} $$
(32)

The stress at the end of time increment can be obtained based on the Hook’s law as follows:

$$ {\boldsymbol{\upsigma}}^{t+\Delta t}={\boldsymbol{\upsigma}}^t+{\mathbf{C}}^e\left(d\boldsymbol{\upvarepsilon} -d{\boldsymbol{\upvarepsilon}}^p\right) $$
(33)

4 FE numerical simulation steps

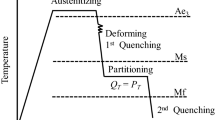
The movement of the punch during the hot stamping process is shown in Fig. 3. It can be seen that there is 4 basic steps which are the following: (a) applying the blank holder force on the blank, (b) move the punch down and forming the blank while the holder and die are stationary, (c) quenching the part which during this process the temperature decreases, (d) springback process which punch moves up and the stresses are released. According to these steps, the U-shaped hot stamping process consist of these computational steps, i.e., (a) applying the blank holder force, (b) numerical simulation of the hot forming process, (c) numerical simulation of the cooling, (d) numerical computation of the springback. Time spans used in each step are as follows: 0.0001 s in applying blank holder force, 0.9 s in hot stamping analysis, 6 s in quenching step, and 3.8 s in analysis of springback [13].

Fig. 3
figure 3

Forming steps and movement of the punch during the hot stamping process (adapted from [13])

Full size image

5 Determination of thermal constants

In order to have accurate thermomechanical FE simulation of the hot stamping process, some thermal constants are needed. The following constants were determined using JMatPro based on chemical composition [34] as follows: thermal expansion coefficient, linear variation from 1.54 × 10−6/K at 25 °C to 1.58 × 10−6/K at 200 °C; heat capacity, linear variation from 0.45 J/gK at 25 °C to 0.52 J/gK at 200 °C; and thermal conductivity, piecewise linear variation of 36.7 W/mK at 25 °C, 36.9 W/mK at 70 °C, 36.8 W/mK at 100 °C, and 36 W/mK at 200 °C. Heat transfer coefficient of metal-air contact is equal to 20 W/m2K and heat transfer coefficient of metal-metal contact is 5 kW/m2K.

6 Contact surfaces

In order to accurate simulation of the hot stamping process, we need to define contact surfaces. Some of these surfaces are in geometrical contact and the others are in thermal contact. There are six contact surfaces as shown in Fig. 4 [13], i.e., (1) geometrical contact surface of die (GCSD), (2) geometrical contact surface of punch (GCSP), (3) geometrical contact surface of blank holder (GCSBH), (4) upper geometrical contact surface of blank (UGCSB), (5) lower geometrical contact surface of blank (LGCSB), (6) thermal contact surface of blank (TCSB). For each contact surface, the approach of heat transfer is different. The corresponding way of heat transfer from blank to tools can be expressed as follows:

$$ {q}_m={h}_{\mathrm{m}m}\left(T-{T}_1\right) $$
(34)

where hmm is the heat convection coefficient of metal-metal contact. T1 is temperature of the tools, T is the temperature of the blank. The equation which describes the heat transfer between the blank to air can be expressed with:

$$ {q}_a={h}_{ma}\left(T-{T}_{\infty}\right) $$
(35)
Fig. 4
figure 4

Definition of geometrical and thermal surfaces and contact pairs

Full size image

In the above equation, hma is the heat convection coefficient between metal and air. Also, T is the blank temperature and T∞ is the temperature of air.

Since the deformations are small in longitudinal direction of the sheet, the position of the points A, B, C, D, E, and F in deformed configuration of the blank in Fig. 4 can be determined in undeformed configuration as shown in Fig. 5. The value of the parameters shown in Fig. 5 are given in the next section.

Fig. 5
figure 5

The position of contact surfaces border in undeformed blank

Full size image

7 Tooling geometry

A schematic view of tools and their dimensions are shown in Fig. 6. As shown in Table 3, dimensions of the original 2D draw-bending test were slightly modified in order to accommodate the thickness of the new material. The springback parameters which should be measured in the future are shown in Fig. 7.

Fig. 6
figure 6

Schematic view of tools and their dimensions for the 2D draw-bending test

Full size image
Table 3 Dimensions for the 2D draw-bending test
Full size table
Fig. 7
figure 7

Schematic of springback measurement method

Full size image

8 Finite element model

The simulation of finite element bending process is performed in the ABAQUS version 2016 software. Due to the symmetry in the model, only half of the model is simulated. In the case of sheet, CPE4RT (4-node plane strain thermally coupled quadrilateral, bilinear displacement and temperature, reduced integration, hourglass control) element and for punch, holder, and die, the analytical rigid bodies are considered. Surface to surface (Explicit) contact is used to define the contact between the tools and blank. Also, penalty tangential behavior is used to define the friction between the tools and blank. The number of elements in the longitudinal direction is equal to 360 and in the thickness direction of the sheet is equal to 4. The sheet holder force is also considered equal to 2.94 kN. The other parameters which used in hot stamping simulation are summarized in Table 4.

Table 4 Parameters used in hot stamping simulation
Full size table

9 Results and discussion

The numerical simulation of the warm U-shaped deep drawing process of DP780 steel sheets was done in the ABAQUS software based on the forward Euler explicit integration scheme. A temperature-dependent Chaboche hardening model and Yld2000-2d yield criterion was used via UMAT and VUMAT user subroutines. In order to validate the present hardening model, a comparison is done with experimental results obtained by [33] in room temperature. The 3D shape of the plate after springback is shown in Fig. 8 a. It can be seen in Fig. 8 b the results obtained based on the Chaboche model have an agreement with experimental data, and the amount of error is represented in Table 5.

Fig. 8
figure 8

a The final shape of the plate after springback at room temperature. b Experimental and predicted springback profiles after U-draw bending at room temperature

Full size image
Table 5 The comparison between the results obtained from the experiment and present FEM method at room temperature
Full size table

Figure 9 shows the distribution of temperature after quenching and before springback for different heating temperatures. It can be seen that the temperature in the area below the holder is the lowest. Also, the temperature in the side wall area has the least variation. The region below the punch has a little deviate from the punch profile, and so the contact between the punch and this region is not quite established. For this reason, no heat is transferred between these two surfaces and the temperature in this region does not change much.

Fig. 9
figure 9

Distribution of temperature for heating temperature (a) Th = 100 °C, (b) Th = 200 °C, (c) Th = 300 °C, (d) Th = 400 °C after quenching and before springback

Full size image

Figure 10 indicates the effect of temperature at the end of heating process on stress distribution of the sheet at the end of quenching process and after springback. It can be seen that with increasing heating temperature, the stress level at the end of quenching process and after springback decreases, as well as the level of stress after the springback decreases.

Fig. 10
figure 10

Distribution of stress for different values of initial hot temperature after quenching (a) Th = 100 °C, (c) Th = 200 °C, (e) Th = 300 °C, (g) Th = 400 °C; and after springback (b) Th = 100 °C, (d) Th = 200 °C, (f) Th = 300 °C, (h) Th = 400 °C

Full size image

Figure 11 reflects the distribution of stress for different heating temperatures after punch stroke and before quenching. By comparing Fig. 10 and Fig. 11, it can be concluded that the level of stress increases after the quenching process.

Fig. 11
figure 11

Distribution of stress for (a) Th = 100 °C, (b) Th = 200 °C, (c) Th = 300 °C, (d) Th = 400 °C before quenching and after punch stroke

Full size image

Figure 12 a and b demonstrate the influence of the heating temperature on predicted springback profile and parameters, respectively. It can be concluded that with increasing the heating temperature, the amount of springback decreases. Also, the heating temperature has the most influence on sidewall curl (ρ) and then θ1. Heating temperature has the least effect on parameter θ2.

Fig. 12
figure 12

a Influence of heating temperature on predicted springback profile. b Influence of heating temperature on predicted springback parameters

Full size image

10 Conclusion

In this paper, the hot stamping process of DP780 steel sheet was simulated based on a novel FE model. For consideration of the hardening behavior of the material, a temperature-dependent Chaboche model and for material anisotropy, Yld2000-2d yield criterion was used. A forming process was simulated in the ABAQUS via the UMAT and VUMAT user subroutines based on the forward Euler explicit integration scheme. The obtained results based on the Chaboche temperature-dependent model had an agreement with experimental results. It was observed that increasing the heating temperature of the sheet causes decreasing the level of stresses. It was seen that the stress level of the sheet after quenching process increases. The distribution of the temperature in region below the holder had the minimum value while the temperature in sidewall and bottom sections of the U-shaped part had the maximum value. Finally, it can be concluded that the amount of springback decreases when heating temperature of the sheet increases.