1 Introduction

Due to the advantages of large materials’ removal rate and high efficiency and accuracy, milling is used as the most common processing technology to shape the thin-walled components widely used in the fields of aerospace and aviation [1]. Regenerative chatter, which is one of the most deleterious phenomena affecting machining operations and decreasing processing quality, is easy to occur during cutting process because of the weak stiffness of the workpiece [2, 3]. Many research efforts have been dedicated to the development of technologies that are able to predict and detect chatter to facilitate the avoidance of chatter during cutting process [4].

Accurate prediction of stability of lobe diagram (SLD), which provides the function between axial depth of cut and spindle speed, is an effective way to guide the selections of the cutting parameters to avoid the chatter. A lot of algorithms including zero-order method [1], semi-discretization method [5], full-discretization method [6], and multiple modes method [7] were proposed. Ren et al. [8] used the semi-discretization method to analyze the stability of thin-wall milling process and gave clearer insight into the dynamics and stability of thin-walled structure. Sun and Jiang [9] predicted chatter stability of the system by an extended second order semi-discretization method. Yan and Zhu [10] presented an improved multi-frequency solution to predict the critical axial dept of cut, and confirmed the good performance of the technique in chatter suppression. However, accurate stability lobe diagram just reflects the physical properties of the cutting system and avoids chatters by selecting proper cutting parameters.

To increase the stability of the cutting process, many techniques were also proposed [11,12,13]. Herranz et al. [14] proposed a working methodology for efficient process planning, which provides several steps that can minimize the bending and vibration effects. Mohring and Wiederkehr [15] presented intelligent fixtures for the mitigation of chatters in milling of thin-walled workpieces. Zhang et al. [16, 17] conducted a feasibility study by submerging the milling system in viscous fluid to mitigate milling chatter. Wan et al. [18] presented a stability improvement method in thin- wall milling by applying tensile prestress to the workpiece.

Besides the suppression strategies described above, there exists other methods focused on designing active or passive dampers to improve the stability of the cutting process [19]. Moradi et al. [20] designed a semi-active tunable vibration absorber to suppress regenerative chatter in milling process, and optimum values of the absorber are determined so that the cutting tool vibrations can be minimized. Zhang et al. [21] proposed a novel semi-active tuned mass damper, which is capable to extend its working frequency band through tuning the stiffness; however, no validation experiments were conducted.

Many efforts have been made to conduct further studies [22,23,24]. Zhang et al. [25] focused on the design of robust controller for chatter suppression, and experimental results show that the designed algorithm is able to suppress chatter. Wang et al. [26] proposed multi-harmonic stiffness excitation and random stiffness excitation method, and implemented milling experiments under stiffness excitation, which validated that the proposed method can suppress chatter effectively. Fei et al. [27] proposed a fixture element to enhance the stiffness of the workpiece in process so that the stability of the milling process could be improved. Yuan et al. [28] proposed a tunable mass damper to suppress the chatters when milling the cylindrical parts. Yang et al. [29, 30] suppressed chatters by designing tunable mass dampers and made good effects in improving the stability of the system.

It should be commented that although the researches mentioned above were devoted to developing effective methods to suppress chatters, they ignored the variety of the dynamic parameters of the workpiece due to the removal of materials. As reported in Refs. [31, 32], both natural frequency and mode shape vary greatly due to the reduction of the mass and the stiffness of the thin-walled workpiece. Thus, different from the existing studies, this paper designs a passive damper to suppress the chatters occurring in thin-wall milling by considering the variety of the dynamics of the workpiece due to the removal of materials. The design criteria considering the various dynamic parameters of the workpiece are described in Section 2. The structures of the passive damper are detailed in Section 3. In Section 4, a series of experiments are conducted with the designed passive damper, which show the good performance of the passive damper in improving machining stability. The article is concluded in Section 5.

2 Design principle considering varying stiffness of the workpiece

The dynamic governing equation of the workpiece to be machined at the initial status is expressed as follows.

$$ \boldsymbol{M}_{0}\ddot{\boldsymbol{X}}(t)+\boldsymbol{C}_{0}\dot{\boldsymbol{X}}(t)+\boldsymbol{K}_{0}\boldsymbol{X}(t)=\boldsymbol{F}_{0}(t) $$
(1)

where M0, C0, and K0 denote the mass, damping, and stiffness matrices of the initial workpiece. \(\boldsymbol {X}\left (t \right )\) is the displacement matrix of the workpiece. \({{\boldsymbol {F}}_{0}}\left (t \right )\) is the cutting force matrix acting on the initial workpiece. The relevant free vibration equation can be written as

$$ \boldsymbol{M}_{0}\ddot{\boldsymbol{X}}(t)+\boldsymbol{K}_{0}\boldsymbol{X}(t)=0 $$
(2)

The eigenvalue equation of Eq. 2 is expressed as follows.

$$ \left( {{\boldsymbol{K}}_{0}}-{{\upomega}_{0}}^{2}{{\boldsymbol{M}}_{0}} \right)\boldsymbol{X}\left( \omega \right)=0 $$
(3)

where ω0 is natural frequency matrix of the initial workpiece. \(\mathbf {X}\left (t \right )\) can be transformed from the physics space to the modal space by the following formula.

$$ \boldsymbol{X}\left( t \right)=\boldsymbol{D}_{0}\boldsymbol{P}_{0}(t) $$
(4)

where D0 is the mass normalized modal shape matrix, which can be obtained by rearranging the eigenvectors related to the eigenvalue ω0. P0(t) is modal displacement matrix.

It should be mentioned that the dynamics of workpiece will be changed as the material of the workpiece is removed, and the dynamic governing equation of the workpiece during process can be expressed as follows.

$$ \boldsymbol{M}_{\text{b}}\ddot{\boldsymbol{X}}(t)+\boldsymbol{C}_{\text{b}}\dot{\boldsymbol{X}}(t)+\boldsymbol{K}_{\text{b}}\boldsymbol{X}(t)=\boldsymbol{F}_{\text{b}}(t) $$
(5)

where Mb, Cb, and Kb are the mass, damping, and stiffness matrices of the workpiece in process. \(\boldsymbol {F}_{\text {b}}\left (t \right )\) is the force matrix acting on the workpiece during process. The free vibration equation associated with Eq. 5 can be expressed as follows.

$$ \boldsymbol{M}_{\text{b}}\ddot{\boldsymbol{X}}(t)+\boldsymbol{K}_{\text{b}}\boldsymbol{X}(t)=0 $$
(6)

To solve the equation quickly, the mass matrix Mb during process can be denoted as the sum of the initial mass matrix M0 and the removal mass matrix ΔM. The removal mass matrix ΔM can be treated as a relatively small value by multiplying a softening coefficient. To reveal the influence of the removed material, the stiffness of the corresponding elements is treated as a relatively small value by multiplying a softening coefficient. The mass and stiffness during process can be expresses as

$$ \begin{array}{@{}rcl@{}} \boldsymbol{M}_{\text{b}}&=&\boldsymbol{M}_{\text{0}}+{\Delta} \boldsymbol{M} \\ \boldsymbol{K}_{\text{b}}&=& \boldsymbol{K}_{\text{0}}+{\Delta} \boldsymbol{K} \end{array} $$
(7)

By substituting Eq. 7 into Eqs. 6, 8 can be obtained as follows.

$$ (\boldsymbol{M}_{0}+{\Delta} \boldsymbol{M})\ddot{\boldsymbol{X}}(t)+(\boldsymbol{K}_{0}+{\Delta} \boldsymbol{K})\boldsymbol{X}(t)=0 $$
(8)

Substituting Eq. 4 into Eq. 8 and then multiplying \(\boldsymbol {D}_{0}^{\text {T}}\) to both sides of Eq. 8 give

$$ \begin{array}{@{}rcl@{}} &&(\boldsymbol{D}_{0}^{\text{T}}\boldsymbol{M}_{0} \boldsymbol{D}_{0}+\boldsymbol{D}_{0}^{\text{T}}{\Delta} \boldsymbol{M}\boldsymbol{D}_{0}) \ddot{\boldsymbol{P}}(t)\\ &&+(\boldsymbol{D}_{0}^{\text{T}}\boldsymbol{K}_{0} \boldsymbol{D}_{0}+\boldsymbol{D}_{0}^{\text{T}}{\Delta} \boldsymbol{K}\boldsymbol{D}_{0})\boldsymbol{P}_{0}(t)=0 \end{array} $$
(9)

Because D0 is a mass normalized matrix, the following equations can be obtained.

$$ \begin{array}{@{}rcl@{}} \boldsymbol{D}_{0}^{\text{T}}\boldsymbol{M}_{0}\boldsymbol{D}_{0}&=&\boldsymbol{I} \\ \boldsymbol{D}_{0}^{\text{T}}\boldsymbol{K}_{0}\boldsymbol{D}_{0}&=&{{\upomega}_{0}^{2}} \end{array} $$
(10)

Substituting Eq. 10 into Eq. 9 leads to

$$ (\boldsymbol{I}+\boldsymbol{D}_{0}^{\text{T}}\boldsymbol{M}_{0} \boldsymbol{D}_{0})\ddot{\boldsymbol{P}}(t)+({{\upomega}_{0}^{2}}+\boldsymbol{D}_{0}^{\text{T}}{\Delta} \boldsymbol{K}\boldsymbol{D}_{0})\boldsymbol{P}_{0}(t)=0 $$
(11)

The eigenvalue equation of Eq. 11 can be denoted as follows.

$$ \left[({{\upomega}_{0}^{2}}+\boldsymbol{D}_{0}^{\text{T}}{\Delta} \boldsymbol{K}\boldsymbol{D}_{0})-\lambda(\boldsymbol{I}+\boldsymbol{D}_{0}^{\text{T}}\boldsymbol{M}_{0} \boldsymbol{D}_{0})\right] \boldsymbol{P}_{0}(\upomega)=0 $$
(12)

where λ is the new eigenvalue of the workpiece during process. The relationship between P0(t) and Pb(t) can be obtained as follows.

$$ \boldsymbol{P}_{0}(t)=\boldsymbol{D}_{\text{r}}\boldsymbol{P}_{\text{b}}(t) $$
(13)

where Dr is the new transformation matrix related to the natural frequency of the workpiece. By substituting Eq. 13 into Eq. 4, the modal matrix during process Db can be obtained as follows.

$$ \boldsymbol{D}_{\text{b}}=\boldsymbol{D}_{\text{0}}\boldsymbol{D}_{\text{r}} $$
(14)

Then, the natural frequency ωb of the workpiece during cutting process can be obtained from the new eigenvalue λ, and the mode shape mb can be extracted from the modal matrix Db.

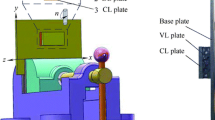
The milling system with a passive damper is illustrated in Fig. 1. To effectively suppress the vibrations, the frequency ratio ν = ωd/ωb between the frequency of the passive damper ωd and the frequency of the workpiece ωb are introduced. The design criterion of equal peaks is used to calculate the optimal parameters of the passive damper, which is described as follows [33].

$$ \nu =\frac{1}{1+\mu} $$
(15)

where μ is the mass ratio between the passive damper md and the targeted mode shape mb. Finally, the optimal frequency of the passive damper can be calculated by

$$ \omega_{\text{d}}=\omega_{\text{b}}\nu $$
(16)
Fig. 1
figure 1

Illustration of the system damped by a passive damper

Full size image

3 Structures of the passive damper

To effectively reduce the vibrations, the passive damper with tunable stiffness is designed according to the principle described in Section 2. The structure of the passive damper is illustrated in Fig. 2. The passive damper mainly consists of five components. c1 is the thin plate. c4 is the mass block, which is fixed on the middle part of the thin plate (c1). The slide blocks (c5) at both sides of c4 can slide along the thin plate, and this characteristic means that the length between the two fixed points can be adjusted. The frequency of the passive damper is adjustable through changing the length of the thin plate. The screws (c2) are used to fix the slide blocks (c5). c3 is the component, which gives a support for the damper. The thin plate (c4) can be moved up and down along the support (c3).

Fig. 2
figure 2

Structures of the passive damper

Full size image

To clearly describe the relationship between the frequency of the passive damper and the length of the thin plate, modal analysis of the passive damper is completed though finite element method. The results of modal analysis are listed in Table 1 and plotted in Fig. 3.

Table 1 The frequency of the passive damper under different length (ld)
Full size table
Fig. 3
figure 3

Results of modal analysis of the passive damper

Full size image

To further show how to suppress the vibrations through the passive damper, the procedure of conduction is summarized as follows.

  1. 1.

    Choose the workpiece and obtain the modal parameters of the initial workpiece by finite element method.

  2. 2.

    Calculate the dynamic modal parameters of the workpiece in process and extract the natural frequency ωb and mode shape mb from the modal parameters by using the method described in Section 2.

  3. 3.

    Design the passive damper, which is schematically shown in Fig. 2, according to the modal parameters of the workpiece.

  4. 4.

    Establish the relationship between the natural frequency ωd and the adjustable length ld of the passive damper.

  5. 5.

    Calculate the mass ratio μ and optimal frequency ωd of the passive damper by using the design principle expressed in Section 2.

  6. 6.

    Adjust the passive damper to the optimal position according to the results of steps (4) and (5).

4 Experimental verification

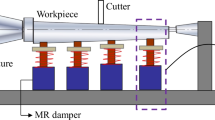
To verify the effectiveness of the proposed method, a series of tests have been conducted on a three-axis CNC machining center. A four-fluted carbide tool with the diameter being 12 mm is used. In the experiments, a microphone is used to acquire the sound signals. Kistler 9255B dynamometer is used to measure the force signals. The experimental setup is illustrated in Fig. 4.

Fig. 4
figure 4

Experimental setup

Full size image

The workpiece with the material being aluminum alloy AL 7075 and the size being 180 mm×80 mm×5 mm is used. It should be pointed out that the workpiece used in the experiments is a thin-walled plate, which has much higher stiffness in X-direction than that in Y -direction. Therefore, the passive damper is mainly designed to focus on the vibrations in Y -direction. Because of this understanding, the illustration of the system damped by the passive damper is only shown to have one degree of freedom in Fig. 1. The radial depth of cut is 2 mm. As the cutting continues, the removal of the materials will be increased, as shown in Fig. 5. The dynamic properties of the workpiece will be changed with the removal of the materials. It is worth noting here that the mode shape plays a significant role on the FRF, and the FRFs change at different cutting points. Thus, in the experiments, after the current tool path of cutting is completed, new mode shape of the specified point in the next tool path is updated by using the method described in Section 2. The natural frequency and normalized mass of the point, which will be cut in the next tool path, are calculated by considering the removal of the materials. The results are listed in Table 2 and plotted in Fig. 6.

Fig. 5
figure 5

Illustration of the removed materials

Full size image
Table 2 Calculation results of the dynamics of the workpiece in process
Full size table
Fig. 6
figure 6

Dynamics of the workpiece in process. a Natural frequency of the workpiece. b Normalized mass

Full size image

The passive damper is attached to the workpiece’ s opposite side of the surface to be machined by Blu. Tack glue. To comprehensively balance the influences of the left and right parts of the workpiece, the passive damper is located at the middle position of the thin-walled plate along the feed direction. Besides, since the upper part of the workpiece has weaker stiffness than the lower part along the height direction, the passive damper should be tried to fix on the relatively higher part of the workpiece. Finally, it should be mentioned that quantitative study of the influence of the location of the passive damper is not the key issue to be studied here, and it remains as a further problem to be deeply detected. The mass of the passive damper is 13.7 g. The mass ratio and optimal frequency of the passive damper are calculated, and the results are listed in Table 3.

Table 3 Calculation results of the optimal frequency of the passive damper
Full size table

Finally, the following comments should be concerned. In actual milling process, the passive damper does not need to be adjusted along a certain tool path. But, after a tool path is completed, the new mode shape of the specified point in the next tool path should be calculated by using the method described in Section 2. Then, the optimal frequency of the passive damper is obtained as Eqs. 15 and 16. The length ld shown in Fig. 2 can be determined according to the relationships between the frequency of the passive damper and the length ld, as shown in Table 1. That is, ld can be tuned by adjusting the two slide blocks (c5) along the plate (c1) to its calculated length. Finally, the thin plate (c1) and two slide blocks (c5) together with the mass block (c4) are adjusted along the supports (c3) to make sure the mass block (c4) is at the opposite side of the specified cutting point in the next tool path to be suppressed. The whole operations are manually carried out.

To show the performance of the passive damper, the 3D stability lobe diagrams without and with passive damper are plotted in Fig. 7. It can be seen that axial critical depths of cut increase obviously when the passive damper works. To further validate the effectiveness of the passive damper, the experiments at three different positions, corresponding to which different ratios of materials are removed, are conducted.

Fig. 7
figure 7

Stability lobe diagrams without and with passive damper. a Without passive damper. b With passive damper

Full size image

It should be mentioned that in the milling process of the cantilevered thin-walled workpiece, the bending mode is the most significant factor that influences the vibrations of the workpiece. Because of this fact, this article aims to design a passive damper for the suppression of the workpiece’ s first order of bending mode. Anyway, the second or other modes also influence the stability of the cutting process, and how to include the influence of these models remains as an open problem to be further studied.

When the height of the material removal is zero, the experiment is conducted at the spindle speed of 3500 rpm. The feed rate is 0.05 mm/tooth. The radial depth of cut is 2 mm. The axial depth of cut is 0.3 mm. The tooth passing frequency is 58.33 Hz. The sound signals and force signals together with their Fourier transformation with and without passive damper are shown in Fig. 8. From the figure, it can be seen that when there is no passive damper, 765.6 Hz and 955.2 Hz occur in the sound signals and 1756 Hz occurs in the force signals, and these frequencies are not integral times of the tooth passing frequency. That means chatters occur during the cutting process and the system is not stable. While the dominant frequency occurs in the sound and force signals are all integral times of the tooth passing frequency when the passive damper is applied to the system.

Fig. 8
figure 8

Experimental results at spindle speed of 3500 rpm when the height of the material removal is zero. “SF” denotes integer times of tooth passing frequency. “CF” denotes chatter frequency. “TMD” denotes tunable mass damper

Full size image

Another group of experiment is conducted when the height of the material removal is 10 mm. In this experiment, the spindle speed is 4000 rpm. The feed rate is 0.05 mm/tooth. The radial depth of cut is 2 mm. The axial depth of cut is 0.3 mm. The tooth passing frequency is 66.67 Hz. The experimental results of sound and force signals together with their Fourier transformation are illustrated in Fig. 9. From the collected signals in Fig. 9, it can be clearly seen that the chatter frequency of 1773 Hz occurred both in sound signals, and force signals are not integral multiples of the tooth passing frequency. That is, the system is not stable when the passive damper is off. Besides, the magnitudes of the sound and force signals without passive damper are much bigger than that with passive damper. This phenomenon shows the good performance of the passive damper.

Fig. 9
figure 9

Experimental results at spindle speed of 4000 rpm when the height of the material removal is 10 mm. “SF” denotes integer times of tooth passing frequency. “CF” denotes chatter frequency. “TMD” denotes tunable mass damper

Full size image

When the height of the material removal is 30 mm, the experiment is conducted at the spindle speed of 4000 rpm. The feed rate is 0.05 mm/tooth. The radial depth of cut is 2 mm. The axial depth of cut is 0.5 mm. The tooth passing frequency is 66.67 Hz. The experimental results are shown in Fig. 10. According to the collected sound and force signals together with their Fourier transformation, it can be seen that the frequencies occurring in the Fourier transformation are all integer multiples of the tooth passing frequency whether the system is with or without the passive damper. This means that there are no chatters during the cutting process under the two conditions. However, from the figure, it can be seen that when the passive damper is on, the magnitudes of the sound and force signals decrease obviously than that without the passive damper. This phenomenon implies the good performance of the passive damper in reducing vibrations.

Fig. 10
figure 10

Experimental results at spindle speed of 4000 rpm when the height of the material removal is 30 mm. “SF” denotes integer times of tooth passing frequency. “CF” denotes chatter frequency. “TMD” denotes tunable mass damper

Full size image

Another experiment at the height of the material removal of 30 mm is conducted under the cutting condition of spindle speed of 6500 rpm. The feed rate is 0.05 mm/tooth. The radial depth of cut is 2 mm. The axial depth of cut is 0.3 mm. The tooth passing frequency is 108.33 Hz. The collected sound and force signals and their Fourier transformation are illustrated in Fig. 11. It can be obviously seen that chatter occurs at the frequency of 1582 Hz both in sound signals and force signals when the system is without the passive damper, while the cutting process is stable when the passive damper is used in the cutting system. What’s more, compared with the sound and force signals without the passive damper, the magnitudes of the sound and force signals are much more smaller. Other two groups of experiments are also conducted at spindle speed of 6500 rpm. The axial depths of cut are increased to 0.8 mm and 1.5 mm when the passive damper is used. The experimental results of these two conditions are shown in Fig. 12. From the Fourier transformations of sound and force signals, it can be seen that the cutting system remains stable though the axial depth of cut is up to 1.5 mm when the passive damper is on. It shows good performance of the passive damper.

Fig. 11
figure 11

Experimental results at spindle speed of 6500 rpm when the height of the material removal is 30 mm. “SF” denotes integer times of tooth passing frequency. “CF” denotes chatter frequency. “TMD” denotes tunable mass damper

Full size image
Fig. 12
figure 12

Experimental results at spindle speed of 6500 rpm when the height of the material removal is 30 mm. “SF” denotes integer times of tooth passing frequency. “TMD” denotes tunable mass damper

Full size image

According to the experiments conducted and stability analysis of the collected sound and force signals together with their Fourier transformation above, it can be obviously seen that the magnitudes of the measured signals are more smaller and no chatter occurs when the designed passive damper is attached to the cutting system. These phenomenon shows the good performance of the designed passive damper in improving the stability of cutting system.

5 Conclusions

Chatters are easy to occur in the milling process of thin-walled components, and thus constitute a harmful source to stable machining. To suppress the vibrations and improve the stability of the cutting system, a passive damper is designed and manufactured with tunable stiffness. The modal parameters of the workpiece during cutting process are derived and the design criterion of equal peaks is used to calculate the optimal frequency of the passive damper. To validate the effectiveness of the proposed method and designed passive damper, a series of experiments are conducted with and without passive damper. During the experiments, the sound signals and force signals are measured and their Fourier transformation are calculated. The results of the experiments show that the cutting system are more stable when the passive damper is used, and it proves the good performance of the passive damper in suppressing chatters and improving the stability of the system.