1 Introduction

Metal cutting has made important developments in recent years; however, chatter remains an important issue because it limits productivity and machining quality. Therefore, the manner in which the stable depth of cut predicted by the stability lobe diagram (SLD) can be improved to increase the maximum material removal rate and avoid and suppress the occurrence of chatter during milling process is a concern.

Variable pitch/helix cutters are a good choice for improving stability [1,2,3,4]. They change the time delays of a dynamic system via uneven pitch/helix angles, which in turn disturb the surface regeneration effect between subsequent cutting edges to increase the stability limit of the milling process.

The effectiveness of variable pitch cutters in suppressing chatter in milling was first confirmed by Slavicek [5]. In a later study, Opitz et al. [6] used average directional factors in considering cutter rotation. The experimental results and predictions showed that variable pitch cutters can considerably increase stability limit. Vanherck [7] considered different pitch variation patterns in their analysis. The simulation results showed the effects of different types of pitch angle on stability limit. The aforementioned studies focused on determining the optimum pitch angle through tool design to maximize stability over a range of spindle speeds. Altintas et al. [8] proposed an analytical stability model suitable for variable pitch cutters. On the basis of this model, they established the geometric design theory of variable pitch cutters. Subsequently, Budak [9, 10] proposed a complete analytical model for optimizing variable pitch cutters. The experimental and machining application results showed that a reasonable pitch angle design during low-speed cutting can considerably improve stability. Olgac and Sipahi [11] analyzed the bounds of stable versus unstable chatter by introducing a cluster treatment of characteristic roots. Given the influence of the variation pitch angle on stability, an optimization model of variation pitch cutter was proposed. Song et al. [12] designed the structural geometry of variable pitch cutters and proposed a design method of variable pitch end mill with high milling stability. In a recent study, Shamoto et al. [13] proposed a method for optimizing pitch angles that simultaneously suppress multimode regenerative chatter. Stepan et al. [14] proposed a numerical method for optimizing pitch angles to improve the ultimate productivity of variable pitch cutters.

In recent years, variable helix cutters have been gradually applied in high-speed milling. Turner et al. [15] simplified a variable helix cutter to a variable pitch milling cutter and proposed an analytical method for quickly predicting the stability of variable helix cutters. However, this approximation can only achieve accurate results with low radial immersions. Similarly, Sims et al. [16] studied the stability of variable pitch and helix cutters. Three modeling methods, namely, semi-discretization (SDM), time-averaged SDM, and time-finite element method were compared. In small radial depths of cut, variable pitch and helix cutters can cause cyclic-fold bifurcation. Jin et al. [17] proposed a method that uses a straightforward integral force model to predict the stability of variable pitch/helix cutters. For special cutters, Dombovari and Stepan [18] proposed a stability prediction model for harmonically varied helix cutters based on the SDM algorithm. To study the applicable conditions of variable helix cutters, Guo et al. [19] established a stability model of variable helix angle cutters and used different types of milling cutter to perform milling experiments on one - and two-degree-of-freedom systems and a thin-walled part. Otto et al. [20] proposed a new model for predicting the stability of variable pitch and variable helix tools with the multi-frequency solution, which considered the nonlinear cutting force behavior and the effect of runout. Niu et al. [21] modeled the dynamic of VPVH tools considering runout. Afterwards, the improved Runge–Kutta (GRK) method was used to solve the multi-regeneration effect caused by the runout; thereby, the stability of the milling process was analyzed. Guo et al. [22] predict the stability with an interpolation method and an integration method, considering the effect of the variable helix and pitch angles. Urena et al. [23] set up an experiment using a variable helix tool to cut the copolymer acetal mounted on an intentionally flexible platform. They verified that the well-designed variable helix tools can offer significant stability performance improvements at higher axial depths of cut.

The aforementioned studies focused on the stability analysis of variable helix cutters. However, few studies have been conducted on optimizing the structure of variable helix cutters to improve the stability region. Yusoff and Sims [24] combined the stability model of a variable helix cutter with an evaluation algorithm and proposed the geometric optimization theory of variable helix cutters. Takuya et al. [25] optimized a variable helix cutter with a regeneration factor. Comak and Budak [26] analyzed the stability of variable pitch and helix cutters and optimized them to maximize chatter stability. They also proposed an improved optimization method of variable pitch milling cutters on the basis of the optimization method in [9].

Although considerable work has been conducted on optimizing variable pitch/helix cutters, further improvement is still needed. Budak [9, 10] first optimized variable pitch cutters using a zero-order analytical method. However, this method is only suitable for predicting the stability of the large radial depth of milling because it ignores the time-varying characteristics of the cutting force coefficient. Frequency domain methods can increase stability; however, optimization results are usually not the final optimal solution. Stepan et al. [14] used the Floquet multiplier to optimize variable pitch cutters; however, they only focused on a specific spindle speed where stability limits are the highest. In the actual machining process, cutting conditions and materials vary due to machining methods. The depth of cut and the spindle speed are different during the milling process. The absolute stability region is the part below the minimum stable depth of cut. In this area, the axial depth of cut is ap < apmin, and the milling process remains stable regardless of how the spindle speed changes. Therefore, the absolute stability limit of a milling system must be increased in the entire spindle speed range, such that a cutter can perform milling with rough and finish machining of different materials. Moreover, previous studies have focused on optimizing variable pitch cutters, and few studies have been conducted to optimize variable helix cutters. Yusoff and Sims [24] optimized variable helix cutters using the average minimum characteristic multipliers (CMs) as the objective function. However, the area of the cutting simulation was extremely small with only one stability pocket. If the cutting area is enlarged, then the average minimum CMs do not guarantee the improvement of the minimum stable depth of cut.

In the present work, maximizing chatter stability limit is improved, and feasibility is assessed by optimizing a variable helix cutter to suppress chatter. A series of experiments with regular cutter, optimal cutter, and other parameters of variable helix cutters are performed to analyze the effectiveness of the proposed approach on milling stability. The structure of this paper is as follows. Section 2 establishes the stability model of variable helix milling and determines the effects of pitch and helix variations on the difference of stability limit. Section 3 proposes an optimization strategy with the maximum absolute stability region. The modal parameters and the cutting force coefficients of a regular cutter are identified via experiments. The theoretical optimization of the milling stability is also achieved. In Sect. 4, the modal parameters and the cutting force coefficients of an optimal cutter are further calibrated via experiments to improve the accuracy of SLDs. A series of experiments are performed, and the experimental results are discussed. The conclusions of this study are drawn in Sect. 5.

2 Stability of milling with a variable helix cutter

This section proposes a stability model of variable helix milling based on SDM [17, 27, 28]. The stability model is simulated, and the effects of pitch and helix variations on stability limit are analyzed.

2.1 Stability analysis with an updated SDM

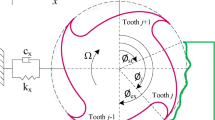
The dynamic model of the two-degree-of-freedom milling process is shown in Fig. 1. The milling cutter is assumed flexible in the x- and y-directions. To study the dynamic behavior in the milling process, the cutter should be divided into several cutting elements along the cutter axis. The mathematical model of the dynamic system can be expressed as

$$ \mathbf{M}\ddot{q}(t)+\mathbf{C}\dot{q}(t)+\mathbf{K}q(t)=\sum \limits_{j=1}^N\sum \limits_{l=1}^Mg\left({\phi}_j\right){\mathbf{K}}_{j,l}\left(q(t)-q\left(t-{\tau}_{j,l}\right)\right) $$
(1)
Fig. 1
figure 1

Schematic of the mechanical model of the milling process

Full size image

Vector q(t) contains the displacement of the cutter tip in the x- and y-directions. M, C, and K represent the modal mass, damping, and stiffness matrixes of the system, respectively. Kj, l is the directional coefficient matrix, which is dependent on the spindle period and axial level in the milling process. N is the number of teeth. A unit step function g(ϕj) determines whether the edge of the cutter is milling.

The geometric model of the helical cutting edges is shown in Fig. 2. The pitch angle between the jth and (j + 1)th cutting edges in the axial direction can be expressed as

$$ {\varphi}_{j,l}(z)=\Big\{{\displaystyle \begin{array}{cc}2\pi +{\phi}_j\left(t,z\right)-{\phi}_N\left(t,z\right)={\phi}_{p1}-z\frac{\tan {\beta}_{j+N-1}-\tan {\beta}_j}{R}& j=1\\ {}{\phi}_j\left(t,z\right)-{\phi}_{j-1}\left(t,z\right)={\phi}_{pj}-z\frac{\tan {\beta}_j-\tan {\beta}_{j+1}}{R}& 1<j\le N\end{array}} $$
(2)

where ϕp1 is the pitch angle between the first and Nth cutting edges at the bottom, ϕpj is the pitch angle between the preceding flutes at the tip of the cutter, βj is the helix angle of the jth cutting edge, and R is the radius of the cutter.

Fig. 2
figure 2

Geometric model of the variable helix cutter

Full size image

Time delay τj, l for the jth cutting edge of the ith cutting element can be expressed as

$$ {\tau}_{j,l}=\frac{\varphi_{j,l}}{\varOmega } $$
(3)

By introducing the system vector \( \mathbf{u}(t)={\left(q(t),\dot{q}(t)\right)}^T \), Eq. (4) with multi-delay can be written as a first-order differential equation, as shown as follows:

$$ {\displaystyle \begin{array}{c}\dot{\mathbf{u}}(t)=\mathbf{A}(t)\mathbf{u}(t)+\sum \limits_{l=1}^M\sum \limits_{j=1}^N{\mathbf{B}}_{j,l}(t)\left[\mathbf{u}(t)-\mathbf{u}\left(t-{\tau}_{j,l}\right)\right]\\ {}\mathbf{A}(t)=\mathbf{A}\left(t+T\right),\kern0.5em {\mathbf{B}}_{j,l}(t)={\mathbf{B}}_{j,l}\left(t+T\right)\end{array}} $$
(4)

where

$$ \mathbf{A}(t)=\left[\begin{array}{cc}0& I\\ {}-\mathbf{K}{\mathbf{M}}^{-1}+{\mathbf{M}}^{-1}\sum \limits_{l=1}^M\sum \limits_{j=1}^N{\mathbf{K}}_{j,l}(t)& -{\mathbf{M}}^{-1}\mathbf{C}\end{array}\right],{\mathbf{B}}_{j,l}(t)=\left[\begin{array}{cc}0& 0\\ {}-{a}_p{\mathbf{M}}^{-1}{\mathbf{K}}_{j,l}(t)& 0\end{array}\right] $$

The first step in the numerical solution is to discretize the time period T into k numbers of discrete time intervals, such that T = k △ t. The time delay term τj, l is discretized into integer mj, l parts of length △t. In [ti, ti + 1], for the initial condition u(ti) = ui, the solution of Eq. (4) can be expressed as

$$ \mathbf{u}(t)={e}^{{\mathbf{A}}_i\left(t-{t}_i\right)}\left[{\mathbf{u}}_i+\sum \limits_{l=1}^M\sum \limits_{j=1}^N{\mathbf{A}}_i^{-1}{\mathbf{B}}_{j,l,i}(t){\mathbf{u}}_{\tau_{j,l,i}}\right]-\sum \limits_{l=1}^M\sum \limits_{j=1}^N{\mathbf{A}}_i^{-1}{\mathbf{B}}_{j,l,i}(t){\mathbf{u}}_{\tau_{j,l,i}} $$
(5)

where

$$ {\displaystyle \begin{array}{l}{\mathbf{A}}_i=\frac{1}{\varDelta t}{\int}_{t_i}^{t_{i+1}}\mathbf{A}(t) dt,{\mathbf{B}}_{j,l,i}=\frac{1}{\varDelta t}{\int}_{t_i}^{t_{i+1}}{\mathbf{B}}_{j,l}(t) dt\\ {}{\mathbf{u}}_{\tau_{j,l,i}}=\mathbf{u}\left(t-{\tau}_{j,l,i}\right)\approx \mathbf{u}\left({t}_i+\varDelta t/2-{\tau}_{j,l,i}\right)\approx {w}_{j,l,i,a}{\mathbf{u}}_{i-{m}_{j,l,i}+1}+{w}_{j,l,i,b}{\mathbf{u}}_{i-{m}_{j,l,i}}\\ {}{w}_{j,l,i,a}=\frac{m_{j,l,i}\varDelta t+\varDelta t/2+{\tau}_{j,l,i}}{\varDelta t},{w}_{j,l,i,b}=1-{w}_{j,l,i,a}\end{array}} $$

where \( {\mathbf{u}}_{i-{m}_{j,l,i}} \) denotes \( \mathbf{u}\left({t}_{i-{m}_{j,l,i}}\right) \), and wj, l, i, a and wj, l, i, b are the weighted factors of \( {\mathbf{u}}_{i-{m}_{j,l,i}+1} \) and \( {\mathbf{u}}_{i-{m}_{j,l,i}} \), respectively.

Substituting \( {\mathbf{u}}_{\tau_{j,l,i}}={w}_{j,l,i,a}{\mathbf{u}}_{i-{m}_{j,l,i}+1}+{w}_{j,l,i,b}{\mathbf{u}}_{i-{m}_{j,l,i}} \) and t = ti + 1 into Eq. (5) yields

$$ {\mathbf{u}}_{i+1}={\mathbf{Q}}_i{\mathbf{u}}_i+\sum \limits_{l=1}^M\sum \limits_{j=1}^N{\mathbf{M}}_{j,l,i,a}{\mathbf{u}}_{i-{m}_{j,l,i}+1}+{\mathbf{M}}_{j,l,i,b}{\mathbf{u}}_{i-{m}_{j,l,i}} $$
(6)

where

$$ {\displaystyle \begin{array}{l}{\mathbf{Q}}_i={e}^{{\mathbf{A}}_i\varDelta t}\\ {}{\mathbf{M}}_{j,l,i,a}=\left(\mathbf{Q}-\mathbf{I}\right){\mathbf{A}}_i^{-1}{\mathbf{B}}_{j,l,i}{w}_{j,l,i,a}\\ {}{\mathbf{M}}_{j,l,i,b}=\left(\mathbf{Q}-\mathbf{I}\right){\mathbf{A}}_i^{-1}{\mathbf{B}}_{j,l,i}{w}_{j,l,i,b}\end{array}} $$

where I denotes the identity matrix. The vector is expressed as follows:

$$ {\mathbf{U}}_i={\left[{\mathbf{u}}_i^T,{\mathbf{u}}_{i-1}^T,...,{\mathbf{u}}_{i-{n}_{\mathrm{max}}+1}^T,{\mathbf{u}}_{i-{n}_{\mathrm{max}}}^T\right]}^T $$

where

\( {n}_{\mathrm{max}}=\max \left({n}_{j,l,i}\right),{n}_{j,l,i}=\frac{\tau_{j,l,i}}{\varDelta t}-\operatorname{mod}\left(\frac{\tau_{j,l,i}}{\varDelta t}\right)+1 \)

According to Eq. (6), a discrete map can be defined as

$$ {\mathbf{u}}_{i+1}={\boldsymbol{\Phi}}_i{\mathbf{u}}_i $$
(7)

where the matrix Φi has the following form:

$$ {\boldsymbol{\Phi}}_i=\left[\begin{array}{cccccc}{\mathbf{Q}}_i& 0& \cdots & 0& 0& 0\\ {}\mathbf{I}& 0& \cdots & 0& 0& 0\\ {}0& \mathbf{I}& \cdots & 0& 0& 0\\ {}\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {}0& 0& \cdots & \mathbf{I}& 0& 0\\ {}0& 0& \cdots & 0& \mathbf{I}& 0\end{array}\right]+\sum \limits_{l=1}^M\sum \limits_{j=1}^N\left[\begin{array}{cccccc}0& \cdots & {\mathbf{M}}_{j,l,i,a}& {\mathbf{M}}_{j,l,i,b}& \cdots & 0\\ {}0& \cdots & 0& 0& \cdots & 0\\ {}0& \cdots & 0& 0& \cdots & 0\\ {}\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {}0& \cdots & 0& 0& \cdots & 0\\ {}0& \cdots & 0& 0& \cdots & 0\end{array}\right] $$
(8)

System stability can be approximated by the finite-dimensional transition matrix, as shown as follows:

$$ {\mathbf{U}}_k=\boldsymbol{\Phi} {\mathbf{U}}_0={\boldsymbol{\Phi}}_{k-1}{\boldsymbol{\Phi}}_{k-2}\cdots {\boldsymbol{\Phi}}_1{\boldsymbol{\Phi}}_0{\mathbf{U}}_0 $$
(9)

The transition matrix Φ can be determined by Φ = Φk − 1Φk − 2⋯Φ1Φ0.

According to Floquet theory, the eigenvalues of Φ, which can be called Floquet multipliers, are calculated from the characteristic equation det(μiΙ − Φ) = 0. The system is stable if all the Floquet multipliers μi are located inside the unit circle of the complex plane; otherwise, it is unstable.

2.2 Effect of pitch and helix angles on stability

In this section, the stability model in Sect. 3 is used to simulate and analyze the effects of variable pitch and helix angles on stability using the cutting force coefficients and modal parameters in [1].

2.2.1 Pitch angle variation

Pitch angle variation mainly adopts two types, which were proposed in the literature [9, 10], namely, alternating pitch variation (APV) and linear pitch variation (LPV). The two models are shown in Fig. 3.

Fig. 3
figure 3

Two types of pitch angle variation: a APV and b LPV

Full size image

(a) APV

$$ \phi =\left[{\phi}_0-\varDelta \phi, {\phi}_0+\varDelta \phi, \cdots, {\phi}_0-\varDelta \phi, {\phi}_0+\varDelta \phi \right] $$
(10)

where \( {\phi}_0=\frac{2\pi }{N} \)

(b) LPV

$$ \phi =\left[{\phi}_0,{\phi}_0+\varDelta \phi, \cdots, {\phi}_0+\left(N-1\right)\varDelta \phi \right] $$
(11)

where \( {\phi}_0=\frac{2\pi }{N}-\frac{\left(N-1\right)\varDelta \phi}{2} \)

2.2.2 Helix angle variation

$$ {\beta}_{j+1}={\beta}_j+\varDelta {\beta}_j,j=1,2,......,N-1 $$
(12)

The SLDs of variable pitch/helix cutters are shown in Figs. 4, 5, and 6.

Fig. 4
figure 4

Effects of variable pitch angles on stability: a APV and b LPV; other parameters: β = 35∘, N = 4, D = 19.05 mm, aD = 0.5

Full size image
Fig. 5
figure 5

Effects of variable helix angles on stability; other parameters: ϕ = 90∘, β = 35∘, N = 4, D = 19.05 mm, aD = 0.5

Full size image
Fig. 6
figure 6

Effects of variable pitch and helix angles on stability: a APV and b LPV; other parameters: β = 35∘, N = 4, D = 19.05 mm, aD = 0.5

Full size image

The SLDs of three variable pitch cutters with APV and LPV are shown in Fig. 4. As the pitch angle changes, the SLDs move to the high-speed cutting area entirely. Absolute stability limits of milling systems caused by variable pitch angle change considerably. Thus, a large absolute stability region can be obtained within a certain speed range by adjusting the pitch angles.

The SLDs of three variable helix cutters with uniform pitch angles are shown in Fig. 5. In comparison with the variable pitch cutter, changing only the helix angles has minimal influence on stability, and the change of the minimum stable depth of cut apmin is not apparent. Therefore, changing only the helix angles is not advisable in actual cutting.

The SLDs of three variable helix cutters with APV and LPV are shown in Fig. 6. As shown in Figs. 4 and 6, the absolute stability limit of the variable helix cutter is higher than that of changing only the pitch angles. Therefore, the maximum absolute stability region can be obtained within a certain speed range by optimizing the pitch and helix angles.

3 Parameter optimization with maximum absolute stability limit

In this section, an optimization algorithm for finding the optimal combination of pitch and helix angles is proposed to improve the absolute stability limit of the variable helix cutter.

3.1 Optimization strategy and results

In [29, 30], the Floquet multiplier provides not only qualitative results (stable/unstable) but also a quantitative measure of stability. In the present study, the Floquet multiplier is used to measure the stability of the variable helix cutter.

The region of stability prediction includes the spindle speed, \( \varOmega \in \left[{\varOmega}_{\mathrm{min}}\kern0.5em {\varOmega}_{\mathrm{max}}\right] \); and the axial depth of cut, \( {a}_p\in \left[0\kern0.5em {a}_{p\max}\right] \). A maximum Floquet multiplier \( {\mu}_{\varOmega, {a}_p} \) exists for any spindle speed and axial depth of cut. The maximum Floquet multiplier \( {\mu}_{\varOmega, {a}_p} \) increases with the axial depth of cut at a certain spindle speed. When the axial depth of cut reaches the maximum value of the range of predicted depth, the maximum Floquet multiplier \( {\mu}_{\varOmega, {a}_p} \) also reaches the maximum value at this speed, such that \( {\mu}_{\varOmega \max }={\mu}_{\varOmega, {a}_{p_{\mathrm{max}}}} \). The smaller the value of μΩmax is, the closer the distance between apmax and the stable depth of cut at a spindle speed; hence, the stable depth of cut at the spindle speed is greater. The stability of this spindle speed is better. The Floquet multiplier can be used to quantitatively measure the distance to the stable depth of cut at a certain spindle speed. The comparison of the magnitude of μΩmax in all speed ranges shows that the maximum value of μΩmax is (μΩmax)max. A minimum stable depth of cut apmin exists in the region of stability prediction, and the spindle speeds at which apmin and (μΩmax)max are located are the same. Therefore, the minimum stable depth of cut apmin is increased to reduce the maximum Floquet multiplier (μΩmax)max, thereby increasing the absolute stability region.

On the basis of this optimization idea, the parameters of the variable helix cutter with four teeth are optimized. The pitch angles are in the form of APV and LPV. The definitions are as follows.

  • Constraint conditions:

  • Pitch angle: 70o ≤ ϕpmin ≤ 90o

  • Helix angle: \( \Big\{{\displaystyle \begin{array}{l}{35}^{\mathrm{o}}\le {\beta}_j,{\beta}_{j+1}\le {45}^{\mathrm{o}}\\ {}{2}^{\mathrm{o}}\le \mid \varDelta {\beta}_j\mid \le {5}^{\mathrm{o}}\end{array}},j=1,2,....,N-1 \)

In addition, when optimizing the cutter with APV, the helix angles alternately vary to ensure the dynamic balance of the cutter, β1 = β3, β2 = β4.

To quantitatively measure stability, a new index called “suppression factors” (SFs) are proposed by taking the Floquet multiplier at the discrete spindle speed points, as shown as follows:

$$ {\mathrm{SF}}_n={\mu}_{\varOmega_n,{a}_{p_{\mathrm{max}}}},n=1,2,\cdots, \frac{\varOmega }{\varDelta \varOmega} $$
(13)

where ΔΩ is the discrete step size of the spindle speed. The objective function is

$$ \min \left({\left\{{\mu}_{\varOmega_1,{a}_{p_{\mathrm{max}}}},{\mu}_{\varOmega_2,{a}_{p_{\mathrm{max}}}},\cdots, {\mu}_{\varOmega_n,{a}_{p_{\mathrm{max}}}}\right\}}_{\mathrm{max}}\right)=\min \left({\left(S{F}_n\right)}_{\mathrm{max}}\right),n=1,2,\cdots, \frac{\varOmega }{\varDelta \varOmega} $$

To identify the optimal combination of pitch and helix angles, a genetic algorithm (GA) is used to find each possible combination and directly search for the global optimal solution. In comparison with other algorithms, GA is a random search algorithm that has the advantages of simple structure, convenient use, speed, and strong robustness. The initial parameter is determined as follows: the population size is 20, the crossover rate is 0.7, the mutation rate is 0.005, and the maximum generation is 20. The results can be obtained as follows.

  1. (a)

    APV

$$ \varDelta \phi =9{.2}^{\mathrm{o}};{\beta}_1={39.8}^{\mathrm{o}},\varDelta {\beta}_1={4.3}^{\mathrm{o}} $$
  1. (b)

    LPV

$$ {\phi}_0=78{.5}^{\mathrm{o}},\varDelta \phi =7{.7}^{\mathrm{o}};{\beta}_1={36.3}^{\mathrm{o}},{\beta}_2={41}^{\mathrm{o}},{\beta}_3={35.5}^{\mathrm{o}},{\beta}_4={43.5}^{\mathrm{o}} $$

3.2 Stability diagrams

To predict SLDs, the frequency response functions (FRFs) of the cutter and the cutting force coefficients must be obtained in advance. Cutting experiments are conducted to calibrate the cutting force coefficients with 6061 aluminum alloy according to the method proposed by Altintas [31]. The tangential and radial cutting force coefficients Ktc and Krc are 717.4 N/mm2 and − 60.4 N/mm2, respectively. The FRFs of the cutter are obtained by impact tests. A four-tooth cutter with 8-mm diameter is selected, the total length of the cutter is 70 mm, and the overhang is 40 mm. Table 1 lists the modal parameters in the x- and y-directions of the cutter.

Table 1 Model parameters in x- and y-directions
Full size table

SLDs are calculated using the method proposed in Sect. 2. The stability charts are determined over a 200 × 100-sized grid of the spindle speed and depth of cut. The discretized number is set as 50, and half-immersion down milling is adopted. The SLDs of the regular cutter and optimal variable helix cutter are shown in Fig. 7.

Fig. 7
figure 7

SLDs of regular and optimal cutters: a APV and b LPV

Full size image

As shown in Fig. 7, the variation of SLDs of the two cutters is evident. The pitch and helix angle variations considerably increase the minimum stable depth of cut apmin.

The linear variation pitch cutter can improve the greater absolute stability region; however, the alternating variation pitch cutter is easier to manufacture, and the dynamic balance is better. Thus, alternating variation pitch cutters are widely used in experimental and actual machining.

4 Experimental verification

4.1 Modification of stability diagrams

The optimized cutter is customized and labeled as cutter 3, whereas the regular cutter and the variable helix cutter with other parameters are labeled cutters 1 and 2, respectively, as shown in Fig. 8. The three cutters are made of carbide. Given the slight difference in cutting force coefficients and modal parameters of the three cutters, using the cutting force coefficients and modal parameters of cutter 1 to predict the SLDs of cutters 2 and 3 will affect the accuracy of the SLDs. The cutting force coefficients and modal parameters of the three cutters are obtained via cutting experiments and impact tests, as shown in Table 2.

Fig. 8
figure 8

Three types of cutter

Full size image
Table 2 Cutting force coefficients and model parameters
Full size table

The SLDs for the three types of cutter are shown in Fig. 9. The comparison of Figs. 7(a) and 9 show that the change of cutting force coefficients and model parameters has minimal effect on the milling stability of the optimal cutter, and apmin is reduced from 3.1 to 3 mm.

Fig. 9
figure 9

Predicted SLDs using regular tool and variable helix tool. Symbols: black square: chatter occurs using cutters 1 and 2 and stable using cutter 3; purple triangle: chatter occurs using cutter 1, and stable using cutters 2 and 3; black star: critical position of three milling cutters; purple star: no chatter occurs with three cutters; blue triangle: chatter occurs using cutter 2, and stable using cutters 1 and 3; blue square: chatter occurs using cutter 1, and stable using cutters 2 and 3

Full size image

4.2 Experimental results and analysis

The machine tool used is the SmartCNC 500 CNC machining center. A dynamometer (Kistler9257A) is fixed on the table of the machining tool. The cutting material is 6061 aluminum alloy, which is preprocessed into an experimental aluminum block and directly fixed to the dynamometer by bolts. Side milling is used for all experiments, and no coolant is used. The sampling frequency is 10,000 Hz.

To verify the correctness of the predicted SLDs and validate the effectiveness of the proposed approach on the suppression of chatter, nine points in Fig. 10 are selected, and the cutting force experiments are performed using a regular cutter and two variable helix cutters at a feed rate of 210 mm/min. The experimental processing parameters and experimental conditions are shown in Table 3.

Fig. 10
figure 10

Experimental results at point A: a cutter 1, chatter; b cutter 2, chatter; c cutter 3, stable

Full size image
Table 3 Milling conditions
Full size table

For simplicity, four out of nine representative points are selected, and the measured milling force signals are compared and analyzed from the time and frequency domains to determine whether chatter occurs during the milling process. The finish surfaces of the workpieces are then compared. The experimental results are shown in Figs. 10, 11, 12, 13, 14, 15, 16, and 17.

Fig. 11
figure 11

Finish surfaces at point A: a cutter 1, chatter; b cutter 2, chatter; c cutter 3, stable

Full size image
Fig. 12
figure 12

Experimental results at point B: a cutter 1, chatter; b Cutter 2, chatter; c cutter 3, stable

Full size image
Fig. 13
figure 13

Finish surfaces at point B: a cutter 1, chatter; b cutter 2, chatter; c cutter 3, stable

Full size image
Fig. 14
figure 14

Experimental results at point C: a cutter 1, stable; b cutter 2, chatter; c cutter 3, stable

Full size image
Fig. 15
figure 15

Finish surfaces at point C: a cutter 1, stable; b cutter 2, chatter; c cutter 3, stable

Full size image
Fig. 16
figure 16

Experimental results at point D: a cutter 1, chatter; b cutter 2, stable; c cutter 3, stable

Full size image
Fig. 17
figure 17

Finish surfaces at point D: a cutter 1, chatter; b cutter 2, stable; c cutter 3, stable

Full size image

For point A (3,000 rpm, 4 mm), the experimental results confirm that the milling process is clearly unstable when cutting with cutters 1 and 2, as shown in Fig. 10a and b, respectively. The chatter frequency of cutters 1 and 2 are 1240 Hz and 1251 Hz, respectively, which are near their natural frequency. However, the milling process is stable when cutter 3 is used. It can be seen that Fig. 10c exhibits that the cutting force is smaller than cutting with other two cutters. Meanwhile, Fourier analysis in Fig. 10c shows that the main components of the cutting force spectrum are tooth passing harmonics. The finish surfaces of the three cutters at point A are shown in Fig. 11. Figure 11a and b show that the finish surfaces of the workpiece processed by cutters 1 and 2 have a vibration trace, poor surface finish, and a burr on the surface. Meanwhile, Fig. 11c shows that the better surface quality can be achieved by cutter 3, and no vibration trace is observed on the machined surface. Consequently, the increased stability of the optimized variable helix cutter is clearly illustrated.

The same phenomenon is observed in point B (4,200 rpm, 4 mm). As demonstrated in Fig. 12a and b, there are significant chatter vibrations in the milling process when cutters 1 and 2 are used. The chatter frequency of cutters 1 and 2 are 1225 Hz and 1246 Hz, respectively, which are near their natural frequency. However, the milling process is stable when cutter 3 is used (Fig. 12c). It is obvious that cutting force oscillations disappeared due to the chatter-free milling process, and the main components of the cutting force spectrum are tooth passing harmonics. Figure 13a and b show that the finish surfaces of the workpiece processed by cutters 1 and 2 have a vibration trace and poor surface finish. Hence, the surface quality processed by cutter 3 is higher than those of the other two cutters, and no vibration trace is observed on the machined surface (Fig. 13c). This result again verifies that the optimized variable helix cutter in milling can suppress chatter.

For point C (6,000 rpm, 3 mm), the milling process is unstable only when cutting with cutter 2, as shown in Fig. 14b. The chatter frequency of cutter 2 is 1267 Hz, which is near its natural frequency. Figure 14a and c show that the tooth passing frequency are dominating in the spectrum analysis. The whole milling process is stable by using cutters 1 and 3. The results shown in Fig. 15a–c manifest that the surface quality processed by cutter 2 is lower than those of the other two cutters. Moreover, the finish surfaces of the workpiece processed by cutter 2 have a vibration trace and poor surface finish.

For point D (7,200 rpm, 3 mm), the milling process is unstable only when cutter 1 is used (Fig. 16a). The chatter frequency of cutter 1 is 1275 Hz, which is near its natural frequency. The milling process is stable when cutters 2 and 3 are used (Fig. 16b and c). The surface quality processed by cutter 1 is lower than those of the other two cutters, and the finish surfaces of the workpiece processed by this cutter have a vibration trace and poor surface finish (Fig. 17a–c).

The SLDs in Fig. 9 show that for point E (5,700 rpm, 4 mm), the stable cutting depths of the three cutters are 4 mm at 5700 rpm. The milling process is stable using the three cutters. However, the point close to the SLDs may be inaccurate because the milling parameters, including cutting force coefficients and modal parameters are insufficiently accurate.

The comparison and analysis of the experimental results verify that the optimized variable helix cutter can suppress chatter, which further proves the feasibility and effectiveness of the cutter optimization method proposed in this study.

5 Conclusions

A stability model of variable helix milling is established by improving the SDM method. An optimization method of a variable helix cutter is proposed using SFs, which is a new index. The optimal combination of the pitch and helix angles is selected by an optimization algorithm in a given cutting parameter region to maximize absolute stability. The optimal variable helix cutter is customized. The cutting force coefficients and modal parameters of the variable helix cutter are obtained via cutting experiments and impact tests. A series of cutting comparison experiments are also performed. The experimental results show that the optimized variable helix cutter has a large absolute stability region, which verifies the accuracy of the stability model and the effectiveness of the optimization method.