1 Introduction

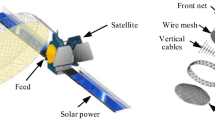
Tension structures are special types of self-stress pin-joint systems composed of tensile and compressive members. Owing to their light weight, simple structure and storage efficiency, tension structures are widely utilized in the fields of architecture and aerospace (Duan 2017; Puig et al. 2010; Volokh 2000). As a typical form of tension structures, mesh reflector antennas are usually composed of a cable-network system (front cable net, rear cable net and tension ties), supporting truss and wire mesh, as shown in Fig. 1 (Orikasa et al. 2013). The cable-network systems are suspended on the supporting truss, whereas the tension ties connect the corresponding nodes of the front and rear cable net to form the required shape. The wire mesh is attached to the back of the front cable net to reflect electromagnetic waves.

Fig. 1
figure 1

Mesh reflector antenna and its component

Full size image

Deployable mesh antennas for future communication and observation applications are required to have high gain and high directivity. The higher the antenna gain and directivity, the stronger the ability to send and receive signals in a particular direction, and the less input power is needed. To meet these space missions, the cable-mesh reflector with high surface accuracy and uniform tension distribution is necessary in the structural design. High surface accuracy can ensure a small geometric error between the actual reflector and the desired ideal reflector, and a uniform tension distribution can reduce the interference due to external environment changes. Thus, the form-finding and optimization design play an indispensable role in mesh reflector antennas. Yang et al. (2017) proposed a minimum length configuration method for cable mesh reflector antennas based on force density method and geometric constraints. Deng et al. (2015) developed a pretension design method for space mesh reflectors considering multiple uncertainties, and the relationship between multi-source errors and cable-tension uncertainty is established. Zhang and Duan (2020) presented an integrated structural-electromagnetic optimization of reflector antennas to reduce the influence of random structural errors on the radiation performance. Yuan et al. (2019) studied a double-loop iterative pretension design method for cable-network antennas to ensure that the reflector surface has a large enough effective area. Based on the force density sensitivity matrix, Zhang and Zhang (2021) introduced a form finding method of cable-mesh reflector antenna considering the interaction between cable networks and supporting truss. The sensitivity matrix of cable net free nodes and truss nodes with respect to force density was derived, and the form-finding process of the reflector antenna was transformed into a sequential quadratic programming problem which can be easily solved. Du and Zhang (2021) developed a robust optimal design method of mesh reflectors considering cable length inaccuracy. The incremental relationship among node position, cable force and cable length was established by finite element method, which reduced the adverse influence of cable net manufacturing and assembly errors on the accuracy of reflector surface. Zhang and He (2022a) proposed a high surface accuracy and pretension design for mesh antennas based on dynamic relaxation (DR) method. The inverse iterative algorithm was used to adjust the original cable length of the cable net in each DR calculation cycle, and a cable-mesh reflector with high precision and equal tension distribution is obtained.

Mesh antennas in orbit are periodically affected by sunlight and earth shadows, whose surrounding temperature is constantly changing (Guo et al. 2016). The thermal deformation of the mesh antennas is inevitable due to the inherent characteristics of thermal expansion and contraction, which deteriorates the surface accuracy and the tension distribution. The above form-finding methods are used for the pretension design for mesh antennas without considering the influence of the space thermal loads, and can only ensure that the mesh antennas have better performance under room temperature condition. Many researches focus on active shape adjustment to improve the on-orbit performance of antenna. Xun et al. (2018) developed an active shape adjustment method for determining the dynamic input voltage profiles of PZT actuators. Song et al. (2020) introduced an adaptive shape control method for antenna reflectors based on feedback error learning algorithm. Lu et al. (2018) proposed a method for modeling and control of membrane mirrors under thermal loads. Three polyvinylidene fluoride (PVDF) patches were pressed on the non-reflective side of the membrane mirror as in-plane actuators. The residual deformation was controlled within microns by using a closed‑loop shape control system. Yuan et al. (2021) proposed a high-precision optimal shape adjustment for cable-network structures. The linear relationship between nodal displacements and undeformed member lengths is established by the singular value decomposition method and the minimum number of actuators and the corresponding layout are determined. Although active shape adjustment can reduce or even completely eliminate the impact of external interference, the actual measurement and adjustment equipment not only greatly increase the structural weight and cost, but also reduce the reliability of the entire antenna system. Therefore, this study mainly focuses on the negative precontrol to reduce the thermal deformation of the mesh antenna. Nie et al. (2019b, 2020) studied an optimal design method of mesh reflector antenna considering truss deformation and thermal effects. The performance of the antenna was improved by minimizing the maximum amplitude of surface errors within the temperature range. Because the shape stability of the reflector surface was not ameliorated in the optimization process, there are still large surface errors under the extreme temperature condition. Yang et al. (2020) put forward the surface shape stability design of mesh reflector antennas by reasonably designing the cross-sectional area of cable element. However, the diversity of cross-sectional area inevitably increases the fabrication complexity of cable-network structures, and the influence of truss deformation was not considered in the design process.

In this study, a thermal design optimization method of mesh antennas considering the interaction between cable net and flexible truss is proposed. The truss model is established by Euler–Bernoulli beam with 6 degrees of freedom and the system equilibrium equation of mesh antenna under thermal loads is introduced. Under the thermal loads, there is an interaction between the cable net and the truss, and the internal elements of the cable net also influence each other. The force density increment equation of the cable net under the space thermal loads is derived by using the analysis strategy of applying thermal loads in two stages. The minimum thermal deformation of the reflector nodes is taken as the optimization objective and the cable tension under extreme temperature condition is constrained to establish thermal design optimization model. The simulation results show that the thermal deformation of the reflector surface has been greatly alleviated under uniform working conditions. The remainder sections are organized as follows. In Section “System equilibrium equation under thermal loads”, the system equilibrium equation of mesh antennas under thermal loads is introduced. In Section “Increment equation of force density under thermal loads”, the force density increment equation of cable net considering space thermal effective is deduced. In Section “Thermal Design Optimization Model of Mesh Reflector Antennas”, a thermal design optimization model for mesh antennas is established. In Section “Numerical example”, the feasibility and effectiveness of the proposed method is proved through numerical examples; Finally, Sect “Numerical example” draws the conclusions.

2 System equilibrium equation under thermal loads

The truss structure of antenna is formed by several groups of rods interconnected by joint hinges. After the antenna is fully deployed, the joint hinges are locked, and there are almost no rotations between the rods. The truss structure can be divided into several groups of beam elements. For the convenience of solution, assuming that the temperature on each beam element is uniformly distributed, the bending moment generated by the non-uniform temperature is 0. The influence of thermal loads on the beam element can be replaced by a pair of axial forces applied at the two end nodes, and then the equilibrium equation of beam element k at temperature T can be expressed as

$$ {\varvec{K}}_{k} \delta_{k} (T) = {\varvec{P}}_{k}^{b} (T) + {\varvec{F}}_{k}^{g} , \, {\varvec{K}}_{k} = {\varvec{T}}_{k}^{T} \tilde{\user2{K}}_{k} T_{k} , \, {\varvec{P}}_{k}^{b} (T) = {\varvec{T}}_{k}^{T} \tilde{\user2{P}}_{k}^{b} (T) $$
(1)

where \({\mathbf{K}}_{k}\) is the stiffness matrix of beam element k in the global coordinate system; \(\delta_{k} (T)\) is the displacement vector of the beam element nodes in the global coordinate system; \({\varvec{F}}_{k}^{g}\) represents the force of cable net on beam element k; \({\varvec{P}}_{k}^{b} (T)\) is the thermal load vector of beam element k at temperature T in the global coordinate system; \({\tilde{\mathbf{K}}}_{k}\) is the stiffness matrix of beam element k in the local coordinate system; \({\mathbf{T}}_{k}\) represents the transformation matrix from local coordinate system to global coordinate system; \(\tilde{\user2{P}}_{k}^{b} (T)\) is the thermal load vector of beam element k at temperature T in the local coordinate system. The nodes at both ends of the beam element have 6 degrees of freedom, respectively, including translation along the three coordinate axes and rotation around the three coordinate axes. Therefore, the thermal load vector in the local coordinate system of the beam element has 12 dimensions, which can be expressed as

$$ {\varvec{P}}_{k}^{b} = [ - E_{b} A_{b} \alpha_{b} (T - T_{0} ) \, 0 \, 0 \, 0 \, 0 \, 0 \, E_{b} A_{b} \alpha_{b} (T - T_{0} ) \, 0 \, 0 \, 0 \, 0 \, 0 \, ]^{T} $$
(2)

where Eb is the elastic modulus of the beam element; Ab is the cross-sectional area of the beam element; \(\alpha_{b}\) is the thermal expansion coefficient of the beam element; T0 represents the design reference temperature.

Through the finite element assembly operation, the above equilibrium relationship is extended to the entire truss structure, and the influence of node rotation vector is eliminated. The truss structure equilibrium equation at temperature T can be expressed as

$$ {\mathbf{K}}_{g} \left[ {\begin{array}{*{20}c} {x_{g} (T) - x_{g0} } \\ {y_{g} (T) - y_{g0} } \\ {z_{g} (T) - z_{g0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{F}}_{x}^{g} } \\ {{\varvec{F}}_{y}^{g} } \\ {{\varvec{F}}_{z}^{g} } \\ \end{array} } \right] + {\varvec{P}}^{b} (T) $$
(3)

where Kg represents the stiffness matrix of the truss after eliminating the rotation vectors of the beam element (Nie et al. 2019a); \({\varvec{P}}^{b} (T)\) represents the thermal load vector acting on the flexible truss; \([{\varvec{F}}_{x}^{g} \user2{ F}_{y}^{g} \user2{ F}_{z}^{g} ]^{T}\) represents the force of the cable net on the truss.

The mesh antenna is in a self-equilibrium state under the tension of the cable net. When the surrounding temperature changes from T0 to T, the mesh antenna under thermal loads reaches a new equilibrium state due to the interaction between truss and cable net. The equilibrium relationship of the forces between the cable net and the truss as well as the deformation coordination relationship must be considered systematically in the process of establishing the equilibrium equation of the mesh antenna under thermal loads. The force density method (Sheck 1974 and Cai et al. 2015) can easily establish the relationship between the boundary cable tension and the boundary nodes of the cable net and transform the system equilibrium equation into a linear expression. Therefore, the force density method in this paper is used to establish the nodal force equilibrium equation the cable network at temperature T, which can be expressed as

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} {{\varvec{x}}_{f} (T)} \\ {{\varvec{x}}_{g} (T)} \\ \end{array} } \right]} & = & {\left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}_{x}^{b} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} {{\varvec{y}}_{f} (T)} \\ {{\varvec{y}}_{g} (T)} \\ \end{array} } \right]} & = & {\left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}_{y}^{b} } \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{f} } & {{\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T)C_{g} } \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} {{\varvec{z}}_{f} (T)} \\ {{\varvec{z}}_{g} (T)} \\ \end{array} } \right]} & = & {\left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{F}}_{z}^{b} } \\ \end{array} } \right]} \\ \end{array} $$
(4)

where Q(T) represents the diagonal matrix of the force density vector q(T) of the cable net at temperature T; \({\varvec{X}}_{f} (T) = [{\varvec{x}}_{f} (T) \, {\varvec{y}}_{f} (T) \, {\varvec{z}}_{f} (T)]^{T}\) are the free node coordinates of cable net; \({\varvec{X}}_{g} (T) =\)\([{\varvec{x}}_{g} (T) \, {\varvec{y}}_{g} (T) \, {\varvec{z}}_{g} (T)]^{T}\) are the boundary node coordinates of cable net; \({\varvec{C}}_{f}\) and \({\varvec{C}}_{g}\) are the topological matrices of free nodes and boundary nodes of the cable net, respectively; \(\left[ {{\varvec{F}}_{x}^{b} \, {\varvec{F}}_{y}^{b} \, {\varvec{F}}_{z}^{b} } \right]^{T}\) represents the force of the flexible truss on the cable net.

For mesh antennas, the force of the flexible truss on the cable net and the force of the cable net on the truss are a pair of interaction forces. The condition of equal size and opposite direction is always satisfied in the process of thermal deformation of antenna.

$$ \left[ {{\varvec{F}}_{x}^{b} \, {\varvec{F}}_{y}^{b} \, {\varvec{F}}_{z}^{b} } \right]^{T} = - [{\varvec{F}}_{x}^{g} {\varvec{F}}_{y}^{g} {\varvec{F}}_{z}^{g} ]^{T} $$
(5)

The coordinate expressions of cable net free node and boundary node of mesh antenna at temperature T can be obtained according to Eqs. (3)–(5).

$$ \left[ {\begin{array}{*{20}c} {{\varvec{x}}_{g} (T)} \\ {{\varvec{y}}_{g} (T)} \\ {{\varvec{z}}_{g} (T)} \\ \end{array} } \right] = \left( {\left[ {\begin{array}{*{20}c} {{\varvec{K}}_{f}^{b} (T)} & {} & {} \\ {} & {{\varvec{K}}_{f}^{b} (T)} & {} \\ {} & {} & {{\varvec{K}}_{f}^{b} (T)} \\ \end{array} } \right] + {\varvec{K}}_{g} } \right)^{ - 1} ({\varvec{K}}_{g} \left[ {\begin{array}{*{20}c} {{\varvec{x}}_{g0} } \\ {{\varvec{y}}_{g0} } \\ {{\varvec{z}}_{g0} } \\ \end{array} } \right] + {\varvec{P}}^{b} (T)) $$
(6)
$$ \left[ {\begin{array}{*{20}c} {{\varvec{x}}_{f} (T)} \\ {{\varvec{y}}_{f} (T)} \\ {{\varvec{z}}_{f} (T)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{f}^{{}} (T)} & {} & {} \\ {} & {{\varvec{K}}_{f}^{{}} (T)} & {} \\ {} & {} & {{\varvec{K}}_{f}^{{}} (T)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{x}}_{g} (T)} \\ {{\varvec{y}}_{g} (T)} \\ {{\varvec{z}}_{g} (T)} \\ \end{array} } \right] $$
(7)
$$ {\mathbf{K}}_{f} (T) = - ({\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T){\mathbf{C}}_{f} )^{ - 1} ({\mathbf{C}}_{f}^{{\text{T}}} {\mathbf{Q}}(T){\mathbf{C}}_{g} ) $$
(8)
$$ {\mathbf{K}}_{f}^{b} (T) = {\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T){\mathbf{C}}_{f} {\mathbf{K}}_{f} (T) + {\mathbf{C}}_{g}^{{\text{T}}} {\mathbf{Q}}(T){\mathbf{C}}_{g} $$
(9)

From the above analysis, as long as the force density vector \({\varvec{q}}(T)\) at temperature T is obtained, the deformation and tension distribution of mesh antenna nodes can be known. At the design reference temperature T0, the thermal load vector \({\varvec{P}}^{b} (T)\) acting on the flexible truss is 0, and the system equilibrium equation is reduced to the system equilibrium equation without considering the space thermal effects (Nie et al. 2019a).

3 Increment equation of force density under thermal loads

The mesh antenna has interaction between flexible truss and cable net under the thermal loads, and there is coupling between cable elements. It is complicated to analyze the influence of thermal loads on the entire mesh antenna directly. Here, the two-stage strategy applying loads to mesh antenna is adopted: first, only the thermal loads are applied to the flexible truss, and the final equilibrium state of the mesh antenna under the interaction between the truss and the cable network is calculated. The incremental force density of the cable network in this state is denoted as \(\Delta {\varvec{q}}_{1}\); then, the thermals loads are applied to the cable net of the above mesh antenna, and the force density increment of the cable network in the new equilibrium state is noted as \(\Delta {\varvec{q}}_{2}\). The final force density increment \(\Delta {\varvec{q}}_{t}\) of the cable net can be expressed by the sum of the force density increments during the two load application process, namely \(\Delta {\varvec{q}}_{t} { = }\Delta {\varvec{q}}_{1} + \Delta {\varvec{q}}_{2}\). The analysis and calculation complexity can be greatly reduced by applying thermal loads step by step, but the design result is the same as that of directly applying thermal loads to the entire mesh antenna. Ignoring the shield of the antenna itself and assuming the uniform temperature distribution of the entire antenna, the force density increment equation of considering the interaction between the cable net and the flexible truss is derived as follows.

3.1 Thermal loads acting on the flexible truss

For the mesh antenna, when the surrounding temperature changes from T0 to T, the truss reaches a new equilibrium state under the combined action of thermal loads and cable-network tension. The new deformation of truss nodes \(\Delta {\varvec{X}}_{g}\) satisfies the following relation.

$$ {\mathbf{K}}_{g} \Delta {\varvec{X}}_{g} = {\varvec{P}}^{b} (T) + \Delta {\varvec{F}}^{g} $$
(10)

where \(\Delta {\varvec{X}}_{g} = [\Delta {\varvec{x}}_{g} \, \Delta {\varvec{y}}_{g} \, \Delta {\varvec{z}}_{g} ]^{T}\) represents the displacement increment of truss nodes; \(\Delta {\varvec{F}}^{g} =\) \([\Delta {\varvec{F}}_{x}^{g} \, \Delta {\varvec{F}}_{y}^{g} \, \Delta {\varvec{F}}_{z}^{g} ]^{T}\) represents the increment of the force acting on the truss by the cable net.

From Eq. (10), it is necessary to obtain the relationship between the increment of force acting on the truss by the cable net and the deformation increment of the truss nodes. The cable-network structures are divided into several groups of cable elements, which are modeled and analyzed according to Hooke's law. Consider a space cable element in the original equilibrium state with the nodes p and q as shown in Fig. 2. The position vectors of the element in the global coordinate system are denoted by xp and xq, while the corresponding nodal force vectors are denoted by Fp and Fq, respectively. Thus, the relationship between the node force vector and the node position vector of the cable element can be expressed as

$$ {\varvec{F}}_{p} = - \frac{{E_{c} A_{c} }}{{L_{k0} }}(L_{k} - L_{k0} )\frac{{{\varvec{x}}_{q} - {\varvec{x}}_{p} }}{{L_{k} }} $$
(11)

where \(E_{c} A_{c}\) is the axial stiffness of the cable element, Lk0 is the initial unstressed element length, and Lk is the stressed element length.

Fig. 2
figure 2

Cable element in equilibrium state

Full size image

The initial unstressed length of the cable element remains unchanged under the thermal loads. Ignoring the influence of higher order terms, the incremental relationship between nodal force and node position can be obtained from (Du and Bao 2013).

$$ \Delta {\varvec{F}}_{k} = {\mathbf{K}}_{ck} \Delta {\varvec{u}}_{k} $$
(12)

Where \(\Delta {\varvec{F}}_{k} = \left[ {\begin{array}{*{20}c} {\Delta {\varvec{F}}_{p} } \\ {\Delta {\varvec{F}}_{q} } \\ \end{array} } \right]\), \(\Delta {\varvec{u}}_{k} = \left[ {\begin{array}{*{20}c} {\Delta {\varvec{u}}_{p} } \\ {\Delta {\varvec{u}}_{q} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Delta {\varvec{x}}_{p} } \\ {\Delta {\varvec{x}}_{q} } \\ \end{array} } \right]\), \({\mathbf{K}}_{ck} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ck} } & { - {\mathbf{K}}_{ck} } \\ { - {\mathbf{K}}_{ck} } & {{\mathbf{K}}_{ck} } \\ \end{array} } \right]\)

$$ \begin{gathered} {\mathbf{k}}_{ck} = \frac{{{\mathbf{d}}{\varvec{F}}_{p} }}{{{\mathbf{d}}({\varvec{x}}_{p} - {\varvec{x}}_{q} )}} \hfill \\ \,\,\,\,\,\,\,\,\,=\,\frac{{E_{c} A_{c} }}{{L_{k}^{3} }}({\varvec{x}}_{p} - {\varvec{x}}_{q} )({\varvec{x}}_{p} - {\varvec{x}}_{q} )^{T} + \frac{{E_{c} A_{c} }}{{L_{k} }}\frac{{L_{k} - L_{k0} }}{{L_{k0} }}{\mathbf{I}}_{3} \hfill \\ \end{gathered} $$
(13)

and I3 is a 3 × 3 identity matrix.

The equilibrium Eq. (12) of the cable-network structures of mesh antenna can be achieved using the standard finite element assembly operation. The boundary nodes of cable net are connected with the supporting truss, whose force conditions are different from those of the internal free nodes. The equilibrium equation is rearranged in the form of first free nodes and then boundary nodes, and can be expressed as

$$ \left[ {\begin{array}{*{20}c} {\Delta {\varvec{F}}^{f} } \\ {\Delta {\varvec{F}}^{b} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{c}^{11} } & {{\mathbf{K}}_{c}^{12} } \\ {{\mathbf{K}}_{c}^{21} } & {{\mathbf{K}}_{c}^{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta {\varvec{X}}_{f} } \\ {\Delta {\varvec{X}}_{g} } \\ \end{array} } \right] $$
(14)

where \(\Delta {\varvec{X}}_{f} = [\Delta {\varvec{x}}_{f} \, \Delta {\varvec{y}}_{f} \, \Delta {\varvec{z}}_{f} ]^{T}\) and \(\Delta {\varvec{X}}_{g} = [\Delta {\varvec{x}}_{g} \, \Delta {\varvec{y}}_{g} \, \Delta {\varvec{z}}_{g} ]^{T}\) are the displacement vectors of free nodes and boundary nodes, respectively; \(\Delta {\varvec{F}}_{f}\) represents the increment of the external load applied to the free node; \(\Delta {\varvec{F}}_{b}\) represents the incremental of reaction force provided by the truss.

Only the flexible truss is subjected to thermal loads, whereas the free nodes of cable net have no external load, which satisfies \(\Delta {\varvec{F}}_{f} = 0\). The relationship between free node displacement and boundary node displacement can be expressed as follows

$$ \Delta {\varvec{X}}_{f} = - ({\varvec{K}}_{c}^{11} )^{ - 1} {\varvec{K}}_{c}^{12} \Delta {\varvec{X}}_{g} $$
(15)

Substituting Eq. (15) into the Eq. (14), the incremental \(\Delta {\varvec{F}}^{b}\) of reaction force provided by the truss can be obtained.

$$ \Delta {\varvec{F}}^{b}\,=\,{\varvec{K}}_{t} \Delta {\varvec{X}}_{g} $$
(16)

where \({\varvec{K}}_{t} = - {\varvec{K}}_{c}^{21} ({\varvec{K}}_{c}^{11} )^{ - 1} {\varvec{K}}_{c}^{12} + {\varvec{K}}_{c}^{22}\).

As the force of the flexible truss on the cable net and the force of the cable net on the flexible truss are a pair of interaction forces, the increment of the force acting on the truss by the cable net under the thermal loads satisfies \(\Delta {\varvec{F}}^{g} = - \Delta {\varvec{F}}^{b}\). Substituting it into Eq. (10), the displacement increment of truss nodes under thermal loads can be obtained.

$$ \Delta {\varvec{X}}_{g} = ({\varvec{K}}_{g} + {\varvec{K}}_{t} )^{ - 1} {\varvec{P}}^{b} (T) $$
(17)

From this, the displacement of the free nodes and boundary nodes of the cable net when the thermal loads act on the flexible truss, the variation of the cable element length can be further acquired. Thus, the corresponding increment of the cable element tension can be expressed as

$$ \Delta {\varvec{F}}_{c} = E_{c} A_{c} \frac{{\Delta {\varvec{L}}}}{{{\mathbf{L}}_{0} }} $$
(18)

where L0 represents the diagonal matrix of the initial unstressed length.

Ignoring the influence of high-order small terms, the relationship between force density increment and tension increment can be approximately expressed as

$$ \Delta {\varvec{F}}_{c} = {\mathbf{L}}\Delta q_{1} + {\mathbf{Q}}\Delta {\varvec{L}} $$
(19)

where L represents the diagonal matrix of the stressed length.

Therefore, when the thermal loads act on the flexible truss, the force density increment equation can be expressed as

$$ \Delta {\varvec{q}}_{1} = {\mathbf{L}}^{ - 1} (\Delta {\varvec{F}}_{c} - {\mathbf{Q}}\Delta {\varvec{L}}) $$
(20)

3.2 Thermal loads acting on the cable net

In our previous work (Zhang and Zhang 2022a; b), the deformation coordination equation of cable net under thermal loads is established by analyzing the relationship between the actual deformation length and the unconstrained deformation length. In the process of the above derivation, it was not assumed that the boundary nodes of the cable net were fixed. The deformation coordination equation is still valid when the research object changes from the cable-mesh reflectors to the mesh antennas.

As the supporting truss is not completely rigid, there is a complex coupling relationship between the cable net and the flexible truss. When the cable net is affected by the thermal loads, the thermal deformation of the cable net nodes occurs and the tension distribution of the cable net is changed. Meanwhile, the equilibrium relationship between the cable net and the truss is also broken, resulting in the structural deformation of the truss. The deformation of the truss will further change the existing state of the cable net. Because the sensitivity matrix established by the force density equation can only consider the interaction between cable elements, but the coupling relationship between cable net and truss is not established, it is not suitable for mesh antenna. We introduce the force density sensitivity matrix (Zhang and Zhang 2022a; b) considering the interaction between the cable net and the flexible truss to replace the force density sensitivity matrix of the cable-network structures. Therefore, when the thermal loads act on the cable net, the force density increment equation can be expressed as

$$ \Delta {\varvec{q}}_{2} = (\frac{{d{\varvec{L}}}}{{d{\varvec{q}}}} - \frac{{{\mathbf{L}}_{0} {\mathbf{L}}}}{{E_{c} A_{c} }})^{ - 1} \alpha_{c} \Delta T{\varvec{L}} $$
(21)

where \(\alpha_{c}\) is the thermal expansion coefficient of the cable element; \(\frac{{d{\text{L}}}}{{d{\text{q}}}}\) represents the sensitivity matrix of cable length with respect to the force density considering the interaction between the cable net and the flexible truss, and the detailed expression is shown in the Eletronic supplementary material.

3.3 Influence of geometric nonlinearity

The mesh antenna is a flexible structure, which has strong geometric nonlinearity. In the case of large deformation of the antenna, the nonlinear relationship between strain and displacement of the beam element is more obvious. Because the linear stiffness matrix of the supporting truss at the initial position is used in the system equilibrium equation, it is only applicable to the case where the geometric nonlinearity has little effect. To ensure that the system equilibrium Eqs. (5)–(8) has more accurate analysis results, the influence of geometric nonlinearity should be minimized in the design process. The geometric nonlinear equation of beam element can be divided into three terms (Liu et al. 1992):

The axial strain produced by axial displacement u and lateral displacement v and w is

$$ \varepsilon_{x}^{1} = \frac{{{\text{d}}u}}{{{\text{d}}x}} + \frac{1}{2}\left[ {(\frac{{{\text{d}}u}}{{{\text{d}}x}})^{2} + (\frac{{{\text{d}}v}}{{{\text{d}}x}})^{2} + (\frac{{{\text{d}}w}}{{{\text{d}}x}})^{2} } \right] $$
(22)

The axial strain caused by curvature \(\frac{{{\text{d}}^{2} v}}{{{\text{d}}x^{2} }}\) is

$$ \varepsilon_{x}^{2} = - y\frac{{{\text{d}}^{2} v}}{{{\text{d}}x^{2} }} $$
(23)

The axial strain caused by curvature \(\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}\) is

$$ \varepsilon_{x}^{3} = z\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(24)

The total axial strain of the beam element is obtained by adding the above three terms, which can be expressed as

$$ \varepsilon_{x} = \frac{{{\text{d}}u}}{{{\text{d}}x}} + \frac{1}{2}\left[ {(\frac{{{\text{d}}u}}{{{\text{d}}x}})^{2} + (\frac{{{\text{d}}v}}{{{\text{d}}x}})^{2} + (\frac{{{\text{d}}w}}{{{\text{d}}x}})^{2} } \right] - y\frac{{{\text{d}}^{2} v}}{{{\text{d}}x^{2} }} + z\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(25)

The linear stiffness matrix of beam element is calculated by linear relationship between axial displacement and axial strain, so the non-axial displacement shall be minimized in the calculation process. First of all, the form-finding design method is used to limit the deformation of the mesh antenna to a small deformation range. If the geometric nonlinearity still has a great influence, the non-axial displacement of the beam element can be constrained in the process of optimization.

4 Thermal design optimization model of mesh reflector antennas

For the paraboloid antenna, the ideal reflector equation is \(z = (x^{2} + y^{2} )/4F\). In the initial design of the cable-mesh reflector, all its nodes are located on the ideal paraboloid. When the surrounding temperature changes, the mesh antenna is deformed under the thermal loads, which causes the reflector node to deviate from the initial design position. The deviation between the deformed reflector surface and the ideal paraboloid is defined as the facet errors, which is used to evaluate the reflector surface accuracy under thermal loads, and can be expressed as

$$ \delta = \sqrt {\sum\limits_{i = 1}^{N} {\iint {[f(x,y) - g_{i} (x,y)]^{2} dxdy/\sum\limits_{i = 1}^{N} {S_{i} } }} } $$
(26)

where \(\delta\) represents the root mean square deviation (RMS) between the deformed reflector surface and the ideal paraboloid; \(f(x,y)\) is the expression of the ideal parabola and \(g_{i} (x,y)\) is the expression of the ith facet on the reflector surface; \(S_{i}\) represents the projected area of the ith facet in the xy-plane; and N is the total number of facets.

The force density vector of the cable net is selected as the design variable, and the cable net configuration is designed reasonably to improve the shape stability of the reflector surface. Denote reflector surface nodes by set H. The displacement increment of reflector node i under thermal loads can be expressed as

$$ \Delta {\varvec{X}}_{i} \user2{ = X}_{i} (T) - {\varvec{X}}_{i} (T_{0} ) $$
(27)

Eliminate the influence of the deformation direction of the nodes, and take the quadratic sum of the node deformation as the objective function, that is,

$$ f = \sum\limits_{i \in H} {\Delta {\varvec{X}}_{i}^{T} } \Delta {\varvec{X}}_{i} $$
(28)

To ensure that the reflector nodes always fall on the paraboloid in the process of optimization, the node positions of the reflector surface is constrained. For any node \(i \in H\), the z-direction deviation from the ideal paraboloid can be expressed as

$$ \delta_{i} = \frac{{x_{i0} \Delta x_{i} + \, y_{i0} \Delta y_{i} \, }}{2F} - \Delta z_{i} + (\frac{{x_{i0}^{2} + y_{i0}^{2} }}{4F} - z_{i0} \, ) = {\varvec{A}}_{i} \Delta {\varvec{u}}_{i} + b_{i} $$
(29)

where \({\varvec{A}}_{i} = [\frac{{x_{i0} }}{2F}, \, \frac{{y_{i0} }}{2F}, \, - 1]\), \(\Delta {\varvec{u}}_{i} = [\Delta x_{i} {, }\Delta y_{i} , \, \Delta z_{i} ]^{T}\), \(b_{i} = \frac{{x_{i0}^{2} + y_{i0}^{2} }}{4F} - z_{i0}\). Let \(\delta_{i} = 0\),\(\begin{gathered} A_{ei} = A_{i} \left[ {\frac{{dx_{i} }}{dq},\,\frac{{dy_{i} }}{dq},\,\frac{{dz_{i} }}{dq}} \right]^{T} \hfill \\ \hfill \\ \end{gathered}\). The z-direction deviation of node i is transformed into a function of force density vector.

$$ \delta_{i} { = }{\varvec{A}}_{ei} \Delta {\varvec{q}} + b_{i} = 0 \, i \in H $$
(30)

where \([\frac{{dx_{i} }}{{d{\text{q}}}} \, \frac{{dy_{i} }}{{d{\text{q}}}} \, \frac{{dz_{i} }}{{d{\text{q}}}}]^{T}\) represents the sensitivity matrix of the coordinate of node i with respect to the force density, and the detailed expression is shown in the Electronic supplementary material.

To avoid large position changes of reflector nodes during the optimization process, which leads to irregular-shaped facets and seriously affects the electromagnetic performance of the antenna, the cable element length of reflector is constrained during the optimization process, as shown in Eq. (31).

$$ \begin{array}{*{20}l} {(1 - \varepsilon )\varvec{L}_{0} \le \varvec{L}_{1} + \Delta \varvec{L} \le (1 + \varepsilon )\varvec{L}_{0} } \hfill \\ {(1 - \varepsilon )\varvec{L}_{0} - \varvec{L}_{1} \le \frac{{{\text{d}}\varvec{L}}}{{{\text{d}}\varvec{q}}}\Delta \varvec{q} \le (1 + \varepsilon )\varvec{L}_{0} - \varvec{L}_{1} } \hfill \\ \end{array} $$
(31)

where \({\varvec{L}}_{1}\) is the cable element length in the current optimization process; \({\varvec{L}}_{0}\) is the cable element length after the form-finding design of the mesh antenna without considering the thermal loads; \(\Delta {\varvec{L}}\) is the length increment of the cable element in the current optimization process; \(\varepsilon\)(\(0 < \varepsilon < 1\)) represents the change degree of cable element length after thermal design optimization and form-finding design.

In addition, the cable net of mesh antenna shall not be relaxed or overloaded under extreme temperature. The cable element tension shall be limited within a reasonable range. After the increment \(\Delta {\varvec{q}}_{t}\) of the force density of the cable net under the thermal loads is obtained, the force density vector at temperature T can be expressed as \({\varvec{q}}(T) = {\varvec{q}}(T_{0} ) + \Delta {\varvec{q}}_{t}\). Substituting it into Eqs. (6) and (7), the coordinates of free nodes and truss nodes of the cable net at temperature T can be obtained, respectively. Then, the tension vector F (T) of the cable element is calculated, as shown in Eq. (32).

$$ {\varvec{F}}(T) = {\mathbf{Q}}(T){\varvec{L}}(T) $$
(32)

where L (T) represents the length vector of the cable element at temperature T.

Assuming that Tmax and Tmin are the upper and lower limits of the temperature interval, respectively, and Fmin and Fmax represent the minimum and maximum tension of the cable element under thermal loads. To ensure that the cable elements in the entire temperature interval are in a reasonable tension range, the cable tension in the temperature interval is sampled and analyzed. Divide the temperature interval \(\left[ {T_{\min } ,T_{\max } } \right]\) into k steps, such as \(\left[ {T_{1} ,T_{2} \cdots T_{k} } \right]\). The cable tension under each temperature condition is guaranteed to be within the required range, as shown below.

$$ {\text{F}}_{\min } \le {\varvec{F}}(T_{i} ) \le F_{\max } {\text{ i = }}1{, }2 \cdots {\text{k}} $$
(33)

Therefore, the thermal design optimization model of mesh reflector antenna can be expressed as

$$ \begin{gathered} {\text{Find }}{\varvec{q}}{ = }[q_{1} ,q_{2} ,...,q_{m} ]^{T} \, \hfill \\ {\text{Min }}f = \sum\limits_{i \in H} {\Delta {\varvec{X}}_{i}^{T} } \Delta {\varvec{X}}_{i} \hfill \\ {\text{ S}}{\text{.t}}{. }A_{ei} \Delta q - b_{i} { = 0 }i \in H \, \hfill \\ {\text{ F}}_{\min } \le {\varvec{F}}(T_{i} ) \le F_{\max } {\text{ i = }}1{, }2 \cdots {\text{k}} \hfill \\ \end{gathered} $$
(34)

The trust-region algorithm is used to solve the above optimization model, and the finite difference method and quasi-Newton method are adopted to obtain the required gradient vector and Hessian matrix of the subproblem. Based on the above solving algorithm and optimization model, the shape stability of the reflector surface has been greatly improved. The detailed thermal optimization design process of the mesh reflector antenna is shown in Fig. 3, which can be summarized as follows:

Fig. 3
figure 3

Thermal optimization design flowchart of mesh Antennas

Full size image

  • Step1: The following conditions are given: initial configuration of the cable-network structures and flexible truss, initial force density vector of cable net \({\varvec{q}}^{0}\), upper and lower limit of cable net tension \(F_{\max }\) and \(F_{\min }\) in temperature interval, and k = 1.

  • Step 2: The increment of force density of cable net is calculated by applying thermal load step by step, and the force density vector \({\varvec{q}}(T)\) at temperature T is obtained. The coordinates of free node and boundary node of cable net at temperature T are calculated by using Eqs. (6) and (7).

  • Step 3: The quadratic sum of the reflector node thermal deformation fk, and the tension vector F of the cable net at extreme temperatures are calculated. If the difference between the absolute values of two adjacent objective functions satisfies \(\left| {f_{k} - f_{k - 1} } \right| < \varepsilon\)(\(\varepsilon\) is a given small value) is satisfied, the process is stopped; otherwise go to Step 4.

  • Step 4: The thermal optimal design model of cable-mesh reflector is established according to Eq. (34). The gradient vector \(g_{k}\) and Hessian matrix \(G_{k}\) with respect to the force density vector are approximately solved by finite difference and quasi-Newton method.

  • Step 5: The trust region subproblem is constructed and solved to determine the optimal step size dk. Calculate the approximation degree \(r_{k} = \frac{{f(q^{k} ) - f(q^{k} + d_{k} )}}{{\varphi_{k} (0) - \varphi_{k} (d_{k} )}}\) of between quadratic model and objective function. If \(r_{k} > \mu\) (\(1 > \mu > 0\)) is satisfied, the force density vector in the next iteration can be expressed as \(q^{k + 1} = q^{k} + d_{k}\); otherwise \(q^{k + 1} = q^{k}\). Let k = k + 1, return to Step 2.

5 Numerical example

The prime focus antenna with the circular configuration (Sun et al. 2022) as shown in Fig. 4 is investigated in this study. The focal length of the front cable net is 8 m and the focal length of the rear cable net is 20 m. The number of segments from the mesh center to the flexible truss was five, and the truss of the mesh reflector used 30 bay rings. The cable element number of the front and rear cable net is 210 × 2, and the element number of tension ties is 61. The materials of cable net and truss are Kevlar and carbon fiber respectively, and other detailed parameters are shown in Table 1. The design reference temperature of mesh antenna is set as 20 °C. The on-orbit temperature range of the mesh antennas can be seen from previous experimental research and simulation analysis, which is about—200 °C–100 °C (Guo et al. 2016), so the temperature interval is set to \(T \in [ - 200,100]\) °C in the following numerical example.

Fig. 4
figure 4

Geometric configuration of the prime focus antenna

Full size image
Table 1 Detailed parameters of the prime focus antenna
Full size table

The effectiveness and feasibility of thermal design optimization method of mesh antennas proved in this study are demonstrated by the comparison with the equal tension method (Zhang and Zhang 2021) and “min–max” method (Nie et al. 2020). Firstly, the equal tension method is used to design the mesh antenna as the initial parameter of thermal optimization design. Due to the limitation of the antenna height, the internal tension of the front net and rear net is set to 25 N and 50 N, and the maximum deformation of the truss is constrained to 15 mm in the equal tension design. The parameters obtained are used to calculate the surface accuracy, node deformation and tension distribution of the mesh antenna at different temperatures. Then, the “min–max” method and the proposed method are adopted to optimize the design of the same mesh antenna. To avoid the relaxation or overload of the cable element during the optimization process, the lower limit of the cable tension of the front and rear net is set to 15 N, the upper limit to 65 N, and the lower limit of the cable tension of the tension ties is set to 2 N in the temperature interval. By comparing the surface accuracy, node deformation and cable tension distribution at different temperatures, the feasibility and effectiveness of the proposed method are proved.

The reflector surface accuracy curves of the three methods in the temperature interval are shown in Fig. 5. For the equal tension method, the worst condition of the reflector is 3.38 mm at − 200 °C, and the optimal condition is 2.47 mm at 20 °C. Because the thermal effects are not taken into account in the design process, the surface accuracy of the worst condition is 36.84% lower than that of the optimal condition. For the “min–max method”, the surface accuracy of the mesh reflector at − 200 °C, −50 °C and 100 °C is 2.92 mm and 2.48 mm, respectively. The worst working condition of the mesh reflector appears at − 200 °C, and the optimal condition appears at − 50 °C. It can be found that the “min–max” method only translates the minimum value of the surface accuracy curve from 20 °C to − 50 °C compared with the equal tension method. The overall trend of the surface accuracy changing with temperature has not been improved, and large surface errors are still easy to occur at extreme temperatures. Compared with the equal tension method and the “min–max” method, although the reflector surface accuracy of the proposed method decreases 2.52 mm from the original 2.47 mm at 20 °C, the sensitivity degree to thermal loads is also greatly reduced. The worst condition of reflector surface accuracy is 2.61 mm at − 200 °C, which is only 3.57% lower than the optimal condition. The large surface errors of the mesh reflector at extreme temperature are avoided.

Fig. 5
figure 5

Reflector surface accuracy curve of three methods in temperature interval

Full size image

Compared with the equal tension method, the surface accuracy of the “min–max” method has been partially ameliorated, but the thermal stability of the reflector nodes has not been improved accordingly. The thermal deformation of the nodes is basically similar to that of the equal tension method. Therefore, the thermal deformation of the mesh reflector of the “min–max” method and the proposed method at -200 °C is taken as an example for discussion and analysis in this section. Figure 6 shows the final equilibrium state of the mesh antenna designed by the "min–max" method at -200 °C, in which Fig. 6a shows the thermal deformation of entire antenna and Fig. 6b shows the thermal deformation of the reflector surface. The minimum thermal deformation of reflector nodes is 1.58 mm, and most of them are above 2.2 mm. The final equilibrium state of the mesh antenna designed by the proposed method at -200 °C is shown in Fig. 7. It can be found that although the deformation of truss nodes has been increased from 15.83 mm to 17.57 mm, the thermal deformation of reflector nodes has been greatly improved. The maximum node deformation of the reflector surface is reduced from the original 2.85 mm to 1.56 mm. The thermal deformation of most nodes is below 1 mm except for the central and the edge nodes. The thermal stability of the reflector surface has been greatly improved in the whole temperature interval.

Fig. 6
figure 6

Final equilibrium state of the mesh antenna designed by the “min–max” method at − 200 °C a Thermal deformation of the entire antenna b Thermal deformation of the reflector surface

Full size image
Fig. 7
figure 7

Final equilibrium state of the mesh antenna designed by the proposed method at − 200 °C. a Thermal deformation of the entire antenna b Thermal deformation of the reflector surface

Full size image

The cable tension distribution of the three methods at different temperature points is shown in Table 2. Since the proposed method fully considers the influence of thermal loads on the tension distribution during the design process, the upper and lower limits of cable tension are guaranteed to be within the required range, thus avoiding the phenomenon of slackening or overload of the cable network under extreme temperatures. The running time of the three methods is also compared and analyzed, as shown in Fig. 8. Matlab Ver. R2012b is used to solve the optimization model. Computations are carried out on a personal computer with a 2.40 GHz Intel(R) Core(TM) i5-1135G7 CPU and 16 GB RAM. Since the equal tension method only needs to consider the surface accuracy at the reference temperature during the design process, the analysis time is very short and takes only 2.1 min. The “min max” method and the proposed method both use the trust region method to solve the optimization model, and the single operation time is not much different, 8.3 min and 8.1 min, respectively. Compared with the equal tension method, the "min–max" method only fine-tunes the reflector configuration, and the thermal stability of the reflector nodes was not improved. Therefore, when the mesh antenna with equal tension is used as the initial configuration for optimization, only 8 iterations are needed to obtain the design results, while the proposed method requires 19 iterations for the larger adjustment of the cable-mesh configuration and thus takes more time.

Table 2 Tension distribution of cable net designed by two methods
Full size table
Fig. 8
figure 8

Analysis time required for three methods

Full size image

6 Conclusion

To solve the problem of optimal design of mesh antenna considering space thermal effects, a thermal design optimization method of mesh antenna considering the interaction between cable net and flexible truss is proposed in this paper. Different from the traditional optimization method that can only ensure the better surface accuracy at a certain temperature point, the proposed method takes the quadratic sum of the reflector node deformation and the cable tension in the thermal environment as the objective function and design constraint, and achieves surface shape stability of the mesh reflector in the whole temperature interval. The coupling relationship between cable net and flexible truss under thermal loads is analyzed systematically, and the equilibrium equation of mesh antennas is established. The two-stage strategy applying thermal loads to the flexible truss first and then to the cable network was adopted, and the force density increment equation of the cable net under thermal loads was firstly derived. Compared with the force density method and the "minimum–maximum" method, the effectiveness and feasibility of the proposed method are proved. The surface accuracy of the worst working condition of the mesh reflector is only 3.75% lower than that of the optimal working condition. The sensitivity degree of the surface accuracy to temperature is greatly reduced, which avoids the large surface error of the mesh reflector at extreme temperatures.