A Gradient-based Sequential Multifidelity Approach to Multidisciplinary Design Optimization

Abstract

Multifidelity design optimization is a strategy that can reduce the high computational cost in cases where the high-fidelity model is too expensive to use directly in optimization. However, current multifidelity approaches cannot handle the high-dimensional problems commonly encountered in industrial settings. Furthermore, they cannot accommodate arbitrary analysis fidelities, directly handle multidisciplinary problems, or provably converge to the high-fidelity optimum. In this paper, we present a practical multifidelity approach that leverages the advantages of conventional gradient-based approaches. Rather than constructing a multifidelity surrogate, we perform a sequence of single-fidelity gradient-based optimizations. The framework determines the appropriate fidelity and updates it during the optimization process. Finally, we demonstrate the proposed approach on a multipoint aerostructural wing optimization problem with over a hundred design variables. The multifidelity approach reduces the computational cost by 59% compared to the high-fidelity approach while obtaining the same numerical optimum.

1 Introduction

Ever since the pioneering work of Haftka (1977) on aerostructural optimization, there have been significant efforts towards improving modeling capabilities within multidisciplinary design optimization (MDO), where increasingly complex analyses are being integrated into an optimization framework. However, more complex modeling incurs a drastically increased computational cost. For example, Brooks et al (2018) performed a large-scale aerostructural optimization with over a thousand design variables and ten flight conditions, which required about 50,000 CPU hours to complete. As we add further analysis capabilities to aircraft MDO, computational costs will likely become prohibitive if only high-fidelity models are used. This is particularly important as MDO is most effectively employed during the conceptual design phase, where rapid turnaround time is crucial for the design team.

In recent years there has been growing interest in multifidelity approaches, where different models with varying levels of accuracy, or fidelities, are combined within the optimization process to reduce overall computational time. Low-fidelity models are cheaper to evaluate but provide less accurate predictions. Together with a model management framework, they form the basis of a multifidelity optimization framework.

In the comprehensive review of multifidelity methods, Peherstorfer et al (2018) distinguished between global and local optimization methods for the first time. In global methods, a search is conducted over the entire feasible domain. In contrast, local methods terminate when a local optimum is found. Typically, global methods do not require gradients, and when supplied with gradient information, local methods can rapidly converge to a local optimum. We use the same characterization below and provide a short review focusing on optimization, particularly for large-scale problems. We then discuss multifidelity methods in the context of multidisciplinary problems and highlight some shortcomings of existing approaches.

1.1 Global and local methods

In global methods, a globally-accurate multifidelity surrogate model is constructed and used during optimization. These approaches are based on Bayesian optimization techniques, relying on the construction of surrogate models. Giselle Fernández-Godino et al (2019) surveyed 178 papers using multifidelity methods and found 73% of them use a multifidelity surrogate model. Unfortunately, surrogate models all suffer from the curse of dimensionality (Viana et al 2014). This has been apparent in the multifidelity optimization field, where applications typically have fewer than 20 design variables (Leifsson and Koziel 2010; Choi et al 2008; Forrester et al 2006; Nguyen et al 2013). This is in direct contrast to high-fidelity aerostructural optimizations with upwards of a thousand design variables (Brooks et al 2018), which are precisely the type of expensive optimizations that would benefit the most from multifidelity methods. Furthermore, most surrogate-based optimization techniques do not leverage gradients, nor are they equipped to handle general non-linear constraints. As such, they cannot verify the satisfaction of the Karush–Kuhn–Tucker (KKT) conditions required for optimality and cannot be shown to be convergent to the high-fidelity optimum. Instead, their termination criteria are commonly based on heuristics.

On the other hand, local methods are only concerned with finding a local minimum. With the help of gradient-based approaches, these methods can be very effective when dealing with many design variables. In this area, the primary method has been trust-region model management (TRMM), which is adapted from the single-fidelity trust-region SQP (sequential quadratic programming) method by replacing the local quadratic model with the low-fidelity model. This was investigated first by Alexandrov et al (2001), who showed that if the low-fidelity model is corrected to satisfy the first-order consistency conditions, this method is provably convergent to the high-fidelity optimum. These requirements are typically met through additive and multiplicative corrections, and the size of the trust region is updated based on the correlation between high and low-fidelity models.

Since then, there have been several developments based on the TRMM approach. Elham and van Tooren (2017) adopted a Pareto filter rather than a penalty parameter when using an augmented Lagrangian approach but was unable to obtain the high-fidelity optimum, and the computation was four times slower than the single-fidelity approach. March and Willcox (2012) combined the trust-region approach with Bayesian calibration to construct a provably-convergent multifidelity method that does not require high-fidelity derivatives. However, the number of function evaluations was still prohibitively high given the lack of gradient information. Gratton et al (2008) proposed a recursive TRMM formulation that allowed for an arbitrary number of fidelities to be used. This approach is reminiscent of multigrid methods in the numerical solution of partial differential equations, where the algorithm switches between coarse and fine grids to accelerate convergence. This method was further extended by Olivanti et al (2019) to include both a gradient-based switching criterion as well as an asynchronous validation scheme and demonstrated on an aerodynamic shape optimization problem with 191 design variables, showing a speed-up factor of 1.3.

Bryson and Rumpfkeil (2018) developed an approach based on TRMM that addressed several shortcomings of the original methodology. Since conventional TRMM uses the low-fidelity model for the local surrogate, no approximate Hessian is kept. Therefore, high-fidelity evaluations are only used to calibrate the low-fidelity output to construct the local surrogate. Instead of discarding those after each step, Bryson et al. maintain the approximate Hessian, which is used in conjunction with line search to pick the next iterate. Furthermore, the optimization reverts to using only the high-fidelity model when the trust-region size is below a threshold to accelerate the optimization convergence at the final stages. This approach was demonstrated in a subsequent paper on an aerostructural optimization problem (Bryson and Rumpfkeil 2019).

Unfortunately, TRMM-based approaches still suffer from some shortcomings. Combining multiple fidelities is a significant challenge because the constraint boundary changes based on the analysis fidelity. As such, most of the results do not include general non-linear constraints. Instead, they either include only design variable bounds or satisfy the constraint (such as the trim constraint) internally within the solver rather than leaving it to the optimizer (Olivanti et al 2019). In other cases, a penalty approach is used to combine the objective and constraints into a single objective function, resulting in an unconstrained optimization problem (Bryson and Rumpfkeil 2019).

1.2 Multifidelity MDO

Existing work on multifidelity optimization methods applied to multidisciplinary systems is unfortunately sparse. Several works mentioned earlier demonstrate their methodology on aerostructural systems (Elham and van Tooren 2017; Bryson and Rumpfkeil 2019) that are inherently multidisciplinary. Still, the low-fidelity aerodynamic model is always coupled with the low-fidelity structural model, resulting in only two distinct fidelities for the overall aerostructural system. As a result, there is no analysis on the tradeoffs of improving the fidelity of either aerodynamics or structures independently. On the other hand, Allaire and Willcox (2014) proposed a methodology for identifying and improving the discipline fidelity that contributed the most error in the objective. However, the approach does not account for the computational cost of each fidelity, nor does it consider the effect of discipline errors on constraints.

A significant difficulty with MDO problems in multifidelity optimization is the lack of hierarchy for model fidelities. For example, while it is clear that a Reynolds-averaged Navier–Stokes (RANS) computational fluid dynamics (CFD) solver has a higher fidelity relative to an Euler solver, it is not clear whether a RANS solver combined with a coarse structural grid would be a higher fidelity compared to an Euler solver using a finer structural grid. Due to the nature of a multidisciplinary problem, many fidelity combinations can arise, posing a challenge to multifidelity methods. Most existing methods cannot even account for more than two possible fidelities in total. They may also suffer from poor scaling when many fidelities are used; for example, they might require a surrogate model to be trained for each fidelity. In addition, there is an implicit assumption that all the given fidelities are useful, which is not true when considering multidisciplinary problems. Few existing methods can analyze all available fidelities and discard those that are not useful (e.g., fidelity 5 in Fig. 3). We focus on effectively identifying and managing fidelity combinations for multidisciplinary systems to tackle this challenge.

1.3 Aim of proposed method

We propose a gradient-based multifidelity optimization framework that leverages the existing high-fidelity MDO approach. We still perform a single gradient-based optimization, but during the process, we periodically evaluate the adequacy of the current model and switch to a better fidelity if necessary. Because we limit the available fidelities to be discipline specific, we first quantify the error in discipline outputs and then propagate them to multidisciplinary system-level outputs. Based on the errors and associated computational cost, an algorithm is proposed to select the appropriate fidelity for the current point in the optimization. Error-based switching criteria trigger the periodic fidelity evaluation. A robust hot-start strategy allows the subsequent optimization to progress smoothly without losing information. The proposed methodology can handle large-scale optimizations with hundreds of design variables and constraints and converge to the same high-fidelity optimum. Many fidelities can be handled, including those that are not necessarily useful, which are automatically filtered. By leveraging low-fidelity models, we can realize significant cost savings.

We note that this type of sequential optimization approach has been employed before, notably by Lyu et al (2015) and later adopted by Bons and Martins (2020). Named the “multi-level optimization acceleration technique,” the authors perform a sequence of optimizations starting from the coarsest grid and switching to a finer grid at the end of each optimization to reduce the number of iterations needed on the finest grid. Similarly, Koziel and Leifsson (2013) performed multi-level optimization with output space mapping applied to airfoil shape optimization. While the principles behind this approach are similar, they lack many of the key ingredients that make the proposed methodology scalable and general to MDO problems.

The following sections introduce the high-fidelity optimization approach and some definitions and terminology, followed by an overview of the proposed multifidelity framework. Finally, we demonstrate the framework on a multipoint aerostructural benchmark problem with over a hundred design variables.

2 Single-fidelity MDO

Before we delve into multifidelity optimization, it is essential to define the terms and concepts for the single-fidelity case. As an example, we look at a two-point aerostructural wing optimization problem, where we optimize the wing considering two operating conditions. The traditional approach to solving these types of optimization problems is by using gradient-based methods together with the multidisciplinary-feasible (MDF) architecture (Martins and Lambe 2013). Unlike gradient-free methods, gradient-based optimization methods can efficiently optimize with respect to hundreds or even thousands of design variables (Yu et al 2018).

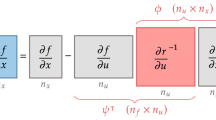
We start with a single-disciplinary analysis, i.e., a mathematical function that maps a set of inputs $\varvec{x}$ to outputs $\varvec{y}$. In this work, we focus on deterministic functions that exhibit a low level of numerical noise. We let $n_x$ be the number of inputs and $n_y$ the number of outputs. In the aerostructural example, there would be two separate disciplinary analyses. For aerodynamics, the inputs could be the angle of attack and twist distribution along a wing. The outputs could be the integrated lift and drag quantities of interest. For structures, the inputs and outputs could be the structural panel thicknesses and the stress distribution, respectively. In the aerostructural case, these two disciplines are also coupled together via surface pressures and structural displacements. The coupled system is typically converged via fixed-point iterations. Once the states converge to the multidisciplinary-feasible solution, we can compute the same discipline outputs $\varvec{y}$ for each discipline. Through the use of the coupled adjoint (Martins et al 2005), we can also compute their derivative with respect to the inputs $\varvec{x}$. The last thing to do is to combine these discipline outputs $\varvec{y}$ into system-level outputs, i.e., the objective f(x) and constraints g(x). Note that typically these functions are analytic expressions of the discipline outputs $\varvec{y}$, and therefore are straightforward to compute. For example, a common objective function in aerostructural optimization is the Breguet range equation, which combines the aircraft weight computed from structures with lift and drag predictions from the aerodynamics. To compute their sensitivities, we can analytically differentiate $\partial f/\partial y$, then apply the chain rule to combine with $\partial y/\partial x$.

However, typical engineering optimizations can involve more than a single multidisciplinary design analysis (MDA). It is common to perform multipoint optimization, where the same design is analyzed at multiple operating conditions to improve robustness. In this case, the different MDAs are entirely parallel and can be analyzed independently, but the converged MDA outputs are combined to compute the system-level quantities f and g. For example, we could use the average fuel burn over several flight conditions as the objective or apply structural constraints from multiple loading conditions. Figure 1 shows the extended design structure matrix (XDSM) diagram (Lambe and Martins 2012) of a two-point, two-discipline MDO problem.

Fig. 1

XDSM diagram of a single-fidelity MDF approach applied to a two-point, two-discipline MDO problem. In this diagram, thin black lines represent process flow, thick gray lines represent data flow, and the numbers in each block refer to the execution order

3 Multifidelity gradient-based MDO framework

It is typical in engineering applications to have multiple analysis tools available that can compute the discipline outputs $\varvec{y}$ to varying degrees of accuracy. Any discussion of accuracy requires a “truth” model to act as a reference, provided by detailed simulations or even experimentation. We assume such a model exists and is known a priori, and can be evaluated as needed to provide the reference for lower-fidelity models. Without loss of generality, we assume this is provided by a known simulation model, which we call the high-fidelity model. Then, the high-fidelity model has zero error by construction.

Given a reference model, we define fidelity to be the accuracy of a given model for a particular input vector $\varvec{x}$ and scalar output y. The fidelity of a model may vary over the design space and depend on the output quantity of interest. For example, Euler-based CFD may be a relatively high-fidelity model for predicting lift, but it is low fidelity in drag because it ignores skin-friction drag. Although higher-fidelity models are commonly expected to be more computationally expensive, it is not always the case. For example, it has been shown that in some cases, XFOIL (Drela 1989) is both cheaper and more accurate than RANS CFD when analyzing airfoils for low Reynolds number flows (Morgado et al 2016), in which case XFOIL should always be used.

In this work, we restrict fidelities to the discipline level, corresponding to a single engineering analysis. The only requirement for such fidelities is that they have the same inputs and outputs such that there is no need to perform design variable mapping between fidelities. In addition, as the framework is based on the MDF formulation used in a gradient-based setting, all available fidelities in each discipline must be fully coupled with all fidelities in the other disciplines, and the coupled derivatives must be available as well.

Fig. 2

XDSM diagram showing the proposed method applied to a single-point MDO problem

In a multidisciplinary setting, determining the available fidelities is a combinatorial problem. Suppose we have three aerodynamic fidelities and two structural fidelities. In that case, there are a total of six possible fidelity combinations for each MDA. In addition, the number of possible system-level fidelity combinations grows even more in a multipoint optimization problem, where the same design is analyzed under multiple operating conditions. This requires novel techniques to handle many possible fidelities at the optimization level.

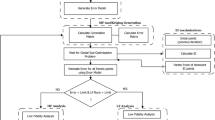
Our proposed framework is based on the single-fidelity MDF approach. We perform a sequence of such single-fidelity MDO, starting from the low-fidelity models and gradually improving the model during optimization until we reach the high-fidelity optimum. The framework tries to answer two questions: When is it time to update the fidelity choice? And what fidelity choice to update to next?

We start by quantifying the errors between the different fidelities in computing the various outputs. We then perform a single-fidelity MDO, starting from the lowest fidelity combinations and monitoring its progress. We stop the optimization when specific error-based termination criteria are met, then update the fidelity. This is a two-step process: we first propagate the errors from discipline outputs to system-level quantities, then construct error metrics to select the subsequent fidelity. We then continue the optimization with updated fidelities. This sequence of single-fidelity optimizations eventually reaches the high-fidelity case, which is allowed to continue until convergence. Figure 2 shows this process applied to a single-point MDO problem. In the following sections, we explain each of the steps in this process in more detail.

3.1 Error quantification

Unlike most existing methods, we do not assume that all available models are useful. Instead, we perform error quantification to assess the suitability of all available fidelities. As mentioned earlier, the fidelity of a given analysis method depends on both the input $\varvec{x}$ and the output $\varvec{y}$. In this work, we opted to neglect the effect of the design variables because we are focused on high-dimensional problems where the costs are prohibitive. Instead, we perform this error quantification process just once at the initial design point $\varvec{x}_0$. Although it is possible to do this quantification every time the fidelity is updated, we found that unnecessary. In all of our test cases, the errors did not change sufficiently to cause a different sequence of fidelities to be selected.

We first perform single-discipline evaluations using each available fidelity at the initial design point and record their outputs. The disciplines need to be evaluated at each operating point for a multipoint problem.

In this work, we use $\ell \in \{0, 1, 2\ldots n_\ell -1\}$ to denote the fidelity used to compute a given quantity, with $\ell =0$ as the high-fidelity reference. We then compute the error for each fidelity $\ell$ and scalar output $y_i$ using

$$\begin{aligned} \delta _{i, \ell } = \vert y_{i, \ell } - y_{i, 0}\vert . \end{aligned}$$

(1)

By construction, $\delta _{i, 0} = 0$. We also record the computational cost $c_i$ for performing each fidelity analysis, measured, for example, in CPU-seconds.

In theory, each model should fall onto the Pareto front of accuracy and computational cost—otherwise, it could be replaced by a cheaper and more accurate model. For example, in Fig. 3 we can see that fidelity 5 is not Pareto-optimal since fidelity 3 is both cheaper and more accurate. There would be no use for such fidelity in this case, and it is removed. Through this filtering process, we can identify and remove fidelities that are non-optimal. The rest of the fidelities form a Pareto front, resulting in a natural ordering. This provides the ordering for $\ell$, where a higher number indicates a decrease in fidelity.

Unlike the field of variable-fidelity optimization, where the fidelity can be arbitrarily controlled, we are not concerned with constructing Pareto-optimal models in this work. We do not examine whether each physics or numerical model choice is appropriate. Instead, we take them as provided and assess them purely on their ability to predict output quantities of interest. This way, the multifidelity framework is problem-agnostic and general for arbitrary MDO problems.

Fig. 3

Notional diagram showing a discipline analysis involving five fidelities, where fidelities 1–4 are Pareto-optimal and 5 is not. This is for a single scalar output; the relative positions of the fidelities could be different for other outputs

Because we do this for each scalar output $y_i$, the outcome may be different for different outputs. We remove a fidelity if at least one of its scalar outputs is not Pareto-optimal. The remaining fidelities now fall onto the Pareto front and can be sorted based on the cost of constructing a hierarchy of discipline fidelities.

This initially quantified error can either be assumed to be constant throughout or updated at the end of each sub-optimization so that fidelity selection is performed with the most up-to-date information. We have not found updating the error to be useful for the optimization problem demonstrated. Hence, the rest of the paper assumes that the error is fixed.

3.2 Error propagation

After quantifying the discipline errors, we propagate them to system-level outputs, which consist of the objective and constraint functions. This allows us to quantify the impact of each discipline’s fidelity on the overall system fidelity combination. Unlike the previous step, this is performed at the end of each sub-optimization because error propagation depends on the current function values.

As hinted earlier in the section, the system-level fidelities are actually fidelity combinations composed of fidelity choices for each discipline and analysis. For example, a two-point aerostructural problem would have a fidelity combination consisting of four choices. We first identify all possible fidelity combinations from which to select the subsequent fidelity combination. In this work, they are all the possible combinations where each discipline’s fidelity is better than or equal to the current fidelity. This allows for simultaneous fidelity improvements in multiple disciplines and skipping certain fidelities. For example, we could skip the medium grid and go directly from the coarse to the fine grid for CFD.

Once we identify the fidelity combinations, we then propagate their discipline errors to system-level objectives and constraints for each of those combinations. To do this, we follow the approach outlined by Allaire and Willcox (2014) and model each discipline output $y_i$ as a normal random variable $\hat{y}_{i, \ell } \sim \mathcal {N}(y_{i, \ell }, \delta _{i, \ell }^2)$. That is, we model the discipline outputs as a normal random variable centered on its discipline output and use its error as the standard deviation. In reality, many of the errors are non-normal and possibly asymmetric. For example, the discretization error in CFD is typically biased such that there is significant skewness to the distribution. This has been demonstrated in NASA’s Drag Prediction Workshop (Levy et al 2013), where the drag coefficient computed by all participating solvers were systematically over-predicted on coarser grids. Of course, if we knew the actual probability distribution function, we would use that directly instead. A normal distribution is a reasonable approximation in the absence of such information.

In reality, these discipline outputs are often correlated and not independent. This is manifested in two ways. First, outputs computed by the same analysis can be correlated. For example, because lift and drag are both functionals computed from the same converged states, a CFD simulation with a significant error in the lift is also more likely to have a more substantial error in drag. Second, outputs computed from different discipline analyses but coupled via MDA would be correlated as well. Taking the aerostructural example, if a CFD simulation had a significant error in the lift, the converged aeroelastic solution would have a different shape. Consequently, the stress distributions on the wing structures would be wrong.

In this work, we only capture the first effect. This is done by extending the probability distribution to a multivariate normal distribution with correlations between specific output quantities. For a given fidelity $\ell$, the multivariate normal distribution used is

$$\begin{aligned} \hat{\varvec{y}} \sim \mathcal {N}(\varvec{y}, \varvec{\Sigma }), \end{aligned}$$

(2)

where the covariance matrix $\varvec{\Sigma }$ is given by

$$\begin{aligned} \varvec{\Sigma }_{i,j} = \rho _{i,j} \delta _{i}\delta _{j}. \end{aligned}$$

(3)

By definition, $\rho _{i,i}=1.0$ since each output is perfectly correlated with itself. For outputs computed from the same analysis, we use a fixed value of 0.9 for $\rho _{i,j}$ throughout this work. We selected a high correlation coefficient because these outputs are computed from the same set of converged state variables. However, we do not attempt to estimate this quantity since doing so would require many function evaluations that could instead be spent on optimization.

After we model the joint probability density function of all the discipline’s outputs, we must propagate them to the objective and constraints. Fortunately, these system-level outputs are typically composed of simple analytic expressions. For example, a common objective used in aerostructural optimization is fuel burn, which is given by

$$\begin{aligned} \mathrm {FB}= m\exp \left( \frac{R\ \mathrm {TSFC}}{V\left( \frac{L}{D}\right) }\right) , \end{aligned}$$

(4)

where lift L, drag D, and mass m are the inputs. The range R, cruise speed V, and thrust-specific fuel consumption $\mathrm {TSFC}$ are constants that remain fixed throughout the optimization.

In this sense, discipline outputs become inputs to these analytic functions that are used to compute the objective and constraints. These discipline outputs are now modeled as normal random variables through the error quantification process. As a result, the system-level outputs, such as fuel burn, also become random variables. We compute the standard deviation of these system-level outputs and use that as the error metric representing the errors introduced by discipline errors. We label system-level errors as $\epsilon _{j,\ell }$ to distinguish them from discipline-level errors $\delta _{i,\ell }$, and use j to index the system-level outputs. In particular, we use $j=0$ denote the objective, and number the constraints as $j\in \{1\ldots n_\text {con}\}$.

Since the functions of interest are analytic and relatively simple, we use the Monte Carlo method to perform the error propagation. We use an adaptive, parallel implementation, where batches of samples are drawn from the joint probability distribution of the discipline outputs $\varvec{y}$, and the resulting mean and standard deviation are monitored. We terminate the Monte Carlo process when the mean and standard deviation changes are smaller than a prescribed absolute or relative tolerance. In this work, we use batches of 10,000 samples and tolerances of $10^{-3}$, which results in around $10^6$ samples on average.

Once we have the errors for objective and constraints for each fidelity combination, we can again apply a Pareto filter to remove certain fidelity combinations, as we did with discipline outputs. In this case, we filter out a fidelity combination if it is not Pareto-optimal for all system-level outputs. This is particularly important in this context as we tend to have many fidelity combinations, and it is helpful to narrow down the possibilities in fidelity selection.

3.3 Fidelity selection

Finally, we construct a single scalar error metric for each fidelity, combining the objective and constraint errors and the cost of evaluating the model. Unlike common criteria used in Bayesian optimization, this metric is not used to select the next sampling point, only the fidelity of the next sub-optimization.

For a given fidelity $\ell$, we first combine the error contributions from the objective and constraints with

$$\begin{aligned} \epsilon _\ell = \epsilon _{0, \ell } + \sum _{j=1}^{n_\text {con}} \lambda _j \epsilon _{j, \ell }, \end{aligned}$$

(5)

where $\lambda _j$ are the Lagrange multipliers associated with constraint j, that are accessed directly from the optimizer.

For constrained optimization, the Lagrange multipliers carry physical significance. At the optimum, the Lagrange multipliers provide the sensitivity of the optimum with respect to each constraint (Nocedal and Wright 2006). If a Lagrange multiplier is large, a small change in the corresponding constraint will cause a significant change in the optimum. Conversely, if a Lagrange multiplier is zero, then the constraint has no effect on the optimum and is therefore inactive by definition. In this case, the Lagrange multipliers provide a natural scaling factor, such that more influential constraints have their errors weighed more heavily, and inactive constraints are automatically ignored. This is similar to the approach by Chen and Fidkowski (2019) in combining errors in the objective and constraints when performing output-based mesh adaptation.

Lastly, we compute the error reduction $\epsilon _\ell ^\text {red}$ relative to the current fidelity, given by

$$\begin{aligned} \epsilon _\ell ^\text {red} = \epsilon _\text {current} - \epsilon _\ell . \end{aligned}$$

(6)

This gives us a measure of how much error we expect to reduce if we switch to each of the possible fidelity combinations. We also normalize $\epsilon _\ell ^\text {red}$ by the cost $c_\ell$ of each fidelity, to give us the normalized error reduction

$$\begin{aligned} \hat{\epsilon }_\ell ^\text {red} = \frac{\epsilon _\ell ^\text {red}}{c_\ell }. \end{aligned}$$

(7)

The fidelity that has the highest normalized error reduction is chosen as the next fidelity combination $\ell _\text {next}$ for optimization:

$$\begin{aligned} \ell _\text {next} = \arg \underset{\ell}\max \, \hat{\epsilon }_\ell ^\text {red}. \end{aligned}$$

(8)

By construction, both the current fidelity and the high-fidelity combination yield zero expected error reduction. This ensures that the algorithm will always eventually select the high-fidelity combination, which will be the final optimization.

Once the subsequent fidelity is chosen, a new optimization is performed, after which the fidelity is selected again. This process is repeated until we arrive at the high-fidelity optimum.

3.4 Switching criteria

In addition to selecting the next fidelity to use, we also need to determine when to switch to the updated fidelity. This is accomplished using optimization tolerances to terminate the current optimization problem and trigger an update to the fidelity selected. Because we use gradient-based optimizers, the proposed criteria are based on the KKT conditions, which are the necessary conditions for the solution of a non-linear optimization problem. The implementation of these conditions typically involves feasibility and optimality tolerances.

It is not necessary to fully converge each sub-optimization since the lower-fidelity optima may not be close to the high-fidelity optimum. Instead, we wish to terminate each sub-optimization at an appropriate point depending on the level of fidelity used—typically earlier for a lower-fidelity model. Therefore, instead of using a fixed tolerance for all sub-optimizations, we developed switching criteria that use the available error estimates of each system-level output (objective and constraints). This allows us to achieve a similar level of convergence for each fidelity relative to the accuracy of the analyses.

The first is an adaptation of the feasibility tolerance based on constraint violation $v_i(x)$, defined as

$$\begin{aligned} v_i(x) = \max \{0, g_i(x) - g_{U, i}, g_{L, i} - g_i(x)\}, \end{aligned}$$

(9)

where $g_i(x)$ are the constraints, and $g_{U, i}$ and $g_{L, i}$ are the upper and lower bounds for each constraint.

For each constraint, we require the violation to be less than a factor $\tau _f$ of the error in predicting that constraint. Recall that we denote the error in the output i for the current fidelity $\ell$ as $\epsilon _{i,\ell }$, which is computed from Monte Carlo error propagation. We place error bounds along each constraint curve, representing the uncertainty in computing these constraints due to the low-fidelity model. Figure 4 shows this graphically for an equality constraint. In the case of an inequality constraint, only the single dashed line within the infeasible region would be present. If every constraint lies within the prescribed error bound, then we have met the feasibility criterion. Mathematically, we formulate the feasibility criteria as

$$\begin{aligned} \max _i \left\{ \frac{v_i(x)}{\epsilon _{i,\ell }}\right\} \le \tau _f. \end{aligned}$$

(10)

Fig. 4

An equality constraint curve within a 2-dimensional design space. The dashed lines represent the error bound on either side of the constraint, showing the effective feasible region in between

The second criterion is an optimality condition, typically based on the objective and constraint gradients. It would be straightforward to apply the same approach as before to the optimality criterion. However, since it is a first-order condition, error estimates of the gradients are needed for each fidelity. Unfortunately, estimating these errors is costly, as it requires adjoint solutions for every output and every existing fidelity. Instead, we replace the optimality condition with a sufficient decrease condition. We monitor the objective decrease between successive major iterations during optimization. We satisfy the optimality criterion when the decrease in the objective $\Delta f$, scaled by the error in the objective, is below a prescribed optimality tolerance $\tau _o$. Mathematically, this criterion is

$$\begin{aligned} \frac{\Delta f}{\epsilon _{0,\ell }} \le \tau _o . \end{aligned}$$

(11)

While the values of $\tau _f$ and $\tau _o$ would affect the timing of each sub-optimization and alter their terminations, we have not found them to cause a large impact on the overall performance of the approach for the aerostructural optimization demonstrated here. Therefore, in this work we use $\tau _o=\tau _f={10^{-4}}$, but these values may have to be tuned for other optimization problems. These switching criteria are applied to every optimization except the final, high-fidelity optimization. In that case, the errors are zero by definition, and the error-based criteria would never be met. Instead, we must revert to using the termination criteria within the optimizer, as done for the single-fidelity optimizations. This ensures that for the final optimization, the optimum found is computed using the high-fidelity model and with a tight convergence tolerance. For a unimodal problem, this would guarantee convergence to the same high-fidelity optimum.

3.5 Optimization

Optimizations can be initialized in three ways. In a cold start, the optimization is initialized with no prior knowledge of the problem, so all the state variables are initialized to default values, except for the initial design variables provided by the user. This is the most common starting strategy taken. In a warm start, partial state information is provided by the user. This could be an initial Hessian approximation or a guess for the active set. In a hot start, the optimizer is initialized with the full state. For a deterministic optimizer, this means that we have all the information to exactly retrace an optimization.

We define optimizer states as variables that completely determine the state at each optimization iteration. Given the same set of states, a deterministic optimizer will always produce the same design for the next iteration and follow the same path within the design space (within machine precision). For an SQP-based optimizer, these states can include Lagrange multipliers, slack variables, the approximate Hessian, and many more. The exact make-up depends on the implementation of a particular optimizer.

In the context of the multifidelity framework developed, efficiently restarting an optimization is crucial to the overall performance. As we switch the fidelity from one to another, we must do so without impeding the progress of subsequent optimizations. By transferring these state variables from a lower-fidelity optimization to a higher one, we use the lower-fidelity model to learn about the optimization problem and provide better estimates for these state variables. We no longer simply use low-fidelity models to obtain a better initial guess for the subsequent optimization. Instead, we are using these models to learn about the overall characteristics of the optimization problem so that fewer iterations are required at the latter stages when more expensive fidelities are used. For example, the approximate Hessian provides curvature information with respect to the augmented Lagrangian. If the low-fidelity model is sufficiently similar to the high-fidelity model, the approximate Hessian can be used to speed up the more expensive optimizations.

For this work, we use the hot start implemented in SNOPT (Gill et al 2005), where the full state within the optimizer is stored at the end of each sub-optimization and loaded into SNOPT at the start of the next sub-optimization. However, because the fidelity is updated in between optimizations, a discontinuity is introduced in the function values, which may cause optimization difficulties. In particular, if the function value is higher under the updated fidelity, the optimizer may have trouble finding a feasible step during line search and may quit immediately after. To address this, we perform an additional function evaluation at the design where the optimization was paused. This updates the function value to that of the new fidelity but preserves other state variables that we want to re-use from the previous optimization.

3.6 Summary

A key focus of the proposed methodology is the quantification of model discrepancy and how it impacts the optimization problem under consideration. The reason for quantifying errors at a discipline level, then propagating them to the system level is that there could be so many possible fidelity combinations that performing an MDA for each would be prohibitively expensive. For example, in the aerostructural test case used in this work, there are 400 combinations for a simple two-point formulation with five aerodynamic and four structural fidelities. An optimization involving 5 flight conditions would have required $20^5={3.2\times 10^{6}}$ MDAs. Instead, we only determine the discipline errors and cheaply propagate them to the system-level outputs. The Monte Carlo evaluations take seconds to complete, compared with the computational time of several hours for an expensive MDA to converge. This approach also provides a well-defined method for selecting the next fidelity in a multidisciplinary context, based on expected error reduction.

4 Computational framework

We use the MACH Framework (MDO of Aircraft Configurations with High-fidelity) to perform aerostructural optimizations (Kenway et al 2014; Kenway and Martins 2014). It uses the MDF formulation of the optimization problem and gradient-based optimizers to perform aerostructural optimizations. We now describe the components of MACH in detail.

4.1 Geometric parameterization and mesh warping

We use pyGeo (Kenway et al 2010) for geometric parameterization. pyGeo uses free-form deformation (FFD) volumes to deform both the aerodynamic surface and structural mesh. We then use IDWarp (Secco et al 2021) to warp the aerodynamic volume mesh based on the surface mesh deformations.

This work does not consider different geometric parameterizations as fidelities, such as using different FFD volumes. We use the same FFD box for all optimizations to keep the same number of design variables to hot-start optimizations.

4.2 Aerostructural analysis and adjoint

The aerodynamic analysis is performed using ADflow (Mader et al 2020), a finite-volume CFD solver with an efficient adjoint implementation suitable for aerodynamic shape optimization. ADflow can solve both the Euler and RANS equations with various turbulence models. In this work, we use two different levels of physics as levels of fidelity: Euler and RANS with the Spalart–Allmaras (SA) turbulence model. For Euler simulations, we also compute a viscous drag correction based on a flat-plate estimate with form factor corrections (Kenway and Martins 2014).

The structure is analyzed using the Toolkit for Analysis of Composite Structures (TACS) (Kennedy and Martins 2014), a finite-element analysis (FEA) solver designed for gradient-based optimizations of thin-walled structures. We use the approach outlined by Kenway et al (2014) to solve the coupled aeroelastic system and compute the coupled adjoint.

4.3 Optimization

We use pyOptSparse (Wu et al 2020), an optimization framework tailored for large-scale gradient-based optimizations that provides wrappers for several popular non-linear optimization packages. In this work, we use the SNOPT optimization package (Gill et al 2005).

5 Aerostructural benchmark problem

We use a multifidelity wing optimization problem as the benchmark. It is a two-point aerostructural optimization, where the aerodynamics and structure are analyzed using various fidelities during optimization. The geometry consists of a single swept wing with an embedded wingbox, shown in Fig. 5. The wingbox is made of 2024 aluminum; the material properties are listed in Table 2.

Fig. 5

Geometric design variables are shown in the upper figure. Each red node indicates an FFD control point, and groups of nodes are manipulated together to form geometric design variables. Structural design variables are visualized in the lower figure, where each design variable controls the panel thickness of a distinct region of the wingbox

We use the cruise flight condition to compute the wing’s performance and the 2.5g maneuver flight condition to size the structure. These flight conditions are listed in Table 1. The design variables consist of two angles of attack, one for each flight condition and seven sectional twist variables that simultaneously warp the CFD and FEA meshes. However, the root twist is not a design variable because we have separate angles of attack for trimming the aircraft. There are also 108 panel thickness variables for the different wingbox components. These geometric and structural design variables are listed in Fig. 5.

Table 1 Operating conditions for the cruise and maneuver points

The objective of the optimization is to minimize the fuel burn $\mathrm {FB}$ given by eq. (4). The drag D and lift L are computed from the cruise point, and the flow speed is computed from the cruise Mach number and altitude. The range R and thrust-specific fuel consumption are given as constants, and the mass m is computed from

$$\begin{aligned} m = 2\times m_\text {struct} + m_\text {extra}, \end{aligned}$$

(12)

where $m_\text {struct}$ is the structural mass of the wingbox as computed by FEA, and $m_\text {extra}$ is a constant value meant to emulate the fuselage and other mass not accounted for in the structural model. All the relevant constants are listed in Table 2.

Table 2 Reference values for the aerostructural test case

Table 3 Optimization problem formulation

There are also several constraints in this problem. We constrain the lift and weight for both the cruise and maneuver flight conditions, taking the load condition into account. We also have manufacturing constraints for the panel thickness variables, such that the difference in thickness between adjacent panels is less than 2.5 mm. These are sparse linear constraints that can be satisfied easily by the optimizer. Structural stress constraints are enforced at the maneuver flight condition. These stress constraints are aggregated using the Kreisselmeier–Steinhauser (KS) function (Lambe et al 2017), ultimately resulting in three constraints: one each for the ribs and spars, upper skin and stringers, and lower skin and stringers. The entire optimization problem formulation is summarized in Table 3.

The structure of the discipline outputs computed at the cruise and maneuver points is shown in Fig. 6, where the different types of correlations are color-coded. As mentioned in Sect. 3.2, the diagonal entries in green are unity by definition. The correlation between outputs computed by the same analysis is shown in blue, and the correlation resulting from the coupled MDA is shown in red. We capture the first two correlations in this work, but not the third.

Fig. 6

Correlation matrix for a two-point aerostructural problem, where all correlations are taken into account. Blue entries indicate correlations between outputs computed by the same analysis, and red entries indicate correlation as a result of the coupled MDA

There are several fidelities available for the aerodynamic and structural disciplines. For aerodynamics, we use both RANS with the SA turbulence model and Euler solutions with a skin-friction correction. In addition, there are different discretizations available: three meshes for RANS and two for Euler, for a total of five fidelities. For structures, there are two discretizations and two finite-element solution orders possible for a total of four fidelities. In total, there are 20 possible aerostructural fidelity combinations for each operating point, giving a total of 400 choices. The available fidelities are listed in Table 4. This shows that even for a small MDO problem, the number of possible fidelity combinations grows quickly. A rigorous and scalable fidelity management framework is needed to handle this increasing complexity.

Table 4 Fidelities available for aerodynamic and structural analyses, together with the number of degrees of freedom and computational cost

6 Results

We perform two optimizations: the first uses the proposed multifidelity approach, and the second uses only the high-fidelity model.

First, we examine the multifidelity results. The process begins with the initial error quantification phase, where we perform single-discipline evaluations to determine the errors in computing discipline outputs. For each of these outputs, we can generate a scatter plot of cost against error for each output and each fidelity shown in Figs. 7 and 8.

Fig. 7

Pareto front for aerodynamic fidelities, showing that not all fidelities are optimal

Fig. 8

Pareto front for structural fidelities, showing that not all fidelities are optimal

We make several observations here. First, not all available fidelities are useful fidelities. For example, the fine Euler fidelity E0 is not Pareto-optimal for computing any aerodynamic quantities and is dominated by R2, the coarse RANS solution. Second, the Pareto-optimality of a fidelity depends on the quantity of interest. For structures, the fidelity O3L1 is not Pareto-optimal for the KS stress constraints but is optimal for computing the structural mass. In the current framework, we still filter out such fidelities as we require each potential fidelity to be Pareto-optimal for all outputs for which it is responsible. Lastly, the scatter plots could be different if analyzed at another design point, resulting in the removal of different fidelities. We do not consider such effects in this work.

After filtering out these non-optimal fidelities, we perform a single-fidelity optimization using the lowest fidelity available. Once terminated via the criteria from Sect. 3.4, we propagate the discipline errors to system-level objectives and constraints. Figure 9 shows the Pareto plot of cost against error, analogous to Figs. 7 and 8 but for system outputs. Each point corresponds to a fidelity combination, and the error is computed through Monte Carlo simulations. After applying another Pareto filter, we compute the composite metric $\hat{\epsilon }_\ell ^\text {red}$. Finally, we select the subsequent fidelity based on this metric.

Fig. 9

Pareto plot of objective errors $\epsilon _{0, \ell }$ against cost for all 400 possible fidelity combinations, showing that many are not Pareto-optimal. The corresponding plot for constraint $\mathrm {KS}_0$ is shown on the bottom

A new optimization is then performed, hot-started from the previous one. This process continues until we reach the final, high-fidelity optimization, which is allowed to continue to completion. Table 5 lists the sequence of fidelities taken, along with the computational costs. For comparison, we perform a reference optimization starting from the same initial design but using only the high-fidelity models. Overall, the multifidelity approach took 41% of the computational cost compared to the single-fidelity approach while effectively finding the same numerical optimum. The difference in the objective between the two designs is $2\times 10^{-3}$kg, for a relative difference of $4\times 10^{-8}$.

Table 5 Sequence of fidelities for the aerostructural optimization, showing the fidelity used, the computational costs, and the number of major iterations taken

A total of nine sub-optimizations were taken, each one hot-started from the previous optimization. As expected, the early, low-fidelity optimizations took many iterations to build up a more accurate approximate Hessian. In contrast, the later optimizations converged in far fewer iterations. As a result, although the number of major iterations was twice as much as the single-fidelity optimization, the overall computational cost was far lower. This also demonstrated the robustness of the hot-start approach that enabled us to perform nine sub-optimizations without losing progress in between.

Looking at the sequence of fidelities chosen, we see that the algorithm preferred to improve the cruise aerodynamics fidelity more than the maneuver analysis. This preference makes sense because both lift and drag values are needed from the cruise point, but only lift is needed for maneuver. Because the error in the lift is typically higher than the error in the drag for a given fidelity, it was more important to improve the cruise aerodynamic fidelity. This is commonly done in single, high-fidelity optimizations, where the maneuver aerodynamics is often analyzed using a lower-fidelity model, such as by using a coarser grid (Brooks et al 2017). Furthermore, structural fidelity is more important for the maneuver point than cruise because it computes all the stress constraints. Naturally, the fidelity selection algorithm improves the maneuver structural fidelity more quickly than the cruise counterpart.

However, some of the selections could improve, particularly for the cruise structural fidelity. The algorithm waited until the final optimization to switch to the high-fidelity structural model for the cruise analysis. This is because the only output directly computed by the cruise structural solver is the structural mass. The mass is computed accurately for all structural fidelities because it is a simple linear computation. This results in an insignificant contribution in the objective error from the mass computation. These two effects, combined with the relative insensitivity of the fuel burn objective with respect to the structural mass (Kenway and Martins 2014), result in the selection algorithm favoring lower-fidelity models for the cruise structural analysis. The error introduced by using a low-fidelity structural model is more than just an inaccurate mass computation. A lower-fidelity structural model would yield inaccurate structural displacements because of the coupled aerostructural analysis. This would result in an inaccurate aeroelastic flying shape and, therefore, inaccurate lift and drag computations. This coupled effect corresponds to the red entries in the correlation matrix shown in Fig. 6, which are not yet accounted for. In the future, we plan to address this issue and improve the sequence of fidelities chosen.

Now, we examine the optimizations in more detail. First, we plot the intermediate designs at the end of each sub-optimization to show the sequence of optimizations. Figure 10 shows the structural panel thicknesses at the end of each sub-optimization. The initial design of uniform thickness is also shown. Similarly, Fig. 11 shows the corresponding structural failure when analyzed with the same fidelity as used in optimization, where a value of 1.0 indicates the yield limit. Despite the loose convergence tolerance of earlier optimizations, their final stress distributions are still quite close to being optimal, with significant regions of the wingbox close to the yield limit. Since the vast majority of the design variables are these structural thicknesses, their rapid convergence is a good indication of the proposed methodology’s effectiveness.

Fig. 10

Sequence of structural panel thicknesses at the end of each sub-optimization, showing the rapid convergence in the early optimizations

Fig. 11

Sequence of stress failure values at the end of each sub-optimization, where a value of 1.0 indicates the yield limit

Next, we plot some design variables over the optimization history in Fig. 12, comparing the progress made by the single and multifidelity approach. We have selected design variables plotted against major iterations throughout the optimization on the top. As expected, the single-fidelity approach took significantly fewer major iterations to arrive at the optimum. However, this is misleading because the earlier iterations in the multifidelity approach are significantly cheaper. When adjusted for the computational cost, the multifidelity approach is much quicker, as shown on the bottom. The earlier, cheaper optimizations required far fewer resources. By the time we start the last few expensive optimizations, the designs are so close to the optimum that only a few iterations are needed.

Fig. 12

Selected design variables during the course of optimizations. Because we hot start each optimization, these lines are continuous. Despite taking more iterations to converge, due to cheaper, lower-fidelity models, the design variables converged more quickly when measured using computational cost

Fig. 13

Selected function outputs during the course of optimizations. The discontinuity is due to the same design being analyzed by different fidelities

Similarly, we plot the optimization history for a few representative outputs in Fig. 13. Unlike design variables, these outputs are not continuous across optimizations since the same design analyzed using different fidelities will yield different outputs. Nevertheless, the outputs still converge relatively quickly when plotted against computational cost.

Fig. 14

Normalized distance from the initial to the final optimum

Figure 14 shows the normalized distance traversed by the two optimizations, which provides a good idea of the progress made throughout the optimizations. Because the design variables vector $\varvec{x}$ is composed of entries of varying magnitudes, the design variables are first scaled element-wise following the scaling factors in Table 6. These scaled design variables $\hat{\varvec{x}}$ are then used to compute a scalar distance metric at each optimization iteration, using

$$\begin{aligned} d(\hat{\varvec{x}}_i) = \frac{\left\| \hat{\varvec{x}}_i-\hat{\varvec{x}}_\text {final} \right\| _2}{\left\| \hat{\varvec{x}}_\text {initial}-\hat{\varvec{x}}_\text {final} \right\| _2}. \end{aligned}$$

(13)

This distance metric is normalized such that the initial design vector $\varvec{x}_0$ is one unit distance away from the final high-fidelity optimum. Throughout the optimizations, the design gradually converges to the final optimum.

Table 6 Normalization factors on the design variables used to compute distances within the design space

From Fig. 14, the multifidelity approach uses the low-fidelity optimizations at the beginning to make significant progress towards the final optimum while using minimal computational resources. The first five optimizations cost less than 1% in total but can obtain a design that is 70% of the distance to the final optimum. However, it is worth noting that not all the optimizations took the design closer to the optimum. For example, the third optimization took the design further away. This is not unexpected since there is no guarantee that the distance will reduce monotonically throughout. Due to the nature of SQP, the optimization will typically follow the constraint boundary once a feasible point is found. This may result in a circuitous path within the design space. Ultimately, as we improve the fidelities used and tighten the termination criteria, we see the optimization rapidly converging to the final optimum.

Fig. 15

Optimization metrics as reported by SNOPT over the course of the optimizations

Lastly, we plot the merit function, the feasibility, and the optimality tolerances for the optimization in Fig. 15, as computed by SNOPT. The merit function is defined as the augmented Lagrangian plus a quadratic penalty term for constraint violations and is used during line search to find an appropriate step length. The feasibility and optimality tolerances are used as termination criteria and are good metrics for judging the progress of the optimization. Because of the efficient hot start, later optimizations in the multifidelity approach can quickly reduce the feasibility and optimality compared with the single-fidelity approach that also used the most expensive high-fidelity model. Furthermore, the feasibility and optimality plots show that the earlier optimizations were not fully converged. Instead, the error-based switching criteria terminated each optimization at an appropriate time without over-converging on the lower-fidelity models.

Overall, we see that the multifidelity approach uses more iterations compared to the single-fidelity approach, but the majority of those iterations were spent on the low-fidelity models. This allowed the optimizer to “learn” the optimization problem by building up the approximate Hessian while moving closer to the final optimum. The final few optimizations using higher-fidelity models took fewer iterations and offered significant computational savings. Ultimately, a 59% cost reduction is achieved while obtaining the same numerical optimum.

7 Conclusion

We present a novel multifidelity approach to perform multipoint, multidisciplinary design optimization. By leveraging existing gradient-based techniques, we preserve key capabilities, such as handling large-scale optimizations with hundreds of design variables and constraints, as well as provable convergence to the high-fidelity optimum. In addition, the framework can handle a large number of fidelities, automatically filtering out those that are not considered useful and selecting appropriate fidelities during optimization.

The approach first quantifies the errors and costs in each fidelity analysis. We then perform a sequence of single-fidelity optimizations, robustly hot-starting the optimization each time to preserve all state variables within the optimizer. Each optimization is terminated by error-based feasibility and optimality criteria. We then propagate the discipline errors to system-level objective and constraint function and construct a single metric used to select the subsequent fidelity. This process is repeated until we arrive at the high-fidelity optimum.

We demonstrate the approach on a two-point aerostructural wing optimization problem, using a mixture of fidelities with varying physics and discretization. A total of nine sub-optimizations were performed, where the chosen fidelities were intuitive to understand from an engineering perspective. For example, the algorithm favored improving the maneuver structural fidelity early because it is both relatively cheap and important. The multifidelity approach arrived at the same numerical optimum using only 41% of the computational cost compared to the high-fidelity approach. The low-fidelity models were effective in making progress towards the high-fidelity optimum and providing a good initial guess for the approximate Hessian and other optimizer states. As a result, few major iterations are needed in the higher-fidelity optimizations, resulting in significant cost savings.

It would be interesting to apply the approach to other large-scale applications in future work to see if similar performance is realized.