Non-newtonian laminar 2D swirl flow design by the topology optimization method

Abstract

The performance of fluid devices, such as channels, valves, nozzles, and pumps, may be improved by designing them through the topology optimization method. There are various fluid flow problems that can be elaborated in order to design fluid devices and among them there is a specific type which comprises axisymmetric flow with a rotation (swirl flow) around an axis. This specific type of problem allows the simplification of the computationally more expensive 3D fluid flow model to a computationally less expensive 2D swirl flow model. The topology optimization method applied to a Newtonian fluid in 2D swirl flow has already been analyzed before, however not all fluids feature Newtonian (linear) properties, and can exhibit non-Newtonian (nonlinear) effects, such as shear-thinning, which means that the fluid should feature a higher viscosity when under lower shear stresses. Some fluids that exhibit such behavior are, for example, blood, activated sludge, and ketchup. In this work, the effect of a non-Newtonian fluid flow is considered for the design of 2D swirl flow devices by using the topology optimization method. The non-Newtonian fluid is modeled by the Carreau-Yasuda model, which is known to be able to accurately predict velocity distributions for blood flow. The design comprises the minimization of the relative energy dissipation considering the viscous, porous, and inertial effects, and is solved by using the finite element method. The traditional pseudo-density material model for topology optimization is adopted with a nodal design variable. A penalization scheme is introduced for 2D swirl flow in order to enforce the low shear stress behavior of the non-Newtonian viscosity inside the modeled solid material. The optimization is performed with IPOPT (Interior Point Optimization algorithm). Numerical examples are presented for some 2D swirl flow problems, comparing the non-Newtonian with the Newtonian fluid designs.

1 Introduction

In order to improve the performance of fluid devices, such as channels, valves, nozzles, and pumps, an optimization method may be used. Particularly, the topology optimization method can be used to obtain a generic optimized shape from a given design domain.

The topology optimization method started with structural optimization. It was adapted for fluid optimization by Borrvall and Petersson (2003) for 2D flow channel design. The adaptation that was performed is that the solid material is modeled by means of a porous medium (Darcy law) instead of varying the material properties as it is done in structural optimization. A high porosity would mean that it is modeling fluid, and a low porosity would mean that it is modeling solid. Intermediate porosity values are allowed in order to relax the optimization problem from binary to real values. This topology optimization approach can also be called “pseudo-density approach,” since it is based on the value of a design variable (called pseudo-density) distributed throughout the entire design domain. Other topology optimization approaches include the “level-set method” (Duan et al. 2016; Zhou and Li 2008), and topological derivatives (Sokolowski and Zochowski 1999; Sá et al. 2016). In this work, the pseudo-density approach is used. Some advantages of the pseudo-density approach are rapid and robust convergence, weak dependence on the initial distribution of the design variable, and dealing with multiple constraints (Deng et al. 2013).

The topology optimization method has already been applied to a wide variety of flow types, such as Stokes flows (Borrvall and Petersson 2003), Darcy-Stokes flows (Guest and Prévost 2006; Wiker et al. 2007), Navier-Stokes flows (Evgrafov 2004; Olesen et al. 2006), slightly compressible flows (Evgrafov 2006), non-Newtonian flows (Pingen and Maute 2010), turbulent flows (Yoon 2016; Dilgen et al. 2018), thermal-fluid flows (Sato et al. 2018; Ramalingom et al. 2018), and unsteady flows (Nørgaard et al. 2016). Some fluid devices that have already been designed through topology optimization are valves (Song et al. 2009), mixers (Andreasen et al. 2009), rectifiers (Jensen et al. 2012), and flow machine rotors (Romero and Silva 2014).

Among the existing fluid flow problems, there is a specific type which comprises axisymmetric flow with a rotation (swirl flow) around an axis, being able to model hydrocyclones, some pumps and turbines, and fluid separators. This specific type of problem allows the simplification of the computationally more expensive 3D fluid flow model to a computationally less expensive 2D swirl flow model. This simplified model has already been applied in topology optimization for Newtonian fluid (water) to design 2D swirl flow devices (Alonso et al. 2018), and Tesla-type pump devices (Alonso et al. 2019).

Since not all fluids feature Newtonian (linear) properties and can exhibit non-Newtonian (nonlinear) effects, the optimized topologies may vary. This is shown in the topology optimization performed by Pingen and Maute (2010) for 2D channel design considering blood flow according to the Carreau-Yasuda model. Topology optimization has also been performed for non-Newtonian fluid for bladed blood pump design (modified Cross model) (Romero and Silva 2017), arterial by-pass grafts (modified Cross model) (Zhang and Liu 2015; Hyun et al. 2014; Kian 2017), roller-type blood viscous micropumps (power-law model) (Zhang et al. 2016), aneurism implants (Jiang et al. 2017), and viscoelastic rectifier design (viscoelastic Oldroyd-B model) (Jensen 2013). A generic non-Newtonian fluid can feature three types of characteristics (illustrated in Fig. 1):

• Stress-dependence: Change in viscosity when under different stress levels, which can be given as shear-thinning (“pseudoplastic” behavior, such as in blood (Cho and Kenssey 1991), activated sludge (Garakani et al. 2011), and ketchup (Bayod et al. 2008)), shear-thickening (“dilatant” behavior, such as the mixture of corn starch and water), or Bingham plastic/ pseudoplastic (such as concrete (Ferraris and deLarrard 1998));

• Viscoelasticity: Viscous and solid elastic behavior when under deformation, in which the shear stress can be expressed in a time-dependent form (differential, rate, or integral) (Quarteroni et al. 2000) (such as in a Bogers fluid (Jensen 2013)). This way, viscoelasticity can model creep, stress relaxation, and hysteresis;

• Time-dependence: Change in viscosity with time when under a given load, which can be given as thixotropy (viscosity decreasing with time) or rheopecty (viscosity increasing with time) (such as in colloidal and particle suspensions) (McArdle et al. 2012; Barnes 1997).

Fig. 1

Possible behaviors for non-Newtonian fluids

Since blood is a non-Newtonian fluid whose rheology has been extensively analyzed (Cho and Kenssey 1991; Quarteroni et al. 2000), features applications in the design of medical devices (Slaughter et al. 2010; Zhang and Liu 2015), and has even been used in topology optimization by various authors (Pingen and Maute 2010; Romero and Silva 2017; Zhang and Liu 2015, 2016; Hyun et al. 2014; Kian 2017), it is the non-Newtonian fluid considered in this work. It is observed that blood features: shear-thinning (due to the formation of macroaggregates (called “roleaux”) at low strain rates (Quarteroni et al. 2000)), viscoelasticity (since younger red blood cells can deform and aggregate more than older red blood cells (Vlachopoulos et al. 2011)), and thixotropy (due to time changes in structural arrangements at the microscopic level (Anand and Rajagopal 2017)). Since blood is not a homogenous fluid, being composed of plasma, red blood cells (erythrocytes), white blood cells (leukocytes), platelets (thrombocytes), lipoproteins, and ions (Behbahani et al. 2009), there are limits to which it can be considered a single continuous fluid. Near walls, there is a thin layer composed of plasma, without any red blood cells, which only features significant effect on the blood viscosity when the fluid flow path is comparable with the size of red blood cells (Fåhræus-Lindqvist effect) (Quarteroni et al. 2000).

Since the Carreau-Yasuda model seems to represent well the rheological properties of blood and also offers high flexibility for adjusting experimental curves, it is the shear-thinning model selected for this work.

Thus, the main objective of this work is to apply the topology optimization formulation to design 2D swirl flow devices considering a non-Newtonian fluid (blood). The objective of the optimization is to minimize the relative energy dissipation considering the viscous, porous, and inertial effects (Alonso et al. 2019; Borrvall and Petersson 2003). The 2D swirl laminar fluid flow modeling is solved by using the finite element method. The traditional material model of fluid topology optimization (Borrvall and Petersson 2003) is adopted by considering nodal design variables. A penalization scheme is introduced for 2D swirl flow in order to enforce the low shear stress behavior of the non-Newtonian viscosity inside the modeled solid material. The implementation is performed in the FEniCS platform, by using the adjoint method for calculating sensitivities (Farrell et al. 2013), IPOPT (Interior Point Optimization algorithm) for solving the optimization problem (Wächter and Biegler 2006), and MUMPS for solving the equations of the weak form of the problem (Amestoy et al. 2001).

This paper is organized as follows: in Section 2, the flow model for the non-Newtonian 2D swirl flow is briefly derived; in Section 3, the weak formulation of the problem is presented together with the finite element modeling; in Section 4, the topology optimization problem is stated by considering the Brinkman model and non-Newtonian penalization; in Section 5, the numerical implementation is briefly described; in Section 6, numerical examples are presented; and in Section 7, some conclusions are inferred.

2 Equilibrium equations

The fluid flow is modeled by the continuity and linear momentum (Navier-Stokes) equations, considering laminar flow, incompressible fluid, and steady-state regime.

2.1 2D swirl flow model

By considering a rotating reference frame, the continuity and Navier-Stokes equations according to the Brinkman model are (Munson et al. 2009; White 2011; Romero and Silva 2014)

$$ \nabla \bullet\textbf{\textit{v}} = 0 $$

(1)

$$ \rho \nabla \textbf{\textit{v}} \bullet\textbf{\textit{v}} = \nabla {\bullet}\textbf{\textit{T}} + \rho \textbf{\textit{f}} - 2\rho (\boldsymbol{\omega}{\wedge}\textbf{\textit{v}}) - \rho \boldsymbol{\omega}{\wedge}(\boldsymbol{\omega}{\wedge}\textbf{\textit{s}}) - \kappa (\alpha )\textbf{\textit{v}}_{\text{mat}} $$

(2)

where v is the relative velocity of the fluid, ρ is the density of the fluid, p is the pressure, μ is the dynamic viscosity, ρ f is the body force per unit volume acting on the fluid, s is position, ∧ is used to denote cross product, − 2ρ(ω∧v) is the Coriolis force, − ρω∧(ω∧s) is the the centrifugal inertial force, and T is the stress tensor given by

$$ \ \ \ \ \ \textbf{\textit{T}} = 2\mu \boldsymbol{\epsilon} - p\textbf{\textit{I}}, {\boldsymbol{\epsilon} = \frac{1}{2}(\nabla \textbf{\textit{v}} + \nabla {\textbf{\textit{v}}}^{T})} $$

(3)

In (2), a porous medium is considered for modeling solid in topology optimization. Thus, a resistance force (Darcy effect) is included (− κ(α)v_mat) (Vafai 2005), which is directly proportional to the fluid velocity in relation to the solid material

$$ \textbf{\textit{f}}_{r} = - \kappa (\alpha)\textbf{\textit{v}}_{\text{mat}} $$

(4)

where κ(α) is the inverse permeability (“absorption coefficient”), v_mat is the velocity in relation to the porous material (v_mat = (v_r, v_𝜃 − ω_matr, v_z), where ω_mat is the rotation of the porous media in relation to the reference frame), and α is the pseudo-density. The pseudo-density can attain values ranging from 0 (solid) to 1 (fluid), and is used as the design variable in topology optimization.

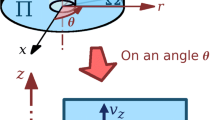
The 2D swirl flow model (“2D axisymmetric model with swirl”) considers axisymmetry and cylindrical coordinates (see Fig. 2). Thus, the position and velocity become

$$ \textbf{\textit{s}} = (r,\ 0,\ z) = r\textbf{\textit{e}}_{r} + z\textbf{\textit{e}}_{z} $$

(5)

$$ \textbf{\textit{v}} = (v_{r},\ v_{\theta},\ v_{z}) = v_{r}\textbf{\textit{e}}_{r} + v_{\theta}\textbf{\textit{e}}_{\theta } + v_{z}\textbf{\textit{e}}_{z} $$

(6)

Fig. 2

Representation of the 2D swirl flow model

Also, from axisymmetry, the derivatives in the 𝜃 direction are zero (i.e., $\frac {\partial (\ )}{\partial \theta } = 0$). The equations for the 2D swirl flow model are further developed in Alonso et al. (2018).

2.2 Non-Newtonian fluid flow model

In this work, the non-Newtonian fluid being considered is blood. The study performed by Gijsen et al. (1999) showed that the main contributor to the blood behavior should be the shear-thinning effect, which is time-independent. In order to model it, the Carreau-Yasuda model is selected, which is capable of adequately representing the blood behavior (Gijsen et al. 1999; Pratumwal et al. 2017; Leondes 2000). The Carreau-Yasuda model is given by (Cho and Kenssey 1991; Bird et al. 1987)

$$ \mu(\dot{\gamma}_{\text{m}}) = \mu_{\infty} + (\mu_{0} - \mu_{\infty}) [1 + (\lambda \dot{\gamma}_{\text{m}})^{a}]^{\frac{n - 1}{a}} $$

(7)

where $\dot {\gamma }_{\text {m}}$ is the shear rate magnitude (also called “scalar shear rate”) (Abraham et al. 2005), λ is a time constant (“characteristic time”), n is an exponential factor, a is the Yasuda coefficient, μ₀ is the maximum dynamic viscosity, and $\mu _{\infty }$ is the minimum dynamic viscosity.

The shear rate magnitude (“scalar shear rate”, $\dot {\gamma }_{\text {m}}$) and the shear stress magnitude (“scalar shear stress”, τ_m) are given by (Lai et al. 2009; Tesch 2013; Arora et al. 2004)

$$ \begin{array}{@{}rcl@{}} \tau_{\text{m}} &=& \mu(\dot{\gamma}_{\text{m}}) \dot{\gamma}_{\text{m}}\\ \dot{\gamma}_{\text{m}} &=& \sqrt{2 \boldsymbol{\epsilon}\bullet\boldsymbol{\epsilon}} \end{array} $$

(8)

where $\boldsymbol {\epsilon } = \frac {1}{2} (\nabla \textit {\textbf {v}} + \nabla \textit {\textbf {v}}^{T})$ is the viscous stress deformation tensor and “∙” is the inner product as defined in Gurtin (1981).

According to Cho and Kenssey (1991) and Pingen and Maute (2010), for blood, the constants in the Carreau-Yasuda model are λ = 1.902 s, n = 0.22, a = 1.5, μ₀ = 0.056 Pa s, and $\mu _{\infty } = 0.00345 \text { Pa s}$. The variation of the dynamic viscosity (μ) in function of the shear rate ($\dot {\gamma }_{\text {m}}$) and the rheological diagram are illustrated in Fig. 3. The corresponding Newtonian fluid model is shown in dashed lines, with a constant viscosity of $\mu = \mu _{\infty } = 0.00345 \text { Pa s}$.

Fig. 3

Non-Newtonian fluid based on the Carreau-Yasuda model for blood flow

2.3 Boundary value problem

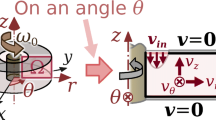
The boundaries for the computational domain when considering a 2D swirl flow model may include the symmetry axis or not, which shown in Fig. 4. Then, the boundary value problem for the 2D swirl flow model can be stated as follows Alonso (2018, 2019).

$$ \begin{array}{@{}rcl@{}} \rho \nabla \textbf{\textit{v}}\bullet\textbf{\textit{v}} = \nabla \bullet\textbf{\textit{T}} (\mu(\dot{\gamma}_{\text{m}})) + \rho \textbf{\textit{f}} - 2\rho (\boldsymbol{\omega}{\wedge}\textbf{\textit{v}})\\ ~~~~~~~~~~~~~~~~~~~~~~ - \rho \boldsymbol{\omega}{\wedge}(\boldsymbol{\omega}{\wedge}\textbf{\textit{s}}) - \kappa (\alpha )\textbf{\textit{v}}_{\text{mat}} && \text{ in } \mathrm{\Omega} \\ \nabla \bullet\textbf{\textit{v}} = 0{\kern5.3pc} && \text{ in } \mathrm{\Omega}\\ \textbf{\textit{v}} = \textbf{\textit{v}}_{in}{\kern4.7pc} && \text{ on } \mathrm{\Gamma}_{\text{in}}\\ {}\textbf{\textit{v}} = \textbf{{0}}{\kern5.3pc} && \text{ on } \mathrm{\Gamma}_{\text{wall}}\\ {v_{r}} = {0} \text{ and } \frac{\partial v_{r}}{\partial r } = \frac{\partial v_{\theta}}{\partial r } = \frac{\partial v_{z}}{\partial r } = \frac{\partial p}{\partial r } = {0} && \text{ on } {\Gamma}_{\text{sym}}\\ \textbf{\textit{T}}(\mu(\dot{\gamma}_{\text{m}})) \bullet \textbf{\textit{n}} = \textbf{{0}}{\kern4pc} && \text{ on } \mathrm{\Gamma}_{\text{out}} \end{array} $$

(9)

where Ω, Γ_in, Γ_wall, Γ_sym, and Γ_out are shown in Fig. 4. A fixed velocity is imposed on the inlet boundary (Γ_in), and the no-slip condition is imposed on the walls (Γ_wall). On the symmetry axis (Γ_sym), the derivatives in relation to the r coordinate are considered to be zero, as well as the radial velocity. The outlet boundary (Γ_out) is modeled by considering a stress-free condition (i.e., open to the atmosphere). $\textit {\textbf {T}}(\mu (\dot {\gamma }_{\text {m}}))$ is the stress tensor (T) considering the non-Newtonian fluid model (7).

Fig. 4

Boundaries for 2D swirl flow devices

3 Finite element method

3.1 Weak formulation

The equilibrium equations of the 2D swirl flow model are solved through the finite element method. By using the weighted-residual and Galerkin methods for the mixed (velocity-pressure) formulation, (Reddy and Gartling 2010; Alonso et al. 2018)

$$ {R}_{c} = {\int}_{\mathrm{\Omega} }[\nabla\bullet\textbf{\textit{v}}]{{\textit{w}}}_{p}rd\mathrm{\Omega} $$

(10)

$$ \begin{array}{@{}rcl@{}} {R}_{m} &=& {\int}_{\mathrm{\Omega} }\left[\rho \nabla \textbf{\textit{v}}\bullet\textbf{\textit{v}} - \rho \textbf{\textit{f}} + 2\rho (\boldsymbol{\omega}{\wedge}\textbf{\textit{v}}) \right.\\ && + \left. \rho \boldsymbol{\omega}{\wedge}(\boldsymbol{\omega}{\wedge}\textbf{\textit{s}})\right]\bullet{\textbf{\textit{w}}}_{v}rd{\Omega} + {\int}_{\mathrm{\Omega} } \textbf{\textit{T}}(\mu(\dot{\gamma}_{\text{m}})){\bullet}(\nabla {\textbf{\textit{w}}}_{v})r d{\Omega}\\ && - \oint_{{\Gamma}}(\textbf{\textit{T}}(\mu(\dot{\gamma}_{\text{m}}))\bullet{\textbf{\textit{w}}}_{v}){\bullet}\textbf{\textit{n}}rd{\Gamma} + {\int}_{\mathrm{\Omega} }{{\kappa }}(\alpha)\textbf{\textit{v}}_{\text{mat}}{\bullet}\textbf{\textit{w}}_{v}rd{\Omega}\\ \end{array} $$

(11)

where c refers to the ”continuity equation”, m refers to the ”linear momentum equation” (i.e., the Navier-Stokes equations), and the test functions are given by w_p for the pressure p, and $\textit {\textbf {w}}_{v} =\left [\begin {array}{ll}{\textit {w}}_{v,r}\\{\textit {w}}_{v,\theta }\\{\textit {w}}_{v,z} \end {array}\right ]$ for the velocity v. As in Alonso (2018, 2019), since the integration domain (2πrdΩ) features a constant multiplier (2π), which does not influence when solving the weak form, (10) and (11) are divided by 2π.

Since the two test functions (w_p and w_v) are mutually independent, (10) and (11) can be summed, leading to a single equation

$$ F = {R}_{c} + {R}_{m} = 0 $$

(12)

3.2 Finite element modeling

For fluid flow, the coupling between the discretizations of the pressure and the velocity may result in instabilities and non-physical oscillations in the pressure (Langtangen and Logg 2016). This can be avoided by choosing a finite element which obeys the LBB (Ladyžhenskaya-Babuška-Brezzi) condition (Girault and Raviart 2012; Guzmán et al. 2013; Brezzi and Fortin 1991). A general proof for the validity of the LBB condition for any constitutive equation and formulation is still lacking (Reddy and Gartling 2010). However, the work done by Galvin (2013) verifies the convergence rates for a non-Newtonian fluid modeled by the Cross model, which is similar to the Carreau-Yasuda model used in this work. A common choice for the finite element choice is using Taylor-Hood elements (see Fig. 5), which are considered very stable and provide 3rd-order spatial accuracy for velocities (Varchanis et al. 2019). The lowest degree Taylor-Hood elements are given by using a 1st degree interpolation for pressure (P₁ element) and a 2nd degree interpolation for velocity (P₂ element). For the pseudo-density (design variable), a 1st degree interpolation (P₁ element) is chosen.

Fig. 5

Finite elements chosen for the state variables (pressure and velocity) and the design variable (pseudo-density)

4 Formulation of the topology optimization problem

4.1 Material model for the inverse permeability

In fluid topology optimization, the aim is to obtain a sufficiently discrete distribution of the pseudo-density in the design domain (0 for solid and 1 for fluid). In order to relax the subtle transition (binary values) between solid and fluid, it is necessary to allow an intermediate porous medium (“gray,” with a pseudo-density between 0 and 1) (real values). Borrvall and Petersson (2003) suggest a convex interpolation function for the inverse permeability:

$$ \kappa (\alpha) = \kappa_{\max} + (\kappa_{\min} - \kappa_{\max})\alpha \frac{1 + q}{\alpha + q} $$

(13)

where the maximum and minimum values of the inverse permeability (κ(α)) are, respectively, $\kappa _{\max \limits }$ and $\kappa _{\min \limits }$. The penalization parameter (q > 0) controls the convexity (relaxation) of the material model. Large values of q mean a less relaxed material model.

4.2 Material model for the non-Newtonian viscosity

When α = 0 (solid), the velocity of the fluid is expected to be minimum, and, therefore, the shear rate magnitude ($\dot {\gamma }_{\text {m}}$) is expected to be near zero. In such case, (7) gives $\mu (\dot {\gamma }_{\text {m}}) \approx \mu _{0}$ (i.e., the viscosity assumes its higher non-Newtonian value). Since even a small fluid velocity value can cause the shear rate magnitude ($\dot {\gamma }_{\text {m}}$) not to approach zero inside the solid material, a penalization scheme is proposed in order to improve the behavior of $\mu (\dot {\gamma }_{\text {m}}) \approx \mu _{0}$ inside the solid material for 2D swirl flow. The penalization scheme consists of changing the non-Newtonian viscosity for 2D swirl flow to the following equation

$$ \mu(\alpha, \dot{\gamma}_{\text{m}}) = \mu_{0} + (\mu(\dot{\gamma}_{\text{m}}) - \mu_{0})\alpha \frac{1 + q}{\alpha + q} $$

(14)

where the viscosity value in the solid is μ₀ and the viscosity value in the fluid is $\mu (\dot {\gamma }_{\text {m}})$ (7). The penalization parameter (q > 0) is the same of (13).

This approach is similar to the one proposed by Pingen and Maute (2010). However, the “solid material viscosity” being imposed here is the “highest” viscosity (μ₀) and not the “lowest” viscosity ($\mu _{\infty }$), which was used by Pingen and Maute (2010). Also, Pingen and Maute (2010)’s penalization was used to counter a coupling issue between the non-Newtonian viscosity and the inverse permeability of the Lattice Boltzmann Method, which is the kinetic approach for modeling fluid flow, while this work uses the hydrodynamic approach for modeling fluid flow (continuity and Navier-Stokes equations) and aims to improve the consistency of the non-Newtonian viscosity with the expected/desired values inside a modeled solid material. A non-Newtonian penalization approach proposed by Hyun et al. (2014) in the context of 2D flow topology optimization says that using the non-Newtonian penalization would avoid numerical instability due to the non-linearity of (7).

Figure 6 shows the material model presented in (14). The upper part of the figure shows a 3D plot of the material model for the non-Newtonian viscosity: when α = 0 (solid), the non-Newtonian viscosity is $\mu (\alpha , \dot {\gamma }_{\text {m}}) \approx \mu _{0}$; when α = 1 (fluid), the non-Newtonian viscosity is $\mu (\alpha , \dot {\gamma }_{\text {m}}) = \mu (\dot {\gamma }_{\text {m}})$ (i.e., (7)). The material model is then represented by the surface connecting the curves of α = 0 (solid) and α = 1 (fluid). The upper part of the figure shows an almost straight line for the material model (high penalization parameter (q)), and the “slice” shown in the lower part of the figure shows some possible values for the penalization parameter (q). As indicated in the lower part of the figure, the “lower limit” of the viscosity ($\mu (\dot {\gamma }_{\text {m}})$) depends on the shear rate magnitude ($\dot {\gamma }_{\text {m}}$): a lower shear rate magnitude means a higher “lower limit” for the viscosity, and a higher shear rate magnitude means a lower “lower limit” for the viscosity.

Fig. 6

Material model for the non-Newtonian viscosity

The main consequence of (14) is that the non-Newtonian viscosity becomes higher and uniform inside a modeled solid material (see Appendix 2). From performed tests, the pressure and velocity values are mostly affected during the topology optimization iterations, while there are still “gray” regions. The effect of the non-Newtonian penalization in the pressure and velocity values becomes small in the final optimized topology (assuming that $\kappa _{\max \limits }$ from (13) is high enough so as to block fluid flow).

Throughout this work, the penalization shown in (14) is referred to as “non-Newtonian penalization.”

4.3 Topology optimization problem

The topology optimization problem can be formulated as follows.

(15)

where f is a specified volume fraction, $V_{0} = {\int \limits }_{\mathrm {\Omega }_{\alpha }}2\pi r d\mathrm {\Omega }_{\alpha }$ is the volume of the design domain (represented as Ω_α), Φ_rel(p(α),v(α), α) is the objective function, and p(α) and v(α) are the pressure and velocity obtained from the solution of the boundary value problem (9), which features an indirect dependency with respect to the design variable α. In this work, the design domain is chosen as the entire computational domain (Ω_α = Ω).

4.4 Objective function

The objective function is chosen as the relative energy dissipation considering inertial effects, as defined in Alonso et al. (2019) for a rotating reference frame, which is based on the energy dissipation defined in Borrvall and Petersson (2003). By considering zero external body forces,

$$ \begin{array}{@{}rcl@{}} \mathrm{\Phi}_{\text{rel}} & =& {\int}_{\mathrm{\Omega} }\left[\frac{1}{2}\mu(\dot{\gamma}_{\text{m}}) (\nabla \textbf{\textit{v}} + {\nabla \textbf{\textit{v}}}^{T})\bullet(\nabla \textbf{\textit{v}} + {\nabla \textbf{\textit{v}}}^{T})\right]2\pi rd{\Omega} \\ & &+ {\int}_{\mathrm{\Omega} }\boldsymbol{\kappa} (\alpha )\textbf{\textit{v}}_{\text{mat}}\bullet\textbf{\textit{v}}2\pi rd\mathrm{\Omega} \\ && + {\int}_{\mathrm{\Omega} } (2\rho (\boldsymbol{\omega}{\wedge}\textbf{\textit{v}}) + \rho \boldsymbol{\omega}{\wedge}(\boldsymbol{\omega}{\wedge}\textbf{\textit{s}}))\bullet\textbf{\textit{v}}2\pi rd\mathrm{\Omega} \end{array} $$

(16)

where $\mu (\dot {\gamma }_{\text {m}})$ is the non-Newtonian viscosity. Note that, since ω = ω₀e_z and from (5), the Coriolis term (2ρ(ω∧v)∙v) is zero.

4.5 Sensitivity analysis

The sensitivity is given by the adjoint method as

$$ \left( \frac{dJ}{d\alpha}\right)^{\text{*}} = \left( \frac{\partial J}{\partial \alpha}\right)^{\text{*}} - \left( \frac{\partial F}{\partial\alpha}\right)^{\text{*}}{\boldsymbol{\lambda}}_{J} $$

(17)

$$ \left( \frac{\partial {F}}{\partial (\textbf{\textit{v}}, p)}\right)^{\text{*}}{\boldsymbol{\lambda}}_{J} = \left( \frac{\partial J}{\partial(\textbf{\textit{v}}, p)}\right)^{\text{*}} \text{(adjoint equation)} $$

(18)

where J = Φ_rel is the objective function (relative energy dissipation), the weak form is given by F = 0, “ * ” represents conjugate transpose, and λ_J is the adjoint variable (Lagrange multiplier of the weak form).

5 Numerical implementation of the optimization problem

The finite element method is implemented in the FEniCS platform (Logg et al. 2012), which uses automatic differentiation and a high-level language in order to represent the weak form and functionals for later assembling of the finite element matrices. In order to implement the topology optimization method, the dolfin-adjoint library (Farrell et al. 2013) is used in order to compute the adjoint model, and IPOPT (Interior-Point Optimization algorithm) (Wächter and Biegler 2006) is used as the optimization algorithm. IPOPT uses a logarithmic barrier term for searching only in the feasible space (i.e., not violating the constraints) and augments it by using a line-search filter method (which avoids having to determine the exact value of the penalty parameter of the logarithmic barrier), and the dolfin-adjoint library has an interface for using it. Since (12) is non-linear, the finite element method is solved through the Newton-Raphson method, by solving the corresponding linearized problems with MUMPS (MUltifrontal Massively Parallel sparse direct Solver) (Amestoy et al. 2001).

The topology optimization method is implemented as shown in Fig. 7. From an initial guess for the pseudo-density distribution in the design domain, a simulation is performed with FEniCS. This initial simulation is used by dolfin-adjoint in order to derive the adjoint model, which is then used in the IPOPT optimization loop. The optimization loop continues until the specified tolerance (convergence criterion) is reached.

Fig. 7

Flowchart illustrating the numerical implementation of the topology optimization problem

In the case the reader uses another software platform in which the dolfin-adjoint library is not available, the corresponding continuous adjoint model for the 2D swirl flow problem is shown in Appendix 1. Since it may be difficult and laborious to derive the continuous adjoint model for the non-Newtonian viscosity of (7), an alternative approach is shown, which uses automatic differentiation only for the sensitivity of the non-Newtonian viscosity.

6 Numerical results

In the numerical results, the fluid is considered as blood, with the non-Newtonian dynamic viscosity ($\mu (\dot {\gamma }_{\text {m}})$) given by (7). Since the compressibility of blood is small, according to Hinghofer-Szalkay and Greenleaf (1987), blood may be assumed as incompressible, with a density (ρ) of 1056 kg/m³.

The finite element meshes are structured, composed of rectangular partitions of 4 triangular elements each (see Fig. 8).

Fig. 8

Distribution of triangular elements in a rectangular partition

In order to have a better numerical conditioning for calculating the weak form, functionals and sensitivities, and also improving the convergence rate, the MMGS (Millimeters-Grams-Seconds) unit system is used, which means that the length and mass units are multiplied by a 10³ factor.

The convergence criterion for the Newton-Raphson method performed for the simulation with MUMPS is based on residuals: absolute tolerance of 10^− 10 and relative tolerance of 10^− 9. The convergence criterion for the optimization is based on a desired tolerance of 10^− 10 for the optimality error of the IPOPT barrier problem, which essentially corresponds to the maximum norm of each KKT condition (Wächter and Biegler 2006).

External body forces are not considered for the numerical examples (ρ f = (0, 0, 0)), and the specified fluid volume fraction (f ) is chosen as 30%. The porous media is assumed with the same rotation as the reference frame, therefore, v_mat = v. Also, $\kappa _{\min \limits } = 0 \text { kg/}(m^{3} s)$. The initial guess for the pseudo-density (design variable) is a uniform distribution of α = f − 1%, where f is the specified volume fraction and 1% is a margin for the initial guess not to violate the volume constraint (because of the numerical accuracy of the calculations). The plots of the optimized topologies consider the values of the design variable α in the center of each finite element. The letter n is used to denote rotation in rpm, and the greek letter ω is used to denote rotation in rad/s.

The pseudo-density (design variable) values of the optimized topologies are post-processed by a threshold function (i.e., a step function):

$$ \alpha_{\text{th}} = \left\{\begin{array}{ll}1\text{ (fluid), if }\alpha \geqslant 0.5\\ 0\text{ (solid), if }\alpha < 0.5 \end{array}\right. $$

(19)

After applying the threshold function, the mesh is cut, removing the solid material (α = 0) from the computational domain (see Fig. 9). This enables the final simulation to be performed with the Navier-Stokes equations without the inverse permeability term (i.e., not including the Brinkman model), thus enabling a comparison of the optimized topologies achieved with different optimization parameters. In all optimized topologies, the final values of the pseudo-density (design variable) are close to the bounds (i.e., to α = 0 and α = 1).

Fig. 9

Post-processing used for the optimized topologies

For simplicity, the Reynolds number is calculated as the maximum value of the local Reynolds number based on the external diameter:

$$ {\text{Re}_{\text{ext}, \ell} = \frac{\mu(\dot{\gamma}) \left|\textbf{\textit{v}}_{\text{abs}}\right| (2 R_{{ext}})}{\rho}} $$

(20)

where $\mu (\dot {\gamma })$ is the non-Newtonian viscosity, which may vary in each position of the computational domain, v_abs is the absolute velocity, which varies in each position of the computational domain, R_ext is the most external radius of the computational domain (it is the “R_ext” of the two first examples, and the “R” of the third example), and ρ is the density.

In some of the numerical examples, a continuation scheme in the optimization parameters is performed for better conditioning the optimization, with a maximum allowed number of optimization iterations defined for each continuation step in the range of 10 to 800. In the beginning of each continuation step, the IPOPT algorithm is restarted.

6.1 Parallel channels

The first example is the design of the classical parallel channels. However, in this case, 2D swirl flow is considered. This example has been extensively treated in 2D flow topology optimization (“double pipe”) since the first fluid topology optimization article (Borrvall and Petersson 2003; Deng et al. 2018), and has even been analyzed for non-Newtonian fluid in a 2D domain (Pingen and Maute 2010). In a 2D swirl flow model, it resembles the horizontal inlet Tesla pump design presented by Alonso et al. (2019). However, it features two inlets and a large axial distance between them. In the present work, two non-rotating inlets are located at a smaller radius, and two outlets are located at a larger radius. The configuration is illustrated in Fig. 10. The flow rate (Q) is equally divided between the two inlets ($Q_{1} = Q_{2} = \frac {Q}{2}$), and the solid material distribution is optimized on the rotating walls.

Fig. 10

Design domain for parallel channels design

The finite element mesh is chosen with 100 radial and 80 axial rectangular partitions of crossed triangular elements, totaling 16,181 nodes and 32,000 elements (see Fig. 11). The input parameters and dimensions of the design domain that are used are shown in Table 1. It can be mentioned that, instead of using a uniformly high discretization in order to be able to simulate the fluid flow behavior, it is also possible to use adaptively refined/coarsened meshes (Adaptive Topology Optimization) (Evgrafov 2015; Duan et al. 2015; Gupta et al. 2020), which may be a better choice for the discretization, but is out of the scope of this work.

Fig. 11

Mesh used in the parallel channels design

Table 1 Parameters used for the topology optimization of the parallel channels

Figure 12 shows a comparison of the non-Newtonian viscosity for the optimized parallel channels designs at 100 rpm without post-processing (i.e., still including the material model). As can be seen, without the non-Newtonian penalization, the non-Newtonian viscosity shows some variation inside the solid material, which may possibly negatively influence the topology optimization. In constrast, when adding the non-Newtonian penalization, the non-Newtonian viscosity inside the solid material is much more consistent with its expected/desired value inside a solid material. The same effect is also observed at other rotations (including 0 rpm), showing that the non-Newtonian penalization may be an interesting approach for topology optimization for non-Newtonian fluid flow.

Fig. 12

Non-Newtonian viscosity in the optimized parallel channels designs for the non-Newtonian fluid flow at 100 rpm before post-processing (i.e., still including the material model) (in log scale). The contours of the optimized topologies are delimited by thin dark lines

A series of optimizations is performed for a sequence of wall rotations by considering non-Newtonian fluid (with non-Newtonian penalization) and Newtonian fluid. Figure 13 shows the objective function (relative energy dissipation) values with respect to the wall rotation for each optimized topology. The objective function values that are shown correspond to the post-processed topology (19). The maximum values for the maximum local Reynolds number ($\max \limits (\text {Re}_{\text {ext}, \ell })$) are given at 500 rpm and are evaluated as 1.21 × 10⁴ (non-Newtonian fluid) and 1.28 × 10⁴ (Newtonian fluid).

Fig. 13

Effect of the wall rotation in the non-Newtonian and Newtonian parallel channels designs

As can be seen in Fig. 13, the optimized channels show a tendency to get closer and thinner near the outlets, for both non-Newtonian and Newtonian fluid flows. The differences between the optimized designs are mainly slightly different curvatures of the parallel channels. As opposed to Borrvall and Petersson (2003) and some of the designs presented by (Pingen and Maute 2010), which perform this optimization for 2D flow, in the present example of 2D swirl flow, the channels are not merged together. This is probably mainly due to the difference in volumes for lower and higher radial positions, which can make the merged channel solution not be a minimum of the objective function. The merged channel solution was not achieved for this example even when reducing the flow rate or further relaxing the penalization parameter (q, of (13)) (i.e., using an even smaller value of q before increasing it, as in Borrvall and Petersson 2003).

In Fig. 13, it can be noticed that the channel width is reduced at larger radii, which is probably due to the volume increase at larger radii (with rate 2πr, due to the 2D swirl flow model), which increases the energy dissipation and, therefore, should have the effect of reducing the channel width. From the optimization iterations and various optimization tests, the axial position (z) of the outlet channels in relation to the outlet heights in the design domain seems to be highly dependent of how the optimization progresses, given that, when the material model is more relaxed (such as with lower values for q or with a “gray” (intermediary) distribution for α), there is an initial influence of the flow of one channel in the other. This “influence” is one of the reasons Borrvall and Petersson (2003) could achieve the merged channel solution in 2D Stokes flow. Because of the higher effect of the rotation in the energy dissipation near the outlets (due to the larger radii in the rotational tangential velocity ω₀r), the effect of the position of the outlet has a smaller sensitivity. Also, since the energy dissipation is not significantly sensitive to small channel curvatures, the topology may possibly stagnate with a non-optimal curvature before reaching a local minimum. These facts together with the “influence of one channel in relation to the other” in initially relaxed configurations of the material model, mean that, depending on the choice of the continuation parameters, different local minima or stagnated topologies can be achieved, such as channels slightly slanted towards or farther from the middle of the design domain, or with curves near the outlets. Even when using a second-order optimization algorithm (IPOPT) (Wächter and Biegler 2006), this problem is still encountered, and different continuations in the material model parameters had to be used in order to achieve straighter channel solutions.

In this numerical example, the solutions with curves near the outlets are worse local minima in relation to straighter channel solutions (i.e., the curves dissipate slightly more energy) and, therefore, are not shown in this numerical example. However, for illustration, one achievable optimized topology is shown in Fig. 14 considering Newtonian fluid flow at 100 rpm with $\kappa _{\max \limits } = 8.0\times 10^{8} \mu _{\infty }$ (kg/(m³s)). It can be noticed that the channels are curved. The optimized topology in this figure considers the continuation in the inverse permeability term starting from q = 0.1 before increasing q, while the optimized topology in Fig. 13 considers the continuation starting from q = 0.05 before increasing q.

Fig. 14

A local minimum optimized topology achievable for the Newtonian parallel channels design at 100 rpm

In Fig. 13, the optimized topologies up to 100 rpm are channels whose walls connect with almost straight inclined lines to the outlets. At 200 rpm, the optimized topologies seem to be local minima attained from the “change” in the format of the optimized topologies that happens between 100 and 300 rpm. From 300 rpm onwards, the optimized topologies start with a small straighter radial distance (r), which may help reducing the energy dissipation near the inlet for higher rotations.

The optimization schemes are shown in Table 2. The values of the optimization parameters are chosen in order for the optimized topologies to be sufficiently discrete and to block fluid flow inside the solid material (as in Alonso et al. (2018)).

Table 2 Reference parameters for the optimization schemes (steps) for the non-Newtonian and Newtonian parallel channels designs

The non-Newtonian viscosities in the optimized parallel channels designs for non-Newtonian fluid flow are plotted in Fig. 15. As can be seen, the increase in the non-Newtonian viscosity is mostly noticeable near the middle of each channel, where the shear stress is smaller. Near the walls, the non-Newtonian viscosity is decreased due to an increase in shear stress on the walls. This behavior is consistent with Fig. 3a. Also, it can be noticed that the non-Newtonian viscosity decreases with higher rotations (i.e., higher Reynolds numbers), which is due to the shear stress increasing under this condition.

Fig. 15

Non-Newtonian viscosities in the optimized parallel channels designs for non-Newtonian fluid flow (in log scale)

The convergence curves for the non-Newtonian and Newtonian designs for 100 rpm are shown in Fig. 16. The maximum Reynolds numbers ($\max \limits (\text {Re}_{\text {ext}, \ell })$) for this case are 2.21 × 10³ (non-Newtonian fluid) and 2.56 × 10³ (Newtonian fluid). The “peak” after 100 iterations corresponds to a change in the penalization parameter (q), as written in Table 2.

Fig. 16

Convergence curves for the non-Newtonian and Newtonian parallel channels designs (100 rpm)

The simulations of the optimized topologies for the non-Newtonian and Newtonian designs for 100 rpm are shown in Fig. 17. As can be seen, the non-Newtonian and Newtonian designs in this case are practically the same. The relative tangential velocity (v_𝜃) is zero on the rotating walls (no-slip condition), since, on the walls, the fluid is rotating, with an absolute tangential velocity of v_𝜃,abs = ω₀r. The simulation of the non-Newtonian design shows that the velocity changes slightly faster (along the channel) than the Newtonian design. This can be noticed by the fact that the relative tangential velocity (v_𝜃) is smaller and for a larger distance, in the Newtonian design.

Fig. 17

Optimized topologies, 3D representations, pressures, and velocities for the non-Newtonian and Newtonian parallel channels designs (100 rpm)

6.2 Two-way channel

The two-way channel consists of the same design applied for parallel channels in the previous Section. However, it is applied to crossed inlets and outlets. This example has already been treated for the 2D swirl flow model in Alonso et al. (2018), considering Newtonian fluid flow (water). The two-way channel is composed of two non-rotating fluid inlets, located at an internal and an external radius. The flow rate (Q) is equally divided between the two inlets ($Q_{1} = Q_{2} = \frac {Q}{2}$), meaning that, since the circumferential area is larger for higher radius, the internal radius inlet features a higher inlet velocity, while the external radius inlet features a smaller inlet velocity. The configuration is illustrated in Fig. 18. The solid material distribution is optimized on the rotating walls.

Fig. 18

Design domain for two-way channel design

The finite element mesh is the same used in the parallel channels design. The input parameters and dimensions of the design domain that are used are shown in Table 3.

Table 3 Parameters used for the topology optimization of the two-way channel

Figure 19 shows a comparison of the non-Newtonian viscosity for the optimized two-way channel designs at 20 rpm without post-processing (i.e., still including the material model). The effect of the non-Newtonian penalization is not so apparent as in the case of the parallel channels design (Fig. 12). The same effect is observed at other rotations (including 0 rpm).

Fig. 19

Non-Newtonian viscosity in the optimized two-way channel designs for the non-Newtonian fluid flow at 20 rpm before post-processing (i.e., still including the material model) (in log scale). The contours of the optimized topologies are delimited by thin dark lines

A series of optimizations is performed for a sequence of wall rotations by considering non-Newtonian fluid (with non-Newtonian penalization) and Newtonian fluid. This is shown in Fig. 20, from the objective function (relative energy dissipation) values with respect to the wall rotation for each optimized topology. As in the parallel channels example, the objective function values that are shown correspond to the post-processed topology (19). The maximum values for the maximum local Reynolds number ($\max \limits (\text {Re}_{\text {ext}, \ell })$) are given at 50 rpm and are evaluated as 1.24 × 10³ (non-Newtonian fluid) and 1.28 × 10³ (Newtonian fluid).

Fig. 20

Effect of the wall rotation in the non-Newtonian and Newtonian two-way channel designs

As can be seen in Fig. 20, the optimized topologies are the topologies connecting the inlets to the nearest outlets, in the form of 180^∘ curved channels, because the topology optimization identified that the curved path would dissipate less energy than the longer straight path. This is probably due to the radially varying volume (with rate 2πr, due to the 2D swirl flow model). Some minor differences can be noticed in the curved channels for non-Newtonian and Newtonian fluid flows, in which the channel side closest to the wall is larger in the Newtonian design in relation to the non-Newtonian design. This is probably due to the size of the zone in which the non-Newtonian effect is apparent. Due to the swirl effect of the fluid near the walls, as the rotation (and the Reynolds number) increases, the channel side closest to the wall slightly decreases in size.

The optimization schemes are shown in Table 4.

Table 4 Reference parameters for the optimization schemes (steps) for the non-Newtonian and Newtonian two-way channel designs

The non-Newtonian viscosities in the optimized two-way channel designs for non-Newtonian fluid flow are plotted in Fig. 21. As in the parallel channel design, the increase in the non-Newtonian viscosity is also mostly noticeable near the middle of the internal radius channel, where the shear stress is smaller. Since the external radius channel portrays a lower fluid velocity, it is under a more noticeable non-Newtonian effect from the fluid inlet. The non-Newtonian effect decreases very little for the internal radius channel with increasing rotations. However, it has a more significant decrease for the external radius channel. Overall, the same effect that is observed for parallel channels design can be seen here, with the non-Newtonian viscosity decreasing under higher rotations (i.e., higher Reynolds numbers).

Fig. 21

Non-Newtonian viscosities in the optimized two-way channel designs

The convergence curves for the non-Newtonian and Newtonian designs for 20 rpm are shown in Fig. 22. The maximum Reynolds numbers ($\max \limits (\text {Re}_{\text {ext}, \ell })$) for this case are 6.57 × 10² (non-Newtonian fluid) and 9.74 × 10² (Newtonian fluid).

Fig. 22

Convergence curves for the non-Newtonian and Newtonian two-way channel designs (20 rpm)

The simulations of the optimized topologies for the non-Newtonian and Newtonian designs for 20 rpm are shown in Fig. 23. As can be noticed, the simulation results for the internal radius channel look similar for the non-Newtonian and Newtonian designs. As for the external radius channel, the pressure drops faster for the Newtonian design, while the relative tangential velocity increases faster in the middle of the channel for the non-Newtonian design.

Fig. 23

Optimized topologies, 3D representations, pressures, and velocities for the non-Newtonian and Newtonian two-way channel designs (20 rpm)

6.3 Two-outlet channel

The two-outlet channel consists of a vertical inlet of rotating fluid, in the condition that there are two possible horizontal outlets. This example has already been treated for the 2D swirl flow model in Alonso et al. (2018), considering Newtonian fluid flow (water). The configuration is illustrated in Fig. 24. The solid material distribution is optimized on the static walls.

Fig. 24

Design domain for two-outlet channel design

The finite element mesh is chosen with 40 radial and 80 axial rectangular partitions of crossed triangular elements, totaling 6,521 nodes and 12,800 elements (see Fig. 25). The input parameters and dimensions of the design domain that are used are shown in Table 5.

Fig. 25

Mesh used in the two-outlet channel design

Table 5 Parameters used for the topology optimization of the two-outlet channel

Figure 26 shows a comparison of the non-Newtonian viscosity for the optimized two-outlet channel designs at 0.05 L/min without post-processing (i.e., still including the material model). The effect of the non-Newtonian penalization is quite apparent and the non-Newtonian viscosity, as in the other examples, is less dispersed and more consistent with its expected/desired value inside a solid material. The same effect is observed for other flow rates.

Fig. 26

Non-Newtonian viscosity in the optimized two-outlet channel designs for the non-Newtonian fluid flow at 0.05 L/min (20 rpm) before post-processing (i.e., still including the material model) (in log scale). The contours of the optimized topologies are delimited by thin dark lines

A series of optimizations is performed for a sequence of flow rates considering a fixed inlet rotation (n_in = 20 rpm) by considering non-Newtonian fluid (with non-Newtonian penalization) and Newtonian fluid. This is shown in Fig. 27, from the objective function (relative energy dissipation) values with respect to the flow rates for each optimized topology. As in the other examples, the objective function values that are shown correspond to the post-processed topology (19). The maximum values for the maximum local Reynolds number ($\max \limits (\text {Re}_{\text {ext}, \ell })$) are given at 0.1 L/min and are evaluated as 1.77 × 10² (non-Newtonian fluid) and 4.06 × 10² (Newtonian fluid). This significant difference in the Reynolds number is due to the predominance of the non-Newtonian effect (i.e., higher viscosity) in the optimized topologies for non-Newtonian fluid flow.

Fig. 27

Effect of the flow rate in the non-Newtonian and Newtonian two-outlet channel designs

As can be seen in Fig. 27, the optimized designs lead the fluid to exit the upper channel, which better minimizes the objective function (relative energy dissipation). By comparing the non-Newtonian with the Newtonian topologies, the curvature of the channel is smoother for the non-Newtonian designs: since the Newtonian fluid has a smaller viscosity, the flow is more guided by its inertia, which means that the first part of the channel can extend longer than the last part of the channel (near the outlet); in the case of the non-Newtonian fluid, the viscosity is higher far from walls, which means that the effect of the fluid inertia is reduced in the middle of the channel, leading the topology optimization to a straighter path to the outlet.

The optimization schemes are shown in Table 6. Lower flow rates may require higher values for $\kappa _{\max \limits }$, since the flow may need more “strength” to form the optimized topology. Higher flow rates may also require it, in order to block the fluid flow inside the solid material. However, if $\kappa _{\max \limits }$ is too high, it may not be possible to achieve a discrete optimized topology, which may lead to a high presence of “gray” (0 < α < 1). This means that there is a compromise in obtaining a discrete optimized topology and blocking fluid flow inside the solid material. Also, the right choice for q may also help stabilizing a discrete optimized topology: Depending on the case, it may be necessary to “relax” the material model (smaller q), which may sometimes lead to a “better local minimum” (as in Borrvall and Petersson (2003)’s double pipe); however, in other cases, when there is no local minimum that can be achieved in this way, this can hinder the achievement of a discrete topology.

Table 6 Reference parameters for the optimization schemes (steps) for the non-Newtonian and Newtonian two-outlet channel designs

The non-Newtonian viscosities in the optimized two-outlet channel designs for non-Newtonian fluid flow are plotted in Fig. 28. At 0.005 L/min, the non-Newtonian effect is easily noticeable, with a higher dynamic viscosity acting over most of the fluid domain. This effect is reduced at higher flow rates, though still keeping a considerable influence.

Fig. 28

Non-Newtonian viscosities in the optimized two-outlet channel designs (in log scale)

The convergence curves for the non-Newtonian and Newtonian designs for 0.05 L/min and 20 rpm are shown in Fig. 29. The maximum Reynolds numbers ($\max \limits (\text {Re}_{\text {ext}, \ell })$) for this case are 5.98 × 10¹ (non-Newtonian fluid) and 2.03 × 10² (Newtonian fluid).

Fig. 29

Convergence curves for the non-Newtonian and Newtonian two-outlet channel designs (0.05 L/min, 20 rpm)

The simulations of the optimized topologies for the non-Newtonian and Newtonian designs for 0.05 L/min and 20 rpm are shown in Fig. 30. As can be noticed in the tangential velocity (v_𝜃) plot, the inlet rotation is “dissipated” along the channel in a “faster” manner for the non-Newtonian design than in the Newtonian design due to the increased viscosity (non-Newtonian effect). Also, the decrease in pressure from the inlet towards the outlet seems to be more uniform in the non-Newtonian design.

Fig. 30

Optimized topologies, 3D representations, pressures, and velocities for the non-Newtonian and Newtonian two-outlet channel designs (0.05 L/min, 20 rpm)

7 Conclusions

In this work, the topology optimization formulation is applied to the 2D swirl flow model, which portrays a smaller computational cost than a 3D model, by considering a non-Newtonian fluid under laminar flow.

The numerical examples illustrate the use of the non-Newtonian formulation compared with the Newtonian formulation. The non-Newtonian formulation considers an additional penalization (non-Newtonian penalization) for 2D swirl flow, which gives a non-Newtonian viscosity distribution in the solid material that is constant and equal to the low-shear stress non-Newtonian viscosity value. This behavior is shown to be coherent with the expected/desired behavior of the fluid inside a modeled solid material.

In topology optimization, from the numerical examples, the effect of using a non-Newtonian fluid model seems to be more significant for designs including “bends” and “axial-radial” flows.

As future work, it is suggested that the non-Newtonian 2D swirl flow model is used for other non-Newtonian fluids, and in specific applications such as in pump/turbine/nozzle design.

Appendices

Appendix 1. Continuous adjoint model for the non-Newtonian 2D swirl flow

The continuous adjoint model for the 2D swirl flow problem is derived as follows. The adjoint (dual) equations for Navier-Stokes flow have already been deduced in Brandenburg et al. (2009). However, in this Appendix, they are particularized for the 2D swirl flow model in a rotating reference frame, and an approach for dealing with the non-Newtonian viscosity is suggested. In the following development, 2D coordinates are considered in the equations, the domain is given in cylindrical coordinates (in which the differential volume and area are given by, respectively, 2πrdΩ and 2πrdΓ), axisymmetry is considered ($\frac {\partial (\ )}{\partial \theta } = 0$), and the differential operators correspond to their cylindrical coordinate system versions (Lai et al. 2009).

The adjoint equation is first presented in Section 4.5 and is based on the Lagrangian function of the optimization problem, which is given by

$$ L((\textbf{\textit{v}}, p), \alpha, (\boldsymbol{\lambda}_{v}, \lambda_{p})) = J((\textbf{\textit{v}}, p), \alpha) - F((\textbf{\textit{v}}, p), \alpha, (\boldsymbol{\lambda}_{v}, \lambda_{p})) $$

(21)

where (v, p) are the state (primal) variables (velocity and pressure), α is the design variable, (λ_v, λ_p) are the adjoint (dual) variables (adjoint velocity and adjoint pressure) (that is, the adjoint variable presented in Section 4.5 separated in its components: λ_J = (λ_v, λ_p)), J((v, p), α) = Φ_rel((v, p), α) is the objective function (relative energy dissipation), and F((v, p), α, (λ_v, λ_p)) is given in (12) (i.e., (10) and (11) without the division by 2π, and with the test functions w_v and w_p replaced by the adjoint variables λ_v and λ_p, respectively).

Then, in order to obtain the weak form of the adjoint equation (F_λ = 0), the equations that compose (21) need to be derived in function of the state variables (v, p), as shown in Section 4.5. This is given by the directional derivative of the Lagrangian function (21), with respect to the state variables (v and p) and in the directions given by $\textit {\textbf {w}}_{\lambda ,v} =\left [\begin {array}{ll}{\textit {w}}_{\lambda ,v,r}\\{\textit {w}}_{\lambda ,v,\theta }\\ {\textit {w}}_{\lambda ,v,z} \end {array}\right ]$ and w_{λ, p} (test functions for the adjoint equations), respectively for each state variable:

$$ F_{\lambda} = L((\textbf{\textit{v}}, p); \underline{(\textbf{\textit{w}}_{\lambda,v}, {\textit{w}}_{\lambda,p})}) = L(\textbf{\textit{v}}; \underline{\textbf{\textit{w}}_{\lambda,v}}) + L(p; \underline{{\textit{w}}_{\lambda,p}}) $$

(22)

where $L(\textit {\textbf {v}}; \underline {{\textit {\textbf {w}}}_{\lambda ,v}})$ is the directional derivative of L with respect to v in the direction of w_{λ, v}, and $L(p; \underline {\textit {w}_{\lambda ,p}})$ is the directional derivative of L with respect to p in the direction of w_{λ, p}.

The dependency of the non-Newtonian viscosity (μ) with respect to the state variables (v, p) can be separated by applying the chain rule. In this case,

$$ \begin{array}{@{}rcl@{}} F_{\lambda} &=& L((\textbf{\textit{v}}, p), \mu(\textbf{\textit{v}}, p); \underline{(\textbf{\textit{w}}_{\lambda,v}, {\textit{w}}_{\lambda,p})}) \\ &=&L((\textbf{\textit{v}}, p); \underline{(\textbf{\textit{w}}_{\lambda,v}, {\textit{w}}_{\lambda,p})})\\ &&+ \frac{\partial L(\mu)}{\partial \mu} \mu((\textbf{\textit{v}}, p); \underline{(\textbf{\textit{w}}_{\lambda,v}, {\textit{w}}_{\lambda,p})}) \end{array} $$

(23)

where $\mu ((\textit {\textbf {v}}, p); \underline {(\textit {\textbf {w}}_{\lambda ,v}, {\textit {w}}_{\lambda ,p})})$ is the directional derivative of μ with respect to (v, p) in the direction of (w_{λ, v}, w_{λ, p}). In the case of the non-Newtonian viscosity given by (7), which does not depend on p, $\mu ((\textit {\textbf {v}}, p); \underline {(\textit {\textbf {w}}_{\lambda ,v}, \textit {w}_{\lambda ,p})}) = \mu (\textit {\textbf {v}}; \underline {\textit {\textbf {w}}_{\lambda ,v}})$. Note that, if $\mu = \mu _{\infty }$ (Newtonian viscosity), $\mu ((\textit {\textbf {v}}, p); \underline {(\textit {\textbf {w}}_{\lambda ,v}, \textit {w}_{\lambda ,p})}) = 0$.

The first term of the weak form of the adjoint equation (23) ($L((\textit {\textbf {v}}, p); \underline {(\textit {\textbf {w}}_{\lambda ,v}, {\textit {w}}_{\lambda ,p}}))$) becomes, after dividing the forward equations by 2π:

(24)

where T(w_{λ, v}, w_{λ, p}) is the stress tensor (3) calculated by substituting v and p by w_{λ, v} and w_{λ, p}, respectively; and the symbols “(+)” and “(–)” serve to indicate the signal that is already considered in the equation and that is multiplying each adjoint form.

The second term of the weak form of the adjoint equation (23) ($\frac {\partial L(\mu )}{\partial \mu } \mu (\textit {\textbf {v}}; \underline {\textit {\textbf {w}}_{\lambda ,v}})$) can be calculated from (11) as, after dividing the forward equations by 2π:

(25)

where $\frac {\partial \textit {\textbf {T}}(\textit {\textbf {v}}, p)}{\partial \mu } = \nabla \textit {\textbf {v}} + \nabla \textit {\textbf {v}}^{T}$. Since it may be difficult and laborious to calculate $\mu (\textit {\textbf {v}}; \underline {\textit {\textbf {w}}_{\lambda ,v}})$ (sensitivity of the non-Newtonian viscosity) from (7) or (14 (or any other non-Newtonian fluid with a more complex constitutive equation), this term may be calculated by automatic differentiation, such as the algorithm used in the FEniCS platform.

From (23), it would be possible to derive the strong form of the adjoint equation (by applying Gauss’s Theorem of Divergence). However, it would require the sensitivity of the non-Newtonian viscosity to be analytically evaluated. Since the finite element method only requires the weak form of the adjoint equation, this step does not need to be performed.

The Dirichlet boundary conditions from (9) assume constant velocity values, which means that their corresponding adjoint boundary conditions are homogeneous (i.e., equal to zero). By also including the Neumann boundary condition, the adjoint boundary conditions become, from (9):

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{v} = \textbf{{0}} ~~~~~~~~~~~~~~~&& \text{ on } \mathrm{\Gamma}_{\text{in}}\\ \boldsymbol{\lambda}_{v} = \textbf{{0}} ~~~~~~~~~~~~~~~&& \text{ on } \mathrm{\Gamma}_{{{\text{wall}}}}\\ {\lambda_{v,r}} = {0} \text{ and } \frac{\partial (\ )}{\partial r } = {0} && \text{ on } \mathrm{\Gamma}_{\text{sym}}\\ \textbf{\textit{T}}({\textbf{\textit{w}}}_{\lambda, v}, {{\textit{w}}}_{\lambda, p}) \bullet \textbf{\textit{n}} = \textbf{{0}} && \text{ on } \mathrm{\Gamma}_{\text{out}} \end{array} $$

(26)

where λ_{v, r} is the radial component of the adjoint velocity (λ_v = (λ_{v, r}, λ_{v, 𝜃}, λ_{v, z})). It can also be mentioned that, in (25), the term which relies on $\left (\frac {\partial \textit {\textbf {T}}(\textit {\textbf {v}}, p)}{\partial \mu }{\bullet }\boldsymbol {\lambda }_{v}\right ){\bullet }\textit {\textbf {n}}$ is zero on Γ_out, because T(v, p)∙n = 0 on Γ_out (9) ($\left (\frac {\partial \textit {\textbf {T}}(\textit {\textbf {v}}, p)}{\partial \mu }{\bullet }\boldsymbol {\lambda }_{v}\right ){\bullet }\textit {\textbf {n}}$$= \left (\frac {\partial \textit {\textbf {T}}(\textit {\textbf {v}}, p)}{\partial \mu }{\bullet }\textit {\textbf {n}}\right ){\bullet }\boldsymbol {\lambda }_{v} = \left (\frac {\partial [\textit {\textbf {T}}(\textit {\textbf {v}}, p){\bullet }\textit {\textbf {n}}]}{\partial \mu }\right ){\bullet }\boldsymbol {\lambda }_{v} = \textbf {{0}}$, since T is symmetric and n does not depend on μ).

Appendix 2. Simulation of the effect of the non-Newtonian penalization

In order to check the effect of the non-Newtonian penalization, a test example of a channel with an obstacle in the middle is simulated (see Fig. 31). The obstacle is modeled by using a rotating material model (ω_mat = ω₀) located in the middle of the channel, the flow rate is 0.5 L/min, the rotation is 20 rpm, and the dimensions are given by: H = 15.0 mm, R = 10.0 mm, r_o = 2.5 mm, and h_o = 2.5 mm. The mesh is the same as the one shown in Fig. 25. The outlet boundary condition is a weak imposition of zero pressure on the outlet, imposing the radial and axial components of the velocity (v_r, v_z) to be perpendicular to the outlet section (i.e., with zero tangential component) (Dirichlet boundary condition), and imposing zero normal stress on the interface (n∙Tn = 0) (Neumann boundary condition). The demonstration of this boundary condition is shown in Alonso et al. (2018) for 2D swirl flow, and in Barth and Carey (2007) for 2D flow.

Fig. 31

Computational domain for the obstacle simulation

When the material model is blocking the fluid flow (i.e., with a sufficiently high value in $\kappa _{\max \limits }$, chosen in this case as $\kappa _{\max \limits } = 2.5 \times 10^{8} \mu _{\infty }$), there is little difference between using only the inverse permeability (“κ(α)”), or using both inverse permeability and non-Newtonian penalization (“κ(α), μ(α)”). This is shown in Fig. 32a. Figure 32b shows the difference fractions for the modeled obstacles, which correspond to the absolute difference of the variable in the cut and modeled obstacles divided by the range of the variable: $f_{x} = \frac {|x_{\text {material}} - x_{\text {cut}}|}{\max \limits (x_{\text {cut}}) - \min \limits (x_{\text {cut}})}$, where x is the variable being considered: relative tangential velocity (v_𝜃), pressure (p) or non-Newtonian viscosity (μ). For the magnitude of the radial-axial velocity ($v_{rz,\text {mag}} = \|\textit {\textbf {v}}_{rz}\| = \|(v_{r}, v_{z})\| = \sqrt {{v_{r}^{2}} + {v_{z}^{2}}}$), the definition is changed to $f_{{v}_{rz,\text {mag}}} = \frac {\|\textit {\textbf {v}}_{rz,\text {material}} - \textit {\textbf {v}}_{rz,\text {cut}}\|}{\max \limits (\|\textit {\textbf {v}}_{rz,\text {cut}}\|) - \min \limits (\|\textit {\textbf {v}}_{rz,\text {cut}}\|)}$. From Fig. 32b: $f_{{v}_{rz,\text {mag}}}$ is mostly small, but features a 0.33 peak near the edge for “κ(α), μ(α)”; $f_{{v}_{\theta }}$ is even smaller, with a maximum value of 0.091; f_p is higher near the edge of the obstacle, reaching a relatively high peak of 0.5 in “κ(α), μ(α)”; and f_μ is higher around the obstacle for “κ(α), μ(α)”. As can be noticed, the highest values of the difference fractions are concentrated near the obstacle / edge of the obstacle. These differences, and, more specifically, the higher values of f_μ on the obstacle, are mainly due to the nodal interpolation used for the design variable (α), which does not exactly match the effect of the “cut obstacle,” such that it “slightly softens” the effect of the edge because of the linear interpolation, and “forces,” when considering the non-Newtonian penalization (“κ(α), μ(α)”), the nodal values of the non-Newtonian viscosity (μ) to the maximum dynamic viscosity value (μ₀).

Fig. 32

Plots of cut and modeled obstacles ($\kappa _{\max \limits } = 2.5 \times 10^{8} \mu _{\infty }$, q = 1000, $\kappa _{\min \limits } = 0$)

The difference between simulation results is more apparent for lower values of $\kappa _{\max \limits }$, which may occur during topology optimization due to the interpolation of the material model (“gray values”). Therefore, $\kappa _{\max \limits }$ is reduced to $\kappa _{\max \limits } = 2.5 \times 10^{6} \mu _{\infty }$ in Fig. 33. From Fig. 33, when including the non-Newtonian penalization (“κ(α), μ(α)”), the radial-axial velocity ((v_r, v_z)) is more reduced inside the modeled obstacle than in the case without the non-Newtonian penalization (“κ(α)”). This is due to the higher and uniform non-Newtonian viscosity inside the modeled obstacle. The relative tangential velocity (v_𝜃) does not show significant differences between both modeled obstacles.

Fig. 33

Plots of cut and modeled obstacles ($\kappa _{\max \limits } = 2.5 \times 10^{6} \mu _{\infty }$, q = 1000, $\kappa _{\min \limits } = 0$)

Therefore, by imposing a uniform non-Newtonian viscosity inside the solid material of the obstacle, the non-Newtonian penalization seems to show a more noticeable effect in the radial-axial velocity ((v_r, v_z)) during topology optimization rather than in its end.