1 Introduction

Additive manufacturing (AM) has opened new opportunities to create parts with unprecedented geometric and material complexity. In AM, parts are fabricated layer by layer, as opposed to a subtractive process (Gibson et al. 2010). Fused deposition modeling (FDM) is one such AM process where a continuous thermoplastic (polymer) filament is deposited layer by layer (see Fig. 1a). With continuously improving materials and technology, FDM is being used today to make functional parts for thermal and structural applications. For example, Fig. 1b illustrates a heat exchanger where FDM’s process capabilities are exploited to achieve large surface-to-volume ratio. Often, the structure can be optimized to reduce material consumption. Further, in such applications, to enhance performance, the polymer is often infused with short (typically, carbon) fibers (Botelho et al. 2003) (Fig. 1c). The functional properties of such short fiber–reinforced polymer (SFRP) components depend significantly on the fiber distribution and orientation. These can be controlled in FDM by suitability modifying the raster path.

Fig. 1
figure 1

Fused deposition modeling of fiber-filled composites

Full size image

The focus of this paper is on the build optimization of such SFRP components. Specifically, the objective is to optimize the build direction, the topology, and fiber orientation (raster path) for thermal applications. While significant progress has been made on each of these topics (for example, see Boschetto and Bottini (2014) and Fernandez-Vicente and Calle (2016)), the objective here is to consider all three factors simultaneously.

Towards this end, the remainder of this paper is organized as follows. The literature is reviewed with a motivating example in Section 2, and research gaps are identified. This is followed by a discussion on problem formulation and derivation of sensitivity equations in Section 3. Results are discussed in Section 4, with a concluding note in Section 6.

2 Literature review

As discussed in the previous section, the objective here is to simultaneously optimize the build direction, the topology, and fiber orientation, to improve functional performance of SFRP parts. Prior work related to the above three build parameters is discussed next.

2.1 Build direction

The build direction plays a significant role in the surface quality, print time, and sacrificial support of FDM components (see (Boschetto and Bottini 2014; Das et al. 2015; Qian 2017; Mohamed et al. 2015; Sanati Nezhad et al. 2010; Zhang et al. 2015). While these are important metrics, the current work focuses on the interplay between build direction and functional performance of the part. Specifically, it is well known that FDM introduces behavioral anisotropy (Mirzendehdel et al. 2018), primarily due to incomplete fusion between adjoint layers. For example, consider Fig. 2a where a heat load is applied on the top surface, and the temperature is fixed at the bottom. Figures 2b and c illustrate two possible build directions. Observe that, in the former, the interlayer resistance is in the direction of heat flow and is therefore not preferable, i.e., the build direction along X (or Y in this example) is preferable from a performance perspective. This simple example illustrates the importance of build direction on part performance. However, the optimal build orientation might not be obvious in many cases (see numerical examples). Researchers have proposed methods to optimize build direction for part performance. For example, Umetani and Schmidt (2013) proposed a structural analysis technique based on a bending moment concept to optimize the build direction; however, isotropic material was assumed for simplicity, i.e., fiber reinforcement was not considered. On the other hand, material anisotropy was considered by Erva (Ulu et al. 2015) where the build direction was optimized to maximize structural safety factor using a surrogate-optimization model.

Fig. 2
figure 2

Build orientation for optimizing functional performance of FDM

Full size image

2.2 Topology

With the advent of AM, there has been significant interest in optimizing the topology to improve part performance. For the above example, with X-axis as the build direction, Fig. 3 illustrates an optimal topology of 50% mass, compared with the original design, with minimal loss in performance. Various techniques such as Solid Isotropic Material with Penalization (SIMP) (Gersborg-Hansen et al. 2006; Bendsoe and Sigmund 2003; Sigmund 2001), level-set (Wang et al. 2003), Evolutionary Structural Optimization (ESO) (Xie and Steven 1993), and topological-sensitivity (Suresh 2010) may be employed for topology optimization. The limitation of prior work is that they assume a pre-defined build direction and typically disregard material anisotropy (see Mirzendehdel et al. (2018) for exception).

Fig. 3
figure 3

The design shown in Fig. 2a is optimized to 50 % of its initial volume

Full size image

Instead of optimizing the topology, researchers have also considered optimizing infill patterns. Martínez et al. (2016) proposed a stochastic method to generate compliant structures with a voronoi infill. Recently, Chougrani et al. (2017) suggested a lattice infill for AM. Wu et al. proposed a two-scale simultaneous optimization of shell-infill in the context of minimizing structural compliance (Jun et al. 2017). Manufacturability of the model has been paid considerable consideration in works such as in Jun et al. (2016) and Qian (2017) . Various attempts have been made to link micro-scale infill topology to the density values obtained through optimization. Multi-scale optimization has been addressed in Yan et al. (2016), Sivapuram et al. (2016), and Yi et al. (2012). Recently, Dapogny et al. (2019) performed a 2D topology optimization considering specific infill patterns with anisotropic behavior.

The focus of this paper is on optimizing the topology, as opposed to finding an optimal infill pattern.

2.3 Fiber orientation/print strategy

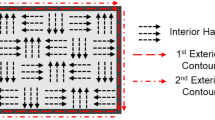
Finally, the print strategy can also have a significant impact on part performance, especially in the case of fiber reinforced polymers (Blok et al. 2018), since (1) fibers preferentially orient in the direction of extrusion of the filament from the print nozzle (Brenken et al. 2018) and (2) fibers add additional strength and thermal conductivity to the material (Liu et al. 2018). Thus, an optimized fiber orientation/print pattern as in Fig. 4 can improve part performance. Towards this end, Raney et al. (2018) recently introduced methods of achieving local site-specific control of fiber orientation. This coupled with development in multi-axis printing (Dai et al. 2018) paves new avenues to realize functionally tailored components with in-situ control of fiber composites. The problem of optimizing fiber orientation angle has been addressed within the context of laminar composites. Discrete material optimization (DMO) is one of the most popular approaches, where a list of a priori directions (e.g., 0∘,± 45∘,± 90∘) (Stegmann and Lund 2005) is used. This avoids local minima but can result in sub-optimal results. Interpolation schemes have also been suggested to overcome this limitation. Alternately, continuous fiber angle optimization (CFAO) has also been proposed (Brampton et al. 2015). This offers greater design freedom but can result in local minima. While the focus has been on laminar composites, there has been a recent increase in targeting these methodologies for AM. More references can be found at Walker and Smith (2003), Luo and Gea (1998), Bendsoe et al. (2008), Huang and Haftka (2005), Gürdal et al. (1999), and Pedersen (1989).

Fig. 4
figure 4

Optimizing the print strategy can improve part performance

Full size image

2.4 Paper contributions

The main contribution of this paper is a comprehensive approach to the build optimization of thermally loaded SFRP components by simultaneously considering the impact of build direction, print topology, and fiber orientation. In particular, the proposed formulation is an extension to the popular SIMP method (Sigmund 2001).

3 Problem formulation

We start by discussing the design variables used in our formulation. This leads to a discussion on the optimization problem, sensitivity analysis, and proposed algorithm.

3.1 Design parameters

3.1.1 Build direction

Due to the incomplete fusion between subsequent layers of deposited material, the thermal conductivity tends to be lower in the direction of the build, leading to transversely isotropic properties. Prajapati et al. (2018) proposed to model the effective thermal conductivity along the build direction via

$$ \frac{1}{k_{z}} = \frac{w_{a} + w_{f}}{w_{a} k_{a} + w_{f} k_{f}} + \frac{R_{c}}{L_{h}} $$
(1)

where kz is the thermal conductivity in the build direction, ka is the thermal conductivity of air, kf is the thermal conductivity of the filament (with no fiber reinforcement), wa is the air gap between rasters, and wf is the width of the raster. Rc is the contact resistance between adjacent layers, and Lh is the layer height. This is illustrated in Fig. 5. Experimental studies show Rc to be in the order of 500 − 2000[μKm2W− 1] leading to kz/kf ≈ 0.6 − 0.8. Similar decrease in mechanical properties has been reported by Knoop and Schoeppner (2015) and Farzadi et al. (2014). Observe that the build-direction anisotropy is different from fiber-induced anisotropy (Zhang et al. 2017).

Fig. 5
figure 5

Illustration showing thermal conductivity of a printed component

Full size image

In our formulation, we assume the part to have an initial build direction along the global Z-axis. We introduce two design parameters α0 and β0 as Eulerian angles to capture the rotation of the build direction about the global X- and Y- axis respectively via (2). These two angle parameters are to be determined by the optimizers.

$$ {\mathbf{b}} = R_{x}(\alpha_{0})R_{y}(\beta_{0}){\mathbf{z}} $$
(2)

where Rx and Ry are standard rotation matrices.

3.1.2 Topology

Next, we consider the parameterization of topology. Here, the evolution of the topology is modeled using classic SIMP where each finite element e is assigned a density value ρe ∈ [0,1]. A density value of one denotes the presence of material, and zero its absence. The density is further penalized by a constant p relating the material property via a power-law:

$$ [K]_{e} = [K_{0}] + {\rho_{e}^{p}}([\hat{K}] - [K_{0}]) $$
(3)

where p = 3, and [k0] is a small thermal conductivity assigned to void elements to prevent singularities.

3.1.3 Fiber orientation

Next, we consider anisotropy due to fiber orientation. Mulholland et al. (2016) reported thermal anisotropy of specific SFRP materials (see Table 1). For example, the baseline conductivity was reported to be 0.26[W/m − K] for PA6-CuF-20, significantly lesser than the fiber-infused counterpart. Here, k∥ is the thermal conductivity achieved along the principal direction of the fibers, leveraging their higher conductivity and k⊥ can be attributed as the thermal conductivity imparted by the filament matrix. Since k⊥/k∥≈ 0.13 − 0.38, it is important to orient the fibers in an optimal fashion.

Table 1 Thermal conductivity of a few SFRPs
Full size table

The finite element formulation used here (see later section) utilizes a geometrically congruent hexahedral (voxel) mesh. Thus, every finite element e is assigned an orientation angle of 𝜃e, on a plane perpendicular to the build direction. This angle will be determined by the optimizer, and the resulting conductivity matrix can be expressed as:

$$ [K]_{e} = R_{\mathbf{b}}(\theta_{e})\hat{K}R_{\mathbf{b}}^{T}(\theta_{e}) $$
(4)
$$ [\hat{K}] = \left[\begin{array}{lll} k_{\parallel} & 0 & 0 \\ 0 & k_{\perp} & 0 \\ 0& 0 & k_{z} \end{array}\right] $$
(5)

where \([\hat {K}]\) is the thermal conductivity matrix along the principal directions assumed to be coincident with the global coordinates of the model. Combining the anisotropy due to layer-wise build (as discussed in the previous section) with that imparted by the fibers, we can see that kz/k⊥≈ 0.08 − 0.31. Further, [Rb(𝜃e)] expresses the orientation of the infill fiber material with respect to the build direction.

3.1.4 Summary

Piecing all the design variables together, we have the effective conductivity given by:

$$ [K]_{e} = [K_{0}] + {\rho_{e}^{p}}(R(\alpha_{0},\beta_{0},\theta_{e})([\hat{K} ] - [K_{0}])R(\alpha_{0},\beta_{0},\theta_{e})^{T} ) $$
(6)

where the rotation matrix is given by:

$$ R(\alpha_{0},\beta_{0},\theta_{e}) = \left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & \cos(\alpha_{0}) & -\sin(\alpha_{0}) \\ 0& \sin(\alpha_{0}) & \cos(\alpha_{0}) \end{array}\right] \left[\begin{array}{lll} \cos(\beta_{0}) & 0 & \sin(\beta_{0}) \\ 0 & 1 & 0 \\ -\sin(\beta_{0}) & 0 & \cos(\beta_{0}) \end{array}\right] \left[\begin{array}{lll} \cos(\theta_{e}) & -\sin(\theta_{e}) & 0 \\ \sin(\theta_{e}) & \cos(\theta_{e}) & 0 \\ 0 & 0 & 1 \end{array}\right] $$
(7)

Observe that (6) combines the effect of build direction (α0 and β0), fiber orientation (𝜃e), and infill density (ρe), resulting in 2n + 2 degrees of freedom where n is the number of finite elements.

3.2 Optimization formulation

We are now ready to formulate the optimization problem. For a typical thermal problem, our objective is to minimize thermal compliance (see Gersborg-Hansen et al. 2006; Gao et al. 2008; Li et al. 1999; Deng and Suresh 2015), subject to a volume constraint:

$$ \begin{array}{@{}rcl@{}} \underset{{\Omega} \subset {\Omega}_{0}}{\min} && C = \int \limits_{\Omega} f {\Theta} d {\Omega} = \boldsymbol{\{f\}}^{T} \boldsymbol{\{{\Theta}\}} \end{array} $$
(8)
$$ \begin{array}{@{}rcl@{}} \text{s.t.} && g(\rho) =\frac{ \int \limits_{\Omega} \rho d{\Omega} }{V^{*}} - 1 \leq 0 \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} && \boldsymbol{ [K] \{ {\Theta} \} = \{ f \} } \end{array} $$
(10)
$$ \begin{array}{@{}rcl@{}} && \alpha_{0} \in [0 , 2\pi] \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} && \beta_{0} \in [0 , \pi] \end{array} $$
(12)
$$ \begin{array}{@{}rcl@{}} && \theta_{e} \in [0 , 2\pi] \quad \forall e \end{array} $$
(13)
$$ \begin{array}{@{}rcl@{}} && \rho_{e} \in [0,1] \quad \forall e \end{array} $$
(14)

Observe that the system is governed by linear equations (10) derived from the finite element discretization of a steady state heat conduction problem. [K] is the stiffness matrix, {Θ} is the temperature field, and {f} is the external heat applied. V∗ in (9) refers to the final volume to be achieved upon optimization. The optimizer used here is the GCMMA (Svanberg 1987); this requires that the design variables be bounded. Thus, thoughthe angular variables (namely α0, β0, and 𝜃e) are periodic, and no bounds are required, limits are imposed as shown. The constraints for the build orientation is given by (11) and (12). The constraint for fiber orientation is given by (13), and (14) sets the limit for density.

3.3 Sensitivity analysis

In order to perform gradient-based optimization, the sensitivity of the objective and constraints, with respect to the design variables is derived in this section.

3.3.1 Objective sensitivity

Recall that the thermal compliance is given by:

$$ \mathcal{C} = \{\boldsymbol{f}\}^{T}\{\boldsymbol{\Theta}\} \equiv \{\boldsymbol{\Theta}\}^{T}[\boldsymbol{K}]\{ \boldsymbol{\Theta}\} $$
(15)

Differentiating (15) with respect to a generic design variable xi, we have

$$ \frac{\partial \{\mathcal{C}\}}{\partial x_{i}} = \frac{\partial \{\boldsymbol{\Theta}\}}{\partial x_{i}}^{T}[\boldsymbol{K}]\{\boldsymbol{\Theta}\} + \{\boldsymbol{\Theta}\}^{T}\frac{\partial [\boldsymbol{K}]}{\partial x_{i}}\{\boldsymbol{\Theta}\} + \{\boldsymbol{\Theta}\}^{T} [\boldsymbol{K}]\frac{\partial \{\boldsymbol{\Theta}\}}{\partial x_{i}} $$
(16)

Neglecting design-dependent loads, we have \( \frac {\partial \boldsymbol {f}}{\partial x_{i}} = \boldsymbol {0}\), (10) is differentiated with respect to design variable xi to get

$$ \frac{\partial \{\boldsymbol{\Theta}\}}{\partial x_{i}} = -[\boldsymbol{K}]^{-1} \frac{\partial [\boldsymbol{K}]}{\partial x_{i}} \{\boldsymbol{\Theta}\} $$
(17)

Inserting (17) into (16) results in:

$$ \frac{\partial \{\mathcal{C}\}}{\partial x_{i}} = -\{\boldsymbol{\Theta}\}^{T}\frac{\partial [\boldsymbol{K}]}{\partial x_{i}}\{\boldsymbol{\Theta}\} $$
(18)

In particular, we have

$$ \frac{\partial [\boldsymbol{K}]}{\partial \rho_{e}} = \iiint\displaylimits_{{\Omega}_{e}}[B]^{T} \frac{\partial [k]_{e}}{\partial \rho_{e}} [B] d {\Omega}_{e} $$
(19)

where [B] is the gradient of the shape function matrix and

$$ \frac{\partial [k]_{e}}{\partial \rho_{e}} = p \rho_{e}^{p-1}([R(\alpha_{0},\beta_{0},\theta_{e})]([\hat{k} ] - [k_{0}])[R(\alpha_{0},\beta_{0},\theta_{e})]^{T} ) $$
(20)

Similarly, the sensitivity with respect to 𝜃e is given by:

$$ \frac{\partial [\boldsymbol{K}]}{\partial \theta_{e}} = \iiint\displaylimits_{{\Omega}_{e}}[B]^{T} \frac{\partial [k]_{e}}{\partial \theta_{e}} [B] d {\Omega}_{e} $$
(21)

where

$$ \begin{array}{@{}rcl@{}} \frac{ \partial [k]_{e}}{\partial \theta_{e}} \!\!&=&\!\! {\rho_{e}^{p}}(\frac{\partial [R(\alpha_{0},\beta_{0},\theta_{e})]}{\partial \theta_{e}}([\hat{k} ] \!- [k_{0}])[R(\alpha_{0},\beta_{0},\theta_{e})]^{T}\\&& + [R(\alpha_{0},\beta_{0},\theta_{e})]([\hat{k} ] - [k_{0}])\frac{\partial [R(\alpha_{0},\beta_{0},\theta_{e})]^{T} }{\partial \theta_{e}} ) \end{array} $$
(22)

The sensitivity with respect to build orientation angle α0 is given by

$$ \frac{\partial [\boldsymbol{K}]}{\partial \alpha_{0}} =\sum \limits_{e} \iiint\displaylimits_{{\Omega}_{e}}[B]^{T} \frac{\partial [k]_{e}}{\partial \alpha_{0}} [B] d {\Omega}_{e} $$
(23)

where \(\frac {\partial [k]_{e}}{\partial \alpha _{0}}\) follows an expression similar to that of (22). The sensitivity with β0 follows suit with α0 and is omitted here for sake of brevity. Further, we note the highly coupled nature of the different design variables and the interplay between density, fiber directions, and build orientation in determining the objective and sensitivities, thus strengthening the argument for the need of a coupled solver.

Note that the sensitivity with respect to the build orientation angles (23) is summed over all elements. This is in contrast to sensitivity with respect to infill densities (20) and fiber orientation (21). In other words, build orientation is global, while infill density and fiber orientation apply to each element.

3.3.2 Constraint sensitivity

The global volume constraint (9) in the discrete form can be expressed as

$$ \frac{\sum \limits_{e} \rho_{e} v_{e}}{ V^{*} } - 1 \leq 0 $$
(24)

where ve is the volume of a discrete element in the congruent hexahedral voxel mesh. The gradient of the global volume constraint with density can be obtained as,

$$ \frac{\partial g}{\partial \rho_{e}} = \frac{v_{e}}{V^{*}} $$
(25)

The sensitivity is zero with respect to 𝜃e,α0, and β0. The box constraints limiting the range of the design variables given by (11), (12), (13), and (14) are considered implicitly by the globally convergent method of moving asymptotes (GCMMA) solver used in this paper (Svanberg 1987). While any finite element solver can be used, an in-house assembly-free solver (Mirzendehdel and Suresh 2015; Yadav and Suresh 2014) is employed here.

3.4 Optimization algorithm

The optimization algorithm utilizes GCMMA (Svanberg 1987) to optimize and an in-house assembly free finite element solver to perform the FEA (Yadav and Suresh 2013). The algorithm followed is described below (algorithm 1):

figure a

4 Numerical experiments

We now demonstrate the proposed method through several examples. The examples considered and the corresponding sub-sections are summarized in Table 2. For example, in Section 4.1.1, we optimize just the topology, by assuming a fixed build direction and fixed fiber orientation. Similarly, in Section 4.1.2, we optimize just the fiber orientation, by assuming a fixed build direction, fixed fiber orientation, topology, and so on. The examples were chosen to highlight the importance of one or more design variables. All experiments were conducted on a desktop PC equipped with an Intel i7 12-core processor with 32 GB RAM running at 3.2 GHz.

Table 2 Summary of various examples considered
Full size table

4.1 Fixed build orientation

In this section, the build orientation is assumed to be fixed, while the topology and/or the fiber orientation are optimized.

4.1.1 Optimization of topology

Consider a plate, with a thickness of 0.5 mm, illustrated in Fig. 6. The thermal boundary conditions are applied as illustrated in Fig. 6, where T = 0∘C and the heat flux Q = 104[W/m2]. The build direction is along the thickness direction. Further, in this subsection, the material is assumed to be isotropic with k = 0.77 [W/m-K], and therefore, the fiber orientation is not relevant. The only design variables are the SIMP densities; the thermal compliance must be minimized for a target volume fraction of 0.5. For finite element analysis, the domain is discretized into 25,000 hexahedral elements (voxels).

Fig. 6
figure 6

Illustration of a plate problem with thermal boundary conditions

Full size image

To optimize the topology, all elements are assigned an initial density of 0.5 (the target volume fraction). The optimization algorithm described earlier is now exploited to find the optimal topology that minimizes the thermal compliance. The optimization terminates when the relative change in the thermal compliance is less than 10− 4. The final topology, together with the convergence, is illustrated in Fig. 7; observe that the topology aligns with the flow of heat, as expected. The solver completed the optimization in 27 iterations, taking a total time of 3.27 min.

Fig. 7
figure 7

Topology and convergence plot for plate problem

Full size image

4.1.2 Fiber optimization

Next, we consider optimizing just the fiber orientation for the above example; the build direction is fixed as before, and the topology is not optimized, i.e., 100% volume. The material is assumed to be PA6-CuF-25 (see Table 1); the anisotropic conductivity is an impetus for preferential fiber orientation. All elements are initially oriented with 𝜃e = 0∘. After optimization, Fig. 8 illustrates convergence and the orientation of the fibers. The solver completed the optimization in 20 iterations, taking a total time of 2.81 min.

Fig. 8
figure 8

Fiber orientation and convergence plot for plate problem

Full size image

4.1.3 Fiber and topology optimization

Next, we combine fiber and topology optimization for the above example. All elements have an initial density of 0.5, and the fibers are oriented at 𝜃 = 0∘. Figure 9 illustrates the convergence and the resulting topology, with fiber orientation. We observe a significant improvement in performance, compared with only optimizing the topology (Section 4.1.1) or the fibers (Section 4.1.2). The solver completed the optimization in 50 iterations, taking a total time of 4.15 min.

Fig. 9
figure 9

Fiber orientation and convergence plot for 2D plate problem

Full size image

4.2 Build orientation and topology optimization

We now illustrate an example where the benefits of optimizing the build direction become evident. Consider the geometry in Fig. 10, where T = 0∘C on the (a subset of the) top face and a heat flux of 103 W/m2 is applied on the bottom face. The material is assumed to be isotropic, i.e., fiber orientation is disregarded. However, observe that depending on the build direction, inter-layer anisotropy will be induced. For example, if the build direction is along Z-axis, then kx = ky = 0.76 [W/m-K] while kz = 0.45 [W/m-K]. For finite element analysis, the domain was meshed with 100,000 elements.

Fig. 10
figure 10

A box geometry with a center hole and associated boundary conditions. All dimensions in mm

Full size image

To isolate the impact of build direction, two sets of optimization studies were carried out. In the first set, the build direction was fixed along Z-axis; observe that this is sub-optimal since the heat sink and source are separated along the Z-axis. The topology was then optimized for 3 different volume fractions: 30%, 50%, and 75%. The final compliances and time taken are reported in the second column of Table 3. In the second set, the build direction was also optimized (with an initial guess along Z-axis). The thermal compliance, together with the optimal build direction and time taken are reported in the third column; the optimal build direction is approximately along X-axis. As one can observe, the compliance reduces significantly when the build direction is optimized. The final topologies at 30% volume fraction from the two sets are shown in Fig. 11.

Table 3 Compliances and computational time with and without build direction optimization
Full size table
Fig. 11
figure 11

Topologies at 30% volume fraction for fixed and optimized build orientation

Full size image

4.3 Sequential vs. simultaneous optimization

In this example, we illustrate the strong interplay between the three sets of design parameters. Consider the geometry and thermal boundary conditions illustrated in Fig. 12, with Q = 10,000[W/m2] and T = 0∘C. As before, we set k∥ = k⊥ = 0.76[W/m − K] and kz = 0.45[W/m − K]. The domain was meshed with 10,000 elements, and the target volume fraction was 0.5. We consider here three optimization scenarios. In the first scenario, we first optimize the build orientation (for full volume), and then optimize the topology and fiber orientation, using the computed build direction. In the second scenario, the build direction and topology are optimized simultaneously, following which the fiber orientation is optimized. Finally, in the third scenario, all three (build, topology, and fiber orientation) are simultaneously optimized.

Fig. 12
figure 12

Geometry and boundary conditions to compare sequential and simultaneous optimization

Full size image

The resulting designs are presented in Fig. 13a–c respectively. The topologies exhibit minor differences, but the optimal build directions are significantly different. Further, in the first scenario, the relative compliance dropped to 0.94 (after optimizing just the build direction taking 23 CG iterations), and then to 0.67 (after optimizing the topology and fiber with 62 CG Iterations), taking a total of 85 CG iterations. In the second scenario, the relative compliance dropped to 0.72 (showcasing the effect of build and topology) which then reduced to 0.61 after 41 and 37 CG iterations respectively, totaling to 78 iterations. Finally, optimizing all three variables simultaneously results in the lowest compliance of 0.58 after 91 CG iterations. Comparing the final compliance of 13 a and c, we note that the combined optimization consumes about 16% more iterations for about 6% gain in performance. This can be attributed to the oscillatory behavior in the convergence of the optimizer and the subjective nature of the problem.

Fig. 13
figure 13

Comparison of sequential and simultaneous optimization

Full size image

4.4 Complete optimization

In this section, we highlight the full potential of the solver by simultaneously optimizing the build direction, topology, and fiber orientation, for the geometry in Fig. 14. The prescribed boundary conditions are a fixed temperature of 0∘C and a heat flux of 104 [W/m2]. We assume the material be PA6-CuF-25 (Table 1) with kz = 0.45 [W/m-K]. The desired volume fraction is 0.3. The design is discretized with 50,000 elements. As before, the initial density of all the elements is 0.3 (desired volume fraction), the orientation of the fibers is 0∘. Several instances of optimization were executed using different initial build orientation; the results are tabulated in Table 4. While the final build direction is almost identical in each case (upto a sign), the final compliances are slightly different. This reflects the sensitivity of the compliance to the build direction.

Fig. 14
figure 14

A triangular block with boundary conditions

Full size image
Table 4 Impact of initial build direction on the optimal build direction and compliance
Full size table

The optimal topology and build direction are illustrated in Fig. 15.

Fig. 15
figure 15

The final topology and build direction upon optimization

Full size image

The compliance convergence (for the fourth build orientation scenario) is plotted in Fig. 16, together with the optimal fiber orientation for one of the cross sections. We observe a sharp decrease in the compliance near the 20th iteration; this can be attributed to the convergence in the build orientation.

Fig. 16
figure 16

The evolution of compliance with iteration. The final topology along with orientation of the fiber at a cross section is shown

Full size image

The convergence of the build direction is illustrated in Fig. 17. We observe that the optimizer considers various orientations to finally arrive at the optimal. Further, we notice that the convergence of the orientation is non-smooth. We conjecture that the oscillatory nature is due to the strong interplay between the build orientation and the evolving topology/ fiber orientation. The solver completed the optimization in 80 iterations taking a total time of 38.5 min.

Fig. 17
figure 17

The convergence of the norm of the difference between the optimal build vector and that at given iteration

Full size image

5 Conclusion

The main contribution of this paper is an integrated framework for the simultaneous optimization of build direction, topology, and fiber orientation of SFRP components. The numerical experiments demonstrated that all three factors must be considered for optimal performance. A global volume constraint was imposed to drive the optimizer towards minimizing compliance. The layer-wise printing paradigm of AM was of central focus, and methods were proposed to include the consequence of anisotropic material properties.

There are several areas for future research. The present formulation does not include several AM-constraints such as overhang surfaces, minimum feature size, and surface finish. Further post-processing (Allaire et al. 2018) might be required to produce smooth transitions in fiber orientation. Generation of machine instructions from the obtained topology and orientation field is also a topic of future research (Steuben et al. 2016).

6 Replication of results

The paper uses the Pareto code, developed at UW-Madison, that has been assigned to the Wisconsin Alumni Research Foundation (WARF). Due to restrictions imposed by WARF, we are unable to provide public access to this software for replication of results.