Topology optimization for microstructural design under stress constraints

Abstract

This work aims at introducing stress responses within a topology optimization framework applied to the design of periodic microstructures. The emergence of novel additive manufacturing techniques fosters research towards new approaches to tailor materials properties. This paper derives a formulation to prevent the occurrence of high stress concentrations, often present in optimized microstructures. Applying macroscopic test strain fields to the material, microstructural layouts, reducing the stress level while exhibiting the best overall stiffness properties, are sought for. Equivalent stiffness properties of the designed material are predicted by numerical homogenization and considering a metallic base material for the microstructure, it is assumed that the classical Von Mises stress criterion remains valid to predict the material elastic allowable stress at the microscale. Stress constraints with arbitrary bounds are considered, assuming that a sizing optimization step could be applied to match the actual stress limits under realistic service loads. Density–based topology optimization, relying on the SIMP model, is used and the qp–approach is exploited to overcome the singularity phenomenon arising from the introduction of stress constraints with vanishing material. Optimization problems are solved using mathematical programming schemes, in particular MMA, so that a sensitivity analysis of stress responses at the microstructural level is required and performed considering the adjoint approach. Finally, the developed method is first validated with classical academic benchmarks and then illustrated with an original application: tailoring metamaterials for a museum anti–seismic stand.

1 Introduction

Nowadays, additive manufacturing allows fabricating high performance components with complex shapes including porous, graded or composite material architecture. It is well–known from nature that the most efficient materials, to address given requirements, are obtained by a tailored distribution of porous or oriented material, e.g. bones or wood structures. The microstructural material distribution defines the macroscopic behavior of the structure. It follows that an appropriate design of the microstructure and its distribution allow for the achievement of desired properties at the macroscopic level.

Since the seminal work by Bendsøe and Kikuchi (1988), porous microstructures have held a prominent importance in the research tied to the design of optimal topologies. Bendsøe and Kikuchi exploited numerical homogenization to compute equivalent elastic properties of parametrized porous microstructures used in the optimization process. Large grey regions frequently occurred in the optimized layouts. These zones were originally interpreted as porous material, thus generating troubles during manufacturing. The interested reader is also referred to the works by Hassani and Hinton (1997, 1998a, b) providing a comprehensive review of the homogenization theory for topology optimization. To overcome this difficulty and generate black and white layouts which were easier to manufacture using classical machine tools, Bendsøe (1989) proposed an efficient material model for porous microstructures. He introduced a power–law to interpolate the material elastic properties and penalize intermediate densities. This material interpolation scheme was later noted as Solid Isotropic Material with Penalization (SIMP), see Bendsøe (1989) and Rozvany et al. (1994), and its physical meaning was afterwards discussed in Bendsøe and Sigmund (1999). Since then, the SIMP model has been largely exploited in various extensions of the topology optimization method, see for instance (Sigmund and Maut 2013) and (Deaton and Grandhi 2014). Homogenization and microstructural design have been receiving a revival interest for several years, as attested by recent works by Xia (2015) or Andreassen et al. (2015).

The homogenization theory plays a key role in engineering problems involving a multiscale character. The method usually assumes that the structure can be described by a periodic Representative Volume Element (RVE) or a Representative Unit Cell (RUC). A distinction between RVE and RUC is provided in Aboudi et al. (2012) and the concept of RUC is exploited in this paper to meet the definition given in the aforementioned contribution. Periodic boundary conditions are imposed on the RUC and the latter is analyzed to extract the effective properties of the microstructure. The method is based on the separation of scales, i.e. the characteristic size of the RUC must be much smaller than the structural dimensions at the macroscopic scale. In-depth explanations of the method can be found in Bensoussan et al. (1978), Sanchez-Palencia (1983), and Suquet (1982) or the equivalent material properties can be computed analytically, although numerical analysis, based on the finite element method, are used for more complex microstructures. Numerical homogenization techniques are further discussed in Guedes and Kikuchi (1990) and Mlejnek and Schirrmacher (1993) or, more recently, in Andreassen and Andreasen (2014), who provide an academic homogenization code.

The pioneering work by Sigmund (1994) initiated a new way of tailoring materials for prescribed properties and extremal features. Taking advantage of topology optimization and the SIMP model as design tools, Sigmund (1994) introduced the concept of inverse homogenization. Numerical homogenization is exploited to extract the equivalent elastic properties of the microstructure through the material distribution process and, comparing the achieved results with respect to target values. However, the target value must be known in advance and this is not always trivial. An alternative formulation consists in directly using the homogenized material properties as objective function while constraining the volume constraint or enforcing additional requirements, see Bendsøe and Sigmund (2003). Later, Sigmund (1999) used the former method for the design of extremal composite materials. This approach was further extended to consider various and more complex fields of applications. Among others, the work of Jensen and Sigmund (2011) addresses the design for optimal electromagnetic and phonic properties. Multiphase elastic materials were explored in the work by Gibiansky and Sigmund (2000), whereas Guest and Prévost (2006) investigated the design for multiple properties such as fluid permeability and stiffness. Sigmund and Torquato (1999) handled the design of microstructures exhibiting prescribed thermal and electrothermal properties, whereas Liu et al. (2016) explored concurrent topology optimization of macrostructures and material microstructures for natural frequency. Jia et al. (2016) used granular micromechanics to cope with the optimal design of materials with micro-scale tension-compression asymmetry. Interested readers may refer to Cadman et al. (2013) for a comprehensive review on the topic.

Besides the numerous compliance–based design formulation in topology optimization, Duysinx and Bendsøe (1998) introduced stress constraints in the framework of density–based topology optimization to assess the structural integrity of the optimized layouts. They proposed a stress criterion for the optimal rank-2 material, before investigating a relevant stress measure to be used along with the SIMP model. In this milestone work, the stress constraints are enforced locally and the well–know singularity phenomenon is overcome through the ε-relaxation (Kirsch 1990; Cheng and Guo 1997). An alternative technique, to address the relaxation of the constraints, is the so–called qp–approach proposed by Bruggi (2008). The latter is based on a suitable choice of the exponents in the interpolations of the local apparent stresses (q) and the stiffness (p) when dealing with the SIMP model and provides a strong relaxation in low density regions, without introducing any bias at full density.

Even if the need for a mathematical relaxation of the constraints is well–known, the issue of efficiency is still not fully solved. To circumvent some numerical burden, Duysinx and Sigmund (1998) introduced global p–norm and p–mean stress measures and proposed to consider a single constraint aggregating the local stress constraints. Although significantly reducing the CPU time, the high non-linearity associated with the global constraint might lead to convergence issues. Other aggregate functions, such as the Kresselmeier–Steinhauser (KS) function used in Yang and Chen (1996) and Luo et al. (2013), were subsequently exploited to try to overcome the high CPU cost. At the crossroad between the local and the global approaches, París et al. (2010) and Holmberg et al. (2013) proposed some clustering approach. The local apparent stress constraints are sorted and aggregated in clusters or groups. Local and global approaches are recovered if the number of clusters is equal to the number of design variables or to one, respectively. The method shows promising results, although its effectiveness may be strongly dependent on the definition of the clusters. Bruggi and Dusyinx (2012) adopted a global compliance constraint in the optimization framework while processing local stress constraints following an active set selection strategy. The CPU time is lower than classical local approaches while allowing for the design of a structure that fulfills stiffness requirements. Recently, Bruggi (2016) extended the approach and adopted stresses as main variables for both the optimization and the analysis problems.

Few investigations on microstructural design subject to stress requirements are available in the literature. Lipton (2006, 2007) employed homogenization solutions in an inverse procedure to identify graded microstructures providing expected structural response while ensuring a local stress control in the vicinity of singularities between structural elements. This method considers local stress amplifications due to the porous microstructure, measured through new multiscale quantities. Microstructural design with stress constraints has also been studied using level set method. One can cite, for instance, the work by Noël and Duysinx (2016), where the topology optimization is performed with a XFEM–level set formulation on benchmarks of the literature as well as multi–inclusion problems. The results show that the method is robust and flexible and can reproduce analytical solutions. The present contribution focuses on the introduction of stress constraints in the SIMP–based material design problem. The authors would like to emphasize that the goal of the paper is to focus on the optimization of the material configuration at microscopic level in order to obtain prescribed stiffness properties while avoiding layouts with high stress concentrations. The pursued objective is to keep the local stresses below a prescribed stress limit thereby enabling to mitigate high stress intensity. Such undesirable features are encountered in theoretical designs, such as rank-2 materials (Bendsøe and Sigmund 2003) or octree lattice structures (Deshpande et al. 2001). Since the far field is not known, i.e. is not computed through a macroscopic finite element analysis, some arbitrary strain fields are applied to produce the stress field within the optimized layouts. Consequently, an arbitrary stress limit is chosen as upper bound of the local stress values and does not stands for the real yield stress of the material. The paper does not constitute an attempt to determine an equivalent plasticity criteria or a first point failure criteria, evaluated in terms of macroscopic (average) stress, to predict the plasticity regime in the periodic cell. Further details are discussed in the subsequent sections of this paper.

The paper is organized as follow. Section 2 recalls the basics of numerical homogenization techniques for periodic microstructures. Section 3 introduces the formalism to tackle stress constraints, adopting a Von Mises stress measure. Section 4 presents the optimization problem addressed in this work. In particular, Section 4.2 derives the sensitivity analysis of the stress constraints in the context of microstructural design. Section 4.3 investigates numerical issues related to the considered optimization problem. Section 5 illustrates the method with classical benchmarks from the literature before investigating application dedicated to seismic insulation device.

2 Homogenization

The homogenization theory was developed to calculate the overall behavior of complex microstructural geometries and evaluate their effective properties at the macroscopic level. Although applicable to heterogeneous media, the particular case of periodic materials, built from the repetition of a RUC in the two or three directions of space, is generally considered as described in Bensoussan et al. (1978), Sanchez-Palencia (1983), and Suquet (1982). Taking advantage of the periodicity, the effective properties of periodic media can be extracted analytically or numerically from the analysis of a single RUC. The homogenization theory of periodic media states that the response of the periodic unit cell is meaningful only if the two considered scales are well separated, i.e. l_RUC ≪ l_macro, where l_RUC and l_macro stand respectively for the RUC length and the characteristic length on which the macroscale loading (or the macroscale deformation gradient) varies in space as showed by Kouznetsova et al. (2001). In practical applications, this assumption might not be verified in the presence of localized actions, e.g. high strain gradient, boundary effects, etc. Nevertheless, the homogenization theory is assumed to remain valid within this work.

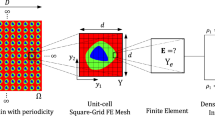
Numerical homogenization techniques refer to the numerical handling of the partial differential equations used to describe highly heterogeneous media, see for instance (Guedes and Kikuchi 1990; Mlejnek and Schirrmacher 1993) or (Andreassen and Andreasen 2014). In the following, we recall the main results useful to our investigations. In particular we address the numerical computation of the homogenized elastic tensor and of the load vector. To avoid any ambiguities between the different stresses at the various scales, we introduce the relations existing between these ones in Fig. 1. At the macroscale, a structural stress Σ can be computed by averaging the stress 〈σ_ij〉 evaluated at the microscale. The microstructural stresses are related to a local stress measure σ_ij that refers to the porous material constituting the RUC. In the present contribution, we only consider the local and the microstructural stresses (σ_ij and 〈σ_ij〉 respectively), since the design domain is restricted to the RUC. The homogenized stress (Σ) is not considered here as our investigation remain focused to the RUC level. More details are provided in Section 4.

Fig. 1

Illustration of separation of scales when considering stress constraints. Within the macrostructure made of repeated periodic unit cells, a structural stress Σ_ij is evaluated as the average of the microstructural stress 〈σ_ij〉 within the RUC. The latter is known by accounting for the local stress measure σ_ij within the porous SIMP material

This work focuses on orthotropic macroscopic materials. Their constituents, at the microscale, are assumed to be linear elastic and their constitutive equation reads:

$$ \boldsymbol{\sigma} = \mathbf{H}\ \boldsymbol{\varepsilon}, $$

(1)

where H is the Hooke’s matrix, σ and ε the microscopic stress and strain respectively.

To evaluate the equivalent homogenized elastic properties and focusing on two dimensional (2D) RUC, three independent strain fields are required: $\boldsymbol {\varepsilon }^{0}_{1} = [1 0 0]^{T}$, $\protect \boldsymbol {\varepsilon }^{0}_{2} = [0 1 0]^{T}$ and $\boldsymbol {\varepsilon }^{0}_{3} = [0 0 1]^{T}$, see for instance (Sanchez-Palencia 1983). We note that for three dimensional problems, six independent strain fields should be applied. An effective way to compute the homogenized elastic properties $\protect H^{H}_{ij}$ is detailed in Bendsøe and Sigmund (2003) and is recalled in (2):

$$\begin{array}{@{}rcl@{}} H^{H}_{ij} &=& \displaystyle \frac{1}{Y} {\int}_{Y}(\boldsymbol{\varepsilon}_{i}^{0}-\boldsymbol{\varepsilon}_{i})^{T}\ \mathbf{H}\ (\boldsymbol{\varepsilon}_{j}^{0}-\boldsymbol{\varepsilon}_{j})\ dY,\\ &&i,\ j = 1,\ 2,\ 3, \end{array} $$

(2)

where Y is the volume of the RUC, $\protect \boldsymbol {\varepsilon }^{0}_{i}$ are the prescribed unit strain fields, and ε_i are the strain fields induced in the RUC when submitted to $\protect \boldsymbol {\varepsilon }^{0}_{i}$.

To satisfy the periodicity of the material, the analysis can be restricted to a single RUC through the application of periodic boundary conditions. Working with regular periodic meshes, boundary conditions are conveniently enforced by the deletion of redundant degrees of freedom (dofs), (see e.g. Sigmund 1994, 1999; Andreassen and Andreassen 2014). Specific procedures, relying on the introduction of Lagrange multipliers (Michel et al. 1998; Miehe and Koch 2002) or polynomial interpolations (Nguyen et al. 2012; Tyrus et al. 2007) were developed to handle more general configurations, such as non–periodic or non–regular meshes.

In this work, the dofs deletion strategy is adopted, as illustrated in Fig. 2. The periodic boundary conditions are enforced by suppressing redundant nodes located at opposite sides of the RUC. Hence, the number of dofs associated to the RUC, and thus the size of the system to solve, are reduced. Eventually, the analysis is restricted to the dashed region in Fig. 2. The obtained displacements u_P can be extended in a post–processing step to recover the initial size of the problem u_NP.

Fig. 2

Enforcing periodic boundary conditions to a square RUC by applying a dofs deletion strategy: corresponding nodes are associated leading to the elimination of redundant dofs

Equation (2) can be rewritten to introduce the displacement field uⁱ undergone by the RUC when acted upon by the unit strain field $\protect \boldsymbol {\varepsilon }_{0}^{i}$:

$$\begin{array}{@{}rcl@{}} H^{H}_{ij} &=& \displaystyle \frac{1}{Y} {\int}_{Y}(\mathbf{u}_{i}^{0}-\mathbf{u}_{i})^{T}\ \mathbf{B}^{T}\ \mathbf{H}\ \mathbf{B}\ (\mathbf{u}_{j}^{0}-\mathbf{u}_{j})\ dY,\\ &=& \displaystyle \frac{1}{Y} (\mathbf{u}_{i}^{0}-\mathbf{u}_{i})^{T}\ \mathbf{K}\ (\mathbf{u}_{j}^{0}-\mathbf{u}_{j}),\\ && i,\ j = 1,\ 2,\ 3, \end{array} $$

(3)

where B is the strain-displacement matrix and K the stiffness matrix associated to the RUC.

To evaluate the displacement field uⁱ, the following static equilibrium equation has to be solved:

$$ \mathbf{K}\ \mathbf{u}_{i} = \mathbf{f}_{i}^{0}, \qquad i = 1,\ 2,\ 3, $$

(4)

where $\protect \mathbf {f}_{i}^{0}$ is the force vector equivalent to the application of the prescribed unit strain field $\protect \boldsymbol {\varepsilon }_{i}^{0}$. The latter can be expressed as:

$$\begin{array}{@{}rcl@{}} \mathbf{f}_{i}^{0} & = & \displaystyle {\int}_{Y} \mathbf{B}^{T}\ \mathbf{H}\ \boldsymbol{\varepsilon}^{0}_{i}\ dY, \qquad i = 1,\ 2,\ 3,\\ & \approx & \displaystyle \sum\limits_{n_{gp}} w_{gp}\ \mathbf{B}^{T}\ \mathbf{H}\ \boldsymbol{\varepsilon}^{0}_{i}\ {\det}\left( \mathbf{J}\right), \end{array} $$

(5)

where w_gp is the weight associated to each Gauss point, det (J) is the determinant of the Jacobian matrix. One should remark that the equivalent force vector $\protect \mathbf {f}^{0}_{i}$ depends on the Hooke’s tensor, itself depending on the design variables, i.e. the densities.

This optimization problem thus involves a design–dependent load.

3 Stress constraints in density–based topology optimization

Handling stress constraints in topology optimization, using the SIMP model, is not straightforward. One faces at least three main difficulties, as reported by Duysinx and Bendsøe (1998). First of all, generalized stress failure criteria for porous media need to be defined. Second the so–called stress singularity phenomenon has to be overcome to prevent the optimization algorithms from removing vanishing members. Finally, the introduction of stress restrictions results in a drastic increase in the problem size and a high CPU time is required to evaluate the local stress constraints and their derivatives.

Duysinx and Sigmund (1998) derived a strength criterion for SIMP–based materials, inspired by the mechanics of layered composites. They computed analytically the stresses in each layer of a reference rank 2 microstructure (micro-stresses) and enforced a Von Mises criterion over them, see also Aboudi et al. (2012). An overall strength domain was defined in terms of macro-stresses and porosity, to introduce the well–known stress criterion for power–law materials.

In this paper, we focus on an RUC made of a porous SIMP material. To perform stress–constrained optimization at the RUC level, the latter must comply with two hypotheses. It should be large enough, compared to the SIMP material scale, to retain the material properties of a bulk medium as stated in Aboudi et al. (2012). Simultaneously, the dimensions of the RUC should remain much smaller than those of the macrostructure, so that the homogenization theory can be exploited to extract the RUC equivalent elastic properties.

Considering that the scale separation is satisfied and that the RUC bulk material properties are known, a stress–constrained optimization framework can be derived. As in Duysinx and Sigmund (1998), we assume that the base material of the porous microstructure is metallic, i.e. has a ductile behavior, and that the local failure can be predicted by a Von Mises criterion. Thus the stress state can be controlled by defining a stress criterion in terms of the computed microstresses and the density unknowns.

Working in a 2D setting and assuming a plane stress state, the equivalent Von Mises stress is expressed as:

$$\begin{array}{@{}rcl@{}} \sigma^{\text{VM}} &=& \sqrt{{\sigma_{x}^{2}} + {\sigma_{y}^{2}} -\sigma_{x}\sigma_{y} + 3\sigma_{xy}^{2}},\\ &=& \sqrt{3\ J_{2}}, \end{array} $$

(6)

where J₂ is the second invariant of the stress tensor.

Performing density–based topology optimization, a well–posed problem is obtained by introducing an interpolation law expressing physical quantities, such as the material stiffness, as a function of the density variables x. As proposed by Bendsøe (1989), the SIMP scheme is adopted in this paper and the components of the elasticity tensor H_ij(x) are given as:

$$\begin{array}{@{}rcl@{}} H_{ij}(x) = x^{p}\ H_{ij}^{0}, \end{array} $$

(7)

where $\protect H_{ij}^{0}$ is the Hooke’s matrix of the solid material, and p the penalization factor taken equal generally to 3 (Bendsœand Sigmund 1999, 2003).

Introducing (7) in (1), the stress tensor can be written as:

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma} = x^{p}\ \mathbf{H}^{0}\ \boldsymbol{\varepsilon} = x^{p}\ \mathbf{T}^{0}\ \mathbf{u}, \qquad \mathbf{T}^{0} = \mathbf{H}^{0}\ \mathbf{B}. \end{array} $$

(8)

Following the approach of Duysinx and Sigmund (1998) and considering a local constraint at the centroid of the e–th element associated with density x_e, the equivalent stress measure reads:

$$ \langle\sigma^{\text{VM}}_{e}\rangle = {x_{e}^{p}}\ \sqrt{\mathbf{u}_{e}^{T}\ \mathbf{M}_{e}^{0}\ \mathbf{u}_{e}} = {x_{e}^{p}}\ \overline{\sigma}^{\text{VM}}_{e} $$

(9)

where

$$ \mathbf{M}^{0}_{e} = \mathbf{T}_{e}^{0,T}\ \mathbf{V}\ \mathbf{T}_{e}^{0}, \quad \mathbf{V} = \left( \begin{array}{ccc} 1 & -1/2 &\quad 0\\ -1/2 & 1 &\quad 0\\ 0 & 0 &\quad 3 \end{array} \right). $$

(10)

A proper failure criterion must be accounted for in the porous SIMP material. Following (Duysinx and Bendsøe 1998), a so–called local stress measure σ_ij is assumed:

$$\begin{array}{@{}rcl@{}} \sigma_{ij}=\langle\sigma_{ij}\rangle/{x_{e}^{q}}, \text{with } q>1. \end{array} $$

(11)

Finally, a suitable stress criterion, to be implemented in a density–based topology optimization framework, is derived:

$$ \frac{\sigma_{e}^{\text{VM}}}{{\sigma_{y}^{0}}} = \frac{\langle\sigma^{\text{VM}}_{e}\rangle}{{x_{e}^{q}}\ {\sigma_{y}^{0}}} = x_{e}^{p-q}\ \frac{\overline{\sigma}^{\text{VM}}_{e}}{{\sigma_{y}^{0}}} \leq 1, $$

(12)

where $\protect {\sigma _{y}^{0}}$ is a prescribed stress limit under which the local stress should remain to mitigate the stress concentrations.

In this work, the design domain is restricted to the RUC and the macroscopic structure is not considered. Nonetheless, it remains legitimate to consider stress constraints to predict failure at the microscopic level. In fact, the homogenization theory assumes well–separated scales, but does not require an infinitesimal dimension of the microstructure, see Sanchez-Hubert and Sanchez-Palencia (1998) and Hassani and Hinton (1997). Since the RUC can keep a finite dimension, we assume that continuum mechanics hypotheses remain valid. Therefore an equivalent Von Mises stress measure can be defined at every point in the microstructure similarly to the works of Gurson (1977) and Michel and Suquet (1993) or Ponte-Castenada and De Botton (1992), where a failure criterion is used to predict plasticity. Conversely to these latter works, a first point failure criterion, as in Duysinx and Bendsøe (1998), is considered here to predict the end of the elastic regime.

4 Optimization framework

The literature devoted to material tailoring mainly focuses on designing metamaterials with prescribed homogenized elastic properties. Optimization problems seek for material distributions in the RUC, which maximize selected stiffness properties. In many examples, achieved designs exhibit small sections or geometrical singularities, where stress concentrations arise causing the layouts to fail even under small structural loads. Detecting and controlling weak design features, i.e. weak in terms of strength, can not be achieved through conventional energy–based formulations, but requires the introduction of stress responses in the optimization problem. In this work, we aim at designing microstructures that exhibit the best overall stiffness properties while keeping the stress state at an admissible level.

Material tailoring problems usually carry out the microstructural design prior to the structural analysis, i.e. the actual structural loads remain undetermined. As the structural strain field is a priori unknown, stress constraints are evaluated for a set of test strain fields. In this context, the bounds imposed on the stress measures are arbitrary. The problem is then formulated as in (13). To deal with the actual stress values under realistic loadings, a second optimization stage could be considered. Optimized layouts would then be subjected to a further optimization step adapting the RUC material volume or the size of the microstructural members to satisfy the material stress limits under the realistic structural strain field.

$$\begin{array}{@{}rcl@{}} P1: & \max & properties\\ & s.t. & stress<bound\\ & & volume< V^{\star} \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} P2: &\min & stress\\ &s.t. & properties>bound\\ & & volume < V^{\star} \end{array} $$

(14)

An alternative formulation, in (14), could minimize the maximum stress measure under a set of test strain fields, subject to restrictions on the volume and the effective stiffness properties. This min–max problem is solved by exploiting the so–called bound formulation, see e.g. Bendsøe and Sigmund (2003), or by replacing the maximum function by a smoothed continuous function, see e.g. Chenm (1985). However, selecting proper bounds for the effective stiffness properties a priori might be difficult from an engineering point of view and would also introduce arbitrary parameters in the problem. From a mathematical perspective, both formulations are equivalent provided that appropriate bounds are prescribed for the volume, the stress constraints or the effective stiffness coefficients. It can be shown that swapping the constraint and the objective results in equivalent problem formulations (see Appendix B). Therefore, enforcing stress constraints does not restrict the general character of the approach developed here. Numerical tests reveal that solving the min–max formulation with MMA has a high computational cost, as a large number stress constraints are active during the first iterations. Constraining the stress responses generally leads to a more computationally effective scheme while using MMA. This observation leads us to consider the formulation presented hereunder, which look for a design with maximum effective stiffness properties subject to volume and stress constraints.

In the following, we address stress–constrained microstructural design through the selected optimization formulation. Special attention is devoted to the sensitivity analysis of the stress constraints. Numerical issues inherent to the problem definition are discussed and detailed: the stress singularity phenomenon, the active restriction strategy and the accuracy of the computed stresses.

4.1 Topology optimization problem

Let’s consider $\protect f(H^{H}_{ij})$ as a generic form of the objective function depending on the target homogenized properties.The resulting 2D optimization problem can be formulated as:

$$\begin{array}{@{}rcl@{}} \displaystyle \min_{\mathbf{x}} \quad & f(H^{H}_{ij}) &\quad i,\ j = 1,2,3 \end{array} $$

(15a)

$$\begin{array}{@{}rcl@{}} \text{s.t.} \quad & \mathbf{K}(\mathbf{x})\ \mathbf{u}_{i} = \mathbf{f}^{0}_{i}(\mathbf{x}),& \quad i = 1,2,3 \end{array} $$

(15b)

$$\begin{array}{@{}rcl@{}} &\mathbf{K}(\mathbf{x})\ \boldsymbol{\chi}_{s} = \mathbf{f}_{s}(\mathbf{x}),& \quad s = 1,\dots,n_{s} \end{array} $$

(15c)

$$\begin{array}{@{}rcl@{}} &x_{e}^{p-q}\ \overline{\sigma}_{e,s}^{\text{VM}} \leq {\sigma_{y}^{0}}, & \quad e = 1, \dots, n_{e} \end{array} $$

(15d)

$$\begin{array}{@{}rcl@{}} &&\quad s = 1, \dots, n_{s} \\ & V(\mathbf{x}) \leq V^{\star}, & \end{array} $$

(15e)

$$\begin{array}{@{}rcl@{}} &0 \leq x_{\min} \leq x_{e} \leq 1, &\quad e = 1, \dots, n_{e} \end{array} $$

(15f)

In (15a),

• (15b)) is used to determine the homogenized properties of the RUC, see (4).

• (15c) refers to n_s load cases applied to the RUC as external strain fields. The load vectors f_s are computed following the same procedure introduced for the evaluation of $\protect \mathbf {f}^{0}_{i}$. These load cases generate stresses within the base cell and the latter ones will be bounded by the imposition of stress constraints.

• (15d) introduces n_e × n_s local stress constraints, where n_e is the number of elements. To reduce the computational effort related to the imposition of a large number of constraints, an active set selection strategy is exploited in this work. The number of constraints n_a, actually supplied to the optimizer, is then lower than the maximum number of constraints n_e × n_s. The adopted selection strategy is further detailed in Section 4.3.

• (15e) enforces a volume restriction on the design.

• (15f) introduces a lower bound x_min on the values of the design variables. This lower bound allows us to avoid a potential singularity of the global stiffness matrix. In Section 5, x_min is fixed to 10^− 3, as recommended by Bendsøe and Sigmund (2003) for raw material exhibiting a Poisson’s ratio equal to 0.3.

As detailed in Sigmund and Petersson (1998), the finite element discretization can be affected by numerical issues such as checkerboard and mesh–dependence. To address these issues, we adopt a density–based filtering technique, as proposed by Bruns and Tortorelli (2001) and Bourdin (2001). The original design variables x_e are mapped into a new set of physical unknowns $\protect \tilde {x}_{e}$:

$$\begin{array}{@{}rcl@{}} \displaystyle \tilde{x}_{e} & = & \displaystyle \frac{{\sum}_{i \in V_{e}} W_{i}\ x_{i},}{{\sum}_{i \in V_{e}} W_{i}},\\ \displaystyle W_{i} & = & \max(0,r_{min}-\text{dist}(e,i)), \end{array} $$

(16)

where V _e is a set of elements located in the neighborhood of the e–th element, dist(e, i) is the distance between the centers of the e −th and i −th elements, r_min is the filter radius. The latter is chosen such that r_min > d_m, where d_m is the element size. For the simulations in Section 5, the filter radius is set to r_min = 2.5 d_m.

4.2 Sensitivity analysis

The microstructural design problem, described in (15a), are solved resorting to gradient–based algorithms and a sensitivity analysis is required. Since the differentiations of homogenized properties are classical results available in the literature (see Bendsøe and Sigmund 2003), they are not further discussed here. This section focuses on the formulation and computation of the sensitivity analysis for imposing stress constraints in the context of density–based techniques.

For each load case s, the derivative of the stress measure for porous SIMP material, proposed in (12), can be written, using the classical chain rule, as :

$$ \frac{\partial\sigma_{e,s}^{\text{VM}}}{\partial x_{k}} = (p-q)\ x_{e}^{p-q-1}\ \overline{\sigma}^{\text{VM}}_{e,s}\ \delta_{ek} + x_{e}^{p-q}\ \frac{\partial \overline{\sigma}_{e,s}^{\text{VM}}}{\partial x_{k}}, $$

(17)

where δ_ek is the Kronecker delta. In the following discussion, the subscript (.)_s is dropped to simplify the notations.

To evaluate the sensitivities, we exploit the adjoint approach:

$$\begin{array}{@{}rcl@{}} \displaystyle \frac{\partial \overline{\sigma}^{\text{VM}}_{e}}{\partial x_{k}} &-& \boldsymbol{\lambda}^{T} \left( \frac{\partial \mathbf{K}}{\partial x_{k}} \boldsymbol{\chi} - \frac{\partial \mathbf{f}}{\partial x_{k}} \right)\\ &+& \left( \frac{d \overline{\sigma}^{\text{VM}}_{e}}{d \boldsymbol{\chi}} -\boldsymbol{\lambda}^{T} \mathbf{K} \right) \frac{d \boldsymbol{\chi}}{d x_{k}} = 0, \end{array} $$

(18)

where λ is the adjoint response.

The implicit part of (18) is eliminated by defining an appropriate adjoint vector λ such that:

$$ \frac{d \overline{\sigma}^{\text{VM}}_{e}}{d \boldsymbol{\chi}} -\boldsymbol{\lambda}^{T} \mathbf{K} = 0. $$

(19)

Finally, the derivatives of $\protect \overline {\sigma }^{\text {VM}}_{e}$ with respect to the design variable x_k is obtained by including the solution of (19) in (18):

$$ \frac{\partial \overline{\sigma}^{\text{VM}}_{e}}{\partial x_{k}} = \boldsymbol{\lambda}^{T} \left( \frac{\partial \mathbf{K}}{\partial x_{k}} \boldsymbol{\chi}-\frac{\partial \mathbf{f}}{\partial x_{k}} \right), $$

(20)

where

$$ \frac{\partial \mathbf{K}}{\partial x_{k}} = p\ x_{k}^{p-1}\ \mathbf{K}_{e}^{0}, \qquad \frac{\partial \mathbf{f}}{\partial x_{k}} = p\ x_{k}^{p-1}\ \mathbf{f}_{e}^{0}. $$

(21)

An evaluation of the pseudo–load λ is required for each active constraint and is expressed as:

$$ \mathbf{K}\ \boldsymbol{\lambda} = -\left[ \frac{\mathbf{M}_{e}^{0}\ \boldsymbol{\chi}_{e}}{\sqrt{\boldsymbol{\chi}_{e}^{T}\ \mathbf{M}_{e}^{0}\ \boldsymbol{\chi}_{e}}} \right]^{T}. $$

(22)

4.3 Numerical issues and remarks

In this section, we discuss some of the issues related to a stress–based topology optimization approach. In particular the prevention of the singularity phenomenon is exposed, as well as the method used to address CPU requirement. Finally we draw a remark concerning the accuracy of the analysis.

Overcoming the singularity phenomenon

To provide mechanical consistency, the same penalization should be adopted for both the stiffness and the local stress interpolations, as explained by Duysinx and Bendsøe (1998). However, under this assumption, gradient–based algorithms are likely to end up in local optima, associated with designs exhibiting massive grey regions. This problem, known as the singularity phenomenon, is due to the presence of degenerated sub–domains, arising within the feasible design space, when handling stress constraints with p = q, as explained in Kirsch (1990) or Cheng and Guo (1997). In this paper, the singularity phenomenon is overcome by adopting a relaxation technique, here the qp–approach proposed by Bruggi (2008). The latter is based on an adequate choice of the penalization q < p. Selecting 2.5 ≤ q < 3 provides a strong relaxation in the regions of low density without introducing any bias at full density. In the examples of Section 5, we fix q = 2.5.

Reducing the computational cost via an active set selection strategy

In this work, we exploit an active set selection strategy to reduce the CPU effort inherent to stress–based optimization problem. During the first iterations, we only consider the constraints, which values are larger than a given threshold, chosen as σ_th,1 = 0.65. The threshold value is then progressively increased to σ_th,2 = 0.95 during the first n_iter iterations here set to n_iter = 10. This strategy results in a modification of the active set of constraints and thus introduces discontinuities in the optimization process, that may trigger convergence issues. However, to the authors knowledge, no such convergence issue was encountered in the numerical investigations. The update rule of the threshold along the iteration process, σ_th(iter), is given in (23)

$$ \sigma_{th}(iter) = {\min}\left( \frac{\sigma_{th,2}-\sigma_{th,1}}{n_{iter}}\cdot iter + \sigma_{th,1}; \sigma_{th,2}\right) $$

(23)

Accuracy of the stress analysis

A crucial issue, when dealing with stress constraints, is the accuracy of the stress analysis. The displacement–based discretization, adopted in this work, is known to suffer from a lack of accuracy in the approximation of the stress field. Moreover, inaccuracy of the evaluated stress field, in the context of density–based topology optimization, is also due to the jagged nature of the optimal structure. Mesh refinement can be used to overcome this issue, but highly increases the CPU time required. Though conventional discretization methods fail to predict exact stress concentration value, they allow detecting the stress peaks locations to mitigate through the optimization process. Interested readers may refer to Le et al. (2010) for a comprehensive review on numerical experiments using displacement–based finite elements. Several research works focus on overcoming these inaccuracy issues in the context of stress–based topology optimization. For example, Bruggi (2016) used stresses as primary variables, whereas Svärd (2015) proposed an interior value extrapolation of the stresses across the boundary of the design.

5 Numerical examples

In this section, the developed methodology of microstructural design with control of the stress level is illustrated with two–dimensional numerical examples. First, some classical benchmarks inspired from the literature are investigated to assess the algorithm. Then, an original material design problem with application to seismic insulation is addressed, involving multiple load cases.

For each example, the discretization of the periodic design domain consists of 64 × 64 square Q4 elements with bi–linear shape functions. The initial periodic base cell presents a circular hole at its center. To validate the choice of the mesh, i.e. make sure that the stress fields are evaluated with a sufficient accuracy, a comparison against a finer mesh (128 × 128 elements) is provided in Appendix A.

The constituent material is assumed linear elastic and isotropic and normalized reference properties are used to carry out the simulations without any loss of generality. In particular, we consider a reference material characterized by a Young modulus E = 1N/m² and a Poisson’s ratio ν = 0.3. The stress limit $\protect {\sigma _{y}^{0}} = 5N/m^{2}$ is enforced in stress–constrained optimization. Strain fields with a suitable magnitude are applied to the unit cell to ensure that the imposed stress constraints become active and are thus effective in removing stress peaks arising within the RUC.

The stress–constrained microstructural design problem in (15a) is solved resorting to the Method of Moving Asymptotes (MMA) developed by Svanberg (1987). The stopping criterion is chosen such that the maximal variation of the design variables between two successive iterations, max(|x^iter+ 1 −x^iter|), should drop to 0.005.

Throughout the paper, the stress maps show the equivalent Von Mises stress normalized by the selected stress limit, i.e. $\protect \overline {\sigma }^{\text {VM}}/{\sigma _{y}^{0}}$. For convenience, identical color bars are used for optimal layouts achieved with and without stress constraints. The proposed procedure is implemented and tested in an academic version of Matlab R2015b.

5.1 Maximization of the bulk modulus

This first example deals with the maximization of the material bulk modulus under hydrostatic loading. This benchmark was extensively studied in the literature, see e.g. Sigmund (1999) and Andreassen et al. (2015), or Noël and Duysinx (2016). This problem consists in finding the optimal contour of a hole in a plate undergoing a single hydrostatic load. Vigdergauz (2001) provided an analytical solution describing the optimal contour of the single hole inclusion depending on its volume. Also, the bulk modulus achieved numerically can be conveniently compared with the theoretical upper bound of Hashin and Shtrikman (1963).

The objective function to be maximized is the equivalent effective bulk modulus, expressed as a linear combination of its homogenized elastic properties as:

$$ f(H^{H}_{ij})=(E_{11}^{H}+E_{22}^{H}). $$

(24)

The boundary conditions, the mesh and the initial configuration are given in Fig. 3. An isotropic strain ε₁ is applied to the periodic cell and considered as a single load case for the enforcement of strength constraints. The problem is solved for different values of the maximum volume V ^⋆ allowed in the RUC.

Fig. 3

Maximization of the bulk modulus under hydrostatic loading: initial guess, mesh and boundary conditions

The results of the optimization procedure, for a target volume V ^⋆ = 0.6, are presented in Fig. 4a and b without and with stress constraints respectively. The relevant maps of the non–dimensional equivalent Von Mises stress measure $\protect \overline {\sigma }^{\text {VM}}/{\sigma _{y}^{0}}$ are given in Fig. 4c and d. The stress map associated with the conventional design in Fig. 4a reports stress concentrations along the hole edge, where $\protect \overline {\sigma }^{\text {VM}}/{\sigma _{y}^{0}}>1$. Conversely, in Fig. 4c, the stress-constrained formulation for bulk maximization leads to a more squared layout, where the maximum stress does not exceed the prescribed limit $\protect {\sigma _{y}^{0}}$.

Fig. 4

Maximization of the bulk modulus under hydrostatic loading: a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map, for the optimized layout without stress constraints; d scaled Von Mises stress map for the optimized layout with stress constraints

According to Vigdergauz (2001) and Grabovsky and Kohn (1995), a family of elliptical shapes evolving from circles, for small cavities, to squares with rounded corners, for large cavities, maximizes the effective bulk while minimizing the stress concentrations around the hole. The optimized shapes shown in Fig. 4a and b are quite similar, and in rather good agreement with the theoretical and numerical results. Nonetheless, the stress-constrained design exhibits a more square-shaped hole, able to modify the stress field so as to satisfy the prescribed stress constraints at the price of a decrease in the objective function value, i.e. the bulk modulus value. These minor shape differences are certainly due to the approach followed in this paper. In fact, we are not solving the original problem of Vigdergauz (2001) and Grabovsky and Kohn (1995), who sought an optimal shape of the hole minimizing the elastic energy or minimizing the stress concentrations around the hole. In this contribution, a prescribed value of the stress limit has to be reached by enforcing stress constraints. This formulation renders the problem more restrictive and steers the optimization towards a less optimal layout. Despite this difference, a solution, consistent with the theoretical expectations and fulfilling the strength requirements, is achieved.

An additional assessment of the achieved layouts can be provided by comparing their bulk modulus with respect to the HS bound $\protect \mathcal {K}_{u}^{HS}$. In the case of plane stress, the equivalent bulk modulus $\protect \mathcal {K}^{H}$ (Bendsøe and Sigmund 1999) is given by:

$$ \mathcal{K}^{H} = \frac{E^{H}}{2\ (1-\nu^{H})}. $$

(25)

The HS upper bound on the bulk modulus $\protect \mathcal {K}_{u}^{HS}$ is expressed as:

$$ \mathcal{K}^{HS}_{u} = \frac{\rho \mathcal{K} \mathcal{G}}{\mathcal{G}+\mathcal{K}\ (1-\rho)}, $$

(26)

where ρ is the material volume fraction, $\protect \mathcal {K}$ and $\protect \mathcal {G}$ are the bulk and the shear moduli of the base material respectively.

Table 1 reports the values of the equivalent bulk modulus computed for the optimal layouts generated for different target volumes V ^⋆, and in particular for the case V ^⋆ = 0.6. Regardless of the adopted formulation, the equivalent bulk modulus $\protect \mathcal {K}^{H}$ matches quite well the corresponding theoretical upper bound $\protect \mathcal {K}^{HS}_{u}$. As expected, for a given volume, the stress–constrained formulation generally finds a layout with a bulk modulus lower than the corresponding one for the unconstrained design. Minor biases with respect to the theoretical bounds may be due to numerical reasons. The refinement of the mesh or the effect of the intermediate densities arising at the interface can lead to a less accurate evaluation of the bulk modulus. A finer mesh and a projection filter could be used to improve the results. Unfortunately, this would have a strong impact on the computational cost of the simulations.

Table 1 Maximization of the bulk modulus under hydrostatic loading: equivalent bulk modulus for the optimized layouts obtained for different volume fractions V ^⋆ and corresponding theoretical Hashin–Shtrikman upper bounds

For the reference mesh with 4096 elements, the number of selected stress constraints at the end of the optimization process $\protect N_{s}^{end}$ is given in Table 1. As can be seen, the number of constraints handled by the optimizer may become non negligible and clearly calls for a compromise between accuracy and efficiency.

5.2 Synthesis of a negative Poisson’s ratio metamaterial

The second example deals with the synthesis of auxetic materials, commonly known as negative Poisson’s ratio materials, as discussed in Evans et al. (1991). As discussed e.g. by Sigmund (1994), Andreassen et al. (2015), and Xia and Breitkopf (2015), the synthesis of material characterized by a negative Poisson’s ratio using topology optimization is a challenging task.

Since early developments on material design, such kind of problems have received a lot of attention both from the theoretical and the practical point of view. Auxetic materials are extremely useful and their particular behavior can be exploited in various applications. Among practical interests, they can be used to design hydrophones as they exhibit a high sensitivity to hydrostatic pressure, as described in Avellaneda (1998), or to design crashworthiness devices for automotive or aerospace engineering, as explained in Liu (2006).

In this work, we investigate the synthesis of negative Poisson’s ratio materials while controlling the stress regime. According to Xia and Breitkopf (2015), the following objective function can be considered:

$$ f(H^{H}_{ij})=\displaystyle E_{12}^{H}-f(\beta)(E_{11}^{H}+E_{22}^{H}), $$

(27)

where f(β) is a scalar function of the parameter β controlling the stiffness of the structure along the principal directions of the plane, being β < 1.

The objective function in (27) is derived as follows. The homogenized Poisson’s ratio can be expressed in term of the homogenized equivalent properties $\protect H_{ij}^{H}$ as:

$$ \nu_{12}^{H} = \frac{E_{12}^{H}}{E_{11}^{H}}, \quad \text{or} \quad \nu_{21}^{H} = \frac{E_{21}^{H}}{E_{22}^{H}}. $$

(28)

Therefore, the objective function to achieve a prescribed Poisson’s ratio value ν^⋆ < 0 can be defined as:

$$ f_{1}(H^{H}_{ij}) = \displaystyle \frac{E_{12}^{H}}{E_{11}^{H}}-|\nu^{\star}|, \quad \text{or} \quad f_{2}(H^{H}_{ij}) = \displaystyle \frac{E_{21}^{H}}{E_{22}^{H}}-|\nu^{\star}|. $$

(29)

If we consider $\protect E_{11}^{H},\ E_{22}^{H} > 0$, minimizing (29) is equivalent to minimizing:

$$ f_{1}(H^{H}_{ij}) = \displaystyle E_{12}^{H} - |\nu^{\star}| E_{11}^{H}, \quad \text{or} \quad f_{2}(H^{H}_{ij}) = \displaystyle E_{21}^{H} - |\nu^{\star}| E_{22}^{H}. $$

(30)

Summing both equations in (30), i.e. f = f₁ + f₂, and thus accounting for stiffness requirements in both directions of the plane, yields:

$$ f(H^{H}_{ij})= \displaystyle(E_{12}^{H}+E_{21}^{H})-|\nu^{*}|(E_{11}^{H}+E_{22}^{H}). $$

(31)

Enforcing $\protect E_{12}^{H} = E_{21}^{H}$, an expression similar to (27) is recovered:

$$ f(H^{H}_{ij})= \displaystyle E_{12}^{H}-\frac{|\nu^{*}|}{2}(E_{11}^{H}+E_{22}^{H}). $$

(32)

The objective function in (32) allows providing stiffness along both principal directions of the plane, thus avoiding the collapse of the microstructure, when synthesizing auxetic materials requiring a negative value of $\protect E_{12}^{H}$.

The difference between (27) and (32) lies in the introduction of the scalar function f(β). During the optimization process, this function f(β) can be held constant or can be updated. To keep a constant value, f(β) = β, with β < 1. Xia and Breitkopf (2015) proposed to use an evolving factor and imposed f(β) = β^iter, being again β < 1 whereas the exponent (.)^iter is the current iteration number. The function f(β) = β^iter tends to zero as the iteration number ^iter increases during the optimization process. This makes the second term in (27) negligible with respect to $\protect E_{12}^{H}$.

The request for stiffness in both principal directions avoids the arising of undesired compliant microstructures but might prevent to achieve a negative Poisson’s ratio. Therefore, the second term in (27) is either set to zero progressively, or kept very small throughout the optimization. Numerical experiments show that using an evolving parameter improves the convergence of the optimization.

The starting point, the mesh and boundary conditions of the optimization problem are presented in Fig. 5. A volume constraint is enforced to achieve V ^⋆ = 0.5. A uniform strain field ε₁ is applied along the x axis, acting as a single load case for the enforcement of strength requirements. Three different sets of parameters are considered as summarized in Table 2.

Fig. 5

Synthesis of material with negative Poisson’s ratio: initial guess, mesh and boundary conditions

Table 2 Synthesis of material with negative Poisson’s ratio: numerical parameters β and ε_x

The optimized layouts obtained considering the objective function in (27) for Case 1, without and with stress constraints enforced in the optimization process, are shown in Fig. 6a and b, respectively. The corresponding normalized stress maps are given in Fig. 6c and d.

Fig. 6

Synthesis of material with negative Poisson’s ratio: a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints; d scaled Von Mises stress map for the optimized layout with stress constraints

The optimized layout in Fig. 6a matches the expected auxetic behavior resorting to thin members connected through compliant hinges. These features are weak from a structural point of view due to the arising of stress concentration, see Fig. 6c. The adoption of the proposed stress–constrained formulation significantly modifies the optimized layout, as shown in Fig. 6b. Thin members and weak connections disappear to fulfill the strength requirements. A similar effect could be alternatively achieved by the introduction of a length–scale control, see e.g. Guest (2009) or Lazarov et al. (2016). However, the enforcement of a minimum length–scale does not account for the stress regime acting in the structure, meaning that it could be ineffective in enforcing prescribed strength requirements all over the domain.

The Poisson’s ratios obtained by the optimized layouts are summarized in Table 3. Surprisingly, the stress–constrained optimization leads to an enhanced auxetic behavior with respect to the unconstrained one. As emphasized in Sigmund (1994, 1995) and Grabovsky and Kohn (1995), material design for auxetic behavior is well–known to be a challenging optimization problem. Due to its high non–convexity, gradient–based algorithms are likely to prematurely stop in undesired local optima. In this particular case, the enforcement of stress constraints steers the minimizing sequence towards a region of the design space where a better optimum exists and a layout, significantly different from the unconstrained one, arises. Thus, one gets a layout free from stress concentration and that exhibits an improved auxetic behavior.

Table 3 Synthesis of material with negative Poisson’s ratio: Poisson’s ratio achieved by the optimized layouts in Figs. 6, 7 and 9

So far Case 1 was considered, i.e. the framework proposed by Xia and Breitkopf (2015) where f(β) = β^iter and the second term of (27) eventually disappears as the number of iterations increases. In the following simulations design problems for which f(β) = β are addressed, that are β = 0.02 (Case 2) and β = 0.1 (Case 3).

Figures 7a and b show the optimized layouts obtained considering a constant function f(β) = β = 0.02, without or with stress constraints, respectively. The corresponding scaled stress maps are presented in Fig. 7c and d. The optimal design without stress constraints is different from the solution of Fig. 6a. Conversely, the stress–constrained formulation achieves a similar topology with respect to the one achieved for Case 1. The four–arm star of Fig. 7b is not far from that seen in Fig. 6b. The relevant Poisson’s ratios are summarized in Table 3. As for the reference design, the enforcement of strength requirements leads to an enhanced auxetic behavior, although this is not generally the case when imposing stress constraints.

Fig. 7

Synthesis of material with negative Poisson’s ratio (β = 0.02): a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints; d scaled Von Mises stress map for the optimized layout with stress constraints

Initializing the stress–based optimization with the density distribution obtained in Fig. 7a, the optimized design shown in Fig. 8a is found. A slight increase in the members thickness allows fulfilling the strength requirements, but yields a drastic reduction in terms of performance, i.e. ν^H = − 0.5515. From a mathematical point of view, this design is sub–optimal with respect to the one previously found using the same stress-constrained formulation. This simple example illustrate that the problem is very sensitive to local optima and that the choice of the initial design has a large influence on the achieved results.

Fig. 8

Synthesis of material with negative Poisson’s ratio: stress–based problem using the density distribution of Fig. 7 as starting point: a optimized layout; b scaled Von Mises stress map for the optimized layout

Figures 9a and b show the obtained layouts and their corresponding scaled stress maps when f(β) = β = 0.1. In this case, the designs achieved neglecting or considering stress constraints exhibit similar topologies. For both problems, a four–arm shape is found, as already seen in Figs. 6b and 7b. Stress requirements induce a modification of the inner hole that is responsible, as expected, for a less enhanced auxetic behavior with respect to the unconstrained optimization, see Table 3.

Fig. 9

Synthesis of material with negative Poisson’s ratio (f(β) = β = 0.1): a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints; d scaled Von Mises stress map for the optimized layout with stress constraints

As a conclusion, starting the optimization from various initial guesses, different solutions are likely to arise when synthetizing auxetic microstructures, see in particular the comprehensive numerical campaign in Xia and Breitkopf (2015). The same conclusion is drawn here for stress–constrained optimization, as illustrated by the stress–based layouts in Figs. 7b and 8a. When the constrained and unconstrained layouts only present slight differences, an expected weakening of the auxetic behavior is observed for the stress–based design, see e.g. Case 3. However, stress constraints can steer the optimizer towards design regions so far unexplored when considering an unconstrained formulation. Due to the high non–convexity of the problem, optimized solutions with improved properties may be achieved, see e.g. Case 1 (Fig. 10).

Fig. 10

Synthesis of material with negative Poisson’s ratio: influence of the selection of β^iter on the convergence of the objective function a without stress constraint; b with stress constraint

5.3 Metamaterial for seismic insulation device

The third example deals with the synthesis of a metamaterial to build a seismic insulation device. A high bulk modulus is required to sustain the weight of an overlaying structure, whereas a low shear modulus allows cutting the horizontal forces in case of an earthquake.

A topology optimization problem can be straightforwardly derived from these requirements. The homogenized bulk modulus of the microstructure should be maximized while an upper bound should be enforced to the homogenized shear modulus, e.g. $\protect \mathcal {G}^{\star } = 0.0013 N/m^{2}$. The design problem reads:

$$\begin{array}{@{}rcl@{}} \displaystyle \max_{\mathbf{x}} & \mathcal{K}(\mathbf{x}) & \end{array} $$

(33a)

$$\begin{array}{@{}rcl@{}} \text{s.t.} & \mathcal{G}(\mathbf{x}) \leq \mathcal{G}^{*}, & \end{array} $$

(33b)

$$\begin{array}{@{}rcl@{}} &\mathbf{K}(\mathbf{x})\ \mathbf{u}_{i} = \mathbf{f}^{0}_{i}(\mathbf{x}),& \quad i = 1,2,3 \end{array} $$

(33c)

$$\begin{array}{@{}rcl@{}} &\mathbf{K}(\mathbf{x})\ \boldsymbol{\chi}_{s} = \mathbf{f}_{s}(\mathbf{x}),& \quad s = 1,\dots,n_{s} \end{array} $$

(33d)

$$\begin{array}{@{}rcl@{}} &x_{e}^{p-q}\ \overline{\sigma}_{e,s}^{\text{VM}} \leq {\sigma_{y}^{0}}, & \quad e = 1, \dots, n_{e} \end{array} $$

(33e)

$$\begin{array}{@{}rcl@{}} &&\quad s = 1, \dots, n_{s} \end{array} $$

(33f)

$$\begin{array}{@{}rcl@{}} &0 \leq x_{\min} \leq x_{e} \leq 1, &\quad e = 1, \dots, n_{e} \end{array} $$

(33g)

Two load cases are considered for the enforcement of strength requirements. Most of its life, the insulator sustains only the weight of the carried structure. In the event of an earthquake, the insulator supports an additional shear loading. The influence of strength requirements on the optimized layouts is assessed investigating the optimization problem with or without the constraints of (33e). In this particular problem, the volume is no longer a design requirement.

The starting point, the mesh and boundary conditions are illustrated in Fig. 11, along with the strain fields related to load case 1 (LC1 - black) and load case 2 (LC2 - red).

Fig. 11

Microstructural design for seismic insulation: initial guess, mesh and boundary conditions

The resulting topologies of the microstructural base cell are rather different when accounting for or neglecting stress constraints, see Fig. 12. If no stress constraint is imposed, thin hinges appear at the corners of the star–shaped hole in the design. When stress constraints are enforced, the star-like hole is preserved, but the members of the layouts are connected by thicker members with a new shape. Table 4 gives the bulk modulus achieved by each one of the tailored microstructures and shows that the stress–based design performs slightly better than the unconstrained one.

Fig. 12

Microstructural design for seismic insulation under the strain fields ε₁ = [2.5,2.5,0] and ε₂ = [0,0,2.5]: a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints (LC1); d scaled Von Mises stress map for the optimized layout with stress constraints (LC1); e scaled Von Mises stress map for the optimized layout without stress constraints (LC2); f scaled Von Mises stress map for the optimized layout with stress constraints (LC2)

Table 4 Microstructural design for seismic insulation: bulk moduli achieved by the optimized layouts under load cases LC1 and LC2

The corresponding non–dimensional stress maps are shown in Fig. 12 for load case LC1 and load case LC2. The thin hinges that allow for the requested shear compliance in the unconstrained design induce stress peaks for LC1 that are not admissible with respect to strength requirements. The introduction of stress constraints in the optimization problem results ins a noticeable reduction of the stress concentration for LC1, as illustrated in Fig. 12d.

Focusing on LC2, both Fig. 12e and f show that the shear load case does not affect the optimization process. In fact, stress constraints are not active for this load case, see also Fig. 14 reporting the number of active constraints for each load case throughout the optimization process.

To further investigate the effect of the shear load case, a stress–constrained optimization with the applied external strain field ε₂ = [0,0,7.5] is considered. The optimized topology, shown in Fig. 13b, remains almost unchanged with respect to the previous one. Minor adaptations are sufficient to handle the increase in the magnitude of LC2, see e.g. the slightly different design in the vicinity of the four corners of the design domain. As expected, the number of active constraints is larger than for the previous optimization case, see Fig. 14.

Fig. 13

Microstructural design for seismic insulation under the strain fields ε₁ = [2.5,2.5,0] and ε₂ = [0,0,7.5]: a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints (LC1); d scaled Von Mises stress map for the optimized layout with stress constraints (LC1); e scaled Von Mises stress map for the optimized layout without stress constraints (LC2); f scaled Von Mises stress map for the optimized layout with stress constraints (LC2)

Fig. 14

Microstructural design for seismic insulation: number of active stress constraints related to both load cases LC1 and LC2 in the course of the optimization process

The bulk moduli found at the end of the optimization are almost the same for both layouts, see Table 4. It must be noticed that the bulk modulus for the optimized solution in Fig. 13 is slightly smaller than for Fig. 12b. This was expected considering that the shear load case has a major importance in this simulation. However, both designs exhibit an increased bulk modulus value with respect to the unconstrained solution.

An additional stress–constrained optimization is performed using the solution in Fig. 13b as starting point. In this case, the achieved topology remains quasi unchanged and slight adaptations are sufficient to reduce the stress peaks, see Fig. 15b. The optimized bulk modulus is equal to $\protect \mathcal {K}^{H} = 0.1021~N/m^{2}$, which is smaller than for the unconstrained problem.

Fig. 15

Microstructural design for seismic insulation under the strain fields ε₁ = [2.5,2.5,0] and ε₂ = [0,0,2.5] with stress constraints and using the density distribution in Fig. 12a as starting point: a starting point, b achieved optimal design

The seismic synthesis problem is arduous as a maximum bulk modulus is sought, while restraining the shear modulus value. It is thus extremely sensitive to local minima, see Section 5.2. Starting from distinct initial guesses, different solutions are likely to arise, see in particular the stress–based layouts in Figs. 13b and 15b. As previously emphasized, stress–constrained layouts are associated with reduced target performance, when they slightly differ from the unconstrained ones. However, stress constraints can steer the optimizer towards design regions unexplored when exploiting the unconstrained formulation. In this particular case, alternative solutions with improved performance are achieved.

6 Conclusion

Enhanced material performance can be achieved by optimizing the material distribution at the microscale. In this work, inverse homogenization problems are solved to tailor porous single–phase microstructures with prescribed elastic properties. Classical density–based optimization is used and, in particular, the SIMP model is adopted to interpolate material properties.

Macroscopic loads applied to the microstructures may induce undesired stress concentrations at the microscale. Stress responses are usually not accounted for in conventional microstructural design approaches. To address this problem, this paper proposes an energy–based stress–constrained optimization formulation to simultaneously maximize target material properties and reduce the stress concentrations at the microstructural level.

Within this work, the macrostructure is not considered and the actual applied macrostructural loads are unknown. Arbitrary test strain fields, representative of the service loads, are thus applied to the microstructure. Therefore, the prescribed stress limits are arbitrary. The resulting approach is thus able to reduce high stress concentrations, but does not fully control the microstress values, which depend on the actual structural strain fields.

Working with periodic microstructures, the homogenization theory is exploited to evaluate the material equivalent properties. Optimization problems are solved resorting to mathematical programming schemes and a sensitivity analysis is carried out considering the adjoint approach. Material tailoring problems are generally associated with design–dependent loads, that induce an additional term in the sensitivity of the equivalent Von Mises stress.

Finally, the proposed approach is validated on classical benchmarks, i.e. the maximization of the material bulk modulus and the design of auxetic microstructures. Then, an original application, including multiple load cases, investigates the design of seismic insulating devices. Although one could expect that accounting for stress restrictions would simply results in a thickening of thin features and weak members at the cost of a volume increase and/or a stiffness performance drop, numerical applications clearly show that the high non–convexity of the problems promotes the convergence towards different local minima, characterized by a small stiffness performance loss, but also by strongly reduced stress concentrations.

Ongoing work aims at introducing stress constraints through a multi–scale approach to enforce strength requirements both at the micro- and at the macroscale. Proceeding this way, it would be possible to simultaneously optimize the material distribution at both scales and to consider the actual strain fields evaluated from the service structural loads. Such an approach would certainly result in a better use of the material. The extension of the proposed approach to account for multiple phases in two–dimensional or three–dimensional design domains is straightforward. Furthermore, non–linear material properties could be considered to synthesize components exhibiting peculiar properties, such as shock absorption.

Appendices

Appendix A

To validate the choice of the reference mesh (64 × 64 elements) used in this contribution, an additional simulation with a finer mesh (128 × 128 elements) is performed. The finer mesh is used to solve the bulk modulus maximization problem described in (15a) with the objective function given in (24). The resulting designs along with their scaled stress maps for both the unconstrained and the stress constrained problems are provided in Fig. 16.

Fig. 16

Maximization of the bulk modulus under hydrostatic loading for a fine mesh , i.e. 128 × 128 elements: a optimized layout without stress constraints; b optimized layout with stress constraints; c scaled Von Mises stress map for the optimized layout without stress constraints; d scaled Von Mises stress map for the optimized layout with stress constraints

The cavity layouts as well as the corresponding stress maps in Fig. 16 are in good agreement with the results obtained with the reference mesh, see Fig. 4. As observed previously, the stress–constrained design leads to a decrease in the bulk modulus values with respect to the unconstrained design, i.e. $\protect \mathcal {K}^{H} = 0.2400~N/m^{2}$ and $\protect \mathcal {K}^{H} = 0.2438~N/m^{2}$ respectively. One should also notice that using a finer mesh yields bulk modulus values closer to the Hashin–Shtrikman theoretical bounds detailed in Table 1.

However, although the quality of the structural responses evaluated is improved, the CPU time drastically increases when using such a fine mesh. Moreover, the number of selected constraints handled by the optimizer at the end of the optimization process is also significantly increased, $\protect N_{s}^{end} = 2649$ over 16384 potential elements. Therefore, the gain in accuracy is obtained at the price of an important loss of efficiency.

For these reasons, the reference mesh is used in this paper as it constitutes a good balance between accuracy, i.e. the stress fields are correctly captured, and CPU time. Finally, one should note that the adopted mesh size is similar to the one used in multiple works addressing stress–based optimization, see e.g. Bruggi and Dusyinx (2012), Collet et al. (2017), Oest and Lund (2017), and Zhang et al. (2017).

Appendix B

For illustration purposes, let us consider two problems: a simple problem (P₁), where we minimize the volume subject to stress constraints, and a second problem (P₂), where we minimize the maximum local stress subject to a volume constraint. The maximum local stress can be approximated by replacing the max function by a smooth continuous function, see e.g. Chenm (1985). By writing down the stationary conditions on the Lagrangians for both problems ((34) and (35)), one can see that problems (P₁) and (P₂) are equivalent, provided that there exists a specific relation between the Lagrange multipliers λ₁ and λ₂. In fact, (P₁) and (P₂) are equivalent if: $\protect \lambda _{1} = \frac {1}{\lambda _{2}}$, i.e. if the Lagrange multipliers are the inverse from one another. Swapping the objective and the constraint is therefore consistent with respect to the mathematical programming approaches, as considered in our paper.

$$(P_{1})\left\{ \begin{array}{lll} \displaystyle \min_{x} & \displaystyle \mathcal{V}\\ \text{s.t.} &\displaystyle \sigma^{\max} \leq \overline{\sigma},& \end{array} \right. (P_{2})\left\{ \begin{array}{lll} \displaystyle \min_{x} & \displaystyle \sigma^{\max}\\ \text{s.t.} &\displaystyle \mathcal{V}\leq\overline{V},& \end{array} \right. $$

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{1}(x,\lambda_{1}) &=& \mathcal{V}+\lambda_{1}(\sigma^{\max}-\overline{\sigma}) \\ \frac{\partial \mathcal{L}_{1}}{\partial x} &=& \frac{\partial \mathcal{V}}{\partial x}+\lambda_{1}\frac{\partial \sigma^{\max}}{\partial x}\qquad\ \ \ = 0\\ \frac{\partial \mathcal{L}_{1}}{\partial \lambda_{1}} &=& \sigma^{\max}-\overline{\sigma} \qquad\qquad\quad \ = 0 \end{array} $$

(34)

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{2}(x,\lambda_{2}) &=& \mathcal{\sigma^{\max}}+\lambda_{2}(\mathcal{V}-\overline{\mathcal{V}})\\ \frac{\partial \mathcal{L}_{2}}{\partial x} &=& \frac{\partial \sigma^{\max}}{\partial x}+\lambda_{2}\frac{\partial \mathcal{V}}{\partial x}\qquad\ \ \ = 0\\ \frac{\partial \mathcal{L}_{2}}{\partial \lambda_{2}} &=& \mathcal{V}-\overline{\mathcal{V}}\qquad \qquad \qquad \ \ = 0 \end{array} $$

(35)

(P₁) and (P₂) are are equivalent if one takes : $\protect \lambda _{1} = \frac {1}{\lambda _{2}}$. Said otherwise, the two optimization problems are equivalent if the Lagrange multipliers are the inverse from one another which make sense since one has swapped the constraint and the objective from one problem to the other.