1 Introduction

Radial Flow Machines are widely spread over the industry, being used in several applications with different scales. They can range from large machines, such as the turbines used in thermoelectric and hydroelectric power plants, to small sized pumps used in medical applications such as auxiliary blood pumps (Aaronson et al. 2012).

Thus, the performance and robustness of these machines are fundamental questions for the industry, wherein small performance improvements can result not only in financial gains for big scale applications but also in an increase of life expectancy in the case of medical devices. These improvements can be done on all parts of the flow machine, such as the rotor, internal valves, bearings, nozzle and others, these parts are illustrated in Fig. 1. However, the rotor stands out for presenting a large influence on the overall performance (Yu et al. 2000). Thus, the rotor design and its functioning evaluation are important parts of the machine conception process.

Fig. 1
figure 1

Exploded view of a generic pump

Full size image

Flow machine optimization comprises from material selection to the better form and position of the blades. In particular, the blade shape optimization has been widely studied. In this process an initial shape is given and an algorithm performs local shape changes in order to improve some characteristic based on the flow around the blade (Lee et al. 2011; Casas et al. 2006).

A number of works in the literature have used optimization techniques applied to these machines with different approaches, obtaining significant efficiency gains (Baloni et al. 2015; Wen-Guang 2011; Derakhshan et al. 2013). All these previous works could obtain an improvement in the flow machine efficiency and they have shown that the rotor is the pump component that mainly influences pump hydraulic performance. A very interesting work of Gȯlcu̇ et al. (2006) shows that a method to increase a pump efficiency is the addition of splitters between the blades, which shows the importance of rotor topology for flow machines.

1.1 Topology optimization

In the topology optimization method for fluids, material is distributed (fluid or solid) over a domain, aiming to maximize (or minimize) an objective function under determined constraints. This method was firstly introduced to fluid domains by Borrvall and Petersson (2003), where they apply the method to 2D flow channel problems, aiming to minimize the energy dissipation over the domain. In this case, the flow is modelled by using the Stokes equations for incompressible flows, without considering body forces, and with low Reynolds numbers.

Evgrafov (2005) reassesses the work of Borrvall and Petersson (2003) and compare the Brinkman model used with a different approach, by considering the fluid viscosity as a problem variable. Evgrafov (2004) also studied the application of topology optimization to slightly compressible fluid. Deng et al. (2013) applies the topology optimization method to the flow channel problem, aiming to minimize the pressure loss, considering Navier-Stokes formulation and the presence of body forces.

In the work of Romero and Silva (2014), topology optimization method has been applied to design flow machine rotors. Diverse configurations of flow machine rotors are proposed by exploring the influence of the initial domain and the effects of changes in the boundary conditions. Another approach to design flow machine rotors is presented in the work of Sá et al. (2017), by exploring the topological derivative concept.

Thus, the optimization of flow machines has been widely studied over the past decades, by using different approaches and obtaining meaningful results. However, from authors knowledge, no work so far has experimentally evaluated the performance of an optimized device designed by using topology optimization. Thus, this work aims to perform the complete development cycle of a small scale pump designed by using topology optimization method based on the density method. For the pump modelling, the Navier-Stokes equations on a rotating reference frame are solved by using finite element method. In the optimization problem, a multi-objective function that aims to minimize the viscous energy dissipation and vorticity is defined considering the volume of fluid as a constraint. The optimized results obtained by using topology optimization are post-processed and manufactured by using a 3D printer, and prototypes are built. An experimental characterization is performed by measuring fluid flow and pressure head given by the pumps. Experimental and computational results are compared with the commercial software ANSYS and the improvement is verified.

This document is organized as follows. In Section 2, the overall process of the development cycle is described. In Sections 3 and 4, the FEM model and the topology optimization process are defined, respectively. In Section 5, the numerical implementation is presented. In Section 6, prototype and the experimental setup are described. In Section 7, the numerical and experimental results are shown. Finally, in Section 8, some conclusions are inferred.

2 Flow machine rotor design methodology

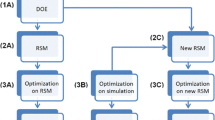
This section explains the overall process and the actions to be taken in order to successfully complete the development steps.

The method involves firstly the requisite definition phase, where a professional that has sufficient knowledge of the application identifies the operational requisites, such as the geometric dimensions, the mass flow and the pressure. Also the characteristics that are important to be optimized are defined, such as vorticity or energy dissipation as well as a corresponding objective function.

The second phase includes to perform the FEM analysis and the topology optimization in order to obtain the optimized designs.

The third phase is composed of the post-processing of topology optimization results (see Fig. 2). Then, the model is passed to a CAD software. The final contour is smoothed by using spline curves in the CAD process. The control points of the spline are chosen in order to maintain the volume the closest possible to the original topology. The contour is reproduced in a circular pattern in a way that maximizes the number of blades without overlap.

Fig. 2
figure 2

Development process of radial flow pump rotor

Full size image

The fourth phase involves building and testing the prototypes. The final design is built by using a 3D printer and the prototype is tested by building the curve pressure head versus the mass flow at the pump outlet.

The following sections describe in detail each phase.

3 Modeling of radial flow machine

The model used in this work is based on the implementation performed by Romero and Silva (2014). Thus, the Navier-Stokes equations are considered with the addition of body forces representing the rotation terms imposed by the rotor. This work considers only Newtonian fluids in the modeling. Also, even though the final model is tested at a high Reynolds flow the design is currently done with a laminar model, however the final verification (experimental and computational) is performed with turbulence models because is quite difficult to manufacture a prototype operating in laminar conditions. However, in this case if the improvement is verified for turbulence conditions, it will occur in laminar conditions too.

The topology optimization method is used by considering only the flow field between blades, without considering the volute influence. Even though the fluid in a real flow machine is three-dimensional, for the case of radial centrifugal impellers, the axial velocity component can be neglected in comparison to the radial and tangential components, hence the flow path can be approximated as a two-dimensional problem (Romero and Silva 2014).

3.1 Equilibrium equations

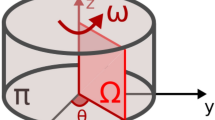
This work considers Newtonian flows, low Reynolds numbers and only steady state analysis, and the incompressible Navier-Stokes equations in a rotating reference frame. The rotational reference system causes the introduction of terms related to the rotary motion of the fluid, such as the relative velocity, and the Coriolis and Centrifugal body forces. Also, by introducing the term κ(α) representing domain porosity, the Brinkman model is obtained (Romero and Silva 2014), given by:

$$ \rho \nabla \mathbf{u} \cdot \mathbf{u} = \nabla \cdot \mathbf{T} + \rho \mathbf{f} -2\rho \boldsymbol{\omega} \times \mathbf{u} - \rho \boldsymbol{\omega} \times \boldsymbol{\omega} \times \mathbf{r} - \kappa(\alpha)\mathbf{u} $$
(1)

where T = −pI + τ is the stress tensor, τ is the viscous stress tensor, given by: τ = μ(∇u + ∇uT). The term u is the relative velocity.

Also, the mass conservation equation is used:

$$ \nabla \cdot \mathbf{u} = \mathbf{0} $$
(2)

It has been suggested that a global Reynolds number is not sufficient to describe the viscous effects within the entire pump and that all parts of the pump must be dealt with separately (Day et al. 2003). Thus, there are different definitions for the Reynolds number (see Barenboim and Vasil’tsov 1965). Usually the “centrifugal” Reynolds number is defined as Re C = ρUR/μ, where U is a reference velocity (U = ω0R), ω0 is the angular velocity, and R is a length scale (here the impeller radius). However, a more suitable definition for this paper is the expression in terms of the pump delivery, given by:

$$ Re_{Q} = \frac{Q}{D \nu} $$
(3)

where Q is the pump mass flow, D is the impeller radius and ν is the kinetic viscosity.

3.2 Finite element method applied to flow machines

The partial differential equations (PDE) shown on the previous section are solved by using the Finite Element Method (FEM) and the weighted residuals procedure of Galerkin’s method is applied to the weak formulation.

The problem is implemented by using the FEniCS environment, in which the weak formulation used as an input to implement the FEM. Thus, here, we describe the weak formulation of the problem, involving Navier-Stokes equations together with a porous media flow, in a rotating reference system considering the steady state (Romero and Silva 2014):

$$\begin{array}{@{}rcl@{}} \mathit{R}_{c} &=& {\int}_{{\Omega}} (\nabla \cdot \mathbf{u} )M d{\Omega}= 0, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} \mathit{R}_{m} &=& {\int}_{{\Omega}} (\rho \mathbf{u} \nabla \mathbf{u}) \cdot \mathbf{W} d{\Omega} \\ && +{\int}_{{\Omega}} \kappa(\alpha)\mathbf{W} \cdot \mathbf{u} d{\Omega} \\ && +{\int}_{{\Omega}} \mathbf{T} : \nabla \mathbf{W} d{\Omega} \\ && +{\int}_{{\Omega}} \mathbf{W} \left[ 2 \rho (\boldsymbol{\omega} \times \mathbf{u}) + \rho \boldsymbol{\omega} \times (\boldsymbol{\omega}\times\mathbf{r} ) \right] d{\Omega} \\ && -{\int}_{{\Omega}} \mathbf{b}\cdot\mathbf{W} d{\Omega} - {\int}_{{\Gamma}} (\mathbf{T} \cdot \mathbf{n}) \cdot \mathbf{W} d{\Gamma}= 0 , \end{array} $$
(5)

where W and M are the test functions and b represents the external body forces, such as gravity. The stress tensor T is given by:

$$ \mathbf{T} = \left[\begin{array}{lllllllllll} -p + 2\mu \frac{\partial u_{1}}{\partial x_{1}} & \mu \left( \frac{\partial u_{1}}{\partial x_{2}} + \frac{\partial u_{2}}{\partial x_{1}} \right)\\ \mu \left( \frac{\partial u_{1}}{\partial x_{2}} + \frac{\partial u_{2}}{\partial x_{1}} \right) & -p + 2\mu \frac{\partial u_{2}}{\partial x_{2}} \end{array}\right] $$
(6)

The finite element method is implemented by using Taylor-Hood elements, where the velocity has a quadratic interpolation and pressure has a linear interpolation, as shown in Fig. 3. The design variable is an elementwise constant.

Fig. 3
figure 3

Triangular Element Interpolation: a Pressure, b Velocity and c Inverse Permeability

Full size image

4 Topology optimization method

4.1 Material model

The material model used in this work is the same of Borrvall and Petersson (2003) and Romero and Silva (2014), which divide the domain in regions between high permeability material, interpreted as pure fluid (α = 1), and low permeability material, representing solid (α = 0):

$$ \kappa(\alpha) = \kappa_{max} + (\kappa_{min}-\kappa_{max})\alpha \frac{1+q}{\alpha+q} $$
(7)

α is the design variable and q is a parameter that controls the curvature of κ. Also, when α ≈ 1 ⇒ κ = κ m i n , it represents a flow of pure fluid, while when α ≈ 0 ⇒ κ = κ m a x , it represents a restricted flow (solid).

4.2 Topology optimization problem

The optimization problem in this work is a multi-objective that includes minimization of energy dissipation in the rotor and minimization of vorticity in the rotor (Romero and Silva 2014). Besides, a volume constraint is defined to restrict the amount of fluid regions on the domain, so a fraction of the domain volume (f|Ω|) is used as an upper bound to create regions of fluid and leaving the remainder to be occupied by solid. Thus,

$$ {\int}_{{\Omega}} \alpha d{\Omega} \leq \mathit{f}|{\Omega}| , $$
(8)

where f is the prescribed volume fraction, a constant between 0 and 1.

4.3 Energy dissipation

Energy loss minimization is very important for a number of applications, specially applications with energy source restrictions, such as portable and small size applications such as cardiac pumps. Thus, minimization of the energy dissipation is one of the objective functions in this work. The energy dissipation that considers the effect of material model is given by Borrvall and Petersson (2003):

$$ {{\Phi}}={\int}_{{\Omega}} \left[ \frac{1}{2} \mu (\nabla\mathbf{u}+\nabla\mathbf{u}^{T}):(\nabla\mathbf{u}+\nabla\mathbf{u}^{T}) + \kappa(\alpha)\mathbf{u}^{2} \right] d{\Omega} , $$
(9)

where u is the relative velocity field on the rotating system.

4.4 Vorticity

Rotating systems have a high tendency to vortex formation that causes a swirl motion on the fluid generating an undesirable vortic current, implying on pressure loss and flow slip. Besides that, this reverse current can cause local cavitation (Fraser 1981).

Vorticity represents the shear stress in the fluid and a high vorticity can damage particles flowing in the current, causing a loss of material integrity, mixing the fluid. It can be hazardous to sensitive fluids such as blood.

In this work, the vorticity is measured in a least-squares sense through the functional given by Berggren (1998), Quarteroni and Rozza (2003), and Abraham et al. (2004):

$$ \mathit{J}(\mathbf{u}) = {\int}_{{\Omega}} |\nabla \times \mathbf{u}|^{2} d{\Omega} = {\int}_{{\Omega}} \left( \frac{\partial u_{2}}{\partial x_{1}}-\frac{\partial u_{1}}{\partial x_{2}} \right)^{2}d{\Omega} $$
(10)

4.5 Multi-objective function

The two objective equations previously defined are combined defining a multi-objective function based on the weighting sum method:

$$ {\Psi}_{obj} = w_{e} {{\Phi}} + w_{v} \mathit{J}, $$
(11)

where Ψ o b j is the multi-objective function, Φ is the viscous energy dissipation term and J is the vorticity. Also, it is considered that w e + w v = 1.

The functionals of the multi-objective function (energy dissipation and vorticity) given by (11) have different orders of magnitude. Thus, in order to reduce these differences, a coefficient can be introduced (Zhu et al. 2014, 2015):

$$ {\Psi}_{obj} = w_{e} {\Phi} + w_{v} \beta_{k} \mathit{J}, $$
(12)

where β k is the weighting factor which changes each iteration k of the optimization algorithm, and is defined as:

$$ \beta_{k} = \frac{{\Phi}_{k-1}}{\mathit{J}_{k-1}}, \quad k\geq 1 $$
(13)

where Φk− 1 and Jk− 1 are the values of Φ and J at the (k − 1)− th iteration, respectively, and k = 0 is the functional values for the initial domain distribution.

5 Numerical implementation

5.1 FEniCS environment

In this work, the FEniCS environment (Logg et al. 2012) is used to solve the equations presented in the previous sections. The resulting FEM system is solved with the MUltifrontal Massively Parallel Sparse direct Solver (MUMPS) (Amestoy et al. 2001). The optimization is solved by firstly calculating the sensitivities, which is obtained here by using the adjoint method implemented by the software dolfin-adjoint (Funke and Farrell 2013). Then, an optimizer is used to update the design variable. In this work, we use the IPOpt optimizer (Wȧchter and Biegler 2006; Wächter 2009), which is a Interior Point Optimization algorithm.

The flow chart of the optimization procedure is represented in Fig. 4. The sequence of steps to solve the optimization involves firstly defining an initial material distribution and the boundary conditions, then the FEniCS routines are called to solve the FEM system returning the solution vector [u1 u2 p]. With this, the functional is evaluated and the dolfin-adjoint is called performing the adjoint problem derivation, in order to calculate the sensitivity of the functional with respect to the design variable. Next, this information is passed to the optimizer IPOpt, that computes the next material distribution over the domain. The process is repeated until the functional value converges, in which case the optimized solution is reached. The convergence criterion used is the design variable change between iterations, and the process converges when the change at each variable is below 10−2:

$$ max\left( |\alpha^{k} - \alpha^{k-1} |\right) \leq 1 \times 10^{-2} $$
(14)
Fig. 4
figure 4

Topology optimization implementation flow chart

Full size image

6 Experimental methodology

This section presents the prototype design for a radial flow pump and also the manufacturing and experimental setup to perform the pump characterization. The prototype built is based on ventricular assist pumps, so it is a small scale pump. The characterization is made by measuring the pump output (pressure, at the inlet and outlet, and mass flow).

6.1 Pump prototype

The prototype consists, essentially, of three parts, the casing, the motor and the rotor. The motor consists of a traditional brushless electric motor. The rotation control is done by manually adjusting the DC source output.

6.1.1 3D printed parts

The prototype case, lid and rotors are built by using a 3D printer Objet30. The materials used are from the Stratasys commercial materials. Two types are used a Translucent Material VeroClear - RGD810, that offers a good dimensional stability, translucency and is rigid (for the lid), and a Opaque Material VeroBlack with similar properties. Casing, lid and rotor are shown in Fig. 5.

Fig. 5
figure 5

3D printed parts

Full size image

6.2 Experimental setup

In order to test the built prototype an experiment is performed. The experiment aims to build the curve pressure head versus mass flow given by the pump. Thus, the experiment consists of a water tank, a flow sensor (Flownetix 100series Smart Ultrasonic Flowmeter) and pressure sensors coupled to the pump. The pump rotation speed is controlled by the source output and observing the encoder. The flow sensor and the hall sensor outputs are read by using an oscilloscope. The scheme representing this assemble is shown in Fig. 6. Figure 7 shows a picture of the experimental site.

Fig. 6
figure 6

Experimental site scheme

Full size image
Fig. 7
figure 7

Experimental site photo

Full size image

The experimental setup has a limitation in the fact that we can operate the pump only at rotations above 1500rpm, thus, even though some region of the rotor may have laminar flows the overall flow will be turbulent. However, as it will be shown in the next section, the optimized topologies do perform well even in the turbulent flow.

7 Results

7.1 Topology optimization results

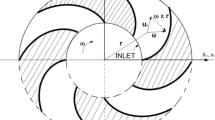
The rotor is modelled as a 2D 100o circular sector, given that the rotor has a radial symmetry, with the blade geometry being repeated in a radial pattern. This angular size is chosen in order to try to obtain a rotor in which 6 blades can fit. The current methodology can not predict the ideal number of blades. Some numerical experiments performed with a full 360o domain, show that the unstructured mesh removes the rotor symmetry and it is more difficult to converge.

The outlet boundary is set to zero over all the external contour so the algorithm can choose where the outlet will be. The inlet velocity is set as a parabolic profile over a 45o opening and profile is calculated so the mass flow entering the domain is 3[l/min]. The other boundaries are set with a no-slip condition to indicate that there would be another blade, i.e. a solid region. The inlet velocity is calculated by:

$$ u_{in} = \frac{Q}{2 \pi r h} \cdot \frac{1}{n_{blades}} $$
(15)

where Q is the mass flow, r is the inner radius, h is rotor height and n b l a d e s is the expected number of blades. In this case we consider a rotor with 5[mm] height and six blades.

Thus, for all cases shown in next sections, the design domain and boundary conditions presented in Fig. 8 are used. The problem is solved by considering that the domain Ω has an inner radius of 0.7[cm] and an outer radius of 1.5[cm]. The fluid (water) has density equal to 1.0[g ⋅ cm−3] and viscosity equal to 0.01[g ⋅ cm−1 ⋅ s−1]. The angular velocity (ω) used is in the z direction and equal to 2500[rpm].

Fig. 8
figure 8

Design domain and boundary conditions

Full size image

The values for κ m a x and κ m i n , from (7), are 1000.0 and 0.0, respectively. The parameter q is firstly defined as 0.01 and then changed to 0.1 to further penalize the gray regions.

The following sections show the topology optimization results for the straight blade initial guess. In all following figures presented, the blue regions represent the fluid domain (α = 1) and the red regions represent the solid region (α = 0).

7.1.1 Straight blade initial guess

Given the domain shown in Fig. 8, it is possible to choose different initial conditions for the optimization process. Thus, in this section an initial domain distribution of a straight blade is used, as shown in Fig. 9. The velocity, pressure, local energy dissipation and vorticity profiles for this initial topology are shown in Fig. 10.

Fig. 9
figure 9

Straight blade 2D optimization: Initial domain

Full size image
Fig. 10
figure 10

Numerical fields for straight blade initial guess

Full size image

The topology optimization results considering equation (11) with different values for the weight factors and a volume constraint of 45% of the volume are shown in Fig. 11. This volume constraint is chosen so the optimized topologies have the same area as the initial guess. The value of this constraint is somewhat arbitrary, and in this case, the constraint is always active on the final topology. This is a common problem in topology optimization and the choice can greatly influence the final result (Sigmund 1997; Nishiwaki et al. 1998; Amigo et al. 2016). The value for each functional, energy dissipation and vorticity, for each result, is shown in Table 1. The table values are calculated by using the 2D model and the entire domain (solid and fluid regions). The results show that there is a Pareto relation between the functionals, i.e., one functional improves in detriment to other. For example, the case with energy and vorticity optimization (Fig. 11b) has a better vorticity value (2479.27), however, a worse energy dissipation (2582.72), when compared with the case with energy dissipation only, that has an energy dissipation of 93.69 and vorticity of 4641.16.

Table 1 Functional values results by considering a 2D straight blade as initial guess
Full size table
Fig. 11
figure 11

Topology optimization results by considering a 2D straight blade as initial guess

Full size image

The result involving the energy dissipation functional as the only objective function (Fig. 11a) shows a topology similar to the traditional curved blades.

Figure 12 shows the velocity, pressure, energy dissipation and vorticity fields for the topology obtained by minimizing energy dissipation functional. Figure 13 shows the same fields for the topology obtained by minimizing the energy dissipation and vorticity functionals.

Fig. 12
figure 12

Numerical fields for topology optimization result considering energy dissipation only as objective function

Full size image
Fig. 13
figure 13

Numerical fields for topology optimization result considering energy dissipation and vorticity as objective function

Full size image

Observing the energy dissipation fields for the three topologies (Figs. 10c, 12c and 13c) we can see that the topology obtained with the energy dissipation functional does not have the lowest peak value, however, the integrated value over the domain is the lowest. In all topologies the highest energy dissipation value occurs near the outlet where the velocity magnitude is also high. In addition, the energy dissipation concentrates near the channel walls, where the velocity gradient is high due to the no-slip condition emulated by the zero velocity inside solid regions.

The vorticity result shows that vorticity can be minimized by introducing regions with intermediate porosity, as it can be seen in Fig. 11b, where the light red region represents an intermediate material between fluid and solid. These regions decelerate the fluid and lower the velocity gradient. The addition of the energy dissipation functional introduces the term relative to the external force of the porous media (κ(α)u ⋅u), which counterposes this intermediate porosity by penalizing it. Thus, the final topology has a more defined contour, however, still having these porous regions near the outlet. Forcing a threshold in the design variable causes the appearance of the blue dots near the outlet (Fig. 11b). Hence, the topology needs to be post-processed before building it.

The pressure has small variations among the different topologies, as observed in Table 1. It is possible to notice that the reduction of the energy dissipation and vorticity do not present a significant effect in the pressure. Thus, the pressure has a stronger correlation with the angular velocity rather than with the rotor topology.

7.2 Experimental results

Considering the optimized result shown in Fig. 11 and the post-processing process described before (Fig. 2), rotors shown in Fig. 14 are manufactured. These rotors have a 30[mm] diameter and blades have a height of 5[mm]. It is important to notice, that due to structural restrictions the final topology is adjusted so the minimal wall width is 1[mm].

Fig. 14
figure 14

Post-processing and rotors built from topology optimization results: a for energy dissipation (Fig. 11a) and b for energy dissipation and vorticity (Fig. 11b)

Full size image
Fig. 15
figure 15

Experimental Curves for the three prototypes

Full size image

7.2.1 Experimental and computational comparison

The experimental results are the curves of pressure by mass flow and can be seen in Fig. 15. This curve is collected by measuring the differential pressure between the pump inlet and outlet and measuring the mass flow.

Comparing the pressure output (Fig. 15), we observe that all models are very close with small differences. The data is collected by fixing a rotation (2500 rpm in this case) and by changing valve in the system.

In these curves, the higher the pressure the higher the viscous energy dissipation. This reasoning is counter-intuitive, however, in the steady state, the dissipation of viscous energy is equivalent to the sum of the power held in the system by the external forces and variation of kinetic energy through the contour (Olesen et al. 2006). That is, the pressure jump between the inlet and the outlet of the pump is related to the dissipation of energy (flow viscous dissipation) - thus, the higher dissipation, the higher pressure jump. Hence, the rotor with straight blades (first column in Fig. 17) has a higher dissipation than the others.

The experimental data can be used to define the boundary conditions of the complete 3D pump computational model, by using the prototype mass flow information to define the model inlet velocity and also setting the rotational speed of the rotor. Then, the pressure at the computational model outlet is set to the experimental pressure measured at the prototype outlet. The verification of the computational model is done by comparing the model pressure gain and the measured pressure gain.

Thus, it is possible to verify the simulation results by modelling the complete 3D pump model with six blades and the casing by using the commercial software ANSYS (Fig. 16). This simulation permits to observe the velocity and pressure distributions over the complete pump model (rotor plus casing) as illustrated in Fig. 17, which shows the absolute velocity and pressure fields for the model. Given these fields the quantities of interest, such as energy dissipation and vorticity, can be calculated.

Fig. 16
figure 16

Complete pump 3D ANSYS model of optimized rotor for energy dissipation

Full size image
Fig. 17
figure 17

ANSYS results for different rotors: Straight blade rotor (first column), Optimized for energy dissipation (second column) and Optimized for energy dissipation and vorticity (third column). a, b, c Velocity field; d, e, f Pressure field; g, h, i Energy Dissipation distribution; and j, k, l Vorticity distribution

Full size image

Even though the formulation used in the optimization considers a laminar model, this simulation considers the Spalart-Allmaras turbulence model, given that the experiment is performed at high rotations and at high Reynolds numbers, characterizing a turbulent flow. However, it is assumed that if an improvement is perceived in the turbulent flow, the same behavior should be expected in laminar flows.

Considering the operational point nearest to the design point of the optimization phase, mass flow of 3[l/min] and 2500[rpm], the simulation is performed in ANSYS for each rotor. The built model uses water as fluid and considers an inlet mass flow and a defined pressure at the outlet. Figure 16 exemplifies the ANSYS model built for the rotor optimized for energy dissipation only. The mesh convergence analysis for each case is shown in the Appendix Appendix. Figure 17 shows the fields for each variable (velocity, pressure, energy dissipation and vorticity) and for each rotor at a xy-plane taken at z = 3.5mm. It is important to notice that the energy dissipation and vorticity are calculated by considering a 3D domain.

Repeating the process for other operational point and for each rotor we can build the pressure versus mass flow curves and compare the experimental and simulated curve, as shown in Fig. 18. We can see that both curves have a good agreement at high mass flow rates, indicating that the computational models represent well the pump prototype behavior for these points.

Fig. 18
figure 18

Comparison between experimental data and simulated point for each rotor: a Straight Blade (Fig. 9), b Opt. for energy dissipation (Fig. 11a) and c Opt. for energy dissipation and vorticity (Fig. 11b)

Full size image

Given that the computational models are verified it is possible to infer that simulations done in the model will reproduce the behavior of the prototype. Thus, the quantities of interest (energy dissipation and vorticity) can be evaluated and compared between the different rotors. The results relative to the energy dissipation and vorticity calculated from the computational models are shown in Fig. 19a and b.

Fig. 19
figure 19

Comparison of energy dissipation and vorticity for each rotor at different points of operation: a Energy dissipation and b Vorticity

Full size image

Observing the curves it is possible to conclude that the optimized rotors have better values for both functionals. The optimized for energy dissipation (Fig. 11a) has average decreases of 66% and 63% for the energy dissipation and vorticity, respectively. While the optimized for both energy dissipation and vorticity (Fig. 11b) has average decreases of 60% and 55% for the energy dissipation and vorticity, respectively.

The topology optimization method reduces the vorticity by creating an intermediate porosity in the final topology, as described before and shown by the dark gray region in Fig. 11b. However, for manufacturing, it is necessary to perform a post-processing of this intermediate porosity, which causes an increase of the vorticity due to changes in the final topology. Thus, the smaller improvement in the vorticity functional of the second optimized rotor (Fig. 14b) is related to the post-processing, given that the numerical results have a region with intermediary porosity that can not be manufactured. The post-processing in this case changed the blade topology by imposing a shape generated by a spline, which changed the optimized contour.

8 Conclusion

The concept of topology optimization is applied to the development of small scale radial pumps, aiming to increase the overall performance and decrease the vorticity of these machines. The complete cycle of development is performed in which a rotary flow machine is modelled, optimized and a small scale prototype is built and tested.

The 3D printer has shown a good synergy with the topology optimization process, being capable of building an operational prototype resulting from the optimization.

The studied example of the straight blade optimization shows that the experimental results are coherent with the computational model, indicating that analysis done in the model would represent the prototype behavior. Also, the optimization shows that the optimized rotors have better values for both objective functions. The rotor designed for energy dissipation minimization presented an average improvement in the order of 66% for the energy dissipation functional and 63% for the vorticity functional. The results concerning the vorticity functional optimization need to be further studied, given that the optimized results with intermediate porosity regions can not be directly manufactured and need to be post-processed, which causes changes in the previous achieved topology and can absorb the improvements obtained with the optimization.

Finally, the proposed process of applying topology optimization to develop radial pump rotors, defined, essentially, by modelling, optimizing, post-processing, 3D printing the prototypes and performing the experimental characterization has been successfully implemented.