1 Introduction

Prestressing steel in concrete beams aims at counteracting the tensile stresses in concrete due to external loads by inducing a permanent internal stress condition which is exploited to enhance the final structural performances. Nowadays, several prestressing technologies are available (e.g. pre-tensioning, post-tensioning and chemical prestressing), and prestressed concrete components are more and more frequently adopted in civil engineering, especially for large buildings and bridge structures. Therefore, a suitable optimization-oriented strategy for structural design would be an effective way for reducing the manufacturing costs while providing design solutions in compliance with modern codes.

The single-objective optimization of continuous partially prestressed concrete beams was studied by Al-Gahtani et al. (1995). In doing so, the authors considered different cross sections and various profiles of the prestressing tendons. A fuzzy-based multi-objective approach for prestressed concrete bridge systems was proposed by Ohkubo et al. (1998). These authors decided to minimize the total construction cost of the bridge sistem and selected the aesthetic feeling as objective function to be maximized. The reliability-based optimization of prestressed concrete beams was addressed by Barakat et al. (2003). In their work, the authors introduced random variables to deal with uncertainties in material properties, loading condition and prestressing force as well as in the models used to predict the structural behavior. The multi-objective optimization of prestressed concrete beams was addressed by Barakat et al. (2004) using the ε-constraint method.

Due to the presence of several nonlinear constraints, the resulting feasible region is likely to be concave and present many local optima, which are often located where one or more constraints are active. Under these circumstances, traditional deterministic approaches can suffer some convergence issues, i.e. they can be trapped into local optimal solutions easily. On the contrary, soft computing strategies inspired by natural behaviors have better global search capability. Moving from this consideration, more recent studies have tried to exploit the superior performances of soft computing algorithms over deterministic methods in the optimum design of prestressed concrete structures. For instance, Aydn and Ayvaz (2010) used a binary-coded genetic algorithm to address the optimum topology and shape design of prestressed concrete bridge girders. Discrete-type design variables were considered in that study. Single-point, two-point and uniform crossover were performed whereas different strategies were adopted to tune the mutation rate iteratively. A standard penalty-based approach was proposed to get the unconstrained version of the original constrained optimization problem. Two heuristic optimization methods, namely the simulated annealing and the threshold accepting algorithms, were performed by Martí and González-Vidosa (2010) for the optimum design of prestressed concrete precast pedestrian bridges. In this study, all variables of the design process are discrete and the analysis is restricted to feasible solutions only. Recently, prestressed concrete flat slabs were designed by El Semelawy et al. (2012) using a genetic algorithm. These authors assumed some design parameters as discrete variables and others as continuous variables. Once again, a penalty-based approach was formulated for handling constraints.

In spite of the complexities in handling constraints for the optimum design of prestressed concrete beams, existing studies in this field basically implement standard penalty-based approaches to carry out the unconstrained version of the original problem (Martí and González-Vidosa 2010), and no significant efforts have been made so far in order to explore more sophisticated strategies. Nonetheless, the performance of the optimization procedures in such class of industrial applications basically depends on the adopted handling constraints mechanisms because the feasible region can be a small non-convex sub-domain of the whole search space. Two are the key features of an efficient numerical strategy for solving constrained opitmization problems. The first goal is to approach the feasible region promptly whereas the second one is to find the feasible optimal solution. In this perspective, the focus here is on investigating an advanced strategy to deal with hard nonlinear constraints in the optimum design of prestressed concrete beams. In the attempt to provide alternative approaches in this field, the paper is concerned with the single-objective constrained optimization using the (μ + λ)-constrained differential evolution algorithm proposed recently by Jia et al. (2013), a soft computing technique which has not been used before in structural optimization applications. The paper has been organized as follows. The structural design of prestressed concrete beams in accordance with ultimate and serviceability limit states from the current European building code (European Committee for Standardisation 2004) is discussed in Section 2. The adopted differential evolution-based optimizer is presented in Section 3. Finally, some numerical results are included in Section 4 in order to discuss the application of the presented approach.

2 Analysis of prestressed concrete beams

Ultimate and serviceability limit states for the optimum design of prestressed concrete beams are presented hereafter. Although design rules from the current European building code (European Committee for Standardisation 2004) have been considered in this study, the presented design methodology can be applied even if a different design code is assumed.

2.1 Geometry and loading conditions

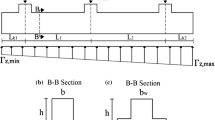
It is considered a pretensioned prestressed concrete beam subjected to in-plane dead and live static loads. The beam is simply supported and a double-T-shaped cross section is assumed (Fig. 1). This section has seven layers of bonded prestressing steel with resultant area A p . The design variables considered in this study deals with the geometry of the cross section and the amount of prestressing steel. Specifically, the design variables of the optimization problems are thefollowing: height of the prestressed beam H, top flange width B t , bottom flange width B b , web thickness b w , top flange thickness t t , bottom flange thickness t b , prestressing force imposed at the jack P. The optimal solution must fulfill some geometrical limitations which are derived from various practical considerations (functionality, fabrication, or aesthetics). The thickness of the top flange must be adequate to transfer the moment whereas the thickness of the bottom flange must be suitable to fit the prestressing steels. Moreover, the variables b w and t t − t b should be defined in order to obtain a good utilization of the section, that is the maximum distance between the limit points. The related constraints can be formulated as follows: b w ≥ 0. 1B t , t t ≥ 0. 08H, t b ≥ t t . Similarly, the width of the bottom flange must be smaller than the width of the top flange ( B b ≤ B t ) whereas the width of the web must be smaller than the width of the bottom flange ( b w ≤ B b ). These constraints directly involve the design variables and restrict their range. The eccentricity of the resultant tendon from the centroidal axis is assumed equal to the bottom limit point. In the case of pretensioning, this condition is required in order to ensure that stresses at transfer in concrete do not exceed the allowable values at the supports. The area of the tendons is calculated as follows:

$$A_{p} = \frac{P}{\sigma_{p,max}}$$
(1a)
$$\sigma_{p,max} = \min \{0.8f_{pk},0.9f_{p0.1k} \}$$
(1b)

where σ p, m a x is the maximum stress applied to the prestressing steel whereas f p k and f p0. 1k are the characteristic tensile strength of prestressing steel and the 0.1 % proof-stress of prestressing steel, respectively. So doing, the maximum force applied to the tendon will not exceed the admissible value.

Fig. 1
figure 1

Double-T-shaped cross section of the prestressed beam

Full size image

2.2 Serviceability limit states

The limits on the tensile and compressive working stresses in concrete are verified at transfer as well as under full service loads (hereafter, compressive stresses are negative values whereas tensile stresses are positive values). In order to satisfy simultaneously the stress limitation and the crack control serviceability limit states, the structural member is designed to remain uncracked. Moreover the formulation herein adopted is independent from the exposure class of the prestressed beam. This choice leads to advantageous results in terms of structural safety, and allows the definition of a clear and effective design methodology. Therefore, in compliance with concrete stress limits specified in the European building code (European Committee for Standardisation 2004, the following stress constraints at transfer are considered:

$$\sigma^{0}_{top,s} \le 0$$
(2a)
$$\sigma^{0}_{bot,s} \ge -0.7f_{ck\tau}$$
(2b)

and they hold for the quasi-permanent load condition. In (2), \(\sigma ^{0}_{top}\) and \(\sigma ^{0}_{bot}\) are the stresses on the top and on the bottom edges of the prestressed section, respectively. Moreover, the subscript s denotes the section at the support whereas f c k τ is the characteristic compressive strength of the concrete at time τ, that is when the prestress is transferred to the concrete. At this stage, the prestressing force is P 0 = α P where α is the reduction coefficient accounting for the immediate loss of prestress due to the elastic deformation of concrete.

At transfer, the prestressing force must satisfy the following constraint:

$$P^{0} \le A_{p} \sigma_{pm0}$$
(3a)
$$\sigma_{pm0} = \min \{0.75f_{pk},0.85f_{p0.1k}\}.$$
(3b)

Similarly, the stress constraints under the full service loads are

$$\sigma_{bot,s} \le 0$$
(4)
$$\sigma_{top,m} \ge -0.45f_{ck}$$
(5)

for the quasi-permanent load condition, whereas the following constraints

$$\sigma_{top,m} \ge -0.60f_{ck}$$
(6)
$$\sigma_{bot,m} \le 0$$
(7)

hold for the characteristic and the frequent load conditions, resepctively. In these equations, f c k is the characteristic compressive strength of concrete and the subscript m denotes the section at the mid-span. The prestressing force is now given by P 0 − ΔP c + s + r , where ΔP c + s + r is the variation of stress in tendons due to creep, shrinkage and relaxation (Fiore et al. 2012, 2013) which is calculated in accordance with the European design code.

2.3 Ultimate limit states

The ultimate flexural strength constraints are of the form:

$$M_{Sd} \le M_{Rd}$$
(8)

where M S d is the bending moment at the mid-span under the ultimate limit states load condition and M R d is the flexural strength of the prestressed section, as it results from the European building code.

The ultimate shear strength constraints are taken into account at the time of the initial prestress and under full service loads. They can be formulated as follows:

$$V_{Sd} \le \min \{ V_{Rd,s}, V_{Rd,max} \}$$
(9)

where V S d is the shear force at the supports, V R d, s is the shear strength provided by transversal shear reinforcement, V R d, m a x is the maximum shear force which can be sustained by the beam, limited by crushing of the compression struts. In particular, checking the shear-compression strength improves the effectiveness of the optimization procedure since it influences the value of the web thickness. Once again, the shear strength values are defined in accordance with European building code recommendations.

2.4 Cost calculation

The optimum design problem is formulated in the aim to reduce the total manufacturing cost of the prestressed beam, i.e. the costs of concrete and prestressing steel. A general formulation of the total manufacturing cost C is the following:

$$C = C_{c}V_{c} + C_{p} \rho_{s} V_{p}$$
(10)

where C c is the cost of concrete per unit of volume, V c is the volume of concrete, C p is the cost of prestressing steel per unit of weight, ρ s is the steel density, V p is the volume of prestressing steel.

3 Optimization procedure

Once the optimization problem has been discussed, the adopted (μ + λ)-constrained differential evolution algorithm is briefly presented. The interested reader is directed to (Jia et al. 2013) for further details, since the description will be restricted here to the most important implementation issues in order to make the paper self-consistent.

3.1 Formulation of the optimization problem

The optimum design of prestressed concrete beams is formulated as single-objective constrained optimization problem:

$$\begin{aligned} \min_{\mathbf{x} \in \mathcal{D}} &\{f(\mathbf{x})\} \\ & s.t. \\ & g_{a}(\mathbf{x}) \le 0. \\ \end{aligned}$$
(11)

In (11), f(x) is the objective function, x is the design vector and g a (x) are constraints of the optimization problem (with \(a=1,\dots ,NC\)). The design vector x is lower bounded by x l and upper bounded by x u. These bounds define the hyper-rectangle 𝒮, that is the total search space of the problem. The best design solution x ∗ is the global minimum of the objective function within the feasible domain \(\mathcal {D} \subset \mathcal {S}\). The objective function f(x) to be minimized is the total cost in (10). The candidate design solution x is assumed as continuous-valued vector. For real applications, the final industrial solution will be obtained by rounding-off the best continuous geometrical data into the design vector x ∗ to the nearest available value (in a conservative sense). This approach does not give less than global optimal results because geometrical data of precast prestressed concrete beams usually vary with a small step within the prescribed range, and thus they can be reasonably assumed as quasi-continuous design variables. Moreover, since the mathematical optimal solution is likely to lie where one or more constraints are strictly satisfied (almost within the machine precision), this strategy will also ensure that the industrial solution to be implemented is slightly more conservative than the theoretical one.

3.2 Basic operations in differential evolution

The differential evolution (DE) is an effective nature-inspired mechanism to solve hard optimization problems, and it has been widely used in structural engineering applications, i.e. (Marano et al. 2013, Quaranta et al. 2010, 2011). It aims at finding the best solution iteratively by manipulating a collection of N P candidate solutions (or individuals) \(\mathbf {x}_{i} = \begin {Bmatrix} x_{i1} & \ldots & x_{ij} & \ldots & x_{in} \end {Bmatrix}\) (with \(i=1,\dots ,NP\)) at each iteration t. The first important operator is the so-called mutation. It works by perturbing a candidate solution by means of the differences between couples of selected individuals. The (μ + λ)-constrained differential evolution is based on the following mutation operators:

$$\mathbf{v}_{i} = \mathbf{x}_{r1} + F(\mathbf{x}_{r2}-\mathbf{x}_{r3}),$$
(12a)
$$\mathbf{v}_{i} = \mathbf{x}_{r1} + F(\mathbf{x}_{r2}-\mathbf{x}_{r3}) + F(\mathbf{x}_{r4}-\mathbf{x}_{r5}),$$
(12b)
$$\mathbf{v}_{i} = \mathbf{x}_{i} + F(\mathbf{x}_{r1}-\mathbf{x}_{i}) + F(\mathbf{x}_{r2}-\mathbf{x}_{r3}),$$
(12c)
$$\mathbf{v}_{i} = \mathbf{x}_{i} + F(\mathbf{x}_{best}-\mathbf{x}_{i}) + F(\mathbf{x}_{r1}-\mathbf{x}_{r2}).$$
(12d)

They are usually named rand/1, rand/2, current-to-rand/1 and current-to-best/1, respectively. In Eq. (12), \(\mathbf {v}_{i} = \begin {Bmatrix} v_{i1} & \ldots & v_{ij} & \ldots & v_{in} \end {Bmatrix}\)is the mutant vector, \(r1,\dots ,r5\) are integers randomly selected from \(\{ 1,\dots ,NP \}\) such that r1 ≠ r2 ≠ r3 ≠ r4 ≠ r5, F is the mutation (or scaling) factor and x best is the best individual in the population. A projection scheme is implemented in order to ensure that v i satisfies all boundary constraints. This operation modifies each out-of-bound component of v i using the rule

$$v_{ij} = \left\{ \begin{array}{ll} 2x^{l}_{j} - v_{ij}\;\text{if}\; {v_{ij} < x^{l}_{j}}\\ 2x^{u}_{j} - v_{ij}\;\text{if} \;{v_{ij} > x^{u}_{j}}\\ v_{ij}\quad \quad\quad\text{otherwise}\\ \end{array} \right.$$
(13)

where \(x^{l}_{j}\) and \(x^{u}_{j}\) are the jth components of x l and x u, respectively.

The (μ + λ)-constrained differential evolution implements a binomial crossover to generate the trial vector u i , thus resulting

$$u_{ij} = \left\{ \begin{array}{ll} v_{ij}\;\;\text{if} \;\;{rand \le CR \;\;\text{or} \;\;j=j_{rand}}\\ x_{ij}\;\;\text{otherwise}\\ \end{array} \right.$$
(14)

where r a n d is a uniformly distributed random number between 0 and 1, j r a n d is a randomly selected integer between 1 to n, C R is the crossover rate.

The iterative strategy stops when a termination criterion is satisfied. In this study, the evolutionary search runs until the maximum number of fitness evaluation is reached (the maximum number of iterations t can be calculated accordingly).

3.3 Improved (μ + λ)-constrained differential evolution algorithm

The pseudo-code of the (μ + λ)-constrained differential evolution by Jia et al. (2013) is described in Algorithm 1. This algorithm implements a special strategy to assess the degree of constraint violation (see Section 3.4), and its functionality mainly depends on two external blocks that will be detailed later. They are:

  • an improved differential evolution (IDE) algorithm which implements several mutation operators simultaneously (see Section 3.5), and

  • the archiving-based adaptive tradeoff model (ArATM) which selects a proper constraint-handling mechanism for each situation (see Section 3.6).

Algorithm 1 (μ + λ-constrained differential evolution

Require: Data for the analysis of the prestressed concrete beam

Require: Control parameters of the optimizer

    Set t = 0 and 𝒜 = Φ (where 𝒜 is the archive)

    The initial population 𝒫 t = {X 1, X 2,…, X μ } is obtained by sampling μ points in 𝒮

    for i←1, μ do

        Get X i ∈ 𝒫 t

        Compute the objective function f(X i )

        Calculate the degree of constraint violation G(X i ) (see Section 3.4)

    end for

    while t ≤ T do

        Generate λ offspring to create the population 𝒬 t using individuals in 𝒫 t (see Section 3.5)

        for i← 1, λ do

            Get X i ∈ 𝒬 t

            Compute the objective function f(X i )

            Calculate the degree of constraint violation G(X i ) (see Section 3.4)

        end for

        Merge 𝒫 i and 𝒬 t , i.e. \(\mathcal {H}_{t} = \mathcal {P}_{t} \bigcup \mathcal {Q}_{t}\)

        Use the archiving-based adaptive tradeoff model (see Section 3.6) in order to select μ potential individuals from ℋ t , thus creating the next population 𝒫 t+1

        t = t + 1

        end while

        return Best (feasible) solution x* ∈ 𝒫 t and the total (minimum) cost of the prestressed concrete beam f(x*)

3.4 Degree of constraint violation

The violations of different constraints may have different magnitudes. Therefore, the ICDE algorithm implements two criteria to assess the degree of constraint violation of each candidate solution within the population. The degree of constraint violation of the candidate solution x i is first defined ∀ a:

$$G_{a}(\mathbf x_i) = \max\{ 0,g_{a}(\mathbf x_i) \}.$$
(15)

Subsequently, the difference Δ is introduced

$$\Delta = \max_{a} \{ \max_{i} \{ G_{a}(\mathbf x_i) \} \} - \min_{a} \{ \max_{i} \{ G_{a}(\mathbf x_i) \} \}$$
(16)

and a flag variable c r i t e r i o n is defined as follows:

$$criterion = \left\{ \begin{array}{l l} 1\;\text{if}\; \Delta \le \eta\\ 2\;\;\text{otherwise}\\ \end{array} \right.$$
(17)

where η is a threshold value, i.e. Δ ≤ η implies that the difference among the violations is not too large.If c r i t e r i o n is equal to 1, then G(x i ) is calculated by summing the degrees of constraint violation G a (x i ) in (15), that is:

$$G(\mathbf x_i) = \sum_{a=1}^{NC} G_{a}(\mathbf x_i).$$
(18)

On the other hand, if c r i t e r i o n is equal to 2, then G(x i ) is

$$G(\mathbf x_i) = \frac{ \sum_{a=1}^{NC} \overline{G}_{a}(\mathbf x_i) }{NC},$$
(19)

where \(\overline {G}_{a}(\mathbf x_i)\) is calculated as follows

$$\overline{G}_{a}(\mathbf x_i) = \frac{ G_{a}(\mathbf x_i) }{ \max_{i} \{ G_{a}(\mathbf x_i) \} }.$$
(20)

The first criterion in (18) is used with the aim of emphasizing the difference among the violations of different constraints when this value is relatively small (Δ ≤ η). On the contrary, the second criterion in (19) is employed when this difference is relevant (Δ > η), in order to allot comparable importance to all constraints.

3.5 Improved differential evolution

The pseudo-code of the IDE algorithm is listed in Algorithm 2. Its main role is to carry out the offsping population 𝒬 t consisting of λ individuals from the parent population 𝒫 t having μ candidate solutions. Differently from the standard DE, the IDE includes several mutation operators simultaneously.

In Algorithm 2, the current-to-rand/best/1 mutation is a new operator which adopts an iteration-dependent criterion to switch from the current-to-rand/1 strategy in (12c) to the current-to-best/1 strategy in (12d). Since the current-to-rand/1 scheme involves individuals randomly chosen from the population, this strategy is able to enhance the global search ability, thus resulting the best choice for the first phase. On the other hand, the current-to-best/1 strategy exploits the information of the best individual in the current population and can speed up the convergence toward the global optimum when the stopping criterion is approached. The current-to-rand/best/1 mutation works as follows:

$$\mathbf v_{i} = \left\{ \begin{array}{l l} \mathbf x_{i} + F(\mathbf x_{r1}-\mathbf x_{i}) + F(\mathbf x_{r2}-\mathbf x_{r3})\; \text{if}\; {t \le \kappa T}\\ \mathbf x_{i} + F(\mathbf x_{best}-\mathbf x_{i}) + F(\mathbf x_{r1}-\mathbf x_{r2})\; \text{otherwise}\\ \end{array} \right.$$
(21)

where κ T is the threshold iteration number ( κ is a positive control parameter less than 1). The third offspring y 3 is finally obtained by applying an improved breeder genetic algorithm mutation to v i with probability P M:

$$y_{3j} = \left\{ \begin{array}{l l} v_{ij} \pm rang_{i} \sum_{s=0}^{15} \alpha_{s} 2^{-s}\;\text{if}\; rand < \frac{1}{n}\\ v_{ij}\quad\quad\quad\quad\quad\quad\quad\quad\quad\text{otherwise}.\\ \end{array} \right.$$
(22)

In (22), r a n d is a freshly generated uniform random number between 0 and 1, \(rang_i=(x^{u}_{i} - x^{l}_i)(1-t/T)^{6}\) is the mutation range, the sign + or − is chosen with probability 0. 5, and α s ∈ {0, 1} is a random number generated with the probability \(p_{r}(\alpha _s=1) = \frac {1}{16}\). Additionally, if the condition t ≤ κ T holds, then (22) is not performed. This implies that y 3 = v i as it results from the current-to-rand/1 scheme in (21).

Algorithm 2 Improved (μ + λ)-differential evolution

Require: Parent population 𝒫 t

Require: Control parameters of the optimizer

     Set 𝒬 t = Φ

     for i ← 1, μ do

          Get x i ∈ 𝒫 t

          Generate the first offspring y 1 using rand/1 mutation scheme in (12a) and binomial crossover

          Generate the second offspring y 2 using rand/2 mutation scheme in (12b) and binomial crossover

          Generate the third offspring y 3 using current-torand/ best/1 mutation scheme in (21) and improved breeder genetic algorithm mutation in (22)

          Update the offspring population, i.e. 𝒬 t = \(\mathcal {Q}_{t} \bigcup \{ \mathbf y_{1}, \mathbf y_{2}, \mathbf y_{3} \}\)

     end for

     return Offspring population 𝒬 t

3.6 Archiving-based adaptive tradeoff model

The combined population \(\mathcal {H}_{t} = \mathcal {P}_{t} \bigcup \mathcal {Q}_{t}\) can include feasible candidate individuals only, infeasible candidate solutions only, both infeasible and feasible candidate individuals. The archiving-based adaptive tradeoff model (ArATM) will select the candidate solutions for the next parent population \(\mathcal {P}_{t+1}\) depending on the specific situation.

Feasible candidate solutions only

When the feasible domain is very large (e.g. bounds of the design variables are too conservative) or the evolutionary search is finishing, it might occur that \(\mathcal {H}_{t}\) only includes feasible candidate solutions. In this case, the objective function values of the feasible candidate solutions in \(\mathcal {H}_{t}\) are compared, and the best μ individuals are collected to create the parent population \(\mathcal {P}_{t+1}\).

Infeasible candidate solutions only

This situation typically occurs at the early stage of the evolutionary search, especially for optimization problems where the feasible domain \(\mathcal {D}\) is very small with respect to the search space \(\mathcal {S}\). In this case, the ArATM model treats the objective function f(x) and the degree of constraint violation G(x) as two objectives which are considered simultaneously, thus obtaining a bi-objective optimization problem. The pseudo-code of the ArATM when infeasible individuals only occur in \(\mathcal {H}_{t}\) is given in Algorithm 3 (the symbol | · | is the cardinality of the set between the vertical bars).

Algorithm 3 ArATM in the event of infeasible individuals only within ℋ t

Require: Combined population ℋ t

Require: Control parameters of the optimizer

     if 𝒜 ≠ ∅ then

          Select randomly randsize individuals from 𝒜 and put them into ℋ t (randsize is a random integer number between 0 and |𝒜|)

     end if

     Set 𝒜 = Φ and 𝒫 t+1 = Φ

     while|𝒫 t+1| < μ do

          Identify non-dominated individuals in ℋ t using Pareto dominance

          Consider the degree of constraint violations in order to sort non-dominated individuals in ascending order

          Select the first half of the non-dominated individuals and store them into 𝒫 t+1

          Remove selected nondominated individuals from ℋ t

     end while

     if |𝒫 t+1| > μ then

          Delete the last (|𝒫 t+1| − μ) individuals in 𝒫 t+1 and store them into ℋ t

     end if

     All individuals in ℋ t are stored into 𝒜

     return New parent population 𝒫 t+1

Both infeasible and feasible candidate solutions

The procedure for this case is the following. First, the indices of the feasible individuals and that of the infeasible candidate solutions are stored into two sets, namely \(\mathcal {Z}_{1}\) and \(\mathcal {Z}_{2}\). Moreover, the best feasible individual x best and the worst feasible individual x w o r s t are identified. Subsequently, the normalized objective function \(\overline {f}(\mathbf x_i)\) is calculated as follows:

$$\overline{f}(\mathbf x_i) = \frac{ f^{\prime} - f^{\prime}_{min} }{ f^{\prime}_{max} - f^{\prime}_{min} }$$
(23)

where

$$f^{\prime} \,=\, \left\{ \begin{array}{l r} f(\mathbf x_i)& \text{if} \;i \in \mathcal{Z}_{1} \\ \max\{ \varphi f(\mathbf x_{best}) \,+\, (1\,-\,\varphi) f(\mathbf x_{worst}), f(\mathbf x_i)\} &\text{if}\;i \in \mathcal{Z}_{2} \end{array} \right.$$
(24a)
$$f^{\prime}_{max} = \max_{z \in \mathcal{Z}_{1} \bigcup \mathcal{Z}_{2} } \{ f^{\prime}(\mathbf x_z) \}$$
(24b)
$$f^{\prime}_{min} = \min_{z \in \mathcal{Z}_{1} \bigcup \mathcal{Z}_{2} } \{ f^{\prime}(\mathbf x_z) \}.$$
(24c)

The symbol φ in (24a) denotes the feasibility proportion of the combined population \(\mathcal {H}_{t}\).

The normalized degree of constraint violation of each candidate solution is defined with reference to the flag variable c r i t e r i o n, thus obtaining

$$\overline{G}= \left\{ \begin{array}{lll}0 &&\text{if}\; i \in \mathcal{Z}_{1}\\ \frac{G(\mathbf{x}_{i})- {G_{min}}}{{G_{max}}- {G_{min}}}&& {\text{if}}\; i \in {\mathcal{Z}_{2}}\; {\text{and}}\;criterion=1\\ G(\mathbf{x_{i}})&&{\text{if}}\;{i}\in \mathcal{Z}_{2}\; {\text{and}}\; criterion=2 \end{array} \right.$$
(25)
$$G_{max} = \max_{z \in \mathcal{Z}_{2} } \{ G(\mathbf x_z) \}$$
(26a)
$$G_{min} = \min_{z \in \mathcal{Z}_{2} } \{ G(\mathbf x_z)\}.$$
(26b)

It is understood that G(x i ) is evaluated as in (18) if c r i t e r i o n = 1 or as in (19) if c r i t e r i o n = 2. The final fitness function f f i n a l (x i ) is then calculated ∀ i as follows:

$$f_{final}(\mathbf x_i) = \overline{f}(\mathbf x_i) + \overline{G}(\mathbf x_i)$$
(27)

where μ individuals with the smallest f f i n a l (x i ) value are selected to create the next parent population \(\mathcal {P}_{t+1}\).

4 Numerical application

The improved (μ + λ)-constrained differential evolution (ICDE) considered in this study is now applied to deal with the optimum design of a prestressed concrete beam. In doing so, design data consistent with typical industrial applications are assumed. Finally, comparisons with genetic algorithms and swarm intelligence-based optimizers are included.

4.1 Problem data and output

Input numerical data for the analysis of the prestressed concrete beam are shown in Table 1 whereas the bounds of the design variables are given in Table 2. Control parameter values in (Jia et al. 2013) are used for the (μ + λ)-constrained differential evolution algorithm, and they are listed in Table 3. The optimization procedure is stopped once a maximum number of fitness evaluations ( F E S) equal to 105 is achieved.

Table 1 Input data for the analysis of the prestressed concrete beam
Full size table
Table 2 Bounds of the design variables
Full size table
Table 3 Control parameter values for (μ + λ)-constrained differential evolution algorithm
Full size table

The minimum cost f m i n and the corresponding optimum design variables x ∗ have been carried out from 25 independent runs. Moreover, the mean value f m e a n , the maximum cost f m a x and the standard deviation f s t d of the objective function have been also calculated. Finally, it has been calculated the ratio χ between the number of runs concluded achiving a feasible final solution and the total number of runs.

4.2 Results and sensitivity analysis

The optimal solution and the above presented performance indices are listed in Table 4. It was found that the minimum manufacturing cost of this prestressed concrete beam is 1,199.30 USD. It is worth noting that the ICDE algorithm achieved an identical (feasible) final solution each time (null f s t d value and χ equal to 100 %). This result was also verified considering 1, 000 independent runs. Therefore, the ICDE exhibits a very remarkable stability. If the optimal industrial solution closest to that calculated by means of the ICDE algorithm is needed, it can be obtained by rounding-off the geometrical dimensions of the optimal design vector to the nearest available value (in a conservative sense). The best industrial solution corresponding to that given in Table 4 might be the following: \(B^{*}_t=\) 730 mm, \(B^{*}_b=\) 475 mm, \(t^{*}_t=\) 130 mm, \(b^{*}_w=\) 155 mm, H ∗ = 1,600 mm, \(t^{*}_b=\) 130 mm. As expected, the industrial solution and the best numerical one are very close each other. So doing, the final industrial solution is slightly conservative than the theoretical one, but this is a desirable result for practical applications because several constraints are active at x ∗.

Table 4 Results obtained by means of ICDE
Full size table

Sample convergence curves of objective function f and feasibility proportion φ are depicted in Fig. 2. The convergence curve of the objective function f shows that the initial manufacturing cost of the prestressed beam is halved at the end of the evolutionary search. The initial value of the feasibility proportion φ was very low in each run (less than 0.05), and most of the times the initial population collected unfeasible candidate solutions only. This reveals that the feasible region \(\mathcal {D}\) in this optimization problem is a small fraction of the total search space \(\mathcal {S}\). Nonetheless, the ICDE was able to find the feasible region as well as the optimal solution herein in a very efficient way.

Fig. 2
figure 2

Convergence curves of objective function f (left) and feasibility proportion φ (right)

Full size image

The convergence of the design variables was also investigated by considering the evolution of the μ candidate solutions during the optimization process. It has been observed that the evolutionary process ends with μ individuals equal to the optimal solution x ∗. Therefore, the whole population converges to the optimum, and the upper and lower envelope of the convergence curves are shown in Fig. 3. Most of the input data in Table 1 depends on the specific problem and cannot be modified on the designer’s preferences. The characteristic cylinder strength of the prestressed concrete f c k is, however, a typical designer’s choice, i.e. larger strength values correspond to more expensive concrete. Therefore, it is somewhat interesting to study the sensitivity of the final solution with reference to f c k . To this end, the variation of the objective function f(x ∗) for different values of the characteristic cylinder strength f c k is plotted in Fig. 4, along with the cost of concrete per unit of volume C c . Although larger concrete strength values correspond to more expensive concrete, Fig. 4 indicates that the total manufacturing cost of the beam decreases as f c k grows up. On using concrete with larger strength values, the cost of concrete per unit of volume increases linearly whereas the corresponding reduction of the cross section is more than linear. As a consequence, concrete having larger f c k values lead to cheaper prestressed concrete beam design.

Fig. 3
figure 3

Envelope of the convergence curves for each design variable

Full size image
Fig. 4
figure 4

Variation of \(f(\mathbf x^{*})\) for different values of \(f_{ck}\)

Full size image

4.3 Comparison with genetic algorithms

Genetic algorithms have been recently employed for the optimum design of prestressed concrete beams, see for instance Refs. (Aydn and Ayvaz 2010; El Semelawy et al. 2012). Therefore, the evolutionary search mechanism based on the Darwinian principle of “survival of the fittest” can be effectively exploited to assess the performance of the ICDE algorithm. To this end, two genetic algorithms are taken into account. The first one is the augmented Lagrangian genetic algorithm (ALGA) with a single population (Conn et al. 1991). The second strategy is the multi-species augmented Lagrangian genetic algorithm (MALGA), a variant of the ALGA in which multiple subpopulations interact during the evolutionary search by means of the so-called migration operator, e.g. Refs. (Monti et al. 2010; Marano et al. 2011). Both genetic algorithm based strategies are stopped once a maximum number of fitness evaluations equal to 105 is achieved and preliminary runs were performed to select the best control parameter values. The total population size for both genetic algorithm based strategies is equal to 50. The scattered crossover function is employed, and the crossover fraction is equal to 0.8. MALGA is performed with 5 subpopulations having the same size. For this optimizer, migration takes place toward the last subpopulation every 5 iterations with a migration fraction equal to 0.2. Results of the comparison between ICDE, ALGA and MALGA are summarized in Table 5.

Table 5 Comparison with genetic algorithms
Full size table

The ICDE does better than the investigated genetic algorithm based techniques, and MALGA performs slightly better than ALGA. Overall, augmented Lagrangian based genetic algorithms show good performances in identifying the feasible region, being the success rate larger than 90 %. However, the genetic-based evolutionary search mechanism demonstrated some weakness in looking for the best feasible solution. The minimum cost obtained using the ICDE is about 2.5 % and 1 % better than the ones calculated using ALGA and MALGA, respectively. It is also observed that the ICDE algorithm is much more stable than ALGA and MALGA. In fact, the final objective function value obtained using these genetic algorithm based strategies fluctuates within a large interval ( f m a x is larger than 1.5 times f m i n ). Moreover, the optimization procedure based on ALGA or MALGA did not carry out a feasible final solution each time because their success rate χ is equal to 92 %. In comparison with the genetic-inspired searching mechanism, mutation schemes within the IDE algorithm combine to provide superior global search ability while preserving the convergence toward the global optimum at the end of the evolutionary process.

4.4 Comparison with swarm intelligence-based optimizers

Particle swarm optimization algorithms mimic the social behaviors of some natural aggregations, such as bird flocking, fish schooling, or swarming of insects. In this study, the performances of two recent swarm intelligence-based optimizers are examined and compared to that obtained using the presented ICDE algorithm (see Table 6. The first method is a chaotic particle swarm optimization (ChPSO) in which the Logistic map is adopted to tune the inertia weight (Chuanwen and Bompard 2005) whereas the Zaslavskii map is used for updating iteratively the acceleration factors (Coelho and Herrera 2007). Moreover, a particle swarm optimizer with passive congregation (PSOPC) is performed He et al. (2004). The swarm size is equal to 50 for, both, ChPSO and PSOPC. The interested reader can found a short description of these optimizers in Ref. (Quaranta et al. 2010), along with all details about the numerical values of the involved control parameters. The static penalty-based approach in Ref. (Aydn and Ayvaz 2010) is adopted (with a penalty factor equal to 1.5) and these algorithms are stopped once a maximum number of fitness evaluations equal to 105 is achieved.

Table 6 Comparison with swarm intelligence-based optimizers
Full size table

Although these swarm intelligence based optimizers were able to compute an objective function value which is not too far from that calculated using the ICDE algorithm, the effectiveness of the penalty-based approach for handling constraints is poor. In fact, the success rate of the ChPSO is 88 %. The final performances of the PSOPC in terms of objective function value are satisfactory, but its success rate is not acceptable. In particular, the PSOPC concluded with a feasible solution only 15 times ( χ equal to 60 %). Numerical results demonstrate that the ArATM is more efficient than static penalty approaches for handling constraints.

5 Conclusions

This paper investigated the application of the (μ + λ)-constrained differential evolution algorithm (ICDE) for the optimum design of prestressed concrete beams. Ultimate and serviceability limit states from the current European building code have been considered, and the manufacturing cost has been assumed as objective function to be minimized. Numerical results and comparisons with different nature-inspired soft computing strategies (genetic algorithms and particle swarm optimization algorithms) have been included. On the basis of this set of results, it can be concluded that:

  • the optimum design of prestressed concrete beams require efficient mechanisms for handling constraints as well as powerful searching strategies;

  • the ICDE algorithm implements a reliable mechanism for finding the feasible region promptly, and its modified differential evolution based strategy performs efficiently;

  • considered swarm intelligence based optimizers provide a final design solution which is cheaper than the one calculated using genetic algorithms;

  • augmented Lagrangian based genetic algorithms are more robust than penalty based particle swarm optimization techniques in achieving the feasible region;

  • the ICDE exhibits improved performances and stability when compared to, both, genetic algorithm based strategies and swarm intelligence based methods.