Efficient surrogate construction by combining response surface methodology and reduced order modeling

Abstract

Response surface methodology is an efficient method for approximating the output of complex, computationally expensive codes. Challenges remain however in decreasing their construction cost as well as in approximating high dimensional output instead of scalar values. We propose a novel approach addressing both these challenges simultaneously for cases where the expensive code solves partial differential equations involving the resolution of a large system of equations, such as by finite element. Our method is based on the combination of response surface methodology and reduced order modeling by projection, also known as reduced basis modeling. The novel idea is to carry out the full resolution of the system only at a small, appropriately chosen, number of points. At the other points only the inexpensive reduced basis solution is computed while controlling the quality of the approximation being sought. A first application of the proposed surrogate modeling approach is presented for the problem of identification of orthotropic elastic constants from full field displacement measurements based on a tensile test on a plate with a hole. A surrogate of the entire displacement field was constructed using the proposed method. A second application involves the construction of a surrogate for the temperature field in a rocket engine combustion chamber wall. Compared to traditional response surface methodology a reduction by about an order of magnitude in the total system resolution time was achieved using the proposed sequential surrogate construction strategy.

1 Introduction

Numerical simulation is currently able to model increasingly complex phenomena. However, it often involves significant computational cost, which hinders its use in some applications requiring frequent calls to the simulation (e.g. optimization, statistical sampling). One way of reducing the computational cost is by using response surface methodology, also known as surrogate modeling, which aims at constructing an approximation of the simulation response based on a limited number of runs of the expensive simulation (Sacks et al. 1989; Queipo et al. 2005; Kleijnen et al. 2005; Chen et al. 2006; Forrester and Keane 2009; Simpson et al. 2010). Multiple surrogate types can be used for fitting the samples, such as polynomial response surface approximations (Myers and Montgomery 2002), kriging (Stein 1999; Simpson et al. 2001; Kleijnen 2009), neural networks (Park and Sandberg 1991; Cheng and Titterington 1994; Goel and Stander 2009) or support vector machines (Mika and Tsuda 2001; Scholkopf and Smola 2002; Smola and Scholkopf 2004).

Some frequently encountered attributes of today’s numerical simulations that render response surface construction more difficult are their high computational cost, the presence of a large number of input variables and the fact that the output of interest may not be a scalar but a high dimensional vector (e.g. the entire displacement field on a structure). The large number of variables is problematic due to the curse of dimensionality, in that the number of simulations required to construct the response surface grows exponentially. This problem is exacerbated when the computational cost of each simulation is high. The dimensionality of the output is problematic because it renders surrogate modeling of the full output difficult in the absence of additional assumptions.

These aspects thus pose the following challenges in terms of response surface construction (Viana et al. 2010):

• i. how to construct the surrogate model as efficiently as possible (i.e. using as few expensive simulations as possible)

• ii. how to construct a surrogate model when the output quantity is not a scalar but a high-dimensional vector (e.g. a pressure field map on an aircraft wing)

To address the first item multiple approaches have been proposed that are based on reducing the number of variables in the input space, which has the effect of decreasing the number of simulations required for the response surface construction. Among such approaches we could mention one-at-a-time (OAT) variable screening (Daniel 1973), global sensitivity analysis (Sobol 1993) or non-dimensional variable grouping (Gogu et al. 2009). The main purpose of these approaches is to remove variables that have negligible impact and regroup as efficiently as possible those that have. For additional details on these and other dimensionality reduction approaches for the input variables we refer the reader to the review in Viana et al. (2010).

The second item (ii.), relative to the dimensionality of the output, can also be addressed by dimensionality reduction approaches, of course in the output space this time. For vector-based response, surrogate modeling techniques that take into account correlation between components are available (Khuri and Cornell 1996) and can in some cases be more accurate than constructing response surfaces for each component independently. For a relatively small dimension of the output vector, methods such as co-kriging (Myers 1982) or vector splines (Yee 2000) are available. However, these are not practical for approximating the high dimensional pressure field around the wing of an aircraft or approximating heterogeneous displacements fields on a complex specimen since these fields are usually described by a vector with thousands to hundreds of thousand components. Fitting a surrogate for each component is even more time and resource intensive and might not take advantage of the correlation between neighboring points.

Reduced order modeling approaches by projection of the response on a reduced basis have proved to be efficient methods for achieving drastic dimensionality reduction in the output space. For example principal components analysis (PCA), also known as proper orthogonal decomposition (POD) or Karhunen–Loeve expansion, allows to determine a reduced-dimensional basis of the output space given a set of output simulation samples. Any output can then be projected on this basis and expressed by its basis coefficients. The challenge of obtaining a surrogate of high dimensional vector-type output quantities can then be solved by constructing response surfaces for the basis coefficients in terms of the design variables of interest. Such an approach has been successfully applied to the multidisciplinary design optimization of aircraft wings (Coelho et al. 2008, 2009; De Lucas et al. 2011), to reliability based design optimization of automotive vehicles (Wehrwein and Mourelatos 2006), to random fields uncertainty representation and propagation (Yin et al. 2009; Singh and Grandhi 2009) as well as to Bayesian identification from full field measurements (Gogu et al. 2012).

The aim of this article is to present a new methodology that can address both points (i. and ii.) more efficiently than existing approaches for problems involving partial differential equations (typically problems solved by the finite elements method). Our method is based on the coupling of the reduced basis modeling approach with the construction phase of a response surface in order to achieve more efficient surrogate construction of complex multidimensional output. To do so, the idea is to (1) solve the full problem, but on a small number of points of the design of experiments, (2) to use these solutions to construct a reduced basis, and (3) to use this reduced basis to build approximate solutions for the other points of the design of experiments, while controlling the quality of the approximations.

The article is organized as follows. We provide in Section 2 an overview of reduced order modeling by projection, i.e. reduced basis modeling, and of its coupling with surrogate modeling as proposed by our method. In Section 3 we give a first application example of the proposed methodology to the identification of orthotropic elastic constants based on full field displacement fields. Section 4 provides a different application example on a thermal problem. Finally, we provide concluding remarks in Section 5.

2 The key points response surface approach

2.1 Reduced basis modeling

Many numerical simulations in the engineering domain involve solving a partial differential equations problem. After space (and time) discretization, the problem often involves a (set of) large linear system(s) of equations.

$$ K(\boldsymbol{u};\boldsymbol{\mu} )=F $$

(1)

with $\boldsymbol {u}\in \mathbb {R}^n$ the unknown state variables and $\boldsymbol {\mu } \in \mathbb {R}^p$ a set of p parameters of interest (material parameters, time...) so that $K:\mathbb {R}^n\times \mathbb {R}^p\to \mathbb {R}^n$, n being the number of state variables. Let us assume that K is such that given any value of the set of parameters $\boldsymbol {\mu }$ a unique solution $\boldsymbol {u}=\boldsymbol {u}(\boldsymbol {\mu } )$ exists.

Model order reduction is a family of approaches that aims at significantly decreasing the computational burden associated with the inversion of system (1). A particular class of model reduction techniques, denoted as reduced basis approaches (or reduced order modeling by projection), aims at reducing the number of state variables of the model by projection on a certain basis. Accordingly, an approximation of the solution is sought in a subspace of dimension m (with usually $m<<n)$, while enforcing the residual to be orthogonal to the same sub-space . Typically, is defined by a so called reduced-basis $\boldsymbol {\Phi }=\left \{\boldsymbol {\Phi } _{1},\ldots ,\boldsymbol {\Phi } _{\mathrm {m}}\right \}$.

The initial problem of (1) is rewritten, as defined by Galerkin conditions, projected onto the reduced basis:

$$ \boldsymbol{\Phi}^TK(\boldsymbol{\Phi} \boldsymbol{\alpha} ,\boldsymbol{\mu} )=\boldsymbol{\Phi}^T\boldsymbol{F} $$

(2)

where $\boldsymbol {\alpha }$ are the reduced state variables, that is the coefficients of vector u expressed in the reduced basis $\boldsymbol {\Phi }$.

If K is linear with respect to its first variable u, the problem of (1) can be written as:

$$ K(\boldsymbol{\mu} )\boldsymbol{u}=\boldsymbol{F} $$

(3)

For example in structural mechanics $K(\boldsymbol {\mu })$ is the stiffness matrix, which usually depends on some parameters of interest $\boldsymbol {\mu }$ (e.g. material properties), u is the displacement vector and F the vector of the forces.

Similarly then, the projected problem of (2) can be written as:

$$ \boldsymbol{\Phi}^TK(\boldsymbol{\mu} )\Phi \boldsymbol{\alpha} =\boldsymbol{\Phi}^T\boldsymbol{F} $$

(4)

At this point it is important to realize that (4) is equivalent to a reduced order model of the initial problem of (3). Indeed, solving the problem of (4) typically involves the inversion of a large system of equations of size n, the size of the stiffness matrix $K(\boldsymbol {\mu })$, which for large scale problems can easily reach hundreds of thousands. On the other hand solving the reduced order model of (4) involves the inversion of a much smaller system of equations of size m, the size of the projected stiffness matrix $\boldsymbol{\Phi}^TK(\boldsymbol {\mu } )\boldsymbol{\Phi}$, which is equal to the dimensionality of the reduced basis m (typically $m<<n$, since m does usually not exceed a few dozen). Solving this reduced order model leads directly to $\boldsymbol {\alpha }$, the coefficients of the solution in the reduced basis.

The problem projected onto the reduced basis thus yields an approximate solution whose accuracy can be quantified by measuring the following residual:

$$ e_{\mathit{rb}}^2 =\frac{\left\| {K(\boldsymbol{\mu} )\boldsymbol{\Phi}\boldsymbol{\alpha} -\boldsymbol{F}} \right\|^2}{\left\| \boldsymbol{F} \right\|^2} $$

(5)

Up to now, the subspace on which the problem is projected, or more precisely one of its basis $\boldsymbol{\Phi}$, was not specified and many different choices are possible for this projection.

For example, eigenmodes of the operators have been used to reduce numerically the size of the problems for applications in dynamics. These approaches are known as modal analysis, Craig–Bampton (Craig and Bampton 1968). In Kerfriden et al. (2011) and Gosselet (2003) the reuse of Krylov subspaces generated during a Krylov iterative solvers was used as a reduced basis. The generalized modes of variables separation techniques (like Proper Generalized decomposition) can also be used in such a context (Ladeveze et al. 2009).

The proper orthogonal decomposition (POD) can also be a way to build a relevant reduced basis in the context of reduced order modeling by projection (Kerfriden et al. 2011; Krysl et al. 2001; Ryckelynck 2005). Indeed, POD (Kunisch and Volkwein 2002) (also known as Karhunen Loeve decomposition (Karhunen 1943; Loeve 1955) or principal component analysis (Hotteling 1933)) is an approach which consists in constructing a reduced basis from a set of solutions, called snapshots. Mathematically, the extraction of the reduced basis from the snapshots is done by singular value decomposition. Generally, the snapshots are the results of full simulations on a set of points.

Note that classical POD-type approaches do not generally go all the way to solving or even formulating the reduced order model of (4). Indeed POD is often used only as a dimensionality reduction approach. Solutions u that were already calculated by solving the full size problem (3) are projected on the POD-reduced basis and expressed in terms of their basis coefficients $\boldsymbol {\alpha }$ thus allowing to express initial solutions u with a drastically reduced dimensionality. Note however that these basis coefficients $\boldsymbol {\alpha }$ can also be obtained by solving the reduced order model of (4), that is by solving the initial problem projected on the reduced basis. This option is not typically used in POD because solving the reduced order model for solutions that are already in the reduced basis (thus for which the full solution is already available) has no interest. However the reduced order model has an interest for obtaining the basis coefficients $\boldsymbol {\alpha }$ at a new point which is not part of the reduced basis. In this case, the reduced order solution is only an approximation and the approximation error can be assessed by the metric provided in (5). The reduced basis modeling approach thus has two major assets: dimensionality reduction by the use of the basis coefficients and computational time reduction for approximating new solutions by the use of the reduced basis model. This paper presents a framework which uses both these aspects in order to more efficiently construct surrogate models.

2.2 Combining response surface methodology with reduced order modeling

The reduced basis modeling approach allows to significantly reduce the dimensionality of a response by expressing it in terms of its basis coefficients $\boldsymbol {\alpha }$ in the reduced basis $\boldsymbol {\Phi}$. To create an approximation of the high dimensional response we will thus construct surrogate models of the basis coefficients $\boldsymbol {\alpha }$. Such an approach, though not novel, addresses challenge ii. presented in the introduction, namely constructing surrogate models of high dimensional responses.

However the issue of the construction cost, mentioned in challenge i. of the introduction, remains a hurdle. We thus propose to further use the reduced basis modeling to also decrease the surrogate construction cost. This is achieved by appropriately choosing some key points of the design of experiments at which the full problem is solved. At all the other points only the reduced order problem (full problem projected on the reduced order basis) needs to be solved. Figure 1 provides the flow-chart of the proposed procedure, that we call the key points response surface approach.

Fig. 1

Flow-chart of the key points response surface construction steps

In the first step the set of points D representing the design of experiments is defined. This set of points will serve both for the reduced dimensional basis extraction using the key points procedure as well as for the construction of the response surface approximations. Since both the key points procedure and the surrogate modeling benefit from a space-filling design, latin hypercube sampling will be used to construct the set D but other sampling methods are possible.

In the second step, full or reduced order simulations are run at the points of the design of experiments. The set of key points, defining the reduced dimensional basis $\Phi$ are denoted by K. The full numerical model is evaluated at the points of set K. On the other hand, at the remaining points (set D-K) an approximation of the response is calculated using the reduced order model (problem solved projected on the reduced dimensional basis $\Phi$). Typically the cardinality of K is one to several orders of magnitude smaller than that of D as will be illustrated in the two application examples in Sections 3 and 4. This is precisely where the interest of the proposed method lies: if the full resolutions need to be carried out only at the points K and that the inexpensive reduced basis model can be used at all the remaining points, this will lead to substantial computational savings for the construction of the surrogate model. Note also that the reduced order approximation satisfies the error criteria $e_{\mathit {rb}}$ (cf. (5)) imposed for the reduced basis modeling, which allows to control the quality of the approximation. Accordingly the set of K is not chosen beforehand but it is determined automatically by the proposed construction procedure such as to verify the error criterion.

At step 3 the full simulation results of the set K are projected onto the basis B to obtain their basis coefficients $\alpha$. For the reduced order simulations of the set D-K we already have the coefficients $\alpha$. Response surface approximations of the basis coefficients $\alpha$ are then constructed.

Finally the accuracy of the approximations is verified in step 4. Two error measures are already available. The first is the criterion $e_{\mathit {rb}}$ on the residuals that was imposed during the reduced order modeling (cf. (5)). The second consists in classical RSA error measures, such as root mean square errors or cross validation errors. An additional cross validation error measure can be considered on the whole procedure itself. The leave-one-out cross validation would consist in applying the key points procedure (steps 1–3 of Fig. 1) not on the entire design of experiment set D but on a subset by leaving one point out. The procedure’s prediction would then be compared to the simulation response at the point that was left out. Note that in the approach we propose we only have the exact finite element solution at the key points (at all the remaining points we only have the reduced basis solution). However since the key points were determined to be the most relevant solutions for constructing the reduced basis it seems appropriate to do the cross validation over these key points only. By doing all possible permutations of leaving a key point out and taking the root mean square of the errors in the prediction we obtain an error measure for the proposed surrogate modeling procedure.

2.3 Construction of the approximation subspace: choosing the key points

At this point we need to choose how to construct the reduced basis. In our approach, similarly to proper orthogonal decomposition (POD), the construction of the reduced basis requires full simulations, but only for a small set of samples, called key points. The choice of these key points is of importance because it has a strong effect on the accuracy of the response surface. Indeed, if the number of key points is too small or poorly chosen, the solutions computed by the reduced model will be inaccurate. Conversely, if the number of key points is too large, the basis would be large which reduces the numerical efficiency. In this paper, we investigate two ways to automatically choose a set of key points, as small as possible, but preserving an imposed accuracy of the reduced order model approximation.

The first approach consists in sequentially browsing the points $\boldsymbol {\mu } _{i}$ of the DoE. For the first point $\boldsymbol {\mu }_{1}$ of the DoE, the full simulation always needs to be carried out and its result $\boldsymbol {u}_{1}$ becomes the first vector of the reduced basis. Then at the point $\boldsymbol {\mu }_{i}$ it is assumed that one has already a reduced basis of size $m_{i}$. The problem for parameter $\boldsymbol {\mu } _{i}$ is then solved by projection on this reduced basis. This corresponds to the inversion of a small system of size $m_{i}$ whose computational cost is low (often negligible) compared to that of the full simulation. The accuracy of the approximate solution thus constructed is evaluated with a measure of the residual error $e_{\mathit {rb}}$. If this indicator is below a certain threshold $\varepsilon _{\mathit {rb}}$, then we move on to the next parameter $\boldsymbol {\mu }_{i+1}$. Otherwise, the complete problem is solved for this point and the associated solution is orthogonalized as shown in (6), normalized and added to the basis.

$$\boldsymbol{\Phi}_k =\boldsymbol{u}_k -\sum\limits_{i=1}^{k-1} {\left\langle {\boldsymbol{u}_k ,\boldsymbol{\Phi}_i} \right\rangle \boldsymbol{\Phi}_i} $$

(6)

Where $\left \langle {\bullet ,\bullet } \right \rangle$ denotes the $L^{2}$ scalar product.

The algorithm for this approach is presented below (Algorithm 1).

This approach, called sequential approach in the sequel, has the advantage of considering points only once, so it has a certain advantage in terms of computation time. However, the choice of reference points (i.e. the key points) is highly dependent on the way the DoE is being browsed. The size of the subspace basis will therefore certainly not be minimal.

A second approach of selecting the key points, inspired from Grepl et al. (2007), consist in building these reference points iteratively at the points where the error is maximum. At iteration k, the basis $^{\mathrm {k}} = {\{}\boldsymbol{\Phi}_{1},{\ldots }, \boldsymbol{\Phi}_{k-1}{\}}$ constructed from the full simulation of the problems with the reference sets of parameters $\left \{ {\boldsymbol {\mu }_1^{\mathit {ref}},...,\boldsymbol {\mu }_{k-1}^{\mathit {ref}}} \right \}$ are supposed to be known. Then an approximation of the solution of all the points of the DoE is computed with the reduced model in projection onto the orthonormal basis ^k. The point where the error $e_{\mathit {rb}}$ is the highest is chosen to be the next key point as shown in (7).

$$ \boldsymbol{\mu}_k^{\mathit{ref}} =\mathop{\arg \max (e_{rb} (\boldsymbol{\mu} ))}\limits_{\mu \in \mathit{DoE}} $$

(7)

A simulation of the problem with the set of parameter $\boldsymbol {\mu }_k^{\mathit {ref}}$ is then performed using the full model. The corresponding solution $\boldsymbol {u}_k^{\mathit {ref}}$ is orthonormalized and added to the reduced basis. Then one proceeds to the next iteration. The algorithm presented below (Algorithm 2) stops when the error is less than the threshold $\varepsilon _{\mathit {rb}}$ everywhere. Unlike the previous approach, the entire DoE is covered at each iteration, but this method, that we call maximum residual approach in the sequel, is supposed to reduce the cardinal of the reduced basis.

3 First application example: material properties identification

3.1 Description of the identification problem

In the present section we apply our proposed surrogate modeling approach to a problem requiring displacement fields, namely the identification problem of the four orthotropic elastic constants of a composite laminate based on full field displacements.

We will use here a simulated experiment of a tensile test on a plate with a hole. The laminated plate has a stacking sequence of $[45, -45, 0]_{\mathrm {s}}$ and the dimensions are given in Fig. 2, with a total plate thickness of 0.96 mm. The applied tensile force is 1200 N. The full field measurement is assumed to take place on the entire $20 \times 20$ mm² area of the specimen. No exact analytical solutions exist for expressing the displacement field, so this problem is solved with an in-house finite element solver based on the gmsh open source mesh generator.

Fig. 2

Simulated experiment specimen geometry and the material orientation axes

The identification problem consists in determining the four orthotropic elastic constants $E_{1}$, $E_{2}$, $\nu_{21}$ and $G_{12}$ of the composite laminate, given that we measure the displacement fields in the X and Y directions (see Fig. 2) over the entire specimen area. Note that the material orientation 1 corresponds to the X direction while the material orientation 2 corresponds to the Y direction.

Since we wanted to test the accuracy of the surrogate modeling approach that we propose within this identification context we chose to use a simulated experiment such as to have reliable reference values for the material properties.

The simulated experiment was obtained by adding a white noise to finite element results that were run with the material properties provided in Table 1. These properties are typical of a graphite/epoxy composite.

Table 1 Material properties for the simulated experiment

The noise on the displacement at each of the mesh nodes was assumed to be Gaussian with zero mean and a standard deviation of 2.5 % of the maximum displacement amplitude.

The displacement fields of the simulated experiment are illustrated in Fig. 3.

Fig. 3

Displacement fields of the simulated experiment

The present identification problem is solved in this work using a model updating approach, which involves finding the material properties that minimize the error expressed in least squares terms between the model prediction and the measurement. Since this identification formulation involves solving a non linear optimization problem it is quite sensitive to computational time of the numerical solution. Note that with current computational resources coupling directly a finite element solver and the optimization routine is possible and would lead on this identification problem to a total computational time of several hours (Silva 2009). While such a computational cost might still be found reasonable in some applications we consider here that a significant reduction in the computational time of the identification is required, such as for example for real-time applications. The presented application example is thus to be seen as a representative example of real-time applications or of larger size finite element problems that would be prohibitive to couple directly with an optimization routine.

In order to reduce the computational time a surrogate modeling approach is chosen, using the key points response surface approach presented in the previous section. We chose this approach since the numerical model of the plate with a hole involves several of the challenge items mentioned in the introduction:

• the numerical model has a relatively high computational cost since no exact analytical solution exists for the displacement fields, thus a finite element model needs to be used

• the output of the simulation and the measurements is not scalar but a high dimensional vector

Since the key points response surface approach allows both to use as few full-size finite element solutions as possible as well as to cope with the high dimensionality of the output, the plate with a hole problem was deemed to be an appropriate application example for this approach.

Within the proposed approach any displacement vector u within the construction bounds is expressed by its approximation $\boldsymbol{\widetilde{u}}$ which is a linear combination of the basis vectors $\boldsymbol{\Phi}_{k}$ determined during the key points procedure:

$$ \boldsymbol{\widetilde{u}}=\sum\limits_{k=1}^K {\alpha_k \boldsymbol{\Phi}_k} =\sum\limits_{k=1}^K {\left\langle {\boldsymbol{U},\boldsymbol{\Phi}_k} \right\rangle \boldsymbol{\Phi}_k} $$

(8)

The synthetic experimental fields are also projected on the basis of the $\boldsymbol{\Phi}_{k}$ vectors leading to the $\alpha_k^{\exp }$ coefficients, that characterize the experiment.

In the identification problem the agreement between the model predictions and the measurements is thus expressed in terms of the agreement of the $\alpha_{k}$ and the $\alpha_k^{\exp }$ coefficients. For reasons that will be explained in the next section it is found that it is advisable to separate the X and Y displacement fields and therefore separate the corresponding X-basis and Y-basis. We denote by $\alpha_{i,k}$ (where i stands for either X or Y) the projection coefficient on the corresponding basis. Accordingly, the identification formulation is written as:

$$ \begin{aligned}[b] &\mathop{\text{Min}}\limits_{\left\{ {E_1 ,E_2 ,\nu_{21} ,G_{12}} \right\}} \;J\left( {E_1 ,E_2 ,\nu_{21} ,G_{12}} \right), \rm{where}\\ J\left( {E_1 ,E_2 ,\nu_{21} ,G_{12}} \right) \\ &\quad =\frac{1}{2}\left({\sum\limits_{k=1}^K {\left( {\alpha_{X,k} (E_1 ,E_2 ,\nu_{21} ,G_{12})-\alpha_{X,k}^{\exp} } \right)^2} } \right. \\ &\qquad \left. {+...\sum\limits_{k=1}^K {\left( {\alpha_{Y,k} (E_1 ,E_2 ,\nu_{21} ,G_{12} )-\alpha_{Y,k}^{\exp} } \right)^2}} \right) \end{aligned} $$

(9)

Efficient surrogate models are constructed using the key points response surface approach for the $\alpha _{i,k}$ coefficients as a function of the four orthotropic material properties of interest for the identification: $E_{1}$, $E_{2}$, $\nu _{21}$ and $G_{12}$. Note that constructing surrogate models for the $\alpha _{i,k}$ coefficients is not the only option. Another possibility would have been to seek a surrogate model of the objective function J and furthermore use it with optimization based sequential metamodel enrichment (Forrester and Keane 2009). However this would have been specific to the identification problem while a surrogate model of the displacement field can have wider applicability and also illustrates the ability of the proposed approach to construct surrogates of entire fields and not just scalar values.

Since the surrogate models for the $\alpha _{i,k}$ coefficients have simple expressions (e.g. polynomial), solving the non-linear least squares problem is computationally very fast. Here the problem was solved using Matlab’s lsqnonlin function, which uses the Levenberg Marquardt algorithm. Note that this algorithm computes the gradients of the objective function by finite differences. Here this gradient calculation did not pose any numerical issues, since the objective function involves smooth polynomial response surface approximations of the basis coefficients. In the absence of such a polynomial fit, it is important to note that the basis coefficients already filter out a large part of the noise in the displacement fields thus facilitating accurate gradient calculations by finite difference. Finally, even when coupling the finite element solution directly with the gradient calculation, the Levenberg Marquardt algorithm was found good enough for accurate identification (Silva 2009).

3.2 Key points response surface implementation

The objective of the present subsection is to construct surrogate models of the basis coefficients under the form $\widetilde {\alpha } _{i,k} \left ( {E_1 ,E_2 ,\nu _{21} ,G_{12}} \right )$ using the key points response surface approach. For this purpose we follow the procedure prescribed in Section 2 (summary in Fig. 1).

In the first step the design of experiments is defined. We use here a Latin hypercube design with 140 points within the bounds provided in Table 2.

Table 2 Bounds for the design of experiments

In the second step the key points approach is applied with an error criterion $e_{\mathit {rb}}$ $=$ 2 * 10⁻³. Either the sequential approach or the maximum residuals approach can be applied.

3.2.1 The sequential approach

The sequential approximation approach led here to using 13 basis vectors. On Fig. 4 the approximation error based on the residual $e_{\mathit {rb}}$ (cf. (5)) is plotted as a function of the experiment number. Recall that in the sequential approach the experiments are covered sequentially. At the beginning the algorithm solves exactly the finite element problem with the parameters of the first point of the DoE and adds the solution vector to the basis used for the reduced order modeling. It then solves the second experiment on projection on this basis and checks if the residual error is higher than the considered threshold ($2 * 10^{-3}$ here). Obviously only one vector for the reduced basis is insufficient to capture the variations of the displacement field for this problem. This can be seen on Fig. 4 by the fact that the residual error for experiment 2 is still significantly above the threshold (red dotted line). In this case the full problem is solved for experiment 2 and the resulting displacement vector is added to the reduced basis. The approach continues sequentially with the following points until the end of the DoE. Each experiment point is first solved projected on the reduced basis. If the corresponding approximation error (residual) is lower than the considered threshold the algorithm moves to the next DoE point. Otherwise the current point is added to the key points (red circle in Fig. 4), meaning that the full problem is solved and the reduced basis enriched by this key point as explained before.

Fig. 4

Plot of the approximation error (log scale) for the sequential approach as a function of the DoE experiment number

On Fig. 4 we can see that the algorithm successively adds to the basis the vectors corresponding to the DoE points number 1 2 3 4 5 6 7 8 9 10 13 25 and 41. One can notice that the first 10 points are considered key points since the reduced-basis is too small to be representative. Then, when the reduced-basis is rich enough, the projected problems are solved accurately without solving the full systems.

3.2.2 The maximum residual error approach

The results of the maximum residual error approach are illustrated in Fig. 5. The color scale represents the approximation error (on a log scale) for each of the 140 points of the DoE (on the abscises axis). On the ordinate axis we have the iteration number until meeting the error criterion. As for the sequential approach, at the beginning of the first iteration the algorithm solves exactly the finite element problem for the first DoE point and adds the solution vector to the basis used for the reduced order modeling. At this initial step we thus have one vector in the basis and at all the remaining points of the DoE the finite element problem are solved approximately on projection on this one vector. One vector is again insufficient to capture the variations of the displacement field for this problem and this can be seen in Fig. 5 by looking at the relative error norm which is higher than 0.1 (−1 on the log scale) for most of the 140 points. For recall we chose a criterion on the error norm of $2 * 10^{-3}$. Having calculated the relative error norms for all the 140 DoE points we chose the point having the highest error (DoE point number μ7 here), solve the finite element problem exactly at this new point and add the solution to the basis, which has now two vectors. We iterate, solving the problem on this expanded basis, calculating the relative error norms and adding the vector with the highest error to the basis until all the DoE points meet the relative error criterion. If at iteration k, the norm of the residual associated with a point P of the DoE is lower than the prescribed criterion, this point is considered to be solved accurately enough with the present basis. Any incremented basis will provide at least the same accuracy. So the point P will not be considered during the following iterations, that is the corresponding residual error will no longer be calculated. This trick contributes to further computational savings.

Fig. 5

Color plot of the approximation error (log scale) as a function of the points of the DoE and the iteration number

On Fig. 5 we can see that we successively add to the basis the vectors corresponding to the DoE points number 1, 117, 135, etc. We can note that once a vector is added to the basis or when the norm of the residual is lower than the prescribed criterion, its error norm for the following iterations remain constant. Indeed, it is no longer considered by the iterative method as it is considered to be solved accurately enough. Also with the iterations that increase the basis dimension we can also note that the relative error norm decreases for all DoE points (darker colors on the plot), until all the points satisfy the $2 * 10^{-3}$ residual error criterion that we considered.

The outputs of step two of the proposed approach are on one hand the exact finite element solutions at the 10 vectors forming the basis and on the other hand the approximate solutions (all satisfying the error criterion) at the 130 remaining points of the DoE. These two outputs are illustrated in boxes number 2 of Fig. 1.

3.2.3 The key points response surface results

The following step (number 3 in Fig. 1) first consists in obtaining the basis coefficients of all the solutions (exact and approximate). These can be obtained either by projecting the exact solutions on the basis or obtained directly but approximately when solving the approximate problem projected on the basis (reduced order model solution). Then response surface approximations are fitted to each of the ten basis coefficient $\alpha _{i,k}$ as a function of the parameters of interest ($E_{1}$, $E_{2}$, $\nu_{21}$ and $G_{12}$ here). Appendix 1 provides details on the physical interpretation of the modal basis for the displacements as well as additional explanations on the key points construction process.

Before presenting the results of the RSA fits we need to make here an important remark specific to the problem considered here, but which would appear to be quite common in mechanical problems, among other. The solution of the finite element problem is a vector containing the displacement fields in both the X and the Y direction. When constructing the key points basis, each basis vectors will also be a juxtaposition of modes in the X and Y direction. Accordingly a basis coefficient will characterize both the displacements in the X and in the Y direction. If seeking a response surface approximation of this basis coefficient directly it would mean that the same response surface equation would govern the variations in both the X displacement field and the Y displacement field. In many complex problems such an assumption would lead to poor results since the variations of the X displacement field are only partly coupled to variations of the Y displacement field. Accordingly we propose in such situations to separate the modes of the X and Y displacement fields and construct the response surface approximations separately for the basis coefficients of the X-displacement modes (X-direction basis vectors) and for the basis coefficients of the Y-displacement modes (Y-direction basis vectors).

The separation of the X and Y displacement modes can be done either concurrently to the key points algorithm or posterior to the algorithm. The posterior approach consists simply in taking the basis vectors obtained with the key points algorithm and split the X and Y displacement components. This leads to separate basis vectors for the X and Y displacement direction.

The concurrent approach is more complex and more code-intrusive but can reduce the size of the basis since it decouples the modes during the numerical problem solving of the reduced basis model. Appendix 2 provides a brief description of the concurrent approach. In the rest of this paper we implement the posterior approach.

The next step consists in fitting a response surface to the basis coefficients $\alpha _{i,k}$. We choose to construct third degree polynomial response surface (PRS) approximations for each coefficient, but any other type of response surface could be used. For this we used Surrogate Toolbox (Viana 2010), a free dedicated toolbox for Matlab. Only the significant terms of the polynomial were kept by imposing a minimum threshold of 2 on the t-values (Student’s t-statistic) for each polynomial coefficient. The final PRS were verified using root mean square error, correlation coefficient and PRESS cross-validation errors (see Appendix 2 for the error metrics obtained).

A final step in the validation of the overall surrogate model consists as described in the last step of Fig. 1, in assessing the cross validation error of the entire procedure consisting in the combination of key points reduced basis construction and subsequent basis coefficient RSA construction. The root mean square of the cross validation error over the 13 key points of the sequential approach is provided in Table 3. The individual errors at each of the cross validation points is quantified by the norm of the error in the displacement field divided by the norm of the displacement field, which thus leads to relative errors.

Table 3 Overall relative cross validation error for the X and Y displacement fields

The errors found are quite acceptable even though slightly higher than the 0.2 % maximum error objective we imposed on the previous steps. It is clear that since we combine the reduced order modeling and the surrogate modeling the overall error can be higher than that of each of the two modeling approaches. The final error found would have to be analyzed independently of the reduced order modeling and surrogate errors and a decision taken whether it is acceptable for the pursued purpose. Otherwise the procedure would have to be repeated with more stringent error criteria on the reduced order modeling and the surrogate procedure. In our case the errors were found acceptable.

Finally we provide an overview of the computational savings achievable with the proposed method. We provide in Table 4 the relative computational times needed for the resolution of the set of systems for the various methods discussed earlier. Note that the computational time was normalized such that the cost of brute force approach is equal to 1.

Table 4 Relative computational cost associated to the resolution of the DoE with the different techniques discussed in the paper

For the brute force method (used as a reference), which consists in computing a full resolution for each experiment of the DoE, the resolution time is equal to one, while the maximum residual method leads to a speed-up of 4.7 and the sequential approach to a speed-up of 9.2. The time taken to solve the linear systems for all the DoE is thus nearly divided by 10 with the sequential method, which is a significant efficiency improvement. Note that in general the higher the number of degrees of freedom in the full problem the more efficient the method is expected to be. Also note that the overall efficiency improvement depends not only on the system inversion but also on the stiffness matrix assembly. Thus depending on the size of the problem and the efficiency of the assembly the overall efficiency improvement may vary.

Considering this speed-up by a factor of almost 10 it can be interesting to compare the computational cost of the key points surrogate based identification with that of a classical surrogate based identification and with an identification coupling directly optimizer and finite element model. This last option was extensively studied for this same open hole test by Silva (2009). Using the Levenberg–Marquardt algorithm for solving this identification problem by direct coupling of the optimizer and the finite element model, Silva found that about 1200 function evaluations (130 optimization iterations) were required for convergence. Replacing the finite element model by a surrogate would lead to negligible surrogate evaluation cost so that the entire computational cost lies in the surrogate construction. In our case this involves 140 function evaluations of the DoE, thus representing about an order of magnitude reduction in the computational cost compared to coupling directly the optimizer with the finite element model. Using the key points approach allows to achieve an additional order of magnitude reduction in the number of function evaluations required.

In the last column of Table 4 the size of the reduced-basis for the different methods are also presented. As one can expect, the maximum residual method lead to a smaller basis (10) than the sequential method (13). Therefore the choice of the method is a compromise between numerical efficiency and reduction and will depend on the application. In the Appendix 1 of the paper an alternative to these two methods was proposed, which consists in performing a sequential approach with two different basis for X and Y components of the displacement, based on partial projections (which we called concurrent XY separation earlier in this section). One can notice in Table 4 that the resolution time is smaller than the maximum residual method, with a speed-up close to 6.6. This last method leads to two reduced-bases whose sizes are different but smaller than that of the sequential method. The fact that two different reduced-basis are used implies that the size of the projected systems are twice bigger than that of the previous sequential method which explains a smaller speed-up compared to the sequential approach. The sequential XY method may thus represent an interesting alternative, even if it is a bit more code intrusive.

3.3 Identification results

The identification framework presented at the beginning of this section is now applied on two test cases based on the simulated experiments illustrated in Fig. 3. The first one is a noise-free simulation obtained with the material properties given in Table 1, denoted reference values. The second one is a noisy experiment obtained with the same material properties but to which a white noise was added to the displacement fields as described at the beginning of this section. Since the white noise component is of aleatory nature we repeat 50 times the identification procedure for the second test case and provide the mean values of the identified properties. Note that once the key points response surfaces constructed, the resolution of the optimization problem was almost instantaneous.

The identification results are provided in Table 5. The reference values are those applied for the simulated experiment.

Table 5 Identified material properties for the two test cases

The identified properties agree very well with the reference values in both test cases. It is worth noting that even in the case of noisy experiments the identification approach still finds on average almost the exact values. This is partly due to the regularization effect of projecting the noisy “experimental” fields on the key points basis.

Note at this point that this regularization greatly reduces the effect of the noise on the displacement fields, rendering the results based on noisy and non-noisy experiments very close to each other. This would not be the case if actual experimental data would be used, but the identification problem is to be seen here just as an illustration of possible applications for a surrogate of the displacement fields.

Also note that other frameworks (e.g. Bayesian) could be used for carrying out the identification but for the same reasons we chose to not detail them in greater depth. The interested reader is referred to Gogu et al. (2012) for details on a Bayesian identification on actual experimental data.

4 Second application example: surrogate of a thermal field

In order to illustrate the applicability and efficiency of the proposed methodology on a large variety of problems and surrogate types an application to the construction of a thermal field surrogate is considered in this section using kriging. Note that only the surrogate construction is sought in this section independently of any identification or other application problem that might involve the thermal field. Indeed the proposed surrogate methodology is independent of the surrogate use that might follow.

The application considered here is the heat transfer through the combustion chamber wall of a rocket engine (Riccius et al. 2004, 2006). A schematic of a typical regeneratively cooled liquid hydrogen (LH2) liquid oxygen (LOX) rocket engine is illustrated in Fig. 6. The regenerative cooling takes place when the liquid hydrogen (LH2) at a temperature of 40 K flows through cooling channels in the combustion chamber wall before entering the injectors as shown in Fig. 6. Determining the temperature field in the combustion chamber wall is important in order to account for the high thermally induced stresses that arise and which can lead to broken cooling channel walls (cf. Fig. 6).

Fig. 6

Schematic of a regeneratively cooled rocket engine combustion chamber. The drawings are not to scale

Due to manufacturing constraints the combustion chamber wall is made of two different sections: an internal side usually made of a copper alloy in which the cooling channels are machined and an external jacket usually made of a Ni alloy (cf. Fig. 6). Convective heat exchange can take place between the combustion chamber gases and the inner side of the combustion chamber wall, between the liquid hydrogen and the cooling channel side of the wall and between the outer environmental temperature and the external side of the combustion chamber wall. The corresponding heat transfer problem is thus parameterized by the following parameters: the conductivity of the inner side of the wall ($k_{\mathit {Cu}}$), the conductivity of the jacket ($k_{\mathit {Ni}}$), the temperature of the gases on the inner side of the combustion chamber ($T_{\mathit {hot}}$), the temperature on the outer side of the combustion chamber ($T_{\mathit {out}}$), the temperature of the cooling fluid ($T_{\mathit {cool}}$), the film convection coefficient on the inner side of the combustion chamber ($h_{\mathit {hot}}$), the film convection coefficient on the outer side of the combustion chamber ($h_{\mathit {out}}$) and the film convection coefficient on the cooling channel side ($h_{\mathit {cool}}$).

We seek in this application example a surrogate of the temperature field in the combustion chamber wall as a function of the previous eight parameters during the stationary regime of the rocket engine.

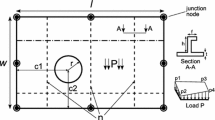
For the design of experiments a finite element model of the combustion chamber wall is used. By symmetry considerations only the discretized segment illustrated in Fig. 6 (right side) is modeled. This time again an in-house finite element solver coded in Matlab is used, but the use of any commercial software is possible given that the “stiffness matrix” can be accessed. The problem’s boundary conditions and finite element mesh is illustrated in Fig. 7.

Fig. 7

Schematic of a regeneratively cooled rocket engine combustion chamber. The drawings are not to scale

The bounds of the design of experiments are provided in Table 6 and a total of 660 points were sampled by latin hypercube.

Table 6 Bounds for the design of experiments of the thermal problem

The key points approach is applied with an error criterion $e_{\mathit {rb}} = 10^{-3}$. The sequential approach leads to a total of 15 basis vectors. The convergence of the residuals error with the experiment number is illustrated in Fig. 8.

Fig. 8

Plot of the temperature surrogate approximation error (log scale) for the sequential approach as a function of the DoE experiment number

As in the previous open hole plate example, using the proposed method, the vast majority of the 660 points of the DoE are evaluated using the computationally inexpensive reduced basis model, only 15 full system resolution being required. An overview and graphical representation of the first three temperature modes (basis vectors) is presented in Appendix 3.

The maximum residuals error approach also requires 14 iterations (and thus 15 basis vectors) to reach the 10$^{-3}$ error criterion as shown in Fig. 9. The figure plots the approximation error indicator based on the residual norm $e_{\mathit {rb}}$ as a function of the iteration number. For iteration i, the approximation errors of the whole set of experiments are plotted as + symbols. The new key point (red circle) at each iteration is the one which corresponds to this maximum residual error. At the end of the procedure all residuals are below the threshold considered.

Fig. 9

Plot of the temperature surrogate approximation error (log scale) as a function of the iteration number in the maximum residuals approach

Given that the same number of basis vectors were obtained by the sequential and the maximum residuals error approach we chose to consider in the rest of this section only the sequential approach basis vectors due to the lower computational effort for obtaining them.

The reduced basis being constructed the next step consists in fitting a surrogate model to the basis coefficients. A kriging model was adjusted for each temperature basis coefficient using Surrogates Toolbox (Viana 2010) (which itself utilizes a modified version of the DACE toolbox).

To validate the entire key points surrogate model cross validation is used again as described in Section 2.2. The root mean square of the cross validation error over the 15 key points was found to be 0.105 %. The individual errors at each of the cross validation points was quantified by the norm of the error in the temperature field divided by the norm of the temperature field, which thus led to relative errors.

Finally we provide an overview of the computational savings achievable with the proposed method for this thermal application problem. Table 7 gives the relative computational times needed for the resolution of the set of systems for the various methods discussed earlier. Note that the computational time was normalized such that the cost of brute force approach is equal to 1.

Table 7 Relative computational cost associated to the resolution of the thermal DoE with the different techniques discussed in the paper

For the brute force method (used as a reference), which consists in computing a full resolution for each experiment of the DoE, the resolution time is equal to one, while the maximum residual method leads to a speed-up of 3.7 and the sequential approach to a speed-up of 10, which is again a significant efficiency improvement. Note that for this problem there is no advantage in using the maximum residual error method since it finds the same reduced basis size as the sequential method.

5 Conclusions

The present article addressed the problem of constructing efficient surrogate models of high dimensional output. We proposed an approach based on the combination of reduced basis modeling and response surface methodology. The reduced basis modeling aims at solving the numerical problem projected on a reduced-dimensional basis, constructed sequentially based on a design of experiments. While such a reduced order modeling approach can be used as a metamodel by itself, even quicker response evaluations can be achieved by coupling the approach with response surface methodology. The proposed approach seeks to construct surrogate models of the basis coefficients that require a reduced number of expensive function evaluations made possible by the key points approach: the full scale (expensive) problem is only solved at a small number of key DoE points, while the reduced order model is used at all the others. Note that this approach is more code-intrusive than classical response surface construction, since the “stiffness” matrix needs to be available. It has however the potential of significant computational cost savings.

We first illustrated our approach on an identification problem of orthotropic elastic constants based on full field displacements. Surrogate models of the displacement fields were constructed using the proposed approach. This surrogate model allowed to have very good accuracy compared to solving the full scale problems each time (relative errors of the order of 0.2 %). Compared to the brute surrogate model the combined approach has roughly the same accuracy but the resolution time of the systems in the DoE was reduced by almost one order of magnitude.

It is also to be noted that we applied here our approach to a problem where the entire high dimensional response was required (the full field displacements or temperature), but note that the presented procedure may also be efficient for scalar responses that are extracted out of a higher dimensional output (e.g. maximum stress extracted out of the full stress map in the structure, or maximum temperature). In such a case our approach would allow to track the maximum even if it changes location on the structure. Compared to classical response surface approximation construction that require full scale problem solving at each design of experiment point our approach still has the potential to greatly reduce the number of required full scale problems solved.

A second application example was presented where a surrogate of a thermal field was sought. This second example in a completely different domain showed that the method is still applicable and similar computational savings were obtained. The proposed method is thus likely to benefit to a wide variety of problems where surrogate models are being sought. Finally it is important to note that the larger the problem (in terms of number of nodes) the higher the potential of the proposed method in terms of surrogate construction speed-up.

Appendices

Appendix 1: Concurrent X-Y separation approach

The concurrent approach for separating the X and Y displacement fields consists in dividing the sets of degrees of freedom (DOF) into two groups: the X and the Y components of the displacement. Each group of DOF can be either projected of its associated reduced-basis $\Phi_{\mathrm {x}}$ and $\Phi_{\mathrm {y}}$ or fully solved independently. Two different errors indicators $e_{\mathit {rb}}$ (as defined in (5)) are defined which quantify the accuracy of the approximation of the X and Y component separately. The two corresponding reduced bases may have different sizes. For solving the problem with a new set of parameters, the system is first solved in projection for both X and Y. Then 3 cases are possible:

• both error indicators are small enough: one switches to the next set of parameters.

• both error indicators are larger than the error criterion: the problem is fully solved. The just computed displacement vector is decomposed on X and Y, and each component is used to enrich the associated reduced-basis.

• one error indicator is small enough but not the other: the problem is partially projected onto the second reduced basis, such that the component which was not accurately approximated is being fully solved. Only the second reduced-basis is enriched by the fully computed component of the solution.

This technique leads to a hybrid problem for which only a part of the DOFs are reduced. For additional details on the practical implementation of the DOF separation the reader is referred to Kerfiden et al. (2012) which implemented a similar separation.

Appendix 2: Displacements modal basis

In the mechanical problem the basis vectors in the X and Y direction have a physical interpretation: they can be seen as displacement modes characterizing the effect of the variations in the mechanical parameters considered ($E_{1}$, $E_{2}$, $\nu_{21}$ and $G_{12}$ here). We illustrate the first three modes in the X and in the Y direction in Fig. 10.

Fig. 10

First three displacement modes obtained using the key points basis construction procedure

The first mode is the dominant mode and has high resemblance with the typical displacement fields (such as the ones illustrated in Fig. 3). That is, if we would only require displacement fields accurate to roughly 90 % (as shown in Fig. 5 after the first iteration) the first displacement mode would be enough. It means that for all displacement fields with parameters within our design space we could express the field as a multiplicative factor times the first mode and have fields that are accurate to about 90 %. The multiplicative factor would of course vary depending on the point within our design space (i.e. depending on the four material properties $E_{1}$, $E_{2}$, $\nu_{21}$ and $G_{12})$. A 10 % error on the displacement fields is however rather on the high side and does not allow capturing finer variations in the displacement fields needed to accurately identify all four material properties. So in order to reduce this error we need to increase the number of basis vectors (modes) utilized and express each field as a linear combination of the displacement modes, each additional mode providing higher accuracy for increasingly finer details of the field. The coefficients of the linear combination vary depending on the design point, thus we seek in the next step to construct response surface approximations of these coefficients as a function of the material properties $E_{1}$, $E_{2}$, $\nu _{21}$ and $G_{12}$. Since we found in the previous paragraphs that we need 10 modes to reach our relative error criterion of 0.2 % we will have to construct 20 response surface approximations in total (ten for the X-displacements and ten for the Y-displacements).

To assess the quality of the polynomial response surface approximation fitted for each basis coefficient we used the error measures provided in Tables 8 and 9. The second row of the tables gives the mean value of the POD coefficient across the design of experiments (DoE). The third row provides the range of variation of the coefficients across the DoE. Row four provides R$^{2}$, the correlation coefficient obtained for the fit, while row five gives the root mean square error among the DoE simulations. The final row gives the PRESS leave one out cross validation error (Allen 1971). Note that approaches other than PRESS exist for assessing the predictive capability of a model, for example the construction of a separate set of validation points. However in this paper we did not seek to guarantee a predictive capability in absolute terms but only relative to the surrogate model whose construction does not use the reduced basis model.

Table 8 Error measures for the polynomial response surface approximations for the basis coefficients of the X-displacements

Table 9 Error measures for the polynomial response surface approximations for the basis coefficients of the Y-displacements

Note also that when assessing the quality of the RSA in Tables 3 and 4, the error measures should be compared not only to the mean value of the coefficients but also to their range. By doing so we notice that all RSAs have a very good quality, both the RMS and the PRESS error satisfying the 0.2 % relative error criterion. Considering such low errors it was not deemed necessary to seek more advanced surrogate models (e.g. kriging, support vector machines, neural networks, etc.) for the basis coefficients.

Appendix 3: Temperature modal basis

As in the mechanical problem the basis vectors of the thermal reduced basis can be represented graphically and have following physical interpretation: the basis vectors can be seen as temperature modes characterizing the effect of the variations in the eight problem parameters considered (conductivities, film convection coefficients and wall temperatures). We illustrate the first three modes in Fig. 11.

Fig. 11

First three temperature modes obtained using the key points basis construction procedure

Again by construction the first mode is the dominant mode, meaning that alone it will explain most of the variations of the temperature fields when the eight parameters of the problem are varied. Of course the subsequent modes are required to catch finer details in the variations of the temperature field and thus meat the $10^{-3}$ error criterion.