1 Introduction

A wide part of the theoretical literature has studied the effects of a change in the size of unfunded pension systems on the growth rate of an economy.Footnote 1 However, only a few papers have considered the impact of the redistributivity of pension systemsFootnote 2 on macroeconomic variables such as the growth rate of the economy. In this paper, the term “redistributivity” is a measure of the indexation of pensions on the wages of agents. A pension system is purely Beveridgian if every agent receives the same pension. Conversely, a pension system is purely Bismarckian if pensions completely depend on the wages of agents. A pension system is mixed if it has a Beveridgian and a Bismarckian component. In the paper of Docquier and Paddison (2003), the more a pension system is Beveridgian, the lower the growth rate of the economy is. Indeed, the more the pension system is redistributive, the less agents decide to educate themselves. In this paper, we do not consider a human capital model. We study the impact of the level of indexation of pensions on wages on the growth rate of an economy in which the physical capital is the only engine of growth. We use an overlapping generations model in which agents differ by their productivity level. We show that the more a pension system is Beveridgian, the higher the growth rate is because of the increase in the aggregate savings. Thus, we complete the literature on pension systems, emphasizing that the structure of pension systems plays a significant role for capital accumulation. This result comes from the fact that the lower indexation of pensions on wages leads agents having the highest wages to increase their savings. Moreover, poor agents decrease their savings because they benefit from a higher pension. Finally, because the productivity level is related to the life expectancy of agents, then the increase in savings of rich agents over-compensates the decrease in savings of poor agents.

Furthermore, this question of the impact of the redistributivity of pension systems is all the more important since countries have adopted very different structures. As reported by Casamatta et al. (2000), or by Sommacal (2006), in France, Germany, and Italy, pension systems are essentially Bismarckian. Conversely, in Canada, the Netherlands, and New Zealand, pension systems are very redistributive. Finally, Japan, the UK, and the USA are in the middle.

2 The model

We assume a closed economy in which, at each period t, two generations overlap: the young and the old. Their respective size is N t and N t − 1. The population grows at a constant rate n, such that N t  = (1 + n)N t − 1. Each agent is randomly endowed with a productivity level a at the beginning of his life. This productivity level belongs to the interval Ω a  = [a  − ,a  + ], with a  +  > a  −. The density function of this variable is denoted by f(a). f(a) is such that \(\int_{\Omega_a}f(a)da=1\). \(\bar{a}\) denotes the average productivity level of the economy:

$$\label{abar} \bar{a}=\int_{\Omega_a}af(a)da $$
(1)

The density function f(a) is assumed to be constant over time and to be exogenously given. Each agent completely lives his first period of lifeFootnote 3 but only a fraction T(a) of his second period of life. We assume that T′(a) > 0, which implies that the productivity level of agents has a positive impact on their length of life.Footnote 4 The average length of life is denoted by:

$$ \bar{T}=\int_{\Omega_a}T(a)f(a)da $$
(2)

The link between productivity and length of life is measured by the covariance:

$$\label{defCov} {\rm COV}_{T(a),a}=\int_{\Omega_a}T(a)af(a)da-\bar{T}\bar{a} $$
(3)

As T′(a) > 0, then we have COVT(a),a > 0. The utility of consumers depends on the consumption flows of the two periods of life. For an agent born in period t endowed with a productivity level a, c t (a) and d t + 1(a)/T(a) denote the first period and the second period consumption flows, respectively. Their utility function has the following form:Footnote 5

$$ \label{eq4} U_t(a)=u(c_t(a))+\beta T(a)u\left(\frac{d_{t+1}(a)}{T(a)}\right), $$
(4)

where β represents the pure time preference factor for the present, and the T(a) in front of their second period utility implies that the longer the length of life is, the more consumers value their utility of this period.

Each agent offers his work during his first period of life inelastically and receives a wage w(a). This wage is taxed at a rate τ t , and the revenues of this tax are used to finance a pay-as-you-go (PAYG) pension system. When an agent is old, he receives a pension p(a). For an agent born in period t, his budget constraints are:

$$ \label{eq5} c_t(a)=w_t(a)(1-\tau_t)-S_t(a) $$
(5)
$$ \label{eq6} d_{t+1}(a)=R_{t+1}S_t(a)+p_{t+1}(a), $$
(6)

with R t + 1 the interest factor and S t (a) the saving function.

We also assume that the utility function has the following form: u(x) = ln (x). Agents maximize Eq. 4 with respect to S t given the budget constraints 5 and 6:

$$\label{defEpargne} S_t(a)=\frac{\beta T(a)w_t(a)(1-\tau_t)}{(1+\beta T(a))}-\frac{p_{t+1}(a)}{(1+\beta T(a))R_{t+1}} $$
(7)

Moreover, we assume a perfect competition on the final good market and on the input markets. The production function of firms is:

$$\label{defFctProd} Y_t=A_tK_t^\alpha\left(L_t\int_{\Omega_a}af(a)da\right)^{1-\alpha} $$
(8)

with 0 < α < 1, K t is the physical capital level, L t is the quantity of labor, and A t is the level of the technology. As in Frankel (1962), we assume \(A_t=A(K_t/L_t)^{1-\alpha}\) to have an endogenous growth model.

As there is perfect competition on each market, firms take wages and interest factors as given. Profit maximization implies the following expressions for prices given that the final good is the numéraire:

$$\label{defR} R_t=A_t\alpha K_t^{\alpha-1}\left(\int_{\Omega_a}af(a)L_tda\right)^{1-\alpha}=A\alpha\bar{a}^{1-\alpha} $$
(9)
$$ w_t=A_t(1-\alpha)K_t^\alpha\left(\int_{\Omega_a}af(a)L_tda\right)^{-\alpha}=A\frac{(1-\alpha)}{\bar{a}^{\alpha}}k_t $$
(10)

The capital level per worker is denoted by k t (k t  ≡ K t /L t ). w t is the wage per efficient unit of work. For agents endowed with a productivity level a, their wage is:

$$\label{defWit} w_t(a)=w_ta=A\frac{(1-\alpha)}{\bar{a}^{\alpha}}ak_t $$
(11)

\(\bar{w}_t\) denotes the average wage of the economy at period t. It has the following expression:

$$\label{defwbar2} \bar{w_t}=\int_{\Omega_a}w_t(a)f(a)da=A(1-\alpha) \bar{a}^{1-\alpha}k_t $$
(12)

We assume a PAYG pension system. The revenues of this system come from a proportional tax on wages: τ. It is used to provide a pension for elderly people. Their pension depends on their wage level and on the average wage of the economy. Their respective weighting is λ and (1 − λ). The first part of this pension represents the Bismarckian component, whereas the second part represents the Beveridgian component of this system (Casamatta et al. 2000). For λ = 0, the pension system is completely Beveridgian because every agent receives the same pension indexed on the average wage of the economy. Conversely, for λ = 1, the pension system is completely Bismarckian because pensions only depend on the wage level of agents. A higher λ increases the Beveridgian component of pension systems.

Consumers receive only a fraction ν (with 0 < ν ≤ 1) of this weighted average, and only during their second period of life T(a). ν denotes the average replacement rate of the pension system. The pension of an agent endowed with a productivity level a is:

$$ p_{t+1}(a)=\nu \left(\lambda w_{t}(a)+(1-\lambda)\bar{w}_{t}\right)T(a) $$
(13)

With Eqs. 11 and 12, we obtain:

$$\label{defPit} p_{t+1}(a)=\nu A(1-\alpha)\frac{k_{t}}{\bar{a}^\alpha}(\lambda a+(1-\lambda)\bar{a})T(a) $$
(14)

We also assume that the government does not use debt. It implies that, for each period, we have:

$$\label{defEqCaisseRetraite} \int_{\Omega_a}\tau_{t+1} w_{t+1}(a)f(a)N_{t+1}da=\int_{\Omega_a}p_{t+1}(a)f(a)N_tda $$
(15)

It is straightforward to show that:

$$\label{defTau} \tau_{t+1}=\frac{\nu}{1+n}\left(\lambda \frac{{\rm COV}_{T(a),a}}{\bar{a}}+\bar{T}\right)\frac{k_t}{k_{t+1}} $$
(16)

The richer agents are, the longer their length of life is. Therefore, an increase in λ (i.e., a decrease in the Beveridgian part of pension systems) increases the indexation of pensions on their wages. It implies that the pension of rich agents increases. Moreover, they benefit from these pensions for a longer period of time than other agents. Consequently, the tax rate has to increase to finance these additional expenditures.

The dynamic equilibrium of our economy is such that the two following conditions are satisfied ∀ t ≥ 0:

$$ K_{t+1}=\int_{\Omega_a}S_t(a)f(a)N_tda $$
(17)
$$ N_t=L_t $$
(18)

Let g t denote the growth rate of the economy (1 + g t  = k t + 1/k t ), and let Ψ t denote the growth factor of the economy (Ψ t  = 1 + g t ). Then, Ψ t and g t are positively correlated. It is straightforward to show that:

$$\begin{array}{lll} &&\displaystyle (1+n)\Psi_t\\ &&=\frac{\beta A(1-\alpha)}{\bar{a}^\alpha}\left(1-\frac{\nu}{1+n}\left(\lambda \frac{{\rm COV}_{T(a),a}}{\bar{a}}+\bar{T}\right)\frac{1}{\Psi_{t-1}}\right) \int_{\Omega_a}\frac{T(a)a}{1+\beta T(a)}f(a)da \end{array} $$
$$\label{defkLT} \qquad\quad\quad -\nu\frac{1-\alpha}{\alpha}\int_{\Omega_a}\frac{\lambda\frac{a}{\bar{a}} +(1-\lambda)}{1+\beta T(a)}T(a)f(a)da $$
(19)

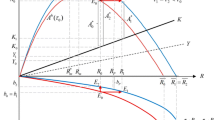
The left-hand side of Eq. 19 is a linear function of Ψ t . As for the right-hand side (RHS), it is an increasing and concave function of Ψt − 1. Moreover, the RHS is such that \(\lim_{\Psi\rightarrow +\infty} \partial {\rm RHS}(\Psi)/\partial\Psi=0\). Consequently, there exist, at most, two steady states (see Fig. 1). Let us assume that the conditions for the existence of these two steady states are verified,Footnote 6 and that the higher growth factor is higher than one. It can be shown that only the higher steady state is stable, that is why we study the properties of that point in the following proposition.

Fig. 1
figure 1

Impact of a decrease in λ

Full size image

Proposition 1

If f(a) > 0 ∀ a ∈ Ω a , then a decrease in λ, i.e., an increase in the Beveridgian part of pension systems, has a positive impact on the growth rate of the economy (g).

Proof

Using Fig. 1, it can easily be shown that Ψ is an increasing function of the Beveridgian part of pension systems if λ has a negative impact on the RHS of Eq. 19. It is obvious that the first element of the RHS is a decreasing function of λ. Moreover, we know that T(a)/(1 + βT(a)) is an increasing function of a. It implies that \(T(a)/(1+\beta T(a))<T(\bar{a})/(1+\beta T(\bar{a}))\) (>), \(\forall a<\bar{a}\) (>). Then, \((a-\bar{a})T(a)/(1+\beta T(a))>T(\bar{a})/(1+\beta T(\bar{a}))(a-\bar{a})\), ∀ a. The second element of the RHS is a decreasing function of λ if the following condition is satisfied: \(\int_{\Omega_a}\frac{a-\bar{a}}{1+\beta T(a)}T(a)f(a)da\geq 0\). We know that \(\frac{a-\bar{a}}{1+\beta T(a)}T(a)f(a)\geq\frac{a-\bar{a}}{1+\beta T(\bar{a})}T(\bar{a})f(a)\), ∀ a ∈ Ω a . Integrating the two sides of this equation over the interval Ω a , the RHS is equal to zero and the condition mentioned above is satisfied.□

Two kinds of effects play a role when we analyze the effects of a decrease in λ. The first effect concerns the impact on the tax rate. Indeed, we have showed that the tax rate is an increasing function of λ. If λ falls, the tax rate decreases for every consumer, which has a positive effect on saving without ambiguity. The second effect concerns the impact on the pension received by each agent. If λ decreases, consumers endowed with a productivity lower than \(\bar{a}\) receive a greater pension, whereas consumers endowed with a productivity higher than \(\bar{a}\) receive a smaller pension. The first group of agents saves less and the second one saves more. Proposition 1 shows that the net effect on saving is positive. Indeed, agents for whom the pension decreases have a longer length of life than the others. Consequently, the increase in the saving of rich agents overcompensates the decrease in the saving of poor agents.