1 Introduction

Until the middle of the 20th century, carpentry wood-to-wood connections were commonly used in construction, with their design and manufacturing aspects based on the experience of skilled wood workers. The Rounded Dovetail Connection (RDC), named after the rounded shape similar to a dovetail (Fig. 1) is adapted to be produced with a CNC-timber processor. RDC are increasingly being used in timber construction, with the most common application being the joist to beam connection (Fig. 2 left). A number of experimental studies on RDC provided valuable insight (Kreuzinger and Spengler 1999; Hochstrate 2000; Bobacz 2002; Tannert et al. 2007; Tannert and Lam 2007, 2009) revealing that failure under shear loading for joist to beam connections was typically brittle, and occurred in the elastic range of the load deformation curve.

Fig. 1 Abb. 1
figure 1

RDC timber members

Schwalbenschwanzzapfenanschluss

Full size image
Fig. 2 Abb. 2
figure 2

RDC application (left) and geometric parameters (right)

SSZ Anwendung (links) und geometrische Parameter (rechts)

Full size image

The complex load transfer mechanism in an RDC is governed by its distinct geometry: dovetail height h 1, flange angle k, dovetail angle a, dovetail width b 1, dovetail depth t, member height h, and member width b (Fig. 2 right). Although RDC were shown to be able to undergo large rotations before failing, the brittle nature of joist failure was independent of loading for similar dovetail geometries (Tannert et al. 2007). The structural performance can potentially be improved by considering its geometrical features as design parameters to reduce concentration of stresses, if detailed knowledge of the stress distribution within the connection is available (Dietsch 2005). The influence of manufacturing parameters including changing moisture content was investigated by Anastas et al. (2008).

Although RDC represent an efficient method for connecting two wooden members and are widely used in praxis, no reliable strength prediction method was available and general acceptance of RDC in the engineering community was delayed. Werner (2002) provided a simplified design method: he examined the load-deformation curves for RDC under shear loading and recommended a deformation limit of 1.5 mm and a design load F adm(Joist) based on the allowable shear stress f s,adm and the effective dovetail area A 1:

$$F_{\mathit{adm}(\mathit{Joist})}=\frac{2}{3}\cdot A_{1}\cdot f_{S,\mathit{adm}}.$$
(1)

Although the approach seems straightforward, it does not allow estimation of RDC capacity, it ignores the interaction of stresses (Dietsch 2005) and neglects the observed dependency of strength on stressed volume (Tannert and Lam 2009). A German general building approval dealing with RDC (DIBt 2007) gives guidance for the dimensioning of RDC produced from glulam and for a series of defined boundary conditions with a method similar to that for notched joints.

Failure modes of timber connections depend on member and connection geometry as well as material type and its associated failure modes. In tension and shear, timber essentially exhibits a linear elastic behaviour, and failure is marked by a brittle fracture. The constitutive behaviour of wood under multi-axial stress states has only been rarely considered (Spengler 1986; Hemmer 1984) and relatively little is known about the associated failure behaviour. Eberhardsteiner (2002) measured the stress-strain behaviour of clear spruce wood under multi-axial loading covering the whole set of distinguishable stress states under plane stress and observed interactions between tension and shear strengths; these interactions were later micro-mechanically explained by Grosse and Rautenstrauch (2004).

For material failure prediction, failure criteria based on either continuum mechanics or fracture mechanics exist. The fracture mechanics approach assumes a pre-existent crack and the conditions for crack growth are usually determined by comparing energy release rates with their critical values. The continuum mechanics approach considers the nature and magnitude of stresses or strains, nowadays usually determined using Finite Element Analysis (FEA) and formerly by analytical formulae. Various failure criteria for wood have been developed, and various in-depth reviews were published, recently by Kasal and Leichti (2005). A commonly applied criterion was proposed by Norris (1962), see Eq. 2:

(2)

where σ X ,σ Y ,σ Z and τ XY ,τ YZ ,τ ZX are the normal and shear stresses, respectively and f X ,f Y ,f Z ,f XY ,f YZ ,f ZX are the material strength parameters.

Although there has been significant further work on failure criteria development, a general and simple unified model for timber is not yet available. Moreover, the existing criteria do not include size effects in timber under multi-axial stresses. One issue for the application of any criterion is the inherent large variability of timber strength parameters, especially if considering strength data (Kasal and Leichti 2005). This limitation must be addressed before failure criteria can be reliably used to predict strength of timber connections.

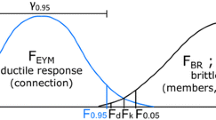
Material strength exhibits a size effect when strength decreases with increasing specimen size under the same test conditions. Three main types of size effects may be distinguished (Bažant 2005): (i) a statistical size effect, due to randomness of strength; (ii) an energetic size effect; and (iii) fractality of fracture or micro-cracks. In materials exhibiting statistical size effect, failure tends to initiate from flaws, which are randomly distributed within the volume; smaller specimens have a lower probability of including such flaws. Size effects are important for the design of real scale structures when the material properties are defined from tests performed on small-scale specimens. For brittle materials, size effects on strength are adequately explained by probabilistic theories such as the Weibull strength theory (Bažant 2005).

The Weibull statistical distribution, introduced by Weibull (1939), has been extensively used in the characterization of mechanical properties of brittle materials. The corresponding probability of survival of a volume subjected to a non-uniform stress distribution, P S , is being calculated as follows:

$$P_{s}=\exp \biggl[-\int_{V}\biggl(\frac{\sigma -\sigma _{0}}{m}\biggr)^{k}dV\biggr]$$
(3)

where, σ is the stress acting over a volume V,m is the characteristic stress or scale parameter, σ 0 is the strength threshold and k is the shape parameter that gives a measure of the strength variability. The parameter m corresponds to the mean stress acting on a particular volume, and has, assuming the Weibull distribution, a probability of survival P s =0.368 (=e −1). The distribution parameters can be estimated by e.g. the maximum likelihood method, least squares/rank regression etc. A particular case of the Weibull distribution is given by setting σ 0 equal to zero, the resulting formulation is called a 2-parameter (2P) Weibull distribution. For the 2P distribution, one consequence of Eq. 3 is that for two volumes V 1 and V 2 submitted to constant stresses σ 1 and σ 2 at failure, assuming equal probabilities of survival, the relationship given in Eq. 4 is obtained:

$$\frac{\sigma _{1}}{\sigma _{2}}=\biggl(\frac{V_{2}}{V_{1}}\biggr)^{1/k}.$$
(4)

Equation 4 allows a direct implementation of size effects in numerical procedures. Since the stresses acting in a specimen are usually multi-axial, the stress operator σ in Eq. 3 can be replaced by a failure criterion.

One of the first documented applications of Weibull theory related to timber was the evaluation of bending strength: Bohannan (1966) showed that the bending strength of wood beams varied with depth and length. Barrett (1974) and Foschi and Barrett (1976) applied Weibull theory to the determination of strength of Douglas fir in tension perpendicular to grain and shear. Larsen and Riberholt (1981) and Colling (1986) confirmed the size effect for shear and perpendicular to grain strength for other timber species. It has been shown (Barrett and Lau 1994) that for timber, k is correlated to the coefficient of variation (CV) using Eq. 5:

$$k=CV^{-1.085}.$$
(5)

Progress has been made towards applications of size effect to a variety of loading conditions and materials, refinements of the statistical basis, and implementation of the theory’s predictions to design standards (Smith et al. 2003). But there are still some fundamental questions towards its applicability: using Weibull theory to analyze components with stress concentrations, capacities can be considerably under-predicted, possibly explained due to the fact that predictions are usually made for one stress component at a time and only for stress states that exhibit elastic-brittle characteristics. There is no allowance for softening of stress peaks under complex multi-axial stress states that accompany stress concentrations (Smith et al. 2003). Nevertheless, recognition of size effects is important when using conventional strength-based failure criteria as shown by Clouston et al. (1998) who implemented Weibull theory into the Tsai-Wu failure criterion to assess size effects in Laminated Veneer Lumber.

In summary, the prediction of RDC capacity is difficult due to the anisotropic and brittle nature of timber, the complex multi-axial stress distribution, and the uncertainties regarding the associated material strength. In this paper the structural performance of RDC is investigated experimentally and numerically. Based on the assumption of size effects, the research is extended with a probabilistic approach to predict RDC capacity.

2 Experimental investigation

2.1 Specimen description

A total of eight experimental series consisting of a main beam and a joist connected by RDC were tested at the Timber Engineering and Applied Mechanics Lab of the University of British Columbia (Tannert 2008). These were divided into two groups of test series, G1 and G2; the difference being the test set up and instrumentation. In G1, three different dovetail heights and three different flange angles were compared to a control geometry. The geometry of the control series was chosen as: flange angle k=15°and dovetail height h 1=119 mm, resulting in a connection back-cut BC (h–h 1) of 65 mm. The three levels of back-cut investigated were 75 mm, 55 mm and 45 mm; the test series were labeled BC75, BC55, and BC45, respectively. The three levels of the flange angle k investigated were 20°,10° and 5°; the test series were labeled A20, A10, and A05, respectively. The remaining parameters were kept constant with b 1=50 mm, depth t=28 mm, and dovetail angle a=15°. In G2, t and a were kept constant as 28 mm and 15°, respectively. The geometric parameters are listed in Table 1.

Table 1 Tab. 1 Geometric parameters of RDC test seriesGeometrieparameter der RDC Testserien
Full size table

2.2 Material

Kiln-dried Western hemlock (Tsuga heterophylla) was used throughout the study. The moisture content (MC) and the apparent density (ρ) of each specimen were determined. Resistance based electrical measurements were used to determine MC; ρ was determined based on the tested specimen weight and volume. The average and standard deviation of MC were 12.6% and 1.6%, respectively. The average ρ was 495 kg/m3 with a standard deviation of 46 kg/m3. A total of 78 specimens were tested, 10 for the control series and 5 for each of the other series in G1, 8 specimens for series A and 14 specimens each for series B and C in G2.

2.3 Methods

The RDC was applied to connect a joist to a main beam (Fig. 3). Since it is the principal loading of RDC for their practical application, shear loading was chosen. The main beam was supported on two 100×100×10 mm3 steel plates, two steel plates on the backside prevented horizontal movement. The main beam was not fixed, thus allowing for some rotation around its longitudinal axis. For the test series in G1, the free end of the joist was supported on a 100×100×10 mm3 steel plate on a spring support with a stiffness of 1 kN/mm, thus simulating an approx. 4 m long beam of the given section. For the test series in G2, the free end of the joist was simply supported on a fixed 100×100×10 mm3 steel plate.

Fig. 3 Abb. 3
figure 3

Test set-up for RDC experiments: G1 (left) and G2 (right)

Skizze des Versuchsaufbaus: G1 (links) und G2 (rechts)

Full size image

For the test series in G1, the load was applied at a distance of 350 mm from the connection and distributed onto the joist with a steel plate with a diameter of 100 mm and a thickness of 10 mm. In G2, the load was applied at a distance of 450 mm. The load was increased up to failure with a constant rate of loading so that failure occurred after approximately six minutes, in accordance with EN-26891 (1991). For the series in G1, no preload was applied, for the series in G2, a pre-load of 1 kN was applied to close any pre-existing connection gaps.

2.4 Instrumentation and measurements

The applied load from the actuator, the force at the support of the free end of the joist, and the vertical displacement on both sides of the connection (as the relative displacements between main beam and joist) were recorded. The force transmitted by the connection was calculated as the difference between the applied load and the load recorded at the free end of the joist. The connection displacement was calculated as the average between the displacements of the two sides.

Two different limit loads were considered: firstly the load that corresponds to a deformation limit which corresponds to the serviceability limit state (F SLS ), set herein to 3 mm (based on the experience of the authors and in consultation with practitioners); secondly the capacity at rupture of the joint (F ULS ), which corresponds to the definition of the ultimate limit state. For RDC that failed before deforming 3 mm, the peak force applied represents F SLS . Besides F SLS and F ULS , the load at crack initiation (F crack ) was determined for the test series in G2 based on measurements of the displacement between upper and lower edges of the joist.

2.5 Experimental results

Within the range of geometric parameters, loading and support conditions investigated, failure was always brittle, occurred in the elastic range, and initiated at the bottom of the dovetail of the joist member (Fig. 4 left). Figure 5 shows the connection load vs. relative vertical connection deformation for all individual specimens of the control series. After the initial slack caused by alignment issues, the load increased linearly until first cracks (visually observed) developed. Further increases of load were associated with stable crack development and larger displacements until brittle failure occurred at capacity. The average of the individual load deformation plots for all series of G1 is shown in Fig. 6. The results exhibit a high variability among the specimens in terms of initial stiffness and capacity. Some specimens showed large initial alignment behaviour with the increasing load after considerable deformations; in other specimens the load started to increase at small deformation.

Fig. 4 Abb. 4
figure 4

Typical failure of RDC (left) and stresses computed by FEA (right)

Typisches Versagen von SSZ (links) und Spannungen aus numerischem Modell (rechts)

Full size image
Fig. 5 Abb. 5
figure 5

Model vs. experimental load deformation curves for control series

Modellierte und experimentelle Last-Verformungskurven der Kontrolltestserie

Full size image
Fig. 6 Abb. 6
figure 6

Model vs. experimental load deformation curves for test series G1

Modellierte und experimentelle Last-Verformungskurven der Testserien G1

Full size image

Table 2 summarizes the results of the recorded variables: F SLS ,F ULS and F crack . The ratio between F crack and F ULS was on average 0.9 for series A and on average 0.8 for series B and C. This coincided with the observation of cracking sounds at a load level of approximately 0.9 of the capacity for the test series of G1.

Table 2 Tab. 2 Capacity of RDC: predicted and experimental results (mean values and standard deviations), and p-values of statistical analysisTraglasten von RDC: Vorhersagen und experimentelle Ergebnisse (Mittelwerte und Standardabweichungen), und p-Werte der statistischen Auswertung
Full size table

In order to check the validity of Eq. 1, the effective dovetail area, A 1, was plotted against the experimentally observed capacity, F ULS , and the serviceability load, F SLS . Figure 7 clearly shows that the linear relationship given in Eq. 1 cannot be supported by the presented research.

Fig. 7 Abb. 7
figure 7

Failure loads of RDC vs. joint size

Traglasten von SSZ in Abhängigkeit der SSZ-Größe

Full size image

Analysis of variance (ANOVA) was carried out to evaluate the effect of the dovetail geometric parameters on F SLS and F ULS . Based on the number of observations, a p-value is calculated and compared to the significance level, α, typically chosen as 0.05 or 0.1 (Montgomery and Runger 2003). If the p-value is smaller than α, then the hypothesis of no differences between means is rejected; this procedure (with α=0.1) was applied, p-values are displayed in Table 2. The dovetail height has a statistically significant effect on F SLS and F ULS . Multiple comparison tests (Least Square Differences) were used to determine which test series exhibit statistical differences. Series BC75 has a significantly lower F ULS than series BC55 and BC45, and a significantly lower F SLS than BC55. The flange angle has a statistically significant effect on F ULS . Multiple comparison tests showed that series A05 has a significantly lower F SLS than all other series.

3 Finite element analysis

3.1 Numerical modeling of timber

Timber is an anisotropic and inhomogeneous material, but for numerical modeling in FEA it is often assumed to be homogeneous. For small specimen obtained relatively far from the pith, the influence of the growth ring curvature is frequently ignored so that properties can be regarded as orthotropic; for specimen with similar height and width, transverse isotropy with identical properties in radial and tangential directions can be assumed. The radial and tangential directions are referred to as perpendicular to grain (⊥), the longitudinal direction is referred to as parallel to grain (∥). Since brittle failure modes initiating within the elastic range dictate the capacity of RDC, the material was regarded as linear elastic and transverse isotropic, with the properties set to: E ∥=E X =12,000 N/mm2 (based on tests, Tannert 2008) and E ⊥=E Y =E Z =600 N/mm2, G XY =G YZ =400 N/mm2, G YZ =40 N/mm2, υ XY =υ XZ =0.02, υ YZ =0.40 in accordance to literature (Barrett et al. 2001; Green et al. 1999).

3.2 Numerical model for RDC

The software ANSYS®(v10) (Ansys 2006) was used in the study applying 3D modelling and 20-node elements. Weighting result accuracy against computing time, the model was divided into different mesh zones, depending on the stress gradients. The finest mesh (5 mm element length) was used along the bottom of the dovetail where the highest stresses were expected. A coarser mesh was used for the remaining parts, with element length varying between 8 and 26 mm. To model the contact between joist and main beam, target and contact surface-to-surface elements were used. Contact stiffness (FKP), penetration tolerance (FTOL), friction coefficient (μ), and the initial connection gap between the connecting members affect result accuracy and convergence. FKP and FTOL are parameters without unit that describe the relative contact stiffness and the allowable penetration, respectively. Based on preliminary investigations (Tannert 2008), FKP was set to 0.02, a value that allowed convergence, and FTOL to 0.5, a value that allowed realistic interpenetration of the surfaces.

Manufacturing tolerances significantly influence the performance of RDC (Anastas et al. 2008). Initial gaps, caused by geometry differences between the two connecting members, have to be considered to model the initial alignment behaviour. Previous work (Tannert 2008) suggested that good agreement between analytical and experimental load response curves can be achieved by modeling a gap of 0.5 mm. The surface quality of the members plays an important role in the behaviour of RDC as it dictates the friction between them. The friction coefficient μ was set to 0.35; similar to previous research (Bobacz 2002; Dietsch 2005), and in the range of values reported in the literature (McKenzie and Karpovich 1968).

3.3 Results of numerical modeling

FEA was used to compute the distribution of stresses in the dovetail section of the joist. The tip of the dovetail is clearly identified as the location of highest stresses which corresponds to the failure locus observed in the experiments (Fig. 4). In the numerical model with elastic material properties, stress singularities are prone to develop at geometrical discontinuities. Furthermore, the magnitude of stress maxima at geometrical discontinuities depend on the chosen mesh—they usually do not converge but increase with mesh refinement. Figure 8 illustrates the occurrence of stress peaks in tension perpendicular to grain stress in the joist member at the bottom of the dovetail tip. The computed curves of the relative connection deformation versus the applied load were compared to the experimental results, see Fig. 5. The numerical model reflects accurately the experimentally observed behaviour.

Fig. 8 Abb. 8
figure 8

Tension perpendicular to grain stress peaks vs. distance to dovetail tip

Zugspannungen rechtwinklig zur Holzfaser in Abhängigkeit vom Abstand zur SSZ

Full size image

3.4 Model validation

The numerical model was validated by comparing results to the experimentally obtained average load displacement curves of all test series in G1 (Fig. 6). The load deformation curves were modeled using their material properties and failure loads as model input. The elastic parameters were adjusted according to the grain orientation ρ and MC (Table 3). Adjustment for MC was done with data from literature (Green et al. 1999); adjustment for ρ was done using previously determined regression data (Tannert 2008). The specimens were modeled with different gaps according to their load displacement response and good agreement between experimental and numerical results was obtained.

Table 3 Tab. 3 Model parameters for test seriesModellparameter der Testserien
Full size table

4 Probabilistic strength prediction

4.1 Strength prediction method

As RDC fail under a combination of stresses, it is necessary to extend the concept of the statistical distribution of the material strength under unilateral stresses (i.e. f T,∥ f T,⊥ f S,∥) towards stresses acting conjunctively. For this purpose, the Norris criterion (Eq. 2) was modified in such a way, that only those stresses that cause brittle failure are considered. A failure stress operator, φ F , was defined:

$$\phi^{2}_{F}=\min\left\{\begin{array}{l}(\frac{\sigma _{X}}{f_{X}})^{2}-(\frac{\sigma _{X}\sigma _{Y}}{f_{X}f_{Y}})+(\frac{\sigma _{Y}}{f_{Y}})^{2}+(\frac{\tau _{XY}}{f_{XY}})^{2},\\[6pt](\frac{\sigma _{Y}}{f_{Y}})^{2}-(\frac{\sigma _{Y}\sigma _{Z}}{f_{Y}f_{Z}})+(\frac{\sigma _{Z}}{f_{Z}})^{2},\\[6pt](\frac{\sigma _{Z}}{f_{Z}})^{2}-(\frac{\sigma _{Z}\sigma _{X}}{f_{Z}f_{X}})+(\frac{\sigma _{X}}{f_{X}})^{2}+(\frac{\tau _{ZX}}{f_{ZX}})^{2}.\end{array}\right.$$
(6)

Idealizing the member under consideration as being constituted by n elements, which for practical reasons coincided with the finite elements used in the FEA, its survival depends on the simultaneous non-failure of all elements i≤n. As a result, for a given applied load, F, the probability of survival can be calculated by Eq. 7:

$$P_{S}(F)=\prod_{i=1}^{n}P_{S,i}(F)$$
(7)

where P S,i (F) is the probability of survival of the constituent element i associated with the applied load F, which can be calculated using Eq. 3. Consequently, if each element i, with a volume V i is subjected to a constant value of the failure function φ Fi , the probability of survival of the whole member is given by Eq. 8:

(8)

Equation 8 can be implemented in a post-processing routine for FEA results (Vallée et al. 2009). To compare predictions with mean values of experimental results, a standard probability of survival of P S =0.5 has to be considered (Towse et al. 1999); the corresponding value of F FEA thus is the predicted capacity. As the approach is probabilistic, deterministic failure predictions cannot be given.

4.2 Determination of material parameters

The brittle material strength properties required for Eq. 6 (i.e. f T,∥,f T,⊥,f S,∥) were determined according to ASTM-D143 (2002). A total of 480 individual tests were carried out, 160 for each of the material properties. These test series were performed on samples exhibiting different stressed volumes, as summarized in Table 4. The experimentally determined mean values, \(\bar{x}\), and the shape parameters, k, corresponding to each test series estimated using Eq. 5 are listed in Table 4. The results are within the range of widely accepted values of softwood (Barrett and Lau 1994; Barrett 1974; Foschi and Barrett 1976). To gather the corresponding statistical parameters for Eq. 3 (k and m), φ F -values corresponding to all specimens were used. As the specimens used for the three different tests exhibited different sizes, the corresponding failure stresses could not be used in one single series. To overcome this formal issue, and according to the lemma resulting from Weibull theory (Eq. 4), all experimentally gathered strengths were first related to an arbitrary reference volume, set herein to V 0=30,000 mm3 (volume of tension perpendicular to grain strength test specimen).

Table 4 Tab. 4 Material strength parametersMaterialkennwerte
Full size table

This procedure resulted in a homogeneous set of data, allowing for a direct comparison of strength data resulting from different test setup, more specifically specimen volumes. Assuming the resulting data to be Weibull distributed, log φ F can be plotted against log (−log [1−P f,i ]), with P f,i =(i−0.3)/(n+0.4), where i is the rank and n the number of samples (Faucher and Tyson 1988), see Fig. 9. Following rank regression on the linear form of the cumulative distribution function the Weibull modulus was found to equal k=4.55, while m=1.124.

Fig. 9 Abb. 9
figure 9

Weibull parameter estimation plot for all experimental results on small specimens

Bestimmung der Weibull Parameter aus den Kleinversuchen

Full size image

4.3 Validation of strength prediction method using ASTM tests

The probabilistic procedure was applied to predict the capacity of the specimens used in the ASTM tests. Only the elements between the loaded areas are considered, as they contain the locus of the failure initiation. Furthermore, the stresses in the other elements are negligible. The comparison of the probabilistic strength prediction and the experimental results is shown in Table 4. The probabilistic method is in excellent agreement with the experiments for the tension parallel to grain and tension perpendicular to grain tests (deviations 4% and 2%), while the deviation for the shear parallel to grain tests is 14%.

4.4 Strength prediction for experimentally investigated RDC

The probabilistic method was applied for the experimental test series on RDC. Since failure occurred in the joist member, only the joist was considered as being constituted by n elements and Eq. 8 was applied to predict the failure load of the RDC. Again, in order to compare predictions with mean experimental values, a standard probability of survival of P S =0.5 was considered in the calculations.

The comparison of the probabilistic strength prediction and the experimental results for RDC strength is shown in Table 2. Excellent agreement was obtained for the tests series in G2, where the actual crack load was measured. For the tests series of GI there is a trend that predicted failure load (F FEA ) is lower than experimental failure load (F EXP ). In addition to F EXP and F FEA , Table 2 also shows the deviation between these two values and the results of t-tests for the hypothesis: F EXP =F FEA . This hypothesis is rejected for those cases where the p-value is smaller than α=0.10 (90% significance level).

4.5 Strength prediction for further RDC configurations

A series of FEA computations was carried out varying the member dimensions (l,b and h) and the dovetail geometry (k,h 1 and b 1). Loading and support conditions were kept constant. The predicted RDC failure loads (F FEA ) and the ratios between them and the effective dovetail area (F FEA /A 1) were computed (Table 5). The results point out that A 1 cannot linearly be used to predict RDC capacities especially when other geometric parameters are varied.

Table 5 Tab. 5 Predicted RDC failure loads for varied geometric parametersVorhergesagte RDC Traglasten für variierte Geometrieparameter
Full size table

5 Discussion

Experimental investigations showed that load deformation response of RDC specimens under shear loading is linear until reaching a load that leads to crack development. For those test series where no preload was applied to close initial connection gaps, minor cutting inaccuracies led to differences in the initial alignment behaviour amongst the individual specimens. Furthermore the specimens show initial connection slackness due to alignment issues resulting in high variability of initial load deformation response. For those test series, where a pre-load was applied, no initial load slip was observed. ANOVA showed that the dovetail height h 1 has a statistically significant effect on the performance of RDC. The capacity increases with increasing h 1 up to an apparent optimum of approx. 2/3 the member height, and then drops again. The flange angle has no statistically significant effect on RDC capacity but because of the observed differences, an angle of 15° is recommended. For all investigated test series, the effective dovetail area was plotted versus the capacity; a non-linear relation was found.

Regarding FEA, the solution convergence is influenced by how the contact is numerically handled and the results accuracy depends strongly on the assigned material properties. Varying the material parameters over a realistic range yielded good agreement between numerical and experimental load deformation curves. The model can be applied for modeling the load-deformation behavior and for probabilistic modeling using the variables as random input parameters.

In the numerical model with elastic material properties, geometrical singularities are accompanied by stress singularities and stress redistribution processes due to stable crack growth cannot accurately be represented. The value of maximum stress is mesh-dependent; as a consequence, a criterion based on maximum stress cannot be used to predict strength of RDC. It was therefore hypothesized that besides the stress magnitude, the stress distributions (stress gradients and volume subjected to high stresses) also influence joint strength. The probabilistic strength prediction method presented in this paper foots, firstly, on a mechanistic based description of the material failure under multiple stresses, and secondly on a companion statistical description of the material strength. Regarding material failure, the adequacy of the Norris criterion has been assessed.

The mechanical parameters needed to formulate the criterion were determined according to ASTM-D143 (2002) on samples exhibiting radically different shapes and volumes. Therefore they had to be brought into a coherent volume, exploiting the assumption that size and strength are correlated using Eq. 4. The validity of the chosen approach has been verified on the strength determination of the small specimen, where the predictions for tension parallel to the grain and tension perpendicular to the grain were very good (deviations of 2% and 4% respectively) while the prediction for shear parallel to the grain was not as good (deviation of 14%). A possible explanation is the fact that no pure state of shear stress is obtained in the experiments. Regarding the statistical description of the material strength, the experimentally gathered data is adequately described by a 2P-Weibull distribution, as shown in Fig. 9; slight deviations from the linear fit do only appear at the lower end of the probability density function (pdf), which are not relevant for the further strength prediction method, since they would lead to slightly underestimate the probability of failure at low stresses.

The accuracy attained by the probabilistic method for the test series in G1 was acceptable (on average around 14%). In G2, the RDC force causing crack initiation—the load that is predicted by the criterion—was measured. Here, the predictions (F FEA ) were in excellent agreement to the experimental results (F EXP ), on average by 3%. The hypotheses: F EXP =F FEA were accepted for all experimental test series. This clearly validates the probabilistic strength prediction method for the range of experimentally investigated geometries. In contrast to the method presented herein, the alternative design procedure, represented by Eq. 1, does only account for one geometrical input parameter, i.e. the dovetail area, and only for the shear strength as sole mechanical input. Because the probabilistic method allows taking into consideration all geometrical parameters, it is possible to investigate the influence of different configurations for structural optimization.

The accuracy of the strength prediction method presented herein is strongly dependent on (i) the quality of the description of the failure criterion, and (ii) the ability of the statistical distribution function to represent the material strength. Regarding (i) an increase of accuracy can be expected by using a less disparate set of tests to determine the material strengths as suggested by ASTM-D143 (2002); using samples that are more comparable in their geometry and volumes, for example a set of off-axis tension tests would allow formulating the failure criterion more straightforwardly. Regarding (ii), a different probability density function (pdf) might be able to model correctly the lower-tail of the distribution; but as the description of the pdf in this area would only affect lowly stressed zones, thus not critical, its impact on the accuracy would almost be negligible.

6 Conclusion

Experimental and numerical investigations have been carried out to study the influence of geometric parameters of rounded dovetail connections (RDC) and a probabilistic method has been developed for the strength prediction of RDC under quasi static shear loading. The following conclusions were drawn:

  1. (i)

    failure mode under shear loading was brittle, occurred in the elastic range of the load deformation response, and initiated at the bottom of the dovetail of the joist;

  2. (ii)

    RDC capacity increases with larger dovetail height, up to an apparent optimum while changing the flange radius only slightly influences RDC performance;

  3. (iii)

    based on the experimental results, the authors recommend producing RDC with flange angles of 15° and dovetail heights of 2/3 the member height;

  4. (iv)

    for numerical models of RDC, the timber can be modelled with linear elastic and transverse isotropic material properties; the actual failure location was confirmed to be the highest stressed part of the model;

  5. (v)

    the comparisons between the numerical and the experimental results showed that the model is reliable in predicting the structural response, suggesting it could be used to develop a numerical based method to predict failure loads;

  6. (vi)

    the modified Norris failure criterion including size effects was shown to be adequate to predict RDC capacity.

    The immediate application of the proposed method is the study of parameter influences on the capacity of RDC; it was shown that the strength increase for larger specimens is not proportional to the dovetail area, which at least questions common methods used by practitioners. Consequently, these findings should be taken into consideration when designing RDC.