Introduction

As living organisms have generally limited resources, they have to divide them between many biological traits which contribute to their survival and reproduction (Stearns, 1992; Roff, 2002). One of the common allocation problems for organisms is the distribution of resources between growth and reproduction (Stearns, 1992; Roff, 2002). It has gained particular interest from experimental ecologists (cf. King and Roughgarden, 1983; Okuda et al., 1998; Roff et al., 2006; Sugiyama and Hirose, 1991; Worley and Harder, 1996) as well as from theoreticians (cf. Heino and Kaitala, 1999; Perrin and Sibly, 1993). For social insects, this allocation problem can be transposed to the colony level, i.e. to the production of workers (growth of the colony) and sexuals (reproduction) (Oster and Wilson, 1978).

On the one hand, breeding queens and males contribute rather directly to the fitness of the members of the colony, because they can reproduce and transmit their genes to new colonies. On the other hand, new workers contribute to the “working force” of a colony, permitting to collect more resources and to produce more sexuals later on. Workers which are produced rather early in the colony cycle may work their entire lifetime and will thus contribute much more to colony fitness than workers produced shortly before the end of the season. The opposite holds true for sexuals of annual colonies. If produced early, they may die before the season ends and before diapause begins. Thus, the relative fitness value of workers and sexuals is time dependent and the optimal allocation strategy will depend on colony size too.

Many models of allocation of resources between growth and reproduction have been developed, but most of them are based on plants and perennial organisms (cf. review in Iwasa, 2000; Perrin and Sibly, 1993). However, it is important to notice that social organisms have a number of specific features, which are not found in plants or solitary organisms, and which may modify the conclusion based on these plant/organism models:

  • The energy which has been allocated to growth (workers) cannot be reallocated later to reproduction (or at least is not easily reallocated).

  • The size of the colony can increase but also decrease, because of mortality of workers.

  • Conflicting interests between queens and workers and between workers themselves often occur, deriving from differences in relatedness between individuals (Oster et al., 1977; Heinze et al., 1994).

Macevicz and Oster (1976) and Oster and Wilson (1978) were the first to investigate the problem of optimal resource allocation for annual colonies of social insects. Their seminal work is often referred to when dealing with colony life cycles (i.e. Beekman et al., 1998; Tschinkel, 1999; Cassill, 2002).

To solve the problem, they used optimal control theory, based on Pontryagin’s maximum principle. This method is rather complex and Mangel and Clark (1988) point out that the method has “many intricate technicalities”, and “unless the problem is particularly simple, the solution must be obtained by numerical computation”. The complexity of the method used, as well as the rather authoritative conclusions might have prevented extensions of the original approach (but see Mitesser et al., 2006, 2007a, b, for extensions; Mitesser et al., 2007a, b, for severe simplification; Beekman et al., 1998, for a mechanistic model; and Cassill, 2002, for a verbal one).

One central conclusion of the work of Oster and Wilson (1978) is that a colony should usually first invest all resources into the production of workers, and then switch completely to the production of sexuals. Such strategies are called “bang–bang strategies”, and the term “determinate growth” is also used for a growth period which ends when reproduction starts. They also predict that a graded transition from pure production of workers to pure investment into sexuals (with an extended phase of mixed investment into sexuals and workers) could occur only under some rather restricted conditions.

Indeed, social insects’ colonies generally start with a growth period or “ergonomic stage”, in which, only workers are produced (Oster and Wilson, 1978). But the “bang–bang” strategy is far from being exclusively met (cf. examples reviewed by Greene, 1984; Mitesser et al., 2007a, b), and many species exhibit “graded strategies” characterised by an extended period during which sexuals and workers are produced simultaneously.

Explanations for graded strategies can be divided into two categories: non-linear relationship between colony size and colony productivity or mortality, and avoidance of risk (bet-hedging), linked to a variability of season length or productivity (cf. Heino and Kaitala, 1999 for a review). Oster and Wilson (1978) already cite non-linearity between size and mortality or productivity of the colony, and bet-hedging as possible explanations, but they focussed on bet-hedging, considering that it should be a better explanation. So did most of the subsequent studies on growth allocation (King and Roughgarden, 1982b; Iwasa, 2000; Mitesser et al., 2007a, b). But in the case of variable season length, which has often been given as the main explanation, the variability necessary to induce an optimal graded strategy is huge, and probably not very realistic (Mitesser et al., 2007a, b).

As we feel that the scarcity of further theoretical studies on the life cycle of colonies of social insects could be related to the methods and conclusions of the Macevicz and Oster (1976) and Oster and Wilson (1978) models, we want to cast them in a new light, providing here not only simpler methods but also more detailed discussion of the biological mechanisms relevant for observed colony dynamics which were absent in the original paper. We also discuss the implication of this model for the evolution of sociality, and illustrate how simple extensions can modify the optimal growth allocation of a colony, leading to graded strategies.

Description of the model

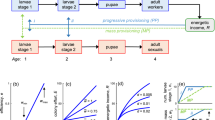
According to the model of Oster and Wilson (1978), colonies can be considered dynamic systems (Fig. 1). The state of the colony is determined at each time t by the number of workers (w) and that of sexuals (s). The number of workers (w) and the individual productivity rate of workers (γ) determine the colony’s rate of acquisition of resources of the colony (productivity of the colony). Acquired resources can in turn be used to produce new workers or sexuals. The time-dependent allocation strategy of the colony is described by the fraction (u) of acquired resources devoted to the production of sexuals at each time. Colony dynamics is governed by two processes: mortality and reproduction. If we assume that workers and sexuals die at rates μ w and μ s, respectively, the temporal development of the colony is thus described by a set of coupled differential equations:

$$ {\frac{{{\text{d}}w(t)}}{{{\text{d}}t}} = (1 - u(t))\gamma w(t) - \mu_{\text{w}} w(t)} $$
(1)
$$ {\frac{{{\text{d}}s(t)}}{{{\text{d}}t}} = u(t)\gamma w(t) - \mu_{\text{s}} s(t)} $$
(2)
Fig. 1
figure 1

Schematic representation of colony dynamics. The resources collected by workers can be allocated either to the production of sexuals (fraction u) or to the production of new workers (fraction 1 − u). Sexuals and workers die at rates μ s and μ w, respectively

Full size image

The colony cycle typically starts in spring with nest founding by inseminated and hibernated females. During the founding phase, the queens work alone and perform all foraging tasks. Those will later be carried out by the workers after their emergence. Thus we start with initial condition w(0) = 1, assuming that the founding queen acts like a single worker until the first eggs have developed into adults.

In this paper, we will focus on the case of an annual colony. The fitness for such colonies can readily be estimated by the total number of sexuals produced by the colony and alive at the end of the season. Like Oster and Wilson (1978), we will thus take this quantity as a measure of total colony fitness, and assume that a colony has to choose an allocation strategy maximising the total number of sexuals alive at the end of the season.

Using both analytical models and dynamic programming models (Mangel and Clark, 1988) we calculated optimal allocation strategies of a colony for a fixed season length (T). We were particularly interested in the influence of the productivity of workers and the mortality of sexuals and workers on optimal allocation strategies.

Constant individual mortality and productivity

Oster and Wilson (1978) start their model analysis with the simple case of constant productivity and mortality, the per capita productivity of workers (γ), the mortality rate of sexuals (μ s) and of workers (μ w) being neither dependent on time nor on colony size. For their analysis, they used optimal control theory (Mangel and Clark, 1988) to calculate the optimal time-dependent allocation strategy (u*(t)). However, we will show that neither optimal control theory nor dynamic programming but only basic calculus is needed to determine the optimal strategy for this case.

The optimal time-dependent allocation strategy (u*(t)) is the strategy which maximises the number of sexuals alive at the end of the season. As sexuals may die before the end of the season, the actual fitness value of each unit resources invested at time (t) into the production of sexuals when approaching the end of the season (Fig. 2) is

$$ {F_{\text{s}} (t) = {\text{e}}^{{ - \mu_{\text{s}} (T - t)}} } $$
(3)
Fig. 2
figure 2

Illustration of the optimal “bang–bang” strategy for an annual colony, with parameters: season length T = 200, productivity γ = 0.035, and mortalities of workers and of sexuals: μ w = 0.015, μ s = 0.01. The upper figure illustrates the optimal allocation strategy, whilst the lower figure illustrates the development of the numbers of sexuals (dashed line) and workers (straight line). The switching time is marked with the vertical bold dotted line. Points and crosses show the results of a corresponding dynamic optimisation approach

Full size image

If the colony produces workers, these workers may subsequently produce sexuals throughout their life. Each unit of resources invested into the production of workers at time (t) may thus provide the fitness increase:

$$ {F_{\text{w}} (t) = \int\limits_{t}^{T} {\gamma {\text{e}}^{{ - \mu_{\text{w}} (t^{\prime} - t)}} \,{\text{e}}^{{ - \mu_{\text{s}} (T - t^{\prime})}} \,{\text{d}}t^{\prime}} } $$
(4)

Towards the end of the season the remaining life span and the reproductive value of workers continuously decrease (Fig. 3). Thus, the colony will eventually switch to the production of sexuals only. Actually, the colony will stop producing workers as soon as the remaining lifetime of a newly produced worker is so short that his lifetime production of sexuals is inferior to the number of sexuals which could be produced directly at the cost of one worker. Evidently, a colony should invest into the production of workers as long as the fitness return from an investment into workers (F w(t)) surpasses that for an investment into sexuals (F s(t)) and switch to the production of sexuals whenever (F w(t s) < F s(t s)). This allows us to calculate the switching time (t s), which corresponds to the solution of F w(t) = F s(t):

$$ {t_{\text{s}} = T - \frac{1}{{\mu_{\text{w}} - \mu_{\text{s}} }}\,{ \ln }\left( {\frac{\gamma }{{\gamma - \mu_{\text{w}} + \mu_{\text{s}} }}} \right)\parallel \gamma - \mu_{\text{w}} + \mu_{\text{s}} > 0} $$
(5)
Fig. 3
figure 3

Fitness gain of an investment into sexuals (bold line, Eq. 4) or into workers (dashed line, Eq. 3), depending on the time of their production, and of the death rates of workers (μ w) and sexuals (μ s). The productivity parameter used for these figures is γ = 0.03, and the length of the season is T = 200. The switching time is marked with the vertical dotted line

Full size image

As can be seen from Eq. 5 and from Fig. 3, there can never be more than one switching point. This results in the typical bang–bang strategy (Fig. 2) already predicted by Macevicz and Oster (1976). A comparison of the analytical result according to Eq. 5 with a dynamic programming approach confirmed our results (Fig. 2).

Note that Eq. 5 will give meaningful predictions only for the case when (a) worker productivity (γ) surpasses the mortality of workers (if the mortality of workers is superior to the productivity, the colony cannot grow), (b) when the predicted switching time is positive (t s > 0), otherwise the season is too short to invest into workers and females should breed solitary. According to L’Hospital’s rule, Eq. 5 gives \( {t_{s} = T - \frac{1}{\gamma }} \) when worker mortality equals sexual mortality.

Lower mortality (μ w) or higher productivity (γ) of workers accelerates the switch from growth to reproduction. A higher mortality of sexuals (μ s), on the contrary, favours a later switching time as sexuals produced later have a higher probability to survive till the end of the season (Fig. 3). Obviously, the advantage of producing sexuals increases with increasing worker mortality (μ w) and decreases when sexual mortality increases. Consequently, the length of the reproductive phase increases with the difference (δ = μ w − μ s) between the mortality of workers and that of sexuals and with increasing worker productivity (γ) (Fig. 4). When worker productivity (γ) is below a critical value it does not pay for the colony to invest into workers because these would produce less than they cost. Thus, the grey area in Fig. 4 marks conditions for non-social behaviour.

Fig. 4
figure 4

Influence of the difference in mortality between sexuals and workers (δ = μ w − μ s) and worker productivity (γ) on the length of the reproductive phase (T − t s) for T = 200. The grey area is the area where the conditions are not met for sociality (γ < μ w − μ s)

Full size image

Rates dependent on colony size

Logistic colony growth (i.e. the dependence of productivity (γ) or mortality (μ) on colony size) has been amongst the favorite candidates for explanations for a graded transition from the ergonomic to the reproductive phase of a colony. As both mechanisms will result in similar patterns, we will, in the following, provide a more detailed analysis of the case of size-dependent productivity (i.e. productivity of individual workers decreases with the size of the colony) and present the results for the case of increasing mortality at the end of this chapter.

With productivity being dependent on colony size:

$$ {\gamma (w) = (\gamma_{0} - \alpha w)} $$
(6)

We can adjust Eqs. 1 and 2 and we get:

$$ {\frac{{{\text{d}}w(t)}}{{{\text{d}}t}} = (1 - u(t))(\gamma_{0} - \alpha w(t))w(t) - \mu_{\text{w}} w(t)} $$
(7)
$$ {\frac{{{\text{d}}s(t)}}{{{\text{d}}t}} = u(t)(\gamma_{0} - \alpha w(t))w(t) - \mu_{\text{s}} s(t)} $$
(8)

Now the size of the colony is limited. During the ergonomic phase, when workers invest only into the production of further workers, colony growth is logistic (Verhulst, 1838):

$$ {w(t) = \frac{{(\gamma_{0} - \mu_{\text{w}} )}}{{\alpha - (\gamma_{ 0} - \mu_{\text{w}} - \alpha )\,{\text{e}}^{{ - (\gamma_{0} - \mu_{\text{w}} )t}} }}} $$
(9)

When per capita productivity decreases with increasing size of the colony, the colony productivity is maximised for colony size w opt:

$$ {w_{\text{opt}} = \frac{1}{2}\left( {\frac{{\gamma_{0} - \mu_{\text{w}} }}{\alpha }} \right)} $$
(10)

The optimal colony size is reduced by α and μ w but increased by γ 0 (Fig. 5). Using Eq. 9 we may determine the time t s1 the colony needs to reach this size:

$$ {t_{{{\text{s}}1}} = \frac{1}{{\gamma_{0} - \mu_{\text{w}} }}\,{ \ln }\left( {\frac{\alpha }{{\gamma_{0} - \mu_{\text{w}} - \alpha }}} \right)} $$
(11)
Fig. 5
figure 5

Influence of the productivity (γ 0) and the mortality of workers (μ w) on the optimal size of the colony (w opt), for two different values of the size dependency factor (α): 0.005 for the left figure, 0.01 for the right one. The grey area indicates combinations of μ w and γ 0 resulting in optimal colony sizes below to 1

Full size image

This time only depends on the productivity function and on the mortality of workers (Fig. 6). As colony productivity decreases when worker number (w) surpasses w opt the colony should not grow above this size. Once it has reached w opt (if season time and colony growth parameters permit it), investment into workers should switch to a mixed investment into sexuals and workers, where the production of workers is limited to the compensation of worker mortality. This compensatory investment u c should be such that 1 − u c = μ w w opt. This results in the remaining investment into the production of sexuals:

$$ {u_{\text{c}} = \left( {\frac{{\gamma_{0} - \mu_{\text{w}} }}{{\gamma_{0} + \mu_{\text{w}} }}} \right)} $$
(12)
Fig. 6
figure 6

Influence of the net productivity during the growth phase: δ = γ 0 − μ w and colony size dependency factor α on the length of the growth phase (t s1)

Full size image

For the switch to the purely reproductive phase, the same argument holds true as in this section for the case of exponential colony growth. Workers should switch to the exclusive production of sexuals as soon as the investment into sexuals generates higher fitness benefit than that into workers. As sexuals may die before the end of the season, the actual fitness for each unit of resources invested into the production of sexuals is given by Eq. 3. However, if worker productivity is dependent on the number of workers, the investment into workers has a twofold effect on colony fitness. On the one hand, it will result in an additional workforce for the colony. In accordance with Eq. 4, the fitness component for the case where worker productivity γ 0(w) is dependent on colony size is

$$ {F_{{{\text{w}}1}} (t) = \int\limits_{t}^{T} {(\gamma_{0} - \alpha w(t))\,{\text{e}}^{{ - \mu_{\text{w}} (t^{\prime} - t)}} \,{\text{e}}^{{ - \mu_{\text{s}} (T - t^{\prime})}} \,{\text{d}}t^{\prime}} } $$
(13)

with colony size depending on time:

$$ {w(t) = \left\{ {\begin{array}{*{20}c} {\frac{{(\gamma_{0} - \mu_{\text{w}} )}}{{\alpha - \left( {\gamma_{0} - \mu_{\text{w}} - \alpha } \right)\,{\text{e}}^{{ - (\gamma_{0} - \mu_{w} )t}} }}} \hfill & {{\text{for}}\;t < t_{{{\text{s}}1}} } \hfill \\ {w_{\text{opt}} } \hfill & {{\text{for}}\;t \ge t_{{{\text{s}}1}} } \hfill \\ \end{array} } \right\}} $$

On the other hand each investment in workers changes the size of the colony and thus decreases the productivity of all other workers. This difference in colony fitness may be calculated as

$$ {\begin{array}{*{20}c} {F_{{{\text{w}}2}} (t) = w(t)((F_{{{\text{colo}}(w + 1)}} ) - (F_{{{\text{colo}}(w)}} ))} \hfill \\ \end{array} } $$
(14)

With colony fitness with additional worker:

$$ {F_{{{\text{colo}}(w + 1)}} = w(t)\int\limits_{t}^{T} {(\gamma_{0} - \alpha (w(t) + 1)\;{\text{e}}^{{ - \mu_{\text{s}} (t - t_{\text{s}} )}} )\,{\text{e}}^{{ - \mu_{\text{w}} (t - t_{\text{s}} )}} \,{\text{e}}^{{ - \mu_{\text{s}} (T - t^{\prime})}} \,{\text{d}}t} } $$

and colony fitness with former worker number:

$$ {F_{{{\text{colo}}(w)}} = w({\text{t}})\int\limits_{t}^{T} {(\gamma_{0} - \alpha w(t)\,{\text{e}}^{{ - \mu_{\text{s}} (t - t_{\text{s}} )}} )\,{\text{e}}^{{ - \mu_{\text{w}} (t - t_{\text{s}} )}} \,{\text{e}}^{{ - \mu_{\text{s}} (T - t^{\prime})}} \,{\text{d}}t} } $$

Thus the total fitness gain from the investment into workers is

$$ {F_{\text{w}} (t) = F_{{{\text{w}}1}} (t) + F_{{{\text{w}}2}} (t)} $$
(15)

In case of investment into sexuals, the fitness gain is

$$ {F_{\text{s}} (t) = {\text{e}}^{{( - \mu_{\text{s}} (T - t))}} } $$
(16)

As the colony should switch to reproduction only when the investment into sexuals generates a higher fitness benefit than that into workers (F s(t) > F w(t)) we get an implicit formulation for the second switching point t s2:

$$ {F_{\text{s}} (t) = F_{\text{w}} (t)} $$
(17)

This equation can only be solved numerically (Fig. 7). However, if we take into account that sexuals live far longer than workers and that worker mortality is much higher than that of sexuals, we may ignore the mortality of sexuals (as has been done by Oster and Wilson, 1978). Moreover, our numerical analysis shows that the mortality of sexuals (μ s) has a negligible influence on the second switching point (i.e. with parameters T = 200, γ 0 = 0.2, α = 0.001, and μ w = 0.005, a change of mortality of sexual from μ s = 0 to μ s = 0.4 gives t s2 = 154.804 instead of t s2 = 154.810). Ignoring the mortality of sexuals (μ s = 0) we can solve Eq. 17 analytically which results in a second switch at

$$ {t_{{{\text{s}}2}} = T + \frac{1}{{\mu_{\text{w}} }}\,{ \ln }\left( {\frac{{( - \gamma_{0} + \sqrt {\mu_{\text{w}} } \sqrt {2\gamma_{0} - \mu_{\text{w}} } )}}{{\mu_{\text{w}} - \gamma_{0} }}} \right)} $$
(18)
Fig. 7
figure 7

Influence of the productivity (γ 0) and the mortality of workers (μ w) on the optimal switching time to the production of sexuals only (t s2), with the parameters: T = 200, α = 0.0008, and μ s = 0.1

Full size image

Figure 7 illustrates how an increasing productivity delays the second switch, whilst an increase of workers mortality either delays (for low mortalities) or accelerates (for already high mortalities) the second switch.

We compared the analytical and numerical solution to the result of a dynamical programming approach, which confirmed the results (see Fig. 8 for one example).

Fig. 8
figure 8

Illustration of the optimal strategy for an annual colony, with parameters: season time T = 200, productivity γ 0 = 0.05, α = 0.0008, and mortalities of workers and of sexuals: μ w = 0.015, μ s = 0.01. The upper figure illustrates the allocation to reproduction, whilst the lower figure illustrates the development of the numbers of sexuals (dashed line) and workers (straight line). The switching times are marked with the vertical bold dotted line, whilst the optimal colony size is marked by the horizontal dotted line. Point and crosses show the results of the dynamic optimisation approach

Full size image

If season time is too short to reach w opt, the colony will adopt a bang–bang strategy, which can be calculated applying a similar method as the one we used in “Description of the model”.

Extending from this, we calculated that with an increasing per capita mortality of workers with increasing colony size:

$$ {\mu (w) = (\mu_{0} + \beta w)} $$
(19)

the optimal colony size becomes w opt:

$$ {w_{\text{opt}} = \frac{1}{2}\left( {\frac{{\gamma_{0} - \mu_{0} }}{(\alpha + \beta )}} \right)} $$
(20)

and the colony growth becomes:

$$ {w(t) = \left\{ {\begin{array}{*{20}c} {\frac{{(\gamma_{0} - \mu_{\text{w}} )}}{{(\alpha + \beta ) - (\gamma_{0} - \mu_{0} - \alpha - \beta )\;{\text{e}}^{{ - (\gamma_{0} - \mu_{0} )t}} }}} \hfill & {{\text{for}}\;t < t_{\text{s1}} } \hfill \\ {w_{\text{opt}} } \hfill & {{\text{for}}\;t \ge t_{\text{s1}} } \hfill \\ \end{array} } \right\}} $$
(21)

t s1 becoming:

$$ {t_{{{\text{s}}1}} = \frac{1}{{\gamma_{0} - \mu_{0} }}\,{ \ln }\left( {\frac{\alpha + \beta }{{\gamma_{0} - \mu_{0} - \alpha - \beta }}} \right)} $$
(22)

Note that in the above equations, α is replaced with the factor (α + μ). Thus, it also permits to consider cases where increasing colony size increases productivity, or decreases workers mortality, as long as (α + μ) is still positive (negative effect of colony size exceeding positive effect).

Discussion

We re-analysed the model of colony growth proposed by Macevicz and Oster (1976). We derived optimal allocation strategies for both constant worker productivity and for worker productivity and mortality dependent on colony size (logistic colony growth). For the latter, an analytical approach predicts mixed strategies whenever worker productivity is sufficiently high and worker mortality is sufficiently low so that colonies can reach optimal size during the ergonomic phase. In this case, colonies will allocate all resources to colony growth until optimal colony size μ characterised by maximal colony productivity μ is reached. Thereafter allocation to worker production is restricted to replacement of dead workers. This phase will last until the expected lifetime productivity of workers becomes less rewarding than direct investment into sexuals. As all workers die at the end of the season, the expected lifetime of workers will necessarily decrease towards the end of season and their lifetime productivity will decrease accordingly. This determines the second switch to the exclusive production of sexuals.

In contrast to Oster and Wilson (1978) who predict (without further detailed investigation of this case) a sigmoid shape of the allocation function for decreasing return to scale, we predict abrupt switches between the three distinct allocation periods. In their article, Macevicz and Oster (1976) already mention that “a logistic-type density dependence (…) can exhibit graded control in certain circumstances”. To model density dependence, they introduce a decrease of productivity with increasing size of the colony. Unfortunately, they restrict the decreasing return to scale to the production of workers, whilst the production of sexuals is not affected by colony size. Thus, their model of density dependence implicitly assumes relative cost of workers to increase with increasing colony size. Fitting this model to a biological case, they concluded that the effect of non-linearity of the size/productivity relation was unlikely to explain the emergence of graded strategies. As increasing relative cost of workers may promote an abrupt switch to reproduction, when workers become too costly, this assumption is likely to account for the difference between their results and ours.

In a different model (discrete time model), Beekman et al. (1998) introduced a limitation of the egg laying rate of the queen in a bumblebee colony model. This approach would also have resulted in logistic colony growth, but the authors neglected the mortality of workers, and only allowed for bang–bang strategies (either full investment in growth or in reproduction) with a single switch. However, in their discussion, they already predicted that mortality of workers might delay the reproduction (the colony would raise more workers to compensate for the loss) or lead to colony strategies with both workers and sexuals being produced simultaneously. They also cite Greene (1984) who showed that there is a graded control in many Polistes species, and note that these species have in fact a high worker mortality. These predictions and observations meet our own conclusions.

The mixed pattern of investment predicted by our model can be considered as a “maintenance” similar to what is described in allocation models for solitary organisms (Perrin and Sibly, 1993). But most of these models consider a constant cost of maintenance with no possibility for the organism to decrease its “maintenance investment” (cf. Kozlowski and Wiegert, 1987; McCauley et al., 1990; Perrin and Sibly, 1993; Perrin et al., 1993; Lika and Nisbet, 2000). However, in insect societies maintenance permits to replace dead workers, and the mortality of workers can hardly be neglected: their life span rarely extends from the beginning till the end of the season (Schmid-Hempel and Schmid-Hempel, 1984; Strassmann, 1985). Amongst the rare analyses having included an effect similar to workers mortality, King and Roughgarden (1982a) introduced a “vegetative loss”. For the case of temporally variable productivity they analyse the influence of vegetative loss on allocation strategies in plants. In their model, however, productivity and loss are linearly related to the size of plants, and consequently, it results in bang–bang strategies only.

Some confusion might arise from the fact that what has generally been considered as “investment into growth” in experimental studies on allocation strategies in social insects is investment into the production of new workers which is not necessarily accompanied by colony growth. Hence, the “mixed investment” generally reported (cf. Greene, 1984) is sometimes only linked to worker production which is a compensation for the mortality of workers, and not an investment into further colony growth. The expressions commonly used in growth allocation studies are themselves often confusing, because different authors use different terminologies, not always with the same meaning (Perrin and Sibly, 1993). Indeed authors often use the terms “graded control” and “mixed strategies” as synonyms of “indeterminate growth”, and the term “bang–bang strategy” as synonym of “determinate growth” (i.e. King and Roughgarden, 1982b; Perrin et al., 1993), mixing up allocation pattern with the pattern of growth. With possible loss of workers, investment into the production of new workers and colony growth are not identical any more, and knowing the pattern of investment is not sufficient to determine the form of growth.

In our model, we studied the effect of a logistic growth on the sexuals versus workers allocation strategy. This logistic growth can either be caused by a decrease of per capita productivity or by an increase in worker mortality with increasing colony size. The existence of a decrease of per capita productivity has been named “Michener’s paradox” (Michener, 1964), as Michener first examined this question and pointed out that it would oppose the evolution of large insect societies. The idea of this decrease in productivity is supported by many studies (Reeve and Keller, 1999; Tschinkel, 1999; Hee et al., 2000; Clouse, 2001; Cassill, 2002; Thomas, 2003; Smith et al., 2007; Stevens et al., 2007; Tindo et al., 2008) and has been defended by many authors, based on verbal arguments (Michener, 1964; Oster and Wilson, 1978), theoretical models (Anderson and Ratnieks, 1999; Jun et al., 2003) and observations of colony growth dynamics (Oster and Wilson, 1978; Houston et al., 1988).

The existence of a decreasing per capita productivity with increasing colony size seems logic as, with limited productivity of the environment, it is evidently impossible that a colony could increase to infinity. However, as some studies failed to show any size effect (Billick, 2001; Shreeves and Field, 2002; Bouwma et al., 2006; Smith et al., 2007) it can be questioned whether insect colonies usually reach sufficiently large sizes to observe a reduction in productivity. Thus, the relation between colony size and per capita productivity is still a debated issue (Jeanne and Nordheim, 1996; Karsai and Wenzel, 1998; Bouwma et al., 2006) and the idea that synergistic effects such as the division of labour between specialised individuals may result in an increase of per capita productivity with colony size has also been defended (Jeanne, 1986; Jeanne and Nordheim, 1996; Naug and Wenzel, 2006).

This debate demonstrates the difficulty to formulate generalities for the per capita productivity, and the lack of experimental data on colony dynamics (Tschinkel, 1991; Clouse, 2001). With the data base we have so far it remains unclear if there is a general pattern for per capita productivity and colony size. Actually, the measurement of both colony size and productivity is difficult, and often destructive for colonies. This makes it necessary to compare numerous colonies at multiple stages and of many sizes (Michener, 1964; Tschinkel, 1991; Smith et al., 2007).

Moreover, there are many ways to evaluate per capita productivity (see review in Clouse, 2001), with varying significance. Productivity is evaluated, e.g., by quantity of food collected (Michener, 1964), number of provisioned nest cells (Michener, 1964; Jeanne and Nordheim, 1996; Karsai and Wenzel, 1998; Clouse, 2001, Smith et al., 2007; Tindo et al., 2008), weight of nest (Karsai and Wenzel, 1998; Clouse, 2001), number of eggs or cocoon (Michener, 1964; Billick, 2001), number of offspring (Billick, 2001; Clouse, 2001), mass of offspring (Jeanne and Nordheim, 1996; Tschinkel, 1993; Karsai and Wenzel, 1998; Clouse, 2001; Strohm and Bordon-Hauser, 2003), number of sexuals produced (Tschinkel, 1993), speed of nest reconstruction (Clouse, 2001), etc. It may be corrected by colony probability of failure (Jeanne and Nordheim, 1996; Smith et al., 2007). Sometimes per capita productivity is evaluated for many colonies at the same time or same state (e.g. Jeanne and Nordheim, 1996; Strohm and Bordon-Hauser, 2003; Tindo et al., 2008) or it is measured many times during colony development (e.g. Billick, 2001; Clouse, 2001; Strohm and Bordon-Hauser, 2003; Smith et al., 2007). The definition of per capita productivity and the methods which should be used are of course depending on the question under study. Jeanne’s request that per capita productivity should be corrected by the proportion of colony failure (Jeanne and Nordheim, 1996; Smith et al., 2007) would be relevant when asking for the evolutionarily optimal colony size. In a study on colony dynamics, colony failure must be handled separately. Correcting individual productivity by colony failure would otherwise result in an underestimation of colony growth.

The other factor which we studied as cause for logistic growth is the mortality of workers. This parameter has been studied even less than productivity, although it should be just as important in order to understand the advantages and drawbacks of sociality. Nevertheless, there are some studies that point to an increase of worker mortality with increasing colony size. Kaspari and O’Donnell (2003) have shown that there can be an increase of mortality of workers by predation, when colonies grow, and Billick (2001) showed that the mortality of workers during winter increases with colony size.

However, limitations to the growth of a colony can also be caused by other factors: i.e. limited size of cavity or shelter used for nests (Hansell, 1987; Billick, 2001), a physiological limit of egg production by the queen (Beekman et al., 1998), parasitism by pathogens (Schmid-Hempel, 1998), or social parasitism (Strohm and Bordon-Hauser, 2003). Moreover, social conflicts between members of a colony may also limit colony growth. A higher number of workers could make it more difficult for the queen to control the reproduction of sisters, or limit worker policing (Nakata and Tsuji, 1996; Kikuta and Tsuji, 1999; Strohm and Bordon-Hauser, 2003), and result in a waste of energy.

Colony size will not only affect further growth of a colony but may also influence the risk arising from predators and parasites threatening the survival of the colony as a whole (Schmid-Hempel, 1998). We did not investigate such potential relationships between colony size and the mortality of the colony. Perrin et al. (1993) studied a case of size-dependent mortality (similar to a destruction of the colony in social insects), and predicted an intermediate optimal strategy if both mortality and productivity increase or decrease with size. But their model is based on plants, and some features may not be relevant for colonies of social insects. Whilst the death of a plant will necessarily result in the death of its reproductive structures, the destruction of the colony can have different effects. It can just prevent future reproduction (but the produced sexuals can have left the colony), but it can also lead to the complete destruction of the sexuals already produced (if they stay in the nest for a time), or it can also lead to a loss of past reproduction, but allow for reconstruction of the nest and future reproduction (Strassmann et al., 1988).

Though their importance has many times been underlined (Oster and Wilson, 1978; Queller, 1989; Gadagkar, 1991), the dynamic properties of colonies are too often neglected in the study of social insects. Population dynamics interact with the evolution of characters and can lead to quite different predictions than simple optimisation models (Stearns, 2000). Thus, the allowance of colony dynamics may significantly modify the predictions for the evolution of traits such as sexual allocation, caste allocation, storage of food, and cooperation. Moreover, as the colony life cycle can itself evolve by evolution of the worker/sexuals allocation strategy, it can co-evolve with all other colony traits. This has already been shown by Bulmer (1981) for sex allocation. Including population dynamics into a model of optimal resource allocation in social insects may be an interesting extension of our approach.

In our study, we assumed that evolution tends to maximise the number of sexuals produced by a colony. However, this corresponds to maximising fitness for the queen. Depending on whether queen or workers control resource allocation, the optimal strategy can differ. This may lead to conflicts between queen and workers, or even amongst workers themselves (cf. Bulmer, 1981). A further analysis, taking into account these differences and genetic aspects could permit to deepen our understanding of intra-colony conflicts, and their changes during the lifetime of a colony.