On The Optimization of Fractional Order Low-Pass Filters

Abstract

This paper presents three different optimization cases for normalized fractional order low-pass filters (LPFs) with numerical, circuit and experimental results. A multi-objective optimization technique is used for controlling some filter specifications, which are the transition bandwidth, the stop band frequency gain and the maximum allowable peak in the filter pass band. The extra degree of freedom provided by the fractional order parameter allows the full manipulation of the filter specifications to obtain the desired response required by any application. The proposed mathematical model is further applied to a case study of a practical second- generation current conveyor (CCII)-based fractional low-pass filter. Circuit simulations are performed for two different fractional order filters, with orders 1.6 and 3.6, with cutoff frequencies 200 and 500 Hz, respectively. Experimental results are also presented for LPF of 4.46 kHz cutoff frequency using a fabricated fractional capacitor of order 0.8, proving the validity of the proposed design approach.

1 Introduction

Fractional calculus is the generalization of the integer calculus, where the same concepts of the integer calculus are applied but with wider generality. Fractional calculus, as a theory, was introduced centuries ago, but it had not been yet used in real applications till a recent time. Only a few decades ago, the fractional calculus broke through into numerous fields of science and engineering [1–4, 6–21, 23, 26–31]. Naming some of such fields, the fractional calculus shared in control engineering [6, 15], robotics [4], electromagnetics [23], biomedical [12] and electrical engineering [16–19, 26–28].

One of the most frequently used definitions for the general fractional derivatives is the Caputo definition [14] described by:

$$\begin{aligned} {D}_0^{\alpha } {f}( {t} )=\frac{1}{{\Gamma }( {{m}-{\alpha }} )}\int \limits _{0}^{\mathrm{t}} {f}^{({{m}} )}( {u} )( {{t}-{u}} )^{{{m}}-{\alpha }-1}{\hbox {d}u}, \end{aligned}$$

(1)

where $\alpha$ is the fractional order, m is an integer, such that $( {{m}-1} )<\alpha <m$, and ${\Gamma }( . )$ is the gamma function.

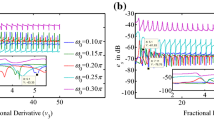
Figure 1 shows the fractional derivative of the functions; $f( x )=x$ in Fig. 1a and $f( x )={\sin }( x )$ in Fig. 1b, when $0\le \alpha \le 1$. The conventional cases are obtained at $\alpha =0\; \& \; \alpha =1$. There is a closed form to calculate the fractional derivative of $f( x )=x$ such that $( {{D}_0^{\alpha } {x}=x^{1-{\alpha }}/{\Gamma }( {2-{\alpha }} )})$. The generalized differentiation of $f( x )={\sin }( x )$ is shown in Fig. 1b, where it can be noticed that the phase of the sine function is shifted in a proportional way with the fractional order ${\alpha }$ as illustrated. The function starts as a sine wave at $\alpha =0$ and moves till it reaches the cosine shape at $\alpha =1$, as known as the integer differentiation of the sine function.

Fig. 1

The fractional derivative of a $f( x)=x$, and b $f( x)={\sin }( x)$

By taking the Laplace transform of (1) under zero initial conditions, the concept of the fractance device can be deduced as follows:

$$\begin{aligned} \mathcal{L}\left\{ {{D}_0^{\alpha } {f}( {t} )} \right\} ={s}^{{\alpha }}\mathcal{L}\left\{ {{f}( {t} )} \right\} \end{aligned}$$

(2)

Based on this transformation, the conventional elements such as resistor, capacitor and inductor are considered as special cases corresponding to ${\alpha }=0,-1$ and 1, respectively. The fractance device, or the so-called constant phase element (CPE), has a constant phase angle, which is independent of frequency, over a wide frequency range.

Figure 2 shows some attempts of the fractance device realization. Figure 2a shows how the half-order capacitor was approximated by the self-similar RC tree, in recursive structure [13]. It was also realized by developing fractal structures on silicon [10] as illustrated in Fig. 2c. Another fabrication process was reported in [1], by providing a thin coating of PMMA film on the electrode surface of a capacitive type probe, as illustrated in Fig. 2b. The fractal admittance was simulated by using some circuits, composed of finite number of conventional elements, like resistance R, capacitor C and inductor L, based on the distributed relaxation time models [21, 29]. Figure 2d shows the equivalent RC tree approximation of the fractional order capacitor, with any order ${\alpha }$. The minimum necessary number of elements’ pairs is illustrated in [21], achieving a bandwidth of 5 decades, with a phase angle error of $\pm 1^{\circ }$, when $| {\alpha } |\in [{0.1-0.9} ]$. For ${\alpha }>1$, the fractional order capacitor (FC) can be realized with the generalized impedance converter (GIC), depicted in Fig. 2e. The fractional order inductor can be also realized using the GIC [22]. Figure 2f shows another way of realizing the fractional inductor with the same order, using a gyrator terminated by a grounded FC, followed by another gyrator.

Fig. 2

Fractional realization of a half-order capacitor with tree implementation, b half-order capacitor with chemical reaction probe, c half-order capacitor with fractal structures, d any general fractional order capacitor with ladder structure, e fractional elements with order ${\alpha }>1$ with generalized impedance converter (GIC) and f fractional elements with order ${\alpha }>1$ with gyrator

Recently, the basic design procedures of the fractional order sinusoidal oscillators, filters and electromagnetic circuits have been modified based on the new fundamentals of the fractional calculus [7, 8, 16–19, 26–28]. The design of the conventional integer order filters is limited to 1st, 2nd, 3rd,...etc. orders, whereas the design of fractional order filters enables the designers to implement any arbitrary filter order such as 1.5 or 2.6. Fractional order filters were first proposed in [18], where the design procedures of the low-pass, high-pass, band-pass and all-pass filters with a single fractional element were introduced. In addition to that, the expressions of the pole frequencies, the quality factor, the right-phase frequencies, and the half power frequencies were derived. The design of the fractional order filter was investigated in a more generalized way in [19], where a fractional order filter design with two fractional elements of the same order was presented.

A fractional order filter design, with dependent orders related by a ratio k, was introduced in [26]. Frequency transformations from the fractional low-pass filter to both fractional high-pass and band-pass filters were also discussed in that work. Two different CCII-based fractional order filters were introduced in [27]. A general procedure to obtain Butterworth filter specifications in the fractional order domain was presented in [28]. The necessary and sufficient condition for designing a fractional order Butterworth filter with a specific cutoff frequency was also derived as a function of the orders. All the fractional order designs proved that the integer order is a very narrow subset from the fractional order domain. Some optimization routines were used in the fractional order low-pass filter design field like in [11], while an approximated fractional order Chebyshev low-pass filter design was introduced in [8].

However, it is easier for practical engineers to use the integer order filters due to the availability of the integer order capacitors in market, as well as the complexity faced in manufacturing fractional ones. Nevertheless, the degree of freedom provided by using the fractional order capacitors makes the design of any fractional order filter possible. This extra degree of freedom increases the design flexibility. Actually, some attempts of manufacturing fractional capacitors already took place in the research phase [1, 9, 10, 30, 31], which will eventually lead to having market-based fractional capacitors, facilitating the design of fractional order circuits later on. The huge interest of researchers in the realization of fractance devices through years offers a great significance that it will be available commercially soon enough [1, 9, 10, 13, 21, 29–31].

This paper introduces a mathematical model for fractional order low- pass filter (FLPF) design. The model provides a tool to describe the filter transition bandwidth, the stop band frequency gain and the maximum allowable peak in the pass band range of the filter. The target of this work is to perform a multi-objective optimization, to find the optimal filter coefficients with the utilization of the extra degree of freedom, provided by the fractional order parameter ${\alpha }$. Three design procedures are investigated throughout the paper: the first procedure is based on controlling the filter transition band width and the stop band frequency gain with no control on the maximum allowable peak in the pass band. The second procedure adds more control over procedure one by introducing restrictions on the maximum peak value. The target of the first two procedures is to find the optimal solution for the desired design specifications. The third procedure implies solving the nonlinear model to find a solution for the desired filter specifications.

This paper is organized as follows: Sect. 2 presents the mathematical model for the FLPF. It also discusses the design procedures for various optimum filter responses with a normalized cutoff frequency 1 rad/s. Section 3 introduces a case study of a FLPF with single negative second-generation current conveyors (CCII-), with a scaled cutoff frequency, suitable for different applications. SPICE simulations and experimental results for some optimal responses are introduced. Finally, Sect. 4 concludes the work.

2 General Specifications and Designs of FLPF

As it is well known, the ideal characteristics of the LPF are non-realizable. However, the filter design can be relaxed through designing within certain tolerable deviations from its ideal behavior as shown in Fig. 3a. Three control parameters can be manipulated to obtain a certain filter response, which are $\epsilon _1 ,\epsilon _2$ and $\epsilon _3$. These parameters, $\epsilon _1 ,\epsilon _2$ and $\epsilon _3$, represent the transition band width, the magnitude response of the stop band frequency and the maximum allowable magnitude in the pass band of the filter response, respectively.

Different filter types, high-pass filter (HPF) and band-pass filter (BPF), can be obtained if a LPF prototype is available. This is achieved using certain transformations as shown in Fig. 3b and Table 1. Figure 3b shows the system block diagram exploring the relation between the LPF, HPF and BPF using two fractional order integrators and a feedback topology. The transfer function of the generalized equal-order fractional order LPF is given by [19]:

$$\begin{aligned} {T}( {{s},{a},{b},{c},{\alpha }} )=\frac{{c}}{{s}^{2{\alpha }}+a{s}^{{\alpha }}+{b}}={}\frac{{c}}{{D}( {{s},{a},{b},{\alpha }} )}, \end{aligned}$$

(3)

where a, b, c are constants and ${\alpha }$ is the fractional order parameter. To achieve a normalized pass band gain, c must be equals to b in the transfer function. The LPF prototype can be easily transformed to HPF with the same fractional order ${\alpha }$, by scaling the transfer function by ( 1 / s ) [26]. The new transfer functions are illustrated in Table 1. By applying the relations in Table 1, the parameters obtained for the low-pass filter, using the proposed procedure, can be simply converted to high-pass filter parameters. The transformation of LPF to a narrow band BPF is simply performed by shifting the low-pass prototype to the new center frequency. Moreover, the transfer function of the BPF $( {{T}_\mathrm{BPF} ( {s} )})$ could be obtained from the transfer function of LPF given by ${T}( {{s},{a},{b},{c},{\alpha }} )$as illustrated in Table 1.

Fig. 3

a Specifications of normalized low-pass filter and b system block diagram of HPF, BPF and LPF with two fractional order integrators and feedback

Table 1 Filter transformations

With ${s}={j}\omega$, and normalized pass band gain ($c=b)$, the following equation could be deduced:

$$\begin{aligned} {D}( {{j}\omega ,{a},{b},\alpha } )= & {} {\omega }^{2{\alpha }}\cos ( {{\alpha \pi }} )+a{\omega }^{{\alpha }}\cos \left( {\frac{{\alpha \pi }}{2}}\right) \nonumber \\&+\,{b}+{j}\left( {{\omega }^{2{\alpha }}\sin ( {{\alpha \pi }} )+a{\omega }^{{\alpha }}\sin \left( {\frac{{\alpha \pi }}{2}} \right) } \right) . \end{aligned}$$

(4)

Fig. 4

a Actual LPF specification, and b numerical simulations of the magnitude and phase responses for the FLPF with $a=0.3789$, $b =0.6695$ with different ${\alpha }$

It is important to define the basic three frequencies which govern the filter behavior depicted in Fig. 4a. The first frequency is the cutoff frequency at which the power drops to half the pass band $| {{T}( {{j}\omega _c } )} |=| {{T}( {{j}\omega _{\mathrm{pass}\;\mathrm{band}} ,{a},{b},{\alpha }} )} |/\sqrt{2}$ described as:

$$\begin{aligned} f_1 \left( {\omega _c ,a,b,\alpha } \right)= & {} \omega _c^{4\alpha } +2a\, \cos \left( {\frac{\alpha \pi }{2}} \right) \omega _c^{3\alpha } +\left( {a^{2}+2b\, \cos \left( {\alpha \pi } \right) } \right) \omega _c^{2\alpha }\nonumber \\&+\,2ab\, \cos \left( {\frac{\alpha \pi }{2}} \right) \omega _c^\alpha -b^{2}\nonumber \\= & {} 0.\end{aligned}$$

(5)

The stop band frequency which controls the slope of the transition band and is calculated by $\left| {{T}\left( {{j}\omega _\mathrm{s} ,{a},{b},{\alpha }} \right) } \right| =\epsilon _2$ which follows:

$$\begin{aligned} f_2 \left( {\omega _\mathrm{s} ,a,b,\alpha ,\epsilon _2 } \right)= & {} \omega _\mathrm{s}^{4\alpha } +2a\, \cos \left( {\frac{\alpha \pi }{2}} \right) \omega _\mathrm{s}^{3\alpha }\nonumber \\&+ \left( {a^{2}+2b\, \cos \left( {\alpha \pi } \right) } \right) \omega _\mathrm{s}^{2\alpha } +2ab \, \cos \left( {\frac{\alpha \pi }{2}} \right) \omega _\mathrm{s}^\alpha +b^{2}-\frac{b^{2}}{\epsilon _2^2 }=0.\nonumber \\ \end{aligned}$$

(6)

The maximum frequency $\omega _\mathrm{max}$ is obtained by solving the equation $(d| {T}( {j}\omega ,{a},{b},{\alpha } ) |/\hbox {d}\omega )_{\omega _\mathrm{max} } =0$, at which the magnitude response has a maximum equal to $\epsilon _3$, above the pass band gain. It can be evaluated using the following equations:-

$$\begin{aligned} f_3 \left( {\omega _\mathrm{max} ,a,b,\alpha ,\epsilon _3 } \right)= & {} \omega _\mathrm{max}^{4\alpha } +2a\, \hbox {cos} \left( {\frac{\alpha \pi }{2}} \right) \omega _\mathrm{max}^{3\alpha } +\left( {a^{2}+2b\, \hbox {cos} \left( {\alpha \pi } \right) } \right) \omega _\mathrm{max}^{2\alpha }\nonumber \\&\quad +\, 2ab\, \hbox {cos} \left( {\frac{\alpha \pi }{2}} \right) \omega _\mathrm{max}^\alpha +b^{2}\left( {1-\frac{1}{\left( {1+\epsilon _3 } \right) ^{2}}} \right) =0, \end{aligned}$$

(7a)

$$\begin{aligned} f_4 \left( {\omega _\mathrm{max} ,a,b,\alpha } \right)= & {} 2\omega _\mathrm{max}^{3\alpha } +3a\, \hbox {cos} \left( {\frac{\alpha \pi }{2}} \right) \omega _\mathrm{max}^{2\alpha } +\left( {a^{2}+2b\, \hbox {cos} \left( {\alpha \pi } \right) } \right) \omega _\mathrm{max}^\alpha \nonumber \\&\quad +\,ab\, \hbox {cos} \left( {\frac{\alpha \pi }{2}} \right) =0, \end{aligned}$$

(7b)

where $f_4 ( . )$ is used to get the maximum frequency $\omega _\mathrm{max}$, while $f_3 ( . )$ is related to the added constraint on the peak which is $( {1+\epsilon _3 } )$, as shown in Fig. 4a.

The purpose of this paper is to exploit the extra degree of freedom provided by the fractional order parameter $\alpha$, to obtain the desired filter response, which is most of the times hard to be achieved by means of integer order elements. Figure 4b illustrates some numerical solutions of the filter magnitude and phase response at fixed values of (a & b) and under three different values of $\alpha$, where different responses are obtained. Note that at $\alpha =1.2$, the response is not stable [20] which is clear from its magnitude and phase responses shown in Fig. 4b. The proposed mathematical model of the nonlinear equations expressed in (5–7) is solved to get the optimal solution of the filter coefficients. The multi-objective optimization produces a range of optimal solutions, which gives the designer the option of choosing the appropriate solution(s). The solver used throughout this paper for optimization is Fminimax which is a very common optimization function used in the MATLAB optimization toolbox. It was used to solve a highly nonlinear system of equations. The function uses the “trust-region-reflective” algorithm [5], with termination tolerances of the function value of $10^{-15}$, and the solution value of $10^{-13}$ and the condition value of $10^{-13}$. The filter is designed with a normalized frequency, $\omega _\mathrm{c} =1\,\hbox {rad}/\hbox {s}$, with a transition band window of $0.5<\epsilon _1 <1$, for different values of $\epsilon _2$ and $\epsilon _3$. Three design procedures of the four equations described in the above section are investigated in this paper, where the first two procedures are optimization ones.

2.1 Design Procedure One

This procedure focuses on the optimization of the cutoff and the stop band frequency equations only. The purpose is to control the transition bandwidth through $\epsilon _1$ and the magnitude response of the stop band frequency $\epsilon _2$, with no control on the peak to get the optimum filter coefficients a,b and fractional order $\alpha$. Therefore, the objective function is:

$$\begin{aligned} {\hbox {minmax}}_{a,b,\alpha } (f_1 ( {1,a,b,\alpha } ),f_2 ( {{\omega }_\mathrm{s} ,a,b,\alpha ,\epsilon _2 } )) \hbox {s.t.}\omega _\mathrm{s} \in [ {1,1+\epsilon _1 } ], \end{aligned}$$

(8)

where the upper and lower limits are chosen as $a,b\in [ {0.01:4} ]$, $\alpha \in [ {0:2} ]$, and $\omega _\mathrm{s} \in [ {0,2.5} ]$.

When $\epsilon _1 =1$, three different optimal solutions are extracted as depicted in Fig. 5a where the filter coefficients are displayed for each solution. The decision of choosing which optimal solution is based on the error in both the cutoff and the stop band frequency equations as illustrated in Fig. 5b.

For example, case 1, when $\epsilon _1 =1$ and $\epsilon _2 =0.065$ with initial point $[ {{a};{b};{\alpha }} ]=[0.3786; 0.8116; 0.5328]$, Fig. 6 shows the filter parameters versus the number of iterations; the optimum solution is reached after 37 iterations. It also shows the error in the cutoff and the stop band frequency equations at each iteration, where it has a maximum value at iteration 1 and reaches its minimum value at the optimal solution at iteration 37.

Fig. 5

Three optimum solutions For $\epsilon _1 =1$ versus different $\epsilon _2$, a filter coefficients, and b error in $f_\mathrm{c}$ and $f_\mathrm{s}$ equations

Fig. 6

Filter coefficients and error versus iterations for $\epsilon _1 =1$ and $\epsilon _2 =0.08$ for case 1

Figure 7 illustrates the filter response of the previous example and the error in the objective functions due to small deviations from the optimal filter coefficients. The filter response is drifting away from the required specifications as a result of the deviation from the optimal coefficients. The error in the functions $( {{f}_1 ,{f}_2 } )=( {3.21\times 10^{-8},6.33\times 10^{-8}} )$ at the optimal solution at $( {{a}_{\mathrm{opt}} ,{b}_{\mathrm{opt}} ,\alpha _{\mathrm{opt}} } )$. A $\pm$10 % deviation is added to ${a}_{\mathrm{opt}}$, while keeping the other parameters the same, results in error in $( {{f}_1 ,{f}_2 } )=( {0.014,0.821} ),( {0.0041,0.754} )$, corresponding to $0.9{a}_{\mathrm{opt}}$, and $1.1{a}_{\mathrm{opt}}$, respectively, as depicted in Fig. 7a. The deviation from ${b}_{\mathrm{opt}}$ results in errors in $( {{f}_1 ,{f}_2 } )=( {0.08,6.44} ),( {0.086,7.1} )$, corresponding to $0.9{b}_{\mathrm{opt}}$, and $1.1{b}_{\mathrm{opt}}$, respectively, as shown in Fig. 7b. Similarly, with the third optimal parameter $\alpha _\mathrm{opt}$, the error in $( {{f}_1 ,{f}_2 } )$ is depicted in Fig. 7c, and it is equal to ( 0.104, 8.92 ), ( 0.0034, 13.77 ), corresponding to $0.9\alpha _{\mathrm{opt}}$, and $1.1\alpha _{\mathrm{opt}}$, respectively.

Figure 8a shows the filter magnitude response versus the radian frequency at one of the optimal solutions when $\epsilon _1 =0.9$, with different values of $\epsilon _2$. The error in the objective functions, at each $\epsilon _2$ is depicted in Fig. 8b. One of the optimal solutions when $\epsilon _1 =0.8$, versus a range of $\epsilon _2 \in [ {0.05,0.1} ]$, is illustrated in Fig. 8d, with their corresponding magnitude response in Fig. 8c. Figure 9 shows the filter magnitude responses at $\epsilon _1 =0.7\, \& \,0.6$ versus the radian frequency and the surface of the response versus $\omega -\epsilon _2$ plane. There is no control over the maximum allowable pass band peak in this design procedure, which will be investigated in the next section.

Fig. 7

Sensitivity of filter coefficients. a ${a}_{\mathrm{opt}}$, b ${b}_{\mathrm{opt}}$, and c $\alpha _\mathrm{opt}$

Fig. 8

a Filter magnitude response for $\epsilon _1 =0.9$, b the error in the optimized functions, c filter magnitude response and d the optimal coefficients for $\epsilon _1 =0.8$

Fig. 9

Filter 3D magnitude response a $\epsilon _1 =0.7$, and b $\epsilon _1 =0.6$

2.2 Design Procedure Two

The second optimization procedure is based on the injection of $\epsilon _1$, $\epsilon _2$ and $\epsilon _3$ as inputs to the optimization tool and get the optimum filter coefficients a, b and $\alpha$, while controlling the maximum peak of the response which is equal to $\epsilon _3$. The optimization function used in this procedure is Fminimax also as in procedure one. Therefore, the objective function is:

$$\begin{aligned}&{\hbox {Minmax}}_{a,b,\alpha } (f_1 ( {1,a,b,\alpha } ),f_2 ( {{\omega }_\mathrm{s} ,a,b,\alpha ,\epsilon _2 } ),f_3 ( {\omega _\mathrm{max} ,a,b,\alpha ,\epsilon _3 } ))\nonumber \\&\qquad \qquad \hbox {s.t.}\omega _\mathrm{s} \in [ {1,1+\epsilon _1 } ],f_4 ( {\omega _\mathrm{max} ,a,b,\alpha } )=0, \end{aligned}$$

(9)

where the upper and lower limits are chosen as $a,b\in [ {0.01:4} ]$, $\alpha \in [ {0:2} ]$, and $\omega _\mathrm{s} \in [ {0,2.5} ]$. Some of the filter optimized solutions of the filter coefficients are illustrated in Table 2.

Figure 10 shows the graphs of the optimized filter parameters for different values of the inputs $\epsilon _1$, $\epsilon _2$ and $\epsilon _3$. For example, Fig. 10a shows the filter parameters for $\epsilon _1 =0.7, \epsilon _{2} =0.11$ versus a range of $\epsilon _3\in [ {0.17,0.22} ]$, while Fig. 10b is for $\epsilon _1 =0.8, \epsilon _{2} =0.1$ versus a range of $\epsilon _3\in [ {0.11,0.2} ]$. Similarly, Fig. 10c is for $\epsilon _1 =0.9, \epsilon _{2} =0.1$ versus a range of $\epsilon _3 \in [ {0.07,0.15} ]$,while Fig. 10d is for $\epsilon _1 =1, \epsilon _{2} =0.1$ versus a range of $\epsilon _3\in [ {0.05,0.15} ]$. It can be noticed that as $\epsilon _1$ is relaxed toward 1, the maximum magnitude of the peak $\epsilon _3$ decreases.

Figure 11a shows the frequency response for $\epsilon _1 =1$ and $\epsilon _{2} =0.08$ for $\epsilon _3 \in [ {0.07,0.15} ]$. The 3D filter response is also shown in Fig. 11a for the same input ranges mentioned. Figure 11b shows the 3D frequency response for $\epsilon _1 =0.9$ and $\epsilon _{2} =0.11$ for $\epsilon _3 \in [0.08,0.15$], presenting the error in the optimized functions.

Table 2 Optimized filter parameters for different $\epsilon$

Fig. 10

Optimized filter coefficients versus $\epsilon _3$ for different $\epsilon _1$ and $\epsilon _2$

Fig. 11

Filter frequency response a for different $\epsilon _3$ range 0.07 to 0.15, b 3D response for (a), c 3D response for different $\epsilon _3$ range 0.08–0.15 and d the error in the optimized functions for (c)

Fig. 12

Optimum filter parameters versus iterations starting from different initial conditions

Figure 12 shows the optimum filter coefficients versus the iterations starting from different initial conditions reaching the same solution for the design specifications $\epsilon _1 =1,\epsilon _2 =0.15$ and $\epsilon _3 =0.15$, where Fig. 12a–c are for coefficients a,b and $\alpha$, respectively. Starting from initial conditions $(a,b,\alpha ,\omega _\mathrm{max} )=(1.5,1.23,0.8,0.9),( {1,1,0.5,0.5} )$ and ( 0.5, 0.5, 1, 0.5 ). After 25 iterations, they all reach the same optimum solution, which is $(1.135254,0.639859,1.118095,0.530829)$.

A sensitivity test is done for the input values $\epsilon _1 =1$, $\epsilon _{2} =0.15$ and $\epsilon _3 =0.15$, where the optimum solution for this case is ${a}=1.135254$, ${b}=0.639859$, ${\alpha }=1.118095$ and ${\omega }_{\mathrm{max}} =0.530829$. Figure 13a shows the filter frequency response at the optimum solution of the parameter a, with the response when this parameter a is varied by $\pm$10 % of its optimum value ${a}_{\mathrm{opt}}$. Figure 13b shows also the error function of the three optimized functions ${f}_1 ,{f}_2$ and ${f}_3$, for $\pm 5\,{\%} a_\mathrm{opt}$, $\pm 10{\,\% a}_{\mathrm{opt}}$ and ${a}_{\mathrm{opt}}$. The error functions $({f}_1 ,{f}_2 ,{f}_3 )$ are equal to (0.176199, 0.667282, 0.04121) for $0.9{a}_{\mathrm{opt}}, (0.0913, 0.349, 0.0214)$ for $0.95{a}_{\mathrm{opt}}$, $(3.871\times 10^{-8},3.87\times 10^{-8},3.87\times 10^{-8})$ for ${a}_{\mathrm{opt}} , (0.0978,0.379,0.023)$ for $1.05{a}_{\mathrm{opt}}$ and (0.201975, 0.788726, 0.047464) for $1.1{a}_{\mathrm{opt}}$. As it is clarified numerically, the minimum error value is achieved at ${a}_{\mathrm{opt}}$, verifying that this is the optimum solution for the provided parameters. Similarly, Fig. 13c–f shows the sensitivity around the parameter ${b}_{\mathrm{opt}}$ and $\alpha _\mathrm{opt}$, respectively.

Fig. 13

Sensitivity of filter coefficients responses and error functions. a, b ${a}_{\mathrm{opt}}$, c, d ${b}_{\mathrm{opt}}$ and e, f $\alpha _\mathrm{opt}$

2.3 Design Procedure Three

This design procedure is based on solving the four equations described in (5–7) together in the four unknowns $\{ {a,b,\alpha ,\omega _\mathrm{max} } \}$ using the MATLAB function Fsolve given a specific $\epsilon _1 ,\epsilon _2$, and $\epsilon _3$ as:

$$\begin{aligned} \hbox {Solve}\{f_1 ( {1,a,b,\alpha } )= & {} 0,f_2 ( {1+\epsilon _1 ,a,b,\alpha ,\epsilon _2 } )=0,f_3 ( {\omega _\mathrm{max} ,a,b,\alpha ,\epsilon _3 } )= 0,\nonumber \\&\quad f_4 ( {\omega _\mathrm{max} ,a,b,\alpha } )=0\}. \end{aligned}$$

(10)

Figure 14 shows the possible solutions for some specific design specifications; such as in Fig. 14a, the filter parameters are shown for $\epsilon _1 =0.7,\epsilon _2 =0.22$ for different values of $\epsilon _3 \in [ {0.155,0.177} ]$, while Fig. 14b shows the solutions for $\epsilon _1 =0.9,\epsilon _2 =0.18$ for different values of $\epsilon _3 \in [ {0.14,0.2}$. Figure 15a shows the frequency response of the filter for $\epsilon _1 =1,\epsilon _2 =0.17$, for different values of $\epsilon _3$ ranges from 0.1 to 0.2 and its 3D response in Fig. 15b. Figure 15c presents the 3D response of the filter for $\epsilon _1 =0.9,\epsilon _2 =0.18$ versus different values of $\epsilon _3$ range 0.11 to 0.2 and the error in the functions for the same values in Fig. 15d.

In all the solutions presented whether optimized in procedure one and two or not as in procedure three, the conventional case, $\alpha =1$ is considered as a special case of the wider range of the fractional order domain. This shows the flexibility offered by the fractional order parameter for the designer to choose whatever response is required for any specific application.

Fig. 14

Filter parameters versus $\epsilon _3$ for different $\epsilon _1$ and $\epsilon _2$

Fig. 15

Filter frequency response a for different $\epsilon _3$ range 0.1–0.2, b its 3D response, c 3D response versus different $\epsilon _3$ range 0.11–0.2 and d the error in the functions for the same values

Fig. 16

a CCII-based Soliman filter, and b CCII- implementation by AD844

3 Case Study

In this section, some of the resultant optimal solutions are applied to a case study of a practical filter to prove the validity of the proposed solutions. SPICE simulation results, stability analysis and experimental results are introduced to validate the theoretical findings. The studied filter is depicted in Fig. 16a, introduced by Soliman [24, 25], and consists of a single second-generation current conveyor (CCII-), with two fractional order capacitors. The CCII- can be implemented by two AD844 as described by Fig. 16b. The filter transfer function (TF) is described by:

$$\begin{aligned} {T}( {s} )=\frac{\frac{1}{{R}_1 {R}_2 {C}_1 {C}_2 }}{{s}^{2{\alpha }}+\frac{( {{C}_1 +{C}_2 } )}{{R}_2 {C}_1 {C}_2 }{s}^{{\alpha }}+\frac{1}{{R}_1 {R}_2 {C}_1 {C}_2 }}. \end{aligned}$$

(11)

From (3) and (11), the relation between circuit component and the filter transfer function parameters are given by:

$$\begin{aligned} a=\frac{( {{C}_1 +{C}_2 } )}{{R}_2 {C}_1 {C}_2 },b=\frac{1}{{R}_1 {R}_2 {C}_1 {C}_2 }. \end{aligned}$$

(12)

The design procedure investigated in the previous section addressed the filter design at normalized cutoff frequency, so frequency scaling is needed to adjust the filter operating frequencies according to the required application. The frequency scaling is done with the assumption that all critical frequencies are scaled to a factor of ${\lambda }$ such that $\omega _\mathrm{new} ={\lambda }\omega _\mathrm{old}$, then the circuit components are scaled according to the following equation [18, 19].

$$\begin{aligned} R_\mathrm{new} =\frac{1}{\lambda ^{\alpha }}R_\mathrm{old}\; or\;C_\mathrm{new} =\frac{1}{\lambda ^{\alpha }}C_\mathrm{old} \end{aligned}$$

(13)

3.1 SPICE Simulation Results

Two optimal solutions are simulated using SPICE, and then one of them is practically built and conducted for experimental verification using a fabricated fractional capacitor as will be shown next. The SPICE macro-model of AD844 is used to simulate the CCII-. The slope of magnitude response of the fractional order filter is $-40\,{\alpha \mathrm{dB}}/{\mathrm{decade}}$.

The first filter specifications chosen to be simulated belong to design procedure two which have $( {\epsilon _1 ,\epsilon _2 ,\epsilon _3 } )=( {0.9,0.25,0.0865} )$ corresponding to $( {{a}_{\mathrm{opt}} ,{b}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}} } )=( {0.3789,0.6695,0.8} )$. With ${\alpha }<1$, the fractional order capacitor is implemented as depicted in Fig. 2d. The circuit parameters are calculated according to the relations shown in (12). To achieve cutoff frequency of 200 Hz, frequency scaling is done where the circuit parameters after the scaling are: ${C}_1 ={C}_2 =1.2\times 10^{-6}$, ${R}_1 =0.782\,\hbox {k}\Omega$ and ${R}_2 =14.586\,\hbox {k}\Omega$. The SPICE circuit simulation of this filter is shown in Fig. 17a , with the SPICE versus numerical at ${f}_\mathrm{c} =\,\hbox {Hz}$.

Fig. 17

LPF magnitude response a SPICE and SPICE versus numerical at $f_\mathrm{c} =200\,\hbox {Hz}$ and b SPICE and SPICE versus numerical at $f_\mathrm{c} =500\,\hbox {Hz}$

The second filter specifications belong to design procedure one, which has $( {\epsilon _1 ,\epsilon _2 } )=( {0.6,0.065} )$ corresponding to $( {{a}_{\mathrm{opt}} ,{b}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}} } )=( 0.931025,0.237018,1.8 )$. The maximum peak value is not controlled during this procedure as the previous simulated case. For ${\alpha }>1$, the GIC can be used with fractional order capacitor to realize the required order [22]. To achieve cut off frequency 500 Hz, the simulated parameters (after frequency scaling) are ${C}_1 ={C}_2 =1.2\times 10^{-9}$, ${R}_1 =830\,\Omega$, ${R}_2 =908\,\Omega$. Figure 17b shows the SPICE simulation, as well as the SPICE versus numerical at ${f}_\mathrm{c} =500\,\hbox {Hz}$. It is clear from the figure that there is a great agreement between the SPICE-simulated response and the numerical response obtained.

3.2 Stability Study

A study of the stability of fractional order systems was investigated in [20]. The study involved a system with characteristic equation as D(s) with two fractional capacitors of the same order. A summary of this study is demonstrated in Table 3, for different cases of stability [20]. All the optimal filter solutions in the three design procedures in Sect. 2 can be studied for stability according to Table 3. To draw the system poles, a transformation from the s-plane to the W-plane is needed according to [20]. The roots are first calculated in the W-plane, and then a mapping is done back to the s-plane, for the physical roots only, where $W={s}^{( {1/m} )}$. The poles are tracked for the case of $( {{a}_{\mathrm{opt}} ,{b}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}} } )=( {0.3789,0.6695,0.8} )$, while ${a}\in [ {0.2-0.5} ]$, with fixed ${b}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}}$. The same is done another time while ${b}\in [ {0.3-0.8} ]$, with fixed ${a}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}}$, as illustrated in Fig. 18, to ensure the system stability. It is obvious that the system is stable at the optimum points and near them as well.

Table 3 Summary of stability conditions

Fig. 18

Poles of the filter simulated case one in the W-plane and the s-plane

Fig. 19

a The practical circuit of the fractional LPF, b the measured Bode plot, and c experimental versus theoretical filter response

3.3 Experimental Results

Figure 19a shows the filter circuit implemented by two AD844 to implement the CCII-. The circuit is built on the NI ELVIS II series, and the kit used is from national instrument which is also used for measuring the filter transfer function. The filter specifications chosen to be verified experimentally are the first simulated case mentioned earlier $( {\epsilon _1 ,\epsilon _2 ,\epsilon _3 } )=( {0.9,0.25,0.0865} )$ corresponding to $( {{a}_{\mathrm{opt}} ,{b}_{\mathrm{opt}} ,{\alpha }_{\mathrm{opt}} } )=( {0.3789,0.6695,0.8} )$. To achieve a cutoff frequency of 4.467 kHz, the parameters (after frequency scaling) are chosen for an equal C design, with ${C}_1 ={C}_2 =1\times 10^{-8},{R}_1 =10\,\hbox {k}\Omega$ and ${R}_2 =200\,\hbox {k}\Omega$. These values are chosen for practical issues, since this is the available fabricated fractional capacitor of order 0.8. The scope output magnitude and phase responses of the filter are demonstrated in Fig. 19b. This shows that for the same filter specifications, the filter can be frequency-scaled to have different ranges of cutoff frequencies. Figure 19c shows the theoretical versus the experimental filter magnitude and phase responses. There is a great matching between the experimental work and the numerical analysis.

Figure 20 shows the Monte Carlo (MC) simulations for the experimental case, where the effect of a 10 % uniform random deviation in the filter coefficients a and b is investigated. The coefficients are function of the practical resistors and capacitors used according to (12). The magnitude response and the phase response are shown in Fig. 20a, b, respectively. This MC analysis is performed over 10,000 iterations.

Fig. 20

Monte Carlo analysis of the experimental case a the magnitude response, and b the phase response

4 Conclusion

The optimization of a fractional order low-pass filter is presented in this work. A mathematical model based on the optimization of a set of nonlinear equations representing the filter specifications is developed. The transition band width, the magnitude response of the stop band frequency and the maximum allowable magnitude of the filter response can all be controlled for any desired filter response according to the required application. All the filter responses achieved cannot be obtained using the ordinary integer order design method, which is a major impact of using fractional elements in designing the proposed LPF. As a case study, a CCII-based fractional LPF is designed with a cutoff frequency equal to 200 and 500 Hz after frequency scaling is performed. A practical circuit is built up for the LPF, and experimental measurements were taken for a cutoff frequency of 4.46 kHz using a fabricated fractional capacitor of order 0.8.