1 Introduction

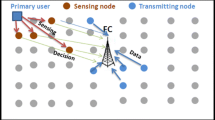
Due to the fixed natural wireless spectrum and the limited battery power of wireless sensor devices, the scarcity of the frequency spectrum and energy-efficiency of these sensor devices are the two major design parameters in any wireless sensor networks (WSNs) [10]. To address these challenges, cognitive radio (CR) is seen as a key enabling technology for the incorporation of dynamic spectrum access in the future wireless networks [20, 27], in which secondary users (SUs) are able to sense the spectrum resource, analyse the spectrum statistics, adjust their transmission parameters, and then access the licensed spectrum dynamically according to the time-varying environment [7]. In a cognitive radio network (CRN), SUs may coexist with primary users (PUs) in two ways: spectrum overlay, which allows SUs to operate only when the spectrum allocated to PUs is sensed as idle, or spectrum underlay, which means that SUs may operate under the noise floor of PUs [29]. In this paper, we focus on spectrum overlay and consider an infrastructure-based CRN, in which there exists a fusion centre (FC) that controls and coordinates the process of spectrum sensing and resource allocation [15].

In the spectrum overlay scheme, spectrum sensing is one of the essential components of CR to detect PUs efficiently and accurately [12]. Due to the multipath fading, the shadow effect, and time-varying natures of wireless channels, it is hard to achieve reliable spectrum sensing by a single SU. To combat these impacts, cooperative spectrum sensing (CSS) has been proposed to improve the spectrum-sensing performance by introducing spatial diversity [17]. The work in Ref. [5] investigated the spectrum-sensing setting for multi-channel CSS under the data fusion rule. In Ref. [24], the authors investigated how to assign SUs to sense multiple channels cooperatively with the hard decision fusion (HDF) schemes. In Ref. [25], cooperation mechanisms and the sensing accuracy-efficiency trade-off problems were elaborated. Our prior work developed an efficient multi-user cooperation framework for multi-channel spectrum sensing in the presence of an imperfect reporting channel [28]. Unfortunately, SUs’ access and transmission may always cause interference to PUs with some probability. Moreover, a well-designed resource-allocation strategy is another effective way to further improve SUs’ throughput and has been widely investigated [11]. The power control based on game theory was studied in Ref. [23] with an interference constraint. In Ref. [22], a survey of resource allocation and scheduling schemes in OFDMA wireless networks was presented. However, previous studies focus solely on the capacity optimization for SUs based on the assumption of the perfect spectrum sensing of PUs’ activities. Furthermore, the spectrum-sensing parameters which affect the spectrum-access opportunities of SUs are conventionally regarded as static and treated independently from the strategies of resource allocation and channel access.

The above spectrum-sensing challenging issues have been investigated recently by jointly considering spectrum sensing, resource allocation, and channel access. The work in Ref. [14] analysed joint optimization of CSS and power allocation in the perfect reporting channels. The work in Ref. [1] developed an adaptive power and rate allocation algorithm for a single-band CR system. In Ref. [19], the optimal power control in single-band CR based on soft decision spectrum sensing was investigated. In Ref. [18], the capacity of a SU under a received power constraint at the primary receiver in the fading environments was analysed for a single band. The work in Ref. [9] investigated the joint design of the power control policy with spectrum access control. In Ref. [16], the resource-allocation and spectrum-sensing problem jointly was formulated in a multi-user competitive setting as a non-convex game. The work in Ref. [21] jointly optimized spectrum access and power allocation in a multi-band CR system assuming that the false alarm and miss detection probabilities on all the channels are known. All these works have motivated us to investigate the joint optimization of resource-allocation configuration with multi-channel spectrum sensing and access.

On the shoulder of the previous valuable works, in this paper, we attempt to exploit the relationship between channel access and power allocation over multi-channel CSS jointly. Considering the imperfect reporting channels, a multi-channel allocation-access framework for multi-user CSS is proposed. In this framework, by exploiting the channel-access and power-allocation mechanisms in CSS, a common matrix model is derived by means of the access factor to describe the multi-user multi-channel allocation-access strategies in CRNs. To effectively assign SUs accessing multiple channels, non-convex optimization problems are formulated for maximization of the opportunistic system throughput under the restraints of the total transmit power, the aggregate interference to the primary system, and the detection probability in both the single-SU and multi-SU systems. By exploiting the hidden convexity of the optimization problems, two iterative algorithms are developed based on alternating optimization in the two scenarios. The performance of the optimal allocation-access CSS mechanism is demonstrated through theory and simulations.

The remainder of the article is organized as follows. The system model for multi-channel CSS is introduced in Sect. 2. In Sects. 3 and 4, the iterative algorithms are developed for optimization of channel-access strategies, the transmit powers, and sensing thresholds in both single-SU and multi-SU systems, respectively. Numerical simulation results are given and discussed in Sect. 5, and Sect. 6 concludes the paper.

2 System Model

Consider the CRN deployment where each geographically nearby M SUs (with the mth pair including secondary transmitter m and secondary receiver m) are interested in detecting the availability of an underutilized spectrum over the K non-overlapping narrowband channels. All the channels are licensed to one PU. Our focus is mainly on joint optimization of CSS and uplink radio resource allocation in the CRN.

Assume that the spectrum occupancy of PU is independent across channels and M SUs rely on spectrum sensing in order to access the channel. Joint of channel access and resource allocation in multi-channel CSS includes three phases: (1) a sensing phase; (2) a reporting phase; and (3) a decision phase. In the sensing phase, each SU makes a local spectrum sensing using energy detection spanning the K channels. In the reporting phase, the SUs report their sensing statistics to a FC in the presence of an imperfect reporting channel. Based on these, the FC determines how the SUs can get access to the channels and broadcasts the resource-allocation decision to SUs in the final phase. In this section, we focus on the sensing-allocation-access strategy for a single-SU case.

2.1 Spectrum Sensing

At the beginning of each time slot, each SU carries out spectrum sensing to get a test statistic for each channel. Let s(n), c, and v(n) be the PU signal, the sensing channel gain between the PU and SU, and the noise of the sensing channel (with zero mean and variance \({\sigma ^2}\)). Then, the received signal at the SU receiver, x(n), can be given in the following binary test hypothesis

$$\begin{aligned} {{\mathcal {H}}_0}:{x}(n)= & {} {v}(n) \end{aligned}$$
(1)
$$\begin{aligned} {{\mathcal {H}}_1}:{x}(n)= & {} {c}s(n) + {v}(n) \end{aligned}$$
(2)

where \(n = 1,2,\ldots ,N\). N denotes the number of samples collected during the signal observation interval (i.e., the sensing period), emphasizing that spectrum-sensing decision is made based on a limited number of signal samples [28].

Assume that the transmitted signal s(n), the channel gain c, and the additive noise v(n) are independent of one another. The channel gains of the PU–SU and SU–FC channels are assumed to be constant over each operation period of interest, which can be justified by the slow-fading nature over these links, where the delay requirement is shorter than the channel coherence time [8]. For the presentation simplicity, the power spectrum density of the primary signal on each channel at the transmitter side is normalized to be 1.

Then, the estimated energy collected by the SU in the kth channel is

$$\begin{aligned} y_k(q) = \sum \limits _{n = qN_\mathrm{s}}^{qN_\mathrm{s}+N - 1} {|x_k(n){|^2}} \end{aligned}$$
(3)

where \(N_\mathrm{s}>N\) indicates the number of samples after which a new spectrum-sensing process starts [4].

According to the central limit theorem [6], for the large N, the statistics \(\{ y_k(q)\}\) are approximately normally distributed with the means \(E(y_k(q)|{{\mathcal {H}}_i}) = N{\delta _i}\) and the variances \(\mathrm{Var}(y_k(q)|{{\mathcal {H}}_i}) = 2N\delta _i^2\), where \(i = 0,1\), \({\delta _0} = {\sigma ^2}\), and \({\delta _1} = |{c}{|^2} + {\sigma ^2}\). Then, the probabilities of false alarm and detection in the kth channel can be approximately expressed as

$$\begin{aligned} P_f({\gamma _k})= & {} Q\left( {\frac{{{\gamma _k} - N{\sigma ^2}}}{{\sqrt{2N} {\sigma ^2}}}} \right) \end{aligned}$$
(4)
$$\begin{aligned} P_\mathrm{d}({\gamma _k})= & {} Q\left( {\frac{{{\gamma _k} - N(|{c}{|^2} + {\sigma ^2})}}{{\sqrt{2N} (|{c}{|^2} + {\sigma ^2})}}} \right) \end{aligned}$$
(5)

where \(\gamma _k\) is the sensing threshold of the kth channel and \({\varvec{\gamma }} = {[{\gamma _1},{\gamma _2},\ldots ,{\gamma _K}]^T}\).

2.2 Channel Access and Resource Allocation

In the resource-allocation strategy, each SU is assigned some portion of spectrum at a certain transmission power. To describe the channel-access model in the multi-channel multi-user scenarios, a common matrix model is derived by means of the access factor \(\rho _k\), where \(\rho _k = 1\) represents the SU assigned to the kth channel and 0 otherwise.

Assume that the channel conditions (flat fading gains) of the secondary links (assumed to be flat fading), denoted as \(h_k\), can be obtained using the channel estimation techniques. Let \(p_k\) denote the allocated powers of the SU in the kth channel. The transmission of the SU over the kth channel is successful if the decision is to transmit over this channel, and no PU is actually present. Then, the aggregate transmission throughput over the K channel if used by the SU is given by

$$\begin{aligned} R(p_k,\rho _k,\gamma _k) = \sum \limits _{k = 1}^K{\left[ 1 - {P_f}(\gamma _k)\right] \rho _k\log \left( 1 + \frac{{|h_k{|^2}p_k}}{{{\sigma ^2}}}\right) } \end{aligned}$$
(6)

where \({\varvec{p}} = {[{p_1},{p_2},\ldots ,{p_K}]^T}\) and \({\varvec{\rho }} = {[{\rho _1},{\rho _2},\ldots ,{\rho _K}]^T}\).

Note that the interference over the kth channel occurs when the SU erroneously misses the presence of PU over that channel. To protect the activity of PU, the aggregate interference over the K channels should be lower than a threshold \(\epsilon \), which can be given as

$$\begin{aligned} I(p_k,\rho _k,\gamma _k) = {\sum \limits _{k = 1}^K {{\rho _k }{p_k}\left[ 1 - {P_\mathrm{d}}(\gamma _k)\right] } } \le \epsilon \end{aligned}$$
(7)

3 Multi-channel Joint Detection

In this section, a joint sensing configuration and allocation-access optimization problem is formulated and addressed in the non-cooperative multi-channel schemes. Subsequently, the non-convex problem is simplified in the several steps, and then an efficient iterative algorithm is proposed.

3.1 Problem Formulation

Here, a joint sensing-allocation-access optimization problem is addressed to maximize the aggregate transmission throughput of secondary network with a transmit power constraint while keeping the interference to PU under a certain bound. Then, the optimization problem under consideration can be formulated as

Problem P1

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{(p_k,\rho _k,\gamma _k)} \quad R(p_k,\rho _k,\gamma _k) \\ s.t. \\ \quad {C1}: \quad {P_\mathrm{d}}(\gamma _k) \ge {\bar{P}_\mathrm{d}} \\ \quad {C2}: \quad {\sum \limits _{k = 1}^K {{p_k} \rho _k\left[ 1 - {P_\mathrm{d}}(\gamma _k)\right] } } \le \epsilon \\ \quad {C3}: \quad \sum \limits _{k = 1}^K {p_k} \rho _k \le P_\mathrm{tot},\quad p_k > 0 \\ \quad {C4}: \quad \rho _k = \{ 0,1\} \\ \end{array} \end{aligned}$$
(8)

where \({\bar{P}_\mathrm{d}}\) is the minimum allowed probability of detection, and the constraint (C3) is the total transmission power constraint with the upper limit \(P_\mathrm{tot}\).

Problem P1 is not convex because the feasible sets (the interference and resource constraint) are not convex. Here, with the linear programming relaxation, the constraint (C4) can be replaced by a weaker constraint, that is, \(0 \le \rho _k \le 1\).

Note that both \(1 - {P_f}(\varvec{\gamma })\) and \(1 - {P_\mathrm{d}}(\varvec{\gamma })\) are the increasing functions of \(\varvec{\gamma }\). And the term \(1 - {P_\mathrm{d}}(\varvec{\gamma })\) should be bounded by \(1- {\bar{P}_\mathrm{d}}\). Consequently, \(R(\varvec{p},\varvec{\rho },\varvec{\gamma })\) achieves its maximal value when \(1 - {P_\mathrm{d}}(\varvec{\gamma })\) reaches its upper bound \(1- {\bar{P}_\mathrm{d}}\). Hence, we have \({P_\mathrm{d}}(\varvec{\gamma }) = {\bar{P}_\mathrm{d}}\) at the optimal point.

Then, Problem P1 can be formulated as

Problem P2

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{(p_k,\rho _k)} \sum \limits _{k = 1}^K {\left[ 1 - {P_f}({\bar{P}_\mathrm{d}})\right] \rho _k\log (1 + {\chi _k}p_k)} \\ s.t. \\ \quad C1: \quad \sum \limits _{k = 1}^K {p_k} \rho _k \le \min \left\{ P_\mathrm{tot},\epsilon /\left[ 1 - {\bar{P}_\mathrm{d}}\right] \right\} \\ \quad C2: \quad 0 \le \rho _k \le 1, \quad p_k > 0\\ \end{array} \end{aligned}$$
(9)

where \({\chi _k} = {{|{h_k}{|^2}} / {{\sigma ^2}}}\), and \({P_f}({\bar{P}_\mathrm{d}})\) can be obtained from (4) and (5) with \(P_\mathrm{d}({\gamma _k}) = {\bar{P}_\mathrm{d}}\).

Note that the objective function and all the constraints of Problem P2 are convex in \(\rho _k\) for the given \(p_k\). Thus, for a given \(p_k\), we conclude that Problem P2 is a convex function in \(\rho _k\). And for a fixed \(\rho _k\), Problem P2 is a concave function of \(p_k\), since \({\log (1 + {\chi _k}{p_k})}\) is concave in \(p_k\), and thus it has a unique solution, which can be found by exploring the Karush–Kuhn–Tucker (KKT) optimality conditions. Then, the optimal \(p_k\) is given by

$$\begin{aligned} {p_k} = {\left[ {\left[ 1 - {P_f}({{\bar{P}}_d})\right] \nu - \frac{1}{{{\chi _k}}}} \right] ^ + } \end{aligned}$$
(10)

where \((\cdot )^+=max\{\cdot ,0\}\) and the water-level \(\nu \) is chosen such that \(\sum \nolimits _{k = 1}^K {p_k} \rho _k =\min \{P_\mathrm{tot},\epsilon /[1 - {\bar{P}_\mathrm{d}}]\}\).

Using (10), the global optimal solution for the maximum aggregate transmission throughput can be found by computing the optimal \(\varvec{p}\) for all the possible choices (\(2^K\)) of \(\varvec{\rho }\). Due to the high complexity of this exhaustive search approach, a suboptimal and efficient algorithm is derived to solve Problem P2 in the next section.

3.2 Iterative Algorithm

There are two kinds of unknowns in Problem P2: the access factor \(\varvec{\rho }\) and the allocated power \(\varvec{p}\). Here, based on the alternating optimization concept [2], we apply the iterative method to achieve a good balance between the unknowns. Since Problem P2 is convex with respect to \(\varvec{\rho }\) and \(\varvec{p}\), the two optimization convex problems can be solved iteratively with the low complexity.

The proposed iterative optimization algorithm for solving Problem P2 is summarized in Algorithm 1. Algorithm 1 is initialized with the equal powers and equal channel-access strategies in all the channels. In each iteration, the optimal \(\varvec{\rho }\) is found for the previously computed \(\varvec{p}\), which can be found from (10) with the fixed \(\varvec{\rho }\). Then, the optimal \(\varvec{p}\) is found for the \(\varvec{\rho }\) obtained by using the efficient numerical techniques such as the interior point method [3] in the previous iteration. \(\varsigma \) is a termination tolerance. Experimentally we have found \(\varsigma =10^{-8}\) to be a good choice.

figure a

Lemma 1

For any choice of system parameters and any feasible initial point of Problem P2, we have:

  1. (a)

    \(R(\varvec{p^{(j)} },\varvec{\rho ^{(j)} })\) is upper bounded, i.e.,

    $$\begin{aligned} R(\varvec{p^{(j)} },\varvec{\rho ^{(j)} }) \le \sum \limits _{k = 1}^K {[1 - {P_f}({\bar{P}_\mathrm{d}})]\log (1 + {\chi _k}{P_\mathrm{tot}})}. \end{aligned}$$
  2. (b)

    \(R(\varvec{p^{(j)} },\varvec{\rho ^{(j)} })\) is non-decreasing in j, i.e.,

    $$\begin{aligned} R(\varvec{p^{(j)} },\varvec{\rho ^{(j)} }) \le R(\varvec{p^{(j)} },\varvec{\rho ^{(j+1)} }) \le R(\varvec{p^{(j+1)} },\varvec{\rho ^{(j+1)} }). \end{aligned}$$
  3. (c)

    Algorithm 1 converges to some \({R^*} = {\lim _{j \rightarrow \infty }}R(\varvec{p^{(j)} },\varvec{\rho ^{(j)} })\).

Proof

Please refer to 1. \(\square \)

Assume that \(\xi \) is the repeated times of the loop in Step 2 for convergence. Experimentally we have found that \(\xi \le 5\) is usually sufficient to obtain the optimal solution. Thus, because of the interior point method [3], the computational complexity of the proposed iterative algorithm is much lower than the exhaustive search method.

4 Cooperative Multi-channel Joint Detection

In this section, we present a cooperation framework for the multi-channel allocation-access CSS, within which SUs can exploit spatial diversity by exchanging local sensing results in order to obtain a more accurate estimate of the unused frequency bands.

4.1 Cooperative Spectrum Sensing

At the nth time instant, let \({c_m^k}\) be the kth sensing channel gain between PU and the mth SU; \({v_m^k}(n)\) be the kth sensing channel noise, which is assumed to be additive white Gaussian with zero mean and variance \(\sigma _v^2\); and \({x_m^k}(n)\) be the PU signal received at the mth SU receiver in the kth sensing channel. Then, the sensing task at any arbitrary SU is formulated as the binary hypothesis test

$$\begin{aligned} {{\mathcal {H}}_0}:{x_m^k}(n)= & {} {v_m^k}(n) \end{aligned}$$
(11)
$$\begin{aligned} {{\mathcal {H}}_1}:{x_m^k}(n)= & {} {c_m^k}s(n) + {v_m^k}(n) \end{aligned}$$
(12)

where \(m = 1,2,\ldots ,M\), \(k = 1,2,\ldots ,K\), and \(n = 1,2,\ldots ,N\).

Then, the estimated energy collected by the mth SU in the kth channel is

$$\begin{aligned} y_m^k(q) = \sum \limits _{n = qN_\mathrm{s}}^{qN_\mathrm{s}+N - 1} {|x_m^k(n){|^2}} \end{aligned}$$
(13)

where \(N_\mathrm{s}>N\) indicates the number of samples after which a new spectrum-sensing process starts.

Assume that the transmitted signal s(n), the channel gain \({c_m^k}\), and the additive noise \({v_m^k}(n)\) are independent of one another. According to the central limit theorem [6], for the large N, the statistics \(\{ y_m^k(q)\}\) are approximately normally distributed with the means \(E(y_m^k(q)|{{\mathcal {H}}_i}) = N{\varDelta _i}\) and the variances \(Var(y_m^k(q)|{{\mathcal {H}}_i}) = 2N\varDelta _i^2\), where \(i = 0,1\), \({\varDelta _0} = {\sigma ^2}\), and \({\varDelta _1} = |{c_m^k}{|^2} + {\sigma ^2}\).

After the statistics \(\{ y_m^k(q)\}\) are transmitted by SUs to the FC through the multipath fading reporting channels, FC will then give a sensing decision with the soft decision fusion (SDF). Assume that the transmissions of the different SUs are orthogonal to one another. The base-band signal at the RF front-end of the FC received from the mth SU can be written as

$$\begin{aligned} q_m^k(n) = \sum \limits _{l = 0}^{{L_g} - 1} {y_m^k(n - l){g_m}(l)} + {u_m}(n) \end{aligned}$$
(14)

where l is the arbitrary sampling instant, the reporting channel noises \({u_m}(n)\) are assumed to be zero mean and spatially uncorrelated additive white Gaussian with variances \({\sigma ^2}\), and \({g_m}(l)\) is the finite multipath channel impulse response with length \(L_g\).

The use of the additive white Gaussian noise model in this work is justified by the slow-changing nature of the channels between the M SUs and their corresponding FC links. Assume that the transmissions of the different SUs are orthogonal to one another and that the transmitted statistics \(\{ y_m^k\} \) are independent of the additive noise \({u_m}(n)\) [28]. Since \(\{ y_m^k\} \) are the normal random variables due to CLT, \({q_m^k}\) are the Gaussian random variables. By considering the hypotheses in (11) and (12), the received signal at the FC can be approximately normally distributed with the means

$$\begin{aligned} E(q_m^k|{{\mathcal {H}}_i}) = N{\varDelta _i}\sum \limits _{l = 0}^{{L_g} - 1} {{g_m}(l)} \end{aligned}$$
(15)

and the variances

$$\begin{aligned} \mathrm{Var}(q_m^k|{{\mathcal {H}}_i}) = 2N\varDelta _i^2\sum \limits _{l = 0}^{{L_g} - 1} {g_m^2(l)} + {\sigma ^2} \end{aligned}$$
(16)

All the individual test statistics \(\{ q_m^k\}\) are used to formulate the resultant detection statistics \(\{ {T^k}\} \) linearly, which can be expressed as

$$\begin{aligned} {T^k} = \sum \limits _{m = 1}^M {\omega _m^kq_m^k} \quad { \mathop {\lessgtr }\limits _{\mathcal {H}_1}^{\mathcal {H}_0}} \quad {\gamma _k} \end{aligned}$$
(17)

where \({\gamma _k}\) is the decision threshold of the kth channel, and the weighting coefficient \(\omega _m^k\) is the combining coefficients for the kth channel.

Then, the probabilities of false alarm and detection in the kth channel can be approximately expressed as

$$\begin{aligned} P_f(\omega _m^k,{\gamma _k})= & {} Q\left( {\frac{{{\gamma _k} - E({T^k}|{{\mathcal {H}}_0})}}{{\sqrt{Var({T^k}|{{\mathcal {H}}_0})} }}} \right) \end{aligned}$$
(18)
$$\begin{aligned} P_\mathrm{d}(\omega _m^k,{\gamma _k})= & {} Q\left( {\frac{{{\gamma _k} - E({T^k}|{{\mathcal {H}}_1})}}{{\sqrt{Var({T^k}|{{\mathcal {H}}_1})} }}} \right) \end{aligned}$$
(19)

where \(E({T^k}|{{\mathcal {H}}_i})\) and \(\mathrm{Var}({T^k}|{{\mathcal {H}}_i})\) are the means and variances of \(\{ {T^k}\}\), respectively, that is,

$$\begin{aligned} E({T^k}|{{\mathcal {H}}_i})= & {} N{\varDelta _i}\sum \limits _{l = 0}^{{L_g} - 1} {{g_m}(l)} \sum \limits _{m = 1}^M {\omega _m^k} \end{aligned}$$
(20)
$$\begin{aligned} \mathrm{Var}({T^k}|{{\mathcal {H}}_i})= & {} \left[ 2N\varDelta _i^2\sum \limits _{l = 0}^{{L_g} - 1} {g_m^2(l)} + {\sigma ^2}\right] \sum \limits _{m = 1}^M {{{(\omega _m^k)}^2}} \end{aligned}$$
(21)

4.2 Channel Access and Resource Allocation

In the resource-allocation strategy, each SU is assigned some portion of spectrum at a certain transmission power. To describe the channel-access model in multi-channel multi-user scenarios, a common matrix model is derived by means of the access factor \(\rho _m^k\), where \(\rho _m^k = 1\) represents the mth SU assigned to the kth channel and 0 otherwise. Assume that each SU is assigned to access several different channels, with each channel being assigned to at most one SU. The mathematical model for this scenario can be given as

$$\begin{aligned} \left\{ \begin{array}{l} \sum \limits _{m = 1}^M {\rho _m^k \le 1} \quad \mathrm{for} \; k = 1,2,\ldots ,K \\ \sum \limits _{k = 1}^K {\rho _m^k \le K} \quad \mathrm{for} \; m = 1,2,\ldots ,M \\ \rho _m^k = \{ 0,1\} \\ \end{array} \right. \end{aligned}$$
(22)

In the design of an efficient distributed cooperative sensing system, the goal is to maximize the system performance measure of interest by controlling the weight coefficient matrix \(\varvec{\omega }\) and the threshold vector \(\varvec{\gamma }\). Just as we did in the previous section, we would like to maximize the opportunistic throughput while satisfying some constraints on the interference to the primary communication system.

Assume that channel conditions (flat fading gains) of secondary links (assumed to be flat fading), denoted as \(h_m^k\), can be obtained using the channel estimation techniques. Let \(p_m^k\) denote the allocated powers of the mth SU in the kth channel. The transmission of the mth SU over the kth channel is successful if the decision is to transmit over this channel and no PU is actually present. Then the (maximum) transmission throughput over the kth channel if used by the mth SU is given by

$$\begin{aligned} R_m^k(p_m^k,\rho _m^k,\omega _m^k,{\gamma _k}) = \left[ 1 - {P_f}(\omega _m^k,{\gamma _k})\right] \rho _m^k\log \left( 1 + \frac{{|h_m^k{|^2}p_m^k}}{{{\sigma ^2}}}\right) \end{aligned}$$
(23)

4.3 Problem Formulation

Consequently, the spatial-spectral joint detection problem is formulated as

Problem P3

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{\left( p_m^k,\rho _m^k,\omega _m^k,\gamma _k\right) } \quad R(p_m^k,\rho _m^k,\omega _m^k,{\gamma _k}) \\ s.t. \\ \quad C1: \quad {P_\mathrm{d}}(\omega _m^k,{\gamma _k}) \ge {\bar{P}_\mathrm{d}} \\ \quad C2: \quad \sum \limits _{k = 1}^K {\sum \limits _{m = 1}^M {\rho _m^kp_m^k\left[ 1 - {P_\mathrm{d}}(\omega _m^k,{\gamma _k})\right] } } \le \epsilon \\ \quad C3: \quad \sum \limits _{k = 1}^K {p_m^k} \rho _m^k \le P_m^\mathrm{tot},\quad p_m^k > 0 \\ \quad C4: \quad \sum \limits _{m = 1}^M {\rho _m^k \le 1} , \quad k = 1,2,\ldots ,K \\ \quad C5: \quad \sum \limits _{k = 1}^K {\rho _m^k \le K} , \quad m = 1,2,\ldots ,M \\ \quad C6: \quad \rho _m^k = \{ 0,1\} \\ \end{array} \end{aligned}$$
(24)

where the constraint (C2) is the aggregate interference over the kth channels with a pre-specified bound \(\epsilon \), and the constraint (C3) is the total transmit power constraint of the mth SU with the upper limit \(P_m^\mathrm{tot}\).

In this scheme, the FC makes the sensing decision by fusing the individual decisions with the soft fusion rules. Here, two conventional SDF optimization schemes for weighting vector setting are presented, namely equal gain combination (EGC) and maximal ratio combining (MRC) [13]. The MRC-based scheme assigns the fractional coefficient weights relative to the corresponding SNR values at the SUs’ receivers with \(\omega _{m,0}^k = SN{R_m} = {{|{c_m^k}{|^2}} / {{\sigma ^2}}}\). In the EGC scheme, the individual weights assigned to the SU signals at the FC are all equal to \(\omega _{m,0}^k = \sqrt{1/M} \). By introducing the variable \(\chi _m^k = {{|h_m^k{|^2}} / {{\sigma ^2}}}\), Problem P3 can be expressed as

Problem P4

$$\begin{aligned} \begin{array}{l} \mathop {\max }\limits _{(p_m^k,\rho _m^k)} \quad R(p_m^k,\rho _m^k) \\ s.t. \\ \quad C1: \quad \sum \limits _{k = 1}^K {\sum \limits _{m = 1}^M {\rho _m^kp_m^k} } \le \min \left\{ \epsilon /[1 - {\bar{P}_\mathrm{d}}],\sum \limits _{m = 1}^M {P_m^\mathrm{tot}} \right\} \\ \quad C2: \quad 0 \le \rho _m^k \le 1, \quad p_m^k > 0 \\ \end{array} \end{aligned}$$
(25)

where \({P_f}(\omega _{m,0}^k,{\bar{P}_\mathrm{d}})\) can be obtained from (18) and (19) with the given \(\omega _{m,0}^k\) and \(P_\mathrm{d}(\omega _{m,0}^k,{\gamma _k}) = {\bar{P}_\mathrm{d}}\).

Although Problem P4 is a non-convex optimization problem, for a fixed \({\varvec{\rho } _m}\), \(m=1,\ldots ,M\), Problem P4 is convex. Thus, from the KKT conditions, the optimal solution can be obtained as

$$\begin{aligned} p_m^k = {\left[ {\left[ 1 - {P_f}(\omega _{m,0}^k,{{\bar{P}}_d})\right] \nu - \frac{1}{{\chi _m^k}}} \right] ^ + } \end{aligned}$$
(26)

where the water-level \(\nu \) is chosen to guarantee \(\sum \nolimits _{k = 1}^K {\sum \nolimits _{m = 1}^M {\rho _m^kp_m^k} } = \min \{\epsilon /[1 - {\bar{P}_\mathrm{d}}]\).

Thus, the global optimal solution of Problem P4 can be found by computing \(\varvec{p}_m\), \(m=1,\ldots ,M\), based on (26) for all the \(2^{MK}\) possible choices of \({\varvec{\rho } _m}\). Similar to the iterative algorithm in Sect. 3, a suboptimal iterative algorithm for solving Problem P4 will be proposed in the next subsection.

4.4 Iterative Algorithm

In Problem P4, for a fixed \({\varvec{\rho } _m}\), the optimal transmit powers \(\varvec{p}_m\) can be obtained from (26). Moreover, for a fixed \(\varvec{p}_m\), Problem P4 can be considered as M independent subproblems (one subproblem for each SU). By solving these M subproblems, the optimal access factor of each sensing SU is obtained for the fixed power-allocation scheme.

Since the M subproblems are identical with Problem P2 in structure, Algorithm 2 is proposed for solving Problem P4 based on the concept of Algorithm 1. In Step 1 of Algorithm 2, we choose a feasible starting point with the equal powers and equal channel-access strategies in all the channels. In the first iteration, the optimal access factor for each SU is obtained in Step 5. And then, for the given access factor, the optimal power-allocation schemes are computed using the waterfilling method (26) in Step 6. Unlike the access factor optimization, the power-allocation optimization is performed jointly for all the sensing SUs. \(\varsigma \) is a termination tolerance. Experimentally we have found \(\varsigma =10^{-8}\) to be a good choice. Assuming the algorithm converges in \(\xi \) iterations, the number of convex subproblems needed to be solved is \((M+1)\xi \). Due to the interior point method, the overall computational complexity of Algorithm 2 is much lower than that of the exhaustive algorithm.

figure b

5 Simulation Results and Discussion

In this section, numerical results are presented to evaluate the performance of the proposed allocation-access CSS mechanism. In our evaluation, we consider a set of SUs sensing the spectrum over \(N=800\) sampling intervals with equal noise variance \({\sigma ^2} = 1\). Notice that \({g_m}\), \({c_m}\), \({c_m^k}\), and \(h_m^k\) are generated randomly for each channel and each SU and assumed to be constant over every sensing time period. Assume that \(P_m^\mathrm{tot} = P_\mathrm{tot}\) for all the SUs.

5.1 Non-cooperative Multi-channel Joint Detection

Here, the performance of multi-channel joint detection with eight channels and a single SU is studied. The first important property to verify is the behaviour of the objective function, obtained by using the optimal channel-access and power-allocation strategies, for any given detection probability value \(\bar{P}_\mathrm{d}\). Figure 1 shows the optimal aggregate transmission throughput versus \(\bar{P}_\mathrm{d}\), with different values of the maximum tolerable interference \(\epsilon \). The behaviours reported in Fig. 1 show that, for the every \(\epsilon \), there exists a value \(\bar{P}_\mathrm{d}^*\) of the detection probability that maximizes the aggregate throughput. The value \(\bar{P}_\mathrm{d}^*\) increases as the interference constraint gets stronger, i.e., \(\epsilon \) decreases.

Fig. 1
figure 1

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\)

Full size image

As an example of channel access and power allocation, the optimal strategies obtained as the solution of Problem P2 using the optimal \(\bar{P}_\mathrm{d}\) are presented in Fig. 2. Subplot (a) and subplot (b) show the optimal channel-access and power-allocation schemes corresponding to the maximum aggregate throughput for \(\epsilon =0.05\), respectively. Subplot (a) indicates that all the eight channels are assigned for the SU’s optimal opportunistic access. And the optimal power allocation in such a case is a multi-level waterfilling varying for each channel. The probability of false alarm for each channel is shown in subplot (c). Comparing with subplots (b) and (c), we can observe that the more power tends to be allocated and the lower probability of erroneous allocation \(P_{f}(\bar{P}_\mathrm{d}^*)\) is achieved, taking into account the channel transfer function as well.

Fig. 2
figure 2

Optimal channel-access and power-allocation strategies for \(P_\mathrm{tot} = 1\)

Full size image

5.2 Cooperative Multi-channel Joint Detection

Next, the scenario of two SUs cooperatively sensing-allocation-access the eight channels by exchanging the summary statistics of their sensed data is considered. Figure 3 shows the optimal power allocation with various sensing schemes: the proposed weighted cooperative sensing (EGC), the traditional unweighted cooperative sensing (HD-OR) [26], and the single-user sensing. It is observed that the spectrum-sensing algorithms with cooperation result in the higher opportunistic rates than the sensing algorithms without cooperation. In addition, the proposed weighted CSS outperforms the cooperative scheme without weighting.

Fig. 3
figure 3

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\) and \(\epsilon = 0.05\)

Full size image

5.3 Multi-channel CSS with Various Fusion Rules

Next, the performance of CSS schemes with four SUs cooperatively sensing the three channels is considered. We compare the fusion decision schemes with both soft (MRC and EGC) [13] and hard decision (HD-OR) rules. Figure 4 shows the optimal power-allocation strategy with the fusion rules under various \(\epsilon \).

As shown in Fig. 4, the better channel utilization (\(1 - {P_f}\)) is obtained when the soft decision scheme is used instead of hard decision. The MRC-based scheme shows the better performance than the EGC scheme due to its adaptability. The MRC scheme assigns the larger weights for the SUs with the high SNRs and the smaller weights for those with the low SNRs; therefore, it controls the contributions of each SU in the overall decision taken at the FC.

Fig. 4
figure 4

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\)

Full size image

5.4 Multi-channel CSS with Various Channel-Access Strategies

We then study the sensing performances with the various channel-access strategies for the four SUs cooperatively sensing the three channels under the EGC fusion rule. The CASE 1 \(\left( {\left[ {\begin{array}{*{20}{c}} {1\mathrm{{ }}0\mathrm{{ }}0\mathrm{{ }}0} \\ {1\mathrm{{ 0 0 0}}} \\ {1\mathrm{{ 0 0 0}}} \\ \end{array}} \right] ^T}\right) \) scenario describes the situation in which all the three channels are assigned for the access of the only one SU, i.e., the first SU. The CASE 2 \(\left( {\left[ {\begin{array}{*{20}{c}} {1\mathrm{{ 0 }}0\mathrm{{ }}0} \\ {\mathrm{{1 }}0\mathrm{{ 0 }}0} \\ {0\mathrm{{ }}0\mathrm{{ }}0\mathrm{{ }}1} \\ \end{array}} \right] ^T}\right) \) scenario describes that a certain SU is assigned to access more than one channels. The CASE 3 \(\left( {\left[ {\begin{array}{*{20}{c}} {1\mathrm{{ }}0\mathrm{{ }}0\mathrm{{ }}0} \\ {0\mathrm{{ }}1\mathrm{{ }}0\mathrm{{ }}0} \\ {0\mathrm{{ }}0\mathrm{{ }}0\mathrm{{ }}1} \\ \end{array}} \right] ^T}\right) \) scenario describes the situation in which each SU is assigned at most one different channel. Figure 5 plots the sensing performances of the three cases. With a certain \(\rho _m^k\) settings, simulation results verify the efficiency of the corresponding model in the channel-access scheme situations. By varying \(\rho _m^k\), the maximum aggregate throughput with the corresponding optimal power allocation could be adjusted to a different extent. The optimal \({\varvec{\rho }}\) setting achieves the optimal power-allocation and spectrum-sensing performance with the proposed joint optimization algorithms.

Fig. 5
figure 5

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\) and \(\epsilon = 0.05\)

Full size image

5.5 Performance of Optimization Algorithm

Then, the performance of the proposed joint optimization algorithms Algorithm 1 and Algorithm 2 is examined by comparing with the two other candidate algorithms. The first candidate algorithm sets the equal channel-access strategies for all the SUs and channels, and the second candidate algorithm allocates equal powers to all the channels. The maximum number of iterations in both Algorithm 1 and Algorithm 2 is set to 10. Figures 6 and 7 illustrate the throughput of the three algorithms mentioned above in both single-SU and multi-SU sensing scenarios, respectively. It is observed that, for all the algorithm schemes, as expected, there exists a value \(\bar{P}_\mathrm{d}^*\) to maximize the aggregate throughput for every \(\epsilon \). The proposed joint optimization algorithms result in the higher aggregate transmission throughput than the two other candidate algorithms.

Fig. 6
figure 6

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\)

Full size image
Fig. 7
figure 7

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\)

Full size image

5.6 Convergence Analysis of Iterative Algorithm

In Figs. 8 and 9, the convergence of Algorithms 1 and Algorithms 2 is investigated. The number of convex/waterfilling problems solved is presented in the horizontal axis, which corresponds to Steps 3–4 of Algorithms 1 and Steps 5–6 of Algorithms 2, respectively. Noticeably, the proposed iterative algorithms converge within the first five times, which shows that the computation complexity of the proposed scheme can meet the real-time requirements.

Fig. 8
figure 8

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\), \(\epsilon = 0.05\), \(\bar{P}_\mathrm{d}=0.93\)

Full size image
Fig. 9
figure 9

Optimal aggregate transmission throughput versus the detection probability for \(P_\mathrm{tot} = 1\), \(\epsilon = 0.05\), \(\bar{P}_\mathrm{d}=0.93\)

Full size image

6 Conclusion

In this paper, a multi-channel jointly CSS, channel-access, and resource-allocation approach is proposed. The channel-access model with the access factor is presented to describe the access strategies of SUs over multiple channels jointly sensing. The multi-channel joint energy detection problem with an imperfect reporting channel is formulated as an optimization problem that the SUs’ aggregate transmission throughput is maximized subject to the constraints of both the interference to the PU and the transmit power consumption. Non-convex problems are formulated for optimization of the sensing thresholds, transmit powers, and access factor strategies in both single and multiple CR systems. Based on the alternating optimization concept, the efficient iterative algorithms are developed to find the global optimal solution. Simulation results show that joint optimization of spectrum sensing, channel access, and power allocation can achieve the better aggregate transmission throughput of SUs compared with equal power-allocation and equal channel-access strategy.