1 Introduction

Two-dimensional(2-D) systems have received considerable attention due to their extensive applications of both theoretical and practical interest in the past several decades [5, 9, 14]. The key feature of a 2-D system is that the information is propagated along two independent directions. Many physical processes, such as image processing [1], signal filtering [8], and thermal processes in chemical reactors, heat exchangers and pipe furnaces [9], have a clear 2-D structure. The 2-D system theory is frequently used as an analysis tool to solve some problems, e.g., iterative learning control [7, 11] and repetitive process control [4, 16]. However, the analysis and synthesis approaches for 2-D systems can not simply extend from existing standard (1-D) system theories because there are many 2-D system phenomena which have no 1-D system counterparts. Thus the study of 2-D systems is an interesting and challenging topic, and a lot of results have been published in the literature. Among these results, Hinamoto [6] established a sufficient condition of the asymptotic stability for 2-D systems, Chen et al. [2] investigated the problem of stability analysis and stabilization for 2-D discrete fuzzy systems via basis-dependent Lyapunov functions, Sebek [15] first addressed the H ∞ control problem for 2-D systems, Du and Xie [3] presented a linear matrix inequality approach to establish several versions of 2-D bounded real lemma.

Delay systems represent a class of infinite dimensional systems largely used to describe propagation and transport phenomena [10]. In some physical processes which are intrinsically 2-D characteristic, delays appear in a natural way since information transmission along time and/or space requires the process of spreading, the presence of delays in a controlled process can also simplify the corresponding process model. Therefore, the control problem for 2-D state delay systems has received some attention. Paszke et al. [12] presented a sufficient stability condition and a stabilization method for linear 2-D discrete state delay systems. Xu et al. [17] proposed an approach to design the optimal H ∞ controller for 2-D discrete state delay systems. However, the above mentioned results on 2-D discrete state delay systems mainly adopted the delay-independent methods, and are more conservative since the delay usually possesses an upper bound in practice. It is worth addressing the delay-dependent stability and H ∞ control problems of 2-D discrete state-delayed systems when the upper bound of the delay can be measured. Xu et al. [18] and Peng et al. [13], respectively, devised a delay-dependent H ∞ state feedback control method and a delay-dependent H ∞ output feedback control method for 2-D state-delayed systems described by the Fornasini–Marchesini (FM) second model. There are no delay-dependent H ∞ control results for 2-D systems in the Roesser model.

In this paper, we first propose a delay-dependent approach to investigate the H ∞ control problem for 2-D discrete state delay systems in the Roesser model. Based on a summation inequality, a sufficient condition for such a system to have a delay-dependent specified H ∞ noise attenuation is also obtained by using LMI approaches, and the condition for the existence of H ∞ controllers is obtained in terms of an LMI. An LMI convex optimization problem is formulated to design a delay-dependent optimal state feedback H ∞ controller. Finally, a simulation example of thermal processes with state delay is given to demonstrate the effectiveness of the proposed results.

2 H ∞ Performance Analysis

Consider an uncertain 2-D discrete linear system with state delay described by the following Roesser model:

(1a)
(1b)

where 0⩽i,j∈Z (where Z denotes a set of integers) are horizontal and vertical coordinates, \(x^{h}(i,j)\in\Re^{n_{1}}\) and \(x^{v}(i,j)\in\Re^{n_{2}}\) are the state vectors, u(i,j)∈ℜm is the input vector, z(i,j)∈ℜp is the noise input which belongs to ℓ 2{[0,∞),[0,∞)}, d 1 and d 2 are unknown positive integers representing delays along horizontal direction and vertical direction, respectively; A, \(A_{d_{1}}\), \(A_{d_{2}}\), B 1, B 2, H and L are constant matrices with appropriate dimensions. The initial condition is defined as follows:

(2)

For the 2-D system (1a)–(1b), assume a finite set of initial conditions, i.e., there exist positive integers L 1 and L 2, such that

$$ \left \{\begin{array}{l@{\quad}l} x(i,j)=0,& \forall j\geqslant L_2,\ i=-d_1,\ -d_1+1,\ldots,0,\\[4pt] x(i,j)=0,& \forall i\geqslant L_1,\ j=-d_2,\ -d_2+1,\ldots,0,\\[4pt] X(0)\in\ell^2,& \mbox{i.e.},\ \|X(0)\|_2<\infty.\\ \end{array} \right . $$
(3)

Denoting \(x(i,j)=[x^{h^{\mathrm{T}}}(i,j) x^{v^{\mathrm{T}}}(i,j)]^{\mathrm{T}}\) and X r =sup{∥x(i,j)∥:i+j=r,i,j∈Z}, we first introduce the definition of asymptotic stability for the 2-D system (1a)–(1b).

Definition 1

The 2-D discrete state delay system (1a)–(1b) is asymptotically stable if lim r→∞ X r =0 with u(i,j)=0, w(i,j)=0 and the initial condition (3).

In order to address the issue of the delay-dependent H ∞ performance, we first define vectors \(t^{h}(i,j)\in\Re^{n_{1}}\) and \(t^{v}(i,j)\in\Re^{n_{2}}\), such that

$$ \left\{ \begin{array}{l} x^h(i+1,j)=x^h(i,j)+t^h(i,j), \\[4pt] x^v(i,j+1)=x^v(i,j)+t^v(i,j). \\ \end{array}\right. $$
(4)

and introduce the following lemma.

Lemma 1

[18]

For any matrices M 1,M 2∈ℜn×n and 0<X∈ℜn×n, and any integer d⩾0, the following summation inequality holds:

(5)

where

$$ \xi(i,j)=\begin{bmatrix} x^h(i,j) \\ x^h(i-d,j) \\ \end{bmatrix},\quad\quad Y=\begin{bmatrix} M_1 \quad M_2 \\ \end{bmatrix}. $$

Definition 2

Consider the uncertain 2-D system (1a)–(1b) with zero input u(i,j)=0 and the initial condition (3). Given a scalar γ>0, integers \(d_{1}^{*}>0\), \(d_{2}^{*}>0\), and symmetric positive definite weighting matrices Q h , \(W_{h}\in\Re^{n_{1}\times n_{1}}\) and Q v , \(W_{v}\in\Re^{n_{2}\times n_{2}}\), the 2-D discrete state delay system (1a)–(1b) with any delays d 1 and d 2 satisfying \(0< d_{1}\leqslant d_{1}^{*}\) and \(0< d_{2}\leqslant d_{2}^{*}\) is said to have an H ∞ noise attenuation γ if it is asymptotically stable and satisfies

$$ \mathcal{J}=\sup_{0\neq (w,X(0)) \in\ell_2}\frac{\|z\|^2_2}{\|w\|^2_2+D_1(d_1^*,j)+D_2(i,d_2^*)}<\gamma^2, $$
(6)

where

The following theorem presents a sufficient condition for the 2-D discrete state delay system (1a)–(1b) with \(0< d_{1}\leqslant d_{1}^{*}\) and \(0< d_{2}\leqslant d_{2}^{*}\) to have a specified H ∞ noise attenuation.

Theorem 1

Given a scalar γ>0 and integers \(d_{1}^{*}>0\) and \(d_{2}^{*}>0\), the 2-D discrete state delay system (1a)–(1b) with u(i,j)=0, \(0< d_{1}\leqslant d_{1}^{*}\), \(0< d_{2}\leqslant d_{2}^{*}\) and the initial condition (3) has an H ∞ noise attenuation γ if there exist matrices \(M_{11}\in\Re^{n_{1}\times n_{1}}\), \(M_{12}\in\Re^{n_{1}\times n_{1}}\), \(M_{21}\in\Re^{n_{2}\times n_{2}}\), \(M_{22}\in\Re^{n_{2}\times n_{2}}\), and symmetric positive definite matrices \(P_{h}\in\Re^{n_{1}\times n_{1}}\), \(P_{v}\in\Re^{n_{2}\times n_{2}}\), \(R_{h}\in\Re^{n_{1}\times n_{1}}\), \(R_{v}\in\Re^{n_{2}\times n_{2}}\), satisfying 0<P h <γ 2 Q h , 0<P v <γ 2 Q v , 0<R h <γ 2 W h , 0<R v <γ 2 W v and

(7)

where

Proof

Define the following Lyapunov–Krasovskii functional for the 2-D system (1a)–(1b):

$$ V \bigl(x(i,j) \bigr)=V_h \bigl(x^h(i,j) \bigr)+V_v \bigl(x^v(i,j) \bigr), $$
(8)

where

and P h >0, P v >0, R h >0, R v >0. It is clear that V(x(i,j)) is positive. Along any trajectory of the system (1a)–(1b) with u(i,j)=0 and w(i,j)=0 the increment △V(x(i,j)) is given by

(9)

Using (4), we have

(10)

Applying Lemma 1, we have the following summation inequalities:

(11)

and

(12)

Substituting (10)–(12) into (9), applying the Schur complement, it follows from the LMI (7) that

$$ V_h \bigl(x^h(i+1,j) \bigr)+V_v \bigl(x^v(i,j+1) \bigr)\leqslant V_h \bigl(x^h(i,j) \bigr)+V_v \bigl(x^v(i,j) \bigr), $$
(13)

holds for any delays d 1 and d 2 satisfying \(0 < d_{1}\leqslant d_{1}^{*}\) and \(0 < d_{2} \leqslant d_{2}^{*}\), where the equality sign holds only when x(i,j)=0.

Let D(r) denote the set defined by

$$ D(r)\triangleq \bigl\{(i,j):i+j=r, i\geqslant 0, j\geqslant 0 \bigr\}. $$
(14)

For any integer r⩾max{L 1,L 2}, it follows from (13) and the initial condition (3) that

(15)

where the equality sign holds only when

$$ \sum_{(i+j)\in D(r)}V\bigl(x(i,j)\bigr)=0. $$

This implies that the whole energies stored at the points {(i,j):i+j=r+1} is strictly less than those at the points {(i,j):i+j=r} unless all x(i,j)=0. Thus, we obtain

$$ \lim_{r\rightarrow \infty }\sum_{(i+j)\in D(r)}V\bigl(x(i,j) \bigr)=0. $$
(16)

It follows that

Consequently, we conclude from Definition 1 that the 2-D discrete state delay system (1a)–(1b) is asymptotically stable for any delays d 1 and d 2 satisfying \(0 < d_{1}\leqslant d_{1}^{*}\) and \(0 < d_{2} \leqslant d_{2}^{*}\).

To establish the H ∞ performance of the 2-D system (1a)–(1b) with the control input u(i,j)=0 for w(i,j)∈ℓ 2{[0,∞),[0,∞)}, it follows from the LMI (7) such that

$$ \triangle V\bigl(x(i,j)\bigr)+z^\mathrm{T}(i,j)z(i,j)- \gamma^2w^\mathrm{T}(i,j)w(i,j)<0. $$
(17)

Therefore, for any integers T 1,T 2>0, we have

(18)

where

For T 1⩾T 2⩾max{L 1+d 1,L 2+d 2}, it follows from (13) and the initial condition (3) that

(19)

Above, the fact that

has been used.

When T 1,T 2→∞, it follows from (17)–(19) that

and

(20)

Since 0<P h <γ 2 Q h , 0<P v <γ 2 Q v , 0<R h <γ 2 W h and 0<R v <γ 2 W v , it follows from Definition 2 that the result of this theorem is true. This completes the proof. □

In the case when the initial condition is known to be zero, i.e., X(0)=0, for all non-zero w(i,j), we have

$$ \| z \|_2<\gamma\| w \|_2, $$
(21)

It follows from the 2-D Parseval’s theorem [3] that (21) is equivalent to

$$ \big\| G(z_1,z_2)\big\|_\infty = \sup_{\omega_1,\omega_2\in[0,2\pi]}\sigma_{\max}\begin{bmatrix} G(e^{j\omega_1},e^{j\omega_2}) \\ \end{bmatrix}<\gamma, $$
(22)

where σ max(⋅) denotes the maximum singular value of the corresponding matrix, and

$$ \begin{array}{l} G(z_1,z_2)=H( \operatorname{diag} \{z_1I_{n_1},z_2I_{n_2}\}-A-[z_1^{-d_1}A_{d_1} z_2^{-d_2}A_{d_2}])^{-1}B_1+L \\ \end{array} $$
(23)

is the transfer function from the noise input w(i,j) to the controlled output z(i,j) for the 2-D system (1a)–(1b).

3 H ∞ Controller Design

Consider the 2-D state delay system (1a)–(1b) and the following controller:

$$ u(i,j)=Kx(i,j) =\left [\begin{array}{c@{\quad}c} K_1 & K_2 \\ \end{array} \right ]\begin{bmatrix} x^h(i,j) \\ x^v(i,j) \\ \end{bmatrix}. \\ $$
(24)

The corresponding closed-loop system is given by

(25a)
(25b)

If there the controller (24) exists such that the closed-loop system (25a)–(25b) is asymptotically stable, and the H ∞ norm of the transfer function (23) from the noise input w(i,j) to the controlled output z(i,j) for the closed-loop system (25a)–(25b) is smaller than γ, then the closed-loop system (25a)–(25b) has a specified H ∞ noise attenuation γ, and the controller (24) is said to be a γ-suboptimal H ∞ state feedback controller for the 2-D state delay system (1a)–(1b) with any state delays d 1 and d 2 satisfying \(0 < d_{1}\leqslant d_{1}^{*}\) and \(0 < d_{2} \leqslant d_{2}^{*}\).

Theorem 2

Given a scalar γ>0 and positive integers \(d_{1}^{*}\) and \(d_{2}^{*}\), if there exist matrices N 11, \(N_{12}\in\Re^{n_{1}\times n_{1}}\), N 21, \(N_{22}\in\Re^{n_{2}\times n_{2}}\), \(N_{1}\in\Re^{m\times n_{1}}\) and \(N_{2}\in\Re^{m\times n_{2}}\), and symmetric positive definite matrices \(\bar{P}=\operatorname{diag}\{\bar{P}_{h},\bar{P}_{v}\}\), \(\bar{R}=\operatorname{diag}\{\bar{R}_{h},\bar{R}_{v}\}\) (where \(\bar{P}_{h}, \bar{R}_{h}\in\Re^{n_{1}\times n_{1}}\) and \(\bar{P}_{v}, \bar{R}_{v}\in\Re^{n_{2}\times n_{2}}\)), such that

(26)

where

then the closed-loop system (25a)–(25b) with \(0 < d_{1}\leqslant d_{1}^{*}\) and \(0 < d_{2} \leqslant d_{2}^{*}\) and the zero initial condition (3) has a specified H ∞ noise attenuation γ, and \(u(i, j ) = [N_{1},N_{2}] \bar{P}x(i, j )\) is a γ-suboptimal state feedback H ∞ controller for the 2-D discrete state delay system (1a)–(1b).

Proof

By applying Theorem 8 and the Schur complement, a sufficient condition for the closed-loop system (25a)–(25b) to have a specified H ∞ noise attenuation γ is that there exist matrices M 11,M 12,M 21,M 22, and symmetric positive definite matrices P h , P v , R h , R v , such that

(27)

where

It follows from (27) that M 12 and M 22 are reversible. Introducing

pre- and post-multiplying the matrix inequality (27) by the matrix \(\operatorname{diag}\{\varPhi^{\mathrm{T}},I, I,I, I, d_{1}^{*}I,d_{2}^{*}I,d_{1}^{*}R_{h}^{-1},d_{2}^{*}R_{v}^{-1}\}\) and \(\operatorname{diag}\{\varPhi,I,I,I,I, d_{1}^{*}I,d_{2}^{*}I,d_{1}^{*}R_{h}^{-1},d_{2}^{*}R_{v}^{-1}\}\) and denoting \(\bar{P}_{h}=P_{h}^{-1}\), \(\bar{P}_{v}=P_{v}^{-1}\), \(\bar{R}_{h}=R_{h}^{-1}\), \(\bar{R}_{v}=R_{v}^{-1}\), \(N_{11}=M_{12}^{-1}M_{11}P_{h}^{-1}\), \(N_{12}=M_{12}^{-1}\), \(N_{21}=M_{22}^{-1}M_{21}P_{v}^{-1}\), \(N_{22}=M_{22}^{-1}\), \(N_{1}=K_{1}\bar{P}_{h}\) and \(N_{2}=K_{2}\bar{P}_{v}\), we see that the matrix inequality (27) is equivalent to the LMI (26). It follows from Theorem 8 that the claim of this theorem is true. This completes the proof. □

Furthermore, an optimization problem can be formulated in

$$ \begin{array}{l@{\quad}l} \min & \lambda=\gamma^2 \\ \mbox{s.t.}& \mbox{(26)}, \\ \end{array} $$
(28)

which minimizes the H ∞ noise attenuation γ of the resulting closed-loop system.

4 An Illustrative Example

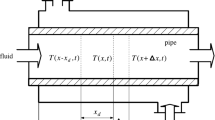
This section applies the main results on H ∞ control to the thermal process of a heat exchanger [9] shown in Fig. 1, which can be expressed in the partial differential equation

(29)

where T(x,t) is usually the temperature at x (space) ∈[0,x f ] and t (time) ∈[0,∞], u(x,t) is a given force function, τ is the time delay, x d is the space delay, a 0, a 1, a 2, b are real coefficients.

Fig. 1
figure 1

The heat exchanger

Full size image

Taking

we write (29) in the form

(30)

Denoting x h(i,j)=T(i−1,j), x v(i,j)=T(i,j), d 1=int(x d /△x) and d 2=int(τ/△t+1) (where int(⋅) is the integer function), it is easy to verify that (30) can be converted into the Roesser model (1a)–(1b) with parameter matrices

Let △t=0.1, △x=0.4, a 0=1, a 1=0.3, a 2=0.4, b=1 and the initial state satisfies the condition (3) for L 1=10 and L 2=10. Considering there exists a disturbance w(i,j) during the thermal exchanging process, the output signal z(i,j) is given to evaluate H ∞ disturbance attenuation performance, the thermal process is modeled in the form (1a)–(1b) with

$$B_1=\begin{bmatrix} 0.04\\ 0.1 \\ \end{bmatrix},\quad\quad H= [\begin{array}{c@{\quad}c} 1 & 1 \\ \end{array} ],\quad\quad L=0.5. $$

Solving the optimization problem (28), when \(d_{1}^{*}=3\) and \(d_{2}^{*}=3\), we can obtain a H ∞ disturbance attenuation γ=0.6728 and a delay-dependent H ∞ controller

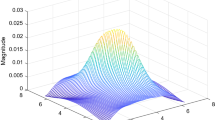
$$ u(i,j)= [\begin{array}{c@{\quad}c} -4.7532 & -9.5389 \\ \end{array} ]x(i,j). $$
(31)

When d 1=3 and d 2=3, the frequency response \(G(e^{j\omega_{1}},e^{j\omega_{2}})\) from the noise input w(i,j) to the controlled output z(i,j) is shown in Fig. 2, and its maximum value is 0.6564 that is smaller than γ.

Fig. 2
figure 2

The frequency response \(G(e^{j\omega_{1}},e^{j\omega_{2}})\)

Full size image

5 Conclusions

This paper has presented a solution to the problem of delay-dependent H ∞ control for 2-D state delay systems described by the Roesser model. Based on the summation inequality for 2-D discrete systems, a sufficient condition for this 2-D system to have delay-dependent H ∞ noise attenuation is proposed in terms of LMIs. Introducing variable substitution, a controller synthesis condition is given in terms of an LMI. A delay-dependent optimal state feedback H ∞ controller is obtained by solving an LMI optimization problem. Finally, a thermal process to serve as a simulation example of 2-D discrete state delay systems is given to illustrate the effectiveness of the proposed results.