MAX MIN Vertex Cover and the Size of Betti Tables

Abstract

Let G be a finite simple graph on n vertices, that contains no isolated vertices, and let $I(G) \subseteq S = K[x_1, \dots , x_n]$ be its edge ideal. In this paper, we study the pair of integers that measure the projective dimension and the regularity of S/I(G). We show that if ${{\,\mathrm{pd}\,}}(S/I(G))$ attains its minimum possible value $2\sqrt{n}-2$ then, with only one exception, ${{\,\mathrm{reg}\,}}(S/I(G)) = 1$. We also provide a full description of the spectrum of ${{\,\mathrm{pd}\,}}(S/I(G))$ when ${{\,\mathrm{reg}\,}}(S/I(G))$ attains its minimum possible value 1.

1 Introduction

In the current trends of commutative algebra, the role of combinatorics is distinguished. Particularly, the combinatorics of finite graphs have created fascinating research problems in commutative algebra and, vice-versa, algebraic methods and techniques have shed new lights on graph-theoretic questions ([10, Chapters 9 and 10]).

Let G be a simple graph over the vertex set $V_G = \{x_1, \dots , x_n\}$ and edge set $E_G$. Throughout the paper, all our graphs are assumed to contain no isolated vertices. Let K be a field and identify the vertices in $V_G$ with the variables in the polynomial ring $S = K[x_1, \ldots , x_n]$. The edge ideal of G, first introduced by Villarreal [16], is defined by

$$\begin{aligned} I(G) = \langle x_i x_j ~\big |~ \{x_i, x_j\} \in E_G\rangle \subseteq S. \end{aligned}$$

Let ${{\,\mathrm{pd}\,}}(G)$ and ${{\,\mathrm{reg}\,}}(G)$ denote the projective dimension and the Castelnuovo–Mumford regularity of S/I(G), respectively. These are fundamental homological invariants that measure the computational complexity of S/I(G). Particularly, ${{\,\mathrm{pd}\,}}(G)$ and ${{\,\mathrm{reg}\,}}(G)$ describe the size of the graded Betti table of S/I(G). Our work in this paper is motivated by the following basic question.

Question 1.1

Given a positive integer n, for which pairs of integers (p, r), does there exist a graph G on n vertices such that ${{\,\mathrm{pd}\,}}(G) = p$ and ${{\,\mathrm{reg}\,}}(G) = r$?

Our approach to Question 1.1 is purely combinatorial in nature. Specifically, we investigate an important graph-theoretic invariant, namely, the maximum size of a minimal vertex cover of G, which we shall denote by $\tau _{\max }(G)$. In graph theory, the two symmetric dual problems, to find a max min vertex cover and to find a min max independent set in a graph, are known to be N P-hard problems and, in recent years, have received a growing attention [1,2,3, 6, 7, 9]. In particular, a result of Costa, Haeusler, Laber and Nogueira [3, Theorem 2.2] proves that

$$\begin{aligned} \tau _{\max }(G) \ge 2\sqrt{n}-2. \end{aligned}$$

(1.1)

The inequality (1.1) gives rise to a somewhat surprising bound, that may have been overlooked, that ${{\,\mathrm{pd}\,}}(G) \ge 2\sqrt{n}-2$; see Corollary 4.2.

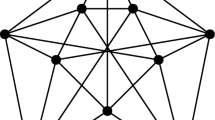
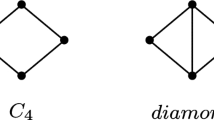
Our first main result shows that if ${{\,\mathrm{pd}\,}}(G) = 2\sqrt{n}-2$ then, with only one exception, we must have ${{\,\mathrm{reg}\,}}(G) = 1$. In fact, since ${{\,\mathrm{pd}\,}}(G) \ge \tau _{\max }(G)$ (see, for example, the proof of Corollary  4.2), we prove the following stronger statement. For a positive integer s, let $H_s$ denote the graph consisting of a complete subgraph $K_s$ each of whose vertex is connected to a set of $s-1$ independent vertices, and these independent sets are pairwise disjoint (see Fig. 1). Let $2K_2$ denote the graph consisting of two disjoint edges and let $C_4$ be the induced 4-cycle.

Theorem 1.2

Let G be a simple graph on n vertices and suppose that n is a perfect square. If $\tau _{\max }(G) =2\sqrt{n}-2$ then we must have either

• (1) $G = 2K_2$ and $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (2,2)$, or

• (2) $G = C_4$ and $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (3,1)$, or

• (3) $G = H_s$, for some $s \in {{\mathbb {N}}}$, and $({{\,\mathrm{pd}\,}}(G),{{\,\mathrm{reg}\,}}(G)) = (2\sqrt{n}-2,1)$.

To establish Theorem 1.2, we characterize all graphs G for which $\tau _{\max }(G) = 2\sqrt{n}-2$, when n is a perfect square. Our classification reads as follows.

Theorem 1.3

Let G be a simple graph on n vertices and suppose that n is a perfect square. Then $\tau _{\max }(G) = 2\sqrt{n}-2$ if and only if G is either $2K_2$, $C_4$ or $H_s$, for some $s \in {{\mathbb {N}}}$.

Theorem 1.2 further leads to the following natural special case of Question 1.1: what is the spectrum of ${{\,\mathrm{pd}\,}}(G)$ for all graphs G, for which ${{\,\mathrm{reg}\,}}(G) = 1$? Our next main result answers this question.

Theorem 1.4

Let $n \ge 2$ be any integer. The spectrum of ${{\,\mathrm{pd}\,}}(G)$ for all graphs G, for which ${{\,\mathrm{reg}\,}}(G) = 1$, is precisely $[2\sqrt{n}-2, n-1] \cap {{\mathbb {Z}}}$.

As an immediate consequence of Theorem 1.4, we show in Corollary 5.6 that for any pair of positive integers (p, r) such that $r \le n/2$ and

$$\begin{aligned} 2 \sqrt{n-2(r-1)}+r-3 \le p \le n-r, \end{aligned}$$

there exists a graph on n vertices such that $({{\,\mathrm{pd}\,}}(G),{{\,\mathrm{reg}\,}}(G)) = (p,r)$.

The paper is outlined as follows. Section 2 collects basic notations and terminology of finite simple graphs that will be used in the paper. In Sect. 3, we start with a simple proof for the inequality (1.1) when G is a gap-free graph, giving the non-experts (in our case, the algebraic readers) a glimpse of why $2\sqrt{n}-2$ appears naturally in the bound for $\tau _{\max }(G)$; see Theorem 3.1. We also construct, for any given $n \in {{\mathbb {N}}}$, a gap-free and chordal graph G such that $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil$, exhibiting that the inequality (1.1) is sharp. Section 4 is devoted to a new proof of the inequality (1.1) in the most general situation; see Theorem 4.1. Our proof is different from that given in [3, Theorem 2.2] and provides structures that we can later on use in the classification for graphs where the equality is attained. Section 5 contains our main results of the paper. We classify graphs G for which $\tau _{\max }(G) = 2\sqrt{n}-2$, in Theorem 1.3, and examine $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G))$ in this case, in Theorem 1.2. We finally show that when ${{\,\mathrm{reg}\,}}(G) = 1$, the spectrum of ${{\,\mathrm{pd}\,}}(G)$ is $[2\sqrt{n}-2, n-1] \cap {{\mathbb {Z}}}$, in Theorem 1.4.

2 Combinatorics of Finite Graphs and Algebraic Invariants

Throughout the paper, G shall denote a finite simple graph on $n \ge 2$ vertices that contains no isolated vertices. Recall that a finite graph G is simple if G has no loops nor multiple edges. We shall use $V_G$ and $E_G$ to denote the vertex and edge sets of G, respectively.

Definition 2.1

Let G be a graph.

• (1) A subset $W \subseteq V_G$ is called a vertex cover of G if $e \cap W \not = \emptyset$ for every edge $e \in E_G$. A vertex cover W is minimal if no proper subset of W is also a vertex cover of G. Set

  $$\begin{aligned} \tau _{\max }(G) = \max \{ |W| ~\big |~ W \text { is a minimal vertex cover of } G\}. \end{aligned}$$

• (2) A subset $W \subseteq V_G$ is called an independent set if for any $u\not =v \in W$, $\{u,v\} \not \in E_G$.

It is easy to see that the complement of a vertex cover is an independent set. Particularly, the complement of a maximum minimal vertex cover is a minimum maximal independent set.

For a subset $W \subseteq V_G$, the induced subgraph of G over W is the graph whose vertex set is W and whose edge set is $\{\{u,v\} ~\big |~ u,v \in W \text { and } \{u,v\} \in E_G\}$. A subset M of $E_G$ is a matching of G if, for any $e \not = e'$ in M, one has $e \cap e' = \emptyset$. The matching number of G is the largest size of a matching in G, and is denoted by $\beta (G)$. A matching M of G is called an induced matching of G if the induced subgraph of G over $\bigcup _{e \in M} e$ has no edges other than those already in M. The induced matching number of G is the largest size of an induced matching G, and is denoted by $\nu (G)$. It is known from [8, 11] that $\nu (G) \le {{\,\mathrm{reg}\,}}(G) \le \beta (G)$.

Definition 2.2

Let G be a graph.

• (1) G is called gap-free if $\nu (G) = 1$. Equivalently, G is gap-free if for any two disjoint edges $e, f \in E_G$, there exists an edge $g \in E_G$ such that $e \cap g \not = \emptyset$ and $f \cap g \not =\emptyset$.

• (2) G is called chordal if every cycle of length at least 4 in G has a chord. That is, for every cycle C of length at least 4 in G, there exist two nonconsecutive vertices u and v on C such that $\{u,v\} \in E_G$.

It is known from [4, 8] that if G is a chordal graph then ${{\,\mathrm{pd}\,}}(G) = \tau _{\max }(G)$ and ${{\,\mathrm{reg}\,}}(G) = \nu (G)$.

Definition 2.3

Let $W \subseteq V_G$ be a subset of the vertices in G. The neighborhood (the set of neighbors) and the closed neighborhood of W are defined by

$$\begin{aligned}&N_G(W) = \{u \in V_G ~\big |~ \exists w \in W: \{u,w\} \in E_G\} \text { and }\nonumber \\&N_G[W] = N_G(W) \cup W. \end{aligned}$$

When $W = \{v\}$, for simplicity of notation, we shall write $N_G(v)$ and $N_G[v]$ in place of $N_G(W)$ and $N_G[W]$. The degree of a vertex $v \in V_G$ is defined to be $\deg _G(v) = |N_G(v)|$. A vertex $v \in V_G$ is called free if $\deg _G(v) = 1$. A leaf in G is an edge that contains a free vertex.

A path is an alternating sequence of distinct vertices and edges (except possibly the first and the last vertex) $x_1, e_1, x_2, e_2, \dots , e_s, x_{s+1}$ such that $e_i = \{x_i, x_{i+1}\}$, for $i = 1, \dots , s$. The length of a path is the number of edges on the path. A path of length s is denoted by $P_s$. A cycle is a closed path. An induced cycle in G is a cycle which is also an induced subgraph of G. An induced cycle of length s is denoted by $C_s$. A complete graph is a graph in which any two distinct vertices are connected by an edge. We shall use $K_s$ to denote a complete graph over s vertices. A graph G is bipartite if there is a partition $V_G = X \cup Y$ of the vertices of G such that every edge in G connects a vertex in X to a vertex in Y. A bipartite graph G with a bi-partition $V_G = X \cup Y$ of its vertices is called a complete bipartite graph if $E_G = \{\{x,y\} ~\big |~ x\in X, y\in Y\}$. We use $K_{r,s}$ to denote the complete bipartite graph whose vertices are partitioned into the union of two sets of cardinality r and s.

Finally, let K be a field and let $S = K[V_G]$ represent the polynomial ring associated with the vertices in G.

Definition 2.4

Let M be a finitely generated graded S module. Then M admits a minimal graded free resolution of the form

$$\begin{aligned}&0 \rightarrow \bigoplus _{j \in {{\mathbb {Z}}}}S(-j)^{\beta _{p,j}(M)} \rightarrow \dots \\&\quad \rightarrow \bigoplus _{j\in {{\mathbb {Z}}}}S(-j)^{\beta _{0,j}(M)} \rightarrow M \rightarrow 0. \end{aligned}$$

The numbers $\beta _{i,j}(M)$ are called the graded Betti numbers of M. The projective dimension and the regularity of M are defined as follows:

$$\begin{aligned}&{{\,\mathrm{pd}\,}}(M) = \max \{i ~\big |~ \exists j: \beta _{i,j}(M) \not = 0\} \text { and }\nonumber \\&{{\,\mathrm{reg}\,}}(M) = \max \{j-i ~\big |~ \beta _{i,j}(M) \not = 0\}. \end{aligned}$$

The graded Betti table of M is an ${{\,\mathrm{pd}\,}}(M) \times {{\,\mathrm{reg}\,}}(M)$ array whose (i, j)-entry is $\beta _{i,i+j}(M)$. When $M = S/I(G)$, we write ${{\,\mathrm{pd}\,}}(G)$ and ${{\,\mathrm{reg}\,}}(G)$ in place of ${{\,\mathrm{pd}\,}}(S/I(G))$ and ${{\,\mathrm{reg}\,}}(S/I(G))$.

3 Gap-Free Graphs and $\lceil 2\sqrt{n} - 2 \rceil$

The goal of this section is to provide the non-experts with an easy understanding of why $2\sqrt{n}-2$ appears naturally in the bound for $\tau _{\max }(G)$. This is demonstrated by a short proof of the inequality (1.1) when G is a gap-free graph. We shall also construct, for any $n \ge 2$, a graph G over n vertices admitting $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil$, showing that the bound for $\tau _{\max }(G)$ in (1.1) is sharp. The graph G constructed will be gap-free and chordal.

Proposition 3.1

If a graph G on n vertices is gap-free, then

$$\begin{aligned} \tau _{\max }(G) \ge \lceil 2\sqrt{n} - 2 \rceil . \end{aligned}$$

Proof

If G is bipartite then $\tau _{\max }(G) \ge n/2 \ge 2\sqrt{n} - 2$. Thus, we can assume that G is a non-bipartite graph. Since G is gap-free, we can also assume that G is a connected graph.

Case 1: G contains a complete subgraph of size at least 3. Let q denote the maximum integer $q \ge 3$ for which G contains a complete subgraph $K_q$. Since $\tau _{\max }(K_q) = q - 1 \ge 2\sqrt{q} - 2$, one can assume that $q < n$. Without loss of generality, suppose that $\{x_1, \ldots , x_q\}$ is the vertex set of such a $K_q$ in G.

We claim that the complete subgraph $K_q$ of G can be chosen such that any vertex $x_j$, for $q < j \le n$, is connected by an edge to a vertex in this $K_q$. Indeed, suppose that this is not the case. Choose such a $K_q$ with the least number of vertices outside of $K_q$ that are not connected to any of the vertices of $K_q$. Let $x_j$, for some $q < j \le n$, be a vertex outside of $K_q$ that is not connected to any of the vertices in $K_q$. Since $x_j$ is not an isolated vertex in G, there exists a vertex $x_k$, for $q < k \not =j \le n$, such that $\{x_j, x_k\} \in E_G$. This, since G is gap-free, implies that $x_k$ must be connected to at least $q - 1$ vertices of $K_q$. In addition, it follows from the maximality of q that $x_k$ must be connected to exactly $q - 1$ vertices of $K_q$. Assume that $x_k$ is connected to $x_1, \ldots , x_{q - 1}$. Let $K_q'$ be the complete subgraph of G over the vertices $\{x_1, \dots , x_{q-1}, x_k\}$.

Consider any vertex $x_l$ outside of $K_q'$ that is connected to a vertex in $K_q$. If $x_l$ is connected to any of the vertices $\{x_1, \dots , x_{q-1}\}$, then $x_l$ is still connected to that vertex in $K_q'$. If $\{x_l, x_q\} \in E_G$ and $\{x_l, x_k\} \not \in E_G$ then, by considering the pair of edges $\{x_l, x_q\}$ and $\{x_j,x_k\}$ and since G is gap-free, we deduce that $\{x_l, x_j\} \in E_G$. This, again since G is gap-free, implies that $x_l$ is connected to at least $q-2$ vertices among $\{x_1, \dots , x_{q-1}\}$. Thus, $x_l$ is connected to a vertex in $K_q'$ (since $q \ge 3$). Hence, the number of vertices outside $K_q'$ that are not connected to $K_q'$ is strictly less than that of $K_q$, a contradiction to the construction of $K_q$.

Now, suppose that each vertex $x_j$, for $q < j \le n$, is connected to a vertex of $K_q$. For $i =1, \dots , q$, let

$$\begin{aligned} W_i = \{j ~\big |~ q < j \le n, \{x_j,x_i\} \in E_G\}, \end{aligned}$$

and set $\omega _i = |W_i|$ (note that the sets $W_i$s are not necessarily disjoint). It is easy to see that a minimal vertex cover of G containing $\{x_1, \dots , x_q\} \setminus \{x_i\}$ must also contain the vertices in $W_i$. Thus, it follows that

$$\begin{aligned} \tau _{\max }(G) \ge \max \{\omega _1, \ldots , \omega _q \} + (q - 1). \end{aligned}$$

Therefore,

$$\begin{aligned} \tau _{\max }(G) \ge \frac{\, n - q \,}{q} + (q - 1) = \frac{\, n \,}{q} + q - 2 \ge 2\sqrt{n} - 2. \end{aligned}$$

Case 2: G does not contain any complete subgraph of size at least 3. Since G is not bipartite, G contains an odd cycle of length $\ell \ge 5$. Since G is gap-free, by considering pairs of non-adjacent edges on this cycle, we deduce that G contains $C_5$ as an induced cycle. Let $x_1, \ldots , x_5$ be the vertices of this $C_5$ in G.

We claim that each vertex $x_i$, for $i > 5$, is connected by an edge to one of the vertices of $C_5$. Indeed, suppose that there exists a vertex $x_i$, for some $i > 5$, that is not connected to any of the vertices of $C_5$. Since G is connected, G has an edge $\{x_i,x_j\}$ for some $j > 5$. Since G is gap-free, either $x_1$ or $x_2$ must be connected to $x_j$. We can assume that $\{x_1,x_j\} \in E_G$. This, since G has no triangle, implies that $\{x_2, x_j\} \not \in E_G$ and $\{x_5,x_j\} \not \in E_G$. For the same reason, at least one of the edges $\{x_3,x_j\}$ and $\{x_4,x_j\}$ is not in G. Suppose that $\{x_4, x_j\} \not \in E_G$. We then have a gap consisting of the edges $\{x_4, x_5\}$ and $\{x_i, x_j\}$, a contradiction.

Now, for $i = 1, \dots , 5$, let $W_i = \{x_k ~\big |~ k> 5 \text { and } \{x_i,x_k\} \in E_G\}$ and set $\omega _i = |W_i|$. Let $b_i = \omega _i+\omega _{i+2}$, where $\omega _{5+j} = \omega _j$. Observe that a minimal vertex cover of G not containing $x_i$ and $x_{i+2}$, for some $1 \le i \le 5$ must contain $W_i \cup W_{i+2}$. Since $b_1 + \cdots + b_5 \ge 2|\bigcup _{i=1}^5 W_i| = 2(n-5)$, it follows that there is $1 \le i \le 5$ with $b_i \ge 2n/5 -2$. Therefore,

$$\begin{aligned} \tau _{\max }(G) \ge 2n/5 + 1 \ge 2\sqrt{n} - 2, \end{aligned}$$

and the result is proved. $\square$

Remark 3.2

In Case 1 of Proposition 3.1, the bound for $\tau _{\max }(G)$ arises from the fact that $\frac{n}{q} + q \ge 2\sqrt{n}$. This is a well known inequality with the equality attainable only if $q = \sqrt{n}$. This gives an explanation as why $2\sqrt{n}-2$ appears naturally as the optimal bound.

Definition 3.3

Given $s \in {{\mathbb {N}}}$, we define $H_s$ to be the graph consisting of a complete graph $K_s$, each of whose vertex is furthermore connected to an independent set of size $s-1$, and these independent sets are pairwise disjoint.

Fig. 1

$H_5$

Example 3.4

The graph depicted in Fig. 1 is $H_s$ for $s = 5$.

The following example gives a graph G over n vertices admitting $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil$ for any $n \ge 2$.

Example 3.5

Let $a > 0$ be an integer with $a^2 \le n < (a + 1)^2$. If $n = a^2$ then let $G_{n} = H_a$. The first graph in Fig. 2 is $G_{25} = H_5$. It is easy to see that $\tau _{\max }(G_n) = 2(a-1) = 2\sqrt{n}-2.$

If $a^2 < n \le a^2 + a$ then let $G_n$ be the graph obtained from $H_a$ by adding a leaf $\{x_i, x_{a^2 + i}\}$ to each vertex $x_i$, for $i=1, \dots , n-a^2$, in the complete subgraph $K_a$ of $H_a$. The second graph in Fig. 2 is $G_{27}$. Then $\tau _{\max }(G_n) = 2a - 1$. Since $a< \sqrt{n} \le \sqrt{a^2 + a} < a + 1/2$, one has $\lceil 2\sqrt{n} - 2 \rceil = 2a - 1 = \tau _{\max }(G_n)$.

If $a^2 + a< n < (a + 1)^2$ then let $G_n$ be the graph obtained from $G_{a^2+a}$ by adding a leaf $\{x_i, x_{a^2 + a + i}\}$ to each vertex $x_i$, for $i = 1, \dots , n-a^2-a$, in the complete subgraph $K_a$ of $G_{a^2+a}$. The third graph in Fig. 2 is $G_{31}$. Then $\tau _{\max }(G_n) = 2a$. Since $a + 1/2< \sqrt{a^2 + a + 1} \le \sqrt{n} < a + 1$, one has $\lceil 2\sqrt{n} - 2 \rceil = 2a = \tau _{\max }(G_n)$.

Fig. 2

Graphs with $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil .$

Note that all graphs constructed here are chordal and gap-free.

4 The Bound $\tau _{\max }(G) \ge 2\sqrt{n} - 2$ for An Arbitrary Graph

In this section, we give a new proof for the inequality (1.1). Our proof is different from that given in [3, Theorem 2.2] and provides information that we could use in the next section to classify graphs for which (1.1) becomes an equality.

Theorem 4.1

Let G be a graph on n vertices. We have

$$\begin{aligned} \tau _{\max }(G) \ge \lceil 2\sqrt{n} - 2 \rceil . \end{aligned}$$

Proof

Since $\tau _{\max }(G) \in {{\mathbb {N}}}$, it suffices to show that $\tau _{\max }(G) \ge 2\sqrt{n}-2$. Let W be a minimal vertex cover of maximum size in G. That is, $|W| = \tau _{\max }(G)$. Our strategy is to construct from W various new minimal vertex covers, keeping in mind that these vertex covers have cardinality at most |W|, to run through all the vertices in G and to relate n to |W|.

We start by partitioning W into $W = A \cup B$ as follows: let $B' = \{w \in W ~\big |~ \deg _G(w) = 1\}$ and set

$$\begin{aligned} B = B' \cup \{v \in W ~|~ N_G(v) \subseteq N_G(B')\} \text { and } A = W\setminus B. \end{aligned}$$

The idea behind this partition is that if a new minimal vertex cover of G does not contain any vertices in B then it must contain $N_G(B) = N_G(B')$.

Observe that $|N_G(B)| \le |B|$. This, particularly, implies that if $A = \emptyset$ then $\tau _{\max }(G) \ge n/2 \ge 2\sqrt{n}-2$. Thus, we shall assume that $A \not = \emptyset$. Set $a = |A|$, $b = |B|$ and $n_b = |N_G(B)| \le b$.

For each vertex $v \in A$, let $M(v) = N_G(v) \setminus (W \cup N_G(B))$. Again, if a new minimal vertex cover is formed by removing v and B from W then it must include M(v) and $N_G(B)$. Consider the maximal sets (with respect to inclusion) of the form M(w) for $w \in A$, and suppose that those maximal sets are $M(w_1), \dots , M(w_t)$, for $w_1, \dots , w_t \in A$. Set $D = A \setminus \{w_1, \dots , w_t\}$ and let $d = |D|$.

Observe further that any vertex in G belongs to at least one of the following sets: $W, N_G(B)$, and $M(w_i)$, for $i=1, \dots , t$. Thus, n can be bounded by giving an upper bound for the cardinality of $M(w_i)$. This is the content of our next claim.

Claim 1. For any $i = 1, \dots , t$, we have $|M(w_i)| \le b+1+d-n_b.$

Proof of Claim

We shall construct a new minimal vertex cover $W'$ by removing $w_i$ and B from W (and, thus, adding $M(w_i)$ and $N_G(B)$) and use the condition that $|W'| \le |W|$ to achieve the desired bound for $|M(w_i)|$.

Set

$$\begin{aligned} D' = \{w \in D ~\big |~ M(w) \not \subseteq M(w_i)\} \cup \{w \in D ~\big |~ ww_i \in E_G\} \text { and } D'' = D \setminus D'. \end{aligned}$$

These sets are introduced because after removing $w_i$ from W and adding $M(w_i)$, the new vertex cover must still contain $D'$; on the other hand, which vertices in $D''$ belong to the new vertex cover depend on the induced subgraph of G on $D''$.

Let H be the induced subgraph of G over $D''$ and let U be a minimal vertex cover of H. Let

$$\begin{aligned} W' = \big [W \cup M(w_i)\cup N_G(B)\big ] \setminus \big [B \cup \{w_i\} \cup (D'' \setminus U)]. \end{aligned}$$

It suffices to show that $W'$ is a minimal vertex cover of G, which then implies that $|W'| \le |W|$; that is,

$$\begin{aligned} |M(w_i)| \le b+1+|D'' \setminus U|-n_b \le b+1+d-n_b. \end{aligned}$$

(4.1)

To see that $W'$ is a vertex cover of G, consider any edge $e = xy \in E_G$. Since W covers G, without loss of generality, we may assume that $x \in W$. If $x \in W'$ then $W'$ covers e. Assume that $x \not \in W'$. This implies that $x \in B \cup \{w_i\} \cup (D'' \setminus U)$. If $x \in B$ then $y \in N_G(B) \subseteq W'$, and so $W'$ covers e. If $x = w_i$ then either $y \in M(w_i) \subseteq W'$ or $y \in W \cup N_G(B)$. Furthermore, if $y \in W$ either y is among the $w_j$, for $j \not = i$, or $y \in D' \subseteq W'$. Thus, in this case, $W'$ also covers e. If $x \in D'' \setminus U$ then, by definition, $M(x) \subseteq M(w_i)$ and $xw_i \not \in E_G$. This implies that at least one of the following happens:

• (1) $y \in M(x)$,

• (2) $y \in \{w_1, \dots , w_t\} \setminus \{w_i\}$,

• (3) $y \in N_G(B)$,

• (4) $y \in D'$,

• (5) xy is an edge in H (which forces $y \in U$).

In any of these cases, we have $y \in W'$.

To see that $W'$ is a minimal vertex cover, consider any vertex cover $W'' \subseteq W'$ of G. Observe that $W''$ does not contain any vertex in $B \cup \{w_i\}$, so $W''$ must contain $N_G(B) \cup M(w_i)$. Also, for any $j \not = i$, $M(w_j) \not \subseteq M(w_i)$. This implies that $M(w_j) \not \subseteq W''$, which forces $w_j \in W''$ for all $j \not = i$. Furthermore, for any $w \in D'$, either $M(w) \not \subseteq W''$ or $ww_i \in E_G$. It then follows that $w \in W''$, i.e., $D' \subseteq W''$. Finally, for any vertex $u \in U$, since U is a minimal vertex cover of H, there exists an edge uv in H such that $v \not \in W'$. This implies that $v \not \in W''$, and so, $u \in W''$. Hence, $W'' = W'$, and $W'$ is a minimal vertex cover of G. $\square$

We proceed with the proof of our theorem by considering two different cases.

Case 1: $B \not = \emptyset$. In this case, Claim 1 gives us

$$\begin{aligned} n&\le \sum _{i=1}^t |M(w_i)| +|A| + |N_G(B)| + |B| \nonumber \\&\le t(b+1+d-n_b) + t+d+n_b+b \nonumber \\&= 2t + t(b+d-n_b) + d+n_b+b \nonumber \\&= 2t + (t-1)(b+d-n_b) + 2(b+d). \end{aligned}$$

(4.2)

On the other hand $\tau _{\max }(G) = t+d + b$.

Observe that, since $b \ge 1$, we have $n_b \ge 1$, and so

$$\begin{aligned} 4n&\le 4\big [2t + (t-1)(b+d-1) + 2(b+d)\big ] \nonumber \\&= 4(t+1)(b+d+1) \le (t+d+b+ 2)^2 \nonumber \\&= (\tau _{\max }(G)+2)^2. \end{aligned}$$

(4.3)

Hence, $\tau _{\max }(G) \ge 2 \sqrt{n}-2$, and we are done.

Case 2: $B = \emptyset$. Observe that, by Claim 1, for each $i = 1, \dots , t$,

$$\begin{aligned} |M(w_i)| \le d+1. \end{aligned}$$

(4.4)

Observe further that if $D = \emptyset$ then it follows from (4.4) that $\tau _{\max }(G) \ge t \ge n/2 \ge 2\sqrt{n}-2$. We shall assume that $D \not = \emptyset$. Since W is a minimal vertex cover of G, it follows that $M(v) \not = \emptyset$ for all $v \in A$. Let $M(D) = \bigcup _{w \in D}M(w) \not = \emptyset$.

To prove the assertion, it suffices to show that

$$\begin{aligned} \big |\bigcup _{i=1}^t M(w_i)\big | \le td+1. \end{aligned}$$

(4.5)

This is because (4.5) then gives

$$\begin{aligned} n \le \big |\bigcup _{i=1}^t M(w_i)| + |A| \le td+1+t+d = (t+1)(d+1), \end{aligned}$$

(4.6)

which implies that $4n \le (t+d+2)^2 = (\tau _{\max }(G)+2)^2$.

To establish (4.5), we partition $\{w_1, \dots , w_t\}$ into the following two subsets

$$\begin{aligned} V_1= & {} \{w_i ~\big |~ M(D) \subseteq M(w_i)\} \text { and }\\ V_2= & {} \{w_i ~\big |~ M(D) \not \subseteq M(w_i)\}. \end{aligned}$$

Consider any $w_i \in V_2$. Since $M(D) \not \subseteq M(w_i)$, there exists a vertex $x \in D$ such that $M(x) \not \subseteq M(w_i)$. Now, apply the same proof as that for Claim 1, for the set $M(w_i)$, observing that $x \in D'$ in this case, and so $|D'' \setminus U| \le d-1$. This implies that $|M(w_i)| \le d$.

Observe, finally, that if $V_1 = \emptyset$ then we have $\big |\bigcup _{i=1}^t M(w_i)\big | = \big |\bigcup _{w_i \in V_2}M(w_i)\big | \le td$, and if $V_1 \not = \emptyset$ then we have

$$\begin{aligned} \big |\bigcup _{i=1}^t M(w_i)\big |&\le \big |\bigcup _{w_i \in V_1}M(w_i)\big | + \big |\bigcup _{w_i \in V_2}M(w_i)| \nonumber \\&\le |M(D)| + (d+1-|M(D)|)|V_1| + d|V_2| \nonumber \\&= d(|V_1|+|V_2|) + 1 - (|M(D)|-1)(|V_1|-1) \nonumber \\&\le td+1. \end{aligned}$$

(4.7)

The result is proved. $\square$

Corollary 4.2

Let G be a graph on n vertices. We have

$$\begin{aligned} {{\,\mathrm{pd}\,}}(G) \ge \lceil 2\sqrt{n}-2\rceil . \end{aligned}$$

Proof

Let $I(G)^\vee$ denote the Alexander dual of the edge ideal I(G) of G. See, for example, [13, Chapter 5] for more details of the Alexander duality theory. By a result of Terai [15, Theorem 2.1], we have

$$\begin{aligned} {{\,\mathrm{reg}\,}}(I(G)^\vee ) = {{\,\mathrm{pd}\,}}(G). \end{aligned}$$

Observe that the minimal generators of $I(G)^\vee$ correspond to the minimal vertex covers in G. Since the regularity is an upper bound for the maximal generating degree, we have ${{\,\mathrm{reg}\,}}(I(G)^\vee ) \ge \tau _{\max }(G)$. Thus, ${{\,\mathrm{pd}\,}}(G) \ge \tau _{\max }(G)$ (see also [4, 12]). The assertion now follows from Theorem 4.1. $\square$

We end this section with a remark that most of the known bounds for ${{\,\mathrm{pd}\,}}(G)$ in the literature are in terms of combinatorial invariants of G. In [4], various upper bounds for ${{\,\mathrm{pd}\,}}(G)$ in terms of n and the degrees of the vertices were given for special classes of graphs. Corollary 4.2 gives a lower bound for ${{\,\mathrm{pd}\,}}(G)$ involving only the number of vertices in G.

5 Classification for $\tau _{\max }(G) = 2\sqrt{n}-2$ and the Spectrum of $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G))$

This section is devoted to our main results. We shall classify graphs G, when n is a perfect square, for which $\tau _{\max }(G)$ attains its minimum value; that is, when $\tau _{\max }(G) = 2\sqrt{n}-2$. We shall also give the first nontrivial partial answer to Question  1.1 on the spectrum of pairs of integers $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G))$. Recall that, for $s \in {{\mathbb {N}}}$, $H_s$ is the graph defined in Definition 3.3.

Theorem 5.1

Let G be a graph on n vertices and suppose that n is a perfect square. Then $\tau _{\max }(G) = 2\sqrt{n}-2$ if and only if G is either $2K_2$, $C_4$ or $H_s$, for some $s \in {{\mathbb {N}}}$.

Proof

It is clear that if G is either $2K_2$, $C_4$ or $H_s$ then $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil$. We shall prove the other implication. Let W be a minimal vertex cover of largest size. That is, $|W| = 2\sqrt{n}-2$. We shall use the same notations as in the proof of Theorem 4.1. Consider the following two possibilities.

Case 1: $B \not = \emptyset$. The proof of Theorem  4.1 shows that $4n = (\tau _{\max }(G)+2)^2$ only if the following conditions are satisfied:

• (1) $t = b+d$ (due to (4.3)),

• (2) $n_b = 1$ (due to (4.3)), and

• (3) $M(w_1), \dots , M(w_t)$ are pairwise disjoint and each has exactly $b+1+d-n_b = b+d$ elements (due to (4.2)).

Fig. 3

G when $B \not = \emptyset$

Condition (3), together with (4.1), implies that $|D''\setminus U| = |D|$. This happens if and only if $D'' = D$ and $U = \emptyset$. Thus, D is an independent set, and for all $i = 1, \dots , t$ and $w \in D$, we have $M(w) \subseteq M(w_i)$ and $ww_i \not \in E_G$. This, together with condition (3) again, implies that either $t = 1$ or $M(w) = \emptyset$ for all $w \in D$.

Suppose that $t = 1$. Condition (1) then implies that $b = 1$ and $d = 0$. In this case, G is either a path of length 3, i.e., $P_3$, or two disjoint edges, i.e., $2K_2$. Note that $P_3 = H_2$.

Suppose that $M(w) = \emptyset$ for all $w \in D$. Since $ww_i \not \in E_G$, it follows that $N_G(w) \subseteq N_G(B)$. This is a contradiction to the construction of B unless $D = \emptyset$. Thus, we have $D = \emptyset$ and $A = \{w_1, \dots , w_t\}$. Let $v_b$ be the only vertex in $N_G(B)$.

Observe that if there exists an i such that $w_iv_b \not \in E_G$, then let

$$\begin{aligned} W' = [W \cup M(w_i)] \setminus \{w_i\}. \end{aligned}$$

It can be seen that $W'$ is a minimal vertex cover of G. Thus, $|W'| \le |W|$, and so we must have $|M(w_i)| = 1$. That is, $b=1$ and $|M(w_j)| = 1$ for all $j = 1, \dots , t$. Therefore, $\tau _{\max }(G) = n/2$. In this case, $\tau _{\max }(G) = 2\sqrt{n}-2$ only if $n = 4$, and we have $t=1$ and $G = 2K_2$.

Assume that $w_iv_b \in E_G$ for all $i = 1, \dots , t$. Observe further that if there are $i \not = j$ such that $w_iw_j \not \in E_G$ then let

$$\begin{aligned} W' = [W \cup M(w_i) \cup M(w_j) \cup N_G(B)] \setminus [B \cup \{w_i,w_j\}]. \end{aligned}$$

It can also be seen that $W'$ is a minimal vertex cover of G. Thus, $|W'| \le |W|$, and we get $|M(w_i)| + |M(w_j)| + 1 \le b+2$. That is, $2b \le b+1$. Therefore, $b=1$ and again $n = 4$. In this case, $G = P_3$.

Suppose, finally, that $w_iw_j \in E_G$ for all $i \not = j$. Clearly, we then have $G = H_{t+1}$, as depicted in Fig.  3 with $t = 4$.

Case 2: $B = \emptyset$. From the minimality of W, it follows that $M(w) \not = \emptyset$ for all $w \in A$. Suppose that $D = \emptyset$. Then (4.4) implies that $|M(w_i)| = 1$ for all $i = 1, \dots , t$. Thus, $\tau _{\max }(G) \ge n/2$, and so $\tau _{\max }(G) = 2\sqrt{n}-2$ only if $n=4$. Therefore, we also have that G is either $P_3$ or $2K_2$.

Suppose that $D \not = \emptyset$. The proof of Theorem 4.1 shows that $4n = (\tau _{\max }(G)+2)^2$ only if the following conditions are satisfied:

• (4) $t = d \not = 0$ (due to (4.6)),

• (5) $M(w_j)$’s are all disjoint for $w_j \in V_2$, $M(w_i)$ and $M(w_j)$ are disjoint for any $w_i \in V_1$ and $j \in V_2$, and $M(w_i)$’s pairwise share exactly M(D) as the set of common vertices (due to (4.7)), and

• (6) either $|M(D)| = 1$ or $|V_1| = 1$ (due to (4.7)).

Consider first the case where $|V_1| = 1$ in condition (6). Without loss of generality, we may assume that $V_1 =\{w_1\}$ and $V_2 = \{w_2, \dots , w_t\}$. In this case, condition (5) states that $M(w_1), \dots , M(w_t)$ are disjoint, $|M(w_1)| = d+1$ and $|M(w_j)| = d$ for $j \ge 2$. Particularly, for all $j \ge 2$,

$$\begin{aligned} M(D) \cap M(w_j) = \emptyset . \end{aligned}$$

(5.1)

Applying (4.1) to $M(w_1)$ implies that D is an independent set in G. Moreover, applying (4.1) to $M(w_j)$, for any $j \ge 2$, gives that $|D''| = d-1$. It follows that, for any $j \ge 2$, there is exactly one vertex w in D such that $M(w) \not \subseteq M(w_j)$ or $ww_j \in E_G$. This and (5.1) force $d = 1$. In this case, G is either a $P_3$ or a $C_4$.

Consider now the case where $|M(D)| = 1$. Let $v_d$ be the only vertex in M(D). In this case, we have $M(w) = M(D) = \{v_d\}$ for all $w \in D$. If $V_2 \not = \emptyset$ then let $v \in V_2$. By condition (6) and applying (4.1) to M(v), we deduce that $|D'' \setminus U| = d-1$. However, $M(w) \not \subseteq M(v)$ for all $w \in D$ by (5.1). Thus, in applying (4.1) to estimate M(v), we have $D'' = \emptyset$. This is the case only if $d = 1$. Thus, $t=d=1$, and we get to a contradiction to the fact that both $V_1$ and $V_2$ are not empty.

Suppose that $V_2 = \emptyset$. Condition (6) states that $M(w_1), \dots , M(w_t)$ pairwise have exactly one vertex $v_d$ in common and each is of size exactly $d+1$. If there are $w_i$ and $w \in D$ such that $ww_i \in E_G$ then, in applying (4.1) to $M(w_i)$, we have that $D' \not = \emptyset$. That is $|D''| \le d-1$, and so $|M(w_i)| \le d$, a contradiction. Hence, $ww_i \not \in E_G$ for all i and all $w \in D$. This shows that the vertices in D are of degree 1. That is, $B \not = \emptyset$, a contradiction. $\square$

Observe that $H_s$ is a chordal and gap-free graph. The conclusion of Theorem 1.3 is no longer true if n is not a perfect square. In fact, for any odd integer $p \ge 3$, there exists a graph G over $n = (p+1)^2/4+1$ vertices that is neither chordal nor gap-free and admits $\tau _{\max }(G) = p = \lceil 2\sqrt{n}-2\rceil$. The following example depicts this scenario when $p = 5$ and $n=10$. The example for any odd $p \ge 3$ and $n = (p+1)^2/4+1$ is constructed in a similar manner.

Example 5.2

Let G be the following graph over 10 vertices (as in Fig.  4). It is easy to see that $\tau _{\max }(G) = 5 = \lceil 2\sqrt{10}-2\rceil$ (the solid black vertices form a minimal vertex cover of maximum cardinality 5). Furthermore, G is neither chordal nor gap-free.

Fig. 4

A graph with $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil$ which is not chordal nor gap-free

The following problem, which we hope to come back to in future work, arises naturally.

Problem 5.3

Characterize all graphs G on n vertices for which $\tau _{\max }(G) = \lceil 2\sqrt{n}-2\rceil .$

Theorem 1.3 furthermore gives us some initial understanding toward Question 1.1.

Theorem 5.4

Let G be a graph on n vertices and suppose that n is a perfect square. If $\tau _{\max }(G) = 2\sqrt{n}-2$ then we must have either

• (1) $G = 2K_2$ and $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (2,2)$, or

• (2) $G = C_4$ and $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (3,1)$, or

• (3) $G = H_s$, for some $s \in {{\mathbb {N}}}$, and $({{\,\mathrm{pd}\,}}(G),{{\,\mathrm{reg}\,}}(G)) = (2\sqrt{n}-2,1)$.

Proof

It follows from Theorem 1.3 that G either $2K_2$, $C_4$ or $H_s$, for some $s \in {{\mathbb {N}}}$. If G is $2K_2$ then $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (2,2).$ If G is $C_4$ then $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (3,1)$.

Suppose that $G = H_s$ for some $s \in {{\mathbb {N}}}$. Recall that $H_s$ is a chordal and gap-free graph. Particularly, the induced matching number of $H_s$ is 1. Thus, by [8, Corollary 6.9], we have ${{\,\mathrm{reg}\,}}(G) = 1$. $\square$

Our next main result serves as a converse to Theorem 1.2; that is, we identify the spectrum of ${{\,\mathrm{pd}\,}}(G)$ when ${{\,\mathrm{reg}\,}}(G) = 1$.

Theorem 5.5

Let $n \ge 2$ be any integer. The spectrum of ${{\,\mathrm{pd}\,}}(G)$ for all graphs G, for which ${{\,\mathrm{reg}\,}}(G) = 1$, is precisely $[2\sqrt{n}-2, n-1] \cap {{\mathbb {Z}}}$.

Proof

By Corollary 4.2, we have ${{\,\mathrm{pd}\,}}(G) \ge 2\sqrt{n}-2$. Observe that any minimal vertex cover of G needs at most $n-1$ vertices, so ${\mathfrak {m}}= (x_1, \dots , x_n)$ is not a minimal prime of I(G). Furthermore, since I(G) is squarefree, it has no embedded primes. This implies that ${\mathfrak {m}}$ is not an associated prime of I(G). It follows that ${{\,\mathrm{depth}\,}}S/I(G) \ge 1$. By Auslander-Buchsbaum formula, we then have ${{\,\mathrm{pd}\,}}(S/I(G)) \le n-1$.

It remains to construct a graph G on n vertices, for any given integer p such that $2\sqrt{n}-2 \le p \le n-1$, for which ${{\,\mathrm{pd}\,}}(G) = p$ and ${{\,\mathrm{reg}\,}}(G) = 1$. By considering the complete bipartite graph $K_{1,n-1}$, the assertion is clearly true for $p = n-1$. Suppose now that $p \le n-2$.

Let $s = \lceil p/2\rceil + 1$ and $T = \lfloor p/2\rfloor + 1$. It can be seen that $sT = \lfloor (p+2)^2/4\rfloor \ge n$. Note further that $s+T = p+2 \le n$. Thus, we can choose t to be the largest integer such that $(s-1)t+T \le n$ (particularly, $1 \le t \le T$), and set $a = (p+2)-(s+t) = T-t$.

Let $K_s$ be the complete graph over s vertices $\{x_1, \dots , x_s\}$. For each $i = 1, \dots , s$, let $W_i$ be a set of $t-1$ independent vertices such that the sets $W_i$s are pairwise disjoint and disjoint from the vertices of $K_s$. For each $i = 1, \dots , s$, connect $x_i$ to all the vertices in $W_i$. Observe further that

• (1) $st+a = (s-1)t+T \le n$, and

• (2) $st + sa = sT \ge n$.

Thus, we can find new pairwise disjoint sets $B_1, \dots , B_s$ of independent vertices, which are also disjoint from the vertices in $K_s$ and $W_i$s, such that $|B_1| = a$ and $|B_i| \le a$, for all $2 \le i \le s$, and $\sum _{i=1}^s |B_i| = n-st$. For each $i=1, \dots , s$, connect $x_i$ to all the vertices in $B_i$. Let G be the resulting graph.

Fig. 5

A graph with $({{\,\mathrm{pd}\,}}(G), {{\,\mathrm{reg}\,}}(G)) = (p,1).$

It is easy to see that G is a chordal and gap-free graph over n vertices. It is also clear to see that $\tau _{\max }(G) = (s-1)+(t-1)+a = p$. By [8, Corollary 6.9], we have ${{\,\mathrm{reg}\,}}(G) = \nu (G) = 1$. Moreover, it follows from [4, Corollary 5.6] (see also [5, Theorem 3.2] and [14, Corollary 3.33]) that ${{\,\mathrm{pd}\,}}(G) = \tau _{\max }(G) = p$. $\square$

For simplicity of the statement of our next result, given an integer $n \ge 2$, let

$$\begin{aligned}&{{\,\mathrm{pdreg}\,}}(n) = \{(p,r) ~\big |\\&\quad \text {there is a graph { G} over { n} vertices}: {{\,\mathrm{pd}\,}}(G) = p, {{\,\mathrm{reg}\,}}(G) = r\}. \end{aligned}$$

Theorem 1.4 basically states that $(p,1) \in {{\,\mathrm{pdreg}\,}}(n)$ for any integer p with $2\sqrt{n}-2 \le p \le n-1$. The next corollary is an immediate consequence of Theorem 1.4.

Corollary 5.6

Let $r \le n/2$ be positive integers. We have $(p,r) \in {{\,\mathrm{pdreg}\,}}(n)$ for any integer p with

$$\begin{aligned} 2\sqrt{n-2(r-1)}+r-3 \le p \le n-r. \end{aligned}$$

Proof

By Theorem 1.4, for any integer $p'$ such that

$$\begin{aligned} 2\sqrt{n-2(r-1)}-2 \le p' \le n-2(r-1)-1, \end{aligned}$$

there is a graph H over $n-2(r-1)$ vertices for which ${{\,\mathrm{pd}\,}}(H) = p'$ and ${{\,\mathrm{reg}\,}}(H) = 1$. Let $H'$ be the graph consisting of $r-1$ disjoint edges. It is easy to see that ${{\,\mathrm{pd}\,}}(H') = r-1 = {{\,\mathrm{reg}\,}}(H')$.

Let G be the disjoint union between H and $H'$. Since the projective dimension and regularity are additive with respect to disjoint unions of graphs, it follows that ${{\,\mathrm{pd}\,}}(G) = p'+(r-1)$ and ${{\,\mathrm{reg}\,}}(G) = 1+(r-1) = r$. The assertion is proved by taking $p' = p - (r-1)$. $\square$

Remark 5.7

One of the referees for this paper asked if the graphs in Corollary  5.6 could be constructed to be connected graphs. We do not know the answer to this natural question.

Note that $\lceil 2\sqrt{n-2(r-1)}\rceil +r-3 \ge \lceil 2\sqrt{n}\rceil -2$. That is,

$$\begin{aligned} \big [\lceil 2\sqrt{n-2(r-1)}\rceil +r-3, n-r\big ] \subseteq \big [\lceil 2\sqrt{n}-2\rceil , n-1\big ]. \end{aligned}$$

In other words, as ${{\,\mathrm{reg}\,}}(G)$ gets larger, the spectrum of ${{\,\mathrm{pd}\,}}(G)$ appears to become smaller. Further computation does suggest that this should be true.

Conjecture 5.8

Let $r,n \ge 2$ be arbirary integers. If $(p,r) \in {{\,\mathrm{pdreg}\,}}(n)$ then $(p,r-1) \in {{\,\mathrm{pdreg}\,}}(n)$.