Natural Time, Nowcasting and the Physics of Earthquakes: Estimation of Seismic Risk to Global Megacities

Abstract

Natural Time (“NT”) refers to the concept of using small earthquake counts, for example of M > 3 events, to mark the intervals between large earthquakes, for example M > 6 events. The term was first used by Varotsos et al. (2005) and later by Holliday et al. (2006) in their studies of earthquakes. In this paper, we discuss ideas and applications arising from the use of NT to understand earthquake dynamics, in particular by use of the idea of nowcasting. Nowcasting differs from forecasting, in that the goal of nowcasting is to estimate the current state of the system, rather than the probability of a future event. Rather than focus on an individual earthquake faults, we focus on a defined local geographic region surrounding a particular location. This local region is considered to be embedded in a larger regional setting from which we accumulate the relevant statistics. We apply the nowcasting idea to the practical development of methods to estimate the current state of risk for dozens of the world’s seismically exposed megacities, defined as cities having populations of over 1 million persons. We compute a ranking of these cities based on their current nowcast value, and discuss the advantages and limitations of this approach. We note explicitly that the nowcast method is not a model, in that there are no free parameters to be fit to data. Rather, the method is simply a presentation of statistical data, which the user can interpret. Among other results, we find, for example, that the current nowcast ranking of the Los Angeles region is comparable to its ranking just prior to the January 17, 1994 Northridge earthquake.

1 Introduction

In this paper, we discuss the idea of nowcasting (Rundle et al. 2016), a term originating from economics and finance. The goal of nowcasting is to determine the current state of the regional system of earthquake faults, or to put it another way, the current state of progress through the recurring regional cycle of earthquakes. This is in contrast to forecasting, which is the calculation of probabilities of future large earthquakes. Our nowcasting approach is based on the use of natural time, a term first used by Varotsos et al. (2005, 2011) and subsequently by Holliday et al. (2006). It has also been proposed that natural time analysis can be used in fields as diverse as biology, medicine, and finance (Varatsos et al. 2005, 2011). We emphasize that the term “earthquake cycle” refers not to events on an individual fault, but to the recurring events in a seismically active region (Sornette and Knopoff 1997).

Earthquake nowcasting builds on the idea that driven threshold systems such as earthquake fault systems often display a power-law distribution of event sizes or magnitudes. While these bursts of activity are observed at all scales, the largest events are usually of most interest. For earthquakes, these largest events are the magnitude 6 + events that cause the most damage and injuries. Interspersed between these largest events are many smaller events of varying sizes and magnitudes.

Taken together, these small and large events are distributed in a scale-invariant power-law statistical distribution of magnitude. The Gutenberg–Richter magnitude–frequency law (Gutenberg and Richter 1942; Scholz 1990) is a simple model of this distribution which is found to be applicable over large spatial domains and over long time intervals. The GR model has two parameters, a and b, which must be fit to the observed data:

$$Log_{10} N = a - bM$$

(1)

where N is the number or frequency of earthquakes having magnitudes larger than M. Typically, b ~ 1.

For the case of earthquake seismicity, we define natural time as the count of small earthquakes (say, 4 ≤ M < 6) since the last large earthquake (say M ≥ 6,). As a simple example of the use of natural time to rank the current hazard of a defined seismically active region, consider the region defined by the circle of radius 100 km around Los Angeles. In California, where b ≈ 0.9, there are then approximately 63 earthquakes 4 ≤ M < 6 for each M ≥ 6 earthquake. Therefore, we can make the general observation that, once 500 such small earthquakes have occurred since the last large earthquake, it would be reasonable to expect that a large earthquake might occur in the relatively near future. Of course, it may be years before that large event might occur, but this is the general idea behind nowcasting.

In fact, we can say that at the present time (October, 2017), there have been 94 earthquakes 4 ≤ M < 6 in that circular region of 100 km around Los Angeles (latitude 34.0522^oN, longitude 118.2437^oW). Just prior to the M6.7 Northridge earthquake on January 17, 1994, there had been 96 earthquakes 4 ≤ M < 6 since the February 9, 1971 M6.6 San Fernando earthquake. On this basis, we can conclude that the nowcast ranking of Los Angeles has returned to its pre-Northridge hazard level.

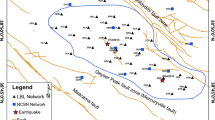
Over smaller spatial domains and shorter time intervals, the actual statistics of the observed number or frequency of earthquakes can depart considerably from the simple model (1). A good example is shown in Fig. 1a, b. On the left in Fig. 1a, we see a map of a large region surrounding the city of San Diego, USA, between 24^o N and 43^o N Latitude, and between 128^o W and 110^o W Longitude. In the center of the map, there is a circle of radius 400 km surrounding the city of San Diego. We then construct the Gutenberg–Richter (GR) number–magnitude statistics in Fig. 1b. The statistics represented by the square symbols are derived from all earthquakes in the large region having magnitudes greater than the completeness magnitude of M3.0 since 1970, at depths less than 200 km, contained within the ANSS Composite Catalog (ANSS 2017).

Fig. 1

a Map of earthquakes having magnitude M ≥ 6.5 near San Diego since 1970. Circle centered on San Diego has radius R=400 km. b GR number–magnitude statistics. The upper blue square symbols are all earthquakes M ≥ 3 for the region as a whole since 1970. The lower green circles are all earthquakes 3 ≤ M< 6.5 since the last M ≥ 6.5 earthquake, which was the M7.2 El Major-Cucapah earthquake on 4/4/2010

The red line in Fig. 1b is the best fitting GR model, where the b value (slope) as shown is 0.91 ± 0.01. The fit of the model is taken between magnitudes M3.25 and M5.5, and we show the extension of the fit line to the X-axis, intersecting that axis at M8.1. The round symbols record similar data for all small earthquakes occurring only after the most recent M ≥ 7.0 earthquake within the 400 km radius circle surrounding San Diego. The blue dashed line is a GR line having the same slope as the red line for the large region b = 0.91.

It can be seen that, whereas earthquake symbols in the large region closely follow the red dashed GR line up to M7.5, recent events in the circular region closely follow the blue dashed line for events less than M4.5. For earthquakes having M > 4.5, the round symbols fall below the blue dashed line. Thus, it would appear that there is a deficit of larger earthquakes that will be eventually filled in by the occurrence of large events, assuming that the GR statistics are the same for both the large and small regions.

There are many other similar examples. In Fig. 2a, b we show images for Athens, Greece. Here, we assume a completeness magnitude of M4.0, and show both the large region, together with the 400 km radius circular region surrounding the city of Athens. A similar pattern of deficit of larger earthquakes (M > 5.5) can be seen for the local events within the circle. It can also be seen that a better estimate of the completeness magnitude is about M ~ 4.5. Yet another example is shown in Fig. 1 of Holliday et al. (2016) for the Tokyo, Japan region.

Fig. 2

a Map of earthquakes having magnitude M ≥ 6.5 near Athens, Greece since 1970. Circle centered on Athens has radius R=400 km. b GR number–magnitude statistics. The upper blue square symbols are all earthquakes M ≥4 for the region as a whole since 1970. The lower green circles are all earthquakes 4 ≤M <6.5 since the last M ≥6.5 earthquake, an M6.5 event on 11/17/2015

2 Statistical Physics of Seismicity: Ergodic Property and Phase Transitions

The fundamental assumption of Holliday et al. (2016) is that a deficiency of large earthquakes within a local region contained within a seismically active larger region will eventually be filled in by the occurrence of large earthquakes. The idea is that the statistics of smaller regions over long times will be the same as the statistics of the larger region over large spatial domains and long times. The basis is the idea that seismic activity is characterized by ergodic dynamics (Ferguson et al. 1999; Tiampo et al. 2003, 2007). Ergodic behavior has been demonstrated for observed seismicity in locations as diverse as California, the Iberian Peninsula, and Eastern Canada.

The ergodic property of seismicity was established using the metric published by Thirumalai and Mountain (1989, 1992). An ergodic system is one in which ensemble averages yield the same result as time averages. In our case, the ensemble average is equivalent to a spatial average, inasmuch as a large seismically active region is regarded as being made up of non-overlapping subdomains of smaller seismically active regions.

The physical picture, common in statistical mechanics of complex systems, is discussed in the papers by Ferguson et al. (1999); Tiampo et al. (2003, 2007). The system evolves on a time-dependent energy landscape (Wales 2004) in which the system resides in one of a large number of scale-invariant free energy minima or “wells” that dot the landscape. Fluctuations within the energy well are associated with the scale-invariant, power-law, small magnitude end of the magnitude–frequency distributions. As the topography of the landscape is constantly evolving, there will occasionally be times when the system escapes from its local energy well in a nucleation event, subsequently landing in another nearby energy well. The nucleation event is associated with a large magnitude earthquake.

This picture of a nucleation event is entirely general, and applies to the dynamics of many statistical physics systems characterized by first-order phase transitions (Rundle et al. 2003). First-order transitions are the mechanisms by which complex dynamical threshold systems evolve by means of sudden, spontaneous events. We note that one of the signatures of fluctuations in energy landscapes is the characteristic, statistical distribution of seismicity averaged over many cycles of activity. Typically, these fluctuations take the form of the Fisher–Stauffer droplet model, which is common in the study of percolation and phase transitions:

$$n\left( s \right) = \frac{{n_{\text{o}} }}{{s^{\tau } }} \exp \left\{ { - \left( {\frac{s}{{s_{\text{o}} }}} \right)^{\sigma } } \right\},$$

(2)

where s is the droplet or cluster size, $n_{\text{o}}$ is a constant, $s_{\text{o}}$ is a scale factor, and $\tau$ and σ are scaling exponents (Stauffer and Aharony 1994; Hoshen and Koppelman 1976). In addition, σ is called the “surface exponent”, since its value characterizes properties of the surface of the nucleating droplets in relation to the bulk or interior of the droplet. For the probability density functions characterizing nearest-neighbor site percolation, $s_{\text{o}}$ is related to the value of the occupation probability and thus to the correlation length of the system.

An important special case of the scaling exponents in (1) occurs when the system is mean field, or even near the mean field condition, in which all components of the system interact over long spatial distances (Stauffer and Aharony 1994; Rundle and Klein 1993; Rundle et al. 2003; Klein et al. 2007). In that case, when interactions are long range, it is found that $\tau = 2.5$, $\sigma = 1$. Near mean field systems in particular are interesting because they imply that phenomena such as metastability and hysteresis are to be expected, together with nucleation droplets that have spatial dimensions on the scale of the correlation length (Klein et al. 2007).

3 Average Earthquake Statistics

As an example, consider the statistics of seismicity averaged over many earthquake cycles in California, where the data are best (Fig. 3). In particular, we will determine the configuration of the average earthquake statistics for “small” magnitude events preceding “larger” magnitude events. We assume a completeness magnitude threshold of M3.0, and determine the average earthquake statistics leading up to large events of M ≥ 5.0, and for M ≥ 6.0. Thus, we are interested in examining earthquake cycles for earthquakes of M ≥ 5.0 and M ≥ 6.0.

Fig. 3

Epicenter maps for California. a All 732 earthquakes since 1932 for M ≥ 5. b All 81 earthquakes since 1932 for M ≥ 6

In Fig. 3, we show the domain of interest, which consists of the region of California–Nevada–Mexico between 32^oN and 45^oN Latitude, and between 114^oW and 130^oW Longitude. Figure 3a shows the 732 M ≥ 5 earthquakes in this region in the catalog, while Fig. 3b shows the 81 earthquakes with M ≥ 6. For the M ≥ 5 earthquake cycles, we construct the GR number–magnitude statistics for all the small events 3.0 ≤ M < 5.0, then normalize by division by 731, the number of M ≥ 5 earthquake cycles. The results are shown in Fig. 4 for Log₁₀ (number) vs. Magnitude.

Fig. 4

Average GR number–magnitude statistics for small earthquakes 3 ≤ M < 5 in California in the region shown in Fig. 3a. Red line shows a fit to the data between magnitudes 3 ≤ M ≤ 5. Green line is a fit to Eq. (5), the droplet model

The red line is a GR fit to the data between the assumed completeness magnitude of M3.0, and M4.5. The green line is a fit to a Fisher–Stauffer droplet-type model equation similar to (2) that we now discuss.

We assume that droplet size can be measured by the elastic energy released during the earthquake, which is the seismic moment of the earthquake. Using base 10 instead of base e, we have:

$$n\left( W \right) = \frac{{n_{\text{o}} }}{{W^{\tau - 1} }}10^{{\left\{ { - \left( {\frac{W}{{W_{\text{o}} }}} \right)^{\sigma } } \right\}}}$$

(3)

for the number of earthquakes having seismic moment larger than W. Equation (2), which is a survivor function, is then approximately valid in the limit of large W _o, which applies to the scaling regime for nucleation and critical phenomena (Stauffer and Aharony 1994).

Using the definition of seismic moment in terms of magnitude (Scholz 1990):

$$1.5M = Log_{10} \left( W \right) - 9.0$$

(4)

we find:

$$Log_{10} [n\left( M \right)] = a - b\;M - 10^{{1.5\sigma \;(M - M_{\text{o}} )}}$$

(5)

where:

$$a = Log_{10} (n_{o} ) {-} 9.0/(\tau - 1)$$

(6)

and

$$b = 1.5/(\tau - 1)$$

(7)

We fit Eq. (3) to the data, using the values of a and b determined by fitting the usual GR (red) line to the small magnitude end between 3.0 ≤ M < 4.5. We see that $b = 0.93 \pm .02$, implying that $\tau \sim 2.61$, near the value of $\tau \sim 2.5$ characteristic of mean field and near mean field systems. Likewise, we find that $\sigma = 1.0 \pm 0.37$, which is the value for mean field systems. The physical significance of this as it relates to earthquakes has been discussed by Klein et al. (2007). We carry out a similar analysis for cycles of earthquakes larger than M ≥ 6 and show the results in Fig. 5. Fitting the data between 3.0 ≤ M < 5.0, we find that $b = 0.90 \pm .01$, thus $\tau \sim 2.67$. In addition, $\sigma = 0.99 \pm 0.38$ as before. Note that Main and Burton (1984) have derived an expression similar to (5).

Fig. 5

Epicenters of 136 earthquakes M ≥ 6.5 since 1970 in a region of size 4000 × 4000 km at depths less than 100 km near Tokyo, Japan. Blue ellipse is a circle of radius 200 km surrounding Tokyo

We point out that many of the earthquakes shown on the maps of Fig. 3 are located far offshore, where there are no seismometers to record small earthquakes. We would, therefore, expect that the completeness threshold for many of these offshore locations would be at magnitudes larger than 3.0. The implication is that the actual b value for the scaling line might be closer to $b\sim 1$, and therefore that $\tau \sim 2.5$.

The fact that these scaling exponents, τ and σ, have values close to their mean field values, indicates that seismicity probably has the ergodic property, and thus that time averages should be equal to ensemble or spatial averages. In turn, this means that the fundamental assumption of nowcasting, and of the forecasting method described in Holliday et al. (2016), has a sound basis. Or put more simply, a deficiency of large earthquakes in the GR statistics, which are not present in Fig. 4, must eventually be filled in by the occurrence of large earthquakes.

4 Application to Megacities: Nowcasting

4.1 Method

In earthquake fault systems, a critical problem is the estimation of the state of stress in the earth, its relation to the failure strength of the active faults in a region, and the rate of stress accumulation (Scholz 1990). Determining the values of these parameters would allow researchers to estimate the proximity to failure of the faults in the region. This would be an answer to the question of “how far along is the region in the earthquake cycle?”. However, it is not possible to determine the state of stress to anywhere near the accuracy needed to answer this question. What can be done is to use proxy data, counts of small earthquakes since the last large earthquake in local regions, and use the statistics of regional events to relate the count of small earthquakes to progress through the regional earthquake cycle.

Our goals are to assign a number to a defined small geographic region at a given time, and to characterize the current potential for a “large” earthquake to occur in the region. We denote the magnitude of the “large” earthquake as $M_{\lambda }$. “Large” in this sense means having the potential to cause damage or injuries if it were to occur close by. We compute the potential using “small” earthquakes, whose magnitude is denoted by M _σ . The large earthquake magnitude is selected by a procedure described below, whereas the small earthquake magnitude is typically set by the catalog completeness level, but can be also viewed as a free parameter within a certain range.

The Gutenberg–Richter magnitude–frequency relation (Gutenberg and Richter 1942) can be used to show that the number of small earthquakes having magnitudes larger than M _σ but less than magnitude $M_{\lambda }$ is on an average a known value N. We can calculate N using the Gutenberg–Richter law for the average number N _avg of earthquakes greater than M:

$$N_{avg} = 10^{a} 10^{ - bM}$$

(8)

where the b value is typically a number near 1 and the value of a is set by the level of seismicity in the region (Scholz 1990).

If we denote by $n_{\sigma }$ the number of earthquakes having magnitude larger than M _σ , and by $n_{\lambda }$ the number of earthquakes having magnitude larger than $M_{\lambda }$, we find:

$$N = \frac{{n_{\sigma } - n_{\lambda } }}{{n_{\lambda } }}$$

(9)

$$N = 10^{{ b\left( {M_{\lambda } - M_{\sigma } } \right)}} {-} 1$$

(10)

As the number of small earthquakes since the last large earthquake increases with time, the likelihood or potential for another large earthquake increases. The number of small earthquakes is often used as a measure of the passage of natural time for the earthquake system (Varotsos et al. 2005; Holliday et al. 2006).

Mathematically, we can express the potential for a large earthquake to occur having magnitude larger than $M_{\lambda }$ by computing the cumulative distribution function (CDF) of small earthquakes of magnitude larger than M _σ but less than $M_{\lambda }$: $M_{\sigma } \le M \le M_{\lambda }$. This CDF can be computed by considering a large geographic region with a substantial number of earthquakes having magnitude $M_{\lambda }$ or larger. The number of large earthquake “cycles” is then 1 less than the number of large earthquakes.

To compute the cumulative distribution, we tabulate the number of small earthquakes for each large earthquake cycle from an appropriate database such as the ANSS earthquake catalog (ANSS 2017), then use this to define the probability density function (PDF) and the cumulative distribution function (CDF) by standard methods (e.g., Bevington and Robinson 2003).

Once we have the CDF, we can then use the current count of small earthquakes $n(t)$ at time t to compute the current value of the CDF, $P\{ n \le n(t)\}$. Note that t is the (calendar) time of the last large earthquake, and n(t) is the number of small earthquakes since the last large earthquake. This value is then assigned at time t as the Earthquake Potential Score (EPS):

$${\text{EPS }} \equiv P\{ n \le n(t)\}$$

(11)

We interpret the EPS as the progress of the small area through the earthquake cycle, and thus the potential for the occurrence of the next large earthquake having magnitude larger than $M_{\lambda }$. By construction, EPS will increase monotonically with time since the last large earthquake. It will reset to ${\text{EPS}} = P\{ n \le n(t = 0)\} = 0$ immediately after the next large earthquake, and then again begin to increase monotonically until the next large earthquake occurs. We note that the nowcasting method does not, a priori, involve a model, it is only a process of tabulating and interpreting data. However, to the extent that the results have meaning, it is a transparent way of estimating the progress of a region through the seismic cycle of large earthquakes.

As an example of these calculations, Fig. 5 shows a map within which is the city of Tokyo, Japan, embedded at the center of a 4000 × 4000 km geographic region. A blue circle of radius 200 km surrounds Tokyo on the map (the circle appears as an ellipse due to the map projection). The large region is used to collect the statistics for the nowcast calculation. Small earthquakes within the circle that have occurred since the last M > 6.5 large earthquake on 07/30/2011 are used to compute the nowcast. All earthquakes, small and large, are constrained to have depths no larger than 100 km.

The corresponding GR number–magnitude statistics are shown in Fig. 6. Note that the completeness magnitude, which has been assumed to be M ≥ 4.0, is actually closer to M ~ 4.5 for the Tokyo region. Recall that whereas the blue square symbols and red line in Fig. 6 represent all earthquakes occurring in the large geographic region, the green circle symbols and blue line represent only the earthquakes occurring within the circular region since the most recent M ≥ 6.5 earthquake in the circle, which was an M6.5 event on 07/30/2011. Also recall that the blue dashed line has the same slope, b = 1.09, as the red dashed line by definition.

Fig. 6

Gutenberg-Richter number-magnitude statistics. The upper blue square symbols are all earthquakes for the Japan region in Fig. 5 since 1970. The lower green circles are all earthquakes in the 200 km radius circle at depths less than 100 km around Tokyo since the last M > 6.5 earthquake, an M6.6 event on 4 November 2011

It should be noted that aftershocks are treated no differently than background seismicity in the natural time counts. The difference is that in clock time, aftershocks are highly clustered in time, whereas in natural time, the events are evenly spaced and not clustered. So in natural time, there is no point in declustering events in time, or for that matter, in space. Nowcasting, therefore, uses all events, without the need to categorize events as aftershocks, background, or some other type.

Figure 7 shows the Earthquake Potential Score for the circular Tokyo region. There have been 917 small earthquakes since the last M6.5 event, corresponding to an EPS score of 92.2%. By this measure, the Tokyo region is near the end of its current earthquake cycle for events M ≥ 6.5.

Fig. 7

Nowcast for M ≥ 6.5 earthquakes within the 200-km circle around Tokyo, Japan, shown in Fig. 6. Green bars are a histogram of the number of small earthquakes arising from the 135 earthquake cycles in the large region. Red curve is the CDF, and blue dashed curve is the Poisson CDF with the same mean. Red dot is the current number of small earthquakes since the last large M6.5 event on 7/30/2011 in the blue circle. Red thermometer on the right side is a pictorial representation of the current state of the earthquake cycle

There were 179 large earthquakes in Fig. 6, thus 178 intervals, which are represented by the binned bars in the histogram. The increasing red curve is the CDF $P\left\{ {n \le n\left( t \right)} \right\}$ constructed from the 178 large earthquake intervals. The dashed blue curve is the Poisson distribution having the same mean as the CDF $P\{ n \le n(t)\}$. The red dot marks the position of the current small earthquake count. There have been 917 earthquakes in the region having magnitudes $M_{\sigma } \ge 4.0$ since the last $M_{\lambda } \ge 6.5$ event on 2011/07/30. The red “thermometer” on the right side is a visual representation of the current cumulative probability (EPS), which is EPS = 92.2%.

4.2 Automated Web Application

To expedite the process of computing and comparing the current relative risk level of various global cities, we have developed a simple automated web application using Python, HTML, CSS and Javascript. The workflow for this app is:

• Python code is invoked to download the data from ANSS, tabulate the nowcast CDF, build and store the images for epicenter map, nowcast, number–frequency relations, and an XML file that is later read by the web app.

• The HTML, CSS and Javascript are then used to access the XML file, display the images, and display and rank the data in tabular form.

A screenshot of this site is shown in Fig. 8 for a large region of 4000 × 4000 km around Taipei, Taiwan. In the next section, we discuss results using this app, and in particular we carry out a simple sensitivity analysis of nowcasting parameters.

Fig. 8

Screenshot of the web app described in the text. Data in the table represent the seven megacities, the current nowcast, and statistical data as described in the accompanying text

The first column of the Table in Fig. 8 contains the city at the center of the 200-km circle embedded within a region of size 4000 × 4000 km. The second column contains the nowcast EPS score computed using the catalog on the date and time listed at the top. The third column contains the date of the most recent M ≥ 6.5 earthquake within the city circle, and the fourth column contains its magnitude. The fifth column contains the count of small earthquakes since the last large earthquake within the city circle. The sixth column is the mean number of small earthquakes between large earthquakes in the large geographic region, and the seventh column is the standard deviation. The eighth and final column is the number of large earthquakes within the large geographic region, so the number of earthquake cycles is 1 less than the number of large earthquakes.

4.3 Sensitivity Analysis

Here, we seek to determine the sensitivity of EPS values to changes in the parameters characterizing the statistics, in particular the size of the region from which the basic statistics are drawn. Tables 1, 2, 3 show data computed for a large region of size 3000 × 3000 km, 2000 × 2000 km, and 1500 × 1500 km, respectively.

The exact choice of parameters will in practice be determined by the uses to which the EPS values are put. All data are computed for a volume containing each city of radius 200 km, depth 100 km, and for large earthquakes of magnitude M ≥ 6.5. Thus, we compute EPS values for M ≥ 6.5 earthquake cycles in the following Tables 1, 2, 3 and 4 that are of the same format of Fig. 8. We then compile the comparisons in Table 4.

Table 1 EPS Statistics for a large region of size 3000 × 3000 km EPS volume for data is 200 km radius circle, depth 100 km large earthquakes arc magnitudes M ≥ 6.5

Table 2 EPS Statistics for a large region of size 2000 × 2000 km EPS volume for data is 200 km radius circle, depth 100 km Large earthquakes are magnitudes M ≥ 6.5

Table 3 EPS Statistics for a large region of size 1500 × 1500 km EPS volume for data is 200 km radius circle, depth 100 km Large earthquakes are magnitudes M ≥ 6.5

Table 4 EPS scores for seven cities and regions of varying sizes for M6.5 earthquakes

Note that the assumed completeness magnitude for the two US cities, Los Angeles and San Francisco, is M3.0, whereas the completeness magnitude for the other cities was set at M4.0. This difference has an interesting effect as we now discuss. Examining Tables 1, 2, 3 and 4, it can be seen that the EPS scores for Tokyo, Taipei, Manila, Lima and Ankara are all fairly consistent, but that the EPS scores for San Francisco and Los Angeles are much larger at the largest geographic region sizes (4000 × 4000 km and 3000 × 3000 km) than they are at the smallest regions sizes (2000 × 2000 km and 1500 × 1500 km).

A difference like this is what one might expect if, in the larger regions, events of magnitude $M\sim 3$ were not recorded. In fact, these larger regions discussed in Table 1 are comprised of a large contribution from offshore earthquakes, which are relatively distant from the nearest land-based seismometers, therefore having a higher expected completeness magnitude. The smaller earthquakes would likely not be recorded as easily as when these events occur on land. Table 4 shows EPS summary data computed for a large region of varying sizes with two different completeness magnitudes for Los Angeles and San Francisco. Completeness magnitude M ~ 4 is the more consistent choice.

5 Discussion and Summary

We have discussed the idea of natural time and applied it to the problem of identifying the current seismic state of a fixed geographic region within its local earthquake cycle, a problem that we refer to as nowcasting. Rather than focusing on a specific fault or several faults, as is typical in geophysics and geology, we focus on the defined set of faults encompassed within the geographic area. This method avoids the developing problem now being recognized, that earthquakes on complex fault systems can jump from fault to fault in complex patterns that are essentially unpredictable in advance (Hamling et al. 2017).

Nowcasting is in fact a concept borrowed from economics and finance. Once the current state of the fault system in the defined area is better understood, it should be possible to better characterize the future state of the region and the calculation of forecast probabilities.

In our nowcasting method, we construct the cumulative probability distribution function (CDF) for the number of small earthquakes between large earthquakes during a sequence of earthquake cycles. These cycles occur in a large region around the area of interest, typically a local region around a specific geographic location. An advantage of this method is that it offers a systematic means of ranking locations as their current exposure to the earthquake hazard. We calculate an Earthquake Potential Score (EPS) that is found from determining the number of small earthquakes since the last large earthquake, then using the CDF found from the regional earthquake cycles. Specifically, if n(t) is the number of small earthquakes since the last large earthquake, the EPS score is defined to be: ${\text{EPS}} = P\{ n \le n(t)\}$, where P is the CDF of small earthquakes occurring between large earthquakes.

We also related the result from previous studies that observed earthquake seismicity indicates ergodic dynamics, that ensemble (spatial) averages should be interchangeable with temporal averages. This implies that the seismicity statistics of local regions over long times should be similar to the seismicity statistics over larger regions on much shorter time scales.

Practical applications of these ideas are straightforward. We constructed an automated web application using HTML, Javascript, CSS and Python to implement the nowcasting paradigm. We then showed that rankings of global cities could be constructed based on ANSS catalog data. We carried out a sensitivity analysis to determine the dependence of hazard rankings on large geographic region size and completeness magnitude. We found that a completeness magnitude of M4.0 gave the most consistent results for the US cities of Los Angeles and San Francisco, as well as for the global cities of Ankara, Lima, Manila, Taipei and Tokyo. For these calculations, we defined the “local” region as a region of radius 200 km around the city, and a maximum earthquake depth of 100 km for hazard from large earthquakes having magnitudes M ≥ 6.5.

One of the limitations of the nowcasting method as described here is related to regions in which the last major earthquake of interest predates the advent of instrumental recordings. In that case, it is not possible to produce a reliable count of the number of small earthquakes since the last large earthquake. An example of this is the case of the earthquakes in the New Madrid seismic zone in Missouri where a series of 4 M > 7 earthquakes occurred during the winter of 1811–1812, well before instrumental records began (Johnston and Schweig 1996). The nowcast risk of this geographic region is difficult to compute directly by the present method.

We conclude that our method offers a rapid and easily reproducible method to estimate the current level of progress through the earthquake cycle for any local region subject to seismic hazard worldwide.