Analysis and Indications on Long-term Forecasting of the Oceanic Niño Index with Wavelet-Induced Components

Abstract

The present paper provides an analysis and a long-term forecasting scheme of the Oceanic Niño Index (ONI) using the continuous wavelet transform. First, it appears that oscillatory components with main periods of about 17, 31, 43, 61 and 140 months govern most of the variability of the signal, which is consistent with previous works. Then, this information enables us to derive a simple algorithm to model and forecast ONI. The model is based on the observation that the modes extracted from the signal are generally phased with positive or negative anomalies of ONI (El Niño and La Niña events). Such a feature is exploited to generate locally stationary curves that mimic this behavior and which can be easily extrapolated to form a basic forecast. The wavelet transform is then used again to smooth out the process and finalize the predictions. The skills of the technique described in this paper are assessed through retroactive forecasts of past El Niño and La Niña events and via classic indicators computed as functions of the lead time. The main asset of the proposed model resides in its long-lead prediction skills. Consequently, this approach should prove helpful as a complement to other models for estimating the long-term trends of ONI.

1 Introduction

El Niño Southern Oscillation (ENSO) is an irregular climate oscillation induced by sea surface temperature anomalies (SSTA) in the Equatorial Pacific Ocean. An anomalous warming in this area is known as El Niño (EN), while an anomalous cooling bears the name of La Niña (LN). ENSO is well recognized as the dominant mode of interannual variability in the Pacific Ocean and it affects the atmospheric general circulation which transmits the ENSO signal to other parts of world; these remote effects are called teleconnections. Variations in the SSTA between warm and cold episodes induce changes in the occurrence of severe weather events, which dramatically affect human activities and ecosystems worldwide (see e.g. Glantz 2001; Hsiang et al. 2011). Therefore, ENSO predictions are of first importance to help governments and industries to plan actions before the occurrence of these phenomena.

Over the last two decades, many models have been proposed for forecasting ENSO by focusing on sea surface temperatures in the so-called Niño 3.4 region ($5^\circ$N–$5^\circ$S, $170^\circ$W–$120^\circ$W, see e.g. Mason and Mimmack 2002; Tippett and Barnston 2008; Zheng et al. 2006; Zhu et al. 2012). At the Climate Prediction Center (CPC), the official ENSO indicator is the Oceanic Niño Index (ONI), which is a 3-month running mean of SSTA in respect to 30-years base periods in this Niño 3.4 area and is the principal measure for monitoring, assessing, and predicting ENSO (CPC 2011). The EN (resp. LN) events are defined by the CPC as a 0.5 $^\circ$C positive (resp. negative) anomaly (called warm (resp. cold) episodes in the following) during at least 5 consecutive overlapping months of ONI. As it can be found in the literature, current predictions of ENSO based on dynamical or statistical models are most often limited to twelve months (e.g. Anthony et al. 2002; Mason and Mimmack 2002; Tippett and Barnston 2008; Zheng et al. 2006; Zhu et al. 2012) and have mixed success rates (Anthony et al. 2002). While it has been argued that accurate ENSO forecasts at longer lead times are out of reach (Fedorov et al. 2003; Thompson and Battisti 2001), some works provide evidence that long-term predictions are actually achievable (Chen et al. 2004; Jin et al. 1994; Desislava Petrova et al. 2016).

This paper fits into the category of long-term predictions. Indeed, we use wavelets to analyze and forecast the ONI signal for lead times ranging from a few months to three years. Wavelets are now well-established tools for signal analysis; their range of applications includes DNA analysis Arneodo et al. (2002), acoustics Saracco et al. (1990), climatology Deliège and Nicolay (2016a), Deliège and Nicolay (2016), Nicolay et al. (2009), Torrence and Compo (1998) to name just a few. Wavelet transforms are provided with a rather strong mathematical theoretical background and with an inverse transform, which is the backbone of reconstruction procedures (see e.g. Daubechies 1992; Daubechies et al. 2011; Mallat 1999). General assertions about the continuous wavelet transform (CWT) and the application to ONI are developed in Sect. 2. The components extracted for reconstructing the signal of interest carry valuable information which is then exploited to derive a simple predictive scheme for ONI, explained in Sect. 3. The prediction skills of the proposed model are then assessed and discussed in Sect. 4. Finally, we draw some conclusions and envisage possible future works in Sect. 5. Let us underline that the proposed approach is independent of any geophysical principles but is based only on the quasi-periodicity of the ENSO signal; the reader interested in physical considerations should consult Desislava Petrova et al. (2016) and the references therein. The philosophy of this paper is to provide a glimpse of the practicability of long-term predictions of ONI and to pave the way for further investigation in this direction.

2 Wavelet Analysis

This section is devoted to a wavelet analysis of ONI, which brings valuable information for modeling and predicting long-term trends of the signal. The principles involved are inspired from Deliège and Nicolay (2016), Nicolay (2011), Nicolay et al. (2009); more details about wavelets and the CWT can be found in e.g. Daubechies (1992), Mallat (1999), Yves Meyer (1993), Torrence and Compo (1998). The ONI signal used throughout the paper can be found at CPC (2011) and the last data considered is the season March–April–May 2016.

2.1 General Statements

First, we recall the basic notions regarding the CWT and explain a major difference between theory and practice. Given a wavelet $\psi$ (i.e. a smooth function with some general properties), the wavelet transform of a function f at time t and at scale $a>0$ is defined as

$$\begin{aligned} W_f(t,a)=\int f(x)\bar{\psi }\left( \frac{x-t}{a}\right) \frac{\mathrm{d}x}{a} \end{aligned}$$

where $\bar{\psi }$ is the complex conjugate of $\psi$. For time-frequency analyzes, one usually chooses a wavelet which is well-located in the frequency domain. In this case, we use the wavelet $\psi$ defined by its Fourier transform

$$\begin{aligned} \hat{\psi }(\nu )=\sin \left( \frac{\pi \nu }{2\Omega }\right) e^{{\frac{-\left( \nu -\Omega \right) ^2}{2}}} \end{aligned}$$

with $\Omega =\pi \sqrt{2/\ln 2}$, which is similar to the Morlet wavelet but with exactly one vanishing moment (Nicolay 2011). Since $\left| \hat{\psi }(\nu )\right| <10^{-5}$ if $\nu \le 0$, we can consider that $\psi$ is a progressive wavelet (i.e. is zero for negative arguments). Progressive wavelets have the convenient property of allowing an easy recovery of trigonometric functions. Indeed, if $\psi$ is such a wavelet and if $f(x)=\cos (\omega x)$, then

$$\begin{aligned} W_f(t,a)=\frac{1}{2}e^{it\omega }\overline{\hat{\psi }(aw)}. \end{aligned}$$

Consequently, at a given time t, if $a^*$ denotes the scale at which the function $a \mapsto \left| W_f(t,a)\right|$ reaches its maximum, then the identity $a^*\omega =\Omega$ holds. The value of $\omega$ can thus be obtained (if unknown) and the function f is recovered with the real part of its wavelet transform:

$$\begin{aligned} f(x)=2\mathfrak {R}(W_f(x,a^*)). \end{aligned}$$

For more complicated signals, it is often necessary to extract several components selected at particular scales of interest. The CWT then allows an almost complete reconstruction of the initial signal with smooth amplitude modulated–frequency modulated (AM–FM) components.

As usual, it is not as simple in practice because of the finite length of the signals. To have an accurate representation of f at a given time t with the CWT, we actually need to know the values of f in a neighborhood of t. Therefore, the signal has to be padded at its edges and the chosen padding irremediably flaws a certain proportion of the wavelet coefficients located at the beginning and at the end of the signal. In the case of the zero-padding of $f(x)=\cos (\omega x)$ ($x\le 0$) and with Morlet-like wavelets, it can be shown that $W_f(t,\Omega /\omega )$ is actually the expected value (as if there were no border effects) multiplied by a complex number $\rho (t)e^{i\theta (t)}$ such that $\rho (t)<1$, $t \mapsto \rho (t)$ is decreasing, $\theta (t)>0$ and $t \mapsto \theta (t)$ is increasing (which makes sense since the coefficients “are trying to converge” to zero as fast as possible). Except for such trivial cases, it is generally impossible to correct the border effects for AM–FM signals. Noticeable improvements can be made in the reconstruction of the initial signal (even at the borders) by iterating the process of computing the CWT and extracting the desired components until almost no energy is drained from the signal anymore (see Appendix A). Nevertheless, the wavelet coefficients still fall short when it comes to extrapolations and forecasts. The signal has to be padded judiciously so that the CWT may produce components that may be suitable for forecasting the signal at longer lead times, as shown in this paper.

2.2 Application to ONI

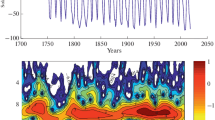
The CWT is applied to ONI and the associated wavelet spectrum (WS) is computed as

$$\begin{aligned} a \mapsto \Lambda (a)=E_t\left| W_f(t,a)\right| \end{aligned}$$

where $E_t$ denotes the mean over time (see Fig. 1). It can be observed that $\Lambda$ displays a significant amount of energy at periods of $\approx 17, 31, 43, 61, 140$ and 340 months, which is globally consistent with previous studies (see Desislava Petrova et al. 2016 and references therein). The associated components extracted from the CWT (with iterations) and named $c_{17},\ldots ,c_{340}$ are plotted in Fig. 2 along with the high-frequency seasonal and annual modes $c_6$ and $c_{12}$. It is important to note that the CWT allows a “flexible” representation of the signal, i.e. these components are actually AM–FM signals. The components $c_{17}, c_{31}, c_{43}, c_{61}$ are near-annual, quasi-biannual and two quasi-quadriennal modes of variability of ENSO and are largely discussed in Desislava Petrova et al. (2016) whereas $c_{140}$ and $c_{340}$ are likely linked with the tropical decadal and interdecadal Pacific variability (see e.g. Okumura 2013).

Fig. 1

Wavelet spectrum of the ONI signal based on data from 1955 to 2016. The main periods governing the signal can be easily identified and range from near-annual to decadal modes of variability

Fig. 2

The initial ONI signal (top) and the components extracted with the CWT and plotted from 1975 to 2016. The last one is displayed since 1950 for better vizualisation

The contribution of a given component c in the signal can be assessed through several indicators. First, the relative energy of c with respect to ONI (denoted s) is computed as

$$\begin{aligned} \epsilon _\mathrm{rel}=\frac{\left\| c\right\| }{\left\| s\right\| }, \end{aligned}$$

where $\left\| .\right\|$ denotes the energy of a signal from the signal analysis point of view, i.e. as the square of the $L^2$ norm. To ensure that c contains pertinent information, we also compute the relative accretion of energy that can be attributed to c as

$$\begin{aligned} \lambda _\mathrm{rel}=\frac{\left\| s\right\| -\left\| s-c\right\| }{\left\| s\right\| }. \end{aligned}$$

Finally, we compute the Pearson correlation coefficient (PCC) between c and s. These indicators can be found in Table 1 and confirm that $c_{17}$, $c_{31}$, $c_{43}$, $c_{61}$ and $c_{140}$ contain most of the information about the variability of ONI. We also calculated these indicators for the reconstructed signal $srec_8$ (sum of the 8 components extracted) and for $srec_4=c_{31}+c_{43}+c_{61}+c_{140}$. The first ones indicate that the reconstruction is almost perfect; we can add that the root mean square error (RMSE) is 0.04. Those related to $srec_4$ show that the low-frequency components capture a significant part of the variability of ONI (with RMSE $=0.349$). This observation is actually the one suggesting that long-term forecasts of ONI should be achievable.

Table 1 Relative energy, relative accretion of energy and correlation associated with the components with respect to ONI

The CWT brings other valuable information that turn out useful for conceiving a model for long-lead forecasts of ONI. Indeed, if we look at Fig. 2, it appears that $c_{31}, c_{43}, c_{61}$ and $c_{140}$ regulating the long-term variations of ONI are relatively stationary and should thus be easily modeled. Regrettably, since the high-frequency components $c_6, c_{12}$ and $c_{17}$ are quite volatile and unpredictable and as the nature of $c_{340}$ is uncertain, these will not be taken into account. Neglecting the high-frequency components can be seen as a “lesser of two evils” choice. On the one hand, trying to model and use them for long-term forecasting is overly hard; our attempts resulted in predictions that were globally worse than without using them because of their variability. On the other hand, omitting them inevitably leads to a loss of accuracy in the timing and intensity of EN and LN events. Besides leaving room for improvements, this second option turned out to be the most appropriate in the context of long-term forecasting of ONI. In consequence, we are led to build initial guesses on future values of the signal based on oscillating components with periods of 31, 43, 61 and 140 months. Their amplitude will be estimated through the wavelet spectrum and considered constant throughout the signal, whereas their phases will be evaluated for each prediction. When the first guess is made, the CWT will be applied to recover amplitude and frequency modulations and to provide a forecast in a natural way. This is detailed in the next section.

3 Forecasting Method

In this study, we focus on forecasting the last two decades of ONI, i.e. from January 1995 to April 2016. Data prior to 1995 is used as training set to calibrate the method. As mentioned, the idea is to construct components $y_i$ ($i \in I=\{31,43,61,140\}$) of the form

$$\begin{aligned} y_i(t)=A_i\cos \left( 2\pi t/i + \phi _i(t)\right) \end{aligned}$$

that can then be extrapolated effortlessly. The amplitudes $(A_i)_{i\in I}$ can be estimated easily with data until 1995. The calculation of the phases $(\phi _i)_{i\in I}$ is more challenging and needs to be done as accurately as possible to have efficient forecasts. The main ideas of the algorithm proposed for the whole procedure are described below and Appendix B shows a more detailed prototype of the code used to construct $y_{43}$. In addition, those auxiliary components $y_i$ and a detailed example of a forecast (through the forecasts of the individual components) are provided with a comparison with the “expected” components as supplementary material.

The values of the initial discrete ONI signal are noted s(t) for $t=1,\ldots ,T$, where s(T) is the last data available for the considered forecast. The forecasting scheme is the following.

• 1. First, we model the decadal oscillation. The amplitude $A_{140}$ is estimated with the WS of s (always until 1995 for the amplitudes) as 0.35 and we set

  $$\begin{aligned} y_{140}(t)=A_{140}\cos (2\pi t/140+2.02). \end{aligned}$$

  The value 2.02 is chosen so that $y_{140}$ is phased with $c_{140}$ in April 1974 (i.e. both reach a minimum).¹

• 2. We now work with $s_1=s-y_{140}$. The WS of $s_1$ gives $A_{61}=0.435$. The idea is to phase $y_{61}$ with the strongest warm events of $s_1$, which occur approximately every 5 years, and anti-phase $y_{61}$ with the weaker warm events occurring in between. More precisely, for each time $t\le T$, we find the position p of the last local maximum of $s_1$ such that $s_1(p)>0.5$. If $s_1(p)>0.9$ then we set

  $$\begin{aligned} y_{61}(t)=A_{61}\cos (2\pi (t-p)/61); \end{aligned}$$

  else

  $$\begin{aligned} y_{61}(t)=-A_{61}\cos (2\pi (t-p)/61). \end{aligned}$$

• 3. We now work with $s_2=s_1-y_{61}$. The WS of $s_2$ gives $A_{31}=0.42$. Now, the idea is to phase $y_{31}$ with the cold events of $s_2$, which occur approximately every 2.5 years. More precisely, for each time $t\le T$, we find the position p of the last local minimum of $s_2$ such that $s_2(p)<-0.5$ and we set

  $$\begin{aligned} y_{31}(t)=-A_{31}\cos (2\pi (t-p)/31). \end{aligned}$$

• 4. We now work with $s_3=s_2-y_{31}$. The WS of $s_3$ gives $A_{43}=0.485$. We set that $y_{43}$ has to explain the remaining warm and cold events of $s_3$ and we proceed as follows. For each time $t\le T$, we find the position p of the last local maximum of $s_3$ such that $s_3(p)>0.5$ and we set

  $$\begin{aligned} y_{43}^1(t)=A_{43}\cos (2\pi (t-p)/43). \end{aligned}$$

  Then we find the position p of the last local minimum of $s_3$ such that $s_3(p)<-0.8$ and we set

  $$\begin{aligned} y_{43}^2(t)=-A_{43}\cos (2\pi (t-p)/43). \end{aligned}$$

  Finally, we define

  $$\begin{aligned} y_{43}=(y_{43}^1+y_{43}^2)/2. \end{aligned}$$

• 5. We extend the signals $(y_i)_{i\in I}$ up to $T+N$ for N large enough (at least the number of data to be predicted). Then

  $$\begin{aligned} y=\sum _{i\in I} y_i \end{aligned}$$

  stands for a first reconstruction (for $t \le T$) and forecast (for $t > T$) of s.

• 6. We set $s(t)=y(t)$ for $t>T$, perform the CWT of s and extract the components $\hat{c}_j$ at scales j corresponding to 6, 12, 17, 31, 43, 61 and 140 months. These are considered as our final AM–FM components and $\hat{c}=\sum _j \hat{c}_j$ both reconstructs (for $t\le T$) and forecasts (for $t>T$) the initial ONI signal in a smooth and natural way.

4 Predictive skills

The predictive skills of the proposed model for the period 1995-2016 are tested in two ways. First, we show that El Niño and La Niña events that occurred during this period could have been anticipated years in advance. Then, we show that the PCC and RMSE of the retrospective forecasts as functions of the lead time are encouraging regarding long-term forecasts.

The predictions of EN and LN events 6, 12, 18, 24, 30 and 36 before the peak of the episode are displayed in Figs. 3 and 4. It can clearly be seen that the trend of the ONI curve can be predicted in advance and thus major EN and LN events can be forecasted long before they happen. One of the most interesting results is about the famous strong event of 1997/98, which is foreseen up to 3 years in advance with a lag of only 3 months. A similar observation can be made regarding the 2009/10 EN for which El Niño conditions are anticipated 2–3 years in advance with a lag of 3 to 6 months. Our model also suggests that the recent strong EN event of 2015/2016 might have been forecasted at least 18 months in advance and even classified as “strong EN” in mid 2014. However, it can be seen that the intensity of the most extreme EN events, e.g. 1997/1998 and 2015/2016, is underestimated. Nevertheless, since the occurrence of strong EN events seems to depend mainly on the local maxima of $c_{61}$, predicting that this component is about to reach a peak could be sufficient to warn of an upcoming strong event. Comparable observations can be made regarding the predictions of LN events, though the lags are generally delays of 3–6 months in this case.

Fig. 3

Forecasts of El Niño events 6 (green), 12 (red), 18 (blue), 24 (orange), 30 (cyan), 36 (magenta) months before the peak of the event. The black curve is the ONI signal. The arrows indicate the moment at which the El Niño condition (SSTA $>0.5\,^\circ$C) is reached

Fig. 4

Forecasts of La Niña events 6 (green), 12 (red), 18 (blue), 24 (orange), 30 (cyan), 36 (magenta) months before the peak of the event. The black curve is the ONI signal. The arrows indicate the moment at which the La Niña condition (SSTA <−$0.5\,^\circ$C) is reached. Note that the LN event of 2000 is a remnant of the one that occurred in 1999 (temperature anomalies do not even reach $0\,^\circ$C in between) and thus begins at the same moment (same black arrow); this observation also holds for the LN events of 2011 and 2012

It is important to recall that seasonality is not taken into account, which contributes to explain the delays and the underestimation of the intensities to some extent. The fact that we use constant amplitudes in the model plays a role as well since the real ONI components are actually AM–FM. This calls for further investigation in the modulations of the amplitudes and their potential phase-locking with their associated component. In addition, it can be asked whether the reference period (1950–1995) used to calibrate the method influences the results. Indeed, an intuitive idea would be to use data up to 2015 to produce a 12 months lead time forecast of the EN event of 2016. Nevertheless, only the amplitudes of the components $y_i$ depend on the training data. Since they are computed as mean amplitudes over 45 years of ONI, they barely change with a slightly larger or smaller reference period. For the record, the amplitudes obtained for the period 1950–2015 differ of at most 0.03 units from those used so far. As a consequence, at the end of the process, the forecast issued with this adaptation is almost identical to the prediction presented here (absolute difference $<0.01$). Hence, it appears that the influence of the reference period is limited and that improving the results in a significant way would require a different approach. Even though there is an exciting challenge ahead in trying to incorporate high-frequency components in the model and to modulate the amplitudes, the long-term trends are recovered and our predictions are satisfying, especially given the long-lead times considered and the simplicity of the model.

In a more “global” approach, we can now focus on the prediction skills of our model as functions of the lead time. For that purpose, the retrospective forecasts at 6, 12, 18, 24, 30 and 36 months lead times are plotted in Fig. 5. As a matter of information, they are computed and displayed from 1975 to show that the model also explains ONI variability prior to 1995 if the values of the amplitudes got in Sect. 3 had been obtained in the mid-70’s (as mentioned the rest of the algorithm does not depend on the training data). As already observed, most EN and LN events can be foreseen from 1 to 3 years in advance. The overall trend of the curve is almost always in agreement with observations, confirming that long-term predictions are possible. Using data until April 2016, we issued a forecast of ONI (plotted in Fig. 5), which predicts a relatively strong LN event during 2017. Finally, the prediction skills of the model are measured with the PCC and RMSE between the forecasted values and the initial signal as functions of the lead time; these indicators are plotted in Fig. 6. It appears that the skills of the model remain relatively stable and decrease slowly rather than abruptly as some other methods (Anthony et al. 2002). Although the performances are not remarkable at short lead times in comparison with Anthony et al. (2002), Desislava Petrova et al. (2016), the most interesting fact is that they are excellent at long lead times (>12 months). This is so because it is designed to capture and predict the long-term variability of the signal. Let us also note that, since ONI has almost zero mean (=0.03), its standard deviation (=0.84) can be viewed as the RMSE-skill of a model for which all the predictions are set to zero. As seen in Fig. 6, our model remains below this threshold while Fig. 6 in Anthony et al. (2002) suggests that it would not necessarily be the case for other models (this should be more carefully investigated since forecasts in Anthony et al. (2002) were actually operational, not retrospective). Consequently, it is necessary to underline that the proposed model should be used in complement with other methods because it brings helpful benefits regarding the long-term predictability of ONI.

Fig. 5

Retrospective forecasts of ONI at 6 (blue) and 12 (red) (then 18 and 24, 30 and 36) months lead time. On the first panel, the green curve is our forecast of ONI (issued in April 2016)

Fig. 6

RMSE and correlation between the forecasted values and the signal as functions of the lead time. The results for the period 1995–2015 are in blue. The green curve represents the results for the period 1975–2015 for the curious minds wondering what would be the skills if the model was applied as it is for a longer period of time. The black line in the first panel is the standard deviation of ONI. Since it has zero mean, this line can be viewed as the skill of a model where all the forecasted values are set to zero

5 Conclusion and Future Work

We carried out a wavelet analysis of the Oceanic Niño Index to detect the main periods governing the signal and to extract the components underlying its variability. The periods and modes in question are globally in agreement with previous studies and bring valuable information for the elaboration of a model predicting the long-term trends of the signal. The proposed model fits in the growing body of evidence suggesting that long-term predictions of ONI are much more possible than previously thought and shows that early signs of major EN and LN events can be detected years in advance. This model could improve our understanding and forecasting skills of EN and LN. More importantly, the proposed technique or, at least, the essence of the algorithm (i.e. phasing appropriate components with warm or cold events), could be combined with other models which are more accurate for short-term predictions. This complementarity could give rise to models able to predict ONI at a large range of lead times.

Future work will consist in incorporating the seasonal (near-annual and annual) variability to improve short-term predictions and the timing and intensity of EN and LN events in long-term forecasts, which remains the main strength of the model. Moreover, we will continue to work on the development of the prediction of the peaks of the components extracted from the CWT, which are the cornerstones of the model and dictate its forecasting skills. The time variations in the periods, phases and amplitudes will also be studied in more detail to improve the predictions. Due to the effects that EN and LN events induce worldwide, predictions 1–2 years ahead could be intelligently used to better prepare for the consequences.

Appendices

Appendix A: Iterations of the CWT

When it comes to extracting components from a signal s as accurately as possible, the CWT can be used several times to sharpen the desired modes. More precisely, if the components of interest are located at scales $(a_i)_{i\in I}$ (for some set of indices I), then at the first iteration one can extract $(c_i^1)_{i\in I}$ as

$$\begin{aligned} c_i^1(t)=2\mathfrak {R}(W_s(t,a_i)). \end{aligned}$$

Then repeat the process, i.e. the CWT and extraction at the same scales $(a_i)_{i\in I}$ but with

$$\begin{aligned} s_1=s-\sum _{i\in I}c_i^1, \end{aligned}$$

get the modes $(c_i^2)_{i\in I}$, repeat with $s_2=s_1-\sum _{i\in I}c_i^2$, and so on. Stop the process when the components extracted are not significant anymore, i.e. at iteration J if

$$\begin{aligned} \max \left\{ \left\| c_i^{J}\right\| ,i\in I\right\} <\alpha \ \max \left\{ \left\| c_i^{1}\right\| ,i\in I\right\} \end{aligned}$$

where $\left\| .\right\|$ denotes the energy (square of $L^2$ norm) of a signal and $\alpha$ is a threshold typically chosen as 0.01. The final components $(c_i)_{i\in I}$ are then obtained as

$$\begin{aligned} c_i=\sum _{j=1}^J c_i^j. \end{aligned}$$

Appendix B: Details for $y_{43}^1$

For simplification, let us write s instead of $s_3$ and y instead of $y_{43}^1$. If y is already known up to time $t-1$, here are the steps describing how to obtain y(t). We note $p(t-1)$ the position of the peak used to generate $y(t-1)=A_{43}\cos (2\pi (t-1-p(t-1))/43)$. We use a variable called lock to prevent abrupt changes from $p(t-1)$ to p(t). To obtain p(t), proceed as follows.

Then $y(t)=A_{43}\cos (2\pi (t-p(t))/43)$. Special mention for $y_{61}$ in order to better synchronize the forecasts with EN events: if it comes that $y_{61}$ reaches a peak before $s_1$, impose that $y_{61}$ stays at $A_{61}$.