Long-Term b Value Variations of Shallow Earthquakes in New Zealand: A HMM-Based Analysis

Abstract

The magnitude–frequency relationship is a fundamental statistic in seismology. Customarily, the temporal variations of b values in the magnitude–frequency distribution are demonstrated via “sliding-window” approach. However, the window size is often only tuned empirically, which may cause difficulties in interpretation of b value variability. In this study, a continuous-time hidden Markov model (HMM) is applied to characterize b value variations of New Zealand shallow earthquakes over decades. HMM-based approach to the b value estimation has some appealing properties over the popular sliding-window approach. The estimation of b value is stable over a range of magnitude thresholds, which is ideal for the interpretation of b value variability. The overall b values of medium and large earthquakes across North Island and northern South Island in New Zealand vary roughly at a decade scale. It is noteworthy that periods of low b values are typically associated with the occurrences of major large earthquakes. The overall temporal variations of b values seem prevailing over many grids in space as evidenced by a comparison of spatial b values in many grids made between two periods with low or high b values, respectively. We also carry out a pre-seismic b value analysis for recent Darfield earthquake and Cook Strait swarm. it is suggested that the mainshock rupture is nucleated at the margin of or right at low b value asperities. In addition, short period of pre-seismic b value decrease is observed in both cases. The overall time-varying behavior of b values over decades is an indication of broad scale of time-varying behavior associated with subduction process, probably related to the convergence rate of the plates. The advance in the method of b value estimation will enhance our understanding of earthquake occurrence and may lead to improved risk forecasting.

1 Introduction

The magnitude–frequency relationship, also known as the Gutenberg–Richter relation, is a fundamental statistic in seismology, which indicates the cumulative number of earthquakes N with magnitude M greater than or equal to $M_c$ follows the log-linear relation:

$$\begin{aligned} \log _{10}N=a-b(M-M_c), \end{aligned}$$

(1)

where a and b are constants and $M_c$ is the magnitude threshold. The constant b, i.e. b value, indicates the relative proportion of the number of small and large earthquakes, corresponding to $\beta$ in the exponential distribution of the magnitudes such as $F(M)=1-{\rm{e}}^{-\beta M}.$ The constant a measures seismicity rate.

The b value has received considerable attention. It is widely believed to reflect the ambient stress state and material heterogeneity. Rock fracture experiments in laboratory show that b is inversely proportional to the applied stress, see Scholz (1968) and Goebel et al. (2013). Field observations in underground mines suggest b is inversely correlated with the stress level. Observed high b values in Alaska and New Zealand subduction zones at depth about 90–100 km are regarded as a result of slab dehydration embrittlement, hence lowering effective stress (Wiemer and Benoit 1996). Nanjo et al. (2012) reports decade-scale decrease in b values prior to the M9-class 2011 Tohoku and 2004 Sumatra megathrust earthquakes. Schorlemmer et al. (2005) suggest the b value varies systematically for different style of faultings and could be used as an indicator of stress state. The relationship is applied for the calculation of recurrence time intervals of earthquakes and mapping magmatic chambers.

In global scale, the b value is typically close to 1. However, significant spatial and temporal heterogeneities of b values in smaller scale are claimed by Wiemer and Benoit (1996), Gerstenberger et al. (2001), Cao and Gao (2002), Wyss et al. (2008) and Nanjo et al. (2012), among many others. Meanwhile, some findings suggest the b value variability is an artifact due to lack of statistical rigor and should be interpreted with caution as a variety of manmade sources of uncertainties exist in the determination of b value, see Kagan (1999), Amorèse et al. (2010) and Kamer and Hiemer (2015). The reasons and interpretations of b value variability are debated.

One popular method to display b value variation over time is the ‘moving-window’ approach, in which the b value is estimated via maximum likelihood method or ordinary least square, usually with a time window centering at current event time and going through the catalogue event by event. The moving-window approach to the b value estimation is simple to implement. However, the tuning parameter, i.e. the window size, is often only selected empirically or manually, causing difficulties in interpretation of b value variability. Typically, the estimated b values resulted from moving-window approach may range from a rapid fluctuated b(t) to nearly a constant by purposely tuning the smoothing parameter, i.e. the window size.

In this study, a model-based approach is applied to demonstrate b value variations for medium to large shallow earthquakes over decades in North Island and northern South Island of New Zealand. The model applied in this analysis is a continuous-time hidden Markov model (CT-HMM), in which the magnitude–frequency distributions switch at several levels according to a latent Markov chain. Hidden Markov models (Zucchini and MacDonald 2009) are popular for its flexibilities in model formulation and wide applicabilities for characterizing regime switching and exploring heterogeneities appearing in time series. With quality catalogue accumulating over decades, it might be timely to display temporal variations of b values via a CT-HMM.

The CT-HMM is formulated in Sect. 3. In Sect. 4, the fittings of a two-state CT-HMM to medium and large shallow events across North Island and northern South Island are demonstrated. It is observed that the estimation is stable over a range of magnitude thresholds, which is ideal for the interpretation of b value variability. We also compare the fit of a two-state CT-HMM with that of a multi-state CT-HMM, a time-homogeneous b value model and a piecewise constant b value model in a number of periods divided roughly according to the time of major network upgrades. The comparison between the two-state CT-HMM and time-homogeneous b value model is implemented via the bootstrap likelihood ratio test. Generally, the temporal variations of b values of medium to large shallow earthquakes over decades in this region are well characterized by a two-state CT-HMM. By utilizing this model, the whole period in study is divided into several episodes characterized by either low or high b values. Finally, in this section, we check whether the occurrence times of strong shallow earthquakes around North Island and northern South Island are associated with the episodes of low b values. The overall b value is an average of b values among different regions across entire North Island and northern South Island, where significant spatial b value variations appear (see Sect. 6). We then carry out a spatial b value analysis to look into the spatial-temporal correlations of b values in Sect. 6. It is demonstrated that the overall temporal variations of b values seem prevailing over many grids in space. Among many possible factors, tectonic stress appears to be the most significant factor that contribute to this large scale of b value variations spatially. However, detailed spatio-temporal b value variations in smaller scale are beyond the scope of the current model to characterize. With quality catalogue data increasing, we then carry out a pre-seismic b value analysis for most recent Darfield earthquake and Cook Strait swarm in Sect. 5. Discussions and concluding remarks are given in Sect. 8.

2 Tectonic Settings, Data and Catalogue Completeness

2.1 Tectonic Settings and Data

Two distinct subduction zones exist in a region of transition for the Australian and Pacific plate boundary. The first stretches along the east coast of North Island from Tonga-Kermadec trench, bend westwards beneath Cook Strait with increasing obliquity of the plate convergence direction, and abruptly terminates roughly at the latitude of Chatham Rise. In this zone, the Pacific Plate is subducting beneath the Australian Plate. In the second zone, the Australian Plate is subducting beneath the Pacific Plate in the southwest of South Island.

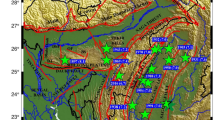
The data set used in this study is obtained from GNS Science of New Zealand via GeoNet (http://www.geonet.org.nz) in the March of 2014. The magnitude is determined by New Zealand version of local magnitude scale. Selected events (Fig. 1) occur either beneath land area or very close to the land, mainly around North Island and northern South Island where shallow events with depth ≤40 km are under good coverage by monitoring networks. The seismic zones under this study are not extended further north, partly because the tectonic setting changes from oceanic–continental convergence to oceanic–oceanic convergence within Tonga-Kermadec trench, and also partly because a discontinuity in seismicity and an offset between Hikurangi and Kermadec trench. Nevertheless, principal reason of excluding events that occurred in the northeast of North Island is lack of detectability and sparsity of the monitoring networks in early periods. The events located in the southwest of South Island are not included in this analysis since the tectonic settings are different. The depth of shallow earthquakes are poorly determined, mainly restricted to 5, 12, 33 km. It is agreed that events restricted to a depth less than 40 km actually occurred in this range, see Gerstenberger and Rhoades (2010). Epicentral distributions and occurrence times are typically highly clustered, see Fig. 1. Figure 1 shows the epicenter distribution of shallow earthquakes ($\ge$40 km) with magnitude greater than 4.5 since 1965 January 1 to 2014 March 20. Events encircled within the solid polygon of Fig. 1 are considered.

Fig. 1

Epicenter distribution of shallow earthquakes (depth $\ge$40 km) with magnitude greater than 4.5 since 1965 January 1–2014 March 20 in NZ catalogue. Events encircled within the polygon with vertexes $(170^{\circ }E, 43^{\circ }S)$, $(175^{\circ }E, 36^{\circ }S)$, $(177.5^{\circ }E, 36^{\circ }S)$, $(180^{\circ }E, 37^{\circ }S)$, $(180^{\circ }E, 38^{\circ }S)$, $(173^{\circ }E, 45^{\circ }S)$ are used in this analysis. Darfield earthquake zone, Cook Strait swarm zone and volcanic zones in central North Island are encircled by dash lines and labeled by “A”, “B” and “C”, respectively

2.2 Catalogue Completeness

Evaluating completeness cutoffs $M_c$ of magnitude is necessary for reliable b value estimation. Some methods are based on the validity of G–R law and fitting G–R relation to the observed frequency–magnitude distributions. The magnitude at which the lower end of the frequency–magnitude distribution departs from log-linear relation of the G–R law is taken as an estimate of $M_c$. Some representative methods such as goodness-of-fit test (GFT) and median-based analysis of the segment slope (MBASS) with software implementation are detailed in Woessner and Wiemer (2005) and Mignan and Woessner (2012). More sophisticated methods were suggested recently by Mignan (2012), Mignan and Chouliaras (2014) through exploring spatial heterogeneities of the completeness cutoffs of the catalogue events. The goodness-of-fit test is measured by the absolute difference of the number of events in magnitude bins between the observed and synthetic or fitted Gutenberg–Richter distribution, normalized by the total number of events. The score of goodness-of-fit test is given by

$$\begin{aligned} R=100-\frac{\sum _i|B_i-S_i|}{\sum _i B_i}100, \end{aligned}$$

where $B_i$ and $S_i$ are the observed and predicted cumulative number of events in each magnitude bin. $M_c$ is found at the first magnitude cutoff at which the score achieves a given confidence level such as 90 or 95%. MBASS method calculates segment slopes of (noncumulative) magnitude–frequency distributions at consecutive points in magnitude range. Then, the sequence of segment slopes are replaced by the corresponding rank statistics. A robust nonparametric test statistic called Wilcoxon–Mann–Withney test or Wilcoxon rank sum test is applied to detect any significant deviation from the median of the segment slopes by summing up the ranks from beginning of the sequence to that point. If this summation at that point obviously deviates from the median at some specified significance levels, i.e. $5\%$, the point is declared as a changepoint of the (noncumulative) magnitude–frequency distribution. The procedure is iterated several times in each segment, which is divided by the identified changepoints. $M_c$ is taken as the changepoint which corresponds to the smallest probability of making type 1 error, i.e. rejecting the null hypothesis. We shall not explain these methods in full detail, but only display the completeness cutoffs of the selected catalogue events determined through GFT and MBASS methods.

Figure 2 indicates the estimation of completeness cutoffs of shallow events between 1965 and 1975 within confine as specified by solid lines in Fig. 1. The left of Fig. 2 demonstrates the residuals of fitted frequency–magnitude distributions by GFT method as a function of minimum magnitude cutoff, with a vertical arrow pointing to the completeness threshold at the first magnitude cutoff when the fit achieves ideal confidence level $(100-R)$%, e.g. 90 or 95%. The right of Fig. 2 displays the median-based analysis of the segment slope for $M_c$ by MBASS method with a vertical dashed line marking the completeness cutoff and the (non)cumulative number of events. The completeness thresholds determined via these two approaches are generally different. Uncertainties of the two estimates are examined via the bootstrap method (Efron and Tibshirani 1994). We sample with replacement from the original data set to obtain 200 bootstrap samples. Then, the magnitude of completeness is calculated for each bootstrap sample. We list the bootstrap estimates of the mean, standard error and quantiles of the completeness thresholds based on 200 bootstrap replications, see Table 1. Among 200 bootstrap replications, the 95% upper confidence limits determined by GFT method is 4.5, which is higher than that given by MBASS method. We choose 4.5, i.e. the 99% upper confidence limit given by GFT method as the completeness threshold for this data set. Lower completeness cutoffs are expected afterwards. The completeness of NZ catalogue is also addressed by Harte and Vere-Jones (1999), Gerstenberger and Rhoades (2010).

Table 1 Bootstrap estimations of the completeness thresholds of shallow events between 1965 and 1975 within confine as indicated in Fig. 2

Fig. 2

The magnitude of completeness of shallow events within confine as indicated in Fig. 1 between 1965 and 1975. The red triangles and black squares in the right panel show the noncumulative and cumulative magnitude–frequency distributions, respectively

3 Hidden Markov Models

The model suggested in this analysis is a continuous time HMM (Zucchini and MacDonald 2009), with the emission distributions being exponentially distributed. Let X(t) be a latent Markov chain specified by the infinitesimal generator matrix ${\bf Q} =(q_{ij})_{r\times r}$ with its (i, j)th element $q_{ij}\ge 0$ for $i\ne j$. Denote the magnitude of an earthquake at $t_i$ by $z_i=M_i-M_0$, which is exponentially distributed with probability density $f_{X_i}(z_i)=\theta _{X_i}\exp (-\theta _{X_i}z_i), z_i\ge 0$. The likelihood of the observations $(Y_i, z_i)_{i=1}^n$ is given by

$$\begin{aligned} L( {\bf Q} , \theta )= {} \pi ' \exp \{ {\bf Q} Y_1\} \Upsilon (z_1;\theta ) \cdots \exp \{ {\bf Q} Y_n\} \Upsilon (z_n;\theta ) {\bf 1} , \end{aligned}$$

(2)

where $\Upsilon (z;\theta )=\text{ diag }(f_1(z),\ldots ,f_r(z)),\theta =(\theta _1,\ldots ,\theta _r)$, $Y_i$ is the inter-event times $t_i-t_{i-1}$, $\pi$ is the initial distribution vector and ${\bf 1}$ is a column vector with all entries being unity, see Roberts and Ephraim (2008) for the case of Gaussian hidden Markov model, and Lu (2016)

Parameter optimization is implemented by maximizing the likelihood through EM algorithm due to some of its appealing properties such as monotonic convergence of the iterations to a local maximum under mild conditions and explicit EM steps for distributions from exponential family. To facilitate evaluation of the likelihood and other statistics, we introduce the forward and backward probabilities. Denote $L_k=\exp \{ {\bf Q} Y_k\}\Upsilon (z_k;\theta ).$ For $0<t<T$, the forward and backward probabilities are written by

$$\begin{aligned} \alpha _t(i)=\pi 'L_1 \cdots L_{N(t)}\exp \{ {\bf Q} (t-t_{N(t)}) \} {\bf e} _i \end{aligned}$$

and

$$\begin{aligned} \beta _t(j)={\bf e} _j'\exp \{ {\bf Q} (t_{N(t)+1}-t)\}\Upsilon (z_{N(t)+1})L_{N(t)+2}\cdots L_n{\bf 1} , \end{aligned}$$

respectively, where ${\bf e} _i$ is a unit column vector with the ith entry being unity and N(t) is the cumulative number of events over [0, t]. The likelihood in terms of this device is obviously $L({\bf Q} , \theta )=\sum \nolimits _{i=1}^r\alpha _t(i)\beta _t(i)$ for all $t\in (0,T)$, see Zucchini and MacDonald (2009).

The explicit EM iterations for $\theta$ is given by

$$\begin{aligned} \hat{\theta }_i=N_i^{*}\left( \sum _{k=1}^n \dfrac{\alpha _{t_k}(i)\beta _{t_k}(i)}{L({\bf Q} , \theta )} z_k\right) ^{-1}, \end{aligned}$$

(3)

where $N_i^{*}=\text{ E }\{N_i|Y_1,\ldots ,Y_n\}=\sum \nolimits _{k=1}^n\alpha _{t_k}(i)\beta _{t_k}(i)/L$ and $N_i$ is the total number of $X_k=i$ for $k=1,\ldots ,n$. The infinitesimal generator of the underlying Markov chain X(t) is updated in EM iterations by

$$\begin{aligned} \hat{q}_{ij}=\frac{\int _0^T\alpha _t(i)q_{ij}\beta _t(j){\rm{d}}t}{\int _0^T \alpha _t(i)\beta _t(i){\rm{d}}t}, \end{aligned}$$

(4)

for $i\ne j, 1\le i,j\le r,$ see Roberts and Ephraim (2008).

One EM iteration is carried out as follows:

• 1. In E-step, update the forward, backward probabilities: let $\alpha _0=\pi ', \alpha _{k}=\alpha _{k-1}\exp \{{\bf {Q}}Y_k\}\Upsilon (z_k), \beta _{n+1}={\bf {1}}$ and $\beta _k=\exp \{{\bf {Q}}Y_k\}\Upsilon (z_k)\beta _{k+1},$ for $k=1,\ldots ,n$.

• 2. Calculate $A_{ij}=\sum \nolimits _{k=1}^n\alpha _{k-1}\int _{t_{k-1}}^{t_k}\exp \{{\bf {Q}}(t-t_{k-1})\}e_ie_j'\exp \{{\bf {Q}}(t_k-t)\}\Upsilon (z_k)\,{\rm{d}}t \beta _{k+1}$, $B_i=\sum \nolimits _{k=1}^n\alpha _k{\bf {e}}_i{\bf {e}}_i'\beta _{k+1}$ and $C_i=\sum \nolimits _{k=1}^n\alpha _k{\bf {e}}_i{\bf {e}}_i' \beta _{k+1}z_k$.

• 3. In M-step, update the parameters by: $\hat{q}_{ij}=q_{ij}^0\frac{A_{ij}}{A_{ii}}, \hat{\theta _i}=\frac{B_i}{C_i}$, where $q_{ij}^0$ is obtained from previous EM steps.

The probabilities of the underlying Markov chain X(t) in state i at time t is given by the smoothing formula such as

$$\begin{aligned} \hat{p}_t(i)\,\hat{=}\,P\{X(t)=i|Y_1,\ldots ,Y_n\}=\dfrac{\alpha _t(i)\beta _t(i)}{\sum \nolimits _{i=1}^r\alpha _t(i)\beta _t(i)}, \end{aligned}$$

(5)

which gives the conditional probability of X(t) sojourn in state i conditioned on observations. Another approach to retrieve the path of latent Markov chain is Viterbi algorithm as set out in general discrete time hidden Markov models, which finds an overall optimal path for the latent Markov chain conditioned on all observations, see Zucchini and MacDonald (2009).

Similarly, $\theta (t)$ may be estimated by

$$\begin{aligned} \hat{\theta }(t)\,\hat{=}\,E\{\theta _{X(t)}|Y_1,\ldots ,Y_n\}=\sum _{i=1}^r \hat{\theta }_i\dfrac{\alpha _t(i)\beta _t(i)}{\sum \nolimits _{j=1}^r\alpha _t(j) \beta _t(j)}. \end{aligned}$$

(6)

Equations (5) and (6) can be used to display the evolution of latent Markov chain X(t) and temporal variations of $\theta$.

4 Modeling the Magnitude–Frequency Distributions via CT-HMM

4.1 Model Fittings via a Two-State HMM

A two-state HMM is fitted to the magnitude–frequency distributions of shallow earthquakes. Two levels of seismicity are corresponding to low or high b values. The parameters of HMM are estimated by maximizing the likelihood (2) through EM algorithm. In all cases, multiple initial values are used in EM iterations to avoid convergence to local maxima. The estimated b values and transition rate matrix $\hat{{\bf {Q}}}$ are listed in Table 2. The log-likelihood of the two-state HMM and the log-likelihood ratio statistics of it over the time-homogeneous b value model are also demonstrated in Table 2. The probabilities of the latent Markov chain sojourn in the first state, i.e. low b value state, are given by (5). Generally, it is sufficient to demonstrate the evolution of the latent Markov chain by interpolating the estimated probabilities of X(t) in the first state at many time points and connect them by straight lines.

Table 2 Two-state HMMs: estimated transition rates $q's$ and b values $b's$

From Table 2, it is noted that greater variability appears in b values upon lowering magnitude thresholds, as indicated in Fig. 3. Figure 3 shows the estimated b values and probabilities of the latent Markov chain in the first state, for magnitude thresholds 4.6–4.8. The estimated b(t) should look exactly the same as the smoothed probabilities of X(t) in the first state when the horizontal axis is raised to $\hat{b}_2$ and $|\hat{b}_1-\hat{b}_2|$ is rescaled to 1. Both of them are displayed with different scales on two sides of vertical axes. From Fig. 3, it is indicated that more detailed b value variations appear after lowering magnitude thresholds. However, for magnitude thresholds 4.8 and 4.7, the periods of low b values and high b values are roughly superimposed. Shallow events with magnitude thresholds above 5 are not considered, as available data in just five decades are limited for a meaningful analysis of b value variations. In addition, shallow events with magnitude below 4.5 are not considered, as the catalogue might be incomplete in early periods. For events with $M_0\ge 4.5$, the $95\%$ bootstrap quantile intervals of $b_1$ and $b_2$ are [0.8, 1.2] and [1.16, 1.7], respectively. There is only slim overlapping of the confidence intervals for two b values. We simulate the same number of events according to the estimated parameters. Then the simulated events are fitted by a two-state HMM using EM algorithm. The procedure is repeated 1000 times to obtain sufficient bootstrap replications. The bootstrap confidence intervals is constructed directly according to the bootstrap replications. Generally, it takes a few days to accomplish the bootstrap simulations.

Fig. 3

The probabilities of X(t) in the first state and b values with vertical axis displayed at the right side of the figure

4.2 Two-State HMM vs. Time-Homogeneous b Values and Three-State HMM

We compare the fit of a two-state HMM with that of the null model, i.e. time-homogeneous b value model, by use of the bootstrap likelihood ratio testing. The merit of this approach is that the exact p values of the statistical hypothesis testing can be approximated at ideal accuracy if the bootstrap sample size is large enough, see Efron and Tibshirani (1994). Note that typical large sample approximation to the distribution of the log-likelihood ratio statistic by $\chi ^2$ distribution is not applicable in this scenario, since under the null hypothesis observations are i.i.d. exponential variables, HMM is nonidentifiable. We turn to the parametric bootstrap methods to approximate the distribution of likelihood ratio statistic under the null hypothesis. In this case, K bootstrap samples are simulated according to the parametric distribution $\hat{P}_{\theta _0}$ under the null hypothesis. Then, each bootstrap sample is fitted by a time-homogeneous b value model and a two-state HMM, respectively. The corresponding likelihood ratio statistic for the K bootstrap samples is computed. If k of these statistics exceed the observed likelihood ratio statistic, then the p value of the test is given by $(k+1)/(K+1)$. For shallow events with magnitude thresholds 4.7 and 4.6, the resulting p values of the bootstrap likelihood ratio test are less than 3% over 300 bootstrap replications. Obviously, a two-state HMM fits the magnitude–frequency distribution much better than a time-homogeneous b value model in this case.

Three-state HMMs are also fitted and compared with two-state HMMs by some information theoretical criterions such as AIC or BIC. It turns out that the gain in log-likelihood of a three-state HMM over a two-state HMM is small, see Table 3. The three-state HMM will not outperform a two-state HMM in terms of AIC or BIC. In addition, part of the entries in the transition rate matrix of the three-state HMM are very close to zero, which strongly suggests lack of information for the corresponding state transitions due to small number of available observations. Generally, a three-state HMM is over-fitted. Higher order HMMs will not be considered further.

Table 3 Three-state HMMs: estimated transition rates $q's$ and b values $b's$

4.3 Two-State HMM vs. Piecewise Constant b Value Model, Residual Analysis

Since the 1960s, major updates of monitoring networks happened three times in New Zealand. One may wonder whether the temporal variations of b values are ascribed to network policy changes. We compare the fit of a two-state HMM with that of a piecewise constant b value model, in which the b value is a constant in a number of periods divided roughly according to the time of major network updates, i.e. 1965–1986, 1987–1999 and 2000 onwards. The log-likelihood of this piecewise constant b value model for shallow events with magnitude greater than 4.5 is 8.58, less than that of the two-state HMM. The two-state HMM obviously outperforms the piecewise constant b value model in terms of AIC. It is also noted from Fig. 4 that none of the state transitions happens immediately after the three major network updates, except for the change happening in the late 1980s. However, no obvious magnitude shift is detected throughout the network upgrades by use of “magnitude signature” techniques, see discussions in Lu and Vere-Jones (2011). Uncertainties in magnitude estimation are not considered in this study (Rhoades 1996), as the full information about the magnitude uncertainties in early periods is lacking.

Fig. 4

The top of the figure is M–T plot for shallow events with magnitude greater than 4.5. The bottom of the figure is the estimated probabilities of X(t) in the first state, i.e. the seismic active state, and also the estimated b values with vertical axis displayed at the right side of the figure. The vertical red lines indicate the occurrence times of large shallow mainshocks

4.4 Associations of Large Shallow Events and b Value Variations

This study indicates decade-long b value variations of New Zealand shallow earthquakes with epicentral distribution indicated in Fig. 1. For magnitude thresholds 4.8 and 4.7, the periods of low(high) b values are roughly superimposed (Fig. 3). After lowering magnitude thresholds to 4.6 (or 4.5), more detailed b value variations appear, see Figs. 3 and 4. The overall pattern of b value variations in time is insensitive to magnitude thresholds, which is ideal for the interpretation of b value variability. For medium size to large events, this analysis suggests b value varies nearly in a timescale of a decade. To characterize small-scale b value variations, it is necessary to lower magnitude thresholds to include smaller events in the study.

From Fig. 4, it is noted that a short period of 1970s, a decade roughly between 1985 and 1995, the late 2000s and afterwards are the periods of low b values. The bottom of Fig. 4 demonstrates the estimated b values and probabilities of the latent Markov chain in the first state for events with magnitude above 4.5. The vertical red lines in this figure indicate the occurrence times of large shallow mainshocks. It is noteworthy that nearly all strong shallow earthquakes or swarms around North Island and northern South Island occurred right in the episodes of low b values (high stress), such as 1984 Bay of Plenty swarm, 1987 Edgecumbe earthquakes, 1994 Arthurs Pass events, 1995 East Cape swarm and most recently, Darfield earthquakes and Cook Strait swarm.

5 Pre-seismic b Value Variations Before Darfield Earthquakes and Cook Strait Swarm

The overall pattern of b value variations for medium size to large earthquakes in decades is well characterized by a two-state HMM. However, detailed b value variations in smaller spatial and temporal scales are often beyond the scope of current models to characterize. We demonstrate the spatio-temporal variations of b values prior to the two most recent major earthquakes, i.e. Darfield earthquakes and Cook Strait swarm. The b value mappings are carried out over grids in size $\frac{1}{5}^{\circ }\times \frac{1}{5}^{\circ }$. For each grid, the b value is evaluated for all events within a rectangle in size $\frac{1}{2}^{\circ }\times \frac{1}{2}^{\circ }$. So, there is a certain degree of overlapping across adjacent grids. The b value map (Fig. 5) prior to 2010 Darfield earthquake shows that M7 mainshock rupture nucleated at the margin of the low b value (high stress) asperity in the Greendale fault zones, propagating eastward to the relatively high b value (low stress) region, stopped near a higher stress or hard region at Banks Peninsula, with all the three largest aftershocks, or mainshocks of secondary aftershocks again located at high b value (low stress) region. The b value map (Fig. 6) prior to 2013 Cook Strait swarm indicates that the doublet with magnitude above 6 actually nucleated right at low b value region.

We also investigate whether there is any change in b values before Darfield earthquake and Cook Strait swarm. Figure 7 indicates the temporal variations of b values within the rectangles as specified by dashed lines in maps 5 and 6. Figure 7a shows the estimated b values before 2010 Darfield earthquake in a scale of 1 year in a box plot. From Fig. 7a, about one and a half year of pre-seismic b value decrease is observed for Darfield mainshock. Figure 7b shows the estimated b values before 2013 Cook Strait swarm in a scale of half a year in a box plot. Again, about one and a half year of pre-seismic b value decrease is observed. For Cook Strait swarm, it is noted that a series of strong foreshocks occurred days before the large doublet.

Fig. 5

The b value map prior to 2010 Darfield M7 earthquake. The time origin is 2005 January 1. The b value mapping is within $(171.5^{\circ }E,173.5^{\circ }E)\times (43^{\circ }S,44^{\circ }S)$. The red star marks the location of 2010 Darfield M7 mainshock. For each small patch with events less than 20 with magnitude above completeness threshold 2.5 determined by GFT method, the b value estimation is default

Fig. 6

The b value map prior to 2013 Cook Strait swarm. The time origin is 2005 January 1. The b value mapping is within $(173.5^{\circ }E,175^{\circ }E)\times (41^{\circ }S,42^{\circ }S)$. The red stars mark the locations of 2013 Cook Strait doublet. For each small patch with events less than 20 with magnitude above completeness threshold 2.5 determined by GFT method, the b value estimation is default

Fig. 7

Temporal variations of b values prior to a 2010 Darfield M7 earthquake and b 2013 Cook Strait swarm for events within confines as indicated in Figs. 5 and 6

6 Spatial Variations of b Values

We also perform a spatial analysis of b values over the most recent decades to look into the spatio-temporal correlations of b value variations. Especially, we investigate the spatial b value variabilities in two phases, i.e. 1996–2000 and 2010–2014, corresponding to the periods of low or high b values, respectively, see Figs. 3 and 4. The b value mapping is carried out over 310 grids in size $\frac{1}{3}^{\circ }\times \frac{1}{3}^{\circ }$. There is no overlapping across adjacent grids in this analysis. In each grid, the b value is estimated for at least 50 events with magnitude above completeness threshold 3, determined via GFT method as aforementioned in Sect. 2.2. Increasing the threshold magnitude further will lead to less available events in each grid and more blank grids with no b value estimations. Typically, the b value estimation is stable over the magnitude thresholds. In this study, we do not consider the depth distribution and just take all the shallow earthquakes with depth less than 40 for the analysis. Generally, the b values show great spatial variabilities, ranging from below 0.8 to above 2 as indicated in Figs. 8 and 9. Figure 8 indicates the spatial b values in “high b value” period. It is noted that over 47 light-colored grids show a b value higher than 1.3, in contrast to only three grids with a b value higher than 1.3 in Fig. 9. Meanwhile, there are 35 deep blue-colored grids showing a b value lower than 1 in Fig. 9, in contrast to only six grids with a b value lower than 1 in Fig. 8. Generally, simple statistics indicate that more than 90% of grids in Fig. 8 show a b value higher than that in the same grid in Fig. 9.

Fig. 8

b value mapping over 1996–2000

Fig. 9

b value mapping over Jan 2010–Mar 2014

These statistics suggest the “low b value” period is featured by systematically more grids showing a low b value than other periods. The pattern is examined across North Island and northern South Island. Nevertheless, the temporal variations of b values are not unanimous across the entire region in study. Typically, some areas show relatively stable b values. Others display greater heterogeneities over these two periods. From Figs. 8 and 9, it is noted that the b values presented in northern South Island are relatively low and lack variability over the two periods, with standard errors less than 0.2 in two cases. With volcanoes located in the central North Island (region C in Fig. 1), most of the high b values ($b\ge 1.3$) appear in this region. In addition, it is noteworthy that b values in North Island show greater variabilities both spatially and temporally, with relatively high means and standard errors in the two periods, see Figs. 8 and 9.

In summary, the overall pattern of temporal variations of b values indicated in HMMs is a feature in large spatial scale as well, as evidenced by the spatial variations of b values in the two periods, i.e. 1996–2000 and 2010–2014. The “low b value” period is characterized by high mean energy release nearly across the entire northern South Island and North Island and relatively frequent occurrences of major shallow earthquakes.

7 Seismotectonic Implications and Speculations

Decade-long b value variations of shallow earthquakes across North Island and northern South Island are indicated in Figs. 3 and 4. Figures suggest that shallow seismicity in this zone with magnitude above 4.5 may be classified into two episodes, low b value periods and high b value periods. Roughly a decade scale of b value variation over the entire region is an indication of large scale of external time-varying behavior associated with subduction process. Among a number of subduction parameters, studies across global major subduction zones suggest that the convergence rate of the plates and the age of the slab are closely related to moment release rate and the occurrence of large earthquakes (Ruff and Kanamori 1980). High seismicity is common when the convergence rate of the plate is fast and the age of the subducted lithosphere is young. At the same time, plate boundaries with slow convergence and subduction of old and cold lithosphere are zones where seismic moment release rate is relatively low and the occurrence of large earthquakes is less frequent. Nevertheless, the timescale of seismicity variation is only about one or two decades, almost negligible when compared with the age of the slab. We suggest that it is the temporal variations of the plate convergence rate, rather than the age of the slab, which is more closely associated with the age-rate-dependent seismicity variations. This line of reasoning is based on the observations that, at many subduction zones globally, both the frequency of a given size earthquake and the seismic moment release rate increase with the convergence rate, see Molnar (1979), Ruff and Kanamori (1980, 1983), McCaffrey (1994, 1997). Other subduction parameters such as subduction zone fault length and fault area also show positive correlations with the convergence rate (Jarrard 1986).

8 Discussion and Concluding Remarks

Decade-long b value variations of shallow earthquakes around North Island and northern South Island are indicated in Figs. 3 and 4. HMM-based b value analysis suggests shallow seismicity may be divided into two episodes, namely low b value periods and high b value periods. The estimation is insensitive to a range of magnitude thresholds. The overall b values around this zone vary roughly at a decade scale. From the bottom of Fig. 4, it is noteworthy that periods of low b values are typically associated with the occurrences of major earthquakes. Correspondingly, periods of high b values are featured by the lack of significant shallow earthquakes and low mean energy release. Although the temporal variations of b values in decades are not unanimous across entire North Island and northern South Island, it is observed that in most grids investigated, spatial b values show nearly simultaneous variations. This is evidenced by a comparison of spatial b values in many grids over two periods with low and high b values, respectively.

Recent decades have seen the occurrences of strong shallow earthquakes frequently (Fig. 4). With quality data available recently, we also perform an analysis of pre-seismic b value variations in smaller spatial and temporal scale, particularly for recent Darfield earthquake and Cook Strait swarm. From the two b value mappings (Figs. 5, 6) preceding 2010 Darfield earthquakes and 2013 Cook Strait doublet, it is suggested that the mainshock rupture is nucleated at the margin of or right at the low b value asperities. In addition, pre-seismic b value decrease at one and a half year scale is observed in both cases.

Sliding-window approach to the b value estimation is widely utilized in practice. However, window size tuning has an unignorable impact on its estimation. The estimation may demonstrate great variabilities, ranging from frequent fluctuations in one case to a lack of variability in another, which is nonetheless irrelevant to the spontaneous b value variations. Optimal window size criterion is customarily not addressed, which may cause difficulties in interpretation of b value variability in practice, as whether the b value variations are artificial due to tuning parameter selection or real remains uncertain. We carry out a decade-long b value analysis via continuous-time hidden Markov models. Model-based b value analysis via bootstrap likelihood ratio testing suggests a two-state HMM fits the pattern much better than the time-homogeneous b value model. Comparing usual model selection criterion such as AIC or BIC for multi-state HMMs suggests that a two-state HMM is sufficient for characterizing the b value variabilities for shallow quakes with magnitude above 4.5 around North Island and northern South Island since 1965. We also rule out the possibility that the b value variations are fully attributed to updates of monitoring networks by comparing the fit of a two-state HMM with that of a piecewise constant b value model segmented according to major updating times of monitoring networks.

We carry out a residual analysis to check whether the model for $M_0\ge 4.5$ is adequate for fitting the observations. Note that the fitted probability density of $z_k$ is given by $\sum \nolimits _{i=1}^r\hat{p}_{t_k}(i)f(z_k, \hat{\theta }_i).$ After transforming $z_k$ by its fitted distribution function $U_k=\sum \nolimits _{i=1}^r\hat{p}_{t_k}(i)F(z_k, \hat{\theta }_i),$ $\{U_k\}$ forms so-called uniform pseudo-residuals on [0, 1]. To identify outliers more explicitly, the uniform pseudo-residuals are further rescaled by $\Phi ^{-1}(U_k),$ which forms the normal pseudo-residuals, where $\Phi$ is the distribution of standard normal. Deviations from N(0, 1) may suggest lack of fit of the model for some of the observations. In this study, nearly all residuals are located within interval $[-3,3]$, except for a few residuals lying left of this interval, which obviously resulted from rounding errors from the original catalogue, see Fig. 10.

The model may overestimate or underestimate b values in some occasions or locations as the model only represents overall averages of b values in a relatively large spatial scale. In much smaller spatial scales, the b value displays great variabilities. For example, volcanic zones in central North Island are regions with active seismicity without major mainshock–aftershock sequences. In this region (region C in Fig. 1), the b value of 38 events with magnitude above 4.5 is 1.7, which is systematically underestimated by HMM. After excluding these events from the original data set, a reanalysis shows no signs of significant changes in b values and transition rates ${\bf {Q}}$. However, our model is simple enough to characterize long-term b value variations in a relatively large spatial scale. The pattern revealed via HMMs is an indication of large scale of external time-varying behavior associated with subduction process. Comparing the moment release rate and the plate convergence rate across global main subduction zones (Ruff and Kanamori 1980; McCaffrey 1994), the temporal variations of b values may be attributed to the temporal variations of the convergence rate of plates. Other key subduction parameters, such as thermal age of the subducting plate, play a less important role in a decade scale of seismicity variations.

Fig. 10

The histogram of normal pseudo-residuals