1 Introduction

The purpose of a seismic hazard study, using available data related to earthquake events, is to determine the specific probability values for seismic activity in a region in the future and combines geological, seismological, and statistical data with other information. Seismic hazard studies are undertaken to obtain long-term predictions of the occurrences of seismic events in a particular region. Most often, the prediction is expressed in the form of probabilities of a specified earthquake magnitude over a period of time, t, or as the expected number of such events. Thus, the number of events over time [0,T] and M define the size of the events; then, that probability is expressed as P{M ≥ m, (0, T)} (Anagnos and Kiremidjian 1988).

Reliable estimation of earthquake hazard in a region requires the prediction of the size and magnitude of future earthquake events and their locations. An incomplete understanding of earthquake phenomena, however, has led to the development of primarily long-term hazard assessment tools relying on the statistical averages of earthquake occurrences without considerations of specific models. One of the most important earthquake hazard parameters is the maximum regional magnitude (M max) and its uncertainty. In addition to M max, two other important earthquake hazard parameters are β value and seismic activity rate or intensity (λ). The “apparent” magnitude (Tinti and Mulargia 1985; Kijko and Sellevoll 1992), which represents the observed magnitude (\(M_{ \hbox{max} }^{\text{obs}}\)), is equal to the “true” magnitude M, plus an uncertainty, ε. The probability distribution of this uncertainty can be modeled by various distribution functions.

A number of statistical techniques and probabilistic models have been already used to estimate earthquake hazard parameters by various researchers. (Wells and Coppersmith 1994; Pisarenko et al. 1996; Kijko 2004; Wheeler 2009; Mueller 2010). Bağci (1996) investigated seismic risk in Western Anatolia between 36° and 41°N and 25° and 31°E using the probabilistic model for earthquake data (1930–1990). Altinok (1991) evaluated the seismic risk of Western Anatolia by applying a probabilistic model. Bayrak and Bayrak (2012, 2013) investigated earthquake hazard potential using different methods for different regions in Western Anatolia.

Earthquakes have posed a persistent threat to life and property in many regions of the world. In Turkey’s Anatolia region, records of devastating earthquakes can be found. A geodynamic complexity and a diversity of faulting regimes can be seen around the Aegean. The western part of the Anatolian plate is one of the most seismically active regions of Turkey. Western Anatolia has seen numerous earthquakes during past years. The consequences of large earthquakes across the globe are a primary motivation for understanding seismic hazard. Particular consideration is given to the appraisal of seismic hazard in the context of Aegean seismotectonics.

The Bayesian method has a special interest that comes from its ability to take into consideration the uncertainty of parameters in fitted probabilistic laws and a priority given to information (Morgat and Shah 1979; Campell 1982, 1983). The advantages of the method used are in its simplicity; it does not require such intermediate steps of investigation as earthquake scenarios, estimates of bimodal recurrence model of magnitude distribution, and bootstrap procedures (Lamarre et al. 1992). Rather, the method is straightforward and needs only a seismic catalog and seismological information.

We applied a procedure developed by Pisarenko et al. (1996) in order to examine earthquake hazard for the 15 different regions of Western Anatolia. For this purpose, earthquake hazard parameters (M max, β value, and activity rate or intensity λ) and their uncertainties are computed. In addition, the quantiles of M max probabilistic distribution in future time intervals of 5, 10, 20, 50, and 100 years are estimated.

2 The Tectonics of Western Anatolia

The Aegean Arc and Western Anatolian Extension Zone play important roles in the geodynamic evolution of the Aegean region and Western Anatolia. Although the North Anatolian Fault is the largest fault system outside of the system, the Aegean Region is observed to commonly experience earthquake movement and is one of the regions with the most rapidly changing shapes in the world (Kahraman et al. 2007). The tectonics of the Aegean region and Western Anatolia have been investigated by a number of researchers (Le pichon and Angelier 1979; Şengör 1987; Barka and Reilinger 1997; Seyzitoğlu and Scott 1992, 1996; Koçyiğit et al. 1999; Şalk and Sari 2000; Kahraman et al. 2007). A number of tectonic and seismotectonic models have been investigated to determine the seismogenic structure of Western Anatolia (Dewey 1988; Seyitoğlu and Scott 1992, 1996; Koçyiğit et al. 1999), and researchers have found that the region has a complex structure (Blumenthal 1962; Brunn et al. 1971, Poisson 1984, 1990; Marcoux 1987; Kissel et al. 1993; Frizon et al. 1995). The structures in Western Anatolia have developed in the directions of NW–SE, NE–SW, N–S, and E–W, and they are oriented in the form of four separate block faults; these structures are called “cross-graben” formations (Şengör et al. 1985; Şengör 1987). The area is currently experiencing an approximately N–S continental extension at a rate of 30–40 mm/year (Oral et al. 1995; Le pichon et al. 1995). The Anatolian plate rotates counterclockwise with an average velocity of 24 mm/year (Mcclusky et al. 2000).

Western Anatolia has developed several graben trending E–W and WSW–ESE, depending on the N–S directional extension tectonics (Dewey and Şengör 1979; Jackson and Mckenzie 1984; Şengör 1982; Şengör et al. 1984). The Aegean Graben System (for example, Küçük Menderes, Büyük Menderes, Gediz, Bakırçay, Simav, Gökova, Kütahya, and Edremit Grabens) generally occurred on E–W trending normal faults and is located trending E–W on a number of graben blocks (Bozkurt and Sözbilir 2004; Yilmaz et al. 2000; Dewey and Şengör 1979; Seyitoğlu et al. 1992).

The eastern part of the region studied includes the NW–SE trending Beyşehir, Dinar, and Akşehir-Afyon Grabens and the NE–SW trending Burdur, Acıgöl, Sandıklı Çivril, and Dombayova Grabens and their bounding faults (e.g., Bozkurt 2001). The Büyük Menderes Graben is located between the Aegean and Denizli and is approximately 200-km long. The eastern end of the graben intersects Pamukkale around the Gediz graben (Ambraseys and Finkel 1995). Western Anatolia corresponds with the normal strike-slip component of NE–SW lines, for example, the Fethiye-Burdur Fault Zone, the Tuzla Fault, and the Bergama Foça Fault. Normal NW–SE faults are located in Southwestern Anatolia. The normal component of the Fethiye–Burdur Fault Zone is a left-lateral strike-slip fault. This fault system is a process of the northeastern Pliny-Strabo system forming the eastern flank of the Aegean Arc (Dumont et al. 1979; Şaroğlu et al. 1987; Price and Scott 1994). The E–W trending Gediz, Büyük Menderes, and Küçük Menderes Faults are located in the central region of Western Anatolia. The Simav, Kütahya, and Eskişehir Faults north of these faults show similar features. The Eskişehir Fault is a WNW–ESE trending fault and is found in the east between Bursa and Afyon. The normal component has a right lateral movement (Şaroğlu et al. 1987). The NE–SW basin is located among S–W and WN–ESE trending normal faults. NE–SW basins are located south of the Izmir Graben, and these trending faults are active. In addition, several NNE–SSW-trending strike-slip faults and N–S-striking active normal faults such as the Bergama-Zeytindağ Fault Zone and the Orhanlı Fault Zone are located in the region (Sözbilir 2002). The Orhanlı Fault Zone is the most continuously traceable fault. Other potentially active faults are the İzmir Fault trending in an E–W direction and the Manisa Fault near Manisa city (Bozkurt and Sözbilir 2006). The Gökova Fault must be traced on a line trending in an E–W direction along the northern coast of Gökova Bay in the southern part of the Western Anatolian zone. The Karaburun-Gulbahce Fault occurs in the Karaburun Peninsula and is believed to be predominantly a strike-slip fault (Şaroğlu et al. 1992; Ocakoğlu et al. 2004, 2005; Aktuğ and Kiliçoğlu 2006).

3 Seismogenic Source Regions and Data

The database used in this work was compiled from several different sources and catalogs such as IRIS (2013), the Incorporated Research Institutions for Seismology (TURKNET 2013), the International Seismological Centre (ISC), and the Scientific and Technological Research Council of Turkey (TUBİTAK); data are provided in different magnitude scales. The catalogs include different magnitude scales (M b body wave magnitude, M s surface wave magnitude, M L local magnitude, M D duration magnitude, and M W moment magnitude), origin times, epicenters, and depth information of earthquakes.

An earthquake data set used in seismicity or seismic hazard studies must certainly be homogenous; in other words, it is necessary to use the same magnitude scale. However, the earthquake data obtained from different catalogs have been reported in different magnitude scales. Therefore, all earthquakes must be redefined in the same magnitude scale. Bayrak et al. (2009) developed several relationships among different magnitude scales (M b body wave magnitude, M s surface wave magnitude, M L local magnitude, M D duration magnitude, and M W moment magnitude) in order to prepare a homogenous earthquake catalog from different data sets. The size of earthquakes that occurred before 1970 are given M s scale in the catalogs compiled in this study. Only, the magnitudes of earthquakes that occurred after 1970 are converted to M s. Finally, we prepared a homogenous earthquake data catalog for M s magnitude using relationships, and we have considered only the instrumental part of the earthquake catalog (1900–2013) for the Bayesian method.

In order to evaluate earthquake risk and/or hazard of a region, foreshocks and aftershocks should be extracted from earthquake catalogs. In other words, it is necessary to decluster the catalogs. In this study, we used the Reasenberg (1985) algorithm which uses interaction zones in space in time to link earthquakes into clusters to decluster the homogenous catalog.

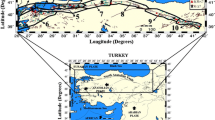
The method is applied in the Western Anatolian region where a vast variation of seismicity and tectonics is observed throughout the region. In this study, we used the regions defined by Bayrak and Bayrak (2012). They divided Western Anatolia into 15 seismic regions on the basis of seismicity, tectonics, and the focal mechanism of earthquakes in order to develop a detailed analysis of seismic hazard in the region with an updated and more reliable earthquake catalog. The regions shown in Fig. 1 are as follows:

Fig. 1
figure 1

Delineation of the 15 different source regions of Western Anatolian the basis of seismicity, tectonics, and focal mechanism of earthquakes. The epicentral distribution of earthquakes of M s ≥ 4 occured during the period 1900–2013 is also shown with the different symbols

Full size image
  1. 1.

    Region: Aliağa Fault.

  2. 2.

    Region: Akhisar Fault.

  3. 3.

    Region: Eskişehir, İnönü Dodurga Fault Zones.

  4. 4.

    Region: Gediz Graben.

  5. 5.

    Region: Simav, Gediz-Dumlupınar Faults.

  6. 6.

    Region: Kütahya Fault Zone.

  7. 7.

    Region: Karova-Milas, Muğla-Yatağan Faults.

  8. 8.

    Region: Büyük Menderes Graben.

  9. 9.

    Region: Dozkırı-Çardak, Sandıklı Faults.

  10. 10.

    Region: Aegean Islands.

  11. 11.

    Region: Aegean Arc.

  12. 12.

    Region: Aegean Arc, Marmaris, Köyceğiz, Fethiye Faults.

  13. 13.

    Region: Gölhisar-Çameli, Acıgöl, Tatarlı Kumdanlı Faults, Dinar Graben.

  14. 14.

    Region: Sultandağı Fault.

  15. 15.

    Region: Kaş and Beyşehirgölü Faults.

4 Method

The technique that was used is described in detail in papers about the method (Pisarenko et al. 1996; Pisarenko and Lyubushin 1999; Tsapanos et al. 2001, 2002; Lyubushin et al. 2002; Tsapanos and Christova 2003; Tsapanos 2003, Lyubushin and Parvez 2010; Yadav et al. 2012). A brief description of the method is given below.

Let R be the value of magnitude (M), which is a measure of the size of earthquakes that occurred in a sequence on a past-time interval (−τ,o):

$$\vec{R}^{\left( n \right)} = \left( {R_{1} , \ldots ,R_{n} } \right), \quad R_{i} \ge R_{0} , R_{t} = { \hbox{max} }\left( {R_{1} , \ldots ,R_{n} } \right), \quad 1 \le i \le n,$$
(1)

where i = 1, 2, …, n and R 0 is the minimum cutoff value of magnitudes (M), i.e., defined by possibilities of registration system, or it may be a minimum value from which the value written in Eq. (1) is statistically representative.

Two main assumptions for Eq. (1) were proposed. The first assumption is that Eq. (1) follows the G–R law of distribution:

$${\text{Prob}}\left\{ {R < r} \right\} = F\left( {\frac{x}{{R_{\text{o}} }},\rho ,\beta } \right) = \frac{{e^{{ - \beta R_{o} }} - e^{{ - \beta_{x} }} }}{{e^{{ - \beta R_{\text{o}} }} - e^{{ - \beta_{\rho } }} }},\quad R_{\text{o}} \le x \le \rho.$$
(2)

Here, ρ is the unknown parameter that represents the maximum possible value of R, for instance, ‘maximum regional magnitudes (M)’ in a given seismogenic region. The unknown parameter b is the ‘slope’ of the Gutenberg–Richter law of magnitude–frequency relationship at small values of x when the dependence (Eq. 2) is plotted on double logarithmic axes.

The second assumption is that λ is an unknown parameter and a Poisson process with some activity rate or intensity λ in the sequence (Eq. 1). If three unknown parameters (ρ, β, and λ) can be written, the full vector is

$$\theta = (\rho ,\beta ,\lambda ).$$
(3)

Apparent magnitude is a magnitude that is observed, i.e., those values that are presented in seismic catalogs. True magnitude is a hidden value and is unknown; it is defined by the formula

$$\bar{R} = R + \varepsilon.$$
(4)

Let (x|δ) be a density of probabilistic distribution of error ε where δ is a given scale parameter of the density and epsilon (ε) value is the error between the true magnitude (R) and the apparent magnitude (\(\bar{R}\)). We can estimate values of true magnitude taking into account different hypotheses about the probability distribution of epsilon (for example, uniform) and about parameters of this distribution. Below, we shall use the following uniform distribution density:

$$n\left( {x|\delta } \right) = \frac{1}{2\delta }, \left| x \right| \le \delta \;\;\;\;\;\;\;\;n\left( {x|\delta } \right) = 0, \left| x \right| > \delta.$$
(5)

Let \(\varPi\) be a priori uncertainty domain of values of parameters θ

$$\varPi = \left\{ {\lambda_{ \hbox{min} } < \lambda \le \lambda_{ \hbox{max} } , \beta_{ \hbox{min} } \le \beta \le \beta_{ \hbox{max} } , \rho_{ \hbox{min} } \le \rho \le \rho_{ \hbox{max} } } \right\}.$$
(6)

We should consider the a priori density of the vector θ to be uniform in the domain \(\varPi.\).

According to the definition of conditional probability, α-posteriori density of distribution of vector of parameters θ is equal to

$$f\left( {\theta |\vec{R}^{(n)} ,\delta } \right) = \frac{{f\left( {\theta ,\vec{R}^{(n)} |\delta } \right)}}{{f\left( {\vec{R}^{(n)} |\delta } \right)}}.$$
(7)

But \(f\left( {\theta |\vec{R}^{(n)} ,\delta } \right) = f\left( {\vec{R}^{(n)} |\theta , \delta } \right) \times f^{a} (\theta )\), where \(f^{a} (\theta )\) is the α priori density of the distribution of vector θ in the domain π. As \(f^{a} (\theta )\) = const according to our assumption and taking into consideration that

$$f\left( {\vec{R}^{(n)} |\delta } \right) = \int\limits_{\pi } {f\left( {\left. {\mathop R\limits^{ \to (n)} } \right|\theta ,\delta } \right)} {\text{d}}\theta.$$
(8)

Then, we will obtain using a Bayesian formula (Rao 1965). The Bayesian formula is as follows:

$$F\left( {\theta |\vec{R}^{(n)} ,\delta } \right) = \frac{{f\left( {\theta |\vec{R}^{(n)} ,\delta } \right)}}{{\int\limits_{\pi } {f\left( {\left. {\mathop R\limits^{ \to (n)} } \right|V,\delta } \right)} {\text{d}}V}}.$$
(9)

An expression for the function \(\left( {f\left( {\left. {\mathop R\limits^{ \to (n)} } \right|\theta ,\delta } \right)} \right)\) should be used in Eq. (9).

In order to use Eq. (9), we must have an expression for the function \(f\left( {\left. {\mathop R\limits^{ \to (n)} } \right|\theta ,\delta } \right)\). With the assumption of Poissonian character sequence in Eq. (1), and independent of its members, should give us

$$f\left( {\vec{R}^{(n)} |\theta ,\delta } \right) = \bar{f}\left( {R_{1} |\theta ,\delta } \right)\ldots\,\bar{f}\left( {R_{n} |\theta ,\delta } \right) \times \frac{{\exp \left( { - \lambda \left( {\theta ,\delta } \right)\tau } \right) \times \left( { - \bar{\lambda }\left( {\theta ,\delta } \right)\tau } \right)^{n} }}{n!}.$$
(10)

Now, we can compute a Bayesian estimate of vector θ:

$$\theta \left( {\vec{R}^{(n)} |\delta } \right) = \;\int\limits_{\pi } {Vf\left( {\left. V \right|\mathop R\limits^{ \to (n)} ,\delta } \right)} {\text{d}}V.$$
(11)

An estimate of maximum value, ρ, is one of the computations of (Eq. 11). We must obtain Bayesian estimates of any of the functions to use a formula analogous to Eq. (11).

One of the computations in (Eq. 11) contains an estimate of maximum value of ρ. Using a formula analogous to Eq. (11), we must obtain Bayesian estimates for any of the functions. The most important are estimates of quantiles of distribution functions of true and apparent values on a given future time interval [0,T], for instance for α quantiles of apparent values

$$\hat{\bar{Y}}\left( {\alpha |\vec{R}^{(n)} ,\delta } \right) = \int\limits_{\pi } {\bar{Y}_{T} \left( {\alpha |V ,\delta } \right)} \times f\left( {\left. V \right|\mathop R\limits^{ \to (n)} ,\delta } \right){\text{d}}V,$$
(12)

\(\hat{Y}_{T} \left( {\delta |\mathop R\limits^{ \to (n)} ,\delta } \right),\) for α quantiles for true values is written analogously to Eq. (12). We must estimate variances of Bayesian estimates (Eqs. 11, 12) using averaging over the density (Eqs. 9, 10). For example:

$${\text{Var}}\left\{ {\hat{\bar{Y}}_{T} \left( {\alpha |\vec{R}^{\left( n \right)} ,\delta } \right)} \right\} = \int\limits_{\pi } {\left( {\bar{Y}_{T} \left( {\alpha |V ,\delta } \right) - \hat{\bar{Y}}_{T} \left( {\alpha |\vec{R}^{\left( n \right)} ,\delta } \right)} \right)}^{2} \times f\left( {\left. V \right|\mathop R\limits^{ \to (n)} ,\delta } \right){\text{d}}V.$$
(13)

First of all, we will set \(\rho_{ \hbox{min} } = R_{\tau } - \delta\). As for the values of ρ max, they depend on the specific data in the series (Eq. 1) and are produced by the user of the method. Boundary values for the slope β are estimated by the formula

$$\beta_{\hbox{min} } = \left( {\beta_{0} \cdot \left( {1 - \gamma } \right)} \right), \beta_{\hbox{max} } = \beta_{0} \cdot \left( {1 + \gamma } \right), \quad 0 < \gamma < 1.$$
(14)

β 0 is the “central” value and is obtained as the maximum likelihood estimate of the slope for the Gutenberg–Richter law

$$\sum\nolimits_{i - 1}^{n} {\ln \left\{ {\frac{{\beta e^{{ - \beta R_{i} }} }}{{e^{{ - \beta R_{\text{o}} }} - e^{{ - \beta R_{\tau } }} }}} \right\}} \to {\text{Max}};\beta ,\beta \varepsilon (0,\beta_{\text{s}} ),$$
(15)

where β s is a rather large value.

For setting boundary values for the t activity rate or intensity (λ) in Eq. (6), we used the following rationale. As a consequence of normal approximation for a Poisson process for a rather large n (Cox and Lewis 1966), the standard deviation of the value λτ has the approximation value \(\sqrt n = \sqrt {\lambda \tau }\). Thus, taking boundaries at ±3σ, we will obtain

$$\lambda_{\hbox{min} } = \lambda_{o} \left( {1 - \frac{3}{{\sqrt {\lambda_{o} \tau } }}} \right), \lambda_{\hbox{max}} = \lambda_{0} \left( {1 + \frac{3}{{\sqrt {\lambda_{0} \tau } }}} \right)\;\;\;\lambda_{0} = \frac{{\bar{\lambda }_{0} }}{{c_{f} \left( {\beta_{0} ,\delta } \right)}}, \bar{\lambda }_{0} = \frac{n}{\tau }.$$
(16)

5 Results and Discussion

Earthquake hazard parameters (maximum regional magnitude M max, β value, and activity rate λ) have been estimated in the examined area using Bayesian statistics provided by Pisarenko et al. (1996) and a homogenous and complete seismic catalog of M s ≥ 4 during the period 1900–2013. The reliability of the estimation of hazard parameters (β value and activity rate or intensity λ) depends upon the time period covered by the instrumental catalog. The Bayesian method requires a priori distribution of unknown parameters, but the a priori distribution is negligible for a large sample. There is an advantage of this method, in that it considers magnitude uncertainties as well in the computation of hazard parameters. There is no priori advantage in using normal or Gaussian distributions, such as Kijko and Sellevoll (1992) did for the estimation of error in magnitudes as also observed by Pisarenko and Lyubushin (1997) and Tsapanos et al. (2001). Therefore, uniform distribution is applied in this analysis. We used the software compiled by Pisarenko and Lyubushin (1997).

The Bayesian approach is a more time consuming method (Pisarenko et al. 1996) but provides more stable results than unbiased approaches. With this purpose, we have also tabulated the maximum observed magnitude (\(M_{\hbox{max} }^{\text{obs}}\)) in Table 1 with other parameters. In this study, the estimated maximum regional magnitudes are in quite good agreement with the maximum observed magnitudes and their differences. The maximum regional magnitude (M max) estimated by this method is comparable and more reliable than the other estimates obtained by different approaches. The close agreement between estimated M max and \(M_{\hbox{max} }^{\text{obs}}\) validates the high quality of data used and appropriateness of the adopted cutoff magnitude. The reliability of the estimation of hazard parameters (β value and activity rate or intensity λ) depends upon the time period covered by the instrumental catalog.

Table 1 The estimates of the Bayesian analysis for the 15 different source regions of Western Anatolia
Full size table

The M max values computed using the Bayesian method are listed in Table 1 and the map showing them is in Fig. 2 for the 15 different regions of Western Anatolia. M max values vary between 6.00 and 8.06. The lowest M max value (\(M_{\hbox{max} }^{\text{Bayes}}\) = 6.00) is estimated for the Kütahya Fault Zone region. The second group of M max values varying between 6.5 and 7.5 and is estimated in the regions of 1, 2, 3, 4, 5, 7, and 9, related to the northern part of Western Anatolia. The third group of M max values varies between 7.5 and 8.0 and is observed in the regions of 8, 11, 12, 13, 14, and 15, related to the southern part of Western Anatolia. Earthquakes larger than 6.8 (Table 1) have occurred in these regions, including the Büyük Menderes Graben, the Aegean Arc, Marmaris, the Köyceğiz-Fethiye Faults, the Tatarlı-Kumdanlı Faults, Dinar Graben, the Sultandağı Fault, and the Kaş-Beyşehirgölü Faults. The largest earthquake in these regions was observed in regions 11 and 12 as 7.1. The highest M max values (8.06) close to the size of the earthquake that occurred in 1926 (Table 1) are computed in region 10, which comprises the Aegean Islands.

Fig. 2
figure 2

The map of distribution of the M max values calculated by Bayesian method for the 15 different source regions of Western Anatolia

Full size image

Bayrak and Bayrak (2013) estimated the values of the upper bound w using the Gumbel III method (GIII) for the 15 different seismogenic source zones used in this study in Western Anatolia. Using this method, w values are considered as M max values for any region. We compared the results of M max values computed from the Bayesian approach in this study with the results found by Bayrak and Bayrak (2013). The distribution of M max (GIII) and M max (Bayes) values is shown in Fig. 3 for the different regions of Western Anatolia. The numerals on the graph represent the region numbers. Using the least squares (LS) method, we developed a relationship between M max values computed by two different methods, as shown in Fig. 3:

$$M_{\hbox{max} } ({\text{Bayes}}) = 0.85 \times M_{\hbox{max} } ({\text{GIII}}) + 1.60.$$
(17)
Fig. 3
figure 3

The relationship between M max(GIII) and M max(Bayes) values for the 15 different source regions of Western Anatolia. The regions are showed the numbers from 1 to 15 on the graph. Straight line is the linear regression and dashed lines are 95 % confidence limits and r is the correlation coefficient

Full size image

The correlation coefficient, r, is approximately 0.90 for Eq. (17). This means that there is a strong relationship between M max values found by the two methods. The straight line in Fig. 3 is the linear regression, and the dashed lines are 95 % confidence limits of the linear regression. Except for region 4 and region 6, the other regions remain in the confidence interval limits. M max values computed from GIII for 15 different seismogenic source regions are larger than those derived using the Bayesian method. Since the observed maximum magnitudes and the level of seismicity in the regions of 4 and 6 (Table 1) are lower than that of other regions, the computed values for these regions are outside confidence limits.

The estimated earthquake hazard parameters (β value and activity rate or intensity λ with events per day) are listed in Table 1. The method provides the mean “apparent” β and λ values as well as the ‘true’ values, which are listed in Table 1. As an example, for the Aliağa Fault region (region 1), we estimated the ‘apparent’ β value as 1.83, while the “true” mean β value was estimated to be 1.84. The mean intensity or activity rate λ is 0.31 (events/day) for “apparent” as well as “true” values. The computed β values vary between 1.70 and 3.08. The highest value is observed in region 13 (the Gölhisar-Çameli, Acıgöl, and Tatarlı Kumdanlı Faults and the Dinar Graben), while the lowest value is observed in region 3 (the Eskişehir and İnönü-Dodurga Fault Zones). Different numbers of earthquakes in different parts of the magnitude–frequency relationship are considered for the estimation of slope β value in the Bayesian method. Therefore, a significant number of earthquakes are used to estimate it for lower magnitude and fewer at larger magnitudes.

The useful probabilistic tools for earthquake hazard evaluation are estimated and demonstrated for 15 seismogenic source regions in Western Anatolia. A posteriori probability density and a posteriori density function for both apparent and true magnitudes M max(T) that will occur in future time intervals of 5, 10, 20, 50, and 100 years are estimated for region 1 (the Aliağa Fault). The a posteriori probability density for the apparent and true magnitudes M max(T) (Fig. 4) as well as the a posteriori probability distribution function for the apparent and true M max(T) magnitudes (Fig. 5), that will occur in future time intervals of 5, 10, 20, 50, and 100 years is illustrated for region 1 seismogenic source region. These figures are useful probabilistic tools in the earthquake hazard analysis in the examined region. We have also calculated ‘tail’ probabilities P(M max(T) > M) of the apparent and true magnitudes for all source regions, but this is shown in Fig. 6 only for region 1 for the future time intervals of 5, 10, 20, 50, and 100 years. The other important quantiles that can be considered for hazard estimation are the ‘tail’ probabilities P(Mmax(T) > M) for the apparent as well as for the true magnitudes. Lastly, we have estimated a posteriori M-quantiles for the 15 source regions in the examined region and for probabilities 0.50, 0.70, and 0.90 in future time intervals of 5, 10, 20, 50, and 100 years. The seismogenic source regions and graphs of their distribution are illustrated (Figs. 7, 8). In these figures, the quantiles of the levels of probability (α = 0.50, 0.70, and 0.90) are shown for each region. We also computed their confidence limits. The quantiles for both apparent and true magnitudes for probabilities of 0.50, 0.70, and 0.90 are estimated and tabulated. It can be observed that the differences between apparent and true magnitude quantiles are very low, and this is due to the good quality of the data used. The time periods T = 50 and 100 years are considered as appropriate time intervals for the estimation of seismic hazard, but anyone interested in shorter periods may obtain the appropriate estimate of M-quantiles. It has been observed that the shorter the time interval, the more appropriate are the results obtained.

Fig. 4
figure 4

A posteriori probability densities of M max(T) for a ‘apparent magnitude’ and b ‘true magnitude’ showing statistical characteristics of seismic hazard parameters for region 1 (Aliağa Fault) in next T = 5, 10, 20, 50, and 100 years

Full size image
Fig. 5
figure 5

A posteriori probability functions of M max(T) for a ‘apparent magnitude’ and b ‘true magnitude’ showing statistical characteristics of seismic hazard parameters for region 1 (Aliağa Fault) in next T = 5, 10, 20, 50, and 100 years

Full size image
Fig. 6
figure 6

‘Tail’ probabilities 1 − ф(M) = Prob(M max(T) ≥ M) for a ‘apparent magnitude’ and b ‘true magnitude’ showing statistical characteristics of seismic hazard parameters for region 1 (Aliağa Fault) in next T = 5, 10, 20, 50, and 100 years

Full size image
Fig. 7
figure 7

Quantiles for ‘apparent magnitudes’ (of 50, 70, and 90 %) of function of distribution of maximum values of M max for a given length T of future time interval for the 15 different source regions of Western Anatolia

Full size image

We have used 110 years of seismic catalogue to calculate earthquake hazard parameters in this study which reveals that the estimates of M-quantiles for next 100 years are reasonable. The apparent and true magnitudes for 50, 70, and 90 % probability levels within the next 5, 10, 20, 50, and 100 years are calculated for all seismogenic regions. The estimated values are listed in Tables 2 and 3. For the next 100 years, the apparent magnitudes with 90 % probability for the 15 different regions in Western Anatolia are found to be 7.09, 6.85, 6.91, 6.38, 6.78, 5.89, 6.96, 7.16, 6.85, 7.65, 7.47, 7.48, 6.75, 6.86, and 7.23, respectively. The true magnitudes for the same parameters for the regions are computed as 7.06, 6.84, 6.87, 6.35, 6.73, 5.81, 6.93, 7.14, 6.83, 7.65, 7.44, 7.45, 6.73, 6.84, and 7.21, respectively. The highest apparent and true magnitude values in these regions are equal to 7.65 and observed in region 10 comprising the Aegean Islands for the next 100 years. If we compare these two tables, it is easy to observe that the values recorded in Table 3 are less than those in Table 2. This is obvious since Table2 includes the magnitudes (apparent) of Table 3 (true) plus the error ε. The differences between these two values are very low, and we believe that this depends upon the quality of the data, which includes minor errors. Therefore, the efficiency of the data included in Tables 2 and 3 and the results of the analysis are almost the same (Fig. 8).

Table 2 The quantiles of the ‘apparent magnitudes’ M max(T) estimated for the levels of probability (1) α = 0.50, (2) α = 0.70, and (3) α = 0.90 for the 15 different source regions of Western Anatolia future T = 5, 10, 20, 50, and 100 years
Full size table
Table 3 The quantiles of the ‘true magnitudes’ M max(T) estimated for the levels of probability (1) α = 0.50, (2) α = 0.70, and (3) α = 0.90 T = 5, 10, 20, 50, and 100 years
Full size table
Fig. 8
figure 8

Quantiles for ‘true magnitudes’ (of 50, 70 and 90 %) of function of distribution of maximum values of M max for a given length T of future time interval for the 15 different source regions of Western Anatolia

Full size image

6 Conclusions

The instrumental earthquake catalog that is homogenous for M s ≥ 4.0 was used during the period 1900–2013 to evaluate earthquake hazard parameters for the 15 seismogenic source regions in Western Anatolia using the Bayesian method. For this purpose, maximum regional magnitude (M max), β value, and the seismicity activity rate or intensity (λ) and their uncertainty are computed. The maximum regional magnitude is one of the most important earthquake hazard parameters; therefore, significance is given to the estimation of this parameter as well as to the quantiles of the M max distribution in a future time interval. The computed M max values are between 6.00 and 8.06, while their uncertain values vary between 0.25 and 0.88. While low values are found in the northern part of Western Anatolia, high values are observed in the southern part of Western Anatolia related to the Aegean subduction zone. The largest value is computed in region 10 comprising the Aegean Islands.

The estimated β values for the 15 different regions of Western Anatolia vary between 1.70 and 3.08. In this method, different numbers of earthquakes in different parts of the magnitude-frequency relationship are taken into account for the estimation of β value. Therefore, a significant number of earthquakes are used to estimate lower magnitude and fewer at larger magnitudes. We estimated earthquake probabilities in the next 5, 10, 20, 50, and 100 years. We also computed a posteriori probability densities of M max(T), a posteriori probability functions of M max(T), and ‘tail’ probabilities Prob(M max(T) ≥ M) for the ‘apparent’ and ‘true’ magnitude values. In addition, we estimated the quantiles of the ‘apparent and true’ magnitudes M max(T) for the levels of probability α = 0.50, α = 0.70, and α = 0.90 for the 15 seismic regions of Western Anatolia in the next T = 5, 10, 20, 50, and 100 years. Considering the estimated parameters, the results indicate that region 10 comprising the Aegean Islands has a very high probability of experiencing a 7.65 magnitude earthquake within the next century.