1 Introduction

Faults are heterogeneous surfaces, with spatially varying friction. Many aspects of fault dynamics can be reproduced by asperity models (Lay et al. 1982; Scholz 1990), assuming that one or more regions of the fault have much higher friction than the adjacent regions. Earthquakes are the result of failure of one or more asperities under the action of tectonic stress.

In the framework of an asperity model, stress accumulation on each asperity, fault slip at asperities and stress transfers between asperities play a key role. Therefore, the dynamical behaviour of faults can be fruitfully investigated by means of discrete models where the basic elements are asperities (e.g. Rice 1993; Turcotte 1997). Discrete fault models include the relevant characteristics of seismic sources, but avoid the too detailed field description of continuum mechanics. An advantage associated with a finite number of degrees of freedom is that one can easily calculate and draw the orbit of the system in phase space, allowing the evolution of the system to be followed in the long term.

Several recent large and medium-sized earthquakes have been the result of failure of two distinct asperities, such as the 1995 Kobe earthquake (Kikuchi and Kanamori 1996; Koketsu et al. 1998), the 2004 Parkfield earthquake (Johanson et al. 2006; Twardzik et al. 2012) and the 2010 Maule, Chile, earthquake (Delouis et al. 2010; Lay et al. 2010; Vigny et al. 2011).

A fault made of two asperities can be modelled by a discrete system that was originally proposed by Nussbaum and Ruina (1987) and further investigated by Huang and Turcotte (1990, 1992), McCloskey and Bean (1992), Sousa (1995), He (2003) and Galvanetto (2004).

The model was discussed by Ruff (1992), who showed graphically some solutions for the failure of a single asperity and the consecutive, but separate, failure of the two asperities. He studied the evolution of some couples of asperities with different degrees of coupling, concluding that the model can reproduce basic features of the activity of a fault, such as variable recurrence times and slip amplitudes.

A more general treatment was given by Turcotte (1997), who showed numerical solutions including the simultaneous motion of asperities. A complete analytical solution was given by Dragoni and Santini (2012). The dynamics of the system has four different modes: a sticking mode and three slipping modes, corresponding to the asperities slipping separately or simultaneously. Any seismic event is due to a certain number and sequence of slipping modes.

However, any fault is subject to stress perturbations in connection with earthquakes generated by neighbouring faults. It has been recognized that stress transfer between seismic faults plays a key role in the behaviour of fault systems (e.g. Stein et al. 1992; Harris 1998; Stein 1999; Steacy et al. 2005). Each earthquake produces a stress redistribution, thus affecting the occurrence times and the magnitudes of subsequent earthquakes. The effects of stress perturbations have been discussed by Belardinelli et al. (2003) for a homogeneous fault.

In the present paper we investigate the effects of stress perturbations on the dynamics of a fault containing two asperities. Since the stress produced by a fault dislocation is strongly inhomogeneous, individual asperities belonging to a fault will be subject to different stress changes. We study how the state of the system is changed by the perturbation, how such a change depends on the initial state and on the components of transferred stress, and how the perturbation affects the subsequent evolution of the system. We neglect viscoelastic effects; these have been considered elsewhere (Amendola and Dragoni 2013) and would not modify the main conclusions of the paper.

As an application of the model, we consider the effect of the 1960 Great Chilean Earthquake on the fault that produced the 2010 Maule earthquake. We evaluate to what extent the stress transferred to this fault changed the occurrence time, the source function and the seismic moment of the Maule earthquake.

2 The Model

We consider a plane fault with two asperities of equal areas, which we name asperity 1 and 2 (Fig. 1). We assume that the fault is embedded in a shear zone that is a homogeneous and isotropic Hooke solid, subject to a uniform strain rate by the motion of two tectonic plates at relative velocity \(v\). According to the premise, we do not determine stress, friction and slip at every point of the fault but, instead, the average values of these quantities on each asperity.

Fig. 1
figure 1

Sketch of the fault model. The states of asperities 1 and 2 are described by their respective slip deficits \(x(t)\) and \(y(t)\). Tangential stresses on the asperities due to tectonic motions are functions of \(x\) and \(y\)

Full size image

We define the slip deficit of an asperity at a certain instant \(t\) of time to be the slip that the asperity should undergo in order to recover the relative plate displacement occurred up to time \(t\). The slip deficit increases when an asperity is stationary and decreases when it slips. We describe the state of the fault by the slip deficits \(x(t)\) and \(y(t)\) of the two asperities.

Due to plate motion, the asperities are subject to tangential forces

$$\begin{aligned} f_1 = - Kx - K_\text{c} (x - y), \quad f_2 = - Ky - K_\text{c} (y - x), \end{aligned}$$
(1)

where \(K\) and \(K_\text{c}\) are constants proportional to the rigidity of the medium, describing respectively the tectonic loading and the coupling between the asperities (Dragoni and Santini 2012).

Fault slip is governed by friction. The rate and state friction laws (Ruina 1983; Dieterich 1994) have been found to be effective in reproducing many aspects of earthquakes and seismicity. In particular, they yield a friction that changes with time during fault slip. Here we are more interested in the spatial distribution of friction on the fault and in its changes produced by stress perturbations. Therefore we use a simpler friction law, assuming that asperities 1 and 2 are characterized, respectively, by static frictions \(f_{\text{s}1}\) and \(f_{\text{s}2}\) and by dynamic frictions \(f_{\text{d}1}\) and \(f_{\text{d}2}\) that are the average values of friction during fault slip.

We introduce nondimensional variables and time

$$\begin{aligned} X = {K x \over f_{\text{s}1}}, \quad Y = {K y \over f_{\text{s}1}}, \quad T = \sqrt{K\over m} t, \end{aligned}$$
(2)

where \(m\) is the mass associated with each asperity. The system is described by four nondimensional parameters defined as

$$\begin{aligned} \alpha = {K_\text{c} \over K}, \quad \beta = {f_{\text{s}2} \over f_{\text{s}1}} = {f_{\text{d}2} \over f_{\text{d}1}}, \quad \epsilon = {f_{\text{d}1} \over f_{\text{s}1}} = {f_{\text{d}2} \over f_{\text{s}2}}, \quad V = {\sqrt{Km} \over f_\text{s}} \,v \end{aligned}$$
(3)

with \(\alpha \ge 0\), \(\beta > 0\), \(0<\epsilon <1\) and \(V>0\). The ratio \(\epsilon\) between dynamic and static friction is chosen to be the same for both asperities. From these parameters we can define a slip

$$\begin{aligned} U = 2 {1 - \epsilon \over 1 + \alpha }, \end{aligned}$$
(4)

which is the maximum slip of asperity 1 when it slips alone, and a time interval

$$\begin{aligned} \Delta T = {U \over V}, \end{aligned}$$
(5)

which is the time required for tectonic motion to accumulate a slip deficit \(U\). The system is subject to the additional constraint

$$\begin{aligned} X\ge 0, \quad Y \ge 0 \end{aligned}$$
(6)

that excludes overshooting during fault slip. We define nondimensional forces

$$\begin{aligned} F_1 = {f_1\over f_{\text{s}1}}, \quad F_2 = {f_2\over f_{\text{s}1}}. \end{aligned}$$
(7)

These can be written in terms of the model variables as

$$\begin{aligned} F_1 = -X - \alpha (X-Y), \quad F_2 = -Y - \alpha (Y-X). \end{aligned}$$
(8)

The system can operate in four different modes, corresponding to stationary asperities (mode 00), motion of asperity 1 (mode 10), motion of asperity 2 (mode 01) and simultaneous asperity motion (mode 11). Each mode is described by a different system of autonomous differential equations: their solutions were given in Dragoni and Santini (2012).

3 Evolution of the System

The evolution of the system can be predicted by calculating the orbits of the representative point in phase space. The conditions for the failure of asperities 1 and 2 are, respectively,

$$\begin{aligned} F_1 = - 1, \quad F_2 = - \beta . \end{aligned}$$
(9)

If we use (8), conditions (9) yield the equations of two lines in the \(XY\) plane, i.e.,

$$\begin{aligned} (1 + \alpha ) X - \alpha Y - 1 = 0, \end{aligned}$$
(10)
$$\begin{aligned} \alpha X - (1 + \alpha ) Y + \beta = 0, \end{aligned}$$
(11)

meeting at a point \(P\): we call them line 1 and line 2, respectively. The sticking region of the system, i.e. the set of points corresponding to stationary asperities, is the quadrilateral \(Q\) (Fig. 2a) defined as the set of solutions of the four inequalities

$$\begin{aligned} X \ge 0, \quad X \le {\alpha \over 1+\alpha } Y + {1\over 1+\alpha }, \quad Y \ge 0, \quad Y \le {\alpha \over 1+\alpha } X + {\beta \over 1+\alpha }. \end{aligned}$$
(12)

If we consider an initial point \(P_0=(X_0,Y_0) \in Q\), its orbit in the sticking region is the line

$$\begin{aligned} Y = X + p, \end{aligned}$$
(13)

where \(p = Y_0 - X_0\). From (8), the difference between the tangential forces on the asperities is

$$\begin{aligned} \Delta F = F_1 - F_2 = (1 + 2\alpha ) p, \end{aligned}$$
(14)

so that \(p\) measures the difference between the forces exerted on the two asperities. The line parallel to (13) through \(P\) is

$$\begin{aligned} Y = X + p_0, \end{aligned}$$
(15)

where

$$\begin{aligned} p_0 = {\beta - 1\over 1 + 2\alpha }. \end{aligned}$$
(16)

This line divides \(Q\) into subsets \(Q_1\) and \(Q_2\), such that the orbits belonging to \(Q_1\) intersect line 1 and those belonging to \(Q_2\) intersect line 2. In the particular case \(p=p_0\), the orbit intersects both lines at \(P\).

In many cases the system passes from mode 00 to mode 10 or 01, then again to mode 00; i.e. it generates an earthquake that is due to the failure of a single asperity. However, there is a set \(S\) of states driving the system to mode 11, i.e. to simultaneous asperity slip (Fig. 2b); \(S\) is the subset of \(Q\) bounded by the lines \(Y=X+p_1\) and \(Y=X+p_2\), with

$$\begin{aligned} p_1 = p_0 - {\alpha U \over 1 + 2\alpha }, \qquad p_2 = p_0 + \beta {\alpha U \over 1 + 2\alpha }. \end{aligned}$$
(17)

4 Stress Perturbations

When a fault slips, it transfers an amount of static stress to neighbouring faults, thus modifying their state of stress. Therefore, any fault is subject to frequent stress perturbations due to the seismic activity of neighbouring faults. If we consider a fault with two asperities, the stress imposed on one asperity by the perturbation will be different from that imposed on the other one, because dislocation stress fields are strongly inhomogeneous. Therefore, the stress difference between the asperities is changed by the perturbation.

We make the following assumptions:

  1. 1.

    Stress is transferred to the fault during the interseismic intervals (this is by far the most probable case, since faults are stationary for most of their lifetime).

  2. 2.

    The stress transfer is instantaneous, taking place over a time interval that is much shorter than an interseismic interval.

  3. 3.

    The state of the fault is sufficiently far from the failure condition and the stress perturbation is sufficiently small that the failure condition is not attained immediately for either asperity.

Suppose that the fault is subject to a stress perturbation when its state is \((X,Y)\). If \(\Delta F_1\) and \(\Delta F_2\) are the changes in tangential forces, the system makes a transition to a state \((X^\prime , Y^\prime )\) with

$$\begin{aligned} X^\prime = X + \Delta X, \quad Y^\prime = Y + \Delta Y, \end{aligned}$$
(18)

where according to (8),

$$\begin{aligned} \Delta X = - {1+\alpha \over 1 + 2\alpha } \,\Delta F_1 - {\alpha \over 1 + 2\alpha } \,\Delta F_2, \end{aligned}$$
(19)
$$\begin{aligned} \Delta Y = - {\alpha \over 1 + 2\alpha } \,\Delta F_1 - {1+\alpha \over 1 + 2\alpha } \,\Delta F_2. \end{aligned}$$
(20)

In phase space, this change in state can be expressed as a vector

$$\begin{aligned} \Delta \mathbf{R} = (\Delta X, \Delta Y). \end{aligned}$$
(21)

The direction of \(\Delta \mathbf{R}\) is related to the position of the dislocation source responsible for the perturbation and to the sign of the tangential stress imposed on the asperities. As a consequence of the perturbation, \(p\) becomes

$$\begin{aligned} p^\prime = p + \Delta p, \end{aligned}$$
(22)

where

$$\begin{aligned} \Delta p = \Delta Y - \Delta X. \end{aligned}$$
(23)

The change in normal stresses produces changes in static friction: if the new frictions are \(f_{\text{s}1}^\prime\) and \(f_{\text{s}2}^\prime\), respectively, we define

$$\begin{aligned} \beta _1 = {f_{\text{s}1}^\prime \over f_{\text{s}1}}, \quad \beta _2 = {f_{\text{s}2}^\prime \over f_{\text{s}1}}. \end{aligned}$$
(24)

The changes in friction are then

$$\begin{aligned} \Delta \beta _1 = \beta _1 - 1, \quad \Delta \beta _2 = \beta _2 - \beta, \end{aligned}$$
(25)

and the conditions (9) for asperity failure become

$$\begin{aligned} F_1 = - \beta _1, \qquad F_2 = - \beta _2. \end{aligned}$$
(26)

Thanks to (8), these yield the equations of lines

$$\begin{aligned} (1 + \alpha ) X - \alpha Y - \beta _1&= 0,\end{aligned}$$
(27)
$$\begin{aligned} \alpha X - (1 + \alpha ) Y + \beta _2&= 0 ,\end{aligned}$$
(28)

meeting at a point \(P^\prime\); we call them line \(1^\prime\) and line \(2^\prime\), respectively. At the same time, the change in friction changes \(p_0\) to

$$\begin{aligned} p_0^\prime = p_0 + \Delta p_0, \end{aligned}$$
(29)

where

$$\begin{aligned} \Delta p_0 = {\Delta \beta \over 1 + 2\alpha } \end{aligned}$$
(30)

with

$$\begin{aligned} \Delta \beta = \Delta \beta _2 - \Delta \beta _1. \end{aligned}$$
(31)

Hence,

$$\begin{aligned} p_0^\prime = {\beta _2 - \beta _1 \over 1 + 2 \alpha }. \end{aligned}$$
(32)

Therefore, the sticking region \(Q\) becomes a different region \(Q^\prime\), which is divided into subsets \(Q_1^\prime\) and \(Q_2^\prime\) by the line \(Y=X+p_0^\prime\). In conclusion, the change in tangential stress modifies the orbit of the system, while the change in normal stress modifies the boundaries of the sticking region. The new sticking region is shown in Fig. 2c, where it is assumed that the frictions of asperities 1 and 2 are increased by amounts equal to \(0.1 f_{\text{s}1}\) and \(0.2 f_{\text{s}1}\), respectively.

Fig. 2
figure 2

The sticking region \(Q\) of the system: a subsets \(Q_1\) and \(Q_2\), from which the failure of asperity 1 or 2 is attained, respectively; b subset \(S\), from which simultaneous asperity failure results; c the sticking region \(Q^\prime\) after a stress perturbation: the thick dashed lines indicate the region before the perturbation (\(\alpha =1\), \(\beta =2\), \(\Delta \beta _1=0.1\), \(\Delta \beta _2=0.2\))

Full size image

5 Changes in Coulomb Stresses

A useful concept in fault mechanics is Coulomb stress (Stein 1999; Gomberg et al. 2000). It is the difference \(\sigma _{\rm C}\) between the tangential traction \(\sigma\) in the slip direction and the static friction \(\tau _\text{s}\) on a fault surface:

$$\begin{aligned} \sigma _{\rm C} = \sigma - \tau _\text{s}. \end{aligned}$$
(33)

Therefore, \(\sigma _{\rm C}\) is negative during an interseismic phase, and an earthquake takes place when \(\sigma _{\rm C}=0\). In general, a stress perturbation produces changes in \(\sigma _{\rm C}\) by changing both \(\sigma\) and \(\tau _\text{s}\).

On a complex fault, we can assign a value of Coulomb stress to each asperity and study how it changes due to stress perturbations. According to (33) and (9), the Coulomb forces on the two asperities are, respectively,

$$\begin{aligned} F_1^{\rm{C}} = - F_1 - 1, \quad F_2^{\rm{C}} = - F_2 - \beta \end{aligned}$$
(34)

or, thanks to (8),

$$\begin{aligned} F_1^{\rm{C}} = (1 + \alpha ) X - \alpha Y - 1, \quad F_2^{\rm{C}} = (1 + \alpha ) Y - \alpha X - \beta. \end{aligned}$$
(35)

They are scalar functions on \(Q\), vanishing on line 1 and line 2, respectively, with \(F_1^{\rm{C}}>F_2^{\rm{C}}\) in \(Q_1\) and \(F_1^{\rm{C}}<F_2^{\rm{C}}\) in \(Q_2\) (Fig. 3). Their gradients are perpendicular to line 1 and to line 2, respectively.

The forces \(F_1^{\rm{C}}\) and \(F_2^{\rm{C}}\) are equal to each other on the line (15), and if we consider a state characterized by the variable \(p\), their difference is

$$\begin{aligned} F_2^{\rm{C}} - F_1^{\rm{C}} = (1 + 2\alpha ) (p - p_0); \end{aligned}$$
(36)

i.e. it is proportional to the difference \(p-p_0\). Therefore, in the states belonging to subset \(S\), driving the system to mode 11, the Coulomb stresses on the two asperities have similar magnitudes.

The changes \(\Delta F_1^{\rm{C}}\) and \(\Delta F_2^{\rm{C}}\) in the Coulomb forces indicate how much the asperities get closer to or farther from the slip conditions. From (34) and (25), these can be written as

$$\begin{aligned} \Delta F_1^{\rm{C}} = - \Delta F_1 - \Delta \beta _1, \quad \Delta F_2^{\rm{C}} = - \Delta F_2 - \Delta \beta _2 \end{aligned}$$
(37)

or

$$\begin{aligned} \Delta F_1^{\rm{C}} = \Delta R [(1+\alpha ) \cos \theta - \alpha \sin \theta ] - \Delta \beta _1,\end{aligned}$$
(38)
$$\begin{aligned} \Delta F_2^{\rm{C}} = \Delta R [(1+\alpha ) \sin \theta - \alpha \cos \theta ] - \Delta \beta _2, \end{aligned}$$
(39)

where

$$\begin{aligned} \theta = \arctan {\Delta Y\over \Delta X}. \end{aligned}$$
(40)

They are plotted in Fig. 4a for a particular choice of the model parameters. The direction of \(\Delta \mathbf{R}\), expressed by the angle \(\theta\), indicates how much the state of the fault gets closer to or farther from the failure conditions given by lines 1 and 2. The relationship between the direction of \(\Delta \mathbf{R}\) and the change in Coulomb stresses is evident if one considers that the gradients of \(F_1^{\rm{C}}\) and \(F_2^{\rm{C}}\) are perpendicular to lines 1 and 2, respectively (Fig. 3). Then, \(\Delta F_1^{\rm{C}}\) is maximum when \(\Delta \mathbf{R}\) is perpendicular to line 1 and points toward it; it vanishes when \(\Delta \mathbf{R}\) is parallel to line 1; it is minimum when \(\Delta \mathbf{R}\) is perpendicular to line 1 but points away from it, and analogously for \(\Delta F_2^{\rm{C}}\).

Equation (36) shows that in mode 00 the distance of an orbit from the line \(Y=X+p_0\) is equivalent to a certain difference between the Coulomb stresses of the two asperities. Therefore, an important quantity for a two-asperity fault is

$$\begin{aligned} \Delta F^{\rm{C}} = \Delta F_2^{\rm{C}} - \Delta F_1^{\rm{C}}. \end{aligned}$$
(41)

Thanks to (38), (39) and (31), this can be written as

$$\begin{aligned} \Delta F^{\rm{C}} = \Delta R\, (1 + 2 \alpha ) (\sin \theta - \cos \theta ) - \Delta \beta, \end{aligned}$$
(42)

which is plotted in Fig. 4b. If \((X,Y) \in Q_1\), perturbations for which \(\Delta F^{\rm{C}}>0\) bring the system nearer to the condition for mode 11 whereas those with \(\Delta F^{\rm{C}}<0\) bring the system farther from that condition. The opposite occurs if \((X,Y) \in Q_2\).

We conclude that \(\Delta p\) measures the change in the asymmetry degree of stress, while \(\Delta \beta\) measures the change in the asymmetry degree of friction that the perturbation brings into the system. While the changes in Coulomb stresses of individual asperities are a measure of how much the asperities get closer to or farther from the slip conditions, the change in the difference between Coulomb stresses indicates how much the system gets closer to or farther from the condition for simultaneous asperity slip.

Fig. 3
figure 3

Coulomb forces \(F_1^{\rm{C}}\) (a) and \(F_2^{\rm{C}}\) (b) on the two asperities, plotted in the sticking region \(Q\) (\(\alpha =1\), \(\beta =2\)). A stress perturbation can be represented as a vector \(\Delta \mathbf{R}\) in \(Q\), changing the values of the Coulomb forces on the asperities

Full size image
Fig. 4
figure 4

Changes in Coulomb forces \(\Delta F_1^{\rm{C}}\) and \(\Delta F_2^{\rm{C}}\) of the two asperities (a) and in their difference \(\Delta F^{\rm{C}}\) (b) as functions of the angle \(\theta\), indicating the direction of vector \(\Delta \mathbf{R}\) (\(\alpha =1\), \(\Delta R=0.1\), \(\Delta \beta _1=0.1\), \(\Delta \beta _2=0.2\))

Full size image

6 Effects of Perturbations

Let us consider how a typical orbit of the system is modified by a perturbation characterized by the values \(\Delta p\), \(\Delta \beta _1\) and \(\Delta \beta _2\). Let \(P_0 \in Q\) be the initial point of the system and \(P_1\) be the point where the unperturbed orbit intersects line 1 or line 2, marking the beginning of a seismic event; For instance, if \(P_0 \in Q_1\), the orbit (13) intersects line 1 at point \(P_1\) with coordinates

$$\begin{aligned} X_1 = 1 + \alpha p, \quad Y_1 = 1 + (1+\alpha ) p. \end{aligned}$$
(43)

However, if the perturbation shifts the initial point \(P_0\) to \(P_0^\prime\), the perturbed orbit is

$$\begin{aligned} Y = X + p^\prime. \end{aligned}$$
(44)

If \(P_0^\prime \in Q_1^\prime\), the orbit intersects line \(1^\prime\) at point \(P_1^\prime\) with

$$\begin{aligned} X_1^\prime = \beta _1 + \alpha p^\prime , \quad Y_1^\prime = \beta _1 + (1+\alpha ) p^\prime. \end{aligned}$$
(45)

The evolution of the system may be very different in the two cases. Different orbits and different sticking regions entail different values of interseismic intervals and slip amplitudes. Moreover, a different asperity may be involved in the earthquake with respect to the unperturbed system, entailing a remarkably different position of the earthquake hypocentre.

In order to calculate the change in the occurrence time of the first earthquake following the perturbation, we consider the case in which the state of the system is in \(Q_1\) (or \(Q_2\)) before the perturbation and in \(Q_1^\prime\) (or \(Q_2^\prime\)) after the perturbation. For the sake of simplicity, we do not consider the particular case in which the state is so close to the boundary between \(Q_1\) and \(Q_2\) that it changes from \(Q_1\) to \(Q_2^\prime\) or from \(Q_2\) to \(Q_1^\prime\) as a consequence of the perturbation.

Let \(T_1\) be the time required for the system to reach line 1 or line 2 at \(P_1\) in the absence of perturbation. If \(P_0=(X,Y) \in Q_1\), we obtain

$$\begin{aligned} T_1 = {1 + \alpha p - X\over V}. \end{aligned}$$
(46)

If a perturbation shifts the system to the point \((X^\prime , Y^\prime )\) and the friction of asperity 1 to \(\beta _1\), the time required to reach line \(1^\prime\) at \(P_1^\prime\) is

$$\begin{aligned} T_1^\prime = {\beta _1 + \alpha p^\prime - X^\prime \over V}. \end{aligned}$$
(47)

The difference between the two times is

$$\begin{aligned} \Delta T_1 = T_1^\prime - T_1 \end{aligned}$$
(48)

or

$$\begin{aligned} \Delta T_1 = {\alpha \Delta Y - (1 + \alpha ) \Delta X + \Delta \beta _1\over V}. \end{aligned}$$
(49)

A comparison with (37) shows that

$$\begin{aligned} \Delta T_1 = - {\Delta F_1^{\rm{C}} \over V}. \end{aligned}$$
(50)

If \(P_0 \in Q_2\), the time \(T_1\) required for the system to reach line 2 at \(P_1\) can be calculated analogously and we obtain

$$\begin{aligned} \Delta T_1 = - {\Delta F_2^{\rm{C}} \over V}. \end{aligned}$$
(51)

If \(\Delta F_1^{\rm{C}}\) or \(\Delta F_2^{\rm{C}}\) is positive, \(\Delta T_1\) is negative and \(T_1\) is reduced: the earthquake occurs earlier. The opposite occurs if \(\Delta F_1^{\rm{C}}\) or \(\Delta F_2^{\rm{C}}\) is negative.

We conclude that the advance or delay of an earthquake produced by a given asperity is proportional to the change in the Coulomb stress of the asperity, in agreement with previous Coulomb failure models (e.g. Gomberg et al. 2000). Figure 4a shows that the same perturbation \(\Delta \mathbf{R}\) can produce very different effects according to whether the state of the system is in \(Q_1\) or in \(Q_2\). Moreover, the evolution of the system can be deeply changed even if the change in Coulomb stress is negligible.

A stress perturbation will also change the moment rate and the seismic moment of the following earthquake. The moment rate can be calculated as

$$\begin{aligned} \dot{M}(T) = M_1 {\Delta \dot{X} + \Delta \dot{Y} \over U}, \end{aligned}$$
(52)

where \(\Delta \dot{X}\) and \(\Delta \dot{Y}\) are the slip rates in the slipping modes and \(M_1\) is the seismic moment due to the slip of asperity 1 by an amount \(U\). The seismic moment is

$$\begin{aligned} M = M_1 {U_1 + U_2 \over U}, \end{aligned}$$
(53)

where \(U_1\) and \(U_2\) are the final slip amplitudes of asperities 1 and 2, respectively. The moment \(M\) as a function of \(p\) was calculated in Dragoni and Santini (2012); it is constant for \(p<p_1\) and \(p>p_2\) and has discontinuities at \(p=p_1\) and \(p=p_2\). After a perturbation, the moment becomes

$$\begin{aligned} M^\prime = M_1 {U_1^\prime + U_2^\prime \over U}. \end{aligned}$$
(54)

The moment change

$$\begin{aligned} \Delta M = M^\prime - M \end{aligned}$$
(55)

can be easily calculated in the absence of simultaneous motion. In this case,

$$\begin{aligned} \Delta M = {\left\{ \begin{array}{ll} M_1 \Delta \beta _1, &{}\quad p<p_1\\ M_1 \Delta \beta _2, &{}\quad p>p_2\\ \end{array}\right. }. \end{aligned}$$
(56)

Therefore, if the system remains outside \(S\) after a perturbation, the change in \(M\) is due solely to the change in friction, hence to the change in normal stress. The greatest change in \(M\) occurs when the initial state belongs to \(S\) or is very close to it. In this case, \(M\) can sensitively increase or decrease. In fact, \(M \ge (\beta _1 + \beta _2)M_1\) in the interval \(p_1 < p < p_2\). In this case, both asperities are involved in the earthquake and the dislocation area is doubled.

7 An Example: The 2010 Maule Earthquake

As an example, we evaluate the effect of the 1960 Great Chilean Earthquake (or Valdivia earthquake) on the fault segment that produced the 2010 Maule earthquake. This earthquake took place in a seismic gap, where the last great earthquake had occurred in 1835 (Campos et al. 2002) and the subduction velocity was estimated to be \(v \simeq 7\) cm a\(^{-1}\) (Ruegg et al. 2009).

The 1960 Valdivia earthquake was a magnitude \(M_w = 9.5\) thrust event producing a rupture 800 km long in southern Chile (Plafker and Savage 1970; Kanamori and Cipar 1974). The 2010 Maule earthquake was a magnitude \(M_w= 8.8\) thrust event that struck central Chile, north of the 1960 rupture (Delouis et al. 2010; Vigny et al. 2011). Slip concentrated on two main asperities situated south and north of the epicentre, with approximately the same areas, which we call asperity 1 and 2, respectively.

The source function of the Maule earthquake was modelled by Dragoni and Santini (2014) as a sequence of modes 10, 11, 01 that can be obtained with \(\alpha =1\), \(\beta =1\), \(\epsilon =0.7\) and \(p= p_\text{a} =-0.07\). This value of \(p\) implies that the state of the system was in \(S\) before the earthquake and that, according to (14), the stress on asperity 1 was greater than that on asperity 2 by an amount equal to 21 % of static friction.

On the basis of the present model, we may try to answer questions such as: What was the stress state on the Maule fault segment after the 1835 earthquake and before the Valdivia earthquake? How large was the advance of the Maule earthquake due to the occurrence of the Valdivia earthquake? Which kind of source function and what value of seismic moment would the Maule earthquake have had if the Valdivia earthquake had not occurred? When would the next earthquake occur in the absence of further perturbations.

To this aim, we calculate the orbit of the system from 1835 to 2010 and extend it into the future. We neglect the 1985 Valparaiso earthquake, which occurred north of the Maule segment, because its seismic moment was much smaller than that of the Valdivia earthquake (Mendoza et al. 1994).

The Maule and Valdivia faults belong to the same plate boundary and have similar strike and dip angles (Fujii and Satake 2013). For the sake of simplicity, we assume that the two faults are coplanar, so that \(\Delta \beta _1 = \Delta \beta _2 = 0\) and the sticking region of the system does not change.

In the first place, we evaluate the tangential stresses \(\Delta \sigma _1\) and \(\Delta \sigma _2\) transferred to asperities 1 and 2 by the Valdivia earthquake. To this aim, we assume that the source is a double couple located at the centre of the higher slip area of the Valdivia fault (Fig. 5); this is of course a rough approximation, but for the present purpose it is enough to give the order of magnitude of the transferred stress. Then, under the assumption that the medium is a Poisson solid,

$$\begin{aligned} \Delta \sigma _1 \approx {M \over 6\pi r_1^3}, \quad \Delta \sigma _2 \approx {M \over 6\pi r_2^3}, \end{aligned}$$
(57)

where \(M\) is the seismic moment of the Valdivia earthquake, and \(r_1\) and \(r_2\) are the distances of asperities 1 and 2 from the assumed source of perturbation.

Then, we evaluate the friction \(\tau _\text{s}\), which is assumed to be the same for both asperities. To this purpose, we consider an event involving only asperity 1, which produces a displacement \(u\) equal to the slip deficit accumulated during an interval \(\Delta t\), corresponding to nondimensional quantities \(U\) and \(\Delta T\) defined in (4) and (5). Then,

$$\begin{aligned} \Delta t = {u \over v} \end{aligned}$$
(58)

and

$$\begin{aligned} u = {U \over U_1} u_1, \end{aligned}$$
(59)

where \(u_1\) is the slip of asperity 1 in the Maule earthquake. The change in force associated with slip \(U\) is calculated from (8) with \(\Delta X = U\) and \(\Delta Y =0\), giving

$$\begin{aligned} \Delta F_1 = - 2(1 - \epsilon ). \end{aligned}$$
(60)

The corresponding stress drop is accumulated in the interval \(\Delta t\), so that the static friction is

$$\begin{aligned} \tau _\text{s} = {\dot{\sigma }\Delta t \over 2(1 - \epsilon )}, \end{aligned}$$
(61)

where \(\dot{\sigma }\) is the stress rate associated with subduction, which can be written as

$$\begin{aligned} \dot{\sigma }= {\mu v \over d}, \end{aligned}$$
(62)

where \(d\) is the width and \(\mu\) is the rigidity of the shear zone. Then,

$$\begin{aligned} \Delta F_1 = -{\Delta \sigma _1\over \tau _\text{s}}, \qquad \Delta F_2 = -{\Delta \sigma _2\over \tau _\text{s}}, \end{aligned}$$
(63)

whence we can calculate \(\Delta X\), \(\Delta Y\) and \(\Delta p\) according to (19), (20) and (23). The changes in Coulomb stress on the two asperities, calculated from (37), coincide with the changes in tangential stress, that is

$$\begin{aligned} \Delta F^{\rm{C}}_1 = - \Delta F_1, \qquad \Delta F^{\rm{C}}_2 = - \Delta F_2. \end{aligned}$$
(64)

The change in the occurrence time of the earthquake is then

$$\begin{aligned} \Delta t_1 = {\Delta T_1 \over \Delta T} \Delta t \end{aligned}$$
(65)

or, thanks to (50) and (42),

$$\begin{aligned} \Delta t_1 = {\Delta F_1 \over U} \Delta t. \end{aligned}$$
(66)

We now introduce appropriate numbers in the formulae in order to draw conclusions about the effect of the Valdivia earthquake on the Maule fault. With \(M=2.7 \times 10^{23}\) N m (Kanamori and Cipar 1974), \(r_1 = 400\) km, \(r_2 = 600\) km, from (57) we find that the Valdivia earthquake imposes stresses \(\Delta \sigma _1 \simeq 224\) kPa and \(\Delta \sigma _2 \simeq 66\) kPa on asperities 1 and 2, respectively. With an average slip \(u_1=13\) m (Delouis et al. 2010) and a ratio \(U/U_1 =1\) (Dragoni and Santini 2014), from (58) we obtain a characteristic time \(\Delta t \simeq 186\) a. With \(\mu = 30\) GPa and \(d = 300\) km, from (61) we obtain a value \(\tau _\text{s} \simeq 2.17\) MPa for the static friction of the asperities. Then, the nondimensional changes in forces on asperities 1 and 2 are \(\Delta F_1 = -0.10\) and \(\Delta F_2 = -0.03\), respectively, entailing \(\Delta p = -0.024\) from (23) and \(\theta \simeq 0.61\) rad from (40).

Hence, the value of \(p\) before the Valdivia earthquake was \(p_\text{b}= -0.046\), showing that the Maule fault was closer to stress homogeneity before 1960, when \(p_\text{b}\) changed to \(p_\text{a}\). According to (41) and (64), the change in the difference between the Coulomb forces of the two asperities was \(\Delta F^{\rm{C}} \simeq -0.07\), not large enough to drive the system out of the subset \(S\) of phase space, entailing simultaneous slip of the asperities. Finally, from (65) the change in the occurrence time was \(\Delta t_1 \simeq - 64\) a, meaning that the occurrence of the Maule earthquake was advanced by this amount of time.

Let \(P_i = (X_i, Y_i)\) be the singular points of the orbit and \(T_i\) the corresponding instants of time, with \(i = 0, 1, 2, \dots\). We define \(P_0\) to be the position of the system just after the 1835 earthquake; \(P_1\) and \(P_2\) the positions just before and after the Valdivia earthquake, respectively; \(P_3\) the position just before the Maule earthquake. We can assume \(T_2=T_1\), because the interval \(T_2 - T_1\) is negligible with respect to the interseismic intervals. The coordinates of points \(P_i\) are then

$$\begin{aligned}&X_3 = 1 + p_\text{a}, \quad Y_3 = 1 + 2p_\text{a}, \end{aligned}$$
(67)
$$\begin{aligned}&X_2 = X_3 - {t_3 - t_2 \over \Delta t} U, \quad Y_2 = Y_3 - {t_3 - t_2 \over \Delta t} U, \end{aligned}$$
(68)
$$\begin{aligned}&X_1 = X_2 - \Delta X, \quad Y_1 = Y_2 - \Delta Y, \end{aligned}$$
(69)
$$\begin{aligned}&X_0 = X_1 - {t_1 - t_0 \over \Delta t}\, U, \quad Y_0 = Y_1 - {t_1 - t_0 \over \Delta t}\, U, \end{aligned}$$
(70)

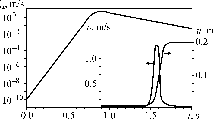
where \(t_0=1,835\) a, \(t_1= t_2= 1,960\) a, \(t_3= 2,010\) a. The orbit is shown in Fig. 6a, and the source function of the 2010 Maule earthquake was approximately that shown in Fig. 7a. The value of \(p\) after the earthquake is \(p_\text{c}=-0.154\), implying a much greater stress inhomogeneity: the stress on asperity 1 is greater than that on asperity 2 by 46 % of static friction. Since \(p_\text{c}<p_1\), the next earthquake would involve only asperity 1.

We can also estimate when the next earthquake will take place, in the absence of perturbations. Let \(P_6\) be the position of the system just after the 2010 Maule earthquake. According to the model, the next earthquake will occur at time

$$\begin{aligned} t_7 = t_6 + {X_7 - X_6 \over U} \Delta t, \end{aligned}$$
(71)

where \(X_6=X_3 - U_1\) and \(X_7 = 1 + \alpha p_\text{c}\). With \(t_6=2{,}010\) a, this results in \(t_7 = 2{,}144\) a.

In the absence of the Valdivia earthquake, the state of the system would have remained at \(p = p_\text{b}\), still such that asperity 1 would have failed first (Fig. 6b). The Maule earthquake would have occurred at time \(t_3 - \Delta t_1\), i.e. in the year 2074, and would have had a different sequence of modes, i.e. 10, 11, 10. The failure of asperity 1 would have been followed by a phase of simultaneous slip of both asperities and then by a short slip of asperity 1 again. The moment rate function would have been very different (Fig. 7b), with a longer duration and a greater seismic moment. From (53), the Maule earthquake would have had moment \(M/M_1=3.01\) instead of \(2.33\), with an increase of about 29 %. After the earthquake, the state of the system would have been \(p_\text{d}=-0.099\), implying a greater stress inhomogeneity, so that the stress on asperity 1 would have been greater than that on asperity 2 by an amount equal to 30 % of static friction. Since \(p_\text{d}>p_1\), the subsequent earthquake would have still involved both asperities.

Fig. 5
figure 5

Sketch of the Maule (left) and the Valdivia (right) faults as envisaged in the model. Arrows indicate the direction of fault slip. The arrow on the Valdivia fault is at the centre of the higher slip area. The star indicates the hypocentre of the Maule earthquake

Full size image
Fig. 6
figure 6

Possible orbits in phase space for the Maule fault, starting from the state \(P_0\) after the 1835 earthquake: a Orbit in the presence of perturbation \(\Delta \mathbf{R}\) due to the 1960 Valdivia earthquake; the segment \(P_3 P_6\) represents the 2010 event, and \(P_7\) is the state at the time of the next earthquake. b Orbit in the absence of perturbation; the segment \(P_1 P_4\) represents the 2010 event, and \(P_5\) is the state at the time of the next earthquake. The sequence of dynamic modes in the 2010 event is different in the two cases (\(\alpha =1\), \(\beta =1\), \(\epsilon =0.7\))

Full size image
Fig. 7
figure 7

Moment rates \(\dot{M}\) of the 2010 Maule earthquakes for the two cases shown in Fig. 5a and b, respectively (\(M_1\) is the moment due to the slip of asperity 1 by an amount \(U\) and \(\omega =\sqrt{1+\alpha }\)). The moment rate in a is the fit of Dragoni and Santini (2014) to observations by Delouis et al. (2010)

Full size image

8 Conclusions

We have considered a fault containing two asperities, a case that is often observed in large and medium-sized earthquakes, and we have studied the effects of a stress perturbation on the dynamics of the system. The fault complexity has consequences that are not present in the case of a homogeneous fault: the perturbation may not only advance or delay the next earthquake generated by the fault, but it can sensitively change the position of the hypocentre, the source duration and the seismic moment. The reason is that the perturbation may change the sequence of dynamic modes of the earthquake.

In particular, we may draw the following conclusions:

  1. 1.

    While the Coulomb stress of an asperity measures the proximity of the asperity to the failure condition, the difference between Coulomb stresses of the two asperities measures the distance from the condition of simultaneous slip. A seismic event will involve both asperities simultaneously only if the difference between their Coulomb stresses is small.

  2. 2.

    When the system is subject to a stress perturbation, the changes in the Coulomb stresses of the asperities are different from each other. The subsequent evolution of the system is controlled by the change in the difference between Coulomb stresses, which measures the changes in the asymmetry degrees of stress and friction and determines which asperity will fail first.

  3. 3.

    The change in the occurrence time of the next earthquake is proportional to the change in the Coulomb stress of the asperity that fails first. The changes in the moment rate and in the seismic moment are determined by the sequence of dynamic modes of the earthquake, the greatest changes taking place when simultaneous slip of asperities is involved.

These conclusions may explain why the earthquakes generated by a fault are not only aperiodic, but are usually different from each other in terms of slip amplitudes, involved areas and position of the hypocentre. These differences are related to the kind of stress perturbations that the fault undergoes during the interseismic intervals. Under the model assumptions, we can calculate the evolution of the system following a perturbation, and from the knowledge of the source function of an earthquake and of the seismic history of neighbouring faults, we can retrieve the state of stress in the past.

The model has been applied to the fault segment of the 2010 Maule earthquake. Several simplifications have been introduced to this aim. Only the two-asperity system that generated the Maule earthquake and the perturbation produced by the 1960 Valdivia earthquake have been considered. The perturbation itself has been evaluated by assuming a point-like source, giving at most the order of magnitude of the imposed stress. However, the key point is that the average stresses imposed on the asperities of the Maule fault are different from each other, and this fact is independent of the model chosen for the source of the stress field. This difference alters the stress distribution on the Maule fault, with remarkable consequences for its subsequent evolution.

With this premise, the model shows that, if the Valdivia earthquake had not occurred, the state of the system resulting from the 1835 earthquake would have remained closer to stress homogeneity, but still be such as to produce the failure of the same asperity first. The Maule earthquake would have occurred many decades later and would have involved a different sequence of modes, with a different moment rate and a greater seismic moment. The Valdivia earthquake changed the state of the system, increasing the degree of stress inhomogeneity. After the 2010 earthquake, a much greater stress inhomogeneity resulted, such that the next earthquake would be due to the failure of only one asperity.

Of course this should not be considered a prediction about the next real earthquake. The aim of the present model was to show the effect of coseismic stress transfer only, while afterslip and viscoelastic relaxation have not be taken into account. The latter may be relevant over time intervals of several decades (e.g. Pritchard and Simons 2006). In a recent paper, Ding and Lin (2014) examined viscoelastic relaxation following the 1960 Valdivia earthquake and found that it may produce stress changes as large as the coseismic stress transfer. Inclusion of viscoelastic deformation in the model will be the subject of future work.