Japan's 2011 Tsunami: Characteristics of Wave Propagation from Observations and Numerical Modelling

Abstract

We use a numerical tsunami model to describe wave energy decay and transformation in the Pacific Ocean during the 2011 Tohoku tsunami. The numerical model was initialised with the results from a seismological finite fault model and validated using deep-ocean bottom pressure records from DARTs, from the NEPTUNE-Canada cabled observatory, as well as data from four satellite altimetry passes. We used statistical analysis of the available observations collected during the Japan 2011 tsunami and of the corresponding numerical model to demonstrate that the temporal evolution of tsunami wave energy in the Pacific Ocean leads to the wave energy equipartition law. Similar equipartition laws are well known for wave multi-scattering processes in seismology, electromagnetism and acoustics. We also show that the long-term near-equilibrium state is governed by this law: after the passage of the tsunami front, the tsunami wave energy density tends to be inversely proportional to the water depth. This fact leads to a definition of tsunami wave intensity that is simply energy density times the depth. This wave intensity fills the Pacific Ocean basin uniformly, except for the areas of energy sinks in the Southern Ocean and Bering Sea.

1 Introduction

On 11 March 2011, at 05:46 UTC, a subduction megathrust earthquake with a moment magnitude M _w = 9.1 occurred 32 km below the ocean floor off the east coast of Honshu, Japan (cf. Song et al. 2012). This earthquake and the generated tsunami killed more that 20,000 in Japan, and caused widespread and lasting devastation and suffering. This unique event was one of the six major earthquakes in the last 60 years (1952–2011), which together account for over half of the seismic energy released during this time period. The other five were off Kamchatka in 1952 (M _w = 9.0), Chile 1960 (9.5), Alaska 1964 (9.4), Sumatra 2004 (9.3) and Chile 2010 (8.8).

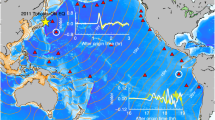
The modern sea level observing network has seen significant improvements in the past decade, allowing more detailed analysis of tsunami wave propagation, transformation and decay. In addition to coastal tide gauges, there are now over 40 DART (Deep-ocean Assessment and Reporting of Tsunamis) instruments (http://nctr.pmel.noaa.gov/Dart/) and several cabled observatories that provide accurate real-time data from bottom pressure recorders (BPRs). The latter include the Japanese cabled stations and NEPTUNE-Canada observatory (http://www.neptunecanada.ca/). Figure 1 shows the locations of most of the DART moorings and several cabled Japanese and NEPTUNE-Canada stations. The 11 March 2011 tsunami was recorded by 32 DART instruments and by the cabled Japanese and Canadian BPR stations.

Fig. 1

Pacific Ocean bathymetry and locations of deep tsunami recorders: black circles denote DART stations with records used in this analysis, while empty circles mark stations with incomplete tsunami records; red triangles mark the Japanese cable stations; blue squares show the NEPTUNE-Canada bottom pressure recorders (BPR). The red star shows the location of the epicenter for the Japan 2011 earthquake, and the red frame outlines the source area further expanded in Fig. 2

Other direct snapshots of tsunami waves crossing the ocean are provided by radar altimeters on board several satellites. It takes about 30–50 min for a polar-orbiting satellite to cross the Pacific Ocean. Thus, in contrast to stationary pressure sensors, the high-precision altimeters on Jason-1, Jason-2 and Envisat satellites record almost instantaneous along-track profiles of the tsunami waves. The available observations are used to improve tsunami models and to study all aspects of the tsunami wave generation, propagation and decay. Much of the fine-tuning of the numerical models is related to realistic characterisation of sea-floor deformation during the earthquake, of detailed ocean bathymetry and of wave energy decay due to turbulent friction in marginal seas and along continental margins.

In this study, we use the available observations from stationary instruments and satellite altimeters to calibrate the numerical model and to study the 2011 Japan tsunami wave propagation and wave field transformation in time and space. Except for some leakage into marginal seas and into other ocean basins (via the straits between Antarctica, Australia and South America), tsunami waves generated in the Pacific Ocean are mostly confined to this ocean, thus allowing examination of physical processes of wave propagation, reflection, scattering and gradual dissipation in a closed basin.

One of the more important aspects is the duration of tsunami wave activity at specific locations. In particular, it is important for the Tsunami Warning System to know not only the timing of the first warning messages, but also the timing of their cancellation. For locations farther away from the source, the first wave may not be the largest. It can be a second, third or even a later wave causing most of the damage. For example, the maximum tsunami wave height at Severo-Kurilsk, Russia, was near 1 m about 5.5 h after the arrival of the first wave, or 1.5 h after the cancellation of the tsunami warning at this location.

It is useful to partition tsunami wave trains into two parts: the leading frontal (head) zone and the trailing (tail) zone. Most of the tsunami sources produce a relatively simple initial sea surface displacement, a dipole consisting of an elongated ridge and a valley. More often than not, the source is near a coast or on a shelf slope, and the outgoing wave is almost simultaneous with its reflection from a shelf break. In the following discussion we can therefore assume that 1 h after the passage of the tsunami front the remaining waves are all in the tail zone.

As the first tsunami wave moves across an ocean in an open arc, its frontal (head) signal decays with distance because of a geometrical effect, but maintains its initial form rather well. However, the waves in the tail are continuously modified and sometimes intensified because of the processes of refraction and multiple reflections from topographic features, such as underwater ridges, valleys, seamounts, islands and coastlines. Thus, over long distances, tsunami wave attenuation from wave transformation becomes very significant. In this work, we use the available observations and numerical model results from the 2011 Japan tsunami to study wave transformation and decay in the Pacific Ocean basin.

2 Numerical Model of 2011 Japan Tsunami Waves

We study the propagation and decay of the Japan 2011 tsunami waves using a numerical tsunami model (Rabinovich et al. 2008) based on the shallow-water finite difference formulation, which is similar to that described by Imamura (1996). This model is set in a Pacific Ocean domain (56S–63N, 120E–70W; Fig. 1) and uses spherical coordinates with a grid size of 2′ and a time step of 2 s. The 2-min seafloor topographic grid was derived from ETOPO2v2 (2006). Tsunami waves simulated by this model were compared with the open-ocean DART and NEPTUNE-Canada BPR data (see next Sect. 2.1), thus verifying the model formulation and the initial tsunami source parameters.

We use a linearised version of the shallow water equations. The corresponding numerical finite-difference approximation is conservative. While this linearisation somewhat limits the accuracy of the model in coastal zones, it allows performing long-term simulations of the wave field, for which non-linear effects are less important, and allows for more control of the energy dissipation in the model.

2.1 Approximation of the Source

In this simulation, we use the finite-fault source model constructed by Hayes (2011). It provides detailed information on the spatial displacements in the area and minimises the uncertainties in the size of the source. The Hayes (2011) analysis was based on a teleseismic waveform approximation (39 teleseismic broadband P waveforms, 22 broadband SH waveforms), which was first converted into displacement by removing the instrument response and bandpass filtering over the 2–330 s period.

The fault plane was defined using the CMT magnitude M _w = 9.0, the USGS location of the hypocenter (142.37E, 38.32N, depth 32 km) and the Global CMT moment tensor solution (http://www.globalcmt.org). The low-angle nodal plane (dip = 10°, strike = 194.4°) was selected as the preferred fault plane, with dimensions of 650 km along strike and 260 km across strike. Long period surface waves were used to improve the resolution and to estimate the downdip variation. The seismic moment release of this model was 4.9 × 10²² N m, somewhat smaller than the Global CMT solution (5.3 × 10²² N m).

Using the equations of Okada (1985), we reformulated the slip distribution from Hayes (2011) into 325 subfaults, 25 × 20 km each (Fig. 2a), with vertical seafloor displacements. Such displacements have a typical dipole structure oriented along the Honshu coast with the uplift zone on the ocean side and the subsidence zone on the island side (Fig. 2b, lower panel). The initial range of vertical displacements is −1.3 to 10.1 m. The classical shallow-water approximation assumes that the sea surface elevation (tsunami source) is the same as the vertical bottom displacement (cf. Kowalik 2008). However, this approximation may not be valid for small-scale sources located in deep water (Kajiura 1963). We therefore used the full three-dimensional Laplace equation to modify the initial sea surface displacement (Fine and Kulikov 2011). This reconstructed displacement is thus smoother (Fig. 2b, upper panel) than the bottom seabed displacement, and its variance is ~90 % of the variance of the seabed displacement.

Fig. 2

a Finite fault model for the 11 March 2011 earthquake in Japan according to Hayes (2011), with slip distribution along the fault plane shown in color. Hypocenter location is denoted by the black star. b The correspondent vertical displacement of the seabed (bottom panel) and the sea surface (upper panel)

2.2 Wave Dissipation in the Model

The main goal of the model used in this study is simulation of the long-term evolution of the tsunami wave field in the Pacific Ocean. The basic ideas of such evolution were presented in Munk (1963), who described wave energy diffusion over all of the Pacific Ocean due to geometric spreading, dispersion, refraction, reflection and scattering processes. Wave energy then continues to decay because of absorption or dissipation of the wave field.

Diffusion redistributes the tsunami energy but does not change the total amount of wave energy in the ocean, while absorption means energy transfer into heat. Figure 3 shows a 6-day record at DART 31413, located off the Mexican coast 12,000 km from the source. Evolution of signal variance at this station clearly shows two processes: the initial decrease in the variance during the first 1–1.5 days changes into a more gradual decrease during the following days. The initial decrease is obviously related to the spreading of tsunami energy, i.e., diffusion, while the subsequent decrease is related to physical dissipation. As was explained in Munk (1963), this later process cannot be due to diffusion because the area of spreading is limited in the World Ocean.

Fig. 3

a Tsunami record from DART 43413 and b sea level variance change with time. The variance was calculated over a moving 6-h window. Solid lines show exponential approximation of the variance change $\sim e^{ - t/\tau }$, where τ is a decay time scale. Horizontal dashed lines mark the observed maximum, the 10 % of the maximum and the level of background noise (~2 × 10⁻⁶ m²)

To simulate absorption in the model, we added a generic linear friction term by rewriting the time derivatives in the momentum equation as

$$ \frac{\partial }{\partial t} \Rightarrow \frac{\partial }{\partial t} + b, $$

(1)

where b = 10⁻⁵ s⁻¹. Introducing such a term in the model leads to an energy balance equation

$$ \frac{\partial E}{\partial t} = - 2bE_{k} - \left( {\nabla \cdot F} \right), $$

(2)

where $E_{k} = \frac{1}{2}\rho H\left( {u^{2} + v^{2} } \right)$ is kinetic energy density, $E = \frac{1}{2}\rho g\zeta^{2} + E_{k}$ is total energy density, $F = \rho Hu\left[ {g\zeta + \frac{1}{2}(u^{2} + v^{2} )} \right]$ is energy flux (per unit of wave front), $\nabla = \frac{\partial }{\partial x}i + \frac{\partial }{\partial y}j$, ρ is water density, H is water column height, u, v are depth-integrated velocity components, ζ is sea level elevation, g is acceleration due to gravity, and x and y are the horizontal coordinates. Equation (2) is valid for both linear and non-linear shallow water equations, as well as for the linear finite-difference analog.

As the total energy is twice the kinetic energy, Eq. (2) states that the energy decay parameter is close to b. This parameter corresponds to an e-folding time scale of 27 h, which is close to the value estimated by Van dorn (1984) for the Pacific Ocean (22 h). Recently, Rabinovich et al. (2011) found a much longer e-folding time scale from their analysis of the 2004 Sumatra event, which was likely related to the additional energy input from the Indian Ocean.

It is important to note that the actual energy decay also includes non-dissipative effects, such as leakage of energy through open boundaries and into shallow seas (e.g., Sea of Okhotsk and Bering Sea). As we see from Fig. 4, it is important to distinguish between the effects of absorption and initial diffusion of wave energy. The larger the distance from the tsunami source, the longer it takes to diffuse the energy after passage of the front, and thus the “effective” (combined) dissipation rate is smaller.

Fig. 4

Tsunami time series at select a DART and b NEPTUNE-Canada BPRs: black lines, observed; red lines, modelled sea level anomalies

3 Comparison Between Observations and Numerical Model Results

3.1 Bottom Pressure Recorders

The deep-ocean observation network includes BPRs at 5 Japanese cabled observatory stations, 32 DART stations and 4 NEPTUNE-Canada nodes. Since this work is about the wave field away from the source, we did not include here the data from the Japanese stations.

The DART sensors are at depths of 3–6 km along the continental margins of the Pacific Ocean, and practically all of them registered the 2011 tsunami. Figure 4a shows examples of tsunami wave trains recorded on 11 March by nine DART instruments (after removing the tides), together with the numerical model-generated waves. In most of these deep-ocean records, there is a distinct transition from a larger wave head (less than 1 h long) to a low-amplitude tail. One possible exception is DART number 51407, located just west of the Big Island of Hawaii. Its record shows a tail with an amplitude comparable to its head, likely because of wave trapping by the islands.

The BPRs of the NEPTUNE-Canada cabled observatory are located off the coast of southern Vancouver Island and northern Washington State at depths 100–2,600 m (Thomson et al. 2011), thus complementing the depth range of DART instruments. Figure 4b shows a comparison between the model and the NEPTUNE observations. The agreement is very good, even though the tsunami waves have travelled a long distance across the Pacific Ocean and their amplitudes have diminished significantly. The good agreement between the model-simulated and the observed tsunami waveforms lends support to the adopted finite fault source model and the choice of parameters in the tsunami model.

3.2 Satellite Altimetry

As was the case during two previous large tsunamis, in Sumatra in 2004 and Chile in 2010, the Japan 2011 tsunami waves were recorded by satellite radar altimeters, thus allowing observing wave transects in space. Using the Radio Altimeter Data System (RADS) archive with standard geophysical corrections (http://rads.tudelft.nl/rads/rads.shtml), we selected four ascending passes for comparison with the numerical model results (Fig. 5). Two of these passes are from Envisat (cycle 100, passes 417 and 419), one from Jason-1 (cycle 338, pass 147) and one from Jason-2 (cycle 99, pass 21).

Fig. 5

Altimeter tracks in the Pacific Ocean (black dashed lines) from a–b Envisat, c Jason-1 and d Jason-2 satellites during the 11 March 2011 tsunami, plotted over the numerical model wave patterns. The corresponding sea level profiles are included in each panel as a function of latitude: model, red lines; altimeter, black. Tsunami fronts are marked by arrows on each profile, while the equator crossing times (UTC) for the altimeter passes are in the top-left corner of each panel

In order to improve the tsunami signal and to separate it from background ocean signals, it is customary to subtract such a background from an altimeter record with tsunami (cf. Okal et al. 1999). However, there is no unique method to calculate this background. One reasonable and simple approach is to assume that, unlike tsunami waves, the ocean anomalies persist on time scales longer than 10 days and to use as background the altimeter signal from a previous cycle (Smith et al. 2005), some combination of previous and subsequent cycles (Gower 2007) or more sophisticated sea level analysis just prior to the tsunami event (Ablain et al. 2006; Hayashi 2008). If the altimeter tsunami signal is sufficiently strong, then it can also be analysed without subtracting the background signals (e.g., Kulikov et al. 2005; Kulikov 2006).

Here we adopted the simple method of subtracting the previous cycle along track data from that during the 2011 tsunami event. This works reasonably well for Jason-1 and Jason-2, with a repeat cycle of 9.9 days. However, the Envisat repeat cycle is 35 days, compared to observed baroclinic time scales for Pacific Ocean eddies of 7–40 days (Stammer 1998), with the shortest time scales (7–10 days) in the Kuroshio/Oyashio Extension region and the longest (25–40 days) in the Equatorial Current and in subtropical eastern boundary currents. Since for most of the ocean the eddy decorrelation time scales are less than 35 days, it makes no sense to use previous cycles as background in Envisat data. Indeed, along track variances of intercycle sea level differences in Jason-1 and Jason-2 data are smaller than the variances of the original data, while for Envisat the opposite is true. Thus, the Envisat anomalies in Fig. 5a, b are shown without subtracting the background. We note in this regard the large anomalies in Envisat traces in Fig. 5b between 30 N and 40 N, which are due to strong sea level variability in the Kuroshio Extension region.

As expected from strong ocean variability at the sea surface, the tsunami signals in altimeter observations are not as clear as in BPR data. Nevertheless, there is relatively good agreement in Fig. 5 between the altimeter-observed and the numerical model-generated signals in the frontal zone, even after the front has travelled about 9 h across most of the Pacific Ocean (Fig. 5d). However, there is much less agreement in the tsunami tail zone. This is not surprising, as after the front has passed, the waves undergo multiple reflections and scattering, making the wave field more chaotic and less predictable.

4 Wave Scattering, Energy Decay and Thermal Equilibrium for Tsunami Waves

The propagation of long waves in the ocean is accompanied by effects of refraction and wave scattering due to reflections by a non-uniform ocean bottom, islands, reefs, etc. Multiple reflections and scattering lead to the stochastization of the wave field, whereby the tsunami waves become incoherent and less predictable. This stochastization is quite evident in Fig. 5, as the area between the front and the tsunami source gradually fills with secondary waves and is transformed into a random wave field.

In order to estimate the temporal evolution of the wave energy field, we calculated the mean energy flux (in Wm⁻¹) during the first hour after arrival at each location of the tsunami front (Fig. 6). It is clearly seen that this frontal wave flux (FWF) is mainly directed to the southeast, toward South America. The FWF decreases with distance and, as a result of the irregular bathymetry, splits into numerous beams. At long distances, the effect of the FWF irregularities becomes even more pronounced.

Fig. 6

Frontal wave flux (in Wm⁻¹) averaged over 1 h during the passage of the front. Colour display is on a logarithmic scale. Black contours mark the distance (in km) from the tsunami source

The decrease with distance in the total FWF is estimated by integrating the FWF passing through equidistant lines in Fig. 6. In the absence of wave scattering and dissipation, this total energy flux should be conserved. However, Fig. 7 shows that this flux decreases exponentially with distance, with an e-folding scale of 4,700 km (0.00021 km⁻¹).

Fig. 7

Total energy flux averaged over 1 h during (red) and up to 4 h after the passage of the front (listed in the legend) as a function of the distance from the source

For secondary waves, the dependence of the total energy flux on distance is quite different. For waves passing through the same equidistant lines for 1–2 h after the passage of the front, the total energy flux actually increases with distance up to 5,000 km from the source and then gradually decreases (Fig. 7). The behaviour of the total energy flux with distance for the following waves, i.e. for waves during 2–3 and 3–4 h after the arrival of the front, is similar to that during the 1–2 h time interval.

The spatial coefficient of 0.00021 km⁻¹ can be converted into a temporal coefficient using the deep-ocean mean wave speed of c = 220 m s⁻¹ (780 km h⁻¹), giving a decay coefficient of 4.6 10⁻⁵ s⁻¹ (a 6-h time scale). This coefficient is larger than can be inferred from the model dissipation parameter. The decrease in the FWF is therefore more related to wave scattering than to the modelled dissipation.

Because scattering does not change the total wave energy, the energy of the secondary waves initially increases. The secondary waves, in turn, also undergo scattering. Such multiple scattering eventually leads to a new equilibrium distribution of the wave energy field.

Equilibrium energy distribution is well known in optics and electromagnetic wave theory as the Rayleigh-Jeans Law (Rayleigh 1900; Jeans 1905), although the wave equipartition theorem was derived by Lord Rayleigh about 30 years earlier for sound waves in a 3-dimensional cavern (Rayleigh 1896). According to this theory, energy is equally distributed among the waves. Thus, the total number of waves in a frequency range (ω, ω + dω) in a unit of volume is

$$ dn_{\omega } = \omega^{2} d\omega /\left( {2\pi^{2} c^{3} } \right) \, $$

(3)

where c is wave speed and ω is angular wave frequency.

The equipartition principle is also well known in seismology for the case of multiple scattering of elastic waves (cf. Margerin et al. 2000). It has been shown that the evolution of energy in a coda of seismic waves is ruled by an equilibration law that states that the ratio of P-wave to S-wave energy densities tends to a constant as the time goes to infinity (Weaver 1982, 1990; Ryzhik et al. 1996; Papanicolaou et al. 1996). This result follows from the wave equipartition theorem, as was the case in optics.

A similar problem has been studied in acoustics by Turner and Weaver (1994a, b). They showed that an equilibration state follows from the equipartition theorem and that the time necessary to reach such equilibration is very dependent on a scattering mechanism.

Coming back to the tsunami wave field, the Pacific Ocean bathymetry is not random. However, because of numerous reflections and scattering, the waves in the basin become less coherent with time and form an equilibrium field—in the same way as in seismology or acoustics. We can therefore expect that after some time a tsunami wave quasi-equilibrium state will be established in this ocean.

Application of the equipartition theorem to the tsunami waves was probably first proposed by Munk (1963), who has discussed the analogy between acoustic waves in a room and tsunami waves in the Pacific Ocean, and presented a two-dimensional version of the Rayleigh-Jeans law. However, he did not consider the spatial distribution of wave energy as a consequence of this law. Efimov et al. (1985) also applied an equipartition principle to characterise the background wave spectra on the Kuril Island shelf. In contrast to background spectra, the tsunami spectra are not stationary in time. However, as was shown above, the effective scattering coefficient is larger than the dissipation parameter; thus tsunami wave spectra are quasi-stationary.

From Eq. (3), the energy density for a three-dimensional wave is inversely proportional to the cube of wave speed c ³. Similarly, in the two-dimensional case (as for the shallow water waves), the number of waves per unit area is

$$ dn_{\omega } = \omega d\omega /\left( {2\pi c^{2} } \right) $$

(4)

According to Eq. (4), the energy is inversely proportional to the square of the phase speed c ², i.e. the water depth H for nearly nondispersive tsunami waves. This is very different from Green’s law, which states that for a progressive wave over slowly changing topography energy density is inversely proportional to the wave speed c, i.e. the square root of the depth H ^1/2 (Green 1837).

The frequency dependence in Eq. (4) is not very important because, in contrast to wind waves, the tsunami waves far from the source are nearly linear. We therefore do not expect energy transfer across the frequency band, and energy at each frequency can be evaluated independently.

Equation (4) leads us to a definition of “wave intensity” I, which is energy density multiplied by the depth:

$$ I \, = \, EH $$

(5)

Wave intensity corresponds to wave energy per wave, i.e. per degree of freedom. When the wave field has reached the equilibrium state, wave intensity should be the same everywhere, regardless of the wave speed or the depth. In this regard, it is interesting to note that wave intensity is analogous to gas concentration in molecular diffusion or to temperature in thermal conductivity. That is, changes in wave intensity create an intensity gradient and a diffusive energy flux, which equalises the intensity everywhere.

The evolution of the tsunami wave intensity in time is displayed in Fig. 8. In the first 12 h (Fig. 8a), the wave intensity distribution is highly nonuniform, corresponding to the non-equilibrium state of the wave field. In Fig. 8b (12–24 h), the wave field is divided into two parts by the 12-h isochron. The eastern part, which includes the front, is still not uniform, while the western part, which includes only the secondary waves, is more diffuse with wave intensity increasing towards the source. Figure 8c (24–36 h) shows the intensity increasing near South America because of reflections from its coast. The remaining area is now more uniform compared to previous time intervals. Finally, Fig. 8d (60–72 h) shows a much more uniform intensity field, with low gradients and intensity slowly decreasing towards the energy sinks in the Southern Ocean, Bering Sea, Sea of Okhotsk and other marginal seas. This figure also shows that even 3 days after the earthquake, tsunami wave intensity remains relatively high near Japan, with the tsunami waves trapped on its shelf slowly releasing energy into the deep ocean.

Fig. 8

Tsunami wave intensity (I) or energy per wave (in kJ m⁻¹) averaged over time intervals of a 0–12 h after the passage of the wave front; b 12–24 h, c 24–36 h and d 60–72 h. Plot density was scaled with a corresponding area-averaged value of I listed in the bottom-left corner of each panel

To check how the modelled wave energy is distributed with depth over time, we calculated the average wave energy for each 30 % change in depth interval (i.e. 50–65 m, 65–84.5 m, etc.) from 50 to 8,000 m, for each 12-h time interval, starting from the time of the earthquake. The results of these calculations are displayed in Fig. 9 for the model (solid lines) and for the observations.

Fig. 9

Tsunami mean energy (E) per unit area as a function of local depth for the same time intervals as in Fig. 8. The coloured lines show the numerical model results, the triangles mark the data from four NEPTUNE-Canada BPRs, and the pluses are for the DART BPRs. Black lines show the theoretical slopes E ∝ H ^−1/2 and E ∝ H ⁻¹

In the first few hours energy distribution is not uniform (Fig. 9), mostly following Green’s Law. As time increases, the total energy decreases because of dissipation and wave radiation through the open boundaries. However, its spatial distribution becomes more uniform (except near the source), thus following more closely the equipartition law. The observed values from NEPTUNE and DART BPRs generally agree with the model results, though the scatter, especially for DARTs, is high.

5 Discussion

In this work we have used a numerical model to describe wave energy decay and transformation in the Pacific Ocean during the 2011 Tohoku tsunami. The numerical model was initialised with the results from a seismological finite fault model, with the along-plane displacements converted to the ocean bottom displacements according to the elastic formula of Okada (1985) and to ocean surface displacements using a three-dimensional Laplace equation.

The tsunami model was validated using deep-ocean bottom pressure records from DARTs, from the NEPTUNE-Canada cabled observatory, as well as data from four satellite altimetry passes. These comparisons show that the model front wave train fits the data very well. However, during later stages point-to-point comparison is no longer possible, as the model waves are not in phase with the observations. This is not a drawback of the model, as the observed waves become more stochastic. In a statistical sense, the model predicts the observed variance rather well, as can be seen in Fig. 4.

The stochastic character of the secondary waves is related to scattering. It was shown that the frontal waves decay exponentially with the distance. The e-folding scale for the frontal energy flux is about 4,700 km, or about 10⁴ km for the corresponding e-folding scale for the amplitude. This value is at the low end of the range found by Ermakov and Pelinovsky (1979). However, their work considered only abyssal seamounts, while the current model includes all the obstacles, such as seamounts, ridges, islands and irregular coastlines.

The multiple scattering and reflection of the waves lead to the so-called diffusive regime, in which the wave field characteristics are determined by its statistical properties. The existence of the diffusive regime for tsunami waves was first mentioned by Munk (1963), who estimated the “diffusion” time scale (i.e., the time to reach the diffusive regime) for the Pacific to be 40 h. This value was estimated from the time needed for the waves to cross the Pacific Ocean and is in relatively good agreement with our findings (see Fig. 8).

As tsunami waves approach the coast, some waves are trapped on the shelf while others radiate back into the open ocean. After some time, additional waves arrive and are trapped on the shelf, which increases the wave energy and, accordingly, also increases wave radiation back into the open ocean. Finally, when the outgoing energy flux is equal to the incoming flux, the equilibrium state is established, and the wave intensity on the shelf is the same as in the open ocean. The time needed to reach such a balance between the incoming and the outgoing waves depends on the characteristics of the shelf (width, length, coastal irregularities, depth, etc.), but not on the basin time scale. This time can therefore be much shorter than that for the Pacific Ocean.

In conclusion, we were able to demonstrate that the temporal evolution of the tsunami wave energy leads to the wave energy equipartition law. This was shown in the case of the 2011 Japan tsunami using statistical analysis and numerical model results, and was adequately confirmed by the observations. Similar equipartition laws are well known for wave multi-scattering processes in seismology, electromagnetism and acoustics. We have also demonstrated that the final near-equilibrium state agrees with such equipartition law: after the passage of the tsunami front, the tsunami wave energy is inversely proportional to the water depth.