1 Introduction

Most of the Kumaon Himalaya in India is characterized by high seismic activity due to the convergence and collision of the northward-moving Indian plate with the Eurasian plate. To assess seismic hazard associated with future large earthquakes it is necessary to determine regional attenuation characteristics of seismic waves released during an earthquake. Attenuation of seismic waves in any region is explained by a dimensionless quantity called quality factor Q (Knopoff 1964). It is seen that Q is probably constant over a large frequency range for homogeneous material and it varies in inhomogeneous media (Vander Baan 2002). For S waves at frequencies 1–25 Hz, Q is proportional to f n with n ranging between 0.6 and 0.8 on an average (Aki 1980; Sato and Fehler 1998). The attenuation property of any medium between earthquake source and observation point is explained by a frequency-dependent quality factor derived from either coda waves, Q c(f) or body waves, Q β(f) and Q α(f).

Different relations between Q β(f) and Q c(f) have been determined by different workers. Dutta et al. (2004) have found that Q β(f) < Q c(f) for frequencies between 0.6 and 3 Hz and Q β(f) > Q c(f) for the frequencies greater than 3 Hz in the south central Alaska region. Castro et al. (2002) has found Q β(f) < Q c(f) for the frequency range 2–3 Hz in central Italy, while it is reverse for the frequencies between 3 and 10 Hz. Results of the work of Yoshimoto et al. (1993) and Sato (1990) indicate strong frequency-dependence of Qβ(f) for frequencies greater than 1.0 Hz. In many studies due to limited data, Q c(f) has been assumed in place of Q β(f) for simulation of strong ground motion. Correct estimation of Q β(f) is required for successful simulation of strong ground motion using various techniques like semi empirical modeling technique (Joshi 2000; Joshi and Midorikawa 2004), composite source modelling technique (Zeng et al. 1994), and stochastic simulation technique (Boore 1983). Therefore, knowledge of Q β(f) for any seismic region is an asset for strong motion simulation. In this paper a method for obtaining the Q β(f) relationship has been presented which uses strong motion data of local events recorded on strong motion network installed in the Pithoragarh region of Kumaon Himalaya, India. Very little work has been done in this part of Himalaya to estimate the shear wave attenuation. Paul and Gupta (2003) have estimated Q c(f) relationship as (92.0 ± 4.7)f 1.0 ± 0.023 using single back scattering model proposed by Aki and Chouet (1975) using short period velocity waveform data. Based on the study of the aftershocks data of the Chamoli earthquake, Mandal et al. (2001) have estimated a Q c(f) as (30.0 ± 0.8)f (1.21 ± 0.03) for the region surrounding the mainshock of the Chamoli earthquake in frequency band 1–24 Hz. Gupta et al. (1995) has estimated Q c(f) for Garhwal Himalaya as 126f 0.95 for the frequency band 1–24 Hz using seven local earthquake (2.4 ≤ M L ≤ 4.9) recorded at five stations which uses 1.0 Hz velocity sensors. These studies used the single backscattering model (Aki and Chouet 1975) to estimate coda Q c(f) relationship for Himalaya. Andrews (1986) has used technique of generalized inversion by decomposing the body wave spectra into source, site and propagation terms. This method does not incorporate source mechanism in the spectral model. It has been demonstrated by Andrews (1986) and Bonamassa and Mueller (1988) that this formulation of gernalised inversion can separates the source and site spectra up to an unresolved degree of freedom, that is, up to an undetermined function of frequency that can be multiplied onto each source spectrum and divided from each site spectrum (Boatwright et al. 1991).

Recently Joshi et al. (2010) has used strong motion data from the Kumaon region to compute the three dimensional distribution of shear wave quality factor. Though the approach gives detailed estimates of the shear wave quality factor, it is difficult to estimate the frequency-dependent quality factor using this technique. A technique has been developed by Joshi (2006) which uses S wave spectra to obtain Q β(f) and corner frequency ‘f c’ of input events for Garhwal Himalaya. In this approach the two-step inversion algorithm was applied to remove site amplification in the accelerogram due to unavailability of sufficient data for site studies in the Garhwal Himalaya. Using this technique Joshi (2006) has estimated Q β(f) = 112 f 97 for Garhwal Himalaya. In the approach given by Joshi (2006) records from events with proper information about seismic moment have been used. This paper uses the data from low magnitude local events recorded on a strong motion network installed in the region. The information about source parameter is limited and needs to be extracted from the inversion algorithm. This paper presents an approach where corner frequency is estimated iteratively from the inversion and seismic moment is computed from the acceleration record after properly correcting the record for site amplification and anelastic attenuation term. Using acceleration spectra as input with known values of corner frequency and seismic moment the inversion algorithm gives estimate of Q β(f) at different frequencies. The least square fit of different values of Q β(f) gives the frequency-dependent shear wave attenuation relation for the region of Kumaon Himalaya.

2 Data

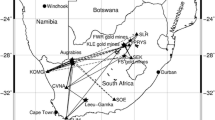
The study area in the present work lies in the Kumaon Himalaya region which is considered to be seismically active. Frequent seismic activity and thrust systems present in this region demonstrate the seismotectonic importance of the region. The Kumaon sector manifests strong deformation and reactivation of some of the faults and thrusts during Quarternary times. This is amply evident by the recurrent seismicity patterns, geomorphic developments and geodetic surveys (Valdiya 1999). This region shows development of all the four morphotectonic zones, which are demarcated by intracrustal boundary thrust of regional dimension. Morphotectonics take into account crustal anisotropy and the state of stress due to plate tectonics, erosion and isostatic rebound (Smith et al. 1999). These zones from south to north are: Siwalik or Sub Himalaya, Lesser Himalaya, Great Himalaya and Tethys Himalaya (Paul and Gupta 2003). Under a major seismicity project funded by the Ministry of Earth Sciences, Government of India, a network of eight strong motion stations has been installed in the highly mountainous terrain of Kumaon Himalaya. Locations of these eight stations along with the geology of the region is shown in Fig. 1. A three-component force balance, short period accelerometer has been installed at all eight stations. In order to have a nearly continuous digital recording mode, the threshold level of instruments were set at a very low value of 0.005% of full scale. The sensitivity of the instrument is 1.25 V/g and full scale measurement is 2.5 V. The purpose of such low threshold level is to record almost every possible local event that occurred during the period of project, i.e., between March 2006 and October 2010. Sampling interval of digital data is kept at 0.01 s. The minimum inter-station distance between these stations is approximately 11 km.

Fig. 1
figure 1

Location of strong motion recording stations installed in the Kumaon Himalaya. The geology and tectonics of the region is after GSI (2000). The strong motion stations of local network and epicenters of the events are denoted by triangle and star, respectively

Full size image

The records collected from the accelerogram have been processed using the procedure suggested by Boore and Bommer (2005). The processing steps involve baseline correction, instrumental scaling and frequency filtering. Instrumental scaling is an important correction which converts counts or m volts recorded by instrument into actual ground acceleration. For the recorder installed by the present network, instrument scaling for NS, EW and vertical components is 1.25 V/g, respectively. After baseline and instrument corrections a filter is applied to remove high frequency noise. In the usual processing of digital records a Butterworth filter with a corner frequency near 80% of final sampling rate (Shakal et al. 2004) is used. In the present work, we have used the data recorded at a sampling rate of 0.01 s; therefore, high frequency cutoff of the Butterworth filter is assumed to be 40 Hz. Low frequency selection of the Butterworth filter remains the most difficult part of strong motion processing. The effect of earthquake magnitude is to raise the response spectrum at low frequencies and subsidize the noise spectrum in the usual strong motion processing band. In order to select the low frequency corner of the Butterworth filter we have selected the data of noise from pre-event memory of the digital record. The frequency at which the ratio of response spectra of the record to noise is equal to 3 (Boore and Bommer 2005) is assumed to be the low frequency of Butterworth filter. Figure 2 shows the effect of processing on the acceleration record.

Fig. 2
figure 2

a Acceleration, b velocity and c displacement waveform of the digitized record of noise taken from prevent memory of the record of event recorded at Dharchula station on 5 May 2006. The d acceleration, e velocity, and f displacement record of signal without filtering. g The pseudo velocity response spectra at 5% damping of noise and signal without filtering. h Acceleration, i velocity and j displacement record of signal after filtering

Full size image

In the present work we have selected 18 local events recorded in the network installed in the Pithoragarh region. The arrival times of primary and secondary phases from these events have been used for localization of events using the HYPO71 program originally developed by Lee and Lahr (1972). The hypocentral parameter of these events and the obtained error in their localization is reported in Table 1. The projection of the ray path of energy released from the source to the recording station used in the present work is shown in Fig. 3. It shows that the ray path of the seismic energy encounters mostly the lesser Himalayan sequence. In the present work both horizontal components, i.e. north-south (NS) and east-west (EW), of strong ground motion have been used for inversion. Processed records that are used for inversion at Dharchula station are shown in Fig. 4. A time window which starts from the onset of the S phase and ends before the arrival of the low frequency surface wave in the record and which covers the entire S phase has been applied to the corrected accelerogram. Selection of S phase is based on visual inspection of entire accelerogram. This sampled window is cosine tapered with 10% taper at both ends (Sharma and Wason 1994). This windowed time series is passed through a FFT operator for computing its Fourier transform. For computing the Fourier transform in the present work we have followed the FFT algorithm given by Cooley and Tukey (1965). The FFT algorithm gives Fourier transform ‘X(k)’ of a real time signal ‘x(n)’ by following expression:

$$ X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {e^{{\frac{ - 2\pi ink}{N}}} x\left( n \right)} $$

where ‘X(k)’ represent a complex series in frequency domain and in the present work amplitude spectrum ‘A m(k)’ is calculated from ‘X(k)’ by using following formula:

$$ A_{\text{m}} \left( k \right) = \sqrt {\left[ {X_{\text{R}} \left( k \right)} \right]^{2} + \left[ {X_{\text{I}} \left( k \right)} \right]^{2} } $$

where ‘X R(k)’ and ‘X I(k)’ represent real and imaginary parts of complex function ‘X(k)’ obtained in the frequency domain. The obtained spectrum is further smoothened using a Laplacian operator before using it as an input to the present algorithm. The complete process of obtaining spectral amplitude from processed time series is shown in Fig. 5.

Table 1 Seismic moment, moment magnitude and hypocentral parameters of events used in the present work and the error obtained in its localisation
Full size table
Fig. 3
figure 3

Projection of ray path of different events recorded at different stations. Star denotes the epicenters of studied earthquakes and triangle denotes the location of recording stations. The tectonics of the region is taken after GSI (2000)

Full size image
Fig. 4
figure 4

Processed NS and EW component of accelerograms of all of the events recorded at the Dharchula station. Star denotes the epicenter of events. Triangle shows the location of recording station. The tectonics of the region is taken after GSI (2000)

Full size image
Fig. 5
figure 5

a Unprocessed accelerogram of the 5 May 2006 event recorded at Dharchula station, b processed accelerogram at Dharchula station, c acceleration spectrum of S phase marked by rectangular block with a time window of 4.0 s, d Discrete value of acceleration spectra used for present inversion. The discrete values of acceleration spectra are shown by small squares

Full size image

3 Inversion

The acceleration spectra of shear waves at a distance R due to an earthquake of seismic moment M o can be given as (Boore 1983; Atkinson and Boore 1998):

$$ A\left( f \right){ = }C \, S\left( f \right)\;D\left( f \right) $$
(1)

where the ‘C’ term is constant at a particular station for a given earthquake, S(f) represents the source acceleration spectra and D(f) denotes a frequency-dependent diminution function which takes into account the anelastic attenuation and attenuation due to geometrical spreading, and is given as (Boore and Atkinson 1987):

$$ D\left( f \right) = \left[ {{\text{e}}^{{ - \pi fR/Q_{\beta } \left( f \right)\beta }} G\left( R \right)} \right]P\left( {f ,f_{\text{m}} } \right) $$

In the above equation P(f,f m) is a high-cut filter that accounts for the observation that acceleration spectra often show a sharp decrease with increasing frequency, above some cutoff frequency f m, that cannot be attributed to whole path attenuation (Boore 1983). Because of the rapid fall of the acceleration spectra after 25 Hz in most of the acceleration records used in the present work, we have used f m as 25 Hz in the analytical form of P(f,f m) given by Boore (1983). The function G(R) represents the geometrical attenuation term and is taken to be equal to 1/R for R < 100 km and equal to 1/(10\( \sqrt R \)) for R > 100 km (Singh et al. 1999). As most of the data used in present work is within R < 100 km, G(R) is used as 1/R in the present work. The term \( {\text{e}}^{{ - \pi fR/Q_{{{\upbeta}}} (f){{\upbeta}}}} \) represents anelastic attenuation. In this term Q β(f) is the frequency-dependent shear wave quality factor. The Eq. (1) serves as the basis for our inversion. For a double-couple seismic source embedded in an elastic medium, considering only S waves, C is a constant for a given station for a particular earthquake and is given as:

$$ C = M_{\text{o}} R_{{{{\uptheta}}\phi }} .{\text{ FS}}.{\text{ PRTITN}}/\left( {4\pi \rho \beta^{3} } \right) $$
(2)

In the above expression, M o is the seismic moment, \( R_{{{{\uptheta}}j}} \) is the radiation pattern, FS is the amplification due to the free surface, PRTITN is the reduction factor that accounts for partitioning of energy into two horizontal components, and ρ and β are the density and the shear wave velocity, respectively. S(f,f c) defines the source spectrum of the earthquake. Using the spectral shape based on ω−2 decay of high frequency proposed by Aki (1967) and Brune (1970), S(f,f c) is defined as:

$$ S\left( {f,f_{\text{c}} } \right) = \left( {2\pi {\text{f}}} \right)^{2} /\left( {1 + \left( {f/f_{\text{c}} } \right)^{2} } \right) $$
(3)

Equation (1) is linearised by taking its natural logarithm. This modifies Eq. (1) as:

$$ \ln A\left( f \right) = \ln C + \ln \left( {S\left( {f ,f_{\text{c}} } \right)} \right) - \pi fR/Q_{{{\upbeta}}} \left( f \right){{\upbeta}} - \ln \left( R \right) $$
(4)

This is now in linearised form with unknown Q β(f) and f c. The term representing the source filter S(f,f c) is replaced with Eq. (3). With an assumption of known values of f c, we are left with only unknown Q β(f), which can be obtained from inversion by minimizing it in a least-squares sense. The least-squares inversion minimizes:

$$ \chi^{2} = \sum \left[ {A_{\text{s}} \left( f \right) - S\left( {f , { }f_{\text{c}} } \right)} \right]^{2} $$
(5)

where S(f,f c) is the theoretical source acceleration spectrum and A s(f) is the source spectrum obtained from the record after substituting parameters Q β(f) obtained from the inversion of Eq. (4). Rearranging known and unknown quantities on different sides, we obtain the following form from the Eq. (5):

$$ - \pi fR/Q_{\beta } \left( f \right)\beta = \ln A\left( f \right) - \ln C - \ln \left( {S\left( {f ,f_{\text{c}} } \right)} \right) + \ln \left( R \right) $$
(6)

Substituting the term related to the source spectrum S(f,f c) as (2πf)2/(1 + (f/f c)2), we obtain:

$$ - \pi fR/Q_{\beta } \left( f \right)\beta = \ln A\left( f \right) - \ln C - \ln \left( {2\pi f} \right)^{2} + \ln \left( {1 + \left( {f/f_{\text{c}} } \right)^{2} } \right) + \ln \left( R \right) $$
(7)

In Eq. (7), the dependence on the corner frequency has been linearised by expanding ln(1 + (f/f c)2) in a Taylor series around f c. Accordingly we obtain the following expression:

$$ - \pi fR/Q_{\beta } \left( f \right)\beta = \ln A\left( f \right) - \ln C - \ln \left[ {\left( {2\pi f} \right)^{2} /\left( {1 + \left( {f /f_{\text{c}} } \right)^{2} } \right)} \right] - \left[ {2/\left( {1 + \left( {f /f_{c} } \right)^{2} } \right)} \right]\left( {f /f_{\text{c}} } \right)^{2} \left( {\Updelta f /f_{\text{c}} } \right) + \ln \left( R \right) $$
(8)

Here Δf c is the small change in the corner frequency and is an unknown quantity that is obtained from the inversion. We obtained the following set of equations at a particular station for the ith earthquake for frequencies f 1, f 2, f 3 ………. f n , where n denotes the total number of digitized samples in the acceleration record:

$$ \begin{array}{*{20}c} { - \pi f_{1} R_{11} /Q_{\beta } \left( {f_{1} } \right)\beta + F\left( {f_{1} ,f_{{{\text{c}}1}} } \right)\Updelta f_{\text{c}} = D_{11} \left( {f_{1} } \right)} \\ { - \pi f_{2} R_{11} /Q_{\beta } \left( {f_{2} } \right)\beta + F\left( {f_{2,} f_{\text{c1}} } \right)\Updelta f_{\text{c}} = D_{11} \left( {f_{2} } \right)} \\ { \vdots \quad \vdots \quad \vdots } \\ { - \pi f_{\text{n}} R_{11} /Q_{\beta } \left( {f_{\text{n}} } \right)\beta + F\left( {f_{\text{n}} ,f_{\text{c1}} } \right)\Updelta f_{\text{c}} = D_{11} \left( {f_{\text{n}} } \right)} \\ \end{array} $$

where F(f,f c) = 2/(1 + (f 1/f c )2)](f 1/f c)2(1/f c) is the term obtained from the expansion of ln(1 + (f/f c)2) in terms of Taylor series around f c. It is found that this function behaves linearly for known values of corner frequency ‘f c’. For this reason in the present work ‘f c’ is used as input parameter and its several possibilities are checked and a final value is selected on the basis of minimum root mean square error (RMSE). For another station, the set of equations will be:

$$ \begin{gathered} - \pi f_{1} R_{12} /Q_{\beta } \left( {f_{1} } \right)\beta + F\left( {f_{ 1} ,f_{\text{c}} } \right)\Updelta f_{\text{c}} = D_{12} \left( {f_{ 1} } \right) \hfill \\ - \pi f_{ 2} R_{12} /Q_{\beta } \left( {f_{2} } \right)\beta + F\left( {f_{ 2} ,f_{\text{c}} } \right)\Updelta f_{\text{c}} = D_{12} \left( {f_{ 2} } \right) \hfill \\ - \pi f_{\text{n}} R_{12} /Q_{\beta } \left( {f_{n} } \right)\beta + F\left( {f_{n} ,f_{\text{c}} } \right)\Updelta f_{\text{c}} = D_{12} \left( {f_{\text{n}} } \right) \hfill \\ \end{gathered} $$
(9)

Subscripts ‘i’ and ‘j’ represent the event and the station number, respectively. In above equation D ij (f i ) is given as:

$$ D_{ij} \left( {f_{i} } \right) = \ln A_{ij} \left( {\omega_{i} } \right) - \ln C_{i} - \ln \left[ {\left( {2\pi f} \right)^{2} /\left( {1 + \left( {f/f_{\text{c}} } \right)^{2} } \right)} \right] + \ln \left( {R_{ij} } \right) $$
(10)

In the matrix form, the above set of equations can be written as:

This can be represented in the following form:

$$ G \, m = d $$
(11)

Model parameters are contained in the model matrix ‘m’ and the spectral component in the data matrix ‘d’. Inversion of the ‘G’ matrix gives the model matrix ‘m’ using Newton’s method as below:

$$ m = \left( {G^{\text{T}} G} \right)^{ - 1} G^{\text{T}} d $$
(12)

The corner frequency is treated as input parameter in the inversion algorithm to maintain the linearity in Eq. (9). We get different solutions for different possibilities of f c. The final solution is that which minimizes RMSE. In the present inversion scheme several possibilities of corner frequencies are checked by iteratively changing corner frequency ‘f c’ in a step of small incremental change of ‘Δf’. The small increment ‘Δf’ considered in the present work is 0.01 Hz. The above inversion is prone to the problems if G T G is even close to singular and for such a case; we prefer the singular value decomposition (SVD) to solve m (Press et al. 1992). Formulation for the SVD is followed after Lancose (1961). In this formulation, the G matrix is decomposed into U p, V p and Λ p matrices as given by Fletcher (1995):

$$ G^{ - 1} = V_{\text{p}} \Uplambda_{\text{p}} U_{\text{p}}^{\text{T}} $$
(13)

where, V p, U p and Λ p are matrices having nonzero eigenvectors and eigenvalues.

The entire scheme of inversion for obtaining f c and Q β(f) is shown in the Fig. 6 in the form of a flow graph. The software QINV, developed by Joshi (2006), has been used in the present work. Seismic moment is one of the most important parameters which is required as an input to the present algorithm. This has been computed from the spectral analysis of the recorded data using Brune’s model (Keilis-Borok 1959; Brune 1970). In this process a time window of a length which covers the entire S phase has been applied to the corrected accelerogram. The sampled window is cosine tapered with 10% taper at both ends (Sharma and Wason 1994). The spectrum of this time series is obtained using FFT algorithm and spectra has been corrected for anelastic attenuation and geometrical spreading term. Using the obtained source spectrum, a long term spectral level has been computed and is used for calculating seismic moment of an earthquake. Based on Brune’s (1970) model, seismic moment M o of an earthquake can be derived from the long term flat level of the displacement spectrum and is given by:

Fig. 6
figure 6

Flow diagram of entire process of inversion (modified after Joshi 2006)

Full size image
$$ M_{\text{o}} = 4\pi \rho \beta^{3} \Upomega_{\text{o}} R/R_{\theta \varphi } $$
(14)

where ρ and β are the density and the S-wave velocity of the medium, respectively, Ωo is the long term flat level of the source displacement spectrum at a hypocentral distance of R and R θφ is the radiation-pattern coefficient. We have used the value of density and S wave velocity as 2.7 gm/cm3 and 3.0 km/s, respectively. As the fault plane solution of the individual events could not be determined owing to the small number of stations, the radiation pattern R θφ was approximately taken as 0.55 for the S wave (Atkinson and Boore 1995).

The data used in the present work consist of various events which have been recorded at different stations. The seismic moment of the input event has been determined from the source displacement spectra of two horizontal components of acceleration record of each event recorded at different stations. The average seismic moment for each event is calculated by using all values of seismic moment at different stations. The initial value of Q β(f) used for obtaining source spectra is that given by Joshi (2006) for Garhwal Himalaya which lies in the proximity of study area. Average value of the seismic moment computed from two horizontal components recorded at several stations is used as an input to the first part of inversion together with the spectra of the S phase in the acceleration record. Several values of the corner frequency have been selected iteratively and are used as input to the inversion algorithm. Root mean square in the obtained and observed data is calculated for each case and the solution corresponding to minimum RMSE gives direct estimate of Q β(f) relation together with the value of corner frequency. One of the important requirements of using Eq. (1) for inversion is that the acceleration spectrum shown in the left hand side of the equation should be free from site amplifications. This can be achieved in two ways (1) by using records from those stations where site amplifications are not effective within the range of frequencies required for the inversion (i.e. rock site), or (2) by removing the site amplifications directly from the acceleration spectra. The first approach is not feasible in our study, as we do not have enough information about the site characteristics at our strong motion sites. Use of the second approach is more suitable for our study; therefore, we have divided the inversion process into two sub-inversions to save computer memory and processing time. In the first part of inversion spectral acceleration data, seismic moment and corner frequency is used as input parameters. Several possibilities of corner frequencies are checked for each input event in this part of inversion. Final values are selected on the basis of minimum RMSE.

In the first part of inversion process, the acceleration spectra without any correction of site amplification is used as an input to the algorithm and Q β(f) relation corresponding to minimum error is obtained. The obtained value of seismic moment, corner frequency and Q β(f) from the first part of inversion are further used for obtaining the residual of theoretical and observed source spectra which are treated as site amplification terms (Joshi 2006). Obtained value of site amplifications are used to correct the acceleration spectra which is now used as input in the second part of the inversion scheme which is similar to the first part. The final outcome from this part is a new Q β(f) relation together with input values of seismic moment and corner frequency of each input. The obtained value of Q β(f) from the second part of inversion is used to calculate source displacement spectra from acceleration record and is further used for computing seismic moment. The process of two-step inversion is repeated for this new estimate of seismic moment and goes on until minimum RMSE is obtained which gives final estimate of Q β(f) at each station. The whole procedure to compute seismic moment after iteratively correcting acceleration spectra is shown in Fig. 7. The obtained source spectra at four different stations are shown in Fig. 8. Moment magnitude and average seismic moment computed from both NS and EW component using final value of Q β(f) and site corrections at each station is given in Table 1.

Fig. 7
figure 7

Flow diagram of entire process to obtain seismic moment

Full size image
Fig. 8
figure 8

a, b and c are the obtained source displacement spectra for an event recorded at four different stations for NS, EW and both components, respectively. Solid line indicates the theoretical spectra defined by Aki (1967)

Full size image

The Q β(f) at each station is calculated using both the NS and EW component of acceleration records. The above scheme of inversion is similar to that used by Joshi (2006) for estimation of Q β(f) for Garhwal Himalaya. The only difference is the consideration of seismic moment from independent sources in the approach given by Joshi (2006). In an attempt to check whether the residual makes sense as a site amplification filter, we have used the technique proposed by Lermo and Chávez-García (1993) to obtain site amplification curves. In this technique, the horizontal-component shear wave spectrum is divided by the vertical-component spectrum at each station to obtain the frequency-dependent site response. This technique is analogous to the receiver function technique applied in the studies of the upper mantle and crust from teleseismic records (Langston 1979). This method is also similar to the Nakamura (1988) method of computing site amplification factors using H/V ratio at single station. The site amplifications obtained at different stations after inversion is shown in Fig. 9.

Fig. 9
figure 9

Site effect at a Dharchula, b Didihat, c Pithoraghar, d Thal and e Tejam stations, respectively. The black and red lines show the site effects obtained by inversion of acceleration records of input events for NS and EW components, respectively. Different lines indicate site effect obtained from residual of input acceleration and source spectra. The shaded area denotes the region between μ + σ and μ − σ of the site amplification obtained using receiver function technique (Lermo and Chávez-García 1993)

Full size image

4 Numerical Experiment for the Data Set

In order to check the stability of the solution and the dependency of results on frequency contents of the input data set, three sets of input data have been used to obtain Q β(f) at Dharchula station which has recorded all events used in the present work. The NS component of the acceleration record has been used for this numerical test. Each set contain six events. The source parameters of these events were calculated from the source displacement spectra computed using initial Q β(f) value as given by Joshi (2006). After obtaining Q β(f) from inversion of spectral acceleration data, source displacement is again computed using obtained value of Q β(f) from inversion. The process goes on until RMS error is minimized. The residual of obtained and theoretical spectra in each step is treated as site amplification and is used further for correcting the acceleration record for the site amplification term. Three input data sets from Dharchula station are separately used and site amplification and Q β(f) is calculated for each set. In order to check the effect of high frequencies on the obtained Q β(f) relation all the data are passed through high cut filter having high cut range of 21.0, 23.0, 25.0 and 30.0 Hz, respectively. Figures 10 and 11 show that almost the same site amplification and Q β(f) relation have been obtained in four different cases for three sets at Dharchula station and minimum error is obtained for a high cut corner of 25.0 Hz frequency. Almost similar results have been obtained for all three sets at similar cutoff frequencies which indicate the stability of the inversion algorithm. The input data, site amplification and Q β(f) obtained from each set at a cut off frequency of 25 Hz are shown in Fig. 12. It is found that almost similar Q β(f) and site amplification has been obtained at Dharchula station for this cutoff for all three sets. Root mean square is also almost similar for all three sets at Dharchula station. In an attempt to check the obtained Q β(f) value by using other horizontal component of acceleration record from same data set, the EW component of acceleration record has been used as input to the inversion algorithm. Table 2 gives the value of RMS error and obtain Q β(f) relation for both NS and EW horizontal component. It is found that almost similar Q β(f) value is obtained for both NS and EW component of acceleration record. The numerical experiment about the dependency of the result in cutoff frequency and data set indicate the stability of the solution obtained in the inversion algorithm.

Fig. 10
figure 10

Site effects obtained from three different sets for the NS component at Dharchula station at frequency range 1–21, 1–23, 1–25 and 1–30 Hz are shown in (a), (b), (c) and (d), respectively. The shaded area denotes the region between μ + σ and μ − σ of the site amplification obtained using receiver function technique (Lermo and Chávez-García 1993)

Full size image
Fig. 11
figure 11

The Q β(f) relationship for the three different sets for NS component at Dharchula station at frequency range 1–21, 1–23, 1–25 and 1–30 Hz are shown in (a), (b), (c) and (d), respectively

Full size image
Fig. 12
figure 12

Input acceleration spectrum for the complete frequency range of three different sets for the NS component at Dharchula station is shown in (a), (d) and (g), respectively. b, e and h show the site effects obtained from different sets at frequency range 1–10 Hz and c, f and i are the Q β(f) relationship for the three different sets at Dharchula station at frequency range 1–25 Hz. The shaded area denotes the region between μ + σ and μ − σ of the site amplification obtained using receiver function technique (Lermo and Chávez-García 1993)

Full size image
Table 2 Q β(f) and RMS error at frequency 21, 23, 25 and 30 Hz obtained from inversion of data for both NS and EW components from three sets of event used at Dharchula station
Full size table

5 Results and Discussion

In the present work six events at each station have been used for inversion process. The iterative inversion is performed at each station independently; the values of corner frequency obtained from the iterative inversion at each station, and detail of all events used at each station, are given in Table 3. It is seen that the obtained value of corner frequency by using an individual data set is almost the same and has very little variations around mean value. The Q β(f) relation obtained using NS and EW component of record independently at each station is given in Table 4. The average Q β(f) relation of form Q 0 f n obtained by using average value of Q β(f) obtained from inversion of NS and EW record at each station is shown in Fig. 13 and given in Table 4. It is found that obtained average relation using average values from inversion of NS and EW component does not differ drastically with the Q β(f) relations obtained individually from NS and EW component. As the study area is covered mostly by sequences of Lesser Kumaon Himalaya, a regional relationship for Kumaon Himalaya has been calculated. In order to calculate regional Q β(f) relation, the Q β(f) values at each frequency obtained from inversion of NS and EW component data is averaged at different station and is plotted in Fig. 14a. The best fit line gives Q β(f) = (29 ± 1.2)f (1.1 ± 0.06) which represents regional attenuation characteristics of Kumaon Himalaya. The deviation of Q 0 and n with respect to their mean values is shown in Fig. 14b and c, respectively. The shaded area in Fig. 14b and c denotes the region deviates from mean to standard deviation, i.e. between μ + σ and μ – σ. The plot of Q β(f) average values versus frequency is shown in Fig. 14a. The RMS error between the input data and data calculated from the regression relation is 0.56, while the linear correlation coefficient is 0.52. It is seen that the calculated value of Q 0 for shear wave attenuation varies between 29 ± 1.2 and n varies between 1.1 ± 0.06, indicating a highly heterogeneous and tectonically active region.

Table 3 Detail of events used for different stations
Full size table
Table 4 The Q β(f) relationship and RMS error obtained at different stations using NS and EW component data relation is developed by using average of Q β(f) obtained from inversion of NS and EW component data
Full size table
Fig. 13
figure 13

Obtained Q β(f) relationship at a Dharchula, b Didihat, c Thal, d Pithoragarh and e Tejam, respectively. The average Q β(f) at different frequencies is taken from the value obtained after inversion of NS and EW components, respectively

Full size image
Fig. 14
figure 14

a Regional Q β(f) relationship for Kumaon Himalaya based on the obtained value of shear wave attenuation at different stations at different frequencies b variation of Q 0 with respect to its mean value c variation of n with respect to its mean value. The shaded area denotes the region between μ + σ and μ − σ

Full size image

The obtained average Q β(f) relation at each station is used for correcting acceleration spectra for anelastic attenuation which is used for computation of source spectra of different events. The seismic moment in the present scheme of inversion is calculated after correcting the acceleration spectra with anelastic attenuation using Q β(f) obtained from inversion in each step of iterative inversion. The average value of seismic moment obtained at different stations is used in the inversion algorithm. This process is repeated for each iterative inversion until error is minimized. The final value of seismic moment obtained for different input events at each station after correction for final Q β(f) for both NS and EW component data is given in Table 5. Using the average relation of Q β(f) = (29 ± 1.2)f (1.1 ± 0.06) developed for Kumaon Himalaya the acceleration spectra is further corrected and seismic moment is calculated from different records and is given in Table 5. The comparison of seismic moment calculated using individual Q β(f) at different stations and average Q β(f) shows that values of seismic moment are almost similar. This shows that Q β(f) = (29 ± 1.2)f (1.1 ± 0.06) can be used for representing attenuation characteristics of the region in broad sense.

Table 5 Seismic moment calculated from source displacement spectra of acceleration record at each station using final Q β(f) at each station and average Q β(f) for Kumaon Himalaya
Full size table

The obtained Q β(f) relations at various stations have been compared with the three dimensional distribution of shear wave quality factor (Q β) of the region obtained by Joshi et al. (2010). The data set in the approach given by Joshi et al. (2010) is small and uses only four events, and it gives attenuation structure at limited frequencies. The obtained Q β(f) value at 2.0 Hz frequency is compared with the three dimensional Q β structure at 2.0 Hz frequency obtained by Joshi et al. (2010) in Table 6. The Q β(f) relations given in Table 6 shows that the obtained value of Q β(f) from present inversion are almost similar with the values obtained by Joshi et al. (2010) at Tejam, Thal, Didihat and Pithoragarh stations while deviation is seen at Dharchula station. The obtained three dimensional structure is highly dependent on the ray path between source and station. Dharchula station is located at the boundary of India and Nepal, and hence has restriction of coverage of only one side for events occurring in Nepal. This may be the cause of deviation of results with an earlier study that uses limited events. Relation between seismic moment and corner frequency has been made by using average value of seismic moment and corner frequency for each event. The relation is plotted in Fig. 15. The logarithmic plot of the seismic moment versus the corner frequency in Fig. 15 shows that the slope of the curve gives a value of −3.0. This gives the scaling law \( M_{\text{o}} \;\alpha \;f_{o}^{ - 3.0} \) which is consistent with the scaling law of spectral parameters given by Aki (1967). The linear relation corresponding to data sets shown in Fig. 15 is given as:

Table 6 Comparison of Q β(f) values developed in present work with Joshi et al. (2010)
Full size table
Fig. 15
figure 15

Relationship between seismic moment and corner frequency of input events used in the inversion algorithm

Full size image
$$ \ln \, f_{\text{c}} = - 0.30\ln \left( {M_{\text{o}} } \right) + 15.8 $$
(15)

A comparison of Q(f) obtained from present work is made with the measurements of Q(f) in other parts of the world and is shown in Fig. 16 and Table 7. In this comparison we have used both shear wave and coda wave attenuation relations depending upon their worldwide availability. It is seen that measurement of Q 0 f n relation provides a basis for dividing different regions into active and stable groups. The parameter Q 0 and n in this relation represent heterogeneities and level of tectonic activity of the region, respectively. Regions with higher n value manifest higher tectonic activity. It is seen from Table 7 that for various active regions, like Hindukush; northwest Himalaya, India; northeast Himalaya, India; Garhwal region, India; Washington state, USA; Garhwal, India; Ishikawa, Japan; Mt. Etna, Italy; and Southern Apennines, Italy, Q 0 and n varies from 18 to 158 and 0.7 to 2.0, respectively (Roecker et al. 1982; Kumar et al. 2004; Gupta and Kumar 2002; Sharma et al. 2009; Havskov et al. 1989; Mandal et al. 2001; Maeda et al. 2008; Giampiccolo et al. 2007; Cantore et al. 2010). For stable regions like Norway, North Iberia and North eastern United state and Southern Canada the value of Q 0 and n varies from 190 to 600 and 0.45 to 1.09, respectively (Kavamme and Havskov 1988; Pujades et al. 1991; Benz et al. 1997). On comparing present relation with other worldwide relations it is seen from Fig. 16b that it falls within the range of values that are justified for tectonically active regions. In the present work we have computed the attenuation of shear waves originating from a shallow depth between 10 and 35 km and hence it indicate high level of tectonic activity due to subducting Himalayan plate over Tibetan plate.

Fig. 16
figure 16

Comparison of Q β(f) relations developed in present work with a that obtained for Indian region, b for worldwide region

Full size image
Table 7 Q(f) Relationship for various Indian and worldwide relations
Full size table

6 Conclusion

In this paper a two-step inversion algorithm for obtaining Q β(f) relations from the strong motion data has been presented. Data of 18 events recorded at five stations located in the Pithoragarh region of Kumaon Himalaya, India from a local strong motion network have been used in this study. The values of Q β(f) obtained at different frequencies at five different stations corresponding to minimum RMS error is used to obtain a regional regression relation of Q β(f) = (29 ± 1.2)f (1.1 ± 0.06) which represent the attenuating property of rocks in the Pithoragarh region of Kumaon Himalayas. Low value of Q 0 and high value of n obtained in the present Q β(f) relation shows that the region is seismically active and characterized by local heterogeneities.