Spectral and Scattering Properties of Quantum Walks on Homogenous Trees of Odd Degree

Abstract

For unitary operators $U_0,U$ in Hilbert spaces ${\mathcal {H}}_0,{\mathcal {H}}$ and identification operator $J:{\mathcal {H}}_0\rightarrow {\mathcal {H}}$, we present results on the derivation of a Mourre estimate for U starting from a Mourre estimate for $U_0$ and on the existence and completeness of the wave operators for the triple $(U,U_0,J)$. As an application, we determine spectral and scattering properties of a class of anisotropic quantum walks on homogenous trees of odd degree with evolution operator U. In particular, we establish a Mourre estimate for U, obtain a class of locally U-smooth operators and prove that the spectrum of U covers the whole unit circle and is purely absolutely continuous, outside possibly a finite set where U may have eigenvalues of finite multiplicity. We also show that (at least) three different choices of free evolution operators $U_0$ are possible for the proof of the existence and completeness of the wave operators.

1 Introduction and Main Results

Recent years have seen a surge of research activity on discrete-time systems described by unitary evolution operators. CMV matrices, quantum walks, Koopman operators of dynamical systems and Floquet operators are classes of such systems having received a lot of attention. This surge of activity has in turn motivated various researchers to develop, or adapt from the self-adjoint setup, mathematical tools suited for the spectral and scattering analysis of unitary operators. Among these tools is the Mourre theory for unitary operators, which has been first introduced in [3] and then further developed in several papers such as [4, 5, 8, 12, 25] (see also the precursor works [15, 21]).

Fig. 1

Homogenous tree of degree 3 with generators $a_1,a_2,a_3$

When the evolution operator U of the system under study is non-trivial, it is often better to start by determining properties of a simpler evolution operator $U_0$ describing the free dynamics and then infer from it properties of U. This is the core idea of perturbation theory for linear operators [16]. However, the operator $U_0$ may be defined in a different Hilbert space than the operator U, as, for instance, when the system has a multichannel structure. In such a case, the perturbation theory has to be adapted accordingly. In the first part of the paper, we collect results in this direction for Mourre theory and scattering theory for unitary operators. Our results are either new or extensions of abstract results of [25, 26], and they can be considered as a unitary analogue of the results of [23] in the self-adjoint case.

In the second part of the paper, we apply our abstract results to quantum walks on homogenous trees of odd degree $d\ge 3$ as defined in [13, 14] (but see also [10, 11] for other definitions of quantum walks on trees). Motivated by recent works on quantum walks on ${\mathbb {Z}}$ [2, 25,26,27], we consider quantum walks with a position-dependent coin admitting a limit at infinity on each main branch of the tree. Since ${\mathbb {Z}}$ is nothing else but a homogenous tree of degree 2, these quantum walks on homogenous trees of degree d are to some extent a generalisation of the anisotropic quantum walks on ${\mathbb {Z}}$ considered in [25, 26].

Here is a more detailed description of the paper. In Sect. 2, we gather the needed results on Mourre theory for unitary operators in one Hilbert space. Given a unitary operator U and a self-adjoint operator A in a Hilbert space ${\mathcal {H}}$, we recall the definitions of commutator classes relative to A, locally U-smooth operators, conjugate operator for U and Mourre estimate for U. We also recall the two main consequences (under some regularity assumptions) of a Mourre estimate for U: the existence of locally U-smooth operators and spectral properties of U (Theorems 2.2 and 2.3).

In Sect. 3, we consider a second unitary operator $U_0$ in a second Hilbert space ${\mathcal {H}}_0$ and assume that an identification operator $J:{\mathcal {H}}_0\rightarrow {\mathcal {H}}$ is given. Then we present an improved version of the results of [25] on the construction of a conjugate operator A for U starting from a conjugate operator $A_0$ for $U_0$. In particular, we determine conditions guaranteeing that the operator $A=JA_0J^*$ is a conjugate operator for U if the operator $A_0$ is a conjugate operator for $U_0$ (Theorem 3.8).

In Sect. 4, we collect results on the existence and completeness under smooth perturbations of the wave operators for the triple $(U,U_0,J)$. We recall the intertwinning property of the wave operators (Lemma 4.1), present criteria for the J-completeness of the wave operators (Theorem 4.5 and Corollary 4.6), prove a chain rule for the wave operators (Lemma 4.7) and finally present a criterion for the completeness, in the usual sense, of the wave operators (Theorem 4.8).

In Sect. 5, we apply the results that precede to quantum walks on homogeneous trees of odd degree $d\ge 3$. We consider quantum walks with evolution operator $U=SC$, where S is a shift and C a position-dependent coin that converge at infinity, on each main branch of the tree, to a constant diagonal matrix $C_i$, $i=1,\ldots ,d$ (Assumption 5.1). This provides evolution operators $U_i:=SC_i$ describing the asymptotic behaviour of U on each main branch of the tree. This also motivates to choose $U_0:=\bigoplus _{k=1}^dU_k$ as a free evolution operator and suggests the definition of the identification operator J. In Sect. 5.1, we construct a conjugate operator for $U_0$ and determine the spectral properties of $U_0$. Using an approach motivated by classical mechanics, we construct a conjugate operator $A_0$ satisfying the homogeneous Mourre estimate

$$\begin{aligned} U_0^{-1}[A_0,U_0]=2. \end{aligned}$$

This relation, together with Mackey’s imprimitivity theorem, implies that $U_0$ is unitarily equivalent to a multiplication operator with purely absolutely continuous spectrum covering the whole unit circle (Proposition 5.6). In Sect. 5.2, we show that the operator $A=JA_0J^*$ is a conjugate operator for U (Lemma 5.9), establish a Mourre estimate for U (Proposition 5.10), obtain a class of locally U-smooth operators (Theorem 5.12) and show that U has at most finitely many eigenvalues, each one of finite multiplicity, and no singular continuous spectrum (Theorem 5.13). To our knowledge, this is the first spectral result of this type for a class of quantum walks on homogeneous trees of degree $d\ge 3$ with position-dependent coin (see [14, Thm. 4.5] for a result on a class of quantum walks on rooted trees of degree 3 with constant coin). Finally, we establish in Sect. 5.3 the existence and completeness of the wave operators for the triple $(U,U_0,J)$ (Theorem 5.14). As a by-product, we infer that the absolutely continuous spectrum of U covers the whole unit circle (Corollary 5.16). Interestingly enough, we also show that two operators different from $U_0$ can be used as a free evolution operator for U, and establish the existence and completeness of the wave operators in these cases too (Corollary 5.15 and Theorem 5.17). Of course, each choice of free evolution operator comes with its pros and cons, see Remark 5.18.

We point out that our proof of the absence of singular continuous spectrum is a key ingredient to establish in the future a weak limit theorem for U. Weak limit theorems are results relating scattering properties of quantum walks to probabilistic properties of the corresponding classical random walks. Typically, these theorems show that if $\mathtt X_n$ is the random variable for the position of a quantum walker at time $n\in {\mathbb {Z}}$, then $\mathtt X_n/n$ converges in law to a random variable $\mathtt V$ as $n\rightarrow \infty$ with probability distribution $\mu _\mathtt V$ given in terms of scattering quantities of the evolution operator of the quantum walk. See [17, 18, 26, 27] for examples of weak limit theorems for quantum walks on ${\mathbb {Z}}$.

To conclude, we emphasise that this work leaves open for future investigations various other interesting problems about quantum walks on homogeneous trees of odd degree. The existence of asymptotic velocity operators, the description of the initial subspaces of the wave operators, the generalisation to coin operators converging to constant coin along more refined partitions of the tree, the extension to rooted trees and the generalisation to coin operators admitting non-diagonal matrix limits at infinity are examples of problems that could be investigated. See the comments (i)–(iv) at the end of Sect. 5.3 for more details.

Notations. ${\mathbb {N}}:=\{0,1,2,\ldots \}$ is the set of natural numbers, ${\mathbb {S}}^1$ the complex unit circle and $\mathrm U(n)$ the group of $n\times n$ unitary matrices. Given a Hilbert space ${\mathcal {H}}$, we write $\Vert \cdot \Vert _{\mathcal {H}}$ for its norm and $\langle \cdot ,\cdot \rangle _{\mathcal {H}}$ for its scalar product (linear in the first argument). Given two Hilbert spaces ${\mathcal {H}}_1,{\mathcal {H}}_2$, we write ${\mathscr {B}}({\mathcal {H}}_1,{\mathcal {H}}_2)$ (resp. ${\mathscr {K}}({\mathcal {H}}_1,{\mathcal {H}}_2)$, $S_2({\mathcal {H}}_1,{\mathcal {H}}_2)$) for the set of bounded (resp. compact, Hilbert–Schmidt) operators from ${\mathcal {H}}_1$ to ${\mathcal {H}}_2$. We also write $\Vert \cdot \Vert _{{\mathscr {B}}({\mathcal {H}}_1,{\mathcal {H}}_2)}$ for the norm of ${\mathscr {B}}({\mathcal {H}}_1,{\mathcal {H}}_2)$, and use the shorthand notations ${\mathscr {B}}({\mathcal {H}}_1):={\mathscr {B}}({\mathcal {H}}_1,{\mathcal {H}}_1)$, ${\mathscr {K}}({\mathcal {H}}_1):={\mathscr {K}}({\mathcal {H}}_1,{\mathcal {H}}_1)$ and $S_2({\mathcal {H}}_1):=S_2({\mathcal {H}}_1,{\mathcal {H}}_1)$.

2 Mourre Theory in One Hilbert Space

A unitary operator U in a Hilbert space ${\mathcal {H}}$ is a surjective isometry, that is, an operator $U\in {\mathscr {B}}({\mathcal {H}})$ satisfying $U^*U=UU^*=1$. Since $U^*U=UU^*=1$, the spectral theorem for normal operators implies that U admits exactly one complex spectral family $E_U$, with support $\mathop {\mathrm {supp}}\nolimits (E_U)\subset {\mathbb {S}}^1$, such that $U=\int _{\mathbb {C}}\mathrm {d}E_U(z)\;\!z$. The support $\mathop {\mathrm {supp}}\nolimits (E_U)$ is the set of points of non-constancy of $E_U$, and it coincides with the spectrum $\sigma (U)$ of U [31, Thm. 7.34(a)]. One can associate in a canonical way a real spectral family to the complex spectral family $E_U$. Indeed, if we let $E^U$ be the spectral measure corresponding to the spectral family $E_U$, then the family ${{\widetilde{E}}}_U$ defined by

$$\begin{aligned} {{\widetilde{E}}}_U(t):= {\left\{ \begin{array}{ll} 0 &{} \hbox {if }t<0\\ E^U\big (\{\mathop {\mathrm {e}}\nolimits ^{is}\mid s\in [0,t]\}\big ) &{} \hbox {if }t\in [0,2\pi )\\ 1 &{} \hbox {if }t\ge 2\pi , \end{array}\right. } \end{aligned}$$

is a real spectral family with support $\mathop {\mathrm {supp}}\nolimits (\widetilde{E}_U)\subset [0,2\pi ]$ which satisfies $U=\int _{\mathbb {R}}\mathrm {d}\widetilde{E}_U(t)\mathop {\mathrm {e}}\nolimits ^{it}$ [31, Thm. 7.36]. Since ${{\widetilde{E}}}_U$ is a real spectral family, the corresponding real spectral measure ${{\widetilde{E}}}^U$ admits a decomposition

$$\begin{aligned} {{\widetilde{E}}}^U={{\widetilde{E}}}^U_{\mathrm{p}}+{{\widetilde{E}}}^U_\mathrm{sc}+{{\widetilde{E}}}^U_{\mathrm{ac}}, \end{aligned}$$

with ${{\widetilde{E}}}^U_{\mathrm{p}}$, ${{\widetilde{E}}}^U_{\mathrm{sc}}$, ${{\widetilde{E}}}^U_{\mathrm{ac}}$ the pure point, the singular continuous and the absolutely continuous components of ${{\widetilde{E}}}_U$, respectively. The corresponding subspaces ${\mathcal {H}}_{\mathrm{p}}(U):=P_\mathrm{p}(U){\mathcal {H}}$, ${\mathcal {H}}_{\mathrm{sc}}(U):=P_{\mathrm{sc}}(U){\mathcal {H}}$, ${\mathcal {H}}_{\mathrm{ac}}(U):=P_\mathrm{ac}(U){\mathcal {H}}$ with $P_\star (U):={{\widetilde{E}}}^U_\star ({\mathbb {R}})$ ($\star =$ p, sc, ac) provide an orthogonal decomposition which reduces the operator U : 

$$\begin{aligned} {\mathcal {H}}={\mathcal {H}}_{\mathrm{p}}(U)\oplus {\mathcal {H}}_{\mathrm{sc}}(U)\oplus {\mathcal {H}}_{\mathrm{ac}}(U). \end{aligned}$$

The sets $\sigma _{\mathrm{p}}(U):=\sigma (U|_{{\mathcal {H}}_{\mathrm{p}}(U)})$, $\sigma _{\mathrm{sc}}(U):=\sigma (U|_{{\mathcal {H}}_{\mathrm{sc}}(U)})$ and $\sigma _\mathrm{ac}(U):=\sigma (U|_{{\mathcal {H}}_{\mathrm{ac}}(U)})$ are called pure point spectrum, singular continuous spectrum and absolutely continuous spectrum of U, respectively, and the set $\sigma _{\mathrm{c}}(U):=\sigma _\mathrm{sc}(U)\cup \sigma _{\mathrm{ac}}(U)$ is called the continuous spectrum of U. We also use the notation $\sigma _{\mathrm{ess}}(U)$ for the essential spectrum of U.

If ${\mathcal {G}}$ is an auxiliary Hilbert space, then an operator $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ is called locally U-smooth on a Borel set $\Theta \subset {\mathbb {S}}^1$ if there exists $c_\Theta \ge 0$ such that

$$\begin{aligned} \sum _{n\in {\mathbb {Z}}}\big \Vert TU^nE^U(\Theta )\varphi \big \Vert _{\mathcal {G}}^2 \le c_\Theta \Vert \varphi \Vert _{{\mathcal {H}}_0}^2\quad \hbox {for all }\varphi \in {\mathcal {H}}, \end{aligned}$$

(2.1)

and T is called U-smooth if (2.1) is satisfied with $\Theta ={\mathbb {S}}^1$. The condition (2.1) is invariant under rotation by $\theta \in {\mathbb {S}}^1$ in the sense that if T is locally U-smooth on $\Theta$, then T is locally $(\theta U)$-smooth on $\theta \Theta$ since

$$\begin{aligned} \big \Vert T(\theta U)^nE^{\theta U}(\theta \Theta )\varphi \big \Vert _{\mathcal {G}}=\big \Vert TU^nE^U(\Theta )\varphi \big \Vert _{\mathcal {G}}\quad \hbox {for all } \varphi \in {\mathcal {H}}. \end{aligned}$$

As in the self-adjoint case, the existence of a locally U-smooth operator can be formulated in various equivalent ways (see [4, Thm. 7.1]). An important consequence of the existence of a locally U-smooth operator T on $\Theta$ is the inclusion $\overline{E^U(\Theta )T^*{\mathcal {G}}^*}\subset {\mathcal {H}}_{\mathrm{ac}}(U)$, where ${\mathcal {G}}^*$ is the adjoint space of ${\mathcal {G}}$ (see [3, Thm. 2.1 & Def. 2.2]).

We now recall some results on Mourre theory for unitary operators in one Hilbert space, starting with definitions and results borrowed from [1, 12, 25]. Let $S\in {\mathscr {B}}({\mathcal {H}})$ and let A be a self-adjoint operator in ${\mathcal {H}}$ with domain ${\mathcal {D}}(A)$. For any $k\in {\mathbb {N}}$, we say that S belongs to $C^k(A)$, with notation $S\in C^k(A)$, if the map ${\mathbb {R}}\ni t\mapsto \mathop {\mathrm {e}}\nolimits ^{-itA}S\mathop {\mathrm {e}}\nolimits ^{itA}\in {\mathscr {B}}({\mathcal {H}})$ is strongly of class $C^k$. In the case $k=1$, one has $S\in C^1(A)$ if and only if the quadratic form

$$\begin{aligned} {\mathcal {D}}(A)\ni \varphi \mapsto \langle A\;\!\varphi ,S\varphi \rangle _{\mathcal {H}}-\langle \varphi ,SA\;\!\varphi \rangle _{\mathcal {H}}\in {\mathbb {C}}\end{aligned}$$

is continuous for the topology induced by ${\mathcal {H}}$ on ${\mathcal {D}}(A)$. The operator associated with the continuous extension of the form is denoted by $[A,S]\in {\mathscr {B}}({\mathcal {H}})$, and it verifies

$$\begin{aligned}{}[A,S]={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{t\rightarrow 0}\;\![A(t),S] \quad \hbox {with}\quad A(t):=\tfrac{1}{it}(\mathop {\mathrm {e}}\nolimits ^{it A}-1)\in {\mathscr {B}}({\mathcal {H}}), \quad t\in {\mathbb {R}}{\setminus }\{0\}. \end{aligned}$$

Three regularity conditions slightly stronger than $S\in C^1(A)$ are defined as follows. S belongs to $C^{1,1}(A)$, with notation $S\in C^{1,1}(A)$, if

$$\begin{aligned} \int _0^1\tfrac{\mathrm {d}t}{t^2}\;\! \big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}S\mathop {\mathrm {e}}\nolimits ^{itA}+\mathop {\mathrm {e}}\nolimits ^{itA}S\mathop {\mathrm {e}}\nolimits ^{-itA}-2S\big \Vert _{{\mathscr {B}}({\mathcal {H}})}<\infty . \end{aligned}$$

S belongs to $C^{1+0}(A)$, with notation $S\in C^{1+0}(A)$, if $S\in C^1(A)$ and

$$\begin{aligned} \int _0^1\tfrac{\mathrm {d}t}{t}\;\!\big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}[A,S]\mathop {\mathrm {e}}\nolimits ^{itA}-[A,S]\big \Vert _{{\mathscr {B}}({\mathcal {H}})}<\infty . \end{aligned}$$

S belongs to $C^{1+\varepsilon }(A)$ for some $\varepsilon \in (0,1)$, with notation $S\in C^{1+\varepsilon }(A)$, if $S\in C^1(A)$ and

$$\begin{aligned} \big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}[A,S]\mathop {\mathrm {e}}\nolimits ^{itA}-[A,S]\big \Vert _{{\mathscr {B}}({\mathcal {H}})} \le \mathrm{Const.}\;\!t^\varepsilon \quad \hbox {for all }t\in (0,1). \end{aligned}$$

As banachisable topological vector spaces, these sets satisfy the continuous inclusions [1, Sec. 5.2]

$$\begin{aligned} C^2(A)\subset C^{1+\varepsilon }(A)\subset C^{1+0}(A)\subset C^{1,1}(A)\subset C^1(A) \subset C^0(A)\equiv {\mathscr {B}}({\mathcal {H}}). \end{aligned}$$

Now, let U be a unitary operator with $U\in C^1(A)$. For $S,T\in {\mathscr {B}}({\mathcal {H}})$, we write $T > rsim S$ if there exists an operator $K\in {\mathscr {K}}({\mathcal {H}})$ such that $T+K\ge S$, and for $\theta \in {\mathbb {S}}^1$ and $\varepsilon >0$, we set

$$\begin{aligned} \Theta (\theta ;\varepsilon ) :=\big \{\theta '\in {\mathbb {S}}^1\mid |\arg (\theta -\theta ')|<\varepsilon \big \} \quad \hbox {and}\quad E^U(\theta ;\varepsilon ):=E^U\big (\Theta (\theta ;\varepsilon )\big ). \end{aligned}$$

With these notations at hand, we can define functions $\varrho ^A_U:{\mathbb {S}}^1\rightarrow (-\infty ,\infty ]$ and ${{\widetilde{\varrho }}}^A_U:{\mathbb {S}}^1\rightarrow (-\infty ,\infty ]$ by

$$\begin{aligned} \varrho ^A_U(\theta )&:=\sup \big \{a\in {\mathbb {R}}\mid \exists \;\!\varepsilon>0~\hbox {such that}~ E^U(\theta ;\varepsilon )U^{-1}[A,U]E^U(\theta ;\varepsilon ) \ge a\;\!E^U(\theta ;\varepsilon )\big \},\\ {{\widetilde{\varrho }}}^A_U(\theta )&:=\sup \big \{a\in {\mathbb {R}}\mid \exists \;\!\varepsilon >0~\hbox {such that}~ E^U(\theta ;\varepsilon )U^{-1}[A,U]E^U(\theta ;\varepsilon ) > rsim a\;\!E^U(\theta ;\varepsilon )\big \}. \end{aligned}$$

In applications, ${{\widetilde{\varrho }}}^A_U$ is more convenient than $\varrho ^A_U$ since it is defined in terms of a weaker positivity condition (positivity up to compact terms). A simple argument shows that ${{\widetilde{\varrho }}}^A_U(\theta )$ can be defined in an equivalent way by

$$\begin{aligned}&{{\widetilde{\varrho }}}^A_U(\theta ) =\sup \big \{a\in {\mathbb {R}}\mid \exists \;\!\eta \in C^\infty ({\mathbb {S}}^1,{\mathbb {R}})~\hbox {such that} ~\eta (\theta )\ne 0~\\&\hbox {and}~\eta (U)U^{-1}[A,U]\eta (U) > rsim a\;\!\eta (U)^2\big \}. \end{aligned}$$

Further properties of the functions ${{\widetilde{\varrho }}}^A_U$ and $\varrho ^A_U$ are recalled in the following lemma.

Lemma 2.1

(Lemma 3.3 of [25]). Let U be a unitary operator in ${\mathcal {H}}$ and let A be a self-adjoint operator in ${\mathcal {H}}$ with $U\in C^1(A)$.

• (a) The function $\varrho ^A_U:{\mathbb {S}}^1\rightarrow (-\infty ,\infty ]$ is lower semicontinuous, and $\varrho ^A_U(\theta )<\infty$ if and only if $\theta \in \sigma (U)$.

• (b) The function ${{\widetilde{\varrho }}}^A_U:{\mathbb {S}}^1\rightarrow (-\infty ,\infty ]$ is lower semicontinuous, and ${{\widetilde{\varrho }}}^A_U(\theta )<\infty$ if and only if $\theta \in \sigma _{\mathrm{ess}}(U)$.

• (c) ${{\widetilde{\varrho }}}^A_U\ge \varrho ^A_U$.

• (d) If $\theta \in {\mathbb {S}}^1$ is an eigenvalue of U and ${{\widetilde{\varrho }}}^A_U(\theta )>0$, then $\varrho ^A_U(\theta )=0$. Otherwise, $\varrho ^A_U(\theta )={{\widetilde{\varrho }}}^A_U(\theta )$.

One says that A is conjugate to U (or that U satisfies a Mourre estimate) at a point $\theta \in {\mathbb {S}}^1$ if ${{\widetilde{\varrho }}}^A_U(\theta )>0$, and that A is strictly conjugate to U (or that U satisfies a strict Mourre estimate) at $\theta$ if $\varrho ^A_U(\theta )>0$. Since ${{\widetilde{\varrho }}}^A_U(\theta )\ge \varrho ^A_U(\theta )$ for each $\theta \in {\mathbb {S}}^1$ by Lemma 2.1(c), strict conjugation is a property stronger than conjugation. We write

$$\begin{aligned} {{\widetilde{\mu }}}^A(U):=\big \{\theta \in {\mathbb {S}}^1\mid {{\widetilde{\varrho }}}^A_U(\theta )>0\big \} \end{aligned}$$

(2.2)

for the subset of ${\mathbb {S}}^1$ where A is conjugate to U, and note that ${{\widetilde{\mu }}}^A(U)$ is open due to the lower semicontinuity of the function ${{\widetilde{\varrho }}}^A_U$ (Lemma 2.1(b)).

The next theorem corresponds to [25, Thm. 3.4]; its formulation has been adapted to be consistent with the definition of locally smooth operators used in this paper. We use the notation $\langle \cdot \rangle :=(1+|\cdot |^2)^{1/2}$ and use the expression ‘spectral gap’ to mean a hole in the spectrum.

Theorem 2.2

(Locally smooth operators). Let U be a unitary operator in ${\mathcal {H}}$, let A be a self-adjoint operator in ${\mathcal {H}}$, and let ${\mathcal {G}}$ be an auxiliary Hilbert space. Assume either that U has a spectral gap and $U\in C^{1,1}(A)$, or that $U\in C^{1+0}(A)$. Suppose also there exist an open set $\Theta \subset {\mathbb {S}}^1$, a number $a>0$ and an operator $K\in {\mathscr {K}}({\mathcal {H}})$ such that

$$\begin{aligned} E^U(\Theta )\;\!U^{-1}[A,U]\;\!E^U(\Theta )\ge aE^U(\Theta )+K. \end{aligned}$$

Then each operator $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ which extends continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle A\rangle ^s)^*,{\mathcal {G}}\big )$ for some $s>1/2$ is locally U-smooth on any closed set $\Theta '\subset \Theta {\setminus }\sigma _{\mathrm{p}}(U)$.

The last theorem of this section has been established in [12, Thm. 2.7]:

Theorem 2.3

(Spectral properties). Let U be a unitary operator in ${\mathcal {H}}$ and let A be a self-adjoint operator in ${\mathcal {H}}$. Assume either that U has a spectral gap and $U\in C^{1,1}(A)$, or that $U\in C^{1+0}(A)$. Suppose also there exist an open set $\Theta \subset {\mathbb {S}}^1$, a number $a>0$ and an operator $K\in {\mathscr {K}}({\mathcal {H}})$ such that

$$\begin{aligned} E^U(\Theta )\;\!U^{-1}[A,U]\;\!E^U(\Theta )\ge aE^U(\Theta )+K. \end{aligned}$$

Then U has at most finitely many eigenvalues in $\Theta$, each one of finite multiplicity, and U has no singular continuous spectrum in $\Theta$.

Remark 2.4

• (a) If the assumptions of Theorem 2.3 are satisfied with $K=0$, then U has no point spectrum in $\Theta$ either, meaning that the spectrum of U in $\Theta$ (if any) is purely absolutely continuous (see [12, Rem. 2.8]).

• (b) An extension of the spectral result of Theorem 2.3 to unitary operators $U\in C^{1,1}(A)$ without the gap assumption can be found in [4, Thm. 2.3]. It would be interesting to see whether such an extension is also possible for the result on locally U-smooth operators of Theorem 2.2 (the result of [4, Prop. 7.1] in this direction holds under an additional assumption which seems unnecessary).

3 Mourre Theory in Two Hilbert Spaces

From now on, in addition to the triple $({\mathcal {H}},U,A)$, we consider a second triple $({\mathcal {H}}_0,U_0,A_0)$ with ${\mathcal {H}}_0$ a Hilbert space, $U_0$ a unitary operator in ${\mathcal {H}}_0$ and $A_0$ a self-adjoint operator in ${\mathcal {H}}_0$. We also assume that an identification operator $J\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ is given.

The regularity of $U_0$ with respect to $A_0$ is usually easy to check, while the regularity of U with respect to A is in general difficult to establish. In the case of self-adjoint operators in one Hilbert space, various perturbative criteria have been developed to tackle this problem, and often a distinction is made between short-range and long-range case. For unitary operators, this distinction consists in treating separately the two terms of the formal commutator $[A,U]=AU-UA$ in the short-range case, or really computing the commutator [A, U] in the long-range case.

In this section, we present an improved version of the results of [25, Sec. 3.2] on the construction of a conjugate operator A for U starting from a conjugate operator $A_0$ for $U_0$ in the short-range case. Before that, we recall a general result about the functions ${{\widetilde{\varrho }}}_U^A$ and ${{\widetilde{\varrho }}}_{U_0}^{A_0}$ when the two-Hilbert space perturbation $V:=JU_0-UJ$ is compact:

Theorem 3.1

(Theorem 3.6 of [25]). Let $({\mathcal {H}},U,A)$, $({\mathcal {H}}_0,U_0,A_0)$ and $J,V\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ be as above, and assume that

• (i) $U_0\in C^1(A_0)$ and $U\in C^1(A)$,

• (ii) $JU_0^{-1}[A_0,U_0]J^*-U^{-1}[A,U]\in {\mathscr {K}}({\mathcal {H}})$,

• (iii) $V\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$,

• (iv) For each $\eta \in C({\mathbb {S}}^1,{\mathbb {R}})$, one has $\eta (U)(JJ^*-1_{\mathcal {H}})\eta (U)\in {\mathscr {K}}({\mathcal {H}})$.

Then one has ${{\widetilde{\varrho }}}_U^A\ge {{\widetilde{\varrho }}}_{U_0}^{A_0}$.

3.1 Short-Range Case

We start by showing how the condition $U\in C^1(A)$ and the assumptions (ii)-(iii) of Theorem 3.1 can be verified in the short-range case. Our approach consists in deducing the desired information for U from equivalent information on $U_0$. The results are thus of a perturbative nature, and the price one has to pay is to impose some compatibility conditions between $A_0$ and A.

Our first proposition is an improved version of [25, Prop. 3.7] that we establish under less assumptions. We make use of the operator

$$\begin{aligned} V_*:=JU_0^{-1}-U^{-1}J\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}}). \end{aligned}$$

Proposition 3.2

Let $U_0\in C^1(A_0)$, assume that ${\mathscr {D}}\subset {\mathcal {H}}$ is a core for A with $J^*{\mathscr {D}}\subset {\mathcal {D}}(A_0)$, and suppose that $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ and $\overline{(JA_0J^*-A)\upharpoonright {\mathscr {D}}} \in {\mathscr {B}}({\mathcal {H}})$. Then $U\in C^1(A)$.

Proof

First, we show that the assumption $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ implies that $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$. Indeed, since $U_0\in C^1(A_0)$, we have

$$\begin{aligned} VA_0\upharpoonright {\mathcal {D}}(A_0) =-UV_*U_0A_0\upharpoonright {\mathcal {D}}(A_0) =-\big (UV_*A_0U_0+UV_*[U_0,A_0]\big )\upharpoonright {\mathcal {D}}(A_0) \end{aligned}$$

with $[U_0,A_0]\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$. Therefore, by using the inclusion $U_0{\mathcal {D}}(A_0)\subset {\mathcal {D}}(A_0)$ and the assumption $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}=B_*\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$, we infer that

$$\begin{aligned} \overline{VA_0\upharpoonright {\mathcal {D}}(A_0)} =-\big (UB_*U_0+UV_*[U_0,A_0]\big ) \in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}}). \end{aligned}$$

Now, we show that $U\in C^1(A)$. For $\varphi \in {\mathscr {D}}$, a direct calculation gives

$$\begin{aligned}&\langle A\;\!\varphi ,U\varphi \rangle _{\mathcal {H}}-\langle \varphi ,UA\;\!\varphi \rangle _{\mathcal {H}}\\&\quad =\langle A\;\!\varphi ,U\varphi \rangle _{\mathcal {H}}-\langle \varphi ,UA\;\!\varphi \rangle _{\mathcal {H}}-\langle \varphi ,J\;\![A_0,U_0]J^*\varphi \rangle _{\mathcal {H}}+\langle \varphi ,J\;\![A_0,U_0]J^*\varphi \rangle _{\mathcal {H}}\\&\quad =\langle \varphi ,VA_0J^*\varphi \rangle _{\mathcal {H}}-\langle V_*A_0J^*\varphi ,\varphi \rangle _{\mathcal {H}}+\big \langle U^*\varphi ,(JA_0J^*-A)\varphi \rangle _{\mathcal {H}}\\&\qquad -\langle (JA_0J^*-A)\varphi ,U\varphi \rangle _{\mathcal {H}}+\langle \varphi ,J\;\![A_0,U_0]J^*\varphi \rangle _{\mathcal {H}}. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \big |\langle \varphi ,VA_0J^*\varphi \rangle _{\mathcal {H}}-\langle V_*A_0J^*\varphi ,\varphi \rangle _{\mathcal {H}}\big | \le \mathrm{Const.}\;\!\Vert \varphi \Vert _{\mathcal {H}}^2 \end{aligned}$$

due to the assumption $J^*{\mathscr {D}}\subset {\mathcal {D}}(A_0)$ and the inclusions $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ and $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$, and we have

$$\begin{aligned} \big |\langle U^*\varphi ,(JA_0J^*-A)\varphi \rangle _{\mathcal {H}}-\langle (JA_0J^*-A)\varphi ,U\varphi \rangle _{\mathcal {H}}\big | \le \mathrm{Const.}\;\!\Vert \varphi \Vert ^2_{\mathcal {H}}\end{aligned}$$

due to the assumption $\overline{(JA_0J^*-A)\upharpoonright {\mathscr {D}}}\in {\mathscr {B}}({\mathcal {H}})$. Finally, since $U_0\in C^1(A_0)$ we also have

$$\begin{aligned} \big |\langle \varphi ,J\;\![A_0,U_0]J^*\varphi \rangle _{\mathcal {H}}\big | \le \mathrm{Const.}\;\!\Vert \varphi \Vert ^2_{\mathcal {H}}. \end{aligned}$$

In consequence, we obtain

$$\begin{aligned} \big |\langle A\;\!\varphi ,U\varphi \rangle _{\mathcal {H}}-\langle \varphi ,UA\;\!\varphi \rangle _{\mathcal {H}}\big | \le \mathrm{Const.}\;\!\Vert \varphi \Vert ^2_{\mathcal {H}}, \end{aligned}$$

which implies that $U\in C^1(A)$ due to the density of ${\mathscr {D}}$ in ${\mathcal {D}}(A)$. $\square$

Our second proposition is an improved version of [25, Prop. 3.8] that we establish under less assumptions. The proposition provides explicit conditions under which assumption (ii) of Theorem 3.1 is verified in the short-range case.

Proposition 3.3

Let $U_0\in C^1(A_0)$, assume that ${\mathscr {D}}\subset {\mathcal {H}}$ is a core for A with $J^*{\mathscr {D}}\subset {\mathcal {D}}(A_0)$, and suppose that $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$ and $\overline{(JA_0J^*-A)\upharpoonright {\mathscr {D}}} \in {\mathscr {K}}({\mathcal {H}})$. Then $U\in C^1(A)$ and

$$\begin{aligned} JU_0^{-1}[A_0,U_0]J^*-U^{-1}[A,U]\in {\mathscr {K}}({\mathcal {H}}). \end{aligned}$$

Proof

First, we note that $U\in C^1(A)$ due to Proposition 3.2. So [A, U] is a well-defined bounded operator. Next, the facts that $U_0\in C^1(A_0)$ and $J^*{\mathscr {D}}\subset {\mathcal {D}}(A_0)$ imply the inclusions

$$\begin{aligned} U_0J^*{\mathscr {D}}\subset U_0\;\!{\mathcal {D}}(A_0)\subset {\mathcal {D}}(A_0). \end{aligned}$$

Using this and the assumptions $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$ and $\overline{(JA_0J^*-A)\upharpoonright {\mathscr {D}}} \in {\mathscr {K}}({\mathcal {H}})$, we obtain for $\varphi \in {\mathscr {D}}$ and $\psi \in U^{-1}{\mathscr {D}}$ that

$$\begin{aligned}&\big \langle \psi ,\big (JU_0^{-1}[A_0,U_0]J^*-U^{-1}[A,U]\big )\varphi \big \rangle _{\mathcal {H}}\\&\quad =\langle \psi ,V_*A_0U_0J^*\varphi \rangle _{\mathcal {H}}+\langle V_*A_0J^*U\psi ,\varphi \rangle _{\mathcal {H}}\\&\qquad +\langle (JA_0J^*-A)U\psi ,U\varphi \rangle _{\mathcal {H}}-\langle \psi ,(JA_0J^*-A)\varphi \rangle _{\mathcal {H}}\\&\quad =\langle \psi ,K_1U_0J^*\varphi \rangle _{\mathcal {H}}+\langle K_1J^*U\psi ,\varphi \rangle _{\mathcal {H}}+\langle K_2U\psi ,U\varphi \rangle _{\mathcal {H}}-\langle \psi ,K_2\varphi \rangle _{\mathcal {H}}\end{aligned}$$

with $K_1\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$ and $K_2\in {\mathscr {K}}({\mathcal {H}})$. Since ${\mathscr {D}}$ and $U^{-1}{\mathscr {D}}$ are dense in ${\mathcal {H}}$, it follows that $JU_0^{-1}[A_0,U_0]J^*-U^{-1}[A,U]\in {\mathscr {K}}({\mathcal {H}})$. $\square$

In the rest of the section, we particularise the previous results to the case $A=JA_0J^*$. This case deserves special attention since it is the most natural choice of conjugate operator A for U when a conjugate operator $A_0$ for $U_0$ is given. However, one needs in this case an assumption that guarantees the self-adjointness of the operator A : 

Assumption 3.4

There exists a set ${\mathscr {D}}\subset {\mathcal {D}}(A_0J^*)\subset {\mathcal {H}}$ such that $JA_0J^*\upharpoonright {\mathscr {D}}$ is essentially self-adjoint, with closure denoted by A.

Assumption 3.4 might be difficult to check in general, but in concrete situations the choice of the set ${\mathscr {D}}$ can be quite natural (see, for example, [25, Lemma 4.9] for the case of quantum walks on ${\mathbb {Z}}$, [22, Rem. 4.3] for the case of manifolds with asymptotically cylindrical ends, or Lemma 5.9 for the case of quantum walks on homogeneous trees). Furthermore, if the operator J is unitary, then Assumption 3.4 is automatically satisfied with the set ${\mathscr {D}}:=J\;\!{\mathcal {D}}(A_0)$.

The two corollaries below follow directly from Propositions 3.2 and 3.3 when Assumption 3.4 is satisfied. They generalise corollaries 3.10 & 3.11 of [25].

Corollary 3.5

Let $U_0\in C^1(A_0)$, suppose that Assumption 3.4 holds, and assume that $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$. Then $U\in C^1(A)$.

Corollary 3.6

Let $U_0\in C^1(A_0)$, suppose that Assumption 3.4 holds, and assume that $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$. Then $U\in C^1(A)$ and

$$\begin{aligned} JU_0^{-1}[A_0,U_0]J^*-U^{-1}[A,U]\in {\mathscr {K}}({\mathcal {H}}). \end{aligned}$$

Remark 3.7

• (a) If needed, the assumption $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ in Proposition 3.2 and Corollary 3.5 can be replaced by the assumption $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$. Indeed, since $U_0\in C^1(A_0)$, we have $U_0^{-1}\in C^1(A_0)$ and

  $$\begin{aligned} V_*A_0\upharpoonright {\mathcal {D}}(A_0) =-U^{-1}VU_0^{-1}A_0\upharpoonright {\mathcal {D}}(A_0) =-\big (U^{-1}VA_0U_0^{-1}+U^{-1}V[U_0^{-1},A_0]\big )\upharpoonright {\mathcal {D}}(A_0) \end{aligned}$$

  with $[U_0^{-1},A_0]\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$. Therefore, by using the inclusion $U_0^{-1}{\mathcal {D}}(A_0)\!\!\subset {\mathcal {D}}(A_0)$ and the assumption $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}=B\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$, we infer that

  $$\begin{aligned} \overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)} =-\big (U^{-1}BU_0^{-1}+U^{-1}V[U_0^{-1},A_0]\big ) \in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}}). \end{aligned}$$

• (b) Similarly, if $V\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$, then the assumption $\overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}} ({\mathcal {H}}_0,{\mathcal {H}})$ in Proposition 3.3 and Corollary 3.6 can be replaced by the assumption $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$. Indeed, if $V\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$ and $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}=B\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$, then we obtain that

  $$\begin{aligned} \overline{V_*A_0\upharpoonright {\mathcal {D}}(A_0)} =-\big (U^{-1}BU_0^{-1}+U^{-1}V[U_0^{-1},A_0]\big ) \in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}}). \end{aligned}$$

By combining the results of Theorem 3.1, Corollary 3.6 and Remark 3.7(b), we obtain a more explicit version of Theorem 3.1 in the case $A=JA_0J^*:$

Theorem 3.8

Let $U_0,U$ be unitary operators in Hilbert spaces ${\mathcal {H}}_0,{\mathcal {H}}$, let $A_0$ be a self-adjoint operator in ${\mathcal {H}}_0$, let $J\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$, and assume that

• (i) there exists a set ${\mathscr {D}}\subset {\mathcal {D}}(A_0J^*)\subset {\mathcal {H}}$ such that $JA_0J^*\upharpoonright {\mathscr {D}}$ is essentially self-adjoint, with closure denoted by A,

• (ii) $U_0\in C^1(A_0)$,

• (iii) $V\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$,

• (iv) $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$

• (v) for each $\eta \in C({\mathbb {S}}^1,{\mathbb {R}})$, one has $\eta (U)(JJ^*-1_{\mathcal {H}})\eta (U)\in {\mathscr {K}}({\mathcal {H}})$.

Then $U\in C^1(A)$ and ${{\widetilde{\varrho }}}_U^A\ge {{\widetilde{\varrho }}}_{U_0}^{A_0}$.

4 Scattering Theory in Two Hilbert Spaces

In this section, we collect results on the existence and completeness under smooth perturbations of the local wave operators for the triple $(U,U_0,J)$. Namely, given a Borel set $\Theta \subset {\mathbb {S}}^1$, we present criteria for the existence and the completeness of the strong limits

$$\begin{aligned} W_\pm (U,U_0,J,\Theta ):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}JU_0^nE^{U_0}(\Theta ) \end{aligned}$$

under the assumption that $V=JU_0-UJ$ factorises as a product of locally smooth operators on $\Theta$. We start by recalling the result of [26, Lemma 2.1] on the intertwining property of wave operators. (In [26], the set $\Theta$ is assumed to be open, but the proof holds for Borel sets too.)

Lemma 4.1

(Intertwining property) Let $\Theta \subset {\mathbb {S}}^1$ be a Borel set and assume that $W_\pm (U,U_0,J,\Theta )$ exist. Then $W_\pm (U,U_0,J,\Theta )$ satisfy for each bounded Borel function $\eta :{\mathbb {S}}^1\rightarrow {\mathbb {C}}$ the intertwining property

$$\begin{aligned} W_\pm (U,U_0,J,\Theta )\;\!\eta (U_0)=\eta (U)\;\!W_\pm (U,U_0,J,\Theta ). \end{aligned}$$

Next, we define the closed subspaces of ${\mathcal {H}}$

$$\begin{aligned} {\mathfrak {N}}_\pm (U,J,\Theta ) :=\Big \{\varphi \in {\mathcal {H}}\mid \lim _{n\rightarrow \pm \infty } \big \Vert J^*U^nE^U(\Theta )\varphi \big \Vert _{{\mathcal {H}}_0}=0\Big \}, \end{aligned}$$

and note that $E^U({\mathbb {S}}^1{\setminus }\Theta ){\mathcal {H}}\subset {\mathfrak {N}}_\pm (U,J,\Theta )$, that U is reduced by ${\mathfrak {N}}_\pm (U,J,\Theta )$, and that

$$\begin{aligned} \overline{\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J,\Theta )\big )}\perp {\mathfrak {N}}_\pm (U,J,\Theta ), \end{aligned}$$

this last fact being shown as in the self-adjoint case, see [32, Lemma 3.2.1]. In particular, we have the inclusion

$$\begin{aligned} \overline{\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J,\Theta )\big )} \subset E^U(\Theta ){\mathcal {H}}\ominus {\mathfrak {N}}_\pm (U,J,\Theta ), \end{aligned}$$

which motivates the following definition:

Definition 4.2

(J-completeness) Assume that $W_\pm (U,U_0,J,\Theta )$ exist. The operators $W_\pm (U,U_0,J,\Theta )$ are J-complete on $\Theta$ if

$$\begin{aligned} \overline{\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J,\Theta )\big )} =E^U(\Theta ){\mathcal {H}}\ominus {\mathfrak {N}}_\pm (U,J,\Theta ). \end{aligned}$$

Remark 4.3

If J is unitary (as, for instance, when ${\mathcal {H}}_0={\mathcal {H}}$ and $J=1_{\mathcal {H}}$), then ${\mathfrak {N}}_\pm (U,J,\Theta )=E^U({\mathbb {S}}^1{\setminus }\Theta ){\mathcal {H}}$, and the wave operators $W_\pm (U,U_0,J,\Theta )$ have closed ranges because they are partial isometries with initial sets $E^{U_0}(\Theta ){\mathcal {H}}_0$. Therefore, the J-completeness on $\Theta$ reduces to the completeness on $\Theta$ in the usual sense, namely $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J,\Theta )\big )=E^U(\Theta ){\mathcal {H}}$. In such a case, the wave operators $W_\pm (U,U_0,J,\Theta )$ are unitary from $E^{U_0}(\Theta ){\mathcal {H}}_0$ to $E^U(\Theta ){\mathcal {H}}$.

The following criterion for J-completeness has been shown in [26, Lemma 2.4] for open sets $\Theta$, but the proof holds for Borel sets too:

Lemma 4.4

If $W_\pm (U,U_0,J,\Theta )$ and $W_\pm (U_0,U,J^*,\Theta )$ exist, then $W_\pm (U,U_0, J,\Theta )$ are J-complete on $\Theta$.

The next theorem corresponds to [26, Thm. 2.5]; its formulation has been adapted to be consistent with the definition of locally smooth operators used in this paper.

Theorem 4.5

(J-completeness of the wave operators). Let $\Theta \subset {\mathbb {S}}^1$ be an open set and let ${\mathcal {G}}$ be an auxiliary Hilbert space. If $V=T^*T_0$ with $T_0\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {G}})$ locally $U_0$-smooth on any closed set $\Theta '\subset \Theta$ and $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ locally U-smooth on any closed set $\Theta '\subset \Theta$, then the wave operators $W_\pm (U,U_0,J,\Theta )$ exist, are J-complete on $\Theta$ and satisfy the relations

$$\begin{aligned}&W_\pm (U,U_0,J,\Theta )^*=W_\pm (U_0,U,J^*,\Theta ) \\&\quad \hbox {and}\quad W_\pm (U,U_0,J,\Theta )\eta (U_0)=\eta (U)W_\pm (U,U_0,J,\Theta ) \end{aligned}$$

for each bounded Borel function $\eta :{\mathbb {S}}^1\rightarrow {\mathbb {C}}$.

Now, by combining Theorems 2.2 and 4.5, we obtain the following criterion for the existence and J-completeness of the local wave operators. We recall that the sets ${{\widetilde{\mu }}}^{A}(U)$, ${{\widetilde{\mu }}}^{A_0}(U_0)$ have been defined in (2.2).

Corollary 4.6

Let $A_0,A$ self-adjoint operators in ${\mathcal {H}}_0,{\mathcal {H}}$. Assume either that $U_0$ and U have a spectral gap and $U_0\in C^{1,1}(A_0),U\in C^{1,1}(A)$, or that $U_0\in C^{1+0}(A_0),U\in C^{1+0}(A)$. Let

$$\begin{aligned} \Theta :=\big \{{{\widetilde{\mu }}}^{A_0}(U_0)\cap {{\widetilde{\mu }}}^{A}(U)\big \} {\setminus }\big \{\sigma _{\mathrm{p}}(U_0)\cup \sigma _{\mathrm{p}}(U)\big \}, \end{aligned}$$

let ${\mathcal {G}}$ be an auxiliary Hilbert space, and suppose that $V=T^*T_0$ with $T_0\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {G}})$ extending continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle A_0\rangle ^s)^*,{\mathcal {G}}\big )$ and $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ extending continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle A\rangle ^s)^*,{\mathcal {G}}\big )$ for some $s>1/2$. Then the wave operators $W_\pm (U,U_0,J,\Theta )$ exist, are J-complete on $\Theta$, and satisfy the relations

$$\begin{aligned}&W_\pm (U,U_0,J,\Theta )^*=W_\pm (U_0,U,J^*,\Theta ) \\&\quad \hbox {and}\quad W_\pm (U,U_0,J,\Theta )\;\!\eta (U_0)=\eta (U)\;\!W_\pm (U,U_0,J,\Theta ) \end{aligned}$$

for each bounded Borel function $\eta :{\mathbb {S}}^1\rightarrow {\mathbb {C}}$.

In the last part of the section, we determine conditions under which the (global) wave operators

$$\begin{aligned} W_\pm (U,U_0,J):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}JU_0^nP_{\mathrm{ac}}(U_0) \end{aligned}$$

are complete in the usual sense; that is, satisfy $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$. When defining the completeness of the wave operators $W_\pm (U,U_0,J)$, the simplest choice would be to require in addition that $W_\pm (U,U_0,J)$ are partial isometries with initial subspaces ${\mathcal {H}}_0^\pm ={\mathcal {H}}_\mathrm{ac}(U_0)$ (as in [7, Def. III.9.24] or [32, Def. 2.3.1] in the self-adjoint case). However, in applications it may happen that the ranges of $W_\pm (U,U_0,J)$ are equal to ${\mathcal {H}}_{\mathrm{ac}}(U)$ but that ${\mathcal {H}}_0^\pm \ne {\mathcal {H}}_{\mathrm{ac}}(U_0)$. In the self-adjoint case, this typically happens for multichannel type scattering processes, in which case the usual criteria for completeness, as [7, Prop. III.9.40] or [32, Thm. 2.3.6], do not be apply. This is why we present below a criterion for the completeness of the wave operators $W_\pm (U,U_0,J)$ without assuming that ${\mathcal {H}}_0^\pm ={\mathcal {H}}_{\mathrm{ac}}(U_0)$.

We start by establishing a chain rule for wave operators analogous to [32, Thm. 2.1.7] in the self-adjoint case.

Lemma 4.7

(Chain rule). Let $U_1,U_2,U_3$ be unitary operators in Hilbert spaces ${\mathcal {H}}_1,{\mathcal {H}}_2,{\mathcal {H}}_3$, let $J_{23}\in {\mathscr {B}}({\mathcal {H}}_2,{\mathcal {H}}_3)$ and $J_{31}\in {\mathscr {B}}({\mathcal {H}}_3,{\mathcal {H}}_1)$, and assume that the strong limits

$$\begin{aligned}&W_\pm (U_3,U_2,J_{23}):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_3^{-n}J_{23}U_2^nP_\mathrm{ac}(U_2)\\&\quad \hbox {and}\quad W_\pm (U_1,U_3,J_{31}):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_1^{-n}J_{31}U_3^nP_\mathrm{ac}(U_3) \end{aligned}$$

exist. Then the strong limits

$$\begin{aligned} W_\pm (U_1,U_2,J_{31}J_{23}) :={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_1^{-n}J_{31}J_{23}U_2^nP_{\mathrm{ac}}(U_2) \end{aligned}$$

exist and satisfy the chain rule

$$\begin{aligned} W_\pm (U_1,U_2,J_{31}J_{23})=W_\pm (U_1,U_3,J_{31})\;\!W_\pm (U_3,U_2,J_{23}). \end{aligned}$$

Proof

For any $n\in {\mathbb {Z}}$, we have the identity

$$\begin{aligned} U_1^{-n}J_{31}J_{23}U_2^nP_{\mathrm{ac}}(U_2) =U_1^{-n}J_{31}U_3^n\big (P_{\mathrm{ac}}(U_3)+1-P_{\mathrm{ac}}(U_3)\big ) U_3^{-n}J_{23}U_2^nP_{\mathrm{ac}}(U_2).\nonumber \\ \end{aligned}$$

(4.1)

But due to the fact that $\big (1-P_\mathrm{ac}(U_3)\big )W_\pm (U_3,U_2,J_{23})=0$ (which can be shown as in the self-adjoint case, see [32, Eq. 2.1.18]), we have for any $\varphi _2\in {\mathcal {H}}_2$ that

$$\begin{aligned} \lim _{n\rightarrow \pm \infty }\big \Vert \big (1-P_\mathrm{ac}(U_3)\big )U_3^{-n}J_{23}U_2^n P_\mathrm{ac}(U_2)\varphi _2\big \Vert _{{\mathcal {H}}_3}=0. \end{aligned}$$

Therefore, we obtain that

$$\begin{aligned}&{{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_1^{-n}J_{31}J_{23}U_2^nP_{\mathrm{ac}}(U_2)\\&\quad ={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_1^{-n}J_{31}U_3^nP_{\mathrm{ac}}(U_3) U_3^{-n}J_{23}U_2^nP_{\mathrm{ac}}(U_2)\\&\quad ={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_1^{-n}J_{31}U_3^nP_{\mathrm{ac}}(U_3) \cdot {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_3^{-n}J_{23}U_2^nP_{\mathrm{ac}}(U_2)\\&\quad =W_\pm (U_1,U_3,J_{31})\;\!W_\pm (U_3,U_2,J_{23}), \end{aligned}$$

which proves the claims. $\square$

We can now present our theorem on the completeness of the wave operators $W_\pm (U,U_0,J)$. It is a unitary analogue of [23, Prop. 5.1] in the self-adjoint case.

Theorem 4.8

(Completeness of the wave operators). Suppose that the wave operators $W_\pm (U,U_0,J)$ exist and are partial isometries with initial set projections $P_0^\pm$. If there is $J'\in {\mathscr {B}}({\mathcal {H}},{\mathcal {H}}_0)$ such that

$$\begin{aligned} W_\pm (U_0,U,J') :={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_0^{-n}J'U^nP_{\mathrm{ac}}(U) \end{aligned}$$

(4.2)

exist and

$$\begin{aligned} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }(JJ'-1)U^nP_{\mathrm{ac}}(U)=0, \end{aligned}$$

(4.3)

then $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$. Conversely, if $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$ and there is $J'\in {\mathscr {B}}({\mathcal {H}},{\mathcal {H}}_0)$ such that

$$\begin{aligned} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }(J'J-1)U_0^nP_0^\pm =0, \end{aligned}$$

(4.4)

then $W_\pm (U_0,U,J')$ exist and (4.3) holds.

Proof

• (i) An application of Lemma 4.7 with $U_1=U_2=U$, $U_3=U_0$, ${\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {H}}$, ${\mathcal {H}}_3={\mathcal {H}}_0$, $J_{23}=J'$ and $J_{31}=J$ implies that the strong limits

  $$\begin{aligned} W_\pm (U,U,JJ') :={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}JJ'U^nP_{\mathrm{ac}}(U) \end{aligned}$$

  exist and satisfy the chain rule

  $$\begin{aligned} W_\pm (U,U,JJ')=W_\pm (U,U_0,J)\;\!W_\pm (U_0,U,J'). \end{aligned}$$

  (4.5)

  In consequence, the equality

  $$\begin{aligned} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }\big (U^{-n}JJ'U^nP_{\mathrm{ac}}(U)-P_\mathrm{ac}(U)\big )=0, \end{aligned}$$

  which follow from (4.3), implies that $W_\pm (U,U,JJ')P_{\mathrm{ac}}(U)=P_{\mathrm{ac}}(U)$. This, together with (4.5) and the equality $W_\pm (U_0,U,J')=W_\pm (U_0,U,J') P_{\mathrm{ac}}(U)$, gives

  $$\begin{aligned} W_\pm (U,U_0,J)W_\pm (U_0,U,J') =W_\pm (U,U,JJ')P_{\mathrm{ac}}(U) =P_\mathrm{ac}(U), \end{aligned}$$

  which is equivalent to

  $$\begin{aligned} W_\pm (U_0,U,J')^*W_\pm (U,U_0,J)^*=P_{\mathrm{ac}}(U). \end{aligned}$$

  This implies the inclusion $\ker \big (W_\pm (U,U_0,J)^*\big )\subset {\mathcal {H}}_{\mathrm{ac}}(U)^\perp$, which together with the fact that the range of a partial isometry is closed leads to the inclusion

  $$\begin{aligned} {\mathcal {H}}=\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )\oplus \ker \big (W_\pm (U,U_0,J)^*\big ) \subset {\mathcal {H}}_{\mathrm{ac}}(U)\oplus {\mathcal {H}}_{\mathrm{ac}}(U)^\perp ={\mathcal {H}}. \end{aligned}$$

  So, one must have $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$, which proves the first claim.

• (ii) For the converse, let $\varphi \in {\mathcal {H}}_{\mathrm{ac}}(U)$. Then we know from the assumption $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$ that there exist $\varphi _0^\pm \in P_0^\pm {\mathcal {H}}_0$ such that

  $$\begin{aligned} \lim _{n\rightarrow \pm \infty }\big \Vert U^n\varphi -JU_0^nP_0^\pm \varphi _0^\pm \big \Vert _{\mathcal {H}}=0. \end{aligned}$$

  (4.6)

  Together with (4.4), this implies that the norm

  $$\begin{aligned}&\big \Vert U_0^{-n}J'U^n\varphi -P_0^\pm \varphi _0^\pm \big \Vert _{{\mathcal {H}}_0}\\&\quad \le \big \Vert U_0^{-n}J' \big (U^n\varphi -JU_0^nP_0^\pm \varphi _0^\pm \big )\big \Vert _{{\mathcal {H}}_0} +\big \Vert U_0^{-n}J'JU_0^nP_0^\pm \varphi _0^\pm -P_0^\pm \varphi _0^\pm \big \Vert _{{\mathcal {H}}_0}\\&\quad \le \mathrm{Const.}\;\!\big \Vert U^n\varphi -JU_0^nP_0^\pm \varphi _0^\pm \big \Vert _{\mathcal {H}}+\big \Vert (J'J-1)U_0^nP_0^\pm \varphi _0^\pm \big \Vert _{{\mathcal {H}}_0} \end{aligned}$$

  converges to 0 as $n\rightarrow \pm \infty$, showing that the wave operators (4.2) exist.

  To show (4.3), we first observe that (4.4) gives

  $$\begin{aligned} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }(JJ'-1)JU_0^nP_0^\pm ={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }J(J'J-1)U_0^nP_0^\pm =0. \end{aligned}$$

  Together with (4.6), this implies that the norm

  $$\begin{aligned} \big \Vert (JJ'-1)U^n\varphi \big \Vert _{\mathcal {H}}&\le \big \Vert (JJ'-1)\big (U^n\varphi -JU_0^nP_0^\pm \varphi _0^\pm \big )\big \Vert _{\mathcal {H}}+\big \Vert (JJ'-1)JU_0^nP_0^\pm \varphi _0^\pm \big \Vert _{\mathcal {H}}\\&\le \mathrm{Const.}\;\!\big \Vert JU_0^nP_0^\pm \varphi _0^\pm -U^n\varphi \big \Vert _{\mathcal {H}}+\big \Vert (JJ'-1)JU_0^nP_0^\pm \varphi _0^\pm \big \Vert _{\mathcal {H}}\end{aligned}$$

  converges to 0 as $n\rightarrow \pm \infty$, showing (4.3).

$\square$

5 Quantum Walks on Homogenous Trees of Odd Degree

In this section, we use the theory of Sects. 2, 3 and 4 to determine spectral and scattering properties of a class of anisotropic quantum walks on homogenous trees of odd degree. We start by recalling from [13] the necessary material for the definition of the quantum walks.

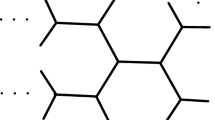
Let ${\mathcal {T}}$ be an homogenous tree of odd degree $d\ge 3$, that is, a finitely generated group ${\mathcal {T}}$ with generators $a_1,\dots ,a_d$, neutral element e and presentation

$$\begin{aligned} {\mathcal {T}}:=\big \langle a_1,\dots ,a_d\mid a_1^2=\dots =a_d^2=e\big \rangle . \end{aligned}$$

See Fig. 1 for an illustration in the case $d=3$, with progress away from e corresponding to multiplication from the right. Using the word length $|\cdot |:{\mathcal {T}}\rightarrow {\mathbb {N}}$ [9, Sec. 6.1], we can define for each $i=1,\dots ,d$ the ith main branch of ${\mathcal {T}}$, that is, the subtree

$$\begin{aligned} {\mathcal {T}}_i:=\big \{x\in {\mathcal {T}}\mid |a_ix|=|x|-1\big \}, \end{aligned}$$

and we can define the sets ${\mathcal {T}}_{\mathrm{e}}$ and ${\mathcal {T}}_{\mathrm{o}}$ of even or odd elements of ${\mathcal {T}}$

$$\begin{aligned} {\mathcal {T}}_{\mathrm{e}}:=\big \{x\in {\mathcal {T}}\mid |x|\in 2{\mathbb {N}}\big \} \quad \hbox {and}\quad {\mathcal {T}}_{\mathrm{o}}:=\big \{x\in {\mathcal {T}}\mid |x|\in 2{\mathbb {N}}+1\big \}. \end{aligned}$$

We write $\chi _{{\mathcal {B}}}$ for the characteristic function of a set ${{\mathcal {B}}}\subset {\mathcal {T}}$. So, $\chi _{{\mathcal {T}}_i}$, $\chi _{{\mathcal {T}}_\mathrm{e}}$, $\chi _{{\mathcal {T}}_{\mathrm{o}}}$ denote the characteristic functions of ${\mathcal {T}}_i$, ${\mathcal {T}}_{\mathrm{e}}$, ${\mathcal {T}}_{\mathrm{o}}$, respectively. We also use the shorthand notations

$$\begin{aligned} \chi _1:=\chi _{{\mathcal {T}}_1\cup \{e\}},\quad \chi _i:=\chi _{{\mathcal {T}}_i}~(i\ge 2),\quad \chi _{\mathrm{e}}:=\chi _{{\mathcal {T}}_\mathrm{e}},\quad \chi _{\mathrm{o}}:=\chi _{{\mathcal {T}}_{\mathrm{o}}}, \end{aligned}$$

which allow to write succinctly two partitions of unity of ${\mathcal {T}}:$

$$\begin{aligned} \sum _{k=1}^d\chi _k\equiv 1 \quad \hbox {and}\quad \chi _\mathrm{e}+\chi _{\mathrm{o}}\equiv 1. \end{aligned}$$

By letting $\ell ^2({\mathcal {T}})$ be the Hilbert space of square-summable functions ${\mathcal {T}}\rightarrow {\mathbb {C}}$ with scalar product

$$\begin{aligned} \langle f,g\rangle _{\ell ^2({\mathcal {T}})}:=\sum _{x\in {\mathcal {T}}}f(x)\overline{g(x)}, \quad f,g\in \ell ^2({\mathcal {T}}), \end{aligned}$$

and $\delta _x$ be the element of the canonical basis of $\ell ^2({\mathcal {T}})$ which sits at $x\in {\mathcal {T}}$ (i.e. $\delta _x(y):=\delta _{x,y}$ for $y\in {\mathcal {T}}$), we can decompose $\chi _1$ as $\chi _1=\chi _{{\mathcal {T}}_1}+\delta _e$.

For $i,j=1,\ldots ,d$, we define the right translation $R_i\in {\mathscr {B}}\big (\ell ^2({\mathcal {T}})\big )$ and the shift $S_{i,j}\in {\mathscr {B}}\big (\ell ^2({\mathcal {T}})\big )$ by

$$\begin{aligned} R_if:=f(\;\!\cdot \;\!a_i),\quad f\in \ell ^2({\mathcal {T}}), \end{aligned}$$

and

$$\begin{aligned} S_{i,j}:=\chi _{\mathrm{e}}R_i+\chi _{\mathrm{o}}R_j. \end{aligned}$$

The operators $R_i$ and $S_{i,j}$ are unitary and satisfy the relations $R_i^{-1}=R_i=S_{i,i}$ and $S_{i,j}^{-1}=S_{j,i}$. Let ${\mathcal {H}}:=\ell ^2({\mathcal {T}},{\mathbb {C}}^d)$ the Hilbert space of square-summable functions ${\mathcal {T}}\rightarrow {\mathbb {C}}^d$ with scalar product

$$\begin{aligned} \langle \varphi ,\psi \rangle _{\mathcal {H}}:=\sum _{x\in {\mathcal {T}}}\langle \varphi (x),\psi (x)\rangle _{{\mathbb {C}}^d}, \quad \varphi ,\psi \in {\mathcal {H}}. \end{aligned}$$

Then the evolution operator of the quantum walk that we consider is the product $U:=SC$ in ${\mathcal {H}}$, where S is the (diagonal unitary) shift operator given by

$$\begin{aligned} S:= \left( {\begin{matrix} S_{1+1,1+2} &{}&{}&{}\\ &{} S_{2+1,2+2} &{}&{} 0\\ 0 &{}&{} \ddots &{}\\ &{}&{}&{} S_{d+1,d+2}\\ \end{matrix}}\right) \quad \hbox {with}\quad S_{d,d+1}:=S_{d,1},~S_{d+1,d+2}:=S_{1,2}, \end{aligned}$$

and C the (unitary) coin operator given by

$$\begin{aligned} (C\varphi )(x):=C(x)\varphi (x),\quad \varphi \in {\mathcal {H}},~x\in {\mathcal {T}},~C(x)\in \mathrm U(d). \end{aligned}$$

We assume that the coin operator C has an anisotropic behaviour at infinity; it converges with short-range rate to d asymptotic coin operators, one on each main branch of ${\mathcal {T}}$, in the following way:

Assumption 5.1

(Short-range). For each $i=1,\ldots ,d$, there exist a diagonal matrix $C_i\in \mathrm U(d)$ and a scalar $\varepsilon _i>0$ such that

$$\begin{aligned} \big \Vert C(x)-C_i\big \Vert _{{\mathscr {B}}({\mathbb {C}}^d)}\le \mathrm{Const.}\;\!\langle x\rangle ^{-(1+\varepsilon _i)} \quad \hbox {if }x\in {\mathcal {T}}_i. \end{aligned}$$

This assumption provides d new evolution operators $U_i:=SC_i$ describing the asymptotic behaviour of U on each main branch ${\mathcal {T}}_i$. It also suggests to define the free evolution operator as the direct sum operator

$$\begin{aligned} U_0:=\bigoplus _{k=1}^dU_k\quad \hbox {in}\quad {\mathcal {H}}_0:=\bigoplus _{k=1}^d{\mathcal {H}}, \end{aligned}$$

and to define the identification operator $J\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ as

$$\begin{aligned} J\;\!\Phi :=\sum _{k=1}^d\chi _k\;\!\varphi _k, \quad \Phi =(\varphi _1,\dots ,\varphi _d)\in {\mathcal {H}}_0. \end{aligned}$$

Using the same notation for functions and the corresponding multiplication operators in ${\mathcal {H}}$, we directly get:

Lemma 5.2

. The adjoint $J^*\in {\mathscr {B}}({\mathcal {H}},{\mathcal {H}}_0)$ is given by

$$\begin{aligned} J^*\varphi =\big (\chi _1\;\!\varphi ,\dots ,\chi _d\;\!\varphi \big ), \quad \varphi \in {\mathcal {H}}, \end{aligned}$$

and satisfies the relations $J^*J=\bigoplus _{k=1}^d\chi _k$ and $JJ^*=1_{\mathcal {H}}$.

Remark 5.3

Choosing $U_0$ as a free evolution operator for U is not the only possibility. Like for other quantum systems with discrete- or continuous-time variable, several choices are possible for the free evolution operator. We will discuss some of them in Sect. 5.3.

5.1 Free Evolution Operator

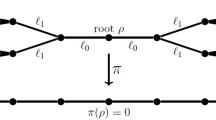
In this section, we construct a conjugate operator for the free evolution operator $U_0$ and determine the spectral properties of $U_0$. For this, one first needs to construct a conjugate operator for the shifts $S_{i,j}$ ($i\ne j$). Following the intuition provided by classical mechanics [28, Sec. 1.1], the approach we use is to define the conjugate operator for $S_{i,j}$ as an operator of the form $S_{i,j}^{-1}[X^2,S_{i,j}]$, where X is an appropriate position observable in $\ell ^2({\mathcal {T}})$ growing along the discrete flow generated by $S_{i,j}$. A natural candidate for X is the operator of multiplication by the word length $|\cdot |$. However, the fact that in general $|\cdot |$ does not take the value 0 on the support of the iterates $S_{i,j}^nf$ ($n\in {\mathbb {Z}},f\in \ell ^2({\mathcal {T}})$) generates technical difficulties. See Fig. 2 for an example where $d=3$, $(i,j)=(1,2)$, $f=\delta _{a_3}$, and the minimum value taken by $|\cdot |$ on the support of the iterates is 1. To correct this issue, one has to use modifications of the word length consisting in $|\cdot |$ composed with a translation making the support of the iterates $S_{i,j}^nf$ pass by the neutral element. (In Fig. 2, this would be the translation by $a_3$.) For each $i\ne j$, the modified word length is defined as

$$\begin{aligned} |\cdot |_{i,j}:{\mathcal {T}}\rightarrow {\mathbb {N}},~~x\mapsto |x|_{i,j}:=\big |x_{i,j}^{-1}x\big |, \end{aligned}$$

where $x_{i,j}$ is the longest word in the reduced representation of x, starting from the left and ending with a letter different from $a_i$ or $a_j$. For instance, if $x=a_1a_2a_3a_2$, then $x_{1,2}=a_1a_2a_3$, and if $x=a_1a_2a_1a_2$, then $x_{1,2}=e$.

Fig. 2

Support of the iterates $S_{12}^n\delta _{a_3}$ ($n\in {\mathbb {Z}}$) when $d=3$

Using these modified word lengths, we can now construct the conjugate operator for $S_{i,j}$. We write $C_{\mathrm{c}}({\mathcal {T}})$ for the set of functions ${\mathcal {T}}\rightarrow {\mathbb {C}}$ with compact support.

Lemma 5.4

(Conjugate operator for $S_{i,j}$). Take $i\ne j$. Then the operator

$$\begin{aligned} A_{i,j}f :=S_{i,j}^{-1}\big [|\cdot |_{i,j}^2,S_{i,j}\big ]f =\big (\chi _{\mathrm{e}}\;\!|\cdot a_j|_{i,j}^2+\chi _{\mathrm{o}}\;\!|\cdot a_i|_{i,j}^2 -|\cdot |_{i,j}^2\big )f,\quad f\in C_{\mathrm{c}}({\mathcal {T}}),\nonumber \\ \end{aligned}$$

(5.1)

is essentially self-adjoint in $\ell ^2({\mathcal {T}})$, with closure also denoted by $A_{i,j}$. Furthermore, one has $S_{i,j}\in C^\infty (A_{i,j})$ with

$$\begin{aligned} S_{i,j}^{-1}[A_{i,j},S_{i,j}]=2\cdot 1_{\ell ^2({\mathcal {T}})}. \end{aligned}$$

Proof

• (i) The equality

  $$\begin{aligned} S_{i,j}^{-1}\big [|\cdot |_{i,j}^2,S_{i,j}\big ]f =\big (\chi _\mathrm{e}\;\!|\cdot a_j|_{i,j}^2+\chi _{\mathrm{o}}\;\!|\cdot a_i|_{i,j}^2 -|\cdot |_{i,j}^2\big )f,\quad f\in C_{\mathrm{c}}({\mathcal {T}}), \end{aligned}$$

  follows from a direct calculation, and the essential self-adjointness of $A_{i,j}$ follows from the fact that multiplication operators are essentially self-adjoint on the set of functions with compact support [20, Ex. 5.1.15]. Now, further calculations give

  $$\begin{aligned}&S_{i,j}^{-1}[A_{i,j},S_{i,j}]f \nonumber \\&\quad =\big \{\chi _{\mathrm{e}}\big (|\cdot a_ja_i|_{i,j}^2-2|\cdot a_j|_{i,j}^2\\&\qquad +|\cdot |_{i,j}^2\big ) +\chi _\mathrm{o}\big (|\cdot a_ia_j|_{i,j}^2-2|\cdot a_i|_{i,j}^2+|\cdot |_{i,j}^2\big )\big \}f, \end{aligned}$$

  and in point (ii), we show that

  $$\begin{aligned}&\chi _\mathrm{e}(x)\big (|xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2\big )\nonumber \\&\quad +\chi _\mathrm{o}(x)\big (|xa_ia_j|_{i,j}^2-2|xa_i|_{i,j}^2+|x|_{i,j}^2\big )=2 \quad \hbox {for all }x\in {\mathcal {T}}. \end{aligned}$$

  (5.2)

  Therefore, it follows that $S_{i,j}^{-1}[A_{i,j},S_{i,j}]=2\cdot 1_{\ell ^2({\mathcal {T}})}$ on $C_\mathrm{c}({\mathcal {T}})$, and since $C_{\mathrm{c}}({\mathcal {T}})$ is a core for $A_{i,j}$ this implies that $S_{i,j}\in C^\infty (A_{i,j})$ with $S_{i,j}^{-1}[A_{i,j}, S_{i,j}]=2\cdot 1_{\ell ^2({\mathcal {T}})}$.

• (ii) To prove (5.2) it is sufficient to show that

  $$\begin{aligned}&|xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2=2\hbox { if } x\in {\mathcal {T}}_{\mathrm{e}} \\&\hbox {and}\quad |xa_ia_j|_{i,j}^2-2|xa_i|_{i,j}^2 +|x|_{i,j}^2=2\hbox { if } x\in {\mathcal {T}}_{\mathrm{o}}. \end{aligned}$$

  We only give the proof of the first identity, since the second one is similar. If $|x|_{i,j}=0$, then $x_{i,j}^{-1}x=e$ and

  $$\begin{aligned} |xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2 =|a_ja_i|^2-2|a_j|^2+0^2 =2. \end{aligned}$$

  If $|x|_{i,j}=1$, then $x_{i,j}^{-1}x=a_i$ or $x_{i,j}^{-1}x=a_j$. In the first case, we get

  $$\begin{aligned} |xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2 =|a_ia_ja_i|^2-2|a_ia_j|^2+1^2 =2, \end{aligned}$$

  and in the second case, we get

  $$\begin{aligned} |xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2 =|a_i|^2-2|e|^2+1^2 =2. \end{aligned}$$

  Finally, if $|x|_{i,j}\ge 2$, then $|xa_j|_{i,j}=|x|_{i,j}+1$ or $|xa_j|_{i,j}=|x|_{i,j}-1$. In the first case, we get $|xa_ja_i|_{i,j}=|x|_{i,j}+2$ and

  $$\begin{aligned} |xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2 =(|x|_{i,j}+2)^2-2(|x|_{i,j}+1)^2+|x|_{i,j}^2 =2, \end{aligned}$$

  and in the second case, we get $|xa_ja_i|_{i,j}=|x|_{i,j}-2$ and

  $$\begin{aligned} |xa_ja_i|_{i,j}^2-2|xa_j|_{i,j}^2+|x|_{i,j}^2 =(|x|_{i,j}-2)^2-2(|x|_{i,j}-1)^2+|x|_{i,j}^2 =2. \end{aligned}$$

  Note that we cannot have $|xa_ja_i|_{i,j}=|x|_{i,j}$ due to the very definition of $|\cdot |_{i,j}$.

$\square$

Using the operators $A_{i,j}$, we can construct a conjugate operator for operators ${{\widetilde{U}}}_0:=SC_0$, where $C_0$ is a diagonal coin operator

$$\begin{aligned} (C_0\varphi )(x):=C_0(x)\varphi (x), \quad \varphi \in {\mathcal {H}}, x\in {\mathcal {T}}, C_0(x)\in \mathrm U(d) \hbox { and diagonal.} \end{aligned}$$

We use the notation $C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d)$ for the set of functions ${\mathcal {T}}\rightarrow {\mathbb {C}}^d$ with compact support and we set $A_{d,d+1}:=A_{d,1}$ and $A_{d+1,d+2}:=A_{1,2}$.

Lemma 5.5

(Conjugate operator for ${{\widetilde{U}}}_0$) The operator

$$\begin{aligned} {{\widetilde{A}}}\;\!\varphi :=\left( {\begin{matrix} A_{1+1,1+2} &{}&{}&{}\\ &{} A_{2+1,2+2} &{}&{} 0\\ 0 &{}&{} \ddots &{}\\ &{}&{}&{} A_{d+1,d+2}\\ \end{matrix}}\right) \varphi , \quad \varphi \in C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d), \end{aligned}$$

is essentially self-adjoint in ${\mathcal {H}}$, with closure also denoted by ${{\widetilde{A}}}$. Furthermore, one has ${{\widetilde{U}}}_0\in C^\infty ({{\widetilde{A}}})$ with

$$\begin{aligned} {{\widetilde{U}}}_0^{-1}[{{\widetilde{A}}},{{\widetilde{U}}}_0]=2\cdot 1_{\mathcal {H}}. \end{aligned}$$

Proof

The essential self-adjointness of ${{\widetilde{A}}}$ on $C_\mathrm{c}({\mathcal {T}},{\mathbb {C}}^d)\subset {\mathcal {H}}$ follows from the isomorphism ${\mathcal {H}}\simeq \bigoplus _{k=1}^d\ell ^2({\mathcal {T}})$ and the fact that the operators $A_{i,j}$ are essentially self-adjoint on $C_\mathrm{c}({\mathcal {T}})\subset \ell ^2({\mathcal {T}})$. Using the same isomorphism, Lemma 5.4 and the relation $[{{\widetilde{A}}},C_0]=0$, one obtains that ${{\widetilde{U}}}_0\in C^\infty ({{\widetilde{A}}})$ with

$$\begin{aligned} {{\widetilde{U}}}_0^{-1}[{{\widetilde{A}}},{{\widetilde{U}}}_0] =C_0^{-1}\big (S^{-1}[{{\widetilde{A}}},S]\big )C_0 =C_0^{-1}(2\cdot 1_{\mathcal {H}})C_0 =2\cdot 1_{\mathcal {H}}. \end{aligned}$$

$\square$

Lemma 5.5, Theorem 2.3 and Remark 2.4(a) imply that ${{\widetilde{U}}}_0$ has purely absolutely continuous spectrum. But more can be said. Since ${{\widetilde{A}}}$ is essentially self-adjoint on $C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d)$, the identity ${{\widetilde{U}}}_0^{-1}[{{\widetilde{A}}},{{\widetilde{U}}}_0]=2\cdot 1_{\mathcal {H}}$ implies that ${{\widetilde{U}}}_0^{-1}{{\widetilde{A}}}\;\!\widetilde{U}_0={{\widetilde{A}}}+2\cdot 1_{\mathcal {H}}$. Using this relation and functional calculus, we obtain for any $s\in {\mathbb {R}}$ and $\gamma \in C({\mathbb {S}}^1)$ that

$$\begin{aligned} \mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{A}}}}\gamma ({{\widetilde{U}}}_0)\mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}} =\gamma \big ({{\widetilde{U}}}_0\mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{U}}}_0^{-1}\widetilde{A}\;\!{{\widetilde{U}}}_0} \mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}}\big ) =\gamma \big ({{\widetilde{U}}}_0\mathop {\mathrm {e}}\nolimits ^{is(\widetilde{A}+2\cdot 1_{\mathcal {H}})}\mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}}\big ) =\gamma (\mathop {\mathrm {e}}\nolimits ^{2is}\widetilde{U}_0).\nonumber \\ \end{aligned}$$

(5.3)

The relation $\mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{A}}}}\gamma (\widetilde{U}_0)\mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}} =\gamma (\mathop {\mathrm {e}}\nolimits ^{2is}{{\widetilde{U}}}_0)$ and Mackey’s imprimitivity theorem [19, Thm. 5] applied to the group ${\mathbb {R}}$ and the subgroup ${\mathbb {Z}}$ imply the existence of a continuous unitary representation $\sigma$ of ${\mathbb {Z}}$ in a Hilbert space ${\mathfrak {h}}_\sigma$ achieving the following: Let $F_\sigma$ be the set of functions $f_\sigma :{\mathbb {R}}\rightarrow {\mathfrak {h}}_\sigma$ such that

• (i) $f_\sigma (n+s)=\sigma (n)f_\sigma (s)$ for all $n\in {\mathbb {Z}}$ and $s\in {\mathbb {R}}$,

• (ii) $\Vert f_\sigma (\;\!\cdot \;\!)\Vert _{{\mathfrak {h}}_\sigma }\in \mathop {\mathrm {L}^2_{\mathrm{loc}}}\nolimits ({\mathbb {R}})$,

• (iii) $f_\sigma$ is strongly measurable,

let $\langle \cdot ,\cdot \rangle _{{\mathcal {H}}_\sigma }$ and $\Vert \cdot \Vert _{{\mathcal {H}}_\sigma }$ be the scalar product and norm on $F_\sigma$ given by

$$\begin{aligned} \langle f_\sigma ,g_\sigma \rangle _{{\mathcal {H}}_\sigma } :=\int _0^1\mathrm {d}s\,\langle f_\sigma (s),g_\sigma (s)\rangle _{{\mathfrak {h}}_\sigma } \quad \hbox {and}\quad \Vert f_\sigma \Vert _{{\mathcal {H}}_\sigma }:=\sqrt{\langle f_\sigma ,f_\sigma \rangle _{{\mathcal {H}}_\sigma }}, \quad f_\sigma ,g_\sigma \in F_\sigma , \end{aligned}$$

and let ${\mathcal {H}}_\sigma$ be the Hilbert space completion of $F_\sigma$ for the norm $\Vert \cdot \Vert _{{\mathcal {H}}_\sigma }$, that is,

$$\begin{aligned} {\mathcal {H}}_\sigma :=\{f_\sigma \in F_\sigma \mid \Vert f_\sigma \Vert _{{\mathcal {H}}_\sigma }<\infty \} /\{f_\sigma \in F_\sigma \mid \Vert f_\sigma \Vert _{{\mathcal {H}}_\sigma }=0\}. \end{aligned}$$

Then there exists a unitary operator ${\mathscr {U}}:{\mathcal {H}}\rightarrow {\mathcal {H}}_\sigma$ satisfying for each $s\in {\mathbb {R}}$ and $\gamma \in C({\mathbb {S}}^1)$

$$\begin{aligned} {\mathscr {U}}\mathop {\mathrm {e}}\nolimits ^{\pi is{{\widetilde{A}}}}{\mathscr {U}}^{-1}=U_\sigma (s) \quad \hbox {and}\quad {\mathscr {U}}\gamma ({{\widetilde{U}}}_0){\mathscr {U}}^{-1}=P_\sigma (\gamma ), \end{aligned}$$

with $U_\sigma$ the induced continuous unitary representation of $\sigma$ from ${\mathbb {Z}}$ to ${\mathbb {R}}$ given by

$$\begin{aligned} \big (U_\sigma (s)f_\sigma \big )(t):=f_\sigma (t+s),\quad s,t\in {\mathbb {R}},~f_\sigma \in {\mathcal {H}}_\sigma , \end{aligned}$$

and $P_\sigma$ given by

$$\begin{aligned} \big (P_\sigma (\gamma )f_\sigma \big )(s):=\gamma (\mathop {\mathrm {e}}\nolimits ^{2\pi is})f_\sigma (s), \quad s\in {\mathbb {R}},~f_\sigma \in {\mathcal {H}}_\sigma ,~\gamma \in C({\mathbb {S}}^1). \end{aligned}$$

Therefore, the operator ${{\widetilde{U}}}_0$ is unitarily equivalent to a multiplication operator with purely absolutely continuous spectrum covering the whole unit circle ${\mathbb {S}}^1$. See [13, Sec. 2.1] for a similar result in the case $C_0=1_{\mathcal {H}}$ obtained by using the matrix representation of S in the canonical basis of ${\mathcal {H}}$. See also [6, 24, 29] for more general results on spectral properties of unitary representations satisfying commutation relations similar to (5.3).

Using what precedes, we can finally construct a conjugate operator for $U_0$ and determine its spectral properties:

Proposition 5.6

(Spectral properties of $U_0$). Let

$$\begin{aligned} A_0\Phi :=\left( \bigoplus _{k=1}^d{{\widetilde{A}}}\right) \Phi , \quad \Phi \in \bigoplus _{k=1}^dC_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d). \end{aligned}$$

• (a) $A_0$ is essentially self-adjoint in ${\mathcal {H}}_0$, with closure also denoted by $A_0$.

• (b) $U_0\in C^\infty (A_0)$ with $U_0^{-1}[A_0,U_0]=2\cdot 1_{{\mathcal {H}}_0}$, and $U_0$ satisfies the imprimitivity relation

  $$\begin{aligned} \mathop {\mathrm {e}}\nolimits ^{isA_0}\gamma (U_0)\mathop {\mathrm {e}}\nolimits ^{-isA_0}=\gamma (\mathop {\mathrm {e}}\nolimits ^{2is}U_0),\quad s\in {\mathbb {R}},~\gamma \in C({\mathbb {S}}^1). \end{aligned}$$

• (c) $U_0$ is unitarily equivalent to a multiplication operator with purely absolutely continuous spectrum

  $$\begin{aligned} \sigma (U_0)=\sigma _{\mathrm{ac}}(U_0)={\mathbb {S}}^1. \end{aligned}$$

Proof

Point (a) follows from Lemma 5.5 and the fact that direct sums of essentially self-adjoint operators are essentially self-adjoint. For point (b), using Lemma 5.5 with ${{\widetilde{U}}}_0=SC_k$ ($k=1,\ldots ,d$), we get the equalities

$$\begin{aligned} U_0^{-1}[A_0,U_0] =\bigoplus _{k=1}^d(SC_k)^{-1}[{{\widetilde{A}}},SC_k] =\bigoplus _{k=1}^d(2\cdot 1_{\mathcal {H}}) =2\cdot 1_{{\mathcal {H}}_0}. \end{aligned}$$

This implies that $U_0\in C^\infty (A_0)$ with $U_0^{-1}[A_0,U_0]=2\cdot 1_{{\mathcal {H}}_0}$, and thus the imprimitivity relation

$$\begin{aligned} \mathop {\mathrm {e}}\nolimits ^{isA_0}\gamma (U_0)\mathop {\mathrm {e}}\nolimits ^{-isA_0}=\gamma (\mathop {\mathrm {e}}\nolimits ^{2is}U_0),\quad s\in {\mathbb {R}},~\gamma \in C({\mathbb {S}}^1). \end{aligned}$$

Finally, using this relation and Mackey’s imprimitivity theorem, one can show point (c) as in the paragraph preceding this proposition. $\square$

5.2 Full Evolution Operator

In this section, we use the theory of Sect. 3 to construct a conjugate operator A for the full evolution operator U starting from the conjugate operator $A_0$ for $U_0$. As a by-product, we obtain a class of locally U-smooth operators and determine spectral properties of U.

We start by showing that the perturbation $V=JU_0-UJ$ is trace class:

Lemma 5.7

The perturbation V factorises as $V=G^*G_0$, with $G_0\in S_2({\mathcal {H}}_0)$ and $G\in S_2({\mathcal {H}},{\mathcal {H}}_0)$. In particular, V is trace class.

Proof

A direct calculation gives for $\Phi =(\varphi _1,\dots ,\varphi _d)\in {\mathcal {H}}_0$

$$\begin{aligned} V\Phi =\sum _{k=1}^d\big (\chi _kSC_k-SC\chi _k\big )\varphi _k =\sum _{k=1}^d\big (S(C_k-C)\chi _k+[\chi _k,S]C_k\big )\varphi _k =G^*G_0\Phi \end{aligned}$$

where

$$\begin{aligned} G_0:=\bigoplus _{k=1}^d\langle \cdot \rangle ^{-(1+\varepsilon _k)/2} \end{aligned}$$

and

$$\begin{aligned} G^*:=DG_0\quad \hbox {with}\quad D\Phi :=\sum _{k=1}^d\big (S(C_k-C)\chi _k+[\chi _k,S]C_k\big ) \langle \cdot \rangle ^{1+\varepsilon _k}\varphi _k. \end{aligned}$$

Therefore, it is sufficient to show that $G_0\in S_2({\mathcal {H}}_0)$ and $D\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$ to prove the claim.

To show that $G_0\in S_2({\mathcal {H}}_0)$, it is sufficient to prove that $\langle \cdot \rangle ^{-s}\in S_2({\mathcal {H}})$ for $s>1/2$ since $\tfrac{1+\varepsilon _k}{2}>1/2$ for each $k=1,\ldots ,d$. Let $(e_i)_{i=1}^d$ be the standard basis of ${\mathbb {C}}^d$. Then the family $(\delta _x\otimes e_i)_{x\in {\mathcal {T}},\,i=1,\ldots ,d}$ is an orthonormal basis of ${\mathcal {H}}$, and a direct calculation gives

$$\begin{aligned} \big \Vert \langle \cdot \rangle ^{-s}\big \Vert _{S_2({\mathcal {H}})}^2 =\sum _{x\in {\mathcal {T}},\,i=1,\ldots ,d} \big \Vert \langle \cdot \rangle ^{-s}(\delta _x\otimes e_i)\big \Vert _{\mathcal {H}}^2 =d\sum _{x\in {\mathcal {T}}}\langle x\rangle ^{-2s} <\infty . \end{aligned}$$

To show that $D\in {\mathscr {B}}({\mathcal {H}}_0,{\mathcal {H}})$, it is sufficient to prove the inclusions $S(C_k-C)\chi _k\langle \cdot \rangle ^{1+\varepsilon _k}\in {\mathscr {B}}({\mathcal {H}})$ and $[\chi _k,S]C_k\langle \cdot \rangle ^{1+\varepsilon _k}\in {\mathscr {B}}({\mathcal {H}})$ for $k=1,\ldots ,d$. The first inclusion follows directly from Assumption 5.1. For the second inclusion, we note that

$$\begin{aligned}&[\chi _k,S]C_k\langle \cdot \rangle ^{1+\varepsilon _k}\nonumber \\&\qquad =S \left( {\begin{matrix} S_{1+1,1+2}^{-1}[\chi _k,S_{1+1,1+2}] &{}&{}&{}\\ &{} S_{2+1,2+2}^{-1}[\chi _k,S_{2+1,2+2}] &{}&{} 0\\ 0 &{}&{} \ddots &{}\\ &{}&{}&{} S_{d+1,d+2}^{-1}[\chi _k,S_{d+1,d+2}]\\ \end{matrix}}\right) \nonumber \\&\qquad \quad C_k\langle \cdot \rangle ^{1+\varepsilon _k} \end{aligned}$$

with

$$\begin{aligned} S_{i,j}^{-1}[\chi _k,S_{i,j}]&=\chi _{\mathrm{e}}\chi _k(\;\!\cdot \;\!a_j)+\chi _{\mathrm{o}}\chi _k(\;\!\cdot \;\!a_i)-\chi _k\\&=\chi _{\mathrm{e}}\big (\chi _{{\mathcal {T}}_k\cdot a_j}+\delta _{k,1}\delta _{a_j}-\chi _{{\mathcal {T}}_k}\big ) +\chi _\mathrm{o}\big (\chi _{{\mathcal {T}}_k\cdot a_i}+\delta _{k,1}\delta _{a_i}-\chi _{{\mathcal {T}}_k}\big ). \end{aligned}$$

But $\chi _{{\mathcal {T}}_k\cdot a_j}=\chi _{{\mathcal {T}}_k}+\delta _e-\delta _{a_k}$ if $j=k$ and $\chi _{{\mathcal {T}}_k\cdot a_j}=\chi _{{\mathcal {T}}_k}$ if $j\ne k$. Therefore,

$$\begin{aligned} S_{i,j}^{-1}[\chi _k,S_{i,j}]&=\chi _\mathrm{e}\big (\delta _{j,k}(\delta _e-\delta _{a_k})+\delta _{k,1}\delta _{a_j}\big ) +\chi _{\mathrm{o}}\big (\delta _{i,k}(\delta _e-\delta _{a_k})+\delta _{k,1}\delta _{a_i}\big )\\&=\delta _{j,k}\delta _e-\delta _{i,k}\delta _{a_k}+\delta _{k,1}\delta _{a_i}\\&=S_{i,j}^{-1}[\chi _k,S_{i,j}]\;\!\chi _{\{e,a_1,\dots ,a_d\}} \end{aligned}$$

and thus

$$\begin{aligned}{}[\chi _k,S]C_k\langle \cdot \rangle ^{1+\varepsilon _k} =[\chi _k,S]C_k\langle \cdot \rangle ^{1+\varepsilon _k}\chi _{\{e,a_1,\dots ,a_d\}} \in {\mathscr {B}}({\mathcal {H}}), \end{aligned}$$

which concludes the proof. $\square$

Next, we show that the assumption (iv) of Theorem 3.8 is satisfied.

Lemma 5.8

One has $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$.

Proof

Take $\Phi =(\varphi _1,\dots ,\varphi _d)\in {\mathcal {D}}(A_0)$. Then it follows from the proof of Lemma 5.7 that

$$\begin{aligned} VA_0\Phi =\sum _{k=1}^d\big (S(C_k-C)\chi _k\widetilde{A}+F_k\big )\varphi _k, \end{aligned}$$

with $F_k:=[\chi _k,S]C_k\chi _{\{e,a_1,\dots ,a_d\}}{{\widetilde{A}}}$ a finite rank operator. In addition, we have

$$\begin{aligned} S(C_k-C)\chi _k{{\widetilde{A}}}\;\!\varphi _k =S(C_k-C)\chi _k\langle \cdot \rangle ^{1+\varepsilon _k} \langle \cdot \rangle ^{-\varepsilon _k} \widetilde{A}\;\!\langle \cdot \rangle ^{-1}\varphi _k \end{aligned}$$

with $S(C_k-C)\chi _k\langle \cdot \rangle ^{1+\varepsilon _k}$ bounded, $\langle \cdot \rangle ^{-\varepsilon _k}$ in the Schatten class $S_\rho ({\mathcal {H}})$ for any $\rho >1/\varepsilon _k$, and $\widetilde{A}\langle \cdot \rangle ^{-1}$ bounded. Indeed, the operator $S(C_k-C)\chi _k\langle \cdot \rangle ^{1+\varepsilon _k}$ is bounded due to Assumption 5.1, the operator $\langle \cdot \rangle ^{-\varepsilon _k}$ belongs to $S_\rho ({\mathcal {H}})$ because

$$\begin{aligned} \big \Vert \langle \cdot \rangle ^{-\varepsilon _k}\big \Vert _{S_\rho ({\mathcal {H}})}^\rho =\sum \limits _{x\in {\mathcal {T}},\,i=1,\ldots ,d}\big \langle \langle \cdot \rangle ^{-\rho \varepsilon _k} (\delta _x\otimes e_i),(\delta _x\otimes e_i)\big \rangle _{\mathcal {H}}=d\sum \limits _{x\in {\mathcal {T}}}\langle x\rangle ^{-\rho \varepsilon _k} <\infty , \end{aligned}$$

and the operator ${{\widetilde{A}}}\langle \cdot \rangle ^{-1}$ is bounded because

$$\begin{aligned} {{\widetilde{A}}}\;\!\langle \cdot \rangle ^{-1} =\left( {\begin{matrix} A_{1+1,1+2}\langle \cdot \rangle ^{-1} &{}&{}&{}\\ &{} A_{2+1,2+2}\langle \cdot \rangle ^{-1} &{}&{} 0\\ 0 &{}&{} \ddots &{}\\ &{}&{}&{} A_{d+1,d+2}\langle \cdot \rangle ^{-1}\\ \end{matrix}}\right) \end{aligned}$$

with

$$\begin{aligned} A_{i,j}\langle \cdot \rangle ^{-1} =\big (\chi _{\mathrm{e}}\;\!|\cdot a_j|_{i,j}^2+\chi _{\mathrm{o}}\;\!|\cdot a_i|_{i,j}^2-|\cdot |_{i,j}^2\big ) \langle \cdot \rangle ^{-1}\in \mathop {\mathrm {L}^\infty }\nolimits ({\mathcal {T}}). \end{aligned}$$

(This last inclusion can be verified as in point (ii) of the proof of Lemma 5.4.) It follows that

$$\begin{aligned} VA_0\Phi =\sum _{k=1}^d(K_k+F_k)\varphi _k, \end{aligned}$$

with $K_k\in S_\rho ({\mathcal {H}})$ and $F_k$ of finite rank. This implies that $\overline{VA_0\upharpoonright {\mathcal {D}}(A_0)}\in {\mathscr {K}}({\mathcal {H}}_0,{\mathcal {H}})$. $\square$

We now define the conjugate operator A for U as in Sect. 3.1 and observe that in our case it coincides with the operator ${{\widetilde{A}}}$ of Lemma 5.5:

Lemma 5.9

(Conjugate operator for U). The operator

$$\begin{aligned} A\;\!\varphi :=JA_0J^*\varphi , \quad \varphi \in C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d), \end{aligned}$$

is essentially self-adjoint in ${\mathcal {H}}$, with closure (also denoted by A) equal to ${{\widetilde{A}}}$.

Proof

Let $\varphi \in C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d)$. Then the identity $\sum _{k=1}^d\chi _k^2\equiv 1$ and the fact that diagonal multiplication operators mutually commute imply that

$$\begin{aligned} A\;\!\varphi =\mathop {\textstyle \sum }\limits _{k=1}^d\chi _k{{\widetilde{A}}}\;\!\chi _k\varphi ={{\widetilde{A}}}\;\!\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _k^2\right) \varphi =\widetilde{A}\;\!\varphi . \end{aligned}$$

Since $C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d)$ is a core for ${{\widetilde{A}}}$, it follows that A is essentially self-adjoint in ${\mathcal {H}}$, with closure equal to ${{\widetilde{A}}}$. $\square$

By combining the results that precede, we can now establish a Mourre estimate for U.

Proposition 5.10

(Mourre estimate for U). One has $U\in C^1(A)$ and ${{\widetilde{\varrho }}}_U^A(\theta )\ge 2$ for all $\theta \in {\mathbb {S}}^1$.

Proof

Theorem 3.8 applies since its assumptions are verified in Proposition 5.6(b) and Lemmas 5.2, 5.7, 5.8, and 5.9. Furthermore, Lemma 2.1(c) and Proposition 5.6(b) imply that ${{\widetilde{\varrho }}}_{U_0}^{A_0}(\theta )\ge \varrho _{U_0}^{A_0}(\theta )=2$ for all $\theta \in {\mathbb {S}}^1$. Thus, $U\in C^1(A)$ and ${{\widetilde{\varrho }}}_U^A(\theta )\ge {{\widetilde{\varrho }}}_{U_0}^{A_0}(\theta )\ge 2$ for all $\theta \in {\mathbb {S}}^1$. $\square$

To infer results for U from the Mourre estimate of Proposition 5.10, one needs to verify a slightly stronger regularity condition than $U\in C^1(A):$

Lemma 5.11

One has $U\in C^{1+\varepsilon }(A)$ for each $\varepsilon \in (0,1)$ with $\varepsilon \le \min \{\varepsilon _1,\dots ,\varepsilon _d\}$.

Proof

We know from Proposition 5.10 that $U\in C^1(A)$. To go further and prove that $U\in C^{1+\varepsilon }(A)$, we need to show that

$$\begin{aligned} \big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}[A,U]\mathop {\mathrm {e}}\nolimits ^{itA}-[A,U]\big \Vert _{{\mathscr {B}}({\mathcal {H}})} \le \mathrm{Const.}\;\!t^\varepsilon \quad \hbox {for all }t\in (0,1). \end{aligned}$$

Using the relations $S^{-1}[{{\widetilde{A}}},S]=2\cdot 1_{\mathcal {H}}$ and $\sum _{k=1}^d\chi _k\equiv 1$, we get for $\varphi \in C_\mathrm{c}({\mathcal {T}},{\mathbb {C}}^d)$

$$\begin{aligned}{}[A,U]\varphi =[{{\widetilde{A}}},SC]\varphi =\big ([\widetilde{A},S]C+S[{{\widetilde{A}}},C]\big )\varphi =\left( 2U+\mathop {\textstyle \sum }\limits _{k=1}^dS[{{\widetilde{A}}},C\chi _k]\right) \varphi . \end{aligned}$$

For the second term, we get

$$\begin{aligned} S[{{\widetilde{A}}},C\chi _k]\varphi =S[{{\widetilde{A}}},(C-C_k)\chi _k]\varphi =S[\widetilde{A}\;\!\langle \cdot \rangle ^{-1},\langle \cdot \rangle (C-C_k)\chi _k]\varphi \end{aligned}$$

where $S\in C^1(A)$ with $[A,S]=S\big (S^{-1}[\widetilde{A},S]\big )=2S$ and

$$\begin{aligned} D_k:=[{{\widetilde{A}}}\;\!\langle \cdot \rangle ^{-1}, \langle \cdot \rangle (C-C_k)\chi _k]\in {\mathscr {B}}({\mathcal {H}}) \end{aligned}$$

(5.4)

due to Assumption 5.1 and the fact that $\widetilde{A}\langle \cdot \rangle ^{-1}\in {\mathscr {B}}({\mathcal {H}})$ (see the proof of Lemma 5.8). Since $C_{\mathrm{c}}({\mathcal {T}},{\mathbb {C}}^d)$ is a core for A, what precedes implies that all the operators in the expression for [A, U] belong to $C^1(A)$, except the operators $D_k$ which we only know to be bounded. Therefore, we have to show that

$$\begin{aligned} \big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}D_k\mathop {\mathrm {e}}\nolimits ^{itA}-D_k\big \Vert _{{\mathscr {B}}({\mathcal {H}})} \le \mathrm{Const.}\;\!t^\varepsilon \quad \hbox {for all }t\in (0,1). \end{aligned}$$

Now, algebraic manipulations as presented in [1, p. 325-326] show that for all $t\in (0,1)$

$$\begin{aligned}&\big \Vert \mathop {\mathrm {e}}\nolimits ^{-itA}D_k\mathop {\mathrm {e}}\nolimits ^{itA}-D_k\big \Vert _{{\mathscr {B}}({\mathcal {H}})} \\&\quad \le \mathrm{Const.}\;\!\big (\Vert \sin (tA)D_k\Vert _{{\mathscr {B}}({\mathcal {H}})} +\Vert \sin (tA)(D_k)^*\Vert _{{\mathscr {B}}({\mathcal {H}})}\big )\\&\quad \le \mathrm{Const.}\;\!\big (\Vert tA\;\!(tA+i)^{-1}D_k\Vert _{{\mathscr {B}}({\mathcal {H}})} +\Vert tA\;\!(tA+i)^{-1}(D_k)^*\Vert _{{\mathscr {B}}({\mathcal {H}})}\big ). \end{aligned}$$

Furthermore, if we set $A_t:=tA\;\!(tA+i)^{-1}$ and $\Lambda _t:=t\langle \cdot \rangle (t\langle \cdot \rangle +i)^{-1}$, we obtain that

$$\begin{aligned} A_t=\big (A_t+i(tA +i)^{-1}A\;\!\langle \cdot \rangle ^{-1}\big )\Lambda _t \end{aligned}$$

with $A\langle \cdot \rangle ^{-1}\in {\mathscr {B}}({\mathcal {H}})$. Thus, since $\Vert A_t+i(tA +i)^{-1}A\;\!\langle \cdot \rangle ^{-1}\Vert _{{\mathscr {B}}({\mathcal {H}})}$ is bounded by a constant independent of $t\in (0,1)$, it is sufficient to prove that

$$\begin{aligned} \Vert \Lambda _t D_k\Vert _{{\mathscr {B}}({\mathcal {H}})}+\Vert \Lambda _t(D_k)^*\Vert _{{\mathscr {B}}({\mathcal {H}})} \le \mathrm{Const.}\;\!t^\varepsilon \quad \hbox {for all }t\in (0,1). \end{aligned}$$

But this estimate will hold if we show that the operators $\langle \cdot \rangle ^\varepsilon D_k$ and $\langle \cdot \rangle ^\varepsilon (D_k)^*$ defined on $C_\mathrm{c}({\mathcal {T}},{\mathbb {C}}^d)$ extend continuously to elements of ${\mathscr {B}}({\mathcal {H}})$. For this, we fix $\varepsilon \in (0,1)$ with $\varepsilon \le \min \{\varepsilon _1,\dots ,\varepsilon _d\}$, and note that $\langle \cdot \rangle ^{1+\varepsilon }(C-C_k)\chi _k\in {\mathscr {B}}({\mathcal {H}})$ due to Assumption 5.1. With this inclusion and the fact that ${{\widetilde{A}}}\;\!\langle \cdot \rangle ^{-1}\in {\mathscr {B}}({\mathcal {H}})$, one infers from (5.4) that $\langle \cdot \rangle ^\varepsilon D_k$ and $\langle \cdot \rangle ^\varepsilon (D_k)^*$ defined on $C_\mathrm{c}({\mathcal {T}},{\mathbb {C}}^d)$ extend continuously to elements of ${\mathscr {B}}({\mathcal {H}})$, as desired. $\square$

We are now in a position to obtain a class of locally U-smooth operators and determine spectral properties of U.

Theorem 5.12

(Locally U-smooth operators). Let ${\mathcal {G}}$ be an auxiliary Hilbert space. Then each operator $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ which extends continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle \cdot \rangle ^{-s}),{\mathcal {G}}\big )$ for some $s>1/2$ is locally U-smooth on any closed set $\Theta '\subset {\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U)$.

Proof

We know from Proposition 5.10 and Lemma 5.11 that for each $\theta \in {\mathbb {S}}^1$ there exists an open set $\Theta _\theta \ni \theta$ for which the assumptions of Theorem 2.2 are satisfied. So, each operator $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ which extends continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle A\rangle ^s)^*,{\mathcal {G}}\big )$ for some $s>1/2$ is locally U-smooth on any closed set $\Theta _\theta '\subset \Theta _\theta {\setminus }\sigma _{\mathrm{p}}(U)$. Since any closed set $\Theta '\subset {\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U)$ is contained in a finite union of closed sets of type $\Theta _\theta '$, we infer that T is locally U-smooth on $\Theta '$ too.

Now, we know from the proof of Lemma 5.8 that ${\mathcal {D}}(\langle \cdot \rangle )\subset {\mathcal {D}}(A)$. Therefore, we have ${\mathcal {D}}(\langle \cdot \rangle ^s)\subset {\mathcal {D}}(\langle A\rangle ^s)$ for each $s>1/2$, and it follows by duality that ${\mathcal {D}}(\langle A\rangle ^s)^* \subset {\mathcal {D}}(\langle \cdot \rangle ^s)^* \equiv {\mathcal {D}}(\langle \cdot \rangle ^{-s})$ for each $s>1/2$. In consequence, any operator $T\in {\mathscr {B}}({\mathcal {H}},{\mathcal {G}})$ which extends continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle \cdot \rangle ^{-s}),{\mathcal {G}}\big )$ for some $s>1/2$ also extends continuously to an element of ${\mathscr {B}}\big ({\mathcal {D}}(\langle A\rangle ^s)^*,{\mathcal {G}}\big )$. This concludes the proof. $\square$

Theorem 5.13

(Spectral properties of U). The operator U has at most finitely many eigenvalues, each one of finite multiplicity, and no singular continuous spectrum.

Proof

Let $\theta \in {\mathbb {S}}^1$. Then we know from Proposition 5.10 and Lemma 5.11 that there exists an open set $\Theta _\theta \ni \theta$ for which the assumptions of Theorem 2.3 are satisfied. Thus U has at most finitely many eigenvalues in $\Theta _\theta$, each one of finite multiplicity, and U has no singular continuous spectrum in $\Theta _\theta$. Since ${\mathbb {S}}^1$ can be covered by a finite number of open sets of type $\Theta _\theta$, it follows that U has at most finitely many eigenvalues, each one of finite multiplicity, and no singular continuous spectrum. $\square$

5.3 Wave Operators

In this final section, we use the results obtained so far to establish the existence and completeness of the wave operators for the triple $(U,U_0,J)$. We also explain why at least two operators different from $U_0$ can be used as a free evolution operator for U, and we establish the existence and completeness in these cases too.

Theorem 5.14

(Completeness, version 1). The wave operators $W_\pm (U,U_0,J):{\mathcal {H}}_0\rightarrow {\mathcal {H}}$ given by

$$\begin{aligned} W_\pm (U,U_0,J):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}JU_0^n \end{aligned}$$

exist and are complete, that is, $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$.

Proof

We know from Lemma 5.7 that V is trace class. Thus, it follows from [30, Ex. 3.8] that $W_\pm (U,U_0,J)$ exist. Similarly, since $J^*U-U_0J^*=U_0V^*U$ is trace class too, the wave operators

$$\begin{aligned} W_\pm (U_0,U,J^*):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U_0^{-n}J^*U^nP_{\mathrm{ac}}(U) \end{aligned}$$

exist too. Now, let $a_\pm ,b_\pm \in {\mathscr {B}}({\mathcal {H}})$ be defined by

$$\begin{aligned} a_\pm \varphi :=W_\pm (U,U_0,J)(\varphi ,\dots ,\varphi ) \quad \hbox {and}\quad b_\pm \varphi :=\sum _{k=1}^d\big (W_\pm (U_0,U,J^*)\varphi \big )_k, \,\, \varphi \in {\mathcal {H}}. \end{aligned}$$

Since ${\mathcal {H}}_\mathrm{ac}(U)\supset \mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,U_0,J)\big )\supset \mathop {\mathrm {Ran}}\nolimits (a_\pm )$, it is sufficient to show that $\mathop {\mathrm {Ran}}\nolimits (a_\pm )={\mathcal {H}}_{\mathrm{ac}}(U)$ to conclude the proof. To achieve this, we need to recall some information: $U_0$ has purely absolutely continuous spectrum by Lemma 5.6(c) and U has at most finitely many eigenvalues and no singular continuous spectrum by Theorem 5.13. So $1_{{\mathcal {H}}_0}=E^{U_0}({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U))$ and $P_\mathrm{ac}(U)=E^U({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U))$, and we have for all $\varphi ,\psi \in {\mathcal {H}}$ the equalities

$$\begin{aligned} \big \langle a_\pm ^*\varphi ,\psi \big \rangle _{\mathcal {H}}&=\big \langle \varphi ,P_{\mathrm{ac}}(U)W_\pm (U,U_0,J)(\psi ,\dots ,\psi )\big \rangle _{\mathcal {H}}\\&=\lim _{n\rightarrow \pm \infty }\sum _{k=1}^d\big \langle \varphi , P_{\mathrm{ac}}(U)U^{-n}\chi _kU_k^n\psi \big \rangle _{\mathcal {H}}\\&=\lim _{n\rightarrow \pm \infty }\sum _{k=1}^d\big \langle U_k^{-n}\chi _kU^nP_{\mathrm{ac}}(U)\varphi , \psi \big \rangle _{\mathcal {H}}\\&=\left\langle \sum _{k=1}^d\big (W_\pm (U_0,U,J^*)\varphi \big )_k,\psi \right\rangle _{\mathcal {H}}\\&=\big \langle b_\pm \varphi ,\psi \big \rangle _{\mathcal {H}}. \end{aligned}$$

Thus $b_\pm$ is the adjoint of $a_\pm$. Furthermore, since

$$\begin{aligned} a_\pm ={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}\mathop {\textstyle \sum }\limits _{k=1}^d\chi _kU_k^n ={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) ^nS^n \end{aligned}$$

with $\sum \nolimits _{k=1}^d\chi _kC_k$ unitary, the operator $a_\pm$ is an isometry and thus has closed range. Also, since

$$\begin{aligned} b_\pm= & {} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }\mathop {\textstyle \sum }\limits _{k=1}^dU_k^{-n}\chi _kU^nP_\mathrm{ac}(U)\\= & {} {{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }S^{-n}\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) ^{-n}U^n E^U({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U)), \end{aligned}$$

we have $\ker (b_\pm )=E^U(\sigma _{\mathrm{p}}(U))$. Combining what precedes, we obtain that

$$\begin{aligned} \mathop {\mathrm {Ran}}\nolimits (a_\pm ) ={\mathcal {H}}\ominus \ker (a_\pm ^*) =E^U({\mathbb {S}}^1){\mathcal {H}}\ominus \ker (b_\pm ) =E^U({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U)){\mathcal {H}}={\mathcal {H}}_{\mathrm{ac}}(U), \end{aligned}$$

as desired. $\square$

The proof of Theorem 5.14 implies in particular that:

Corollary 5.15

(Completeness, version 2). The operators $a_\pm :{\mathcal {H}}\rightarrow {\mathcal {H}}$ given by

$$\begin{aligned} a_\pm :={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}J_nS^n, \quad J_n:=\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) ^n, \end{aligned}$$

exist, are isometric and satisfy $\mathop {\mathrm {Ran}}\nolimits (a_\pm )={\mathcal {H}}_{\mathrm{ac}}(U)$.

Corollary 5.15 means that the operators $a_\pm$ are complete wave operators, with time-dependent identification operators $J_n$, for the pair (U, S). This shows that if one uses the matrix powers $\big (\sum \nolimits _{k=1}^d\chi _kC_k\big )^n$ as time-dependent identification operators, then the (pretty simple) shift S can be chosen as a free evolution operator for U.

Corollary 5.16

One has $\sigma _{\mathrm{ac}}(U)={\mathbb {S}}^1$.

Proof

Let $U_+:=(a_+)^*Ua_+$. Since $a_+$ is unitary from ${\mathcal {H}}$ to ${\mathcal {H}}_\mathrm{ac}(U)$, we have

$$\begin{aligned} \sigma _{\mathrm{ac}}(U) =\sigma \big (U\upharpoonright {\mathcal {H}}_{\mathrm{ac}}(U)\big ) =\sigma \big ((a_+)^*Ua_+\big ) =\sigma (U_+). \end{aligned}$$

So it is sufficient to show that $\sigma (U_+)={\mathbb {S}}^1$ to prove the claim. Let $\varphi \in {\mathcal {H}}$. Then the definition of $a_+$, the intertwining property of $W_+(U,U_0,J)$, and Lemma 5.2 imply that

$$\begin{aligned} U_+\varphi&=\sum _{k=1}^d\big (W_+(U_0,U,J^*)W_+(U,U_0,J)U_0(\varphi ,\dots ,\varphi )\big )_k\\&={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \infty }\sum _{k=1}^d\big (U_0^{-n}J^*JU_0^n (U_1\varphi ,\dots ,U_d\varphi )\big )_k\\&={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \infty }S^{-n}\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) S^{n+1}\varphi . \end{aligned}$$

This, together with the fact that $[\widetilde{A},\sum \nolimits _{k=1}^d\chi _kC_k]=0$ and the imprimitivity relation (5.3), implies for $s\in {\mathbb {R}}$

$$\begin{aligned} \mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{A}}}}U_+\mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}}&={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \infty }\big (\mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{A}}}}S\mathop {\mathrm {e}}\nolimits ^{-is\widetilde{A}}\big )^{-n} \left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) \left( \mathop {\mathrm {e}}\nolimits ^{is{{\widetilde{A}}}}S\mathop {\mathrm {e}}\nolimits ^{-is{{\widetilde{A}}}}\right) ^{n+1}\\&={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \infty }(\mathop {\mathrm {e}}\nolimits ^{2is}S)^{-n}\left( \mathop {\textstyle \sum }\limits _{k=1}^d\chi _kC_k\right) (\mathop {\mathrm {e}}\nolimits ^{2is}S)^{n+1}\\&=\mathop {\mathrm {e}}\nolimits ^{2is}U_+. \end{aligned}$$

So $U_+$ is unitarily equivalent to $\mathop {\mathrm {e}}\nolimits ^{2is}U_+$ for each $s\in {\mathbb {R}}$, and thus $\sigma (U_+)={\mathbb {S}}^1$. $\square$

Combining Theorem 5.13 and Corollary 5.16, we infer that the spectrum of U covers the whole unit circle and is purely absolutely continuous, outside possibly a finite set where U may have eigenvalues of finite multiplicity.

Interestingly enough, a third choice of free evolution operator is yet possible for the proof of the existence and completeness of the wave operators, namely the operator $\widetilde{U}_0:=S\sum _{k=1}^d\chi _kC_k:$

Theorem 5.17

(Completeness, version 3). The wave operators $W_\pm (U,{{\widetilde{U}}}_0):{\mathcal {H}}\rightarrow {\mathcal {H}}$ given by

$$\begin{aligned} W_\pm (U,{{\widetilde{U}}}_0):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }U^{-n}(\widetilde{U}_0)^n \end{aligned}$$

exist, are isometric and are complete, that is, $\mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,{{\widetilde{U}}}_0)\big )={\mathcal {H}}_{\mathrm{ac}}(U)$.

Proof

The coin operator $C_0:=\sum _{k=1}^d\chi _kC_k$ is diagonal. So we know from Sect. 5.1 that ${{\widetilde{U}}}_0$ has purely absolutely continuous spectrum covering the whole unit circle ${\mathbb {S}}^1$. Furthermore, calculations similar to that of Lemma 5.7 show that the perturbation $\widetilde{U}_0-U=S\sum _{k=1}^d\chi _k(C_k-C)$ is trace class. Therefore, we obtain from [30, Ex. 3.8] that the wave operators

$$\begin{aligned} W_\pm (U,{{\widetilde{U}}}_0) \quad \hbox {and}\quad W_\pm (\widetilde{U}_0,U):={{\,\mathrm{{\mathrm{s-lim}}}\,}}_{n\rightarrow \pm \infty }({{\widetilde{U}}}_0)^{-n}U^nP_{\mathrm{ac}}(U) \end{aligned}$$

exist. And the operators $W_\pm (U,{{\widetilde{U}}}_0)$ are isometric. Since $1_{\mathcal {H}}=E^{{{\widetilde{U}}}_0}({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U))$ and $P_{\mathrm{ac}}(U)=E^U({\mathbb {S}}^1{\setminus }\sigma _{\mathrm{p}}(U))$, it follows from Remark 4.3 and Lemma 4.4 that

$$\begin{aligned} \mathop {\mathrm {Ran}}\nolimits \big (W_\pm (U,{{\widetilde{U}}}_0)\big ) =E^U({\mathbb {S}}^1{\setminus }\sigma _\mathrm{p}(U)){\mathcal {H}}={\mathcal {H}}_{\mathrm{ac}}(U), \end{aligned}$$

as desired. $\square$

Remark 5.18

Each choice of free evolution operator comes with its pros and cons. The shift S is a very simple operator, but the corresponding complete, isometric, wave operators $a_\pm$ are not easily interpretable since they are defined with time-dependent identification operators. The operator $\widetilde{U}_0=S\sum _{k=1}^d\chi _kC_k$ is simple, and the corresponding complete, isometric, wave operators $W_\pm (U,{{\widetilde{U}}}_0)$ are intuitive. But ${{\widetilde{U}}}_0$ does not encode in separate Hilbert spaces the multichannel structure of the scattering system. The d scattering channels are summed together in the Hilbert space ${\mathcal {H}}$ via the matrix $\sum _{k=1}^d\chi _kC_k$. Finally, the operator $U_0$ is simple, encodes in separate Hilbert spaces the multichannel structure of the scattering system, and the corresponding complete wave operators $W_\pm (U,U_0,J)$ are intuitive. But the operators $W_\pm (U,U_0,J)$ are not isometric. We expect them to be partial isometries with non-trivial initial subspaces ${\mathcal {H}}_0^\pm \subset {\mathcal {H}}_0$ defined in terms of some asymptotic velocity operators, as in the case of anisotropic quantum walks on ${\mathbb {Z}}$ (see the discussion below).

To conclude, we list some interesting generalisations and problems left open by this work on quantum walks on trees:

• (i) As mentioned in Remark 5.18, it would be interesting to determine the initial subspaces ${\mathcal {H}}_0^\pm \subset {\mathcal {H}}_0$ on which the wave operators $W_\pm (U,U_0,J)$ are isometric. As for anisotropic quantum walks on ${\mathbb {Z}}$ [26, Prop. 3.4], we expect these subspaces to be defined in terms of some asymptotic velocity operators for the operators $U_i=SC_i$ ($i=1,\ldots ,d$). However, on trees of odd degree $d\ge 3$, there are no canonical position operators coming to mind allowing to define straightforwardly asymptotic velocity operators. So, one might have to do something new in order to determine the subspaces ${\mathcal {H}}_0^\pm$.

• (ii) It would be interesting to consider the case of quantum walks with coin operator converging at infinity to constant coins along partitions of the tree ${\mathcal {T}}$ different from the one considered here. In this first work on the topic, we used for simplicity the partition of ${\mathcal {T}}$ into its d main branches, but many other more refined choices of partitions into subtrees are possible.

• (iii) In the case $d=3$, for evolution operators $U=SC$ with constant coin operator $C\in \mathrm U(3)$, it has been shown in [14, Sec. 2] that one can impose boundary conditions that restrict the configuration space of the quantum walker to a rooted tree, while preserving the unitarity of U. It would be interesting to generalise this restriction procedure to evolution operators with non-constant coin operators and determine which results of this paper still hold in that modified setup.

• (iv) In this work, we have treated coin operators that converge on each main branch of ${\mathcal {T}}$ to a constant diagonal unitary matrix, whereas in the case of quantum walks on ${\mathbb {Z}}$ the authors of [25, 26] have covered coin operators that converge at infinity to arbitrary constant unitary matrices. This is explained by the fact that on ${\mathcal {T}}$ there is not any explicit Fourier transform allowing to diagonalise non-diagonal asymptotic operators. So, the construction of a conjugate operator based on the Fourier transform presented in [25, Sec. 4.1] is not possible here. That being said, each cyclic subspace of $\ell ^2({\mathcal {T}})$ of the form ${\overline{\mathop {\mathrm {Span}}\nolimits }}\{S_{i,j}^n\delta _x\mid n\in {\mathbb {Z}}\}$ is isomorphic to $\ell ^2({\mathbb {Z}})$, and thus admits a Fourier transform [13, Lemma 2.2]. Therefore, it would be worth investigating if these implicit Fourier transforms can be used to construct a conjugate operator suitable for quantum walks on ${\mathcal {T}}$ with coin operators converging on each main branch of ${\mathcal {T}}$ to an arbitrary constant unitary matrix.