1 Introduction

In recent years, with the development of geothermal energy, deep geological burial of nuclear waste and underground coal gasification, the damage and failure characteristics of rock masses under thermal effects have also become research hotspots in rock mechanics [1,2,3]. The mechanical properties and microstructure of a natural rock mass will change under the influence of thermal stress at high temperatures [4,5,6]. Numerous experimental efforts have been carried out to investigate the influence of high temperature on the failure characteristics and mechanical properties of rock under a compressive stress state. For example, Chen et al. [7] and Yang [8] conducted uniaxial compression experiments on granite after treatments at different temperatures, and the relationships of peak strength, peak strain, elastic modulus and crack damage and temperature were discussed. Meng et al. [9] studied the evolution of the thermocracking and permeability of granite at different high temperatures under triaxial compression conditions with different confining pressures. Zhu et al. [10] conducted uniaxial compression tests on granite with different heating–cooling (H–C) cycles, and the influence of H–C cycles on the mechanical properties of granite was analysed. Based on water quenching and conventional triaxial compression tests, Yin et al. [11] investigated the effect of H–C cycles on the cracking mechanisms and mechanical behaviour of granite under different confining pressures. After fully recognizing the deterioration mechanism of H–C cycles on rock properties, some scholars have attempted to establish an accurate damage model to reflect the damage behaviour under cyclic H–C treatments. At the theoretical level, a coupled thermohydromechanical model was presented by Hassen [12] to simulate the transient creep strain of the load-induced thermal strain of concrete during a H–C cycle with a concomitant applied load. Jiang et al. [13] proposed a statistical damage constitutive model of red sandstone after heating and water-cooling cycles based on the Weibull distribution theory. Zhou et al. [14] proposed a constitutive model of rocks subjected to cyclic stress and high-temperature conditions based on statistical damage theory, and the damage constitutive model was extended with the Weibull distribution. The existing theoretical models of rocks or rock-like materials under H–C cycle treatment with complex calculation formulas and parameters, at the same time, the fitting effect of mechanical behaviour compaction stage after thermal damage of rock material is not ideal. But all of them provided a solid foundation for the theoretical research in this paper.

At the same time, a considerable amount of attention has also been devoted to the effect of H–C on fracture toughness, shear behaviour, tensile strength, etc. [15,16,17,18,19,20]. To investigate the effect of high temperatures on the fracture mechanical behaviour of rock masses, Yin et al. [15] conducted a mixed-mode fracture test on heat-treated granite, and the effect of the high-temperature treatment on the granite I + II mixed-mode fracture toughness was discussed. Meng et al. [16] carried out mechanical tests on semicircular bend (SCB) specimens at real-time high temperatures and found that the effective fracture process zone (FPZ) size of the crack tip increased with increasing temperature. Based on a series of direct shear tests on sandstone after high-temperature treatment, Zhang et al. [17] investigated the variation pattern of shear strength, friction coefficient and shear stiffness under different temperature conditions. Zhao et al. [18] and Zhai et al. [19] conducted direct shear tests on artificially fractured granite and artificially healed fractured granite after high-temperature exposure, respectively. The weakening pattern of the shear properties of granite with different shear surfaces under high-temperature action was revealed. Xiong et al. [20] carried out splitting tensile tests on high-temperature-treated rock-like materials and discovered that their tensile strength deteriorated with increasing temperature.

With the help of various advanced techniques such as nuclear magnetic resonance (NMR) techniques [21, 22], acoustic emission (AE) monitoring techniques [23] and scanning electron microscopy (SEM) techniques [24, 25], the microdamage deterioration mechanism of rocks after high-temperature treatment has also been investigated and discussed in the literature [15, 16, 21,22,23,24,25]. For example, by using NMR techniques, Li et al. [21] examined the changes in the pore structure and mechanical properties of sandstone after high-temperature treatment, and the results showed a significant increase in the porosity and permeability of sandstones after thermal treatment. Based on SEM results, Chen et al. [24] found that the connections between minerals in granite weaken with increasing heat treatment temperature. Wu et al. [25] also investigated the changes in the microstructure of granite after thermal treatments by using SEM and found that both the number and opening of microcracks increased with increasing temperature. Kong et al. [23] analysed the development and evolution of internal cracks and the time domain of AE signals in rocks after thermal treatments, and they concluded that the phase characteristics of AE time series can correspond to five stages of rock thermal deformation and fracture.

Previous studies have promoted the understanding of the effects of high temperatures on the microstructure and mechanical behaviour of rock masses, and as mentioned earlier, determining the evolutionary laws of rock microstructure and mechanical behaviour under high temperatures is important for ensuring the stability of rock engineering construction in high-temperature environments [1]. However, the majority of current research has focused on the physical and mechanical properties of rocks after being exposed to high temperatures once, and only a minimal number of scholars have investigated the changing microstructure and mechanical properties of rocks after cyclic H–C treatment. In the case of geothermal energy systems, during the long-term heat extraction process, multiple alternating hot and cold cyclic effects lead to fracture expansion or secondary fractures, which change the permeability and stability of the geothermal reservoir [26,27,28]. Thus, to reveal the evolution of the microstructure and mechanical properties of bedrock under cyclic H–C effects, the damage deterioration mechanism and damage constitutive modelling of red sandstone under cyclic H–C treatments were investigated in this paper. First, red sandstone specimens were subjected to cyclic H–C treatment, and then a series of mechanical uniaxial compression tests were carried out, with monitoring of the mechanical behaviour of the microcracks using the AE technique. Then, by using SEM, the microstructure of the sandstone fracture surfaces was obtained after different numbers of H–C cycles, and the influence of the H–C cycles on the mesoscopic characteristics was analysed. Finally, the cyclic H–C damage variables were defined and calculated, and a coupled statistical damage constitutive model was deduced to consider the cyclic H–C effects and the loading effects. The parameter closely related to the number of H–C cycles was especially considered in the proposed model.

2 Experiment procedure

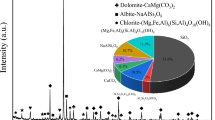
In this research, uniform red sandstone was selected for the test material in this research, as shown in Fig. 1, with the X-ray powder diffraction (XRD) results of the red sandstone. The mineral components of the red sandstone are primarily quartz (48.84%), calcite (11.82%), feldspar (23.79%), chlorite (4.03%), mica (6.66%), anhydrite (3.42%), and haematite (1.44%). These specimens were processed into a standard cylindrical shape with dimensions of 50 mm (diameter) × 100 mm (height). According to the sample preparation method recommended by ISRM [29], all end faces of each sample were smoothed to ensure that the two flatness errors were less than 0.02 mm.

Fig. 1
figure 1

Photographs of the specimens and the XRD results

Full size image

All the specimens were divided into three groups, and the specimens were exposed to temperatures of 200, 500 and 600 °C. All the specimens were heated to the target temperature in a high-temperature muffle furnace (as shown in Fig. 2). To investigate the effect of H–C cycles on the mechanical behaviour of the specimens, each temperature was reached for 5, 10, 15, and 20 H–C cycles. Specimens were placed into a high-temperature muffle furnace for different H–C cycle treatments; for each H–C cycle number, two specimens were tested.

Fig. 2
figure 2

Cyclic H–C experiment of red sandstone

Full size image

The H–C cycle–temperature curve is shown in Fig. 3. In each H–C cycle, the initial temperature of the heating process was the ambient temperature (25 °C), and the specimens were heated to the target temperature at a constant rate of 5 °C/min and then kept at a constant temperature for 2 h. Finally, the samples were removed and cooled to ambient temperature in the natural environment.

Fig. 3
figure 3

Cyclic H–C treatment of a sample

Full size image

The mechanical test procedure is shown in Fig. 4. Each uniaxial compression test was conducted on a servo-controlled test system (WHY-CTS600), and the loading rate setting was 0.12 mm/min. During loading, the stress, vertical displacement and AE events are recorded simultaneously via a data acquisition system. After failure, the mesoscopic characteristics of the fracture surface were scanned and analysed through a Siri200 field emission scanning electron microscope.

Fig. 4
figure 4

Mechanical test procedure

Full size image

3 Experimental results

3.1 Strength, deformation characteristics and cumulative damage variables

Figure 5 exhibits a few stress–strain curves of the specimens after different H–C treatments. Figure 5 shows that all of the stress–strain curves are concave during the initial loading period, mainly reflecting the closure of internal microcracks during loading. With the increase in the number of H–C cycles, the slope of the stress–strain curve decreases obviously, which means that the damage inside the specimen is more obvious with the increase in the number of H–C cycles. This also indicates that the uneven expansion of minerals during the H–C cycles leads to damage to the sandstone matrix and degradation of the strength.

Fig. 5
figure 5

Stress–strain curves of the specimens after different number of H–C cycles

Full size image

The peak strength of specimens with different temperatures and H–C cycle numbers is shown in Fig. 6. Zero means that the specimen did not undergo H–C cycling and that it was directly subjected to a uniaxial compression test. Figure 6 shows that the thermal treatment has an obvious influence on the peak strength of the specimens, and when the number of cycles is constant, the peak strength decreases with increasing temperature. For each temperature tested (200, 500 and 600 °C), the peak strength of the specimens decreased with an increasing number of H–C cycles. Especially for the specimen tested at 600 °C, the peak strength showed a trend of accelerated decline after five H–C cycles.

Fig. 6
figure 6

Change curve of average peak strength with the number of H–C cycles

Full size image

Damage mechanics considers that the damage of the material is the result of the accumulation of damage in the microscopic unit and is reflected in the change in macroscopic physical and mechanical parameters. The accumulation of damage and deterioration occurred in the rock during H–C cycles, and the difference in rock damage and deterioration degree is shown in its peak tangent modulus, as shown in Fig. 5. Therefore, according to macroscopic damage mechanics theory, the cumulative damage variable Dn of specimens with different H–C cycles can be represented by the change in the peak tangent modulus [14], which is defined as:

$$D_{n} = 1 - \frac{{E_{n} }}{{E_{0} }}$$
(1)

where \(E_{0}\) is the peak tangent modulus of a specimen that does not undergo cyclic H–C treatment, \(E_{n}\) is the peak tangent modulus of a specimen after n cycles of H–C, and n is the cycle number.

Figure 7 shows the damage variables of the specimens after different numbers of H–C cycles. Clearly, for each temperature value, the damage variables increased with the number of H–C cycles. At the same time, different from the specimens tested at 200 and 500 °C, the damage variables of the specimens tested at 600 °C show a trend of accelerated growth with an increasing number of H–C cycles. This also indicates that the damage accumulation in rock under H–C cycling is not only related to the number of cycles but also affected by the temperature value. When the temperature reaches 600 °C, the damage accumulation effect increases significantly with the increase in the number of cycles.

Fig. 7
figure 7

Average damage variable \(\overline{D}_{n}\) of different numbers of H–C cycles at different temperatures

Full size image

3.2 Tangent modulus-strain curve and microcrack closure behaviour

Figure 8a shows a typical stress–strain curve of a specimen obtained during a uniaxial compression test, and the corresponding relationship between the tangent modulus and axial strain is shown in Fig. 8b. The tangent modulus characterizes the real-time relationship between stress and axial strain under rock loading and reflects the damage process of internal microstructures [30]. It also reveals the development of cracks in the rock specimen and the mechanical response characteristics of cracks at various stages under loading. By using the moving average data processing method, the strong variations in the original data were eliminated, and the tangent modulus-strain curve was obtained (Fig. 8b).

Fig. 8
figure 8

a Stress–strain curves of red sandstone without cyclic H–C treatment and b tangent modulus-strain curve

Full size image

For each stage in Fig. 8a, based on the tangential modulus, the damage process of the internal microstructures was revealed. For stage AB, the tangential modulus increases from 0 to 2.8 GPa and exhibits little fluctuation (Fig. 8b), which indicates that the cracks closed. This stage is the crack closure stage, and \(\varepsilon_{{{\text{cc}}}}\) \(\sigma_{{{\text{cc}}}}\) at point B are called the crack closure strain and crack closure stress, respectively. In stage BC, the axial stress curve increases nearly linearly with increasing axial strain (Fig. 8a), and the tangent modulus fluctuates greatly in this stage (Fig. 8b), which indicates that the initiation and expansion of microcracks occurred inside the specimen. After point C, the tangent elastic modulus decreases continuously and fluctuates obviously (Fig. 8b), which means that unstable expansion occurred in the cracks, and the number of cracks increased rapidly in this stage. Therefore, stage CD is also called the unstable crack propagation stage.

Figure 9 shows the typical tangent modulus-strain curves of the specimens after H–C cycles, and the crack closure strain \(\varepsilon_{{{\text{cc}}}}\) of the specimens treated with different temperatures and H–C cycles is also exhibited in Fig. 9. Clearly, for each temperature, with an increasing number of H–C cycles, the slope of the tangent modulus-strain curve obviously decreases. At the same time, with an increasing number of H–C cycles and increasing temperature, the crack closure stress \(\sigma_{{{\text{cc}}}}\) and corresponding crack closure strain \(\varepsilon_{{{\text{cc}}}}\) show obvious differences. To facilitate comparison and analysis, the two eigenvalues are extracted, as shown in Fig. 10.

Fig. 9
figure 9

Tangent modulus-strain curves of the samples after H–C cycles at different heating temperatures

Full size image
Fig. 10
figure 10

The crack closure stress and strain of the specimens after H–C cycles

Full size image

Figure 10 shows the crack closure stress \(\sigma_{{{\text{cc}}}}\) and stress \(\varepsilon_{{{\text{cc}}}}\) of specimens that underwent treatments with different temperatures and H–C cycle numbers. Overall, with increasing temperature, \(\sigma_{{{\text{cc}}}}\) exhibits a growth trend. At the same time, \(\sigma_{{{\text{cc}}}}\) also increased with increasing H–C cycle times. The crack closure strain \(\varepsilon_{{{\text{cc}}}}\), similar to the crack closure stress \(\sigma_{{{\text{cc}}}}\), increases with increasing H–C cycle number and temperature. According to Ji et al. [30], the higher \(\sigma_{{{\text{cc}}}}\) and \(\varepsilon_{{{\text{cc}}}}\) of the specimen are, the more difficult it is to close the internal cracks completely. Therefore, it can be concluded that the cyclic H–C treatments promoted the development of fractures in the specimen, and the microcrack density also increased with increasing H–C cycles and temperature.

3.3 Failure characteristics

Figure 11 shows the red sandstone specimens after different numbers of H–C cycles at 600 °C. Figure 11a shows that when the number of H–C cycles is 5, the appearance of the specimen does not change significantly. However, with the increase in the number of H–C cycles, a small area of spalling began to appear on the surface of the specimen after 10 cycles (Fig. 11b), and the spalling of the specimen surface was more serious when it reached 20 cycles (Fig. 11d). During the heating process, thermal stress was generated and promoted the expansion of existing microcracks. The mineral particles expanded by heat later shrank during the cooling process, but some mineral crystals were still connected, and the large difference between the specific heat capacity and thermal expansion coefficient of each mineral crystal made the cooling and shrinking process of the specimen unable to occur freely [31, 32], so residual compressive stresses developed within these red sandstone specimens during the cooling process. The specimens also developed more microcracks under the influence of residual compressive stress [33, 34]. The phenomenon of crack initiation and propagation inside a specimen became increasingly serious with an increasing number of H–C cycles, as found from the SEM results of the fracture surface of the specimen, which are shown in Fig. 12.

Fig. 11
figure 11

Red sandstone after different numbers of H–C cycles at 600 °C: a 5 cycles; b 10 cycles; c 15 cycles; d 20 cycles

Full size image
Fig. 12
figure 12

SEM results of the fracture surfaces of specimens after different H–C cycles at 600 °C

Full size image

Figure 12a shows the scanning result for the specimen that did not undergo H–C cycles. Clearly, there are a certain number of microcracks in the sandstone. After H–C treatment, the microstructure of the sandstone was changed. After 5 H–C cycles, microcrack groups were generated (Fig. 12b). The length of intergranular microcracks in a specimen increased with an increasing number of H–C cycles, accompanied by the appearance and expansion of a small amount of transgranular microcracking, as shown in Fig. 12c. When the number of H–C cycles reaches 15, both the number of transgranular microcracks and the microcrack spacing increase, as shown in Fig. 12d. With further increases in the number of H–C cycles, the intergranular microcracks and transgranular microcracks expand and interpenetrate after 20 cycles, as shown in Fig. 12e. It can be concluded that the increase in the crack closure stress and strain of the specimen is the result of the combined effect of the increase in the intergranular microcrack spacing and the number of intragranular microcracks.

The internal structure of red sandstone changes under the action of H–C cycles, which also leads to the transformation of the macroscopic fracture mode of the specimen. Figure 13 shows the failure modes of the specimens after different numbers of H–C cycles at 600 °C. It can be seen from the test results that the failure mode of the specimen changes with the number of H–C cycles. For the specimen with fewer than 10 H–C cycles, all manifested mainly macroscopic shear failure (Fig. 13a–c). With the increase in the number of H–C cycles, the failure mode of the specimen gradually changed from shear failure to splitting failure. Especially for the specimen with 20 cycles, there was no shear failure plane observed; instead, several axial splitting bands and visible end fractures formed (Fig. 13e). The main reason for this phenomenon is that the microcracks initiated and expanded under cyclic H–C. Under uniaxial loading, the microcracks connected, which led to the transformation of the macrofracture mode of a specimen. After 20 H–C cycles, due to the increase in the number of cracks and expansion of cracks in the specimen, splitting failure occurred with the connection of microcracks.

Fig. 13
figure 13

Failure modes of specimens under uniaxial compression: a without H–C cycles; b 600 °C and 5 cycles; c 600 °C and 10 cycles; d 600 °C and 15 cycles; e 600 °C and 20 cycles

Full size image

3.4 AE characteristics

The AE waveforms generated by rupture events provide information related to crack rupture patterns [35]. To classify active cracks, two AE metrics, namely, RA values (angle of rise) and AF values (average frequency), which are related to the shape of the AE waveform, were used to distinguish between tensile and shear cracks [36, 37], as shown in Fig. 14a. To further analyse the fracture characteristics of the specimens treated with different numbers of H–C cycles, RA and AF were used to classify the cracking pattern of red sandstone specimens during loading. The two AE indicators are calculated as follows:

$$RA = {{RT} \mathord{\left/ {\vphantom {{RT} A}} \right. \kern-\nulldelimiterspace} A}$$
(2)
$$AF = {C \mathord{\left/ {\vphantom {C D}} \right. \kern-\nulldelimiterspace} D}$$
(3)
Fig. 14
figure 14

The cracking classification based on RA and AF values

Full size image

where RT is the rise time, A is the maximum amplitude, D is the duration of the AE waveform and C is the total number of AE waveforms over a threshold.

In this study, a line with a slope of 0.5 kHz/ms/v is used to distinguish tensile cracks from shear or hybrid cracks [38]. As shown in Fig. 14b, due to the high scattering of the raw data, the classification of cracking patterns is not obvious. Therefore, the kernel density estimation (KDE) method is used to visualize the RA and AF data. This method can better identify the concentration area of AF and RA values and clearly visualize data points. Kernel density clouds for crack classification in the crack propagation stage at 600 °C for different numbers of H–C cycles are shown in Fig. 15. For the kernel density clouds in Fig. 15, different concentration areas are represented by different colours: red and yellow represent the maximum density of data points, and blue represents the minimum density of data points. Without H–C cycles, the RA value varies from 0 to 400 ms/v, and the AF value ranges from 0 to 330 kHz, which proves that both tensile and shear/mixed cracking events occurred in the loading process. Similar to Fig. 15a, the kernel density cloud for the specimen with 5 H–C cycles under 600 °C (Fig. 15b) also indicates that considerable shear or mixed cracking events still occurred in the failure process of these specimens. When the H–C cycles reached 10 cycles, the proportion of shear fracture decreased significantly, and tensile fracture gradually became dominant (Fig. 15c). It can also be found from Fig. 13c that when the number of cycles is 10, the spalling of the specimen surface is obvious, in addition to the shear failure plane. With a further increase in H–C cycles, the crack cracking pattern changes from shear mixed rupture to tensile cracking. In particular, for the specimen that underwent 20 cycles (Fig. 15e), tensile cracking events played a dominant role during the crack propagation stage. This result is also consistent with the macrofracture characteristics in Fig. 13e, in which splitting (tensile) failure played a dominant role.

Fig. 15
figure 15

Kernel density contour map of crack failure classification after different cyclic H–C treatments at 600 °C

Full size image

4 Statistic constitutive model

4.1 Mechanism and constitutive model for coupling H–C cycles and load

As mentioned earlier, the internal microdefects and cracks in the red sandstone expand and initiate more new cracks under the alternating effect of thermal expansion and contraction during cyclic H–C treatment. During the loading process, the damage inside the specimen will further accumulate until macrofailure occurs. In this study, to investigate the coupling mechanism of cyclic H–C treatments and loading on red sandstone, the coupled damage process was discretized into three different stages, as shown in Fig. 16. At the same time, the strain equivalence principle was applied to derive the total damage variables for the coupling effect of cyclic H–C treatments and loading. To facilitate analysis, according to Lemaitre [39], the damage variable in terms of damage area can be defined as follows:

$$D = \frac{{S_{0} - S_{{\text{d}}} }}{{S_{0} }}$$
(4)
Fig. 16
figure 16

Schematic diagram of the effective load and effective stress area distribution of rock in three different states

Full size image

where D is the damage variable, \(S_{0}\) is the total cross-sectional area and \(S_{{\text{d}}}\) is the undamaged cross-sectional area.

Assuming that the damage variable of rock material under cyclic H–C treatment is \(D_{n}\), the damage variable of rock under an axial load is \(D_{{\text{l}}}\), and the total damage variable of rock material after cyclic H–C treatment and loading is \(D_{{{\text{nl}}}}\), then the damage variables at each stage can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {D_{n} = \frac{{S_{0} - S_{{{\text{dn}}}} }}{{S_{0} }}} \\ {D_{{\text{l}}} = \frac{{S_{{{\text{dn}}}} - S_{{{\text{dnl}}}} }}{{S_{dn} }}} \\ {D_{{{\text{nl}}}} = \frac{{S_{0} - S_{{{\text{dnl}}}} }}{{S_{0} }}} \\ \end{array} } \right.$$
(5)

where \(S_{0}\) is the total effective cross-sectional area, \(S_{{{\text{dn}}}}\) is the undamaged effective cross-sectional area of the specimen after cyclic H–C treatment, and \(S_{{{\text{dnl}}}}\) is the undamaged effective cross-sectional area of the specimen after a combination of cyclic H–C treatment and loading.

As mentioned before, the coupled damage process was discretized into three different stages in this study (Fig. 16). The first is the initial damage stage, the second is the damage state of the rock after n H–C cycles, and the third is the damage state of the rock specimen suffering from n H–C cycles and axial loading. According to the strain equivalence principle proposed by Lemaitre [40], the following can be obtained:

$$\overline{\sigma }_{0} S_{0} = \overline{\sigma }_{n} S_{{{\text{dn}}}} = \overline{\sigma }_{{{\text{nl}}}} S_{{{\text{dnl}}}}$$
(6)

where \(\overline{\sigma }_{0}\) and \(S_{0}\) are the effective stress and effective force area of the rock material in the first state (natural state), \(\overline{\sigma }_{n}\) and \(S_{{{\text{dn}}}}\) are the effective force and effective force area of the rock material in the second state (after cyclic H–C treatments) and \(\overline{\sigma }_{{{\text{nl}}}}\) and \(S_{{{\text{dnl}}}}\) are the effective force and effective force area of the rock material in the third state (with the combination of cyclic H–C treatment and axial loading). Combining Eqs. (5) and (6), the following can be obtained:

$$\left\{ {\begin{array}{*{20}c} {\overline{\sigma }_{{{\text{nl}}}} = (1 - D_{{\text{l}}} )\overline{\sigma }_{n} } \\ {\overline{\sigma }_{n} = (1 - D_{n} )\overline{\sigma }_{0} } \\ {\overline{\sigma }_{{{\text{nl}}}} = (1 - D_{{{\text{nl}}}} )\overline{\sigma }_{0} } \\ \end{array} } \right.$$
(7)

and

$$D_{{{\text{nl}}}} = D_{n} + D_{{\text{l}}} - D_{n} D_{{\text{l}}}$$
(8)

To facilitate the analysis, the following assumptions are made:

  1. (1)

    This paper considers only the damage and deterioration of rock specimens caused by cyclic H–C treatment and axial loading, and the initial damage of the specimen is defined as 0.

  2. (2)

    The microcellular intensity follows the statistical law of the Weibull function.

Because of the random distribution of cracks and pores in rock materials, the mechanical properties of rock specimens cannot be described by a single characteristic value. Considering the uneven distribution of the microelement strength in heterogeneous rocks, the microelements inside the rock will be randomly damaged under the action of external loads, so it is a reasonable and effective approach to subject the overall variation in microelement strength to some statistical distribution [41,42,43]. According to Wang et al. [43], the expression based on the rock microelement strength obeying the Weibull distribution is proposed as

$$\phi (\varepsilon ) = \frac{m}{\alpha }\left( {\frac{\varepsilon }{\alpha }} \right)^{m - 1} \exp \left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]$$
(9)

where \(\phi \left( \varepsilon \right)\) is the strength probability corresponding to the base element at a microstrain, \(\varepsilon\) is the microstrain of the base element, and \(\alpha\) and m are the Weibull statistical distribution parameters. Then, at a certain stress \(\sigma\) level satisfying \(\varepsilon = 0\), \(D_{{\text{l}}} = 0\), and the damage variables \(D_{{\text{l}}}\) under a load are obtained from Eq. (10) as follows:

$$D_{{\text{l}}} = \int\limits_{0}^{\varepsilon } {\phi (\varepsilon )} {\text{d}}\varepsilon = 1 - {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(10)

With Eqs. (1), (8) and (10), the expression of the total damage variable \(D_{{{\text{nl}}}}\) can be expressed as:

$$D_{{{\text{nl}}}} = 1 - \frac{{E_{n} }}{{E_{0} }}{\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(11)

According to the strain equivalence hypothesis proposed by Lemaitre [39], the damage constitutive relationship of red sandstone after cyclic H–C treatment is:

$$\sigma = E_{n} \varepsilon {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(12)

The typical stress–strain curve of red sandstone under uniaxial compression is shown in Fig. 17 and can be divided into three stages: the crack closure stage (OA), linear elastic stage (AB) and yield stage (BC). For the crack closure stage (OA), the stress–strain curve of the specimen is a concave function rather than a linear function, indicating that the tangent modulus gradually increases at this stage (Fig. 5) and that there is a process of crack closure inside the specimen, so this stage is a negative damage process.

Fig. 17
figure 17

Typical stress–strain curves of red sandstone under uniaxial compression after cyclic H–C treatments

Full size image

As loading continued, the internal microdefects and cracks of the specimen were compacted at point A. Therefore, for the linear elastic stage (AB), the stress–strain curve is an approximately linear function. In the yield stage (BC), new cracks were generated in the specimen, and the cracks continued to expand under loading. The specimen underwent damage: the total damage increased, the bearing capacity weakened and the tangent modulus decreased. Clearly, the stress–strain curve in the crack closure stage presents an obvious power function trend. At the same time, as mentioned earlier, the crack closure strain increased with an increasing number of H–C cycles. Then, Eq. (12) cannot reflect the stress–strain relationship at this stage. Therefore, to ensure that the model reflects the mechanical properties of the specimens more realistically, the damage correction factor i was introduced to correct the total damage variable of the specimen:

$$1 - D_{{{\text{nl}}}}^{^{\prime}} = i\left( {1 - D_{{{\text{nl}}}} } \right)$$
(13)

where \(D_{{{\text{nl}}}}^{^{\prime}}\) is the corrected total damage variable of the specimen and i is a correction factor related to the rock type and determined as a function of the shape of the specimen during the compaction phase.

Based on the shape function of the specimen in the compaction stage, it can be considered a higher-order power function [30, 43]. Combined with the shape of the specimen during the compaction phase, the correction factor is expressed as:

$$i = \varepsilon^{k}$$
(14)

Therefore, the modified expression for the total damage variable is:

$$D_{{{\text{nl}}}}^{^{\prime}} = 1 - \frac{{E_{n} }}{{E_{0} }}\varepsilon^{k} {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(15)

The modified expression for the damaged structure is:

$$\sigma = E_{n} \varepsilon^{{\left( {1 + k} \right)}} {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(16)

The expressions of the model parameters can be obtained from:

$$\left. {\frac{{{\text{d}}\sigma }}{{{\text{d}}\varepsilon }}} \right|_{{(\varepsilon_{{\text{p}}} ,\sigma_{{\text{p}}} )}} = 0,\quad \sigma_{{\text{p}}} = E_{n} \varepsilon_{{\text{p}}}^{{\left( {1 + k} \right)}} {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}}$$
(17)

and the modified uniaxial compression intrinsic model of the rock is:

$$\left\{ {\begin{array}{*{20}c} {\alpha = {{\varepsilon_{{\text{p}}} } \mathord{\left/ {\vphantom {{\varepsilon_{{\text{p}}} } {\left( {\ln \frac{{E_{n} \varepsilon_{{\text{p}}}^{{\left( {1 + k} \right)}} }}{{\sigma_{{\text{p}}} }}} \right)^{\frac{1}{m}} }}} \right. \kern-\nulldelimiterspace} {\left( {\ln \frac{{E_{n} \varepsilon_{{\text{p}}}^{{\left( {1 + k} \right)}} }}{{\sigma_{{\text{p}}} }}} \right)^{\frac{1}{m}} }}} \\ {m = {{\left( {1 + k} \right)} \mathord{\left/ {\vphantom {{\left( {1 + k} \right)} {\ln \frac{{E_{n} \varepsilon_{{\text{p}}}^{{\left( {1 + k} \right)}} }}{{\sigma_{{\text{p}}} }}}}} \right. \kern-\nulldelimiterspace} {\ln \frac{{E_{n} \varepsilon_{{\text{p}}}^{{\left( {1 + k} \right)}} }}{{\sigma_{{\text{p}}} }}}}} \\ {\sigma = E_{0} \left( {1 - D_{n} } \right)\varepsilon^{{\left( {k + 1} \right)}} {\text{e}}^{{\left[ { - \left( {\frac{\varepsilon }{\alpha }} \right)^{m} } \right]}} } \\ \end{array} } \right.$$
(18)

where α and m are Weibull statistical distribution parameters and \(\varepsilon_{{\text{p}}}\) and \(\sigma_{{\text{p}}}\) are the peak strain and peak stress, respectively. \(E_{n}\) is the peak tangent modulus of the rock after n H–C cycles.

4.2 Validation of the damage constitutive model and parametric analysis

The reliability and rationality of the damage constitutive model were verified based on the uniaxial compression test results given above. Figure 18 shows the comparison between the test curves and theoretical curves. As shown in Fig. 18, the theoretical curve fitted by the derived damage constitutive model is basically similar to the experimental curves, and the peak stress, peak strain and peak tangent modulus of the two kinds of curves are also basically the same. At the same time, the crack closure deformation of the specimens treated with different numbers of H–C cycles can be well reflected by the proposed model.

Fig. 18
figure 18

Test curve and theoretical curve for different numbers of cycles

Full size image

In general, the fitted curve is consistent with the experimental curve at each stage, and the mechanical parameters, such as peak stress, peak strain and tangent modulus, are also highly consistent. Therefore, the damage constitutive model of the coupling effect of the cyclic H–C treatment and loading of red sandstone proposed in this paper is in line with the actual situation (Table 1).

Table 1 Mechanical parameters of the rock samples and corresponding damage constitutive model parameters under different numbers of H–C cycles
Full size table

The damage statistical constitutive model based on the Weibull distribution proposed in this paper mainly considers three parameters: k, α and m. α and m reflect the magnitude of the macroscopic statistical mean strength and the concentration of the distribution of the microelement strength within the rock material, respectively [41, 42, 44]. As shown in Fig. 19, when the heating treatment temperature is 200, 500 and 600 °C, parameters α and m generally decrease with increasing H–C cycles, indicating that the distribution concentration degree of the microelement strength inside the red sandstone decreases after the H–C treatment, and that specimen develops from brittle to ductile. The function fitting was carried out according to the characteristics of the data points. It was found that the properties of red sandstone specimens with a higher heating temperature are easier to change under cyclic H–C treatment. The value of the newly introduced correction coefficient k increases with the increase in the number of H–C cycles, as shown in Fig. 20.

Fig. 19
figure 19

Variation in the statistical parameters α and m with the number of cyclic H–C treatments

Full size image
Fig. 20
figure 20

Variation in the model correction coefficient k with the number of cyclic H–C treatments

Full size image

The crack compacting phase of the stress–strain curve particularly pronounced for severely thermal damaged porous rock materials. To further illustrate the advantages of the model proposed in this paper, the Liu et al. [45] model and Jiang et al. [13] model were applied to describe the experimental data and were compared with the proposed model (see Fig. 21),which still presents a higher consistency with the experimental curves in contrast to the other two models. Two error measurements, including the root mean squared error (RMSE) and regression R-square value (R2), were adopted to evaluate the reliability of the proposed model. Equations of these error measurements are given in Eq. (19).

$$\left\{ {\begin{array}{*{20}c} {R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {(y_{{{\text{model}}}} - y_{{{\text{test}}}} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {(y_{{{\text{test}}}} - y_{{{\text{average}}}} )^{2} } }}} \\ {{\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {(y_{{{\text{model}}}} - y_{{{\text{test}}}} )^{2} } }}{n}} } \\ \end{array} } \right.$$
(19)
Fig. 21
figure 21

Comparison of experimental and theoretical curves of different constitutive models

Full size image

\(y_{{{\text{test}}}}\), \(y_{model}\) and \(y_{{{\text{average}}}}\) indicate the test value, the model value and the average value, respectively. The R2 and RMSE were calculated as follows:

$$25\;^{ \circ } {\text{C}},0\;{\text{cycles}}\left\{ {\begin{array}{*{20}c} {R^{2} } & {{0}{\text{.9809}}\;{\text{(Proposed}}\;{\text{model)}} > 0.8929\;{\text{(Jiang}}\;{\text{model)}} > - 0.0736\;{\text{(Liu}}\;{\text{model)}}} \\ {{\text{RESM}}} & {7.0872{\text{(Proposed}}\;{\text{model)}} < 8.6238\;{\text{(Jiang}}\;{\text{model)}} < {27}{\text{.0661}}\;{\text{(Liu}}\;{\text{model)}}} \\ \end{array} } \right.$$
(20)
$$600\;^{ \circ } {\text{C}},\;5\;{\text{cycles}}\left\{ {\begin{array}{*{20}c} {R^{2} } & {{0}{\text{.9266}}\;{\text{(Proposed}}\;{\text{model)}} > 0.5147\;{\text{(Jiang}}\;{\text{model)}} > - 1.4603\;{\text{(Liu}}\;{\text{model)}}} \\ {{\text{RESM}}} & {5.{50501}\;{\text{(Proposed}}\;{\text{model)}} < 12.9827\;{\text{(Jiang}}\;{\text{model)}} < {29}{\text{.2322}}\;{\text{(Liu}}\;{\text{model)}}} \\ \end{array} } \right.$$
(21)
$$600\;^{ \circ } {\text{C}},15\;{\text{cycle}}s\left\{ {\begin{array}{*{20}c} {R^{2} } & {{0}{\text{.9554}}\;{\text{(Proposed}}\;{\text{model)}} > 0.6320\;{\text{(Jiang}}\;{\text{model)}} > - 1.1893\;{\text{(Liu}}\;{\text{model)}}} \\ {{\text{RESM}}} & {2.{9960}\;{\text{(Proposed}}\;{\text{model)}} < 8.6107\;{\text{(Jiang}}\;{\text{model)}} < {21}{\text{.0023}}\;{\text{(Liu}}\;{\text{model)}}} \\ \end{array} } \right.$$
(22)
$$600\;^{ \circ } {\text{C}},20\;{\text{cycles}}\left\{ {\begin{array}{*{20}c} {R^{2} } & {{0}{\text{.9167}}\;{\text{(Proposed}}\;{\text{model)}} > 0.5276\;{\text{(Jiang}}\;{\text{model)}} > - 1.3492\;{\text{(Liu}}\;{\text{model)}}} \\ {{\text{RESM}}} & {2.{5279}\;{\text{(Proposed}}\;{\text{model)}} < 6.0212\;{\text{(Jiang}}\;{\text{model)}} < {1}3.4278\;{\text{(Liu}}\;{\text{model)}}} \\ \end{array} } \right.$$
(23)

A greater R2 reflects less data deviation, while a smaller RMSE reflects a more reliable estimation. It can be concluded from the comparison in Fig. 21 and Eqs. (20)–(23) that the model proposed in this paper is more reliable and more stable for higher numbers of H–C cycles than the other two models and that the overall error is smaller at the initial loading stage. Therefore, the damage statistical constitutive model proposed in this paper is more suitable for rocks with large porosity changes.

5 Conclusion

To investigate the damage deterioration of the red sandstone specimen after H–C cycling, cyclic H–C experiments and uniaxial compression tests were conducted. The influences of cyclic H–C action on the strength, deformation characteristics, damage variables and failure characteristics of sandstone specimens were analysed. At the same time, a statistical constitutive model of the damage of the cyclic H–C treated specimens under loading was proposed, and finally, the model was validated using experimental data. The main conclusions are as follows:

  1. (1)

    The thermal treatment had an obvious influence on the peak strength of the specimens, and when the number of cycles is constant, the peak strength decreased with increasing temperature. For each temperature tested, the damage variables increased with the number of H–C cycles. The damage accumulation in rock under cyclic H–C was not only related to the number of cycles but also affected by the temperature. When the temperature reached 600 °C, after 5 H–C cycles, the peak strength showed a trend of accelerated decline, and the damage accumulation effect increased significantly with the increase in the number of cycles.

  2. (2)

    With an increasing number of H–C cycles, the slope of the tangent modulus-strain curve obviously decreased, and both the crack closure stress \(\sigma_{{{\text{cc}}}}\) and crack closure strain \(\varepsilon_{cc}\) increased. The cyclic H–C treatment promoted the development of fractures in the specimen, and both the transgranular microcracks and the microcrack spacing increased. With the increase in the number of H–C cycles, the failure mode of a specimen gradually changed from shear failure to splitting failure.

  3. (3)

    A coupled damage evolution equation of red sandstone under cyclic H–C treatment and loading was derived based on the principle of strain equivalence. The damage correction coefficient was introduced to modify the total damage evolution equation. The crack closure deformation of the specimens treated with different numbers of H–C cycles were well reflected by the proposed model, and the mechanical parameters, such as the peak stress, peak strain and tangent modulus, were also highly consistent. Finally, a comparative analysis with previous models was carried out, and the model proposed in this paper was more reliable and stable.