Velocity model of the Hronov-Poříčí Fault Zone from Rayleigh wave dispersion

Abstract

The Hronov-Poříčí Fault Zone (HPFZ) is an active tectonic area with regularly occurring shallow earthquakes up to magnitude 5. For their exact locations, at least an average velocity model of the area is needed. A method of measuring local phase velocities of surface waves using the array of stations deployed permanently in the HPFZ is introduced. Seven regional and teleseismic events are selected to represent different backazimuths of propagation. Applicable range of periods is estimated for each event. The coherency of the waves reaching the array is constraining the short period range. The dimension of the array is a limiting factor for the long-periods. A dispersion curve of Rayleigh wave phase velocity measured at the vertical component and characterizing 1D properties of the target area is determined using the seven measurements for the interval from 1 to 40 s. An isometric method is used to invert the determined dispersion curve for shear and longitudinal velocity distribution from the surface to the depth of 65 km.

1 Introduction

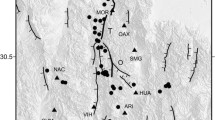
The Hronov-Poříčí Fault Zone—the area of our study—belongs to the second most seismically active region of the Bohemian Massif. As well as the West Bohemia/Vogtland zone, it is also affected by young—up to Early Quaternary—tectonic movements and it is characterized by shallow intraplate seismicity. The region situated on the NE margin of the Bohemian Massif, is approximately 40–60-km wide and 150-km long and comprises of a number of NW-SE and NNW-SSE striking faults. The HPFZ itself is more than 30-km long striking NW-SE. For more detailed tectonic overview, see Valenta et al. (2008) and Kolínský et al. (2012). Figure 1 presents the topography settings and location of four station array around the HPFZ. Stars denote the local events detected and localized by Kolínský et al. (2012).

Fig. 1

Topografic map of the target area. Four broadband seismic stations are shown as well as the events detected and localized by Kolínský et al. (2012). Mutual interstation distances are depicted. The Hronov-Poříčí Fault Zone is shown by a bold black line

For a long time, the HPFZ has been an object of geophysical observations. The strongest historical earthquake occurred there in 1901 (Woldřich 1901) with a magnitude of approximately 4.6, see also Málek et al. (2008) and Stejskal et al. (2007). Apart from the seismic activity, CO₂-rich mineral springs can be found in the area. Other studies in recent years have also been concerned about geomorphological research (Stejskal et al. 2006) and geoelectrical profiling (Valenta et al. 2008). The region surrounding the HPFZ and other structures of the NE margin of the Bohemian Massif have been studied by paleostress analysis (Nováková 2010, 2014), by GPS monitoring (Schenk et al. 2010) and by paleoseismic survey (Štěpančíková et al. 2010). Contribution to the seismic activity monitoring of the whole region is given by Špaček et al. (2006).

Hydrological wells are monitored and groundwater levels measured in the vicinity of HPFZ (Brož et al. 2009; Stejskal et al. 2007, 2009). The latest contribution describing the results of hydrological and seismic observations has been made by Kolínský et al. (2012). In their study, 12 seismic events with magnitudes from 0.1 to 1.5 were detected and localized in the period from 2009 to 2011. The knowledge of the velocity model of the area is crucial for proper localization of small earthquakes. In the latter study, only a homogeneous model has been used. In the present paper, we propose a new layered 1D model of both shear and longitudinal velocity constructed for the target area and based on the surface wave phase velocity measurement. As the seismic monitoring is still ongoing, this model will be used for localization of new events as well as for the previously detected earthquakes relocation.

Inverting phase velocities of surface waves is an alternative method for velocity model estimating, if there is not enough data for seismic tomography from the body waves. Surface waves provide good sensitivity for structural parameters in the horizontal direction. Their ability of resolving vertical contrasts is limited. However, by proper inversion problem parameterization, sufficiently accurate distribution of seismic velocities with depth can be achieved. Moreover, surface waves provide a determination of shear wave velocities or both shear and longitudinal ones, which is an advantage in comparison to the common refraction and reflection studies. The measurement of phase velocities (station-station) instead of group velocities (source-station) allows us to use broader period range for the target area than it would be possible using local sources. Local sources can provide proper spatial coverage, but they produce only short periods of seismic waves. Regional and teleseismic sources produce longer waves, but they have unusable long propagation paths when measuring the group velocity. Hence, by the use of surface wave phase velocities for a broad period range, we are able to determine the model of the HPFZ for depths down to 65 km. It even overreaches the depths where local earthquakes occur (8–23 km, see Kolínský et al. 2012). Such a model has not been available for this region yet. The only attempt to determine the shear wave velocity of the crust and the uppermost mantle in the area of HPFZ was provided by Wilde-Piórko et al. (2005) using receiver function technique beneath the DPC station (SE part of the target region, see Fig. 1).

The method of measuring phase velocities across the HPFZ is based on two approaches: We measure the time differences between two records of the same wave at each pair of neighboring stations, similarly to how it has been commonly used in many studies (e.g., Kolínský et al. 2011; Bourova et al. 2005; Hwang and Yu 2005.). Then, we apply an array approach to determine both the absolute value of the phase velocity and the direction of propagation of each wavelength among all the stations at once.

Surface wave phase velocities have been used for a long time to study structural parameters of the rock massifs. The two-station method relies on an assumption that surface waves propagate along a known great circle path and they cross two stations where the phase difference can be computed. An advantage of the two-station method is that the origin time of the event is not needed because only relative time shifts between the stations enter the velocity measurement. The first attempts to use the two-station method were provided by Nafe and Brune (1960). Although many techniques have evolved since these very beginnings of analysis, some of the principles proposed by the referenced work are still valid and used also in our study. We also deal with problems of proper ridge identification in spectrograms arising from cycle-skip uncertainty. We also use a priori information about the reasonable velocities of longer period waves to identify the number of cycles between the stations. We still need to compare measurements from different events at different sets of stations to confirm the reliability of the results. Brune and Dorman (1963) provided an inversion of phase velocities for medium velocities beneath the Canadian Shield, which can be considered as one of the first attempts to use the phase velocities for structural studies. Lateral heterogeneities were studied by Knopoff and Mal (1967) using an array of stations by applying the two-station method at different pairs of stations. Isse et al. (2000) measured phase velocities across the Philippine Sea by the two-station method as well. Another example of the modified two-station method is given by Mitra et al. (2006) for the South Indian Shield. They used the method, when the seismogram at the farther station was expressed as a convolution of the seismogram at the nearer station with a filter describing the properties of the interstation structure. As an example of other studies, we can further mention He et al. (2004) who inverted two-station paths crossing a small region into tomographic maps for periods from 4 to 15 s.

The two-station method suffers from a requirement that the interstation path coincides with the great circle path of the wave propagation. It reduces the applicability and accuracy not only because a limited number of events can be used for each station pair, but also because we do not know the true propagation path which can significantly differ from the geometrical one. These problems were partly overcome for example by Bourova et al. (2005), who measured the two-station paths across the Aegean Sea. Corrections of the true propagation direction were incorporated using the array approach. Kolínský et al. (2011) also provided the two-station measurement of several short profiles across the Bohemian Massif and introduced another original method of correction of the phase velocities for the true backazimuth propagation depending on the wave period. They used phase velocity dispersion curves determined at two pairs of stations in the same region with slightly different azimuths. Under the assumption that both dispersion curves should be similar, they provided a correction of the propagation backazimuths so that both curves really match each other. However, even this approach still requires some limitating assumptions and cannot be used for any station configuration.

In our present study, we use an array approach for measuring the phase velocities. It allows us to use events in any direction and even without the knowledge of the event location, origin time, or backazimuth.

Array techniques have been used for surface wave measurements in the last two decades, too. A comparison of phase velocities measured along the great circle paths and those obtained by the array approach was provided by Alsina et al. (1993) for the Iberian Peninsula. Stange and Friederich (1993) proposed a method for estimating structural properties of the crust and upper mantle using a network of nine stations.

In case of the HPFZ, we are looking for a 1D structural model, since it can be easily used for local events localization. Moreover, the number of stations in the area is limited so that a laterally heterogeneous model cannot be constructed. Our approach is similar to the one used by Hwang and Yu (2005). They also used an array of stations to measure phase velocities beneath Taiwan. Plane waves were considered as propagating across the array, and simple geometrical approach was used to determine phase velocity dispersion curves. This allows them to use long-period surface waves for local study and to estimate the shear wave velocity down to the depth of 200 km. A similar approach was also used by Gaždová et al. (2008) although group velocities instead of the phase ones were used in their paper.

2 Data set

Four seismic stations have been operating in the HPFZ in recent years. Dobruška-Polom (DPC) and Úpice (UPC) stations are operated by the Institute of Geophysics, Academy of Sciences of the Czech Republic (ASCR). Ostaš (OSTC) and Chvaleč (CHVC) stations are operated by the Institute of Rock Structure and Mechanics, ASCR. All four stations are part of the Czech Regional Seismic Network with online real-time data transfer to the Institute of Geophysics in Prague. Stations are situated around the HPFZ, see Fig. 1. All four stations are now equipped with broadband Streckeisen seismometers. OSTC and CHVC stations use the RUP acquisition system (Brož and Štrunc 2011). See Table 1 for other details about the stations. For the processing, all records are resampled to 25 Hz.

Table 1 Seismic stations used for the study

The stations are located within different geological environments. OSTC and CHVC stations are build in the Czech part of the Intrasudetic Depression—a deep post-orogenic sedimentary basin filled with sediments from Lower Carboniferous up to Cretaceous. The thickness of the sediments exceeds 4,000 m (Tásler 1979; Mastalerz 1995) and locally even more. Both Tásler (1979) and Mastalerz (1995) reported thickness of only the Lower Carboniferous itself to reach even 6,000 m.

UPC station is situated in the Krkonoše Piedmont Basin—also the post-orogenic Carboniferous sedimentary basin. However, the thickness of sediments is much lower than in the Intrasudetic Depression—e.g., Martínek et al. (2006) reports thickness of about 1,800 m. DPC station is located within the Orlice-Kladsko Crystalline Unit.

The primary function of the stations is to monitor local microearthquakes, and so, they were deployed in a quadrangular array around the HPFZ. The array shape is sufficiently convenient also for a surface wave study: to compute both the backazimuth and absolute value of phase velocity at least a triangular array is needed to cover any (even unknown) direction of propagation. Array dimensions are marked in Fig. 1.

Six earthquakes and one mine burst (Poland, near the town of Lubin) were selected for the processing, see Table 2 for details. Geometrical great circle backazimuths and distances are given just for the station CHVC as an example. The number of events was chosen to be high enough to provide reliable estimate of uncertainties and to represent different propagation backazimuths and spectrum of wavelengths and to be low enough to enable careful processing and analysis by the authors manually without using any procedures as black boxes. Events were selected for the period starting from the beginning of 2011 until March 2013.

Table 2 Events used for the study

Because Guralp seismometer characteristic is not sufficiently stable for periods above 30 s and hence it does not enable precise phase velocity measurement, OSTC station was not used for the computation in case of the Crete event. It was used for the Italy A event as only limited period range up to 28 s was analyzed there. In case of the Poland event, no surface waves shorter than 3.5 s were detected by the UPC station and so, for this event, only three stations were used as we wanted to extend the dispersion curve towards shorter periods as much as possible.

All computational programs used in this study has been originally developed by the authors starting with the preprocessing viewers and ellipsoid distance computation and including filtering, tapering of the records, phase time shift computations, and inversion procedures.

3 Filtering and applicable period ranges

We use the vertical component only, and thus, Rayleigh waves are analyzed. Rayleigh waves depend on both v _s and v _p , which can be determined from their dispersion curve. Moreover, the vertical component does not suffer from the unknown true backazimuths and hence uncertain rotation of horizontal components. So, the vertical component fulfills the needs of our aim.

As a first step, record at each station is processed and analyzed separately. We follow the procedure described by Kolínský and Brokešová (2007) and further developed by Kolínský et al. (2011). The classical method of Fourier transform-based multiple-filtering is applied to analyze the dispersive records. Non-constant relative resolution filtering is used (Dziewonski et al. 1969). Example of such procedure is shown in Fig. 2. Left plots depict an original spectrum (grey line) with four selected Gaussian filters (dashed black lines) with varying width. Around 100 filters are actually used during the analysis. Towards higher frequencies, the filters are wider. The width of the filters does not only depend on frequency, but it is further adjusted according to the real properties of given signal from analyzed event so that optimal resolution is achieved both in frequency and time domains, see Kolínský (2004). Resultant filtered spectra (solid black lines) correspond to the original spectrum weighted by the Gaussian filters. As symmetric Gaussian filters are applied to a generally asymmetric spectrum, the frequencies which prevail in the filtered spectra do not generally match the central frequencies of the filters (Dziewonski et al. 1972). We solve this by estimating the instantaneous frequency (Levshin et al. 1989) which is computed using the analytical signal corresponding to each filtered quasimonochromatic signal. Right plots in Fig. 2 show the time representations of the filters (dashed lines) from the left plot with their envelopes computed as a modulus of the analytical signal. The envelopes correspond to the energy carried by the signal at given frequency. Distribution of these envelopes in the frequency-time plane is called spectrogram.

Fig. 2

Filtering in the frequency domain and tapering in the time domain. The left plots show the raw spectrum of the event from the Greenland Sea (grey line) with four weighting Gaussian filters (dashed lines) and corresponding four resultant filtered spectra (solid black lines). The right plots show time representations of the filters from the left plot. The dashed lines represent quasimonochromatic signals and their envelopes, and solid lines show tapered signals and corresponding envelopes

At this stage, a comparison of the records from all stations is useful. As we need to compare properties of the signals both in the frequency and time domains and as it is not convenient to plot four spectrograms over each other, we proposed another approach. All maxima of all envelopes are picked, and we plot only these maxima in the frequency-time diagram, forming ridges corresponding to different modes, see Figs. 3 and 4. Four different colors represent maxima picked at four stations.

Fig. 3

Spectrogram ridges for four stations. The example is computed for the record of the event from Poland. Different colors represent different station spectrograms. Bold grey lines delineate dispersion curve of the Rayleigh wave fundamental mode. For the UPC station (red dots), the ridge is found only for 3.4–12 s. For the other three stations, broader range of 1.0–12 s can be used

Fig. 4

Spectrogram ridges for four stations. The example is computed for the record of the event from Bulgaria. Fundamental mode for all stations is identified in a broad period range between 7–60 s. However, the short-period part of the records does not provide sufficient coherency among the stations. Long-period waves are beyond the capability of the array. Hence, a limited range of 13.3–40 s was used for the phase velocity measurement

Figure 3 depicts the envelope maxima for the Poland event. For the group velocity measurement, epicenter coordinates and origin time are used. However, for further phase velocity measurement, these event parameters are not needed. We see that in the range from 3.5 up to 12 s, all four stations show coherent fundamental mode ridges (bold grey lines). However, looking at the periods lower than 3.5 s, we are not able to find continuation of the fundamental mode ridge for the UPC station (red dots). This approach enables to decide, which period range for which stations can be used for further relative phase velocity measurement. We also see, that even for the other three stations (DPC, CHVC, and OSTC), the fundamental ridge is not smooth between 3 and 4 s. As it is shown in the next sections, we have good evidence that ridges in both period intervals below and above 3.5 s really belong to the fundamental mode. So, for the Poland event, we selected a period interval from 1 to 12 s for the phase velocity measurement. Considering velocities of waves around 1 s to be 2 km/s, their wavelength is around 2 km. In case of our array aperture, we deal with 5 to 15 wavelength cycles between the stations. It would be not possible to decide which number of the cycles is the correct one, considering only the shortest wavelengths separately. However, as we describe below, we use a procedure which allows us to determine the correct number of cycles even for such short waves.

Figure 4 shows the same diagram for the Bulgaria earthquake. Fundamental mode of group velocities was found for all four stations in the interval from 7 to 60 s. However, periods below 13.5 s are not coherent enough to allow reliable relative phase velocity measurement. On the other hand, even if the periods above 40 s are still very coherent, we cannot use them for the measurement of the phase velocities by such a small array. Assuming the group velocity of nearly 4 km/s and the period of 40 s, the wavelength is nearly 160 km. We measure only less than 1/4 of the wavelength for the waves longer than 40 s in case the waves propagate along the longest distance of our array and 1/15 of the wavelength in case of propagation in the direction of the smallest distance. As the determination of quasimonochromatic signal phases at both stations is affected by errors relatively increasing for longer waves, the mutual phase differences are distorted by a subtraction of two close numbers with high relative errors. In other words, the array measures the long wavelengths as one single station. So, due to the given design of the array, waves longer than 40 s are not used in our computation even for the events where clear fundamental modes were detected for periods as long as 60 or 80 s.

Table 2 gives the applicable period range for each event. For events, where the upper boundary is set to 40 s, the group velocity fundamental modes were actually found to be longer and we truncated the range due to the geometry of the array as in the case of the Bulgaria event. Lower boundaries of period ranges are selected according to the possibility of correct cycle number determination in case of the Poland event, or according to the sufficient coherency in case of more distant events (all other six events). Actually, we carried out the phase velocity measurement described in the next section for broader period range toward shorter waves at first, and according to the results, we truncated the phase velocity curves at the reliable period afterwards.

4 Phase velocity measurement

To provide the phase velocity measurement, we select the wavegroups corresponding to the fundamental mode. After the filtration in the frequency domain described in the previous section, we provide a tapering in the time domain. The right plot in Fig. 2 shows the selection of the wavegroups for four filters. As described earlier, dashed lines depict the quasimonochromatic signals and their envelopes. Bold lines show the tapered part of the signals with their tapered envelopes. The width of the time window depends on period—it is wider towards longer periods. It corresponds to the filters in the frequency domain being wider towards higher frequencies. Figure 5 summarizes both procedures. Left 3D plot shows the original spectrogram of the Greenland Sea earthquake record with time signal at the bottom and its spectrum along the left vertical axis. Right part of Fig. 5 shows the frequency time filtered spectrogram with corresponding filtered spectra along the right vertical axis and with corresponding time representation at the bottom. This wavegroup, filtered in the frequency domain and tapered in the time domain, represents the fundamental mode surface wavegroup—compare it with the original seismogram on the left. For all stations, records of given event are filtered by the same filters in the frequency domain and tapered by the same way in the time domain.

Fig. 5

Left plot: spectrogram of the Greenland Sea earthquake record with a seismogram and a spectrum plotted along the corresponding axes of the spectrogram. Right plot: spectrogram of the same record filtered and tapered along the fundamental mode. A corresponding seismogram and spectrum are also shown. Both spectrograms have the same color scale. The same bold black lines in both spectrograms represent the group velocity dispersion curve

At this stage, we have quasimonochromatic signals for a selected period range tapered around the fundamental mode ridge at all stations. Figure 6 gives an example of the Italy B event. Four top plots show raw seismograms at all stations. Middle 39 plots depict the filtered signals, and bottom plots represent filtered fundamental wavegroups as on the right bottom plot in Fig. 5 for the Greenland Sea event. Signals from DPC, OSTC, and UPC stations in Fig. 6 are shifted in time with respect to the CHVC station so as if the waves propagate along the geometrical great circle path with velocity of 3.6 km/s. We can see that longer period waves really match each other. In contrast, the waves of periods shorter than 15 s still do not correspond because their velocity is lower and also the true propagation direction does not coincide with the great circle backazimuth.

Fig. 6

Quasimonochromatic signals of the event from Italy B. The colors represent the four stations. Raw seismograms are shown at the top of the plot, 39 signals filtered in the frequency domain at the stated periods and tapered in the time domain along the fundamental mode are in the middle, and resulting fundamental surface wavegroups are shown at the bottom. The records are shifted in time with respect to the CHVC station with a lag corresponding to the propagation along the great circle path with a velocity of 3.6 km/s

The measurement of time differences between quasimonochromatic signals is accomplished according to the method described by Kolínský et al. 2011. Filtered and tapered quasimonochromatic signals are shifted in time sample by sample, and their correlation is computed for each time shift. One of the stations is set as a reference one, and time shifts corresponding to the highest correlation are determined consecutively for the other (three) stations. The time range of quasimonochromatic signal shifting is set according to the interstation distance so that it covers the delay of the lowest expected velocity as if the wave propagates right from one station to the other in case of the two most distant stations in the array. At this stage, we do not know the propagation direction, so the slowest case (longest time) is assumed. All other possible propagation directions result in shorter apparent time differences.

Several correlation maxima are found for pairs of quasimonochromatic signals of periods shorter than 13 s. This represents the uncertainty of an unknown number of cycles between the stations. For longer waves, this uncertainty vanishes as only one or fewer cycles take place for each station pair. A priori estimates of long-period velocities were used to select the proper number of wavelengths between the two stations, for example by Isse et al. (2000). We apply the same approach. We plot all the possible time differences (dispersion curves for travel times), and we select a quasimonochromatic signal of sufficiently long period so that only one time difference corresponds to an a priori estimated phase velocity. Usually, a period longer than 10 s is enough. For such long periods, other correlation maxima produce velocities which are several times lower than those a priori assumed.

Then we follow the continuous dispersion curve towards shorter periods. Thus, we select the proper dispersion curve even for waves much shorter than the interstation distance. Practically, this applies only for the Poland and Italy A events; as for the other ones, only longer periods are used.

The goal of the following step is to determine the true velocities and directions of surface wave propagation. Assuming the wave is planar, knowing the array geometry (interstation distance vector ${\overrightarrow{s}}_i$ for i-th station) and having the measured time differences Δt _i , we have a set of equations for two unknowns of the slowness vector ${\overrightarrow{p}}_i$ for each period:

$$ \begin{array}{ll}{\overrightarrow{s}}_i\cdot {\overrightarrow{p}}_i{\left|{}_k=\varDelta {t}_i\right|}_k\hfill & \mathrm{for}\;i-\mathrm{th}\;\mathrm{station}\;\mathrm{and}\;k\hbox{-} \mathrm{th}\;\mathrm{period}\hfill \end{array} $$

In case of an array of four stations, three time differences are determined with respect to the selected reference station and hence, three equations for two unknowns are available. A minimum number of stations needed for such computation is three—this applies to the Poland and Crete events in our study. In this minimalistic array geometry, we have just two equations for the two unknowns and hence, the solution is unique. In case of four stations, linear regression is used to determine the slowness vector of each quasimonochromatic signal. As a result, we have both the absolute value of the phase velocity as well as its direction.

Results of measurement and computation are given in Fig. 7. Phase velocities including true propagation backazimuths are shown. For each event, we consecutively set each of the stations as a reference one. It effectively represents a jackknife testing as for each event, we have four different measurements. For each reference station, three time differences are measured. Moving to the other station and considering it as a new reference one, only one of the time differences is the same as in the previous case and two others are different. Providing such repeated procedure for all the stations, we have four results. The differences of the four results give us an estimate of the observation errors. The waves are not strictly planar, each time difference based on correlation has its own error and linear regression still keeps unresolved time residua for each station pair. Figure 7 shows these consecutive measurements by the same color for each event. We can see that towards longer waves, the scatter of the measurements is higher. Georgia earthquake represents the worst results. In case of Poland and Crete events, where only three stations are used, the procedure is the same. However, the scatter of their results is almost none because it is always possible to fit a plane into three points. Therefore, theoretically, all three dispersion curves should be exactly the same. Figure 7 also shows that the mutual differences between the measurements using different events are greater towards longer waves.

Fig. 7

Determined dispersion curves. The colors represent different events. For each event, four (or three) dispersion curves are given corresponding to the measurement with respect to different stations. The solid black line shows the average dispersion curve representing a 1D characteristic of the target area. Errors of measurement for each period are given as the maximal scattering of all the measurements represented by the average of four (or three) measurements for each event

As a 1D characteristic of the target area, we compute an average dispersion curve shown by solid black line in Fig. 7. Its errors are estimated as the maximum deviation of determination for the given period from all events considering an average dispersion curve for each event (not shown in the figure). This keeps the uncertainty of dispersion curve determination identified by different events but eliminates the outlying errors of jackknife computations for each event. In case of the short-period part, where only one event was measured and hence no span of values is available, an error of 0.02 km/s is added.

Figure 8 shows the dispersion of backazimuths. Again, as in Fig. 7, we show all four (or three) measurements for each event (solid lines). Dashed lines represent geometrical great circle backazimuths. We again see that the Georgia event suffers from the highest backazimuth scatter.

Fig. 8

Backazimuths of propagation depending on periods. The solid lines show four (or three) measurements for each event. The dashed lines represent geometrical great circle backazimuths. For each event, these geometrical backazimuths are given for all stations. However, for more distant events, these values are close to each other

Figure 9 summarizes the results of phase velocity measurement. For each station and for each event, a set of color vectors is plotted. The color scale represents the periods of the waves in the whole range between 1 to 40 s. The direction of the vectors represents the measured phase velocity propagation backazimuths, and the length of the vectors corresponds to the absolute value of the phase velocity. Circles around each station denote the scaling of the velocities. Geometrical great circle backazimuths are also drawn for used events.

Fig. 9

The determined backazimuths and velocities show nearly the same pattern for all seven events at all four stations. The color scale represents periods in a range from 1 to 40 s. Length of the vectors represents the absolute value of the phase velocity, and their directions show the backazimuths. Blue, green and red circles denote three values of phase velocity, compare with Fig. 7. Geometrical backazimuths are given for all the events and stations, compare with Fig. 8

5 Inversion

To obtain the structural velocity of the HPFZ, we invert the determined dispersion curve shown in Fig. 7. We follow the procedure described by Kolínský and Brokešová (2007), which was used also by Kolínský et al. (2011) and by Gaždová et al. (2014). As an inversion technique, an isometric method (IM) is used. It is a fast algorithm developed by Málek et al. (2005) and tested by Málek et al. (2007). It combines features of several standard inverse methods, particularly the simplex method, Newton’s least squares method and simulated annealing. Typical tasks which are effectively solved by the IM are weakly nonlinear problems with tens of parameters. IM was successfully utilized in the above mentioned studies for inversion of dispersion curves.

The inversion is solved for 1D layered medium with v _p , v _s , and density being the parameters of each layer. The forward problem is solved by the modified Thomson-Haskell matrix method; see Thomson (1950), Haskell (1953) and Proskuryakova et al. (1981). During the inversion, the phase velocity dispersion curve is computed many times and the distance between theoretical and determined dispersion curve (misfit function) is minimized.

Surface waves depend predominantly on shear wave velocity, and hence, the inversion searches for the shear wave velocity directly. Starting model is set as a shear wave velocity piece-wise constant increasing with depth using the absolute value of the velocity in the first layer and a constant step for each successive layer. Many tests showed that the result does not depend on the starting model. However, by setting appropriate starting values, we can significantly lower the computational time. The starting model is set by trial and error approach: we change the two parameters manually (shear wave velocity of the first layer and the velocity step between the layers) so that the forward modeling produces a theoretical dispersion curve approximately matching the velocity range of the determined dispersion curve. This is usually achieved after a few trials. We can further constrain the inversion by prescribing the range of shear wave velocity difference between two neighboring layers. If this difference is allowed to be high, the inversion produces a curve which matches the observation well. However, the shear wave velocity distribution with depth usually shows unreliable oscillations between the layers when implausibly high velocity in one layer is balanced by implausibly low velocity in the next layer. By constraining the inversion too strongly, we may force the result to copy the starting model with no good match to the measured data.

In case of HPFZ phase velocity dispersion curve inversion, the starting model is chosen so that the shear wave velocity in the first layer of 100-m thickness is 1.3 km/s and in each next layer, this velocity is of 0.2 km/s higher. The constraining range in which the inversion procedure searches the velocity, is set to ±0.2 km/s from the starting velocity for the first layer. For the next layers, we prescribe that their difference from the neighboring upper layer can vary in the range from −0.2 to +1.2 km/s. It means, we a priori assume that the velocity increases with depth more than it decreases. This range is connected to the actual value in each layer and not to the starting model during the inversion. So, even strong low velocity zones can still be found. These constraints are very loose and do not influence the results as it has been proved by testing different values of them. However, they still avoid the unreliable oscillation of the velocity distribution.

Longitudinal velocity is strongly constrained and related to the shear wave velocity by the v _p /v _s ratio, as the Rayleigh wave propagation does not depend on the v_p significantly. The ratio is set to be 1.73 for the starting model, and the inversion is allowed to search for its final value in the range of ±0.05 from the starting value. Density is kept unchanged during the inversion. It is set to the value of 2.3 g/cm³ for the uppermost layer and to increase piece-wisely down to the half-space to the value of 3.58 g/cm³. The lowest values refer to Cretaceous and Permo-Carboniferous sediments (Ibrmajer and Suk 1989), whereas the highest values to olivine rich rocks of the upper mantle.

The layer thicknesses are set manually and are not changed during the inversion. However, several tests are made before the final layer layout is chosen. As we have no a priori information about the velocity model, we set a high number of layers for the preliminary tests to check how the inversion behaves and what velocity distribution with depth can be expected. Then, by contrast, we use a very limited number of layers to check the depth of Moho discontinuity. Finally, we use a set of 16 layers of increasing thickness above the half-space that corresponds to the decreasing resolution capability of longer periods of surface waves to the depth.

The inversion of the dispersion curve is highly non-unique. Nearly the same dispersion curves can be obtained in different structural models. It means that the minimum of the misfit function in the model space is very shallow. As the IM uses random values of parameters to generate new models, we obtain slightly different results even for the same starting parameters. To overcome this non-uniqueness of the inversion process, we use the method tested in Kolínský and Brokešová (2007), Kolínský et al. (2011) and used also in Gaždová et al. (2014). Inversion is computed many times, and mean velocity distribution with its standard deviation is then determined from all runs. To estimate the needed number of runs, we tested several pairs of inversion sets. We looked for such a number of runs, for which there was no difference in the resultant mean shear wave velocity distributions between the two testing sets. We found the number to be 20. For the final run, we use 50 inversions to be conservatively high above the estimated level. Figure 10 shows the determined dispersion curve from Fig. 7 by a bold black dashed line with errors. Dispersion curve corresponding to the mean velocity distribution is depicted by solid red line, and the absolute scatter of all inversion runs is drawn by dashed blue lines.

Fig. 10

Inversion fitting. The black dashed line shows the determined dispersion curve with errors, the same as in Fig. 7. The solid red line is the dispersion curve corresponding to the mean resultant velocity distribution and blue dashed lines represent the absolute scatter of all 50 inversion trials. The solid green lines show the curves corresponding to the mean low and mean high structure velocity estimates

The mean velocity distribution has several properties which differentiate it from single inversion runs. It is robust and not depending on particular random IM generation of the model as described above. In addition, it is also smoother than most of the single runs. The smoothness can be easily described quantitatively: for each particular inversion results as well as for the resultant mean distribution, an average of velocity contrasts between all layers is computed. This average of velocity contrasts is lower for the mean velocity distribution than for most of the single inversion result. The situation is plotted in Fig. 11. Open circles denote 50 inversion results in the average of velocity contrasts—misfit plane. Vertical axis shows the phase velocity misfit as an average value for one dispersion point. This “one point misfit” is used to allow comparing results for different dispersion curves with different numbers of determined points. Horizontal axis represents an average contrast between the shear wave velocities again related to the one layer boundary. Minimum, maximum, and mean values of both quantities are shown as well as the slope of the distribution. The filled black dot represents the position of the result for the mean velocity distribution. Its position is closest to the lowest value in terms of the 2D distribution of both quantities.

Fig. 11

Distribution of the results of 50 inversion runs (open circles) in the average of velocity contrasts—misfit plane for shear wave velocity-depth distribution. Minimum, maximum, and mean values of both quantities are given as well as the slope of the distribution. Filled black dot represents the position of the result for the mean velocity distribution

6 Results

During the inversion, sharper velocity contrast is allowed and may occur in an arbitrary depth. However, the unavoidable consequence of this multilayer approach is that the possible sharp velocity contrast of the real medium is blurred among several layers in a resulting model, see the tests in Kolínský et al. (2011).

Before the detailed layering of the model was used, we provided another test. Because the preliminary results showed a very smooth course of the structural velocities with depth, we were suspicious if the Moho discontinuity could not be blurred by the inversion. Thus, we constructed a very simplified three-layered model above the half-space with only two 1-km-thick layers near the surface and considering the whole crust as the third layer. The upper mantle was considered to be the half-space below these three layers. We tested 26 models where the manually set Moho discontinuity was changing its depth from 20 to 45 km with a 1-km step. We tried to resolve the appropriate depth of the Moho and to force the velocity contrast between the crust and the upper mantle to concentrate to the single layer boundary. The results of this test are presented in Fig. 12. For each of the 26 models, its misfit (the distance between the determined and the fitted dispersion curve) is plotted to the corresponding depth. We see that indication of Moho is possibly pronounced in the depths of 35 or 37 km where the misfit is the lowest. However, the misfit distribution with depth has no clear trend and so the depth is very uncertain. The velocity contrast is Δv _s  = 0.58 km/s and Δv _p = 1.08 km/s for the depth of 35 km and Δv _s = 0.58 km/s and Δv _p = 0.97 km/s for the depth of 37 km. However, this contrast, even not so high, is still overestimated by these models due to the lack of velocity gradient both in the crust and below the Moho.

Fig. 12

A set of 26 three-layered models for both v _p and v _s and misfit values for each prescribed Moho discontinuity depth

After that, we construct a 16-layer model above the half-space as described above and provide the whole procedure for estimating the structural velocities. One of the layer boundaries is set to 37 km—the possible Moho depth. We determine the shear and longitudinal wave velocities distribution with depth shown in Fig. 13 and summarized in Table 3. Mean velocities which result from the 50 inversion runs are shown by red lines and their standard deviations by blue lines. We notice a slightly increased uncertainty below the steep velocity gradient in the depth of 4 km and then again a gradually increasing scatter of velocities below the depth of 23 km. These standard deviations are relatively narrow; however, they still represent mostly the uncertainties caused by the inversion procedure itself rather than by the measurement.

Fig. 13

Resultant 1D velocity model. The solid red lines represent shear and longitudinal velocity, the blue lines show standard deviations of the results with respect to 50 inversion trials. Grey shaded areas shows the range of the mean low and mean high (green) estimates. The colors correspond to Fig. 10. All values are given also in Table 3. Purple dots represent the shear wave velocity distribution determined by Wilde-Piórko et al. (2005) for the DPC station

Table 3 Resultant shear and longitudinal velocities with v _p/v _s and low and high estimates for the HPFZ

To reveal the uncertainties of the model which are based on the errors of dispersion curve determination, we provide a conservative estimate of the lowest and the highest possible velocity distributions. We assume that, in the worst case, the whole determined dispersion curve is systematically shifted down (or up) to the limits given by the error bars in Figs. 7 and 10. We follow exactly the same inversion procedure as for the average determined dispersion curve with 50 inversion runs, and we compute two new velocity distributions corresponding to this low and high phase velocity dispersion curves. The results are shown by grey shaded areas in Fig. 13. The edges of the shaded areas (green lines) correspond to these extreme structural velocity distributions. Table 3 summarizes these estimates too. The absolute difference of the bigger of the two low/high estimates from the mean model is attached in the last two columns of the Table 3 for both wave types. Phase velocity dispersion curves corresponding to these low and high models are shown in Fig. 10 by green lines.

From Table 3, we see that for depths lower than 14 km, the velocities are sometimes switched. The low estimate produces higher velocities than the mean distribution, and the high estimate produces lower velocities. However, they are always in the range of the standard deviation of the mean model. This is due to the fact that measurement errors of the short-period part of the curve are generally lower than those towards the longer periods, and so, all three computations provided the same results in terms of their standard deviations for shorter periods—see coinciding green and red curves in Fig. 10 for periods 1–6 s as well as nearly the same velocities of all three models for depths shallower than 14 km. A systematic difference of the results is observed below the depth of 18 km where the low estimates of both v _s and v _p give lower values of structural velocities and the same applies for the high estimates which give higher values.

7 Comparison and discussion

Dispersion curve of a broad period range is determined, thanks to the use of the events in distances from 100 km up to 2,500 km. Nearer events lack long periods as they do not evolve so close to the epicenter (Poland), or because the events are of lower magnitude—see the magnitude and period ranges of Italy A and Italy B (Table 2) which are both of nearly the same distance. In case of distant events, shorter periods are attenuated or too scattered. Combining different epicentral distances and magnitudes allowed the construction of the dispersion curve which would not be possible to determine using only one event.

Measured backazimuths show continuous dependence on the period varying around the geometrical ones as shown in Fig. 8. For longer waves, they are almost identical with the great circle backazimuths for Greenland Sea and Italy B events. For Crete and Bulgaria events, coming from almost the same direction, for periods above 19 s, both measurements are systematically shifted towards higher backazimuths compared with the great circle ones. However, waves of periods below 19 s are significantly different for both events trending towards higher backazimuths in case of Crete and towards lower backazimuths in case of the Bulgaria earthquake. This could be caused by different epicentral distances and hence by different crustal properties along both paths. Georgia earthquake represents an event with the most varying measured backazimuths with the highest scatter. This is probably due to the long epicentral distance (although not the longest) and due to the complicated crustal structure along the paths from Caucasus to the Bohemian Massif. Poland event shows distinct deviation of short-period backazimuths below 3.5 s both from the longer period range and from the geometrical great circles. Also, the group velocity dispersion curves of this event are of complicated shape, see Fig. 3. The possibility of fundamental mode being misidentified with the first higher mode was excluded both by careful analysis of the dispersion ridge smooth behavior and by the fact that for the higher mode, the phase velocities would be significantly higher than those for the fundamental one. The velocities measured for Poland event for waves shorter than 3.5 s are, instead, significantly lower than those above 3.5 s, see Fig. 7.

Concerning the resultant velocity model in Fig. 13, the steep velocity gradient in the first 5 km well corresponds to the estimated sedimentary thickness of the Intrasudetic Depression—thicknesses exceeding 4 km were reported by Tásler (1979) and Mastalerz (1995) as stated before. This thickness also corresponds to the thickness of sediments derived from the gravity data (Bouguer anomalies) by Majdański et al. (2007). They, however, did not consider this value to be trustworthy, because it did not fit their tomography results.

Moho discontinuity is not implicated in our resultant model. Surface wave dispersion curve inversion smoothes sharp discontinuities when many layers are used for the model. However, even by searching the Moho depth considering only limited number of layers, only weak implication of Moho around the depths of 35 or 37 km was found, see Fig. 12, with a relatively small velocity contrast between the crust and upper mantel. This contrast is further blurred in the resultant model; however, the final model represents the velocity-depth distribution with higher accuracy and lower misfit. Majdański et al. (2007) give the Moho depth for the area of our interest around 33 km with an uncertainty of ±2 km.

For direct comparison, we chose the results published by Wilde-Piórko et al. (2005) because they focused on shear wave velocities as a contrast to other studies which dealt only with longitudinal velocities. Receiver functions technique was used to determine the structure down to the 60-km depth for selected stations across the Bohemian Massif. In Fig. 13, we reprint the shear wave velocity distribution for the DPC station by purple dots. It can be seen, that both velocity distributions are generally similar with the exception of the uppermost crust (1–5 km). The receiver functions did not image the high gradient beneath the DPC, which reflects the actual geological situation. The DPC station itself is located apart from the center of the array within the crystalline massif while the other three stations are situated within the Intrasudetic Depression with several kilometers of sedimentary cover. In the range between 5 and 9 km, velocities of both models are the same. Below this depth, receiver functions show both the low (10–26 km) and the high velocity zones (27–51 km) as more pronounced. It may be due to the fact that dispersion curve inversion smoothes the possible contrasts. However, even in the DPC receiver function model, the Moho discontinuity is only weakly pronounced by the gradient between 24 and 34 km.

8 Conclusion

The average phase velocity dispersion curve is determined for the HPFZ. Waves propagating from different sources with different backazimuths are used for the broad spectrum from 1 to 40 s. Computation is provided using the array technique which utilizes relative time shifts between the local stations and allows to determine simultaneously both the absolute value of the phase velocity as well as its true propagation backazimuth for each wavelength independently of the source parameters of the given event. Errors of the measurement are estimated. Inversion of the dispersion curve provides a determination of vertical distribution of seismic velocities v _s and v _p down to the depth of 65 km for the target area. Conservative low and high estimates are computed to show the range of possible velocity uncertainties. Down to the depth of 18 km, this model has a very low level of uncertainty, which enables us to use it for the local event localization.