Subsistence, Substitutability and Sustainability in Consumption

Abstract

We propose a representation of individual preferences with a subsistence requirement in consumption, and examine its implications for substitutability and sustainability. Specifically, we generalize the standard constant-elasticity-of-substitution (CES) utility specification for manufactured goods and environmental services, by adding a subsistence requirement for environmental services. We find that the Hicksian elasticity of substitution strictly monotonically increases with the consumption of environmental services above the subsistence requirement, and approaches the standard CES value as consumption becomes very large. Whether the two goods are market substitutes depends on the level of income. We further show that the subsistence requirement may jeopardize the existence of an intertemporally optimal and sustainable consumption path. Our results have important implications for growth, development and environmental policy.

1 Introduction

We develop a general and formal conceptual framework to examine the effect of a subsistence requirement in the consumption of environmental services on substitutability between manufactured goods and environmental services as well as the conditions for sustainable development.

The economic study of subsistence requirements in consumption has a rich history and dates back to Klein and Rubin (1947/48), Samuelson (1947/48), Geary (1950) and Stone (1954). More recently, subsistence requirements have been shown to be relevant in the growth, development and environmental economics literature (e.g. Garner 2010; Heal 2009a, b; King and Rebelo 1993; Kraay and Raddatz 2007; Matsuo and Tomoda 2012; Pezzey and Anderies 2003; Ravn et al. 2008; Steger 2000; Strulik 2010).

A common understanding of the term subsistence, as expressed for example in the Merriam-Webster English dictionary, is “the minimum (as of food and shelter) necessary to support life”. In the economic literature, subsistence is often conceptualized within a single consumption good framework to, inter alia, analyse savings behaviour, growth rates and the process of development (e.g. King and Rebelo 1993; Steger 2000; Strulik 2010). Moreover, the idea is applied in bivariate utility functions, where the subsistence requirement is related to abstract minimum consumption levels in order to analyse human capital formation (Matsuo and Tomoda 2012), or specifically as minimum nutrition levels. The latter is the case in Pezzey and Anderies (2003), who analyze the stability or collapse of resource based societies, such as the Easter Island civilization. Closest to our understanding of subsistence in terms of environmental services is Heal (2009a: 279), who suggests that utility derives from the consumption of manufactured goods as well as environmental services, and that there is a subsistence requirement of those environmental services—including water, air, and food—necessary for survival.

There is an on-going conceptual discussion on the notion of subsistence requirements (Alkire 2002; Heal 2009a, b; Max-Neef et al. 1991; Rauschmayer et al. 2011; Steger 2000). In particular, Sharif (1986: 555) has argued that it must go beyond a mere consideration of basic physical needs to encompass the “lowest standard of social desirability [concerning] the needs of physical and mental survival”.

Accordingly, we here understand subsistence as more than mere survival, namely as a minimum consumption level of a subsistence good characterizing individual preferences. Below that minimum level, the individual attaches absolute priority to subsistence; only above the subsistence level does the individual consider trade-offs with other goods. Such subsistence certainly includes the consumption of a certain amount of food, water and air, but may also include immaterial components, such as cultural ecosystem services.

Substitutability between different consumption goods and capital stocks plays a crucial role in environmental, resource, and sustainability economics (Markandya and Pedroso-Galinato 2007; Traeger 2011; Baumgärtner and Quaas 2010; Pezzey and Toman 2002; Quaas et al. 2013). It marks the core distinction between weak and strong sustainability (Gerlagh and van der Zwaan 2002; Neumayer 2010). We focus on substitutability in consumption and, in an application, restrict the analysis of sustainability to the discussion of intergenerational equity in the sense of non-declining utility over time.

The prevalent distinction between weak and strong sustainability in consumption rests on a simple constant-elasticity-of-substitution (CES) utility function with an environmental and a manufactured good, and concerns the question whether environmental services are necessary and essential to satisfy non-declining welfare over time. In this CES-framework, substitutability is determined by exogenous parameters, and can take any value between non-substitutability (a CES of zero) and perfect substitutability (a CES of infinity), where the case of a CES value of unity is often considered to mark the threshold between weak and strong sustainability. Several alternative models of variable substitutability have been formally studied so far. Gerlagh and van der Zwaan (2002) focus on the finiteness in terms of growth of consumption of environmental goods, while assuming that the consumption of manufactured goods can grow without bound. This allows them to distinguish short-term (instantaneous) and long-term substitutability and to assess long-term substitutability via the maximal utility level achievable with unlimited growth in the consumption of manufactured goods for a given consumption of the environmental good. Dupoux and Martinet (2015) assume that the substitutability between manufactured consumption goods and environmental quality is context-dependent and depends on the amounts of the two types of goods. Fenichel and Zhao (2015) assume that one can invest into a knowledge stock to increase the elasticity of substitution.

Here, we follow a proposal by Heal (2009a, b) and amend the utility function by introducing a subsistence requirement in terms of environmental services. This allows for non-substitutability to hold, i.e. a range of the consumption of the environmental good to exist where the utility function represents a lexicographic ordering. In this sense, our above definition of a subsistence requirement can be interpreted as an absolute limit to substitution between the two goods. Indeed, directly incorporating such a subsistence requirement in the consumption of environmental services may capture best the rationale underlying the prevalent discussions on limited substitutability (see Drupp 2015 for a more detailed discussion). For example, Dasgupta (2001:125) reminds us that “a large part of what the natural environment offers us is a necessity”. Heal (2009a, b) specifically suggests to examine substitutability between an environmental and a manufactured good in the presence of a subsistence requirement in terms of the environmental good by extending a CES utility function through including a survival threshold. Without providing a formal examination, Heal (2009a:279) conjectures that “the elasticity of substitution is not constant but depends on and increases with welfare levels.”

In this paper, we generalize and formalize this conjecture by Heal (2009a, b) and explore its implications for the economics of sustainability. We find that the Hicksian elasticity of substitution is non-constant and, above the subsistence threshold, strictly monotonically increases with the consumption of the environmental subsistence good or income. However, whether or not the goods are market substitutes does not only depend on the Hicksian elasticity of substitution but also on the level of income and the subsistence requirement. In a subsequent step, we apply this subsistence model to the analysis of optimal and sustainable use of a renewable natural resource. We find that a subsistence requirement may jeopardize the existence of an optimal consumption path that is also sustainable in the sense of non-declining utility over time and consumption being above the subsistence requirement.

2 A Model of Subsistence and Substitutability

There are two composite goods, an environmental service S with a subsistence requirement $\bar{S}$, and a manufactured consumption good X. The consumer’s preferences are represented by a utility function for $S,X\ge 0$:

$$\begin{aligned} U(S,X)=\left\{ \begin{array}{ll} U_l(S)&{}\quad \text {for}\ S\le \bar{S}\\ U_h(S,X)&{}\quad \text {else} \end{array}\right. \end{aligned}$$

(1)

where $U_l(S)$ strictly increases with S and $U_h(S,X)$ is twice continuously differentiable, strictly increasing in both arguments and strictly quasi-concave. Furthermore, the individual always prefers to be in the domain where the subsistence requirement is satisfied, i.e.

$$\begin{aligned} \inf \limits _{S> \bar{S},X\ge 0}U_h(S,X)>\sup \limits _{0\le S\le \bar{S}}U_l(S)\ . \end{aligned}$$

(2)

This represents the idea of a subsistence requirement in the consumption of environmental services: for $S\le \bar{S}$ the individual is not willing to consider trade-offs between the subsistence good S and the other good X, but lexicographically prefers more of S.¹

As an interesting and handy specification of $U_h(S,X)$ we suggest, following Heal’s (2009a, b) idea, a generalized modification of the Stone–Geary function (Geary 1950; Stone 1954) and the CES-function (Solow 1956; Arrow et al. 1961). Specifically, this extends an otherwise standard bivariate CES utility function by including a subsistence requirement $\bar{S}$ in terms of environmental services:² $^{,}$ ³

$$\begin{aligned} U_h(S,X)= \,\, \left[ \alpha \left( S-\bar{S}\right) ^{\theta }+ (1-\alpha ) X^{\theta }\right] ^{1/\theta }\,\, \quad \text {with}\quad -\infty <\theta \le +1,\ 0<\alpha <1\ . \end{aligned}$$

(3)

For $\bar{S}=0$, i.e. without subsistence requirement, this function reduces to the usual CES utility function, which contains as special cases perfect substitutes ($\theta =+1$), Cobb-Douglas ($\theta =0$) and perfect complements ($\theta \rightarrow -\infty$).

As a measure of substitutability between the two goods, we use the elasticity of substitution introduced by Hicks (1932[1963]), Robinson (1933) and Hicks and Allen (1934a, b).⁴

Definition 1

The elasticity of substitution is given by:

$$\begin{aligned} \sigma (S,X) \ := \ \frac{MRS}{X/S}\ \frac{d\,(X/S)}{d\,MRS}\ , \end{aligned}$$

(4)

where

$$\begin{aligned} {\textit{MRS}} \ := \ -\left. \frac{d\,X}{d\,S}\right| _{U(S,X)=\text {const.}} \quad =\quad \frac{\displaystyle \frac{\partial \,U(S,X)}{\partial \,S}}{\displaystyle \frac{\partial \,U(S,X)}{\partial \,X}}\ . \end{aligned}$$

(5)

The Hicksian elasticity of substitution measures substitutability between two goods along an indifference curve, as the elasticity of the ratio of the amounts of the two goods in a given allocation with respect to the marginal rate of substitution (MRS) between the two in that allocation. This is the most basic and a rather general measure of substitutability. In contrast to some more sophisticated measures it does not rely on further assumptions on individual behavior or institutional context, but characterizes individual preferences per se (Bertoletti 2005; Frondel 2011; Stern 2011).

Fig. 1

Sets of indifference curves for $\theta =0.5$ (left), and $\theta =-0.5$ (right) in the presence of a subsistence requirement $\bar{S}$ (dashed line). The dotted blue 45$^{\circ }$ line highlights that preferences are non-homothetic. (Color figure online)

For utility function (1), the MRS (5) is not defined in the domain $S\le \overline{S}$. As the individual is not willing to trade off S for X when $S\le \overline{S}$, we plausibly extend Definition 1 by defining $\sigma$ to be equal to zero for all $S\le \overline{S}$.

Following Hicks (1932 [1963: 296]), we define the elasticity of substitution for the affinely homothetic utility function (3) with respect to the true origin ($S=0,X=0$; see Fig. 1). This is in contrast to Brown and Heien (1972) or Beckman and Smith (1993), who define the elasticity of substitution with respect to the subsistence requirement bundle ($S=\bar{S},X=0$), thus confining themselves to a standard CES setting.

3 Results

In this section, we derive the Hicksian elasticity of substitution between the two composite goods, environmental services and manufactured goods, analyse its properties in preference space (Sect. 3.1), and subsequently examine substitutability in a market setting (Sect. 3.2). Both settings are of relevance to the economic analysis of environmental services, as some, but by far not all, of environmental goods and services are traded on markets.

3.1 Subsistence and Substitutability in Preference Space

To start with, we recover the standard case discussed in the literature. For $\bar{S}=0$, i.e. without subsistence requirement, utility function (1) with specification (3) reduces to the usual CES utility function with

$$\begin{aligned} \sigma (S,X)=\frac{1}{1-\theta }=\text {const.} \end{aligned}$$

(6)

The parameter $\theta$ completely determines the elasticity of substitution, with the special cases of perfect substitutes ($\theta =1$; $\sigma =\infty$), Cobb-Douglas ($\theta =0$; $\sigma =1$) and perfect complements ($\theta \rightarrow -\infty$; $\sigma =0$).

If, in contrast to this well-established case, there is a finite subsistence requirement in the consumption of environmental services, one obtains:

Proposition 1

For $\bar{S}>0$, the elasticity of substitution of utility function (1) with specification (3) is given by

$$\begin{aligned} \displaystyle \displaystyle \sigma (S,X) \ = \ \left\{ \begin{array}{ll} \quad 0&{}\text {for}\ S \le \bar{S}\\ \displaystyle \frac{1}{1-\theta }\,\left[ 1-\frac{ \displaystyle (1-\alpha )\displaystyle \frac{\bar{S}}{S}}{\alpha \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta }+(1-\alpha )}\right] &{}\text {else.} \end{array}\right. \ . \end{aligned}$$

(7)

Proof

See Appendix 1. $\square$

By (extended) Definition 1, the elasticity of substitution is zero as long as the subsistence requirement, $S>\bar{S}$, is not yet satisfied. In the domain where subsistence consumption is satisfied, the value of $\sigma$ is in particular determined by the parameter value of $\theta$ and the amounts consumed of both goods (S, X), and the subsistence requirement $\bar{S}$.

Proposition 2

For $S>\bar{S}$, $\sigma (S,X)$ (Eq. 7) has the following properties:

$$\begin{aligned} 0\quad <\quad \sigma (S,X)< & {} \frac{1}{1-\theta }\quad \text {for all}\ S,X \end{aligned}$$

(8)

$$\begin{aligned} \sigma (S,X)\rightarrow & {} 0\quad \text {for}\ \theta \rightarrow -\infty \end{aligned}$$

(9)

$$\begin{aligned} \frac{d\,\sigma (S,X)}{d\,S}> & {} 0\quad \text { for }\theta \ge 0\end{aligned}$$

(10)

$$\begin{aligned} \sigma (S,X)\rightarrow & {} \begin{Bmatrix} 0 \\ \alpha \\ \frac{1}{1-\theta } \end{Bmatrix} \quad \text {for}\ S\rightarrow \bar{S}\ \ \ \ \text {and}\ \ \theta \gtreqqless 0 \end{aligned}$$

(11)

$$\begin{aligned} \sigma (S,X)\rightarrow & {} \frac{1}{1-\theta }\quad \text {for}\ S\rightarrow \infty \end{aligned}$$

(12)

$$\begin{aligned} \frac{d\,\sigma (S,X)}{d\,\bar{S}}< & {} 0\quad \text { for }\theta \ge 0\end{aligned}$$

(13)

$$\begin{aligned} \sigma (S,X)\rightarrow & {} \frac{1}{1-\theta }\quad \text {for}\ \bar{S}\rightarrow 0\end{aligned}$$

(14)

$$\begin{aligned} \sigma (S,X)\rightarrow & {} +\infty \quad \text {for}\ \theta \rightarrow 1 \end{aligned}$$

(15)

Proof

See Appendix 2. $\square$

The elasticity of substitution is positive, but for all levels of consumption of the two goods strictly smaller than the standard non-subsistence CES value (Properties 8, 9). That is, the subsistence requirement shifts the relationship between the two goods towards (stronger) complementarity.

For non-negative values of $\theta$ the elasticity of substitution in any given allocation is the greater, the higher the consumption of S (Property 10). This confirms Heal’s (2009a:279) conjecture that the elasticity of substitution increases with the welfare level—for a given level of X, welfare is monotonically increasing in S. As the consumption of S approaches the subsistence requirement from above, the elasticity of substitution approaches zero for $\theta >0$, is equal to the share $\alpha$ of S for $\theta =0$, and approaches the CES value for $\theta <0$ (Property 11). As consumption of the subsistence good goes to infinity, the elasticity of substitution approaches the CES value (Property 12). This is an intuitive result: The subsistence threshold becomes irrelevant in this case and we are back in the standard CES setting.

For non-negative values of $\theta$ the elasticity of substitution is the smaller, the higher the subsistence requirement (Property 13), i.e. a stronger subsistence requirement shifts the relationship between the two goods towards (stronger) complementarity. In the limit case where no subsistence requirement exists, the elasticity of substitution approaches the CES value (Property 14). When $\theta$ approaches unity, the elasticity of substitution becomes infinite, irrespectively of the level of consumption of $S>\bar{S}$ or X (Property 15): Above the subsistence threshold, the two goods are perfect substitutes at the margin for $\theta =1$.

Fig. 2

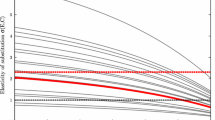
Elasticity of substitution $\sigma (S,X)$ (Eq. 7) as a function of consumption of the subsistence good S for $\theta =0.5$ (left) and $\theta =-0.5$ (right). The subsistence requirement $\bar{S}$ is depicted by the dashed line

Figure 2 shows a plot of $\sigma (S,X)$ (Eq. 7) as a function of S for different signs of $\theta$. Importantly, for $\theta >0$ (Fig. 2 left), a subsistence good that is a substitute to the other good when available in large quantity ($\sigma >1$ for high S), can change to become a complement as its availability is reduced ($\sigma <1$ low S).⁵ An obvious example would be water.

In contrast, for $\theta <0$ (Fig. 2 right) the subsistence good is a complement to the other good at all levels of S.

3.2 Subsistence and Substitutability in a Market Setting

Having analyzed the elasticity of substitution in preference space, we now add institutional context to the analysis by invoking a competitive-market setting with given income m and prices $p_S$ and $p_X$. The utility-maximizing allocation of the two goods under the budget constraint is then given by the respective Marshallian demand functions $S^{\star }(m, p_S, p_X)$ and $X^{\star }(m, p_S, p_X)$.

Proposition 3

The elasticity of substitution in the utility-maximizing allocation, $\sigma ^{\star }:= \sigma (X^{\star } , S^{\star })$, has the following properties:

$$\begin{aligned} \sigma ^{\star }=0 \quad \text { for } \quad m \le p_S \bar{S}\ . \end{aligned}$$

(16)

For $m > p_S \bar{S}$, the following holds:

$$\begin{aligned} 0\quad <\quad \sigma ^{\star }< & {} \frac{1}{1-\theta } \end{aligned}$$

(17)

$$\begin{aligned} \frac{d\,\sigma ^{\star }}{d\, m}> & {} 0 \end{aligned}$$

(18)

$$\begin{aligned} \sigma ^{\star }\rightarrow & {} \frac{\alpha }{\alpha +(1-\alpha ) \left[ \frac{\alpha }{1-\alpha }\frac{p_X}{p_S}\right] ^{\frac{\theta }{\theta -1}}}\,\frac{1}{1-\theta } <\frac{1}{1-\theta } \quad \text { for } \quad m \rightarrow p_S\,\bar{S}\end{aligned}$$

(19)

$$\begin{aligned} \sigma ^{\star }\rightarrow & {} \frac{1}{1-\theta } \quad \text { for } \quad m \rightarrow \infty \end{aligned}$$

(20)

$$\begin{aligned} \frac{d\,\sigma ^{\star }}{d\, \bar{S}}< & {} 0 \end{aligned}$$

(21)

For $\theta >0$, there is a threshold value of income

$$\begin{aligned} m^P=p_S\,\bar{S}\,\frac{1-\theta }{\theta }\,\left( \frac{1-\alpha }{\alpha }\right) ^{\frac{1}{1-\theta }}\,\left( \frac{p_S}{p_X}\right) ^{\frac{\theta }{1-\theta }} \end{aligned}$$

(22)

such that

$$\begin{aligned} \sigma ^{\star }\lesseqqgtr 1 \quad \text {for}\quad m\lesseqqgtr m^P. \end{aligned}$$

(23)

Proof

See Appendix 3. $\square$

Property (16) is by (extended) Definition 1: the elasticity of substitution between the two goods in the optimal allocation is zero as long as income is not high enough to afford a consumption level satisfying the subsistence requirement.

Properties (17)–(21) correspond to the statements of Proposition 2 about $\sigma (S,X)$ but are considerably stronger, as they now hold for all values of the CES-parameter $\theta$. In particular, for $m>p_S \bar{S}$ the elasticity of substitution in the optimal allocation strictly monotonically increases with income (Property 18) and decreases with the subsistence requirement (Property 21).

Again, the elasticity of substitution approaches the standard CES value as income goes to infinity (Property 20). However, for finite income, the elasticity of substitution between the two goods is strictly lower in the presence of a subsistence requirement compared to the CES case (Property 17).

For $\theta > 0$, there is a threshold level of income $m^P$ (Eq. 22), so that the two goods are substitutes (complements) in terms of the Hicksian elasticity of substitution for incomes above (below) $m^P$ (Property 23). As stated previously, the subsistence requirement shifts the relationship between the two goods towards complementarity. It depends on the level of income whether or not this effect is strong enough to turn substitutes ($\sigma >1$ in the absence of a subsistence threshold) into complements. For a sufficiently small income, $m<m^P$, the subsistence requirement has an effect strong enough that the two goods become complements. This threshold $m^P$ increases with the subsistence requirement $\bar{S}$ and the price of the subsistence good $p_S$, it decreases with the price of the other good $p_X$.

Finally, we analyze whether the two goods are market substitutes (complements) in the sense that if the price of one good increases the demand for the other goods increases (decreases):

Proposition 4

For $m> p_S \overline{S}$, the cross-price effects on the Marshallian demand of the two goods are as follows:

$$\begin{aligned} \frac{d\,S^{\star }}{d\, p_X}&\gtreqqless \, 0&\quad \text {for} \quad \theta \gtreqqless 0\ ,\end{aligned}$$

(24)

$$\begin{aligned} \frac{d\,X^{\star }}{d\, p_S}&< 0&\quad \text {for} \quad \theta \le 0\ . \end{aligned}$$

(25)

For $\theta >0$, there exists a threshold value of income

$$\begin{aligned} m^M=\frac{p_S\,\bar{S}}{\theta }+m^P \end{aligned}$$

(26)

such that

$$\begin{aligned} \frac{d\,X^{\star }}{d\, p_S} \lesseqqgtr 0\quad \text {for}\quad m\lesseqqgtr m^M. \end{aligned}$$

(27)

Proof

See Appendix 4. $\square$

Fig. 3

Optimal consumption of S and X for low income (left, $m=1.7$) and high income (right, $m=5$) in the case $\theta =0.5$ and $\overline{S}=1$. The subsistence requirement $\bar{S}$ is depicted by the black dashed line, indifference curves as solid red lines, and budget constraints in dotted blue for $p_X=1$ and two values of $p_S$, $p_S^1=0.8$ and $p_S^2=1$. At low income (left), an increase of $p_S$ from $p_S^1$ to $p_S^2$ decreases demand for X; at high income (right), the same increase of $p_S$ increases demand for X. (Color figure online)

Whether S is a market-substitute for X only depends on the sign of the CES parameter $\theta$ (Result 24). The effect of an increase of $p_S$ on the demand for X is more nuanced: X is a market-complement for S if $\theta \le 0$ (Result 25). For $\theta >0$, whether X is a market-substitute for S depends on all model parameters,⁶ and in particular on income: X is a substitute for S only for sufficiently high income, and a complement otherwise (Result 27).

The threshold value of income $m^M$ (Eq. 26) that determines market substitutability is a simple additive extension to the income threshold that determines the Hicksian elasticity of substitution (Eq. 22). The threshold level $m^M$ increases with the subsistence requirement $\bar{S}$ and the price of the subsistence good $p_S$, it decreases with the price of the other good $p_X$. The intuition behind Result (26) is that as the price of the subsistence good increases, it requires higher income to meet the subsistence requirement, thus also shifting the market-substitutability relationship towards complementarity (see Fig. 3).

4 Application: Sustainable Consumption

In this section, we illustrate the effect of the subsistence requirement for an environmental service on the sustainable use of a renewable resource. This is a standard problem of resource economics and relevant, for example, for fishery or forestry. It is well known that for standard resource properties and a standard utility function with no subsistence requirement an intertemporally optimal consumption path exists, which is also sustainable if the initial resource stock is not larger than the steady-state stock size (Clark 1990). We show here that a subsistence requirement in an otherwise standard setting may jeopardize this result: with a subsistence consumption requirement it becomes more ambitious to have an optimal consumption path that is also sustainable, and it may even be that no such path exists.

To this end, we study an intertemporal optimization problem where the environmental service $S_t$ at time t is the harvest from the current stock $R_t$ of a renewable resource. We employ utility function (1) as the instantaneous utility function. For the sake of focus and simplicity, we assume that the manufactured consumption good is exogenously supplied in constant quantity, $X_t=\bar{X}$ for all t.

The intertemporally optimal harvesting/consumption path $\{S_t\}$ is the solution to the following problem:

$$\begin{aligned} \begin{array}{lll} \displaystyle \max _{\{S_t\}}\int \limits _0^T U(S_t,\bar{X})\,e^{-\delta \,t}\,dt &{}\quad \text { subject to}&{} \quad \dot{R}_t=g(R_t)-S_t\ ,\\ &{}&{}\quad R_0\ge 0\ \text {given}, \end{array} \end{aligned}$$

(28)

with time horizon $T>0$, discount rate $\delta >0$, and $g(\cdot )$ being the natural growth function of the resource stock which fulfills the standard assumptions $g(0)=0$, $g(K)=0$ for some carrying capacity $K>0$, $g(R)>0$ and $g''(R)<0$ for all $R\in (0,K)$. The instantaneous utility function U(S, X) is of the subsistence type (Eq. 1). For $U_h(S,X)$, we assume specification (3), which implies that $U_h(S,X)\ge 0$. We further assume $U_l(S)<0$ (to assure that property (2) holds), $U_l'(S)>0$ and $U_l''(S)<0$ for all $S\in (0,\bar{S})$.

The current-value Hamiltonian for problem (28) is

$$\begin{aligned} H_t=U(S_t,\bar{X})+\lambda _t\,\left( g\left( R_t\right) -S_t\right) \ , \end{aligned}$$

(29)

from which we derive the first-order conditions for an interior solution

$$\begin{aligned} \frac{\partial U(S_t,\bar{X})}{\partial S}&=\lambda _t\ ,\end{aligned}$$

(30)

$$\begin{aligned} \frac{\dot{\lambda }_t}{\lambda _t}+g'\left( R_t\right)&=\delta \ , \end{aligned}$$

(31)

together with given $R_0\ge 0$ and the transversality condition $\lambda _T\,R_T=0$.

Before we discuss the existence and sustainability of a solution, we define two particular stock sizes for reference. First, the stock size $R_\delta$ is defined by

$$\begin{aligned} g'\left( R_\delta \right) =\delta \ . \end{aligned}$$

(32)

Second, the stock size $\underline{R}$ is implicitly defined as the smaller of the two solutions of

$$\begin{aligned} g\left( \underline{R}\right) =\bar{S}\ , \end{aligned}$$

(33)

if two solutions exist. As illustrated by Fig. 4, $\underline{R}$ may be smaller or larger than $R_\delta$, depending on the natural growth dynamics of the resource.

Fig. 4

Phase diagrams for optimal resource use with subsistence requirement. Parameter values are $\delta =0.15$, $\alpha =0.5$, $\bar{S}=0.12$, $\bar{X}=1$; and $g(R)=r\,R\,(1-R)$ with $r=0.6$ (left panel) and $r=0.5$ (right panel)

We are now equipped to formulate the following proposition.

Proposition 5

• 1. If $R_0<\underline{R}$ there exists a $\bar{T}>0$ such that for $T>\bar{T}$ optimization problem (28) has no solution satisfying $S_t>\bar{S}$ for all $t\le T$.⁷

• 2. If $R_0>\underline{R}$ optimization problem (28) has a solution satisfying $S_t\ge \bar{S}$ for all $t\le T$ and all $T>0$. In particular,

  • (a) if $g(R_\delta )>\bar{S}$ the optimal steady-state stock size is $R_\delta$ and the optimal steady-state harvest rate is $g(R_\delta )>\bar{S}$;

  • (b) if $g(R_\delta )<\bar{S}$ the optimal steady-state stock size is $\underline{R}$ and the optimal steady-state harvest rate is $g(\underline{R})=\bar{S}$.

Proof

See Appendix 5. $\square$

Proposition 5 states that an optimal consumption path that exceeds the subsistence requirement at all times exists if and only if the initial resource stock is large enough. If the initial resource stock is not large enough, the optimal consumption path exceeds the subsistence requirement at all times only if the time horizon is not too large.

It follows directly from the defining Eq. (33) and the assumptions on the growth function g(R) that

$$\begin{aligned} \frac{d\underline{R}}{d\bar{S}}&=\frac{1}{g'(\underline{R})}>0\quad \text {and} \end{aligned}$$

(34a)

$$\begin{aligned} \lim \limits _{\bar{S}\rightarrow 0}\underline{R}&=0\ . \end{aligned}$$

(34b)

Hence, the larger the subsistence requirement $\bar{S}$ for the environmental service, the larger the range of initial stock sizes $R_0$ and time horizons T for which optimization problem (28) has no solution with $S_t>\bar{S}$ for all $t\le T$ (cf. Proposition 5, statement 1). Conversely, for $\bar{S}=0$, optimization problem (28) simplifies to a standard problem in renewable-resource economics, which always has a solution (Clark 1990).⁸

The substitution parameter $\theta$ has no effect on the optimal steady state, which is not surprising for a renewable resource model without harvesting costs. It has, however, an effect on the optimal transition dynamics, as illustrated in Fig. 4.

We now bring to this setting the notion of sustainability in consumption. As sustainability is about the long-term future, we let $T\rightarrow \infty$ in optimization problem (28).

Definition 2

A consumption path $\{S_t\}$ is called sustainable if and only if for all $t>0$, $dU(S_t,\bar{X})/dt\ge 0$, i.e. utility is non-declining over time, and $S_t>\bar{S}$, i.e. the subsistence requirement is satisfied at all times.

Because manufactured-goods consumption is constant over time, $dU(S_t,\bar{X})/dt\ge 0$ is equivalent to $\dot{S}_t\ge 0$, which, in turn, is equivalent to $\dot{R}_t\ge 0$ along an optimal path. That is, along an optimal consumption path, non-declining utility is equivalent to a non-declining resource stock. In the simple setting considered here, thus, Definition 2 of sustainability comprises both weak and strong sustainability.⁹ With this notion of sustainability, we arrive at the central proposition of the application.

Proposition 6

If $R_0<\underline{R}$ or $g(R_\delta )<\bar{S}$, there exists no optimal consumption path that is sustainable.

Proof

See Appendix 6. $\square$

Proposition 6 states that an optimal consumption path that forever exceeds the subsistence requirement and that leads to non-declining utility over time (“sustainable consumption”) is not feasible if the initial resource stock or the growth rate of the renewable resource are too low (cf. right panel of Fig. 4). This sustainability problem is in addition to the well known sustainability problem under standard utility assumptions (that is, an initial resource stock that is too large; cf. Footnote 8), and is due to the subsistence threshold $\bar{S}$.

While an empirical quantification or real-world application of the theoretical model analyzed here is beyond the scope of this paper, it is a relevant area of future research. Clearly, in many cases of natural resource use worldwide we have a situation where harvested ecosystem services provide subsistence for people, e.g. food, water or life-support regulating services, and where the resource stocks by now are at a critically low level as a consequence of past mismanagement and overuse. Then, Proposition 6 suggests that sustainable development (in the sense of Definition 2) may simply be impossible under the economic and ecological constraints assumed in the model—namely if the current resource stock, or its growth rate, is below some critical value that depends on the subsistence threshold. Having an empirical estimate of these parameter values is therefore crucial for sustainability policy.

5 Conclusions

We have proposed a formal description of individual preferences with a subsistence requirement in consumption in an otherwise standard CES utility specification. We have studied how substitutability between an environmental service subsistence good and another manufactured good depends on the subsistence requirement and the level of consumption of the two goods. Furthermore, we have applied this model to analyze the effect of the subsistence requirement on the sustainable management and consumption of a renewable resource.

We find that (i) a subsistence requirement shifts the substitutability relationship between goods towards complementarity; (ii) the Hicksian elasticity of substitution is equivalent to the non-subsistence CES value only if the subsistence good or income is available in an infinite amount; (iii) above the subsistence threshold, the elasticity of substitution strictly monotonically increases with income; (iv) whether the two goods are market substitutes or complements depends on the level of income and the subsistence requirement; (v) in an otherwise standard renewable resource management problem, a subsistence requirement may jeopardize the existence of an optimal consumption path that is also sustainable. While our analysis is set in the framework of a specific functional form—a simple extension of an otherwise standard CES utility function—our main results remain valid under more general preference specifications.

Our key result that with a subsistence requirement, substitutability between different consumption goods is non-constant but increases with the consumption of the subsistence good or individual income, has important implications for growth, development and environmental policy. These need to be explored by further research, and we can think of several fruitful areas.

First, the role of income distribution for the Pareto-efficiency of market equilibrium allocations needs to be reassessed for preferences characterized by a subsistence requirement. One could examine a two-household model in which one household may have an insufficient budget to meet the subsistence requirement. This may lead, inter alia, to poverty traps in subsistence economies.

Second, since substitutability between manufactured goods and environmental services is a key issue in the appraisal of climate policies (Heal 2009a, b; Sterner and Persson 2008), the application of our model may have directly relevant implications for the optimal management of climate change due to higher relative prices of environmental services. In this vein, Drupp (2015) applies this model to dual discounting of ecosystem services and manufactured goods.

Third, the standard result of growth and resource economics by Solow (1974) that a constant consumption path forever is feasible even if production essentially depends on a non-renewable resource needs to be qualified: if the Solowesque constant consumption level is below the subsistence threshold, one would not like to think of that solution as “sustainable”.

Fourth, the explicit discussion of environmental services that are necessary to meet human subsistence needs is related to, and may contribute to, the discussion of critical natural capital and safe minimum standards (Ciriacy-Wantrup 1952; Bishop 1978; Ekins 2003). Moreover, our results are analogously relevant for substitutability in production, when some part of natural capital is ‘critical’.

Fifth, in the prominent discussion of sustainable development, the distinction between weak and strong sustainability is vindicated on the grounds of different degrees of substitutability between human-made and natural capital and the respective services (Neumayer 2010; Traeger 2011). With our preference-model in a general-equilibrium setting, the distinction between weak and strong sustainability becomes endogenous, as the elasticity of substitution depends on the level of income.

Appendices

Appendix 1: Proof of Proposition 1

With utility function (3), the marginal rate of substitution for $S>\bar{S}$ (Eq. 5) is

$$\begin{aligned} {\textit{MRS}} = \frac{\displaystyle \frac{\partial \,U_h(S,X)}{\partial \,S}}{\displaystyle \frac{\partial \,U_h(S,X)}{\partial \,X}} = \frac{\alpha }{1-\alpha } \left[ \frac{ S- \bar{S}}{ X} \right] ^{ \theta -1} = \frac{\alpha }{1-\alpha } \left[ \frac{S}{X}\left( 1-\frac{\bar{S}}{S}\right) \right] ^{\theta -1}\ , \end{aligned}$$

(35)

so that

$$\begin{aligned} \frac{{\textit{MRS}}}{(X/S)}= \frac{\alpha }{1-\alpha } \left( \frac{S}{X}\right) ^{\theta }\left( 1-\frac{\bar{S}}{S}\right) ^{\theta -1} \end{aligned}$$

(36)

and

$$\begin{aligned} \frac{d\,{\textit{MRS}}}{d\,(X/S)}= & {} \frac{\alpha (\theta -1)}{1-\alpha } \left[ \frac{S}{X}\left( 1-\frac{\bar{S}}{S}\right) \right] ^{\theta -2} \left\{ \frac{d(S/X)}{d(X/S)}\left( 1-\frac{\bar{S}}{S}\right) + \frac{S}{X}\frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\right\} \end{aligned}$$

(37)

$$\begin{aligned}= & {} \frac{\alpha (\theta -1)}{1-\alpha } \left[ \frac{S}{X}\left( 1-\frac{\bar{S}}{S}\right) \right] ^{\theta -2} \left\{ -\left( \frac{X}{S}\right) ^{-2}\left( 1-\frac{\bar{S}}{S}\right) + \frac{S}{X}\frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\right\} .\quad \end{aligned}$$

(38)

With (36) and (38), the elasticity of substitution (4) becomes

$$\begin{aligned} \sigma (S,X)= & {} \frac{{\textit{MRS}}}{X/S}\ \frac{d\,(X/S)}{d\,{\textit{MRS}}} = \frac{{\textit{MRS}}}{X/S}\ \left( \frac{d\,{\textit{MRS}}}{d\,(X/S)}\right) ^{-1} \end{aligned}$$

(39)

$$\begin{aligned}= & {} \left( \frac{S}{X}\right) ^{\theta }\left( 1-\frac{\bar{S}}{S}\right) ^{\theta -1} \frac{1}{\theta -1}\ \left[ \frac{S}{X}\left( 1-\frac{\bar{S}}{S}\right) \right] ^{2-\theta }\nonumber \\&\times \left\{ -\left( \frac{X}{S}\right) ^{-2}\left( 1-\frac{\bar{S}}{S}\right) + \frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\frac{S}{X}\right\} ^{-1}\end{aligned}$$

(40)

$$\begin{aligned}= & {} \frac{1}{1-\theta }\left\{ 1-\frac{\frac{X}{S}}{\left( 1-\frac{\bar{S}}{S}\right) } \frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\right\} ^{-1}\ . \end{aligned}$$

(41)

To calculate the remaining derivative, we transform the problem from the standard variables (S, X) into the following variables (w, v):

$$\begin{aligned} w&:=\frac{X}{S}\end{aligned}$$

(42)

$$\begin{aligned} v&:= \alpha \left( S-\bar{S}\right) ^\theta + (1-\alpha ) X^\theta , \end{aligned}$$

(43)

where w is the ratio of the two consumption goods and v is a monotonic transformation of the utility function, so that $v={\textit{constant}}$ is equivalent to $U(S,X)={\textit{constant}}$. Derivatives under the constraint $U(S,X)={\textit{const}}.$, i.e. along an indifference curve, are now taken along $v={\textit{const}}.$, or $dv=0$.

From (43), using (42), we have

$$\begin{aligned} \left( 1-\frac{\bar{S}}{S}\right)&=\left[ \frac{v}{\alpha S^\theta }- \frac{1-\alpha }{\alpha } w^\theta \right] ^{\frac{1}{\theta }} \ , \end{aligned}$$

(44)

such that

$$\begin{aligned}&\displaystyle \frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)} =\frac{d\left[ \frac{v}{\alpha S^\theta }- \frac{1-\alpha }{\alpha } w^\theta \right] ^{\frac{1}{\theta }}}{dw}\end{aligned}$$

(45)

$$\begin{aligned}&\displaystyle =-\left[ \frac{v}{\alpha S^\theta }- \frac{1-\alpha }{\alpha } w^\theta \right] ^{\frac{1}{\theta }-1}\,\left( \frac{v}{\alpha S^{\theta +1}}\,\frac{dS}{dw}+ \frac{1-\alpha }{\alpha }w^{\theta -1}\right) \end{aligned}$$

(46)

Totally differentiating (43), and using $dv=0$, yields

$$\begin{aligned}&0&=\theta \,\left[ \alpha \left( S-\bar{S}\right) ^{\theta -1}+ (1-\alpha )w^\theta \, S^{\theta -1}\right] \,dS+\theta (1-\alpha )\,S^\theta \,w^{\theta -1}\,dw \end{aligned}$$

(47)

$$\begin{aligned} \Leftrightarrow&\frac{dS}{dw}&=-\frac{(1-\alpha )S^\theta \,w^{\theta -1}}{\alpha \left( S-\bar{S}\right) ^{\theta -1}+(1-\alpha )w^\theta \, S^{\theta -1}} \end{aligned}$$

(48)

Using (46) and (48), we have:

$$\begin{aligned}&-\frac{\frac{X}{S}}{\left( 1-\frac{\bar{S}}{S}\right) } \frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\nonumber \\&\quad = \frac{\frac{X}{S}}{\left( 1-\frac{\bar{S}}{S}\right) }\,\left[ \frac{v}{\alpha S^\theta }- \frac{1-\alpha }{\alpha } w^\theta \right] ^{\frac{1}{\theta } -1}\,\left( \frac{v}{\alpha S^{\theta +1}}\,\frac{dS}{dw}+ \frac{1-\alpha }{\alpha }w^{\theta -1}\right) \end{aligned}$$

(49)

$$\begin{aligned}&\quad =-\frac{X}{S}\,\left( 1-\frac{\bar{S}}{S}\right) ^{-\theta }\,\left( \frac{v}{\alpha S^{\theta +1}}\,\frac{(1-\alpha )S^\theta \,w^{\theta -1}}{\alpha \left( S-\bar{S}\right) ^{\theta -1}+(1-\alpha ) S^{\theta -1}\,w^\theta }-\frac{1-\alpha }{\alpha }w^{\theta -1}\right) \end{aligned}$$

(50)

$$\begin{aligned}&\quad =-\left( \frac{X}{S}\right) ^\theta \,\left( 1-\frac{\bar{S}}{S}\right) ^{-\theta }\, \left[ \frac{v(1-\alpha )}{\alpha ^2 S\,\left( S-\bar{S}\right) ^{\theta -1}+\alpha (1-\alpha ) X^{\theta }}- \frac{1-\alpha }{\alpha } \right] \end{aligned}$$

(51)

$$\begin{aligned}&\quad =-X^\theta \,(S-\bar{S})^{-\theta }\, \left[ \frac{v(1-\alpha ) - \alpha (1-\alpha ) S\,\left( S-\bar{S}\right) ^{\theta -1} - (1-\alpha )^2 X^{\theta }}{\alpha ^2 S\,\left( S-\bar{S}\right) ^{\theta -1}+\alpha (1-\alpha ) X^{\theta }} \right] \end{aligned}$$

(52)

$$\begin{aligned}&\quad =-X^\theta \,\left( S-\bar{S}\right) ^{-\theta }\, \frac{(1-\alpha )\left( S-\bar{S}\right) ^{\theta }- (1-\alpha ) S \left( S-\bar{S}\right) ^{\theta -1}}{\alpha S\,\left( S-\bar{S}\right) ^{\theta -1}+ (1-\alpha ) X^{\theta }}\end{aligned}$$

(53)

$$\begin{aligned}&\quad =(1-\alpha )X^\theta \,\frac{\frac{S}{S-\bar{S}}-1}{\alpha S \left( S-\bar{S}\right) ^{\theta -1}+ (1-\alpha )X^\theta } . \end{aligned}$$

(54)

Plugging this into (41) yields

$$\begin{aligned} \sigma (S,X)&=\frac{1}{1-\theta }\left\{ 1-\frac{\frac{X}{S}}{\left( 1-\frac{\bar{S}}{S}\right) } \frac{d\left( 1-\frac{\bar{S}}{S}\right) }{d(X/S)}\right\} ^{-1}\end{aligned}$$

(55)

$$\begin{aligned}&=\frac{1}{1-\theta }\left\{ 1+(1-\alpha )X^\theta \,\frac{\frac{S}{S-\bar{S}}-1}{\alpha S \left( S-\bar{S}\right) ^{\theta -1}+ (1-\alpha )X^\theta } \right\} ^{-1}\end{aligned}$$

(56)

$$\begin{aligned}&=\frac{1}{1-\theta }\,\left[ \frac{\alpha S\left( S-\bar{S}\right) ^{\theta -1}+(1-\alpha )X^\theta }{\alpha S\left( S-\bar{S}\right) ^{\theta -1}+(1-\alpha )X^\theta \,\frac{S}{S-\bar{S}}}\right] \end{aligned}$$

(57)

$$\begin{aligned}&=\frac{1}{1-\theta }\,\left[ \frac{\alpha \left( \frac{S-\bar{S}}{X}\right) ^{\theta -1}+(1-\alpha )\frac{X}{S}}{\alpha \left( \frac{S-\bar{S}}{X}\right) ^{\theta -1}+(1-\alpha )\frac{X}{S-\bar{S}}}\right] \end{aligned}$$

(58)

$$\begin{aligned}&= \frac{1}{1-\theta }\,\left[ 1-\frac{ (1-\alpha )\displaystyle \frac{\bar{S}}{S}}{\alpha \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta }+(1-\alpha )}\right] . \end{aligned}$$

(59)

Appendix 2: Proof of Proposition 2

Results (8), (9), (11), (12), (14) and (15) can easily be verified.

Proof of Result (10):

$$\begin{aligned} \frac{d\,\sigma }{d\, S}= \frac{1}{1-\theta }\, \frac{1-\alpha \bar{S}}{S^2}\,\frac{\left[ \displaystyle \alpha \left( \frac{\theta S}{X} \left[ \frac{S-\bar{S}}{X}\right] ^{\theta -1}+ \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta }-1 \right) +1 \right] }{\left( 1-\alpha + \alpha \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta }\right) ^2} >0\quad \text { for }\theta \ge 0. \end{aligned}$$

(60)

Proof of Result (13):

$$\begin{aligned} \frac{d\,\sigma }{d\,\bar{S}}= \frac{1}{\theta -1}\, \frac{1-\alpha }{S}\,\frac{\left[ \displaystyle \frac{\theta \alpha \bar{S}}{X} \left[ \frac{S-\bar{S}}{X}\right] ^{\theta -1}+ (1-\alpha )+ \alpha \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta } \right] }{\left( 1-\alpha + \alpha \displaystyle \left[ \frac{S-\bar{S}}{X}\right] ^{\theta }\right) ^2} <0\quad \text { for }\theta \ge 0. \end{aligned}$$

(61)

Appendix 3: Proof of Proposition 3

The consumer requires $m= p_S \bar{S}$ to meet her subsistence needs $\bar{S}$. This means that up to this level of income she is not willing to substitute S for X, i.e. $\sigma ^{\star }=0$. For $m> p_S \bar{S}$, she faces the utility maximization problem

$$\begin{aligned} {\max \limits _{S, X} \, U_h(S,X)} \qquad \text {s.t.} \qquad p_S S + p_X X \le m\ . \end{aligned}$$

(62)

The Lagrangian and first-order conditions are:

$$\begin{aligned} {\mathcal {L}}(S,X, \mu )= & {} \left[ \alpha \left( S-\bar{S}\right) ^{\theta }+ (1-\alpha ) X^{\theta }\right] ^{1/\theta } + \, \mu (m - p_S S - p_X X ) \end{aligned}$$

(63)

$$\begin{aligned} \frac{\partial \, {\mathcal {L}}}{\partial \, S}= & {} 0 \ \Leftrightarrow \ \alpha (S- \bar{S})^{(\theta -1)} \left[ \alpha (S- \bar{S})^{\theta } + (1- \alpha ) X^{\theta } \right] ^{(1/\theta -1)} = \mu p_S\end{aligned}$$

(64)

$$\begin{aligned} \frac{\partial \, {\mathcal {L}}}{\partial \, X}= & {} 0 \ \Leftrightarrow \ (1-\alpha ) X^{(\theta -1)} \left[ \alpha (S- \bar{S})^{\theta } + (1- \alpha ) X^{\theta } \right] ^{(1/\theta -1)} = \mu p_X \end{aligned}$$

(65)

$$\begin{aligned} \frac{\partial \, \mathcal { L}}{\partial \,\mu }= & {} 0 \ \Leftrightarrow \ p_S S + p_X X = m \end{aligned}$$

(66)

From conditions (64) and (65), we obtain

$$\begin{aligned} \frac{\alpha }{1-\alpha } \left[ \frac{ (S- \bar{S})}{ X} \right] ^{\theta -1} = \, \frac{p_S}{p_X} . \end{aligned}$$

(67)

Rearranging gives

$$\begin{aligned} X = (S- \bar{S}) \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} }\ . \end{aligned}$$

(68)

Inserting (68) into (66) and solving for S yields the Marshallian demand function

$$\begin{aligned} S^{\star }(m, p_S, p_X)= \frac{m+ p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } }{ p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } }\ . \end{aligned}$$

(69)

Inserting (69) into (68) yields the Marshallian demand function

$$\begin{aligned} X^{\star }(m, p_S, p_X) = \frac{m- p_S \bar{S} }{ p_X + p_S \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ -\frac{1}{ \theta -1} } }\ . \end{aligned}$$

(70)

Inserting (69) and (70) into Eq. (7) yields the Hicksian elasticity of substitution in the utility-optimal allocation ($X^{\star }$, $S^{\star }$):

$$\begin{aligned} \displaystyle \displaystyle \sigma ^{\star }= & {} \displaystyle \frac{1}{1-\theta }\,\left[ 1-\frac{ \displaystyle (1-\alpha )\,\bar{S} \, \, \displaystyle \frac{ p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } }{m + p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } } }{(1-\alpha )+\alpha \displaystyle \left[ \frac{\displaystyle \frac{m+ p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } }{ p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } } -\bar{S}}{\displaystyle \frac{m- p_S \bar{S} }{ p_X + p_S \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-1}{ \theta -1} } } }\right] ^{\theta }}\right] \end{aligned}$$

(71)

$$\begin{aligned} \displaystyle \displaystyle= & {} \displaystyle \frac{1}{1-\theta }\,\left[ 1-\frac{ (1-\alpha )\,\bar{S} \, \, \left( p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } \right) }{ \left( m + p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } \right) \left( \alpha \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-\theta }{ \theta -1} } +(1-\alpha ) \right) } \right] \end{aligned}$$

(72)

$$\begin{aligned}= & {} \frac{1}{1-\theta }\,\left[ \frac{m \left( (1-\alpha ) + \alpha \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-\theta }{ \theta -1} } \right) }{ (1-\alpha ) \bar{S} \left( p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } \right) + m \left( (1-\alpha ) + \alpha \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-\theta }{ \theta -1} } \right) } \right] \ .\nonumber \\ \end{aligned}$$

(73)

Solving the equation $\sigma ^{\star }=1$ for $m=m^P$ we obtain (22).

From Eq. (73) it can easily be seen that as income m goes to infinity, the elasticity of substitution $\sigma ^{\star }$ approaches standard CES result in absence of a subsistence requirement:

$$\begin{aligned} \displaystyle \sigma ^{\star } \rightarrow \frac{1}{1-\theta } \quad \text {for}\ m\rightarrow \infty \ . \end{aligned}$$

(74)

Furthermore, the elasticity of substitution monotonically increases with income,

$$\begin{aligned} \frac{d\,\sigma ^{\star }}{d\, m}= \, \frac{1}{1-\theta }\, \left[ \frac{ (1-\alpha ) \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{2\theta +1}{ \theta -1} } \left( p_X + p_S \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } \right) \left( (1-\alpha ) + \alpha \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{\theta }{ \theta -1} } \right) }{ \left( \alpha m + (1-\alpha ) \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{\theta }{ \theta -1} } \left( m + p_S \bar{S} + p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1}} \right) \right) ^2 } \right] >0. \end{aligned}$$

(75)

and decreases with an increasing subsistence requirement

$$\begin{aligned} \frac{d\,\sigma ^{\star }}{d\, \bar{S}}= \, \frac{1}{\theta -1}\, \left[ \frac{ (1-\alpha ) m \left( p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } \right) \left( (1-\alpha ) + \alpha \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{\theta }{ \theta -1} } \right) }{ \left( \alpha m \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{\theta }{ \theta -1} } + (1-\alpha ) \left( m + p_S \bar{S} + p_X \bar{S} \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1}} \right) \right) ^2} \right] <0. \end{aligned}$$

(76)

Appendix 4: Proof of Proposition 4

The cross-price derivatives of the Marshallian demand functions for S and X are obtained from Eqs. (69) and (70) and have the following properties:

$$\begin{aligned} \frac{d\,S^{\star }}{d\, p_X}= & {} \frac{\theta }{\theta -1}\, \left[ \frac{ ( p_S \bar{S} - m) \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1} } }{ \left( p_S + p_X \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{1}{ \theta -1}} \right) ^2 } \right] \quad \gtreqqless \, 0 \quad \text {for} \quad \theta \gtreqqless 0 \end{aligned}$$

(77)

$$\begin{aligned} \frac{d\,X^{\star }}{d\, p_S}= & {} \frac{1}{\theta -1}\, \left[ \frac{ \bar{S} \left( (1-\theta ) p_X + p_S \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-1}{ \theta -1} } \right) - \theta m \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-1}{ \theta -1} } }{ \left( p_X + p_S \left[ \frac{\alpha }{1-\alpha } \frac{p_X}{p_S} \right] ^{ \frac{-1}{ \theta -1}} \right) ^2 } \right] , \end{aligned}$$

(78)

with

$$\begin{aligned} \frac{d\,X^{\star }}{d\, p_S}&\left\{ \begin{array}{r} \rightarrow \infty \\ =-(1-\alpha )\frac{\overline{S}}{p_X} < 0 \\ < 0\end{array}\right\} \,&\quad \text {for} \quad \theta \begin{Bmatrix} \rightarrow 1 \\= 0 \\ < 0 \end{Bmatrix}. \end{aligned}$$

(79)

Solving the equation $dX^{\star }/dp_S=0$ for m, we obtain (26). It is further easy to verify that $\frac{d^2 X^{\star }}{dp_S dm}>0$ for $\theta >0$.

Appendix 5: Proof of Proposition 5

Use $S_t^\star$ to denote the solution of the optimization problem (28) that satisfies $S_t^\star >\bar{S}$ for all $t\le T$, and $R_t^\star$ to denote the corresponding development of the resource stock. Then $R_t^\star \le \hat{R}_t$ where the dynamics of $\hat{R}_t$ are described by $\dot{R}_t=g(R_t)-\bar{S}$ with $R_0^\star =\hat{R}_0=R_0$ given. Furthermore,

$$\begin{aligned} \frac{\partial \hat{R}_0}{\partial t}=g\left( \hat{R}_0\right) -\bar{S}<0 \end{aligned}$$

(80)

and hence

$$\begin{aligned} \frac{\partial \hat{R}_t}{\partial t}&=g\left( \hat{R}_t\right) -\bar{S}<0 \end{aligned}$$

(81)

$$\begin{aligned} \frac{\partial ^2\hat{R}_t}{\partial t^2}&=g'\left( \hat{R}_t\right) \, \frac{\partial \hat{R}_t}{\partial t}<0. \end{aligned}$$

(82)

Thus there must be some $\hat{T}<\infty$ where $\hat{R}_t=0$, and hence $R_t^\star =0$ for all $t>\hat{T}$. This contradicts the assumption $S_t^\star >\bar{S}$ for all $t>\bar{T}$ with $\bar{T}\le \hat{T}$.

Appendix 6: Proof of Proposition 6

Because of Proposition 5 (statement 1), an optimal solution where the subsistence requirement is exceeded forever, i.e. with $T\rightarrow \infty$, exists only for $R_0>\underline{R}$. In this case, Proposition 5 (statement 2b) implies that if $g(R_{\delta })<\underline{R}$ the optimal harvest rate is $S_t=\bar{S}=const.$ and the optimal steady state stock level is $\underline{R}$, which is monotonically approached (Acemoglu 2009). Thus, the subsistence requirement is not exceeded at any time.