Keywords

1 Introduction

In the recent times, the development of the smart homes has drastically increased with the availability of various smart sensors and energy-efficient resources. Several smart devices like the smartphones, televisions, HVAC (heating, ventilation, and air conditioning) systems, etc., have contributed to the growth of these smart homes. These technologies employ several sensors for acquiring data from varying locations. So, it is quite difficult to infer the actual location of a target sensor node (SN) due to the ubiquity of scattering objects and multiple transmission paths. Thus, for transmission in indoor environments (IEs), the ultra-wideband (UWB) technology is considered to be the most reliable approach for facilitating communication between the smart devices [1,2,3,4, 26]. The UWB technology has marked a prime development in wireless communication industries, with the ability to support high data rate transmission over a short range. It also consumes less power which makes it an energy-efficient choice for personal area networks (PANs). The time of arrival (TOA)-based ranging is used distinctively with the UWB technology for localizing the sensors in a wireless sensor network (WSN). The TOA ranging can make complete utilization of the high bandwidth and appropriately manages the time delay resolution of the UWB technology [14, 15].

In IEs, the data transmission path between the source and the sink can be located either by using a line of sight (LOS) or non-line of sight (NLOS) propagation. In smart homes, the NLOS propagation indicates a lack of direct communication path between the source and the sink, due to the presence of obstacles, viz., furniture and walls. A major concern with indoor complex networks is the transmission of data over the UWB channel in NLOS environments. The execution of a TOA-based UWB communication relies on accessibility of a direct signaling path between the source and the sink [10]. Thus due to the ambiguity in the existence of an explicit data path between the source and the sink, the TOA localization can exhibit significant variations in its range.

In this paper, we employ a straightforward approach to characterize the variations in range by using the well-known Tsallis’ entropy framework. This framework was proposed to depict the consolidation of the power-law behavior and tail fluctuations of dynamical systems in statistical mechanics [5,6,7,8,9]. We first consider the localization of SNs by using the UWB-based TOA approach to infer the location of an SN. In IEs, the uncertainties in range caused due to multiple paths can be characterized by using the proposed model, i.e., the \(q-\)Gaussian distribution which is determined by maximizing the Tsallis entropy. Here, we consider a network of sensor nodes supporting multipath transmission; thus, a prior information about the location of a set of SNs is essential in order to infer the location of other SNs in the network. Therefore, by using an efficient sensor localization techniques, the initial cost associated with the deployment of SNs, as well as the cost for powering each node in a WSN, can be reduced greatly. As we are considering a multipath UWB communication between the SNs, the prime source of error is due to the presence of multiple paths between the transmitter and the receiver. Therefore, due to the presence of these errors originating from various points in a WSN, the estimates obtained using the TOA localization get degraded [10, 16]. So, it becomes quite challenging and inevitable to characterize the variations in range for multipath communication channels. Here, we employ maximum Tsallis’ entropy framework subjected to the normalization constraint, and the first two moment constraints, which yields the \(q-\)Gaussian distribution. The different values of the non-extensive parameter q characterize the variations in range. Beck and Cohen [18] proposed a superstatistics framework for modeling complex systems, by averaging over the environmental fluctuations. Thus by following [18], we design a mixture model for the variations in range by incorporating the fluctuations caused due to multipath components.

We also present a robust technique for estimation of the parameters corresponding to the PDFs of the mixture model and the proposed model, in order to characterize the synthetic data.

The rest of this paper is as follows: Sect. 2 illustrates the problem statement. In Sect. 3, we derive the \(q-\)Gaussian distribution using the maximum Tsallis’ entropy framework. The parameter estimation techniques corresponding to the mixture model and our proposed model are discussed in Sect. 4. Section 5 deals with the characterization of range for different values of q. Finally, in Sect. 6 we provide the conclusion and future works.

2 Problem Statement

When a signal travels from the sender (or transmitter) to a receiver, then its propagation time can be estimated by using the TOA technique. Generally, TOA estimation is used along with UWB technology for an energy-efficient ranging in IEs with multiple propagation paths. We use localization of SNs to quantify the signal obtained from a heterogeneous set of sensors. Figure 1 illustrates the deployment of several SNs in a smart home. These SNs are positioned abundantly throughout the smart home and can be used to sense diverse indoor environments.

Fig. 1
figure 1

Deployment of multiple sensors in a smart home environment

Full size image
Fig. 2
figure 2

Variations in range under the presence of multiple paths in IEs

Full size image

Figure 2 shows the existence of multiple transmission paths in ubiquity of several interfering objects. These signals undergo scattering and reflection due to interference of several objects present in an indoor environment. The interfering objects scatter the waves while being transmitted from the transmitter (Tx) to the receiver (Rx) which leads to difficulty in identifying the actual location of a target node.

We can model the UWB channels having multipath components by utilizing the impulse response [11], i.e.,

$$\begin{aligned} h\left( t \right) = \sum \limits _{l = 0}^m {{a_l}\delta \left( {t - {\tau _l}} \right) }, \end{aligned}$$
(1)

where \({a_l}\) is the amplification factor for the lth multipaths and \({\tau _l}\) represents the time delay of the channel.

Therefore, using Eq. (1), the received signal corresponding to the TOA estimate can be characterized using [13] as

$$\begin{aligned} {r_{i,l}}\left( t \right) = \sum \limits _{i = 0}^n {\sum \limits _{l = 0}^m {{a_{i,l}}s\left( {t - {\tau _ {i,l}}} \right) + {n_ {i,l}}\left( t \right) } }, \end{aligned}$$
(2)

where \(s \left( t \right) \) represents the transmitted signal and \({n_ {i,l}}\left( t \right) \) denotes the additive white Gaussian noise. Thus, it can be observed that under NLOS conditions these channels reflect dense multipath effects and time delays which may affect the overall performance of the system.

Let us consider the sensor nodes to be deployed in an indoor environment. If we consider the TOA ranging for determining the location of the sensor nodes, then their range can be given as

$$\begin{aligned} {r_i} = d_i + {n_i}\,,\,\,\,\,i = 0,1,2, \ldots , n, \end{aligned}$$
(3)

where \({r_i}\) is the measure of the range between a source and receiver for ith sensor nodes and \({d_i}\) is the distance between the source and the ith sensor and can be stated as

$$\begin{aligned} {d_i} = ||x - {x_1}|{|_2} = \sqrt{{{\left( {x - {x_i}} \right) }^2} + {{\left( {y - {y_i}} \right) }^2}}, \end{aligned}$$
(4)

here, \(\left( x,y \right) \in X\) is a set of remote source locations and \(\left( {x_i},{y_i} \right) \in {X_i}\) is the set of recognized coordinates of the ith sensor, and \({n_i}\) is the additive white Gaussian noise, such that \({n_i} \sim N \left( 0, {\sigma _i}^2 \right) \).

Thus if we characterize the range in terms of a Gaussian distribution [19], then its probability density function (PDF) can be expressed as

$$\begin{aligned} f({r_i}) = \frac{1}{{\sqrt{2\pi } {\sigma _i}}}{{\mathrm{e}}^{ - \frac{{{{\left( {{r_i} - {d_i}} \right) }^2}}}{{2{\sigma _i}^2}}}}, \end{aligned}$$
(5)

where \({r_i} \sim N \left( {d_i}, {\sigma _i}^2 \right) \), with \({\sigma _i}^2\) representing the variance corresponding to \({r_i}\).

However, the variations \(\left( {\sigma _i}^2 \right) \) in the range \({r_i}\) can be characterized by inverse Gamma distribution [17, 18, 20]. So, the parameter \({\sigma _i}\) can be considered to be a random variable such that

$$\begin{aligned} {\beta _i} = \frac{1}{{{\sigma _i}^2}} \sim Gamma \left( {a,b} \right) , \end{aligned}$$
(6)

where a and b are the shape and scale parameters, and \({\beta _i}\) is the inverse of the variations caused in the range for ith SNs.

Let \(g\left( {{\sigma _i}} \right) \) be the variational range distribution and be defined as

$$\begin{aligned} g\left( {{\sigma _i}} \right) = \frac{1}{{{b^a}\Gamma \left( a \right) }}{\beta _i}^{a - 1}{{\mathrm{e}}^{ - \frac{{{\beta _i}}}{b}}},\,\,\,\,{\beta _i} \ge 0. \end{aligned}$$
(7)

The PDF for the gamma distribution in compliance with the synthetic data is illustrated in Fig. 5.

The unconditional distribution of range is obtained by averaging over the gamma distribution [17, 25],

$$\begin{aligned} p\left( {{r_i}} \right) = \int \limits _0^\infty {f\left( {{r_i}|{\sigma _i}} \right) g\left( {{\sigma _i}} \right) {\text {d}}{\sigma _i}}, \end{aligned}$$
(8)

where \({f \left( {r_i}|{\sigma _i} \right) }\) is the conditional probability distribution of \({r_i}\) for a given \({\sigma _i}\).

Now, we have

$$\begin{aligned} p\left( {{r_i}} \right) = \int \limits _0^\infty {\sqrt{\frac{{{\beta _i}}}{{2\pi }}} } {{\mathrm{e}}^{ - \frac{{{\beta _i}{{\left( {{r_i} - {d_i}} \right) }^2}}}{2}}}\frac{1}{{{b^a}\Gamma \left( a \right) }}{\beta _i}^{a - 1}{{\mathrm{e}}^{ - \frac{{{\beta _i}}}{b}}}\frac{1}{2}{\left( {{\beta _i}} \right) ^{ - \frac{3}{2}}}{\text {d}}{\beta _i}. \end{aligned}$$
(9)

So, the probability distribution corresponding to the variations in range observed in an indoor multipath environment is given as

$$\begin{aligned} p\left( {{r_i}} \right) = \frac{{\Gamma \left( {a - 1} \right) }}{{2\sqrt{2\pi } {b^a}\Gamma \left( a \right) }}{\left[ {\frac{1}{b} + \frac{{{{\left( {{r_i} - {d_i}} \right) }^2}}}{2}} \right] ^{ - \left( {a - 1} \right) }}. \end{aligned}$$
(10)

The above mixture model along with the synthetic data is shown in Fig. 6.

3 Proposed Model

In order to obtain accuracy in inferring the location of SNs in an IE, we need to characterize the variations in the measurement of the range observed due to multipath components. If we consider \({r_i}\) to be a random variable, then by applying Tsallis entropy [6, 7, 21,22,23], the uncertainties in the range obtained in Eq. (3) can be characterized through the non-extensive parameter q and is expressed as

$$\begin{aligned} {S_q}\left( {{r_i}} \right) = \frac{{1 - \int \nolimits _{ - \infty }^\infty {\left[ {f_q}\left( {{r_i}} \right) \right] ^q} {\text {d}}{r_i} }}{{q - 1}} . \end{aligned}$$
(11)

Here, we investigate the probability distribution corresponding to the variations in range for smart home sensors by maximizing the Tsallis entropy framework subjected to the normalization constraint and the moment constraints.

Thus, the constraint for normalization can be given as

$$\begin{aligned} \int \limits _{ -\infty }^\infty {{f_q}} \left( {{r_i}} \right) {\text {d}}{r_i} = 1. \end{aligned}$$
(12)

The first two constraints for the moments of \({r_i}\) can be specified as

$$\begin{aligned} \int \limits _{ - \infty }^\infty {{f_{\mathrm{es}}}} \left( {{r_i}} \right) {r_i}{\text {d}}{r_i} = \mu , \end{aligned}$$
(13)

and

$$\begin{aligned} \int \limits _{ - \infty }^\infty {{f_{\mathrm{es}}}} {\left( {{r_i} - \mu } \right) ^2}{\text {d}}{r_i} = {\sigma ^2}, \end{aligned}$$
(14)

where \(\mu \) and \({\sigma ^2}\) indicate the mean and variance.

Therefore, the probability distribution in Eqs. (13) and (14) corresponding to any probability \({f_q}\) can be expressed as

(15)

where \({f_{\text {es}} \left( {{r_i}} \right) }\) denotes the escort probability and is used to represent the asymptotic decay of q moments. Since we are using a parameter q, so the type of expectation used for defining the variations in the range is called the \(q-\)expectation. Thus, by considering the Lagrangian, for any stationary SN, we can optimize the range of the received signal as

$$\begin{aligned} \begin{aligned} L\left( {{f_q},{r_i}} \right)&= \frac{{1 - \int _{ - \infty }^\infty {{f_q}} {{\left( {{r_i}} \right) }^{^q}}{\text {d}}{r_i}}}{{\left( {q - 1} \right) }} + {\omega _1}\left( {1 - \int \limits _{ - \infty }^\infty {{f_q}} \left( {{r_i}} \right) {\text {d}}{r_i}} \right) \\&\quad + {\omega _2}\left( {\mu - \int _{ - \infty }^\infty {{r_i}{f_{\text {es}}}\left( {{r_i}} \right) {d_i}} } \right) + {\omega _3}\left( {{\sigma ^2} - \int _{ - \infty }^\infty {{f_{\text {es}}}} {{\left( {{r_i} - \mu } \right) }^2}{\text {d}}{r_i}} \right) , \end{aligned} \end{aligned}$$
(16)

where \({\omega _1},{\omega _2}\) and \({\omega _3}\) are the Lagrangian parameters. Now by employing the Euler–Lagrange equation, we have

$$\begin{aligned} \frac{{\partial L}}{{\partial {f_q}\left( {{r_i}} \right) }} - \frac{{\text {d}}}{{{\text {d}}{r_i}}}\left( {\frac{{\partial L}}{{\partial {f_q}'\left( {{r_i}} \right) }}} \right) = 0 \end{aligned}$$
(17)

Thus, by using Eq. (17) in association with Eqs. (11)–(16), we have

(18)

where \(z = \sigma \sqrt{\frac{{\left( {3 - q} \right) \pi }}{{q - 1}}} \frac{{\Gamma \left( {\frac{{3 - q}}{{2q - 2}}} \right) }}{{\Gamma \left( {\frac{1}{{q - 1}}} \right) }}\) and is called the normalization constant. From Eq. (18), we obtain the maximum value for the entropy probability distribution corresponding to the variations in range of the TOA estimate.

4 Parameter Estimation

In this section, we discuss the parameter estimation for the mixture model obtained in Eq. (10) and the proposed \(q-\)Gaussian distribution obtained in Eq. (18). The shape parameter ‘a’ and scale parameter ‘b’ of the mixture distribution can be estimated through the probability distribution of ‘\({\sigma _i}\)’. The random variable \({\sigma _i}\) is defined as

$$\begin{aligned} {\sigma _i} \left( {{r_i}} \right) \equiv {\left[ {\frac{1}{N} \sum \limits _{\tau = 1}^N {\left| {{v_\tau }\left[ {t:t + \tau } \right] } \right| } } \right] ^2},\,\,\,\,i = 1,2,\ldots ,n, \end{aligned}$$
(19)

where N is the number of samples per time stamp \(({\tau })\) and \({v_\tau }\) represents the variations in the range within the interval \(\left[ {t,t + \tau } \right] \).

The estimate of non-extensive parameter ‘q’ can be expressed through the generalized Jensen–Shannon (JS) symmetric measure. Thus, the symmetric JS divergence measure can be defined as

$$\begin{aligned} \begin{aligned} {\text {JS}}\left( {{f_q}\left( {{r_i}} \right) ||g\left( {{r_i}} \right) } \right)&= \frac{1}{2}{\text {KL}}\left( {{f_q}\left( {{r_i}} \right) ||\frac{{{f_q}\left( {{r_i}} \right) + g\left( {{r_i}} \right) }}{2}} \right) \\&\quad + \frac{1}{2}{\text {KL}}\left( {g\left( {{r_i}} \right) ||\frac{{{f_q}\left( {{r_i}} \right) + g\left( {{r_i}} \right) }}{2}} \right) \end{aligned} \end{aligned}$$
(20)

where \(KL\left( . \right) \) is the generalized Kullback–Leibler measure. This measure provides the distance between the proposed distribution \({f_q}\left( {r_i} \right) \) and the empirical distribution \(g\left( {{r_i}} \right) \) [7, 24]. Thus, the KL measure is given as

$$\begin{aligned} {\text {KL}}\left( {{f_q}\left( {{r_i}} \right) ||g\left( {{r_i}} \right) } \right) = \sum \limits _{k = 1}^n {{f_{{q_k}}}} \left( {{r_i}} \right) {\log _2} \left| {\frac{{{f_q}\left( {{r_i}} \right) }}{{{g_k}\left( {{r_i}} \right) }}} \right| \end{aligned}$$
(21)

The optimal value corresponding to the non-extensive parameter q is attained at which the symmetric JS divergence is minimum.

Thus, the optimal value of the \({\hat{q}}\) estimate provides a closed agreement between the synthetic data and the proposed theoretical distribution. Therefore, the optimal value of q is estimated as

$$\begin{aligned} \hat{q} = \mathop {\arg \min }\limits _{q \in \left( {1,3} \right) } \left\{ {{\text {JS}}\left( {{f_q}\left( {{r_i}} \right) ||g\left( {{r_i}} \right) } \right) } \right\} \end{aligned}$$
(22)

5 Results and Discussion

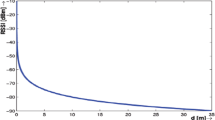
In this section, we plot the PDF for the maximum entropy obtained in Sect. 3 for the different values of q, viz., \(q=1.5\) (proposed model), \(q=1.37\) and \(q=1.45\). It can be observed that at \(q=1.5\), our model successfully captures the variations in range caused due to indoor multipath propagation. It is worth noting that for \(q=1.5\) (as shown in Fig. 3), the model exhibits the long memory behavior and extensively entails the extreme fluctuations in the range. In order to validate our model, we generate synthetic data using MATLAB incorporating multipath components. Figure 4a shows the trend plot for the synthetic data with a sample size of 1000, and Fig. 4b shows its respective histogram. We transformed the variations in range for indoor environments to the gamma distribution, obtained in Eq. (7), and its compliance with the synthetic data is shown in Fig. 5. In IEs, the presence of dense multipath and the ubiquity of NLOS conditions causes degradation in the estimation of TOA. From Fig. 6, it can be observed that our proposed framework captures the dense multipath components of the generated signal even at the tail end. From the above discussions, we can draw an inference that when \(q=1.5\), the model provides a better characterization for the uncertainties in the TOA estimation. Further, we can obtain greater precision for estimating the range of SNs, using TOA with resolutions for providing more accuracy in temporal and multipath components.

Fig. 3
figure 3

\(q-\)Gaussian PDFs for different values of q, viz., \(q=1.5\) (proposed model), \(q=1.37\) and \(q=1.45\)

Full size image
Fig. 4
figure 4

a Representation of the trend plot with sample size 1000. b Representation of histogram corresponding to the trend plot

Full size image
Fig. 5
figure 5

Representation of the gamma PDF in convergence with the synthetic data for \(a=9.04432\) and \(b=0.0285463\)

Full size image
Fig. 6
figure 6

Fitting of PDFs for the mixture model for \(a=9.04432\) and \(b=0.0285463\) along with the proposed \(q-\)Gaussian model over the synthetic data for uncertainties in range, obtained for \(q=1.5\) with \(\mu =0.0428\) and \(\sigma =1.4138\).

Full size image

6 Conclusion and Future Work

In this paper, we discussed the UWB-based TOA localization and variations in its range for indoor environments. We characterized the variations in range for TOA localization by using Tsallis’ entropy framework. The maximized Tsallis entropy subjected to the first two moment constraints (i.e., mean and variance) along with the normalization constraint is derived. It is observed that our model captures the variations in the localization range in the existence of dense multipaths in indoor environments. Our proposed \(q-\)Gaussian model operates well over the synthetic data in contrast to the mixture model. It is observed that the \(q-\)Gaussian distribution provided a better characterization of the variations in the localization range for \(q=1.5\). This paper also presented a new approach for estimation of parameters corresponding to the mixture model and our proposed model, by minimizing the JS symmetric measure between the two models and the synthetic data.

In the future, we will provide an intrinsic stochastic differential equation (SDE) model and its corresponding Fokker–Planck equation, to entail the variations in the localization range for densely positioned indoor environments.