A Panorama of Iterated Revision

Abstract

In 1985, David Makinson, together with Carlos Alchourron and Peter Gärdenfors published an article, the now renowned “AGM paper”, that gave rise to an entire new area of research: Belief Revision. The AGM paper set the stage for studying belief revision and provided the first fundamental results in the area. There was however one aspect of belief revision that was not addressed in the AGM paper: iterated belief revision. Since 1985, there have been numerous attempts to tackle this problem. In this chapter, we shall review some of the most influential approaches to the problem of iterated belief revision, and discuss their strengths and shortcomings.

1 Introduction

Almost three decades ago, David Makinson, together with Carlos Alchourron and Peter Gärdenfors published their classical work on the logic of theory change, the renowned “AGM paper” Alchourron et al. (1985). From this paper the area of Belief Revision was born and hundreds of future publications drew inspiration from it and contributed to the development of the field. Yet in this survey we will not focus on what the AGM did do, but rather on what it left out: iterated belief revision.

Let us set the stage with an example. Vasiliki is an archeologist participating in an excavation of an ancient temple near Athens. One day her trowel hits on an ancient Greek vase. The vase is a typical third century BC Greek vase. The design, the painting, the archeological layer it was discovered in, all confirm without doubt that the vase was made in Greece some 2300 years ago. The big surprise however came when Vasiliki looked inside the vase. A small stone tablet with Maya script inscribed on it was lying inside! The discovery was mind-blowing. To the young enthusiastic archeologist, eager to make a name for herself, this was without doubt concrete proof that Columbus was not the first European to reach America. The ancient Greeks had beat him by 1800 years! History books had to be rewritten! Vasiliki spent the night thinking of all the changes that had to be made in our theories about ancient Greeks (and perhaps ancient Mayas).

The theory developed by Alchourron, Gärdenfors, and Makinson, was designed to address precisely these kind of scenarios. A rational agent receives new reliable information $\varphi$ that (in principle) contradicts her initial belief set $K$; the agent is thus forced to move to a new belief set $K*\varphi$ containing $\varphi$. Moreover, the new belief set $K*\varphi$ has to be a rational change to $K$ given $\varphi$. The inner workings of the transition from $K$ to $K*\varphi$ are studied and formalized in the AGM paper, setting the stage for a plethora of exciting results to follow over the next three decades.

Yet, Vasiliki’s story doesn’t end here. The next day, Vasiliki tells her friend Margarita of her discovery. Margarita was more cautious in her reaction. She tells Vasiliki that the local museum is hosting an exhibition of ancient Mayan artifacts, and that this may have something to do with her tablet. Still, Vasiliki refuses to make the connection, and holds on to her theory of an ancient Greek Columbus. Yet her theory survived only another few hours. On the 8 o’clock news that evening Vasiliki finds out that the police had arrested a man who had confessed to having stolen an ancient Greek vase and a Maya tablet from the local museum, both of which he had hidden in a hole he dug at the very spot Vasiliki made her discovery.

Surprising as it may sound, the AGM paper doesn’t cater for Vasiliki’s later revision. At first, this seems very strange. Since the AGM framework formalizes correctly one-step belief revision, why can’t we use the AGM models for a sequence of revisions, simply by treating such a sequence as a series of one-step revisions? The short answer is that by doing so, we are essentially assuming that each one-step revision in the series is independent from the rest, thus failing to capture the fact that all these one-step revisions are performed by the same rational agent, and therefore have to be related. The way that these one-step revisions are related to one-another is a hot topic that has led to many interesting proposals, the most influential of which we shall review in this survey.¹

2 Preliminaries

Let us first fix some notation and terminology. Throughout this article we shall be working with a propositional language $L$ in which the agent’s beliefs as well as the new information will be expressed.² Sometimes we shall refer to $L$ as the object language.

For a set of sentences $\Gamma$ of $L$, we denote by $Cn(\Gamma )$ the set of all logical consequences of $\Gamma$, i.e. $Cn(\Gamma ) = \{\varphi \in L$: $\Gamma \vdash \varphi \}$. A theory $K$ of $L$ is any set of sentences of $L$ closed under $\vdash$, i.e. $K= Cn(K)$. We shall denote the set of all theories of $L$ by $\text {I}\!{{\text {K}}_L}$. A theory $K$ of $L$ is complete iff for all sentences $\varphi \in L$, $\varphi \in K$ or $\lnot \varphi \in K$. We shall denote the set of all consistent complete theories of $L$ by $\text {I}\!{{\text {M}}_L}$. For a set of sentences $\Gamma$ of $L$, $[\Gamma ]$ denotes the set of all consistent complete theories of $L$ that contain $\Gamma$. Often we shall use the notation $[\varphi ]$ for a sentence $\varphi \in L$, as an abbreviation of $[\{\varphi \}]$. For a theory $K$ and a set of sentences $\Gamma$ of $L$, we shall denote by $K+\Gamma$ the closure under $\vdash$ of $K\cup \Gamma$, i.e. $K+\Gamma = Cn(K\cup \Gamma )$. For a sentence $\varphi \in L$ we shall often write $K+\varphi$ as an abbreviation of $K+\{\varphi \}$. Finally, the symbols $\top$ and $\bot$ will be used to denote an arbitrary (but fixed) tautology and contradiction of $L$ respectively.

3 The AGM Postulates for Belief Revision

In the AGM paradigm the process of belief revision is modeled as a function $*$ mapping a theory $K$ and a sentence $\varphi$ to a new theory $K*\varphi$. Of course certain constraints need to be imposed on $*$ in order for it to capture the notion of rational belief revision correctly. A guiding intuition in formulating these constraints has been the principle of minimal change according to which a rational agent ought to change her beliefs as little as possible in order to (consistently) accommodate the new information.

In Gärdenfors (1984), a set of eight postulates, known as the AGM postulates for belief revision,³ which are now widely regarded to have captured much of what is the essence of rational belief revision:  

• $(K*1)$ $K*\varphi$ is a theory of $L$.

• $(K*2)$ $\varphi \in K*\varphi$.

• $(K*3)$ $K*\varphi \subseteq K+ \varphi$.

• $(K*4)$ If $\lnot \varphi \not \in K$ then $K+ \varphi \subseteq K*\varphi$.

• $(K*5)$ If $\varphi$ is consistent then $K*\varphi$ is also consistent.

• $(K*6)$ If $\vdash \varphi \leftrightarrow \psi$ then $K*\varphi = K*\psi$.

• $(K*7)$ $K*(\varphi \ \wedge \psi ) \subseteq (K*\varphi ) + \psi$.

• $(K*8)$ If $\lnot \psi \not \in K*\varphi$ then $(K*\varphi ) + \psi \subseteq K*(\varphi \wedge \psi )$.

Any function $* : \text {I}\!{{\text {K}}_L}\times L \mapsto \text {I}\!{{\text {K}}_L}$ satisfying the AGM postulates for revision $(K*1)$–$(K*8)$ is called an AGM revision function. The first six postulates $(K*1)$–$(K*6)$ are known as the basic AGM postulates (for revision), while $(K*7)$–$(K*8)$ are called the supplementary AGM postulates.

Postulate $(K*1)$ says that the agent, being an ideal reasoner, remains logically omniscient after she revises her beliefs. Postulate $(K*2)$ says that the new information $\varphi$ should always be included in the new belief set. $(K*2)$ places enormous faith on the reliability of $\varphi$. The new information is perceived to be so reliable that it prevails over all previous conflicting beliefs, no matter what these beliefs might be. Postulates $(K*3)$ and $(K*4)$ viewed together state that whenever the new information $\varphi$ does not contradict the initial belief set $K$, there is no reason to remove any of the original beliefs at all; the new belief state $K*\varphi$ will contain the whole of $K$, the new information $\varphi$, and whatever follows from the logical closure of $K$ and $\varphi$ (and nothing more). Essentially $(K*3)$ and $(K*4)$ express the notion of minimal change in the limiting case where the new information is consistent with the initial beliefs. $(K*5)$ says that the agent should aim for consistency at any cost; the only case where it is “acceptable” for the agent to fail is when the new information in itself is inconsistent (in which case, because of $(K*2)$, the agent can’t do anything about it). $(K*6)$ is known as the irrelevance of syntax postulate. It says that the syntax of the new information has no effect on the revision process; all that matters is its content (i.e. the proposition it represents). Hence, logically equivalent sentences $\varphi$ and $\psi$ change a theory $K$ in the same way.

Finally, postulates $(K*7)$ and $(K*8)$ are best understood taken together. They say that for any two sentences $\varphi$ and $\psi$, if in revising the initial belief set $K$ by $\varphi$ one is lucky enough to reach a belief set $K*\varphi$ that is consistent with $\psi$, then to produce $K*(\varphi \wedge \psi )$ all that one needs to do is to expand $K*\varphi$ with $\psi$; in symbols $K*(\varphi \wedge \psi )= (K*\varphi )+\psi$. The motivation for $(K*7)$ and $(K*8)$ comes again from the principle of minimal change. The rationale is (loosely speaking) as follows: $K*\varphi$ is a minimal change of $K$ to include $\varphi$ and therefore there is no way to arrive at $K*(\varphi \wedge \psi )$ from $K$ with “less change”. In fact, because $K*(\varphi \wedge \psi )$ also includes $\psi$ one might have to make further changes apart from those needed to include $\varphi$. If however $\psi$ is consistent with $K*\varphi$, these further changes can be limited to simply adding $\psi$ to $K*\varphi$ and closing under logical implications—no further withdrawals are necessary.

As already mentioned, the AGM postulates are widely accepted as sound properties of rational belief revision. Notice however that all postulates refer to a single belief set $K$; no constraints are placed to relate future revisions with past ones.⁴ We will have more to say about this in Sect.  5.

For the sake of readability from now on we shall restrict our attention only to revision by consistent epistemic input $\varphi$; i.e. we assume $\not \vdash \lnot \varphi$. We note however that most approaches discussed herein can also deal with the limiting case of revising by an inconsistent sentence.

4 Epistemic Entrenchment

Suppose that two different rational agents hold the same beliefs $K$ and they receive the same information $\varphi$. Will the two agents revise $K$ in the same way? The answer in general is no. The reason is that extra-logical factors come into play that may lead the agents to respond differently to $\varphi$. Hence the AGM postulates do not determine a single rational revision function but a whole family of them. The choice of the “right” function for a particular scenario depends on the extra-logical factors mentioned above (see Gärdenfors and Makinson (1988), Peppas (2008) for details). These extra-logical factors essentially assign an epistemic value to the agent’s individual beliefs which determine their fate during revision.

Considerations like these led Gärdenfors and Makinson (1988) to introduce the notion of epistemic entrenchment as a means of encoding the extra-logical factors that are relevant to belief revision. We note that originally epistemic entrenchment was introduced as a constructive model for another type of belief change called, belief contraction. Nevertheless because of the close connection between belief contraction and belief revision (see Gärdenfors and Makinson (1988), Peppas (2008) for details), epistemic entrenchment can also be regarded as a constructive model of belief revision and this is how we shall treat it herein.

Intuitively, the epistemic entrenchment of a belief $\psi$ is the degree of resistance that $\psi$ exhibits to change: the more entrenched $\psi$ is, the less likely it is to be swept away during revision by some other belief $\varphi$. Formally, epistemic entrenchment is defined as a preorder $\le$ on $L$ satisfying the following axioms:  

• (EE1) If $\varphi \le \psi$ and $\psi \le \chi$ then $\varphi \le \chi$.

• (EE2) If $\varphi \vdash \psi$ then $\varphi \le \psi$.

• (EE3) $\varphi \le \varphi \wedge \psi$ or $\psi \le \varphi \wedge \psi$.

• (EE4) When $K$ is consistent, $\varphi \not \in K$ iff $\varphi \le \psi$ for all $\psi \in L$.

• (EE5) If $\psi \le \varphi$ for all $\psi \in L$, then $\vdash \varphi$.

Axiom (EE1) states that $\le$ is transitive. (EE2) says that the stronger a belief is logically, the less entrenched it is. At first this may seem counter-intuitive. A closer look however will convince us otherwise. Consider two beliefs $\varphi$ and $\psi$ both of them members of a belief set $K$, and such that $\varphi \vdash \psi$. Then clearly, if one decides to give up $\psi$ one will also have to remove $\varphi$ (for otherwise logical closure will bring $\psi$ back). On the other hand it is possible to give up $\varphi$ and retain $\psi$. Hence giving up $\varphi$ produces less epistemic loss than giving up $\psi$ and therefore the former should be preferred whenever a choice exists between the two. Thus axiom (EE2). For axiom (EE3) notice that, again because of logical closure, one cannot give up $\varphi \wedge \psi$ without removing at least one of the sentences $\varphi$ or $\psi$. Hence either $\varphi$ or $\psi$ (or even both) is at least as vulnerable as $\varphi \wedge \psi$ during revision. We note that from (EE1)–(EE3) it follows that $\le$ is total; i.e. for any two sentences $\varphi , \psi \in L,\,\varphi \le \psi$ or $\psi \le \varphi$.

The final two axioms deal with the two ends of this total preorder $\le$, i.e. with its minimal and its maximal elements. In particular, axiom (EE4) says that in the principal case where $K$ is consistent, all non-beliefs (i.e. all the sentences that are not in $K)$ are minimally entrenched; and conversely, all minimally entrenched sentences are non-beliefs. At the other end of the entrenchment spectrum we have all tautologies, which according to (EE5) are the only maximal elements of $\le$ and therefore the hardest to remove.

Given a belief set $K$ and an epistemic entrenchment $\le$ associated with $K$ (which encodes all the extra-logical factors that are relevant to belief revision), we can fully determine the new belief set $\,K\,*\varphi$ for any epistemic input $\varphi$ by means of the following condition:  

• (E*) $\psi \in K*\varphi$ iff $(\varphi \rightarrow \lnot \psi ) < (\varphi \rightarrow \psi )$.

Loosely speaking, (E*) can be interpreted as follows: the presence of a belief $\psi$ in $\,K\,*\phi$ is fully determined by its epistemic entrenchment relative to its negation, under the assumption $\varphi$. That is, $\psi \in K\,*\phi$ iff assuming $\varphi$, the belief $\psi$ is more entrenched than its negation.

From the results obtained by Gärdenfors and Makinson in (1988) it follows that the class of revision functions induced from epistemic entrenchments via (E*) corresponds precisely to the family of AGM revision functions (see also Rott (1991); Peppas and Williams (1995)). In other words, epistemic entrenchment is a sound and complete model of the extra-logical factors relevant to AGM revision.

4.1 System of Spheres

Building on earlier work by Lewis (1973), Grove (1988), introduced another constructive model for belief revision based on a structure called system of spheres. Like an epistemic entrenchment, a system of sphere is essentially a preorder. However the objects being ordered are no longer sentences but consistent complete theories.

Fig. 1

A System of Spheres

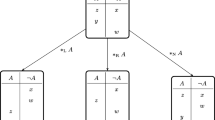
Given an initial belief set $K$ a system of spheres centered on $[K]$ is formally defined as a collection $S$ of subsets of $\text {I}\!{{\text {M}}_L}$, called spheres, satisfying the following conditions (see Fig. 1)⁵:  

• (S1) $S$ is totally ordered with respect to set inclusion; that is, if $V, U\in S$ then $V\subseteq U$ or $U\subseteq V$.

• (S2) The smallest sphere in $S$ is $[K]$; that is, $[K] \in S$, and if $V\in S$ then $[K] \subseteq V$.

• (S3) $\text {I}\!{{\text {M}}_L}\in S$ (and therefore $\text {I}\!{{\text {M}}_L}$ is the largest sphere in $S)$.

• (S4) For every $\varphi \in L$, if there is any sphere in $S$ intersecting $[\varphi ]$ then there is alsoa smallest sphere in $S$ intersecting $[\varphi ]$.

Intuitively a system of spheres $S$ centered on $[K]$ represents the relative plausibility of consistent complete theories, which in this context play the role of possible worlds: the closer a consistent complete theory is to the center of $S$, the more plausible it is. Conditions (S1)–(S4) are then read as follows. (S1) says that any two worlds in $S$ are always comparable in terms of plausibility. Condition (S2) tells us that the most plausible worlds are those compatible with the agent’s initial belief set $K$. Condition (S3) says that all worlds appear somewhere in the plausibility spectrum. Finally condition (S4), also known as the Limit Assumption, is of a more technical nature. It guarantees that for any consistent sentence $\varphi$, if one starts at the outermost sphere $\text {I}\!{{\text {M}}_L}$ (which clearly contains a $\varphi$-world) and gradually progresses towards the center of $S$, one will eventually meet the smallest sphere containing $\varphi$-worlds.⁶ The smallest sphere in $S$ intersecting $[\varphi ]$ is denoted $c(\varphi )$. In the limiting case where $\varphi$ is inconsistent, $c(\varphi )$ is defined to be equal to $\text {I}\!{{\text {M}}_L}$.

Suppose now that we want to revise $K$ by a sentence $\varphi$. Intuitively, the rational thing to do is to select the most plausible $\varphi$-worlds and define through them the new belief set $K*\varphi$:  

• (S*) $K*\varphi = \bigcap (c(\varphi )\cap [\varphi ])$

Condition (S*) is precisely what Grove proposed as a means of constructing a revision function $*$ from a system of spheres $S$. Moreover Grove proved that the functions so constructed coincide with the functions satisfying the AGM postulates. Hence, like an epistemic entrenchment, a system of spheres is also a sound and complete model of the extra-logical factors relevant to belief revision.

Notice that there is an obvious connection between systems of spheres and preorders on possible worlds. In particular, let us call a preorder$\le$ in $\text {I}\!{{\text {M}}_L}$ inductive iff every non-empty subset of $\text {I}\!{{\text {M}}_L}$ has a minimal element. For any belief set $K$ and system of spheres $S$ centered on $[K]$ we can derive an inductive total preorder on possible worlds $\le$ as follows:  

Fig. 2

What we need for Iterated Belief Revision

• $(S{\le })$ $r\le r'$ iff every sphere of $S$ containing $r'$ also contains $r$.

If $*$ is the revision function (at $K)$ induced from $S$, then it is not hard to verify that

• $(\le {*})$ $K*\varphi$ = $min([\varphi ],\le )$.⁷

Conversely, for any theory $K$ and inductive total preorder $\le$ whose minimal worlds are all the $K$-worlds, we can construct by means of the condition $(\le {S})$ below, a system of spheres $S$ centered on $[K]$ such that the revision function $*$ induced from $S$ at $K$ is identical to the revision function induced from $\le$ at $K$ (via condition $(\le {*})$).  

• $(\le {S})$ $V\in S$ iff there is an $r\in \text {I}\!{{\text {M}}_L}$ such that $V= \{ r'\in \text {I}\!{{\text {M}}_L}: ~ r' \le r\}$.

Given the inter-definability of systems of spheres and inductive total preorders, in the rest of the article we shall switch back and forth between the two as the need arises. Moreover, for the rest of the article, all preorders are assumed to be inductive, unless explicitly stated otherwise.

5 The Problem of Iterated Revision

As already noted, when a rational agent performs a sequence of revisions, the individual steps in this sequence must somehow be related. Returning to the introductory example, the fact that Vasiliki responded to her discovery of a Maya tablet in an ancient Greek vase by adopting the belief of an ancient-Greek-Colombus (rather than, say, that the tablet and the vase were fake), may very well be related to her subsequent decision to hold on to this belief even when faced with the information of a local museum displaying Maya artifacts. Unfortunately, the AGM postulates tell us very little about the relationship between the individual steps of a sequence of revisions.

The problem can be expressed more formally as follows. Consider a theory $K$ coupled with a structure encoding extra-logical information relevant to belief change, say, a system of spheres $S$ centered on $[K]$. Suppose that we now receive new information $\varphi$, such that $\varphi \not \in K$, thus leading us to the new theory $K*\varphi$. Notice that $K*\varphi$ is fully determined by $S$ and $\varphi$, and moreover, as Grove has shown, the transition from the old to the new belief set satisfies the AGM postulates. So far, so good. This however is as far as the classical AGM paradigm can take us. If at this point we receive further evidence $\psi$ that is inconsistent with $K*\varphi$ (but not self-contradictory), we have no means of producing $K*\varphi *\psi$. What we are missing is a new system of spheres $S'$ associated with $K*\varphi$ that would determine our revision policy at this point (see Fig. 2).⁸

Presumably, the new system of spheres $S'$ would be a rational offspring of $S$ and $\varphi$. Even if $S'$ in not fully determined by $S$ and $\varphi$, it should at least be constrained by them. More generally, the problem of iterated revision is the problem of formulating constraints that capture the dynamics of the structure used to encode one-step revision policies (be it a system of spheres, an epistemic entrenchment, or any other mathematical object with a similar function). The rest of this article reviews (some of) the best known proposals.

6 Iterated Revision with Enriched Epistemic Input

Spohn (1988), was one of the first to address the problem of iterated belief revision, and the elegance of his solution has influenced most of the proposals that followed. This elegance however comes with a price; to produce the new preference structure from the old one, Spohn requires as input not only the new information $\varphi$, but also the degree of firmness by which the agent accepts the new information. Let us take a closer look at Spohn’s solution (to simplify discussion, in this section we shall consider only revision by consistent sentences on consistent theories).

To start with, Spohn uses a richer structure than a system of spheres to represent the preference information related to a belief set $K$. He calls this structure an ordinal conditional function (OCF). Formally, an OCF $\kappa$ is a function from the set $\text {I}\!{{\text {M}}_L}$ of possible worlds to the class of ordinals such that at least one world is assigned the ordinal $0$. Intuitively, $\kappa$ assigns a plausibility grading to possible worlds: the larger $\kappa (r)$ is for some world $r$, the less plausible $r$ is.⁹ This plausibility grading can easily be extended to sentences: for any consistent sentence $\varphi$, we define $\kappa (\varphi )$ to be the $\kappa$-value of the most plausible $\varphi$-world; in symbols, $\kappa (\varphi )$ = min$(\{ \kappa (r):$ $r\in [\varphi ] \})$.

Clearly, the most plausible worlds of all are those whose $\kappa$-value is zero. These worlds define the belief set that $\kappa$ is related to. In particular, we shall say that the belief set $K$ is related to the OCF $\kappa$ iff $K$ = $\bigcap \{r\in \text {I}\!{{\text {M}}_L}$: $\kappa (r) = 0 \}$. Given a theory $K$ and an OCF $\kappa$ related to it, Spohn can produce the revision of $K$ by any sentence $\varphi$, as well as the new ordinal conditional function related to $K*\varphi$. The catch is, as mentioned earlier, that apart from $\varphi$, its degree of firmness $d$ is also needed as input. The new OCF produced from $\kappa$ and the pair $\langle \varphi , d\rangle$ is denoted $\kappa *\langle \varphi , d\rangle$ and it is defined as follows¹⁰:

• (CON) $\kappa *\langle \varphi , d\rangle (r)\,=\,\left\{ \begin{array}{ll} \kappa (r) - \kappa (\varphi ) &{} \text{ if } r\in [\varphi ] \\ ~ &{} ~ \\ \kappa (r) - \kappa (\lnot \varphi ) + d~~~~~ &{} \text{ otherwise } \end{array} \right.$

Essentially condition (CON) works as follows. Starting with $\kappa$, all $\varphi$-worlds are shifted “downwards” against all $\lnot \varphi$-worlds until the most plausible of them hit the bottom of the rank; moreover, all $\lnot \varphi$-worlds are shifted “upwards” until the most plausible of them are at distance $d$ from the bottom (see Fig. 3). Spohn calls this process conditionalization (more precisely, the $\langle \varphi , d\rangle$ -conditionalization of $\kappa )$ and argues that is the right process for revising OCFs.

Fig. 3

Spohn’s Conditionalization

Conditionalization is indeed intuitively appealing and has many nice formal properties, including compliance with the AGM postulates¹¹ (see Spohn 1988, Gärdenfors 1988, Williams 1994). Moreover notice that the restriction of $\kappa$ to $[\varphi ]$ and to $[\lnot \varphi ]$ remains unchanged during conditionalization, hence in this sense the principle of minimal change is observed not only for transitions between belief sets, but also for their associated OCFs.

There are however other ways of interpreting minimal change in the context of iterated revision. Williams (1994) proposes the process of adjustment as an alternative to conditionalization. Given an OCF $\kappa$, Williams defines the $\langle \varphi , d\rangle$ —adjustment of $\kappa$, which we denote by $\kappa {\circ }\langle \varphi , d\rangle$, as follows:

• (ADJ) $\kappa {\circ }\langle \varphi , d\rangle (r)$ = $\left\{ \begin{array}{ll} 0 &{} \text{ if } r\in [\varphi ]\text{, } d> 0\text{, } \text{ and } \kappa (r) = \kappa (\varphi ) \\ ~ &{} ~ \\ d&{} \text{ if } r\in [\lnot \varphi ]\text{, } \text{ and } \kappa (r) = \kappa (\lnot \varphi ) \text{ or } \kappa (r) \le d \\ ~ &{} ~ \\ \kappa (r) ~~~~~ &{} \text{ otherwise } \end{array}\right.$

Adjustment minimizes changes to the grades of possible worlds in absolute terms. To see this, notice that in the principal case where $\kappa (\varphi ) > 0$ and $d> 0$,¹² the only $\varphi$-worlds that change grades are the most plausible ones (wrt $\kappa )$, whose grade becomes zero. Moreover, the only $\lnot \varphi$-worlds that change grades are those with grades smaller that $d$, or, if no such world exists, the minimal $\lnot \varphi$-worlds whose grade becomes $d$. Like conditionalization, adjustment satisfies all AGM postulates for revision. The process of adjustment was further developed in Williams (1996) and Benferhat et al. (2004), with the introduction of maxi-adjustment and disjunctive maxi-adjustment respectively.

The entire apparatus of OCFs and their dynamics (conditionalization or adjustment) can be reproduced using sentences rather than possible worlds as building blocks. To this end, Williams (1994) defined the notion of ordinal epistemic entrenchments functions (OEF) as a special mapping from sentences to ordinals, intended to encode the resistance of sentences to change: the higher the ordinal assigned to sentence, the higher the resistance of the sentence. As the name suggests, an OEF is an enriched version of an epistemic entrenchment (in the same way that an OCF is an enriched version of a system of spheres). Williams formulated the counterparts of conditionalization and adjustment for OEF and proved their equivalence with the corresponding operation on OCFs.

In Nayak (1994), Nayak took this line of work one step further. Using the original epistemic entrenchment model to encode sentences resistance to change, he considers the general problem of epistemic entrenchment dynamics. The novelty in Nayak’s approach is that the epistemic input is no longer a simple sentence as in AGM, or even a sentence coupled with a degree of firmness as in OCF dynamics, but rather another epistemic entrenchment; i.e. an initial epistemic entrenchment $\le$ is revised by another epistemic entrenchment $\le '$, producing a new epistemic entrenchment $\le *\le '$. Notice that because of (EE4) (see Sect.  4), an epistemic entrenchment uniquely determines the belief set it relates to; we shall call this set the content of an epistemic entrenchment. Hence epistemic entrenchment revision should be interpreted as follows. The initial epistemic entrenchment $\le$ represents both the original belief set $K$ (defined as its content) as well as the preference structure related to $K$. The input $\le '$ represents prioritized evidence: the content $K'$ of $\le '$ describes the new information, while the ordering on $K'$ is related (but not identical) to the relative strength of acceptance of the sentences in $K'$. Finally, $\le *\le '$ encodes both the posterior belief set as well as the preference structure associated with it.

The construction of $\le *\le '$ is motivated by what is now known as lexicographic revision, defined in terms of systems of spheres as follows.¹³ Consider two systems of spheres $S$ and $S'$, with the former representing the initial belief state, and the latter the epistemic input. Let $B1, B2, B3, \ldots$ be the bands of $S$, and $A1, A2, \ldots$ the bands of $S'$.¹⁴ The revision of $S$ by $S'$ is defined to be the system of spheres composed by the following bands (after eliminating the empty sets): $A1\cap B1,\,A1\cap B2,\,A1\cap B3,\,\ldots ,\,A2\cap B1,\,A2\cap B2,\,A2\cap B3,\,\ldots$

Nayak’s induced operators satisfy (a generalized version of) the AGM postulates for revision. Compared to Williams’ OEFs dynamics, Nayak’s work is closer to the AGM tradition (both use epistemic entrenchments to represent belief states and plausibility is represented in relative rather than absolute terms). On the other hand however, when it comes to the modeling epistemic input, Nayak departs even further than Williams from the AGM paradigm; an epistemic entrenchment (used by Nayak) is a much more complex structure than a weighted sentence (used by Williams), which in turn is richer than a simple sentence (used in the original AGM paradigm).

7 Iterated Revision with Simple Epistemic Input

This raises the question of whether a solution to iterated revision can be produced using only the apparatus of the original AGM framework; that is, using epistemic entrenchments (or systems of spheres or selection functions) to model belief states, and simple sentences to model epistemic input.

7.1 The DP Approach and its Sequels

One of the most influential proposals to this end is the work of Darwiche and Pearl (“DP” for short), (1997). The first important feature of this work is that, contrary to the original approach of Alchourron, Gärdenfors and Makinson (but similarly to Spohn (1988), Williams (1994), Nayak (1994)), revision functions operate on belief states, not on belief sets. In the present context a belief state (also referred to as an epistemic state) is defined as a belief set coupled with a structure that encodes relative plausibility (e.g., an epistemic entrenchment, a system of spheres, etc.). Clearly a belief state is a richer model that a belief set. Hence it could well be the case that two belief states agree on their belief content (i.e. their belief sets), but behave differently under revision because of differences in their preference structures. For ease of presentation, and although this is not required by Darwiche and Pearl, in the rest of this section we shall identify belief states with systems of spheres; note that given a system of spheres $S$ we can easily retrieve its belief content–simply notice that $c(\top )$ is the smallest sphere of $S$ and therefore $\cap c(\top )$ is the belief set associated with $S$.¹⁵ We shall denote this belief set by $B(S)$; i.e. $B(S)$ = $\cap c(\top )$. We may sometimes abuse notation and write for a sentence $\varphi$ that $\varphi \in S$ instead of $\varphi \in B(S)$.:

With these conventions, $*$ becomes a function that maps a system of spheres $S$ and a sentence $\varphi$, to a new system of spheres $S\,*\,\varphi$. Darwiche and Pearl reformulated the AGM postulates accordingly to reflect the shift from belief sets to belief states¹⁶:

• (S*1) $S*\varphi$ is a system of spheres.

• (S*2) $\varphi \in B(S*\varphi )$.

• (S*3) $B(S*\varphi ) \subseteq B(S+ \varphi )$.

• (S*4) If $\lnot \varphi \not \in B(S)$ then $B(S+ \varphi ) \subseteq B(S*\varphi )$.

• (S*5) If $\varphi$ is consistent then $B(S*\varphi )$ is also consistent.

• (S*6) If $\vdash \varphi \leftrightarrow \psi$ then $B(S*\varphi ) = B(S*\psi )$.

• (S*7) $B(S*(\varphi \ \wedge \psi )) \subseteq B((S*\varphi ) + \psi )$.

• (S*8) If $\lnot \psi \not \in B(S*\varphi )$ then $B((S*\varphi ) + \psi ) \subseteq B(S*(\varphi \wedge \psi ))$.

With this background, Darwiche and Pearl introduced four additional postulates to regulate iterated revisions¹⁷:

• (DP1) If $\varphi \vdash \chi$ then $(S*\chi )*\varphi$ = $S*\varphi$.

• (DP2) If $\varphi \vdash \lnot \chi$ then $(S*\chi )*\varphi$ = $S*\varphi$.

• (DP3) If $\chi \in S*\varphi$ then $\chi \in B((S*\chi )*\varphi )$.

• (DP4) If $\lnot \chi \not \in S*\varphi$ then $\lnot \chi \not \in B((S*\chi )*\varphi )$.

Postulate (DP1) says that if the subsequent evidence $\varphi$ is logically stronger than the initial evidence $\chi$ then $\varphi$ overrides whatever changes $\chi$ may have made. (DP2) says that if two contradictory pieces of evidence arrive sequentially one after the other, it is the latter that will prevail. Notice that according to (DP1) and (DP2), the latter piece of evidence $\varphi$ prevails in a very strong sense: $\varphi$ fully determines, not just the next belief set, but the entire next belief state (alias system of spheres), overriding any effects that the former piece of evidence may have had in either of them. (DP3) says that if revising $S$ by $\varphi$ causes $\chi$ to be accepted in the new belief state, then revising first by $\chi$ and then by $\varphi$ cannot possibly block the acceptance of $\chi$. Finally, (DP4) captures the intuition that “no evidence can contribute to its own demise” Darwiche and Pearl (1997); if the revision of $S$ by $\varphi$ does not cause the acceptance of $\lnot \chi$, then surely this should still be the case if $S$ is first revised by $\chi$ before revised by $\varphi$.

Apart from their simplicity and intuitive appeal, postulates (DP1)–(DP4) also have a nice characterization in terms of systems-of-spheres dynamics. First however some more notation: for a system of spheres $S$, we shall denote by $\le _S$ the preorder induced from $S$ by $(S\le )$. Moreover $<_S$ denotes the strict part of $\le _S$.

Darwiche and Pearl proved that there is a one-to-one correspondence between (DP1)–(DP4) and the following constraints on system-of-spheres dynamics:

• (DPS1) If $r, r' \in [\varphi ]$ then $r~ \le _{S*\phi } r'$ iff $r~ \le _S r'$.

• (DPS2) If $r, r' \in [\lnot \varphi ]$ then $r~ \le _{S*\phi } r'$ iff $r~ \le _S r'$.

• (DPS3) If $r\in [\varphi ]$ and $r' \in [\lnot \varphi ]$ then $r~ <_S r'$ entails $r~ <_{S*\phi } r'$.

• (DPS4) If $r\in [\varphi ]$ and $r' \in [\lnot \varphi ]$ then $r~ \le _S r'$ entails $r~ \le _{S*\phi } r'$.

Theorem 1

(Darwiche and Pearl 1997 ). Let $S$ be a belief state and $*$ a revision function satisfying the (DP-modified) AGM postulates. Then $*$ satisfies (DP1)–(DP4) iff it satisfies (DPS1)–(DPS4) respectively.

In a way, Darwiche and Pearl were forced to make the shift from belief sets to belief states, for otherwise, as pointed out by Lehmann (1995), (DP2) would have conflicted with the AGM postulates.¹⁸ For instance, let $p, q$ be propositional variables, and define $K\,=\,Cn(\emptyset )$ and $K'\,=\,Cn(\{p\})$. From $(K*1)$–$(K*8)$ it follows that $K'*\lnot q\,=\,K *(p\wedge \lnot q)$. Therefore, $(K'*\lnot q)*q\,=\,(K * (p\wedge \lnot q)) * q$. On the other hand, from (DP2) we derive that $(K'*\lnot q)*q\,=\,K'*q$, and similarly, $(K * (p\wedge \lnot q)) * q\,=\,K * q$. Moreover from (K*1)–(K*8) it follows that $K'* q\,=\,K'+q\,=\,Cn(\{p,q\})$, whereas, $K * q\,=\,K+q\,=\,Cn(\{q\})$. Hence, $(K'*\lnot q)*q \ne (K*(p\wedge \lnot q))*q$ Contradiction.

Nayak et al. (2003), proposed another way to reconcile (DP2) with the AGM postulates that does not require moving away from belief sets. It does however require two other changes to the original formulation of belief revision. Firstly, $*$ is defined as a unary rather than a binary function, mapping sentences to theories. That is, each theory $K$ is assigned its own revision function which for any sentence $\varphi$ produces the revision of $K$ by $\varphi$. We shall denote the unary revision function assigned to $K$ by $*_K$ and the result of revising $K$ by $\varphi$ as $*_K(\varphi )$. This change in notation will serve as a reminder of the unary nature of revision functions adopted in Nayak et al. (2003) Notice that this reformulation of revision functions does not require any modification to the AGM postulates, since all of them refer only to a single theory $K$.

The second modification to revision functions proposed in Nayak et al. (2003) is that they are dynamic; i.e. they could change as new evidence arrives. The implications of this modification are best illustrated in the following scenario. Consider an agent whose belief set at time $t_0$ is $K_0$, and who receives a sequence of new evidence $\varphi _1, \varphi _2, \ldots , \varphi _n$ and performs the corresponding $n$ revisions that take him at time $t_n$ to the belief set $K_n$. Suppose now that it so happens that $K_n = K_0$; i.e. after incorporating all the new evidence, the agent ended up with the theory she started with. Because of the dynamic nature of revision functions in Nayak et al. (2003), it is possible that the revision function assigned to $K_0$ at time $t_0$ is different from the one assigned to it at time $t_n$. Hence although the evidence $\varphi _1, \varphi _2, \ldots , \varphi _n$ did not change the agent’s beliefs, they did alter her attitude towards new epistemic input.

These two modifications to revision functions take care of the inconsistency between (DP2) and the AGM postulates when applied to belief sets. There is however another problem with (DP1)–(DP4) identified in Nayak et al. (2003). Nayak et al. argue that (DP1)–(DP4) are also too permissive; i.e. there are revision functions that comply with both the AGM and DP postulates and nevertheless lead to counter-intuitive results. Moreover, an earlier proposal by Boutilier (1993, 1996), which strengthens (DP1)–(DP4) still fails to block the unintended revision functions (and introduces some problems of its own–see Darwiche and Pearl (1997)). Hence Nayak et al. proposed the following addition to (DP1)–(DP4) instead, called the Conjunction Postulate:  

• (CNJ) If $\chi \wedge \varphi \not \vdash \bot$, then $*_{*_K(\chi )}^\chi (\varphi )$ = $*_K(\chi \wedge \varphi )$.

Some comments on the notation in (CNJ) are in order. As usual, $K$ denotes the initial belief set, and $*_K$ the unary revision function associated with it. When $K$ is revised by a sentence $\chi$, a new theory $*_K(\chi )$ is produced. This however is not the only outcome of the revision of $K$ by $\chi$; a new revision function associated with $*_K(\chi )$ is also produced. This new revision function is denoted in (CNJ) by $*_{*_K(\chi )}^\chi$. The need for the superscript $\chi$ is due to the dynamic nature of $*$ (as discussed earlier, along a sequence of revisions, the same belief set may appear more than once, each time with a different revision function associated to it, depending on the input sequence).

Postulate (CNJ) essentially says that if two pieces of evidence $\chi$ and $\varphi$ are consistent with each other, then it makes no difference whether they arrive sequentially or simultaneously; in both cases the revision of the initial belief set $K$ produces the same theory.

Nayak et al. show that (CNJ) is consistent with both AGM and DP postulates, and it blocks the counterexamples known at the time. In fact (CNJ) is strong enough to uniquely determine (together with (K*1)–(K*8) and (DP1)–(DP4)) the new revision function $*_{*_K(\chi )}^\chi$. A construction of this new revision function from $*_K$ and $\chi$ is given in Nayak et al. (2003)

Yet, some authors have argued, Zhang (2004), Jin and Thielscher (2005), that while (DP1)–(DP4) are too permissive, the addition of (CNJ) is too radical (at least in some cases). Accordingly, Jin and Thielscher proposed a weakening of (CNJ), which they call the Independence postulate Jin and Thielscher (2005, 2007). The Independence postulate is formulated within the DP framework; that is, it assumes that belief states rather than belief sets are the primary objects of change¹⁹:

• (Ind) If $\lnot \chi \not \in S*\varphi$ then $\chi \in B((S*\chi )*\varphi )$.

The Independence postulate, apart from performing well in indicative examples (see Jin and Thielscher (2005)), also has a nice characterization in terms of system of spheres dynamics:

• (IndR) If $r\in [\varphi ]$ and $r' \in [\lnot \varphi ]$ then $r~ \le _S r'$ entails $r~ <_{S*\phi } r'$.

Theorem 2

(Jin and Thielscher 2005 ). Let $S$ be a belief state and $*$ a revision function satisfying the (DP-modified) AGM postulates. Then $*$ satisfies (Ind) iff it satisfies (IndR).

  The Independence postulate can be shown to be weaker than (CNJ) and in view of Theorems 1, 2, it is clearly stronger than (DP3) and (DP4). Jin and Thielscher show that (Ind) is consistent with the AGM and DP postulates combined.

7.2 Conflicts

Despite the popularity of the DP approach and the remedies introduced to fix its initial problems, their is still some controversy surrounding the DP postulates. One of the latest criticisms comes in the form of a result proving that the DP postulates are in conflict with another important aspect of belief revision; namely, the desideratum that beliefs that are not relevant to the new information should be immune to the revision process.

As noted by Parikh in (1999), the AGM postulates are too liberal in their treatment of relevance, and hence he proposed an extra postulate called (P) to supplement them presented below. First some notation: for any sentence $x,\,L_x$ denotes the (unique) smallest language in which $x$ can be expressed:

• (P) If $K= Cn(x \wedge y)$, where $x, y$ are sentences of disjoint languages $L_x$, $L_y$ respectively, and moreover $\varphi \in L_x$, then $K*\varphi = (Cn(x)\circ \varphi )+y$, where $\circ$ is a revision function over the language $L_x$.

Hence (P) essentially says that, if the initial belief set can be split into two parts $x$ and $y$ of disjoint languages $L_x$ and $L_y$, then the revision of $K$ by any epistemic input in $L_x$ leaves the $y$-part of $K$ unaffected. Although (P) may not tell the whole story of relevance-sensitive belief revision, it is surely an intuitive first step.

At first glance postulate (P) appears to be unrelated to iterated revision and consequently to the DP postulates. Yet, in Peppas et al. (2008), using the semantics of (P) developed in Peppas et al. (2004), proved that (P) is in conflict with each one of the DP postulates:

Theorem 3

(Peppas et al. 2008 ). In the presence of the AGM postulates, postulate (P) is inconsistent with each one of the postulates (DP1)–(DP4).

It should be noted that according to the above result, the DP postulates are in conflict with (P) not only as a whole, but also in isolation. Of course Theorem 3 can be interpreted as a liability for axiom (P) rather than the DP postulates. Nevertheless, until the issue is settled, the DP postulates (and axiom (P)) remain contestable.

7.3 Enriched Epistemic States

Next we turn to two approaches to Iterated Belief Revision that, while keeping the epistemic input simple, use richer structures to model epistemic states.

The first is a distance-based approach by Lehmann, Magidor, and Schlechta (or LMS for short), Lehmann et al. (2001). The LMS proposal is based on a simple and very intuitive idea: introduce an priori notion of distance $d$ between possible worlds, and use $d$ to derive the preorders associated with the initial belief set $K$ as well as with all future belief sets resulting from $K$ via iterated revisions. Formally, $d$ is a function that maps any two possible worlds $r$ and $r'$ to a real number $d(r,r')$ ²⁰ which is to be interpreted as a measure of how far away $r'$ looks from the standpoint of $r$.

Let us take a concrete example to illustrate the LMS approach. Suppose that the object language $L$ is built from two propositional variables $p$ and $q$, that give rise to four possible worlds $r_0 = Cn(\{p,q\}),\,r_1 = Cn(\{p,\overline{q}\}),\,r_2 = Cn(\{\overline{p}, q\})$, and $r_3 = Cn(\{\overline{p},\overline{q}\})$.²¹ Moreover assume that the distance $d$ between these worlds is the Euclidean distance between the corresponding points in Fig. 4.

Fig. 4

Distances Between Possible Worlds

Suppose that the initial belief state is $r_0$. Then according to Fig. 4, the world closest to $r_0$ is $r_1$, followed by the worlds $r_2, r_3$ which are equidistant from $r_0$. Hence the preorder associated with $r_0$ is $r_0 \le r_1 \le r_2, r_3$. Future preorders can likewise be derived. If for example $r_0$ is revised by $\overline{p}$, the new preorder $\le '$ associated with $r_0 * \overline{p}$ is $r_2, r_3 \le ' r_1 \le ' r_0$.²² More generally, the preorder $\le$ derived from a distance $d$ which is associated with a belief set $K$, can be defined as follows:

• (d$\le$) $r\le r'$ iff there is a $w\in [K]$ such that, for all $w'\in [K],\,d(w,r) \le d(w', r')$.

LMS assume very little about the properties of the distance function $d$. In fact they assume even less that what are generally considered reasonable properties of distance, committing themselves only to the following assumption:

• (d1) $d(r, r')\,=\,0$ iff $r= r'$.

If in addition to (d1), $d$ satisfies the property (d2) below, it is called symmetric:  

• (d2) $d(r, r')\,=\,d(r', r)$.

It can be shown that under property (d1) alone, all revision functions induced from distance functions $d$ satisfy the AGM postulates. The converse however is not true; there exist AGM revision functions that cannot be constructed by any distance function. Lehmann, Magidor, and Schlechta provided an exact characterization of the class of AGM functions that can be constructed from distance functions. Herein we shall present only the representation result related to symmetric distance functions, and only for the special case of finitary propositional languages (i.e. propositional language $L$ built from finitely many propositional variables). For similar results on more general cases, the reader is referred to Lehmann et al. (2001).

When the object language $L$ is finitary, any theory $K$ can be represented as the logical closure of a single sentence (i.e. all theories are finitely axiomatizable). Hence for condition (d*) below, we shall abuse notation and extend the application of the disjunction operator to theories with the understanding that for any two theories $K$ and $K',\,K\vee K'$ denotes the disjunction of sentences $\chi$ and $\chi '$ whose logical closure equals $K$ and $K'$ respectively.

• (d *) If $K_0$ is consistent with $K_1\,*\,(K_0\vee K_2),\,K_1$ is consistent with $K_2\,*\,(K_1\vee K_3)$, . . . , and, $K_{n-1}$ is consistent with $K_n*(K_{n-1}\vee K_0)$, then $K_1$ is consistent with $K_0\,*\,(K_n\vee K_1)$

Theorem 4

(Lehmann et al. 2001 ). An AGM revision function $*$ can be constructed from a symmetric distance function $d$ over possible worlds, iff $*$ satisfies (d*).

The key feature of the LMS approach is the use of a belief-set-independent meta-structure, namely a distance function $d$, to derive all preorders necessary to guide present and future revisions. Recently, Booth and Meyer (2011) also developed such a meta-structure with similar aims, which however is quite different from a distance function.

The basic idea in Booth and Meyer (2011), is to construct for each possible world $r$, a “positive” and “negative” clone, denoted $r^+$ and $r^-$ respectfully. The set of all such “signed” possible worlds is denoted by $\text {I}\!{{\text {M}}_L}^\pm$; moreover, $\text {I}\!{{\text {M}}_L}^+$ and $\text {I}\!{{\text {M}}_L}^-$ denote the sets of positively and negatively signed possible worlds respectfully (and hence $\text {I}\!{{\text {M}}_L}^\pm = \text {I}\!{{\text {M}}_L}^+ \cup \text {I}\!{{\text {M}}_L}^-)$.

The intuition behind signed possible worlds is given by the following passage from Booth and Meyer (2011):

$\ldots$ when we compare two different worlds $x$ and $y$ according to preference, often we are able to imagine different contingencies, according to whether all goes well in $x$ and $y$ or not. Our idea is to associate to each world $x$ two abstract objects $x^+$ and $x^-$, with the intuition that $x^+$ represents $x$ in positive circumstances, while $x^-$ represents $x$ in negative circumstances.

Against this background, Booth and Meyer introduced a preorder $\preccurlyeq$ over signed worlds, which is the meta-structure alluded to above. In particular $\preccurlyeq$ is defined as a total preorder in $\text {I}\!{{\text {M}}_L}^\pm$ such that for all possible worlds $r, w$,

• $(\preccurlyeq 1)$ $r^+ \prec r^-$

• $(\preccurlyeq 2)$ $r^+ \preccurlyeq w^+$ iff $r^- \preccurlyeq w^-$

Let us call a total preorder in $\text {I}\!{{\text {M}}_L}^\pm$ that satisfies $(\preccurlyeq 1)$–$(\preccurlyeq 2)$ a signed preorder.²³ Signed preorders provide the model proposed by Booth and Meyer for epistemic states.

The best way to understand a signed preorder $\preccurlyeq$ and its role in iterated revision is through a graphical representation proposed in Booth and Meyer (2011). Suppose that each possible world $r$ is represented by a “stick” of a fixed length whose left and right endpoints correspond to $r^+$ and $r^-$ respectively (Fig. 5). The sticks are positioned in such a way as to reflect the preorder $\preccurlyeq$ over the endpoints. For instance, from Fig. 5 it follows that $r_1^+ \approx r_2^+ \prec r_3^+ \prec r_4^+ \prec r_5^+$, and $r_1^- \approx r_2^- \approx r_4^+ \prec r_3^-$.

Fig. 5

Signed Possible Worlds

From the preorder $\preccurlyeq$ over signed worlds, one can extract a preorder $\le$ over plain worlds, essentially by taking the projection of $\preccurlyeq$ over $\text {I}\!{{\text {M}}_L}^+$. More formally, $\le$ is defined as total preorder in $\text {I}\!{{\text {M}}_L}$, constructed from $\preccurlyeq$ as follows:

• (Def-$\le$) For all $r,w\in \text {I}\!{{\text {M}}_L}$, $r\le w$ iff $r^+ \preccurlyeq w^+$

The preorder $\le$ extracted from $\preccurlyeq$ plays the role of a system of spheres.²⁴ Hence, the minimal worlds wrt $\le$ define the agent’s current beliefs $K$, and for any epistemic input $\varphi$, the revision of $K$ by $\varphi$ is defined as $K* \varphi = \bigcap (min([\varphi ],\le ))$. As for the rest of $\preccurlyeq$, it is used to determine the preorder associated with the revised belief set $K\,*\,\varphi$. In particular, depending on whether a world $r$ satisfies the new evidence $\varphi$ or not, its plausibility relative to the new belief set $K\,*\,\varphi$ is identified with the plausibility of its positive or negative clone respectively. More formally, let $\vartheta _\varphi (r)$ denote $r^+$ if $r\vdash \varphi$, and $r^-$ otherwise. Then the preorder $\le '$ associated with the revised belief set $K\,*\,\varphi$ is defined as follows:

• (Def-$\le '$) For all $r,w\in \text {I}\!{{\text {M}}_L}$, $r\le ' w$ iff $\vartheta _\varphi (r) \preccurlyeq \vartheta _\varphi (w)$.

There are two features of the above approach to iterated revision, let us call it the BM approach, that should be noted.²⁵ Firstly, the new information $\varphi$ is not always included in the revised belief set $K*\varphi$; this places the BM approach in the realm of non-prioritized belief revision Hansson (1998). Secondly, the BM approach still comes short of a complete solution to the problem of iterated belief revision. In particular, notice that while the signed preorder $\preccurlyeq$ associated with the initial belief set $K$, fully determines the system of spheres related to $K$, as well as the system of spheres associated with $K*\varphi$ (for any input $\varphi )$, it doesn’t go any further than that; systems of spheres associated with future belief sets $K*\varphi *\psi$ remain unknown. What is needed to complete the picture is a method of cascading the signed preorder $\preccurlyeq$ to future belief sets. Booth and Meyer have already made important steps in this direction, Booth and Meyer (2011).

8 Other Approaches

The models discussed so far are among the most influential in the iterated revision literature. Other important works on the subject are briefly presented in this section (although the list is far from complete).

Ferme’s and Rott’s approach to iterated belief revision, Ferme and Rott (2004), can loosely speaking be described as follows. Let $\le$ be a total preorder on possible worlds representing the agent’s initial belief state, and let $\varphi$ be the new information received by the agent. Like Spohn, Ferme and Rott require information about the firmness of $\varphi$, in addition to $\varphi$ itself. Unlike Spohn however, firmness is not specified as an ordinal number (which Ferme and Rott argue is intuitively unclear), but through a reference sentence $\psi$. In particular, the epistemic input comes as a pair of sentences $(\varphi ,\psi )$ which essentially instructs the agent to revise the initial belief state $\le$ in such a way so that at the new belief state $\le '$, not only is $\varphi$ accepted, but it is accepted with the same firmness as $\psi$ (i.e. $\varphi ,\,\psi$ are equally entrenched). This can be achieved as follows. Let $r_{\lnot \psi }$ denote any minimal $\lnot \psi$-world wrt $\le$. Ferme and Rott construct $\le '$ from $\le$ by moving all $\lnot \varphi$-worlds to the left of $r_{\lnot \psi }$, at the same layer as $r_{\lnot \psi }$.²⁶ The approach is intuitively appealing and has many nice features. At the same time, it also has a number of shortcomings (for example, the preorders tend to become coarser, which among other things entails that one “can never build up an informative belief state from the state of complete ignorance” Ferme and Rott (2004)).

In Delgrande and Schaub (2003), propose a constructive approach to belief revision that includes a solution to the problem of iterated revision as a by-product. In particular, for a theory $K$ and a sentence $\varphi$, the revision of $K$ by $\varphi$ is constructed as follows. Firstly, a new theory $K'$ is built from $K$ by replacing every atom $p$ with a new atom $p'$. Observe that $\varphi$ is consistent with $K'$ (even if it is inconsistent with $K)$ since the two are expressed in terms of disjoint languages. Starting with the (consistent) set $K'\cup \{\varphi \}$, one goes through the list of original atoms $p$ and corresponding new atoms $p'$, progressively adding assertions of the form $p \equiv p'$ for as long as consistency is maintained. Let us denote by $EQ$ a maximal set of such assertions $p \equiv p'$ that can be consistently added to $K'\cup \{\varphi \}$. Delgrande and Schaub define the revision of $K$ by $\varphi$ as the projection of $Cn(K'\cup \{\varphi \}\cup \{EQ\})$ to the original language of $K$. If there is more than one maximal set of assertions $EQ$ that is consistent with $K'\cup \{\varphi \}$, we can either use one of them (chosen by a selection function), or take the intersection of $Cn(K'\cup \{\varphi \}\cup \{EQ\})$ for all such $EQ$s. The former is called choice revision and the latter skeptical revision.²⁷ Observe that since $K*\varphi$ is defined for every $K$ and $\varphi$, this approach provides a solution both for one-step and for iterated belief revision.

In Delgrande et al. (2006), take a different approach to iterated revision. Given an initial belief base $\varphi _0$, and a sequence of observations $\varphi _1; \varphi _2; \ldots ; \varphi _n$, the revision of $\varphi _0$ by the sequence is defined as the prioritized merging of the multiset $\{(\varphi _0,r_0), (\varphi _1,r_1)$, $\ldots ,\,(\varphi _n,r_n) \}$, where each $r_i$ represents the reliability degree of the corresponding sentence $\varphi _i$. Observe that in the special case where $r_0 < r_1 < \cdots < r_n$, prioritized merging conforms with an assumption widely used in the iterated revision literature: recent observations are assumed to have priority over earlier ones. Delgrande, Dubois and Lang prove that most of the well known postulates for iterated revision (except (DP2)) are consequences of the postulate they propose for prioritized merging.

All the works discussed so far assume that the agent under consideration is situated in a static world. Recently, iterated belief revision has also been studied in the context of a dynamic environment. In particular, consider an agent operating in a world that changes due to actions taken by the agent herself or by other agents. Let us denote by $K$ the agent’s beliefs about the initial state of the world. If the agent is informed of an action that brought about $\varphi$, she has to modify $K$ accordingly via a process known as belief update.²⁸ Moreover, in addition to actions that change the state of the world (ontic actions), there are also sensing actions, through which the agent acquires information about the world without changing it. The effects of sensing actions are modeled in terms of belief revision. We note that some sensing actions can indirectly reveal information about past world states, leading to an interesting interplay between alternating revisions and updates. Such scenarios have been studied by Hunter and Delgrande (2005, 2007), as well as by Shapiro et al. (2000) (the latter in the context of situation calculus).

In a different direction, considerations related to iterated belief revision are starting to be studied in a dynamic epistemic logic setting Baltag and Smets (2009). Finally, there is also important work on iterated contraction (see for example Chopra et al. (2008), Ramachandran et al. (2012)).

9 Conclusion

Important steps have been made towards a general solution to the problem of iterated revision. On the other hand, there is still some controversy over the appropriateness of the proposed approaches and no signs of convergence towards a “standard” model (like AGM is for one-step revision).

Part of the reason for this has to do with the lack of consensus over the “right” input for iterated revision. As we have seen in this survey, input can vary from being a plain sentence, to a sentence coupled with an ordinal number, to an entire preorder on sentences.²⁹

A second source of difficulty in the way that most proposals in the literature approach the problem of iterated revision is the following. To solve the problem of iterated revision (regardless of the type of input we employ) one will ultimately have to specify a relationship between the meta-structure $\mathcal {U}$ that guides one-step revisions at the initial time-point, with the meta-structure $\mathcal {U'}$ resulting after revision.³⁰ Any solution that uniquely determines $\mathcal {U'}$ from $\mathcal {U}$ and the epistemic input, runs the risk of not being general enough. On the other hand, if $\mathcal {U'}$ in not fully determined from $\mathcal {U}$ and the epistemic input, then a meta-meta-structure is needed to select between the different options for $\mathcal {U'}$. This however leads to a vicious circle since one would then have to develop a model for the dynamics of the meta-meta-structures (with similar problems to confront).

Clearly, there are still important pieces missing from the puzzle of iterated belief revision. One should treat this as an opportunity rather than a liability: exciting new results on the subject are waiting to be discovered!