Modeling Spatial Effects on Childhood Mortality Via Geo-additive Bayesian Discrete-Time Survival Model: A Case Study from Nigeria

Abstract

Childhood mortality is an important indicator of overall health and development in a country. It is the result of a complex interplay of determinants at many levels, and as such several studies have recognized that, for instance, maternal (Caldwell 1979; Cleland and van Ginneken 1988), socio-economic (Castro-Leal et al. 1999; Wagstaff 2001), and environmental (Wolfe and Behrman 1982; Lee et al. 1997) factors are important determinants of childhood mortality. However, only a few studies have incorporated environmental factors that are spatial in nature and derived from geographic databases, such as distances from households or communities (Watson et al. 1997).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Childhood mortality is an important indicator of overall health and development in a country. It is the result of a complex interplay of determinants at many levels, and as such several studies have recognized that, for instance, maternal (Caldwell 1979; Cleland and van Ginneken 1988), socio-economic (Castro-Leal et al. 1999; Wagstaff 2001), and environmental (Wolfe and Behrman 1982; Lee et al. 1997) factors are important determinants of childhood mortality. However, only a few studies have incorporated environmental factors that are spatial in nature and derived from geographic databases, such as distances from households or communities (Watson et al. 1997).

While the commonly used approaches, such as correlation coefficients and regression analysis may produce statistical outcomes and measures of association, which are limited to a particular location, these relationships cannot be readily generalized for other locations within a country. In order to determine that the observed social phenomena are not distributed in a spatially random manner, spatial analysis is employed. Spatial analysis could be defined as a quantitative data analysis, which focuses on the role of space and relies explicitly on spatial variables in order to explain or predict the phenomenon under investigation (Cressie 1993; Chou 1997). It tests theories that stress that the location of an individual influences social attitudes and behaviour, and that observed social phenomena are not distributed in a spatially random fashion (Weeks 2004). Studies of childhood mortality in developing countries using aggregated data and methodologies that ignore spatial dimensions run the risk of explaining very little of the variations in mortality rates as well as masking spatial variations. For instance, results of the 2003 Nigeria Demographic and Health Survey (NDHS), disaggregated by geopolitical zones, shows that the infant mortality rate (IMR) for the period 10–14 years preceding the 2003 NDHS (1989–1993) at the national level was 113 per 1,000 live-births, while the corresponding IMR for the then four geopolitical zones was North East (129/1,000), North West (136/1,000), and South East (74/1,000), South West (81/1,000) (NPC 2004).

Crude under-five mortality rates stratified by districts (states) are displayed in Table 3.1, and reveal wide variations between districts within the same geopolitical region, information that would otherwise be “hidden” in the overall picture of crude mortality rate for that region or states had spatial analysis not been carried out, thereby exemplifying the significance of spatial analysis.

Table 3.1 Under-five mortality rates (per 1,000) by older states (districts) in Nigeria for 0–4 years prior to the survey (1999–2003)

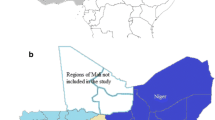
This chapter is intended to account simultaneously for spatial and time-varying effects on childhood mortality by employing a geo-additive Bayesian model with dynamic and spatial extensions of discrete-time survival models in estimating temporal and spatial variation in the determinants of childhood mortality, as well as any associations between risk factors and childhood mortality in the presence of spatial correlation. To ignore this correlation would mean an underestimation of the variance of the effects of risk factors (Weeks 2004). The impact of some determinant factors of child survival is allowed to vary over time, as well as allowing for non-linear effects of some covariates on child survival. This model introduces appropriate smoothness priors for spatial and non-linear effects, as well as Markov chain Monte Carlo simulation techniques (Gelfand and Smith 1990; Smith and Roberts 1993), used to estimate the model parameters. The models are subsequently used to examine spatial variation in childhood mortality rates in Nigeria, and explore district-level clustering of mortality rates across both space and time (Fig. 3.1). This chapter will however be limited to the older 31 states (i.e. states created before 1996) due to lack of spatial data including the last five states. Figure 3.1 displays spatial distribution of mortality rates (per 1,000) across these states/districts for crude neonatal mortality (panel b); crude peri-natal mortality (panel c); crude infant mortality (panel d); crude child mortality (panel e); and crude under-five mortality (panel f).

Fig. 3.1

Map of Nigeria (a) and spatial distribution of mortality rates across the 36 states/districts (b–f), in Nigeria 1999-2003 (Source: Table 3.1)

2 Study Area and Study Population

Nigeria, with a 2006 population of 140 million people, is the most populous country in Africa (Onuah 2006). It is also the tenth largest country by population in the world. The country lies on the west coast of Africa between 4° and 14° North latitude and 2° and 15° East longitude, and is bordered by Benin, Niger, Chad, Cameroon, and the Gulf of Guinea. It has a landmass extending over 923,768 km² and is located on the eastern terminus of the bulge of West Africa (Population Resource Centre 2000). With an average density of approximately 124 persons per square kilometer (Ali-Akpajiak and Pyke 2003) Nigeria is one of the most densely populated countries in the world. The spatial distribution of the population is uneven, with some areas of the country sparsely inhabited while other areas are densely populated. With the exception of Lagos, which has the highest population density in the country, the South East of Nigeria has the highest densities. Sixty four percent of the population is concentrated in the rural areas (Ali-Akpajiak and Pyke 2003). Nigeria is made up of 36 states (districts) and a Federal Capital Territory at Abuja. The 36 states are grouped into six geopolitical zones (regions). The mean temperature ranges between 25 °C and 40 °C, and rainfall ranges between 2,650 mm in the Southeast and less than 600 mm in some parts of northern Nigeria that lies mainly in the Sahara desert. These climatic differences give rise to both vegetational differences ranging from mangrove swamp forest in the Niger delta and Sahel grassland in the North, and different soil conditions. This results in a variation in agricultural produce and natural resources in the different parts of Nigeria. A map of Nigeria indicating the geographical location of the states (districts) is shown in Fig. 3.1.

3 Geo-Additive Bayesian Discrete-Time Survival Model

3.1 The Basic Model

Let T denote a discrete survival time, where t є {1, …, q + 1} represents the t th month after birth and let x _i  = (x ₁ , …, x _t ) denote the history of a covariate up to month t. The discrete-time conditional probability of death at month t is then given by

$$ \uplambda (\mathrm{t},{{\mathrm{x}}_{\mathrm{i}}})=\mathrm{pr}(\mathrm{T} = \mathrm{t}\ |\mathrm{T}\ \geq \mathrm{t},\ {{\mathrm{x}}_{\mathrm{i}}}),\quad \mathrm{t} = 1,\ldots,\mathrm{q}. $$

(3.1)

Survival information on each child is recorded by (t _i, δ _i ), i є {1, …, N}, where t _i є {1, …, 60} is the child’s observed survival time in months, and δ _i is a survival indicator with δ _i  = 1 if child i died, and δ _i  = 0 if it is still alive. Therefore for δ _i  = 1, t _i is the age (in months) of the child at death, and for δ _i  = 0, t _i is the current age of the child (in months) at the time of interview.

The assumption is non-informative censoring as applied by Lagakos (see Lagakos1979), so that the risk set R _t includes all individuals who are censored in interval ending in t. A binary event indicator is then defined as:

$$ \begin{gathered} {{\mathrm{y}}_{\mathrm{i}\mathrm{t}}}\{\mathrm{i}\,\varepsilon\,{{\mathrm{R}}_{\mathrm{t}}},\,\,\mathrm{t}=1,\,\,\ldots,\,{{\mathrm{t}}_{\mathrm{i}}}\} \hfill \\ {{\mathrm{y}}_{\mathrm{i}\mathrm{t}}}=\{1\,\,\,\mathrm{if}\,\mathrm{t}={{\mathrm{t}}_{\mathrm{i}}}\,\mathrm{and}\,{\delta_{\mathrm{i}}}=1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\{0\,\,\,\,\,\,\mathrm{otherwise}, \hfill \\ \end{gathered} $$

(3.2)

The event of death of individual i could then be considered as a sequence of binary “outcomes” – dying at age t (y _it = 1) or in the case of survival beyond age t (y _it = 0). Such formulation yields a sequence of 0 s and 1 s indicating survival histories of each child at the various time points.

3.2 Incorporation of Fixed-, Time-Varying and Spatial-Effects

Parallel with the sequence of 0 s and 1 s, the values of relevant explanatory variables x_it = (x _i1 , …, x _it ), i =1, 2, … could be recorded. These variables may be fixed over time, for example sex, place of residence; or may vary over time, for example breastfeeding of a child, at time t.

The indicator y _it could be linked to the covariates x _it by an appropriate link function for binary response model such as probit, logit or multinomial link function, and a predictor η _it (x _it ). Assuming that y _it has a binomial distribution and using a probit link function for i є Rt, the probability of death for a child i is denoted by:

$$ \Phi (\upeta_{\mathrm{it})} = \mathrm{pr}\ (\mathrm{y_{it}} =1|\mathrm{x_{it}}). $$

(3.3)

The usual form of the predictor is

$$ \upeta_{\mathrm{it}} = \mathrm{f}_0\ (\mathrm{t})+\mathrm{x_{it}}\ \upbeta $$

(3.4)

where the baseline effect f ₀ (t), t =1, 2, … is an unknown, usually non linear, function of t to be estimated from data and β is the vector of fixed covariate effects. In parametric framework, the baseline hazard is often modelled by a few dummy variables, which divide the time-axis into a number of relatively small segments or by some low-order polynomial. In practice however, it is difficult to correctly specify such parametric functional forms for the baseline effects in advance. Non-parametric modelling based on some qualitative smoothness restrictions offers a more flexible framework to explore unknown patterns of the baseline.

Restriction to fixed effects alone might not be adequate in most cases, due to the covariates whose value may vary over time. The predictor in (3.4) is subsequently extended to a more flexible semi-parametric model, which could accommodate time-varying effects. On further inclusion of another expression to represent spatial effects, this semi-parametric predictor is given by

$$ \upeta_{\mathrm{it}} = \mathrm{f}_0(\mathrm{t})+\mathrm{f}_1(\mathrm{X})+\mathrm{f}(\mathrm{t})\mathrm{X_{it}}+\mathrm{f}_{\mathrm{spat}}(\mathrm{s_i})+\mathrm{X_{it}}\ \upbeta. $$

(3.5)

Here, f ₀ (t) is the baseline function of time, and f ₁ is a nonlinear effect of metrical covariate X. The effects, f (t), of the covariates in X _it are time-varying, while X _it comprises fixed covariates whose effect is represented by the parameter vector β; and f _spat is the non-linear spatial component of, for instance, district s (s =1, …,S), where the child lives. The spatial effects f _spat (s _i ) may be further split-up into spatially correlated (structured) and uncorrelated (unstructured) effects of the form f _str (s _i ) + f _unstr (s _i ). The fundamental reason behind this is that a spatial effect is a surrogate of many unobserved influencing factors, some of which may obey a strong spatial structure while others may only be present locally. The analyses in this chapter are based on (3.4) and (3.5), and would be subsequently referred to as “constant fixed effects model” and “geo-additive model” respectively.

3.3 The Estimation Process

The functions f ₀, f ₁ , and f are smooth over by second-order random walk priors using the MCMC techniques implemented in BayesX (Fahrmeir and Lang 2001a, b; Brezger et al. 2002).

Letf = {f (1),…,f (m),m ≤ n} be a vector of corresponding function evaluations at the observed values of x. The general form of the prior for f would be:

$$ \mathrm{f} |\uptau^2\ \upalpha \exp \big( { - 1/2\uptau^2(\mathrm{f}_2\ \mathrm{f}/\mathrm{Kf})} \big) $$

(3.6)

where K is a penalty matrix that penalizes too abrupt jumps between neighbouring parameters. In most cases, K is rank deficient, therefore the prior for f is improper.

Traditionally, the smoothing parameter is equivalent to the variance parameter τ ², which controls the trade-off between flexibility and smoothness. A highly dispersed but proper hyperprior is assigned to τ ² so as to estimate the smoothness parameter simultaneously with f. A proper prior for τ ² is required in order to obtain a proper posterior for f (Hobart and Casella 1996). In the event of the selection of an Inverse Gamma distribution with hyper-parameters a and b, (τ ² ∼ IG (a, b)), a first- and second-order random walk priors for f would be defined respectively by:

$$ \mathrm{f}(\mathrm{t})=\mathrm{f}(\mathrm{t}-1)+\mathrm{u}(\mathrm{t}),\,\,\mathrm{and}\ \mathrm{f}(\mathrm{t})=2\mathrm{f}(\mathrm{t}-1)-\mathrm{f}(\mathrm{t}-2)+\mathrm{u}(\mathrm{t}), $$

(3.7)

with Gaussian errors u(t) ∼ N (0;τ ²) and diffuse priors f(1) α const, or f(1) and f(2) α const, as initial values. A first order random walk penalizes abrupt jumps f(t) − f(t − 1) between successive states, and a second order random walk penalizes deviations from the linear trend 2f(t − 1) − f(t − 2). The trade-off between flexibility and smoothness of f is controlled by the variance parameter τ ². This chapter adopts the approach of estimating the variance parameter and the smoothing function simultaneously; this is achieved by introducing an additional hyperprior for τ ² at a further stage of the hierarchy. A highly dispersed but proper Inverse Gamma prior, p (τ ² ) ∼ IG (a; b) is chosen, with a = 1 and b = 0.005. Similarly, a highly dispersed Inverse Gamma prior is defined for the overall variance σ².

For the spatially correlated or structured effect, f _str (s), s = 1,…,S, Marked random field priors common in spatial statistics are chosen (Besag et al. 1991) of the form

$$ \begin{aligned} \mathrm{f_{str}}(\mathrm{s})|\,\mathrm{f_{str}}(\mathrm{r}),\,\mathrm{r}&\ne \mathrm{s},\,\tau^{2}{}_{\mathrm{str}}\,\sim\,\mathrm{N}\left( {\sum {\mathrm{f_{str}}(\mathrm{r})/\,\mathrm{N}\mathrm{s},\,\tau^{2}{}_{\mathrm{str}}/\mathrm{Ns}} } \right) \hfill \\ & \qquad r\varepsilon \partial s \end{aligned} $$

(3.8)

where N _s is the number of adjacent regions, and r є ∂s indicates that region r is a ‘neighbour’ of region s. Therefore the conditional mean of f _str (s) is an unweighted average of function valuations for neighbouring regions. In addition, the variance parameter τ ² _str controls the degree of smoothness.

For a spatially uncorrelated (unstructured) effect, f _unstr, s = 1, …,S, common assumptions are that the parametersf _unstr (s), are i.i.d. Gaussian:

$$ {f_{\mathrm{unstr}}}(s)|{\tau^2}_{\mathrm{unstr}}\sim N(0,\ {\tau^2}_{\mathrm{unstr}}). $$

(3.9)

Variance or smoothness parameters τ ² _j , j = str, unstr, are also considered as unknown in a fully Bayesian analysis, and are therefore estimated simultaneously with the corresponding unknown functions f _j . As such, hyperpriors are assigned to them in a second stage of the hierarchy by highly dispersed Inverse Gamma distributions p (τ ² _j ) ∼ IG (a _j , b _j ) with known hyperparameters a _j and b _j .

Standard choices for the hyperparameters are a = 1 and b = 0.005 or a = b = 0.001. The results of the illustration in this chapter are however not sensitive to the choice of a and b, and the later choice is close to Jeffrey’s non-informative prior. Fully Bayesian inference is based on the posterior distribution of model parameter, which is not a known form. As such, MCMC sampling from full conditionals for nonlinear effects, spatial effects, fixed effects and smoothing parameters is used for posterior analysis. For the nonlinear and spatial effects, the sampling scheme of Iterative Weighted Least Squares (IWLS) implemented in BayesX (see Brezger et al. 2002) is applied. This is an alternative to the general Metropolis–Hastings algorithms based on conditional prior proposals, suggested first by Knorr-Held (1999) in the context of state space models as an extension to Gamerman (1997), and given in more detail in Knorr-Held and Rue (2002).

An essential task in the model-building process is the comparison of a set of plausible models, for instance, rating the impact of covariates and assessing whether their effects are time-varying or not; or comparing geo-additive models with simpler parametric alternatives. The measure of complexity and fit suggested by Spiegelhalter et al. (2002) is adopted in this chapter for comparison, and the model that takes all relevant structure into account while remaining parsimonious is selected.

The Deviance Information Criteria (DIC), which may be used for model comparison, is defined as

$$ \overline{\mathrm{DIC}}(\mathrm{M}) = \mathrm{D}(\mathrm{M}) + \mathrm{pD}. $$

(3.10)

Therefore, the posterior mean of the deviance $\overline{D}(M)$ is penalized by the effective number of model parameters pD. Models could be validated by analyzing the DIC, which is smaller in models with covariates of high explanatory value.

3.4 Advantages of the Bayesian Geo-additive Model

There are several potential advantages of the Bayesian geo-additive model described above over the more conventional approaches such as, discrete-time Cox models with time-varying covariates and fixed or random districts effects, or the standard 2-level multilevel modelling with unstructured spatial effects (Goldstein 1999). In the conventional models, it is assumed that the random components at the contextual level (district in this case) are mutually independent. In practice however, these approaches specify correlated random residuals (see Langford et al. 1999), which is contrary to the assumption. Furthermore, Borgoni and Billari (2003) point out that the independence assumption has an inherent problem of inconsistency. They argue that if the location of the event matters, it is only logical to assume that areas close to each other are more similar than areas that are far apart. In addition, treating groups (in this case, districts) as independent is unrealistic and may lead to poor estimates of the standard errors. As Rabe-Heskesth and Everitt (2000) stipulate, standard errors for between-district factors are likely to be underestimated as a result of observations from the same districts being treated as independent, and thereby increasing the apparent sample size. In contrast, standard errors for within-district factors are likely to be overestimated (see also Bolstad and Manda 2001). Demographic and Health Survey data on the other hand are based on the random sampling of districts that introduces a structured component, which allows for the borrowing of strength from neighbors in order to cope with the posterior uncertainty of the district effect and obtain estimates for areas that may have inadequate sample sizes or are not represented in the sample. In order to highlight the advantages of the Bayesian geo-additive model approach used in this chapter, and examine the potential bias incurred when ignoring the dependence between aggregated spatial areas, several models shall be fitted with, and without the structured and random components, as seen in the illustration below.

4 Illustration: Spatial Modelling of Under-Five Mortality in Nigeria

4.1 Data Set

Data from the 2003 Nigeria Demographic and Health Survey (NDHS) was used in this chapter. The sample included 7,620 women aged 15–49 years, and all men aged 15–59 in a sub-sample of one-third (i.e. 2,346) of the households. The data contains 6,029 children born within 5 years prior to the survey, which came from 3,725 mothers who contributed between 1 child and 6 children. Technical details of the survey have been reported in the official 2003 NDHS report (NPC 2004). From the data collected, a retrospective child file consisting of all children born to the sample women was generated, of these, 1,559 children died before their fifth birthday. Each live birth and each subsequent child health outcome contains information on the household and each parent, thereby constituting the basic analytic sample.

The response variable used in this chapter is:

$$ {y_{\mathrm{it}}}=\left\{ {\begin{array}{*{20}{l}} {1:\ \ \ \mathrm{if}\ \mathrm{child}\ i\,\mathrm{dies}\ \mathrm{in}\ \mathrm{month}\ t} \\[4pt] {0:\ \ \ \mathrm{if}\ \mathrm{child}\ i\,\mathrm{survives}\ \mathrm{beyond}\ \mathrm{time}\ t,} \\ \end{array}} \right.$$

(3.11)

4.2 Specification and Measurement of Variables

On the basis of previous studies, a selection of theoretically relevant variables was chosen as covariates of childhood mortality, and these include: mab, mother’s age at birth of the child (in years) – nonlinear; dobt, duration of breastfeeding – time-dependent; dist, district (state) in Nigeria – spatial covariate; X, vector of categorical covariates, such as: sex of the child (male or female), asset index (low, middle or higher income household), place of residence (urban or rural), mother’s educational level (no education, primary, secondary of higher), place of delivery (hospital or home/other), preceding birth interval long birth interval [≥24 months], or short birth interval [<24 months], antenatal visits during pregnancy (at least one visit, or none), marital status of mother (single or married), and district level mortality rate per 1,000 (at least 6 children, or at less than six children per woman).

The last levels of each covariate were selected as reference or baseline levels; descriptive statistics of covariates used in the analysis are shown in Table 3.2. Available statistics suggest that child mortality levels in Nigeria exhibit wide geographic disparities (NPC 2000, 2004), with the northern regions and rural areas generally having higher childhood mortality rates compared to the southern regions and urban areas respectively. While the focus of previous studies in Nigeria have mainly been on effect of individual and household factors in explaining childhood mortality differences in the country, they have largely neglected the impact of small area variations and community-level variables (see Iyun 1992; Adetunji 1994; Folasade 2000; NPC 2004).

Table 3.2 Descriptive statistics of covariates used in the analysis, Nigeria Demographic and Health Survey, 2003

The aim of this present chapter is to highlight the regional- and district-level variations in under-five mortality in Nigeria, while improving current knowledge of district-level socio-economic and demographic determinants (thereby warranting the inclusion of a geographic location [districts] covariate). It is also intended to assist policy makers in evaluating and designing programme strategies needed to improve child health services, and reduce childhood mortality levels in Nigeria.

4.3 Statistical Method

An analysis and comparison of simpler parametric probit models, and probit models with dynamic effects, pr (y _it = 1|x _it) = Ф (η _it), was made for the probability of dying in month t, i.e. the conditional probability of a child dying, given the child’s age in months, the district where the child lived before death, and covariates in X above, is modeled with the following predictors:

$$ M1:{\eta_{\mathrm{it}}}={f_0}(t) + {X_{\mathrm{it}}}\beta$$

$$ M2:{\eta_{\mathrm{it}}}={f_0}(t) + {f_1}(\mathrm{mab})+f(t){X_{\mathrm{it}}}+{f_{\mathrm{unstr}}}(\mathrm{dist}) + {f_{\mathrm{str}}}(\mathrm{dist}) + {X_{\mathrm{it}}}\beta $$

The fixed effects in model M1 include all covariates described above with constant fixed effects. Mother’s age at birth was split into three categories as shown in Table 3.2, and duration of breastfeeding was included as dichotomous (0, 1) variable. Model M2 will be superior to model M1 because Model M2 accounts for the unobserved heterogeneity that might exist in the data, all of which cannot be captured by the covariates (see Madise et al. 1999).

The effects of f ₀ (t), f ₁ and f(t) are estimated using second-order random walk prior, and Markov random field priors for f _str (s). The analysis was carried out using BayesX-version 0.9 (Brezger et al. 2002), a software for Bayesian inference based on Markov Chain Monte Carlo simulation techniques. The sensitivity of the effects to choice of different priors for the non-linear effects (P-splines) and the choice of the hyperparameter values a and b are investigated.

Previous studies, for example, Berger et al. (2002), have shown that breastfeeding is an important factor. In order to assess its effect, a time-varying indicator variable (see Kandala 2002), that takes the value 1 in the months a child is breastfed, and 0 otherwise, is generated. In addition, temporal and spatial variations in the determinants of child mortality are also assessed. Common choices for discrete survival models are the grouped Cox model and probit or logit models. For this chapter, probit model for discrete survival data is used because binary response models (3.3) can be written equivalently in terms of latent Gaussian utilities, which lead to very efficient estimation algorithms. In addition, since survival time in the DHS data set is recorded in months and the longest observation time for this study is limited to 60 months, the data naturally contain a high amount of tied events. A constant hazard within each month is assumed.

At the exploratory stage, a probit model with constant covariate effects (M1) for the effects of breastfeeding and mother’s age are fitted with a view to compare them to the dynamic probit models (M2).

5 Results

5.1 Fixed Effects

The estimates of posterior odds ratio of the fixed effect parameters for under-five mortality in Nigeria (Model 2) together with their standard errors and quantiles are presented in Table 3.3. Results indicate that children living in urban areas at lower risk of dying than children living in rural areas (posterior odds ratio 0.54), with positive corresponding 2.5 %- and 97.5 % quantiles indicating that the effect is statistically significant. Boys are only slightly at higher risk of dying than girls (posterior odds ratio 1.08), and the corresponding 2.5 %- and 97.5 % quantiles are both positive. The results also show that a short birth interval significantly reduces a child’s chances of survival, as children with birth interval 25+ months were at lower risk of dying compared to those < 25 months (posterior odds ratio 0.71), the effect being statistically significant. In comparison to children whose mothers had no antenatal visits during pregnancy, children whose mothers had at least one antenatal visit were at lower risk of dying; the effect being statistically significant.

Table 3.3 Posterior Odds ratio of the fixed effect parameters for under-five mortality in Nigeria (Model 2)

Children delivered in hospitals were at slightly lower risk of dying compared to children born at home or elsewhere (posterior odds ratio 0.95). Findings also indicate that child survival is associated with economic status of the household; while children living in households within the 2nd and 4th quintiles were significantly at lower risks of dying compared to those in the 1st quintile (richest households), those living in households within the 3rd quintile had a slightly higher risk of dying (posterior odds ratio 1.09) compared to those in the 1st quintile. Mothers’ education, was associated with child survival and works in the expected direction (with children of uneducated mothers having 50 % higher risk). Partner’s education, on the other hand, was insignificant.

Children of single mothers were at higher risk of dying (posterior odds ratio 1.27) compared to children whose mothers were married; both quantiles were positive, and therefore the relationship was significant. Remarkably, the larger the household size, the lower the risk of the children dying. Children living in medium-size households (posterior odds ratio 0.99), and those living in large-size households (posterior odds ratio 0.96), were at lower risk of dying compared to children living in small-size households; both relationships had positive quantiles and were therefore significant.

5.2 Baseline Effects

The estimated nonlinear effect of child’s age (baseline time) and the time-varying effects, modelled and fitted through Bayesian P-splines are shown in Fig. 3.2. The posterior means are presented within 80–95 % credible intervals, and show that starting from a comparably high level in the first month, the baseline effect remains more or less constant until 25–26, and 40–41 months, where they peak. These observed peaks are likely to be caused by a “heaping” effect from the large number of deaths reported at these times (probably resulting from incorrect reporting of large number of deaths at these ages).

Fig. 3.2

Estimated nonlinear effect of baseline time. Shown is the posterior mean within 80–95 % credible intervals

5.3 Time-Varying Effects

Figure 3.3 displays the time-varying effect of breastfeeding in Nigeria, and indicates that breastfeeding is on average associated with lower risk of mortality within the first 16–18 months using 80–95 % credible intervals. However, given the wide range of the 80–95 % credible region at the end of the observation period (most likely due to fewer numbers of cases), the results beyond 18 months should be interpreted with caution.

Fig. 3.3

Estimated nonlinear effect of time-varying effect of breastfeeding. Shown is the posterior mean within 80–95 % credible intervals

5.4 Nonlinear Effects

Figure 3.4 shows the non-linear or time-varying effect of mother’s age at birth of the child. Children with younger mothers (<20 years) and older mothers (>35 years) have higher (but statistically insignificant) risk of dying compared to children of mothers within the middle age group (22–34 years). Figure 3.4 also shows that children of mothers 42–48 years are even at higher risk of dying compared to children of mothers <20 years.

Fig. 3.4

Estimated nonlinear effect of mother’s age at child’s birth. Shown is the posterior mean within 80–95 % credible intervals

Fig. 3.5

Estimated odd ratio of total residual spatial states effects for under-five mortality in Nigeria. Dark coloured – high risk. Grey coloured – low risk

5.5 Spatial Effects

Posterior means of the estimated residual spatial states effects on under-five mortality in Nigeria are presented in Fig. 3.5. This map shows a strong spatial pattern, which suggests that survival chances of children under-5 years of age are highest within the North Western (Sokoto, and Kebbi) and South Western (Lagos) regions compared to the other regions. On the other hand, the survival chances of children under-5 years are lowest among children from Jigawa, Taraba, Delta, Rivers and Adamawa states compared to the children from the rest of the states. A comparison between the under-five mortality rates (Table 3.1) and the estimated odds ratio (Fig. 3.5) reveals the emergence of a clear spatial pattern of under-five mortality risk with the residual effects in Fig. 3.5. Therefore, failure to take into consideration the posterior uncertainty in the spatial location (states or districts) would invariably lead to an overestimation of the precision in predicting childhood mortality risks in unsampled districts. The spatial effects could therefore be interpreted as representing the cumulative effect of unidentified or unmeasured additional covariates that may reflect impacts of environmental and socio-cultural factors.

6 Discussion and Conclusion

After controlling for the spatial dependence in the data, almost all the covariates associated with under-five mortality in the fixed part of the model were found to have effects in the expected directions. A remarkable finding however, is that children in larger households are at slightly lesser risk of dying compared to children in small households; this may not be unconnected with factors that might contribute to a household’s propensity to experience childhood deaths such as the burden of child ill-health and mortality being borne by only a small fraction of all households (Madise and Diamond 1995); household income (Vella et al. 1992); maternal education (Cleland and van Ginneken 1988); physical access to care (Kuate Defo 1996); and rural as opposes to urban setting (Sastry 1997).

The time-varying effects of breastfeeding emphasize the importance of breastfeeding, which is widely believed to be the most beneficial source of infant nutrition for the attainment of health and well-being of the infant (Weimer 2001). Results of this study show a lowered risk of mortality associated with breastfeeding within the first 16–18 months. However, results at the end of the observation period do not provide reliable information on the dynamic effect of breastfeeding (due to few cases), and should therefore be interpreted with caution. Results of the nonlinear effect of mother’s age at the birth of the child are in the expected direction, emphasizing the risk associated with younger mother (also seen in Alam 2000) and late childbirth (see Hobcraft et al. 1985), especially the higher risk associated with children of women aged 42–48 years.

The estimated residual spatial effects for under-five mortality in Fig. 3.5 show clear differences between the significantly better survival chances of children in the North West (Sokoto, and Kebbi) and South West (Lagos) regions compared to the North East (Adamawa, Taraba, Yobe, Borno), South South (Delta, Rivers, Akwa Ibom) and South East (Enugu) regions. These state patterns are similar to analysis of poverty in Nigeria in which the Northeast zone had the highest poverty incidence with 67.3 %, followed by the Northwest with 63.9 %; the South South zone had the highest poverty rates (55 %) among the southern states, while the lowest poverty rates were recorded in the South East at 34.2 %, followed by Southwest with 43.0 % (National Bureau of Statistics 2005).

While some of these effects have been shown using traditional parametric methods, using Bayesian geo-additive models uniquely shows subtle differences when analysing for small-area spatial effects. Though the spatial effects do not show causality, careful interpretation could identify latent and unobserved factors that directly influence mortality rates. This geographic semi-parametric approach therefore appears to be able to discern subtle influences of the determinants, and identifies district-level clustering of under-five mortality.

The variation in the probability of childhood survival in Nigeria is spatially structured. This implies that adjusted mortality risks are similar among neighbouring states or districts, which may partly be explained by general health care practices, similar prevalence of common childhood diseases, and the residual spatial variation induced by variation in unmeasured district-specific characteristics (which any standard 2-level model with unstructured spatial effects assuming independence among districts would yield estimated that lead to incorrect conclusions).