Keywords

1 Introduction

Cone Penetration test (CPT) is a widely used in situ test for calculation of soil parameters like relative density, friction angle and stiffness modulus [1, 2]. Cone penetrometer test was primarily limited to soft soils but with the application of enhanced functionalities like piezocone CPT with pore water pressure measurement and modern jacking techniques, it is possible to use CPT for wide variety of soils and for soft rocks as well.

There are various analytical methods available to study cone penetration in dense sand which includes bearing capacity theory by limit plasticity [3–5], cavity expansion theory [6–8] and strain path method [9]. Laboratory chamber studies [10–13] have also been carried out to study penetration of cone in soil media.

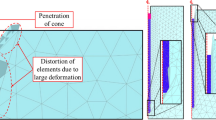
Advances in numerical computation software have encouraged various researchers to simulate difficult real life geotechnical problems in a numerical model. With use of finite element analysis it is possible to implement any type of constitutive model with increased accuracy even with difficult geometry. Finite element method has been used by researchers [14–16] to simulate cone penetration test. Finite element formulation of cone penetration is very advantageous because it takes into account the effect of soil stiffness and compressibility, considers the effect of initial stresses, calculates the stresses during penetration with reasonable accuracy, and no assumption of failure modes is required, and utilizes various constitutive models to simulate behavior of soil. But cone penetration involves large distortion of mesh in high strain concentration area around the cone tip which leads to loss of accuracy as the penetration depth is increased. The cone penetration has been analyzed as a bearing capacity problem by some researchers [3, 17] assuming Mohr-Coulomb failure criterion of soil. Vesic [8] incorporated the application of kinematic field for soil which has similar movements as proposed in cavity expansion theory [8]. Baligh analyzed the cone to be surrounded by an incompressible, inviscid fluid to determine the deformation pattern of soil around the cone and calculating the theoretical strain and pore water distribution in soil using these deformation patterns. Another approach to calculate the response of very soft cohesive clays was developed using conformal mapping technique for analytical calculations of strain rates around the cone tip assuming an inviscid fluid flow [18]. But the results from both these methods [18, 19] have limited validity because of the assumptions taken for simplification of problem. The deformation patterns assumed in bearing capacity theory and cavity expansion theory are not justified by the experimental observations. Application of kinematic field to soil nodes accounts for stress calculation in later stages of analysis but it is not justified because of its inability to account for initial stress state of soil.

With more advanced numerical computation techniques, an Eulerian part is introduced in finite element analysis. A study of cone penetration is considered by Van Den Berg et al. [15] using Arbitrary Lagrangian Eulerian (ALE) methodology for layered deposit. The objective of Van Den Berg et al. [15] was limited to application of ALE technique in analyzing layered soil medium rather than analysis of cone penetration simulation. Van Den Berg et al. [15] assumed the cone to have rigid boundary conditions and the soil to move around the cone tip in specified displacement field. This application of ALE technique created a new benchmark in finite element models to calculate the effect of large scale deformation in soil domain. Van Den Berg et al. [15] started his analysis by placing the cone in a pre-bored hole which may result in underestimation of horizontal stresses on cone. However the work by Van Den Berg et al. [15] was also limited by prescribed displacement field of soil around the cone tip.

The adaptive remeshing technique for simulation of finite deformation is used with explicit iteration method which is more effective than implicit iteration. It is because of the fact that the analysis run time is directly proportional to the mesh size in explicit analysis whereas it is directly proportional to the square of the wave front times the number of degrees of freedom [20] in implicit analysis. Thus it is possible to simulate a model with very fine mesh in the expected zone of effect for penetration while carrying out ALE adaptive remeshing technique. Adaptive remeshing used by Susila and Hryciw [21] established a reasonable axisymmetric numerical model to simulate finite scale deformation which occurs during cone penetration.

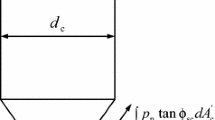
Huang et al. [22] simulated a numerical model for cone penetration in cohesionless soil. Huang et al. [22] used basic mathematical equations to separate the cone resistance from sleeve friction resistance. These equations are used in this study to separate the cone resistance from sleeve friction. The resistance to penetration of cone consists of two terms. The first term is the resistance encountered by the conical area which is termed as cone resistance and second is the resistance encountered by the sleeve of the cone which is called sleeve friction. A mathematical correlation is used in this study to separate these values. According to Huang et al. [22],

$$ F_{\text{t}} = F_{\text{c}} + F_{\text{s}} $$
(1)

where, F t is total force experienced during penetration of cone, F c is cone resistance encountered in terms of force and F s is sleeve resistance encountered during penetration. Out of these two components of total force, the most important engineering design parameter is the cone resistance expressed in form of stress,

$$ q_{\text{c}} = 4F_{\text{c}} /{\varvec{\uppi}}d_{\text{c}}^{ 2} $$
(2)

where, q c is the cone tip resistance, d c is the diameter of cone.

To separate F c from F t, the interface friction angle is set to zero and total force is determined during penetration (refer Fig. 1). Thus the obtained force with interface friction angle equal to zero is equal to cone resistance without any frictional resistance, i.e. F c |ϕsc=0 = F t |ϕsc=0. It is to be noted that when the interface friction is not zero, then there will be a component of interface friction in addition to F c |ϕsc=0.

Fig. 1
figure 1

Illustration of contact interface friction angle to cone resistance

Full size image

Now to account for the contribution of interface friction in cone resistance, we will multiply the cone resistance at zero friction (\( \bar{q}_{\text{c}} \)) with a cone tip factor η so that,

$$ q_{\text{c}} =\upeta\bar{q}_{\text{c}} $$
(3)

where, q c is the actual cone tip resistance and as per,

$$ \begin{aligned} q_{\text{c}} A_{\text{c}} & = \int\limits_{{A^{\prime}_{\text{c}} }} {p_{\text{n}} \left( {\sin \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right) + \cos \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right)\tan\upphi_{\text{sc}} } \right)} dA_{\text{c}}^{{\prime }} \\ & = \left( {\sin \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right) + \cos \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right)\tan\upphi_{\text{sc}} } \right)\int\limits_{{A^{\prime}_{c} }} {p_{\text{n}} dA_{\text{c}}^{{\prime }} } \\ & \quad {{q_{\text{c}} A_{\text{c}} } \mathord{\left/ {\vphantom {{q_{\text{c}} A_{\text{c}} } {\bar{q}{}_{\text{c}}A_{\text{c}} \Rightarrow\upeta = 1 + \cot \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right)}}} \right. \kern-0pt} {\bar{q}{}_{\text{c}}A_{\text{c}} \Rightarrow\upeta = 1 + \cot \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right)}}\tan\upphi_{\text{sc}} \\ \end{aligned} $$
(4)

where, \( A_{\text{c}}^{{\prime }} \) represents tip area of cone. According to Huang et al., a factor υ is introduced in this equation to account for effect of dilation angle:

$$ \upeta = 1 +\upupsilon\cot \left( {{\upalpha \mathord{\left/ {\vphantom {\upalpha 2}} \right. \kern-0pt} 2}} \right)\tan\upphi_{\text{sc}} \quad 0. 7<\upupsilon < 1. 1 $$
(5)

where υ is a fitting parameter determined through least-square fit method. A value of 0.86 is chosen in this study for υ which is used in Eq. (5) based on numerical CPT data and least square fit method as discussed by Huang et al. [22].

The objective of this study is to perform cone penetration analysis numerically accounting for finite scale deformation occurring in soil domain as a result of cone penetration. In this study, numerical simulation of cone penetration in different relative densities of sand has been carried out using three dimensional nonlinear finite element program (ABAQUS) and the coupled Eulerian-Lagrangian (CEL) method. Herein, soil domain has been modelled using Eulerian elements and the cone has been modelled using Lagrangian elements. The stress-strain response of soil is simulated using the Mohr-Coulomb constitutive model and the cone is modelled as steel with rigid body properties. The elasto plastic deformation of soil is presented and output in the form of cone tip resistance is used for establishing a relationship between cone tip resistance and mean effective stress.

2 Geometry and Mesh

The numerical model presented in this study is prepared by taking advantage of the symmetry of problem. The soil domain is modelled as a quarter cylindrical domain of height 3.5 m and radius 0.5 m. The cone is modelled as 0.031 m long and apex angle 60° as presented in Table 1. The soil domain has a void section of 50 cm in the upper part as shown in Fig. 2 to model the flow of material displaced by the insertion of cone. Up to 1 m penetration of cone is considered in the present work.

Table 1 Material and geometrical properties of cone
Full size table
Fig. 2
figure 2

Mesh diagram of CPT model

Full size image

3 Modelling Details

Boundary and Initial Conditions: The velocity of nodes at the bottom of the soil domain is kept zero in all active degree of freedoms. The outer surface of cylindrical domain is kept constrained from horizontal motion of nodes i.e. in x and y directions, the velocities are zero. Symmetric boundary conditions are applied on the plane of symmetry in model. The x-plane of symmetry in the model restricts the velocity of nodes in the x-direction but allow the nodes to move in the y and z-directions. Similarly the velocity of nodes in y-direction is kept zero for y-plane of symmetry while keeping the velocity in the x and z directions to be free.

Initial stresses are defined in the model based on the density of soil and surcharge applied at the soil void interface. The earth pressure coefficient at rest (K 0 = 1 – sin ϕ′) is used to calculate the horizontal stresses at any given depth. A reference point is defined in this analysis to control the motion of rigid body cone. Six active degrees of freedom have been specified at the reference point. Initial conditions in the form of velocity are applied to this rigid body reference point to control the motion of cone. This reference point has been assigned a constant velocity of penetration in z-direction and all other five degrees of freedom have been assigned zero velocity throughout the analysis.

Loading: There are two types of loading applied in this study to account for the effect of gravity and surcharge loading. The effect of gravity is introduced by specifying an acceleration of 10 m/s2 in negative z-direction for the material assigned section in the Eulerian part.

The second type of loading used herein is the application of surcharge at the soil-void interface. This surcharge is applied to study the effect of higher depth of soil penetration without modelling the complete depth of soil medium. For example, a surcharge of 80 kPa represents that the soil void interface is located at a depth of 4 m in soil domain of unit weight 20 kN/m3. Different values of surcharge are used in this study to study the dependence of cone tip resistance on the surcharge applied.

Analysis: Two types of analysis are carried out for one simulation of cone penetration. One analysis is carried out with frictionless interface and the other with frictional interface and interface friction angle equal to two-third of soil friction angle. The analyses are carried out till a constant value of tip resistance is achieved. Then the Eqs. (3) and (5) are used to calculate the cone resistance from this constant value corresponding to frictionless analysis and sleeve resistance is calculated by subtracting cone resistance from the total resistance obtained by frictional analysis.

4 Material Modelling

Soil domain in this study is modelled using Mohr-Coulomb plasticity criterion with parameter specified in Table 2 depending on the relative densities of sand. The Young’s modulus is maintained constant in the soil domain. The cone is modelled as a rigid body which will not undergo any deformation during analysis. A reference point is generated in space to control the motion of cone which is needed to assign a constant velocity of penetration to cone.

Table 2 Soil parameters for various types of sands used in this study
Full size table

The following simplified relationship is used to calculate the dilation angle (ψ) for different types of sands having different friction angles [23]:

$$ \uppsi =\upphi^{\prime } -\upphi_{\text{cv}} $$
(6)

where ϕ′ denotes the friction angle for sand and ϕcv denotes critical state friction angle equal to 30°. The general contact algorithm in Abaqus and penalty contact with interface friction angle equal to two-third of sand friction angle is used between cone and soil to define the contact between cone and the surrounding soil.

5 Results and Discussions

Calibration: The calibration of the numerical model is presented to prove that the analysis is independent on the size of elements in mesh and velocity of penetration. Table 3 shows description of three different types of mesh used in this study to calibrate the numerical model. Figure 3a shows the output from three different numerical models with different size of mesh in the form of total force required to penetrate the cone in soil domain. These analyses are performed for contact interface friction angle equal to two-third of the friction angle for dense sand. Based on these results, the medium mesh is chosen in this study to simulate the cone penetration problem.

Table 3 Description of mesh size
Full size table
Fig. 3
figure 3

Calibration of numerical model a mesh independency (with frictional interface) and b velocity independency (with smooth interface)

Full size image

The second step of calibration in this study is performed to ensure that the results are independent of the velocity of cone penetration. Figure 3b shows result in form of total force required to penetrate the cone in soil domain. A velocity of 0.4 m/s is chosen for further analysis of cone penetration. This velocity is preferred because it will decrease the CPU time and increase the economy of analysis.

The main emphasis in this study is given on the tip resistance encountered by the cone tip during cone penetration in cohesionless soil. Tip resistance is calculated by using Eq. (3) with results obtained from frictionless interface between soil and cone. However, distribution of total global sleeve friction is also presented in this study. In this study the sleeve friction is calculated for the complete shaft which is penetrated in the soil domain. Thus the contact area between cone tip and soil remains constant after the full penetration of cone tip but the contact area between sleeve and soil keeps on increasing with increasing penetration depth. Figure 4 shows distribution of cone tip resistance and global sleeve friction for dense sand (ϕ = 37.5°). The graph shows that at the penetration depth of 1 m, magnitude of cone resistance is equal to 6,876 kPa as compared to the sleeve friction value of 12 kPa. The average value of friction ratio for 1 m penetration is recorded as 0.72 %. Based on Robertson and Campanella [24], soil with friction ratio 0.72 % and cone resistance as 6,876 kPa will be classified as sandy soil. According to Douglas and Olsen [25], soil will be classified as non-cohesive coarse grained soil. This value of friction ratio and cone resistance justifies the material modelling of soil as dense sand.

Fig. 4
figure 4

Distribution of a cone resistance; b sleeve friction for dense sand with zero surcharge

Full size image

The variation of sleeve friction along the sleeve length is also considered in this analysis. Figure 5 shows the stress distribution on the sleeve at penetration depth of 0.35 m. The values on y axis represent the distance of points from the conical part of cone. The distribution shows a constant value of 2 kPa for penetration depth of 0.35 m with zero surcharge and dense sand (ϕ = 37.5°).

Fig. 5
figure 5

Stress distribution along sleeve

Full size image

Figure 6 shows the variation of horizontal stresses at fixed points in soil domain. These points are chosen at depths of 0.25, 0.50 and 0.75 m. The values of stresses are plotted on logarithmic scale because of very high value of stress corresponding to an individual point when the cone passes through that point. This distribution shows that there is very high increase in horizontal stresses when the cone passes through a particular point but as the cone goes down, the sleeve resistance come into play and the horizontal stresses become constant which is unaffected by further penetration of cone.

Fig. 6
figure 6

Distribution of horizontal stresses for three fixed nodes in numerical model (dense sand with zero surcharge)

Full size image

The analysis is performed for different values of surcharge \( \upsigma_{{{\text{v}}0}}^{{\prime }} \) like 40, 80, 160 and 240 kPa in order to simulate different depths of soil. The Eq. (7) given by Clausen et al. [26] is used to calculate the relative density of soil for applied surcharge and the obtained cone resistance q c because the Mohr Coulomb model does not take into consideration of soil relative density. According to Clausen et al. [26], the relative density D R of soil is,

$$ D_{\text{R}} = 0.4\;\ln \left[ {\frac{{q_{\text{c}} }}{{22.\sqrt {\upsigma_{\text{v0}}^{{\prime }} p_{\text{a}} } }}} \right]\quad \quad p_{\text{a}} = 100\;{\text{kPa}} $$
(7)

The equation by Clausen et al. [26] is used to present the results of current study in terms of relative density of sand. This relative density of sand depends on the stress conditions and compressibility of soil. The compressibility of the soil is in turn dependent on the change in void ratio divided by the change in stress. The average of these relative densities for a particular soil type is taken and then that type of soil is symbolized by this average relative density. Table 4 shows the value of averaged relative density as obtained from Clausen et al. [26]. The results of finite element analyses are then compared with that reported in Baldi [2] in terms of averaged relative densities as calculated from Eq. (7). Figure 7 shows the comparison between current study and Baldi [2]. The comparison shows good agreement between current study and Baldi [2] for sands with same relative density.

Table 4 Relative densities of sands under study as calculated according to Clausen et al. [26]
Full size table
Fig. 7
figure 7

Comparison between present study and Baldi [2] with D R calculated from Clausen et al. [26]

Full size image

The next comparison is made between results from current study and various results from bearing capacity theory, calibration chamber testing and cavity expansion solutions. Results from bearing capacity solution of Durgunoglu and Mitchell [4, DM], cavity expansion solutions from Collins et al. [27] combined with correlation of Yasafuku and Hyde [28], YH&C); cavity expansion solution of Collins et al. [27] combined with bearing capacity factor correlation of Ladanyi and Johnston [29], LJ&C); average chamber correlation of Houlsby et al. ([13], HH); and experimental results from Yu and Mitchell [30] are compared with current solution by CEL analysis in this section (Fig. 8). The comparison between normalized stresses (\( q_{\text{c}} /\upsigma_{\text{v0}}^{{\prime }} \)) for surcharge value 240 kPa shows good agreement between the results.

Fig. 8
figure 8

Comparison between experimental data and predicted cone factor solution for several studies with current study for 240 kPa

Full size image

6 Conclusions

As observed in the numerical analysis, the CEL procedure is very well suited for problems involving large deformation. The successful representation of cone penetration test using CEL proves that CEL is a potential tool for large deformation in Geotechnical Engineering.

Herein, numerical simulation of cone penetration test is performed to understand the response of cohesionless soil for different relative density values. The material is modelled using the Mohr-Coulomb failure criteria and the response of soil is studied. Comparison with existing numerical results and experimental data show that the response of numerical model presented in this study is reasonable for intermediate depths of cone penetration. The relationships derived in this study are purely numerical and proper site investigation and consultation must be sought before using these results.