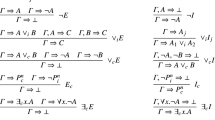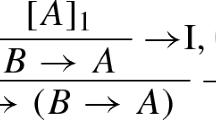A Semantical View of Proof Systems

Abstract

In this work, we explore proof theoretical connections between sequent, nested and labelled calculi. In particular, we show a semantical characterisation of intuitionistic, normal and non-normal modal logics for all these systems, via a case-by-case translation between labelled nested to labelled sequent systems.

E. Pimentel—Funded by CNPq, CAPES and the project FWF START Y544-N23.

1 Introduction

The quest of finding analytic proof systems for different logics has been the main research topic for proof theorists since Gentzen’s seminal work [5]. One of the best known formalisms for proposing analytic proof systems is Gentzen’s sequent calculus. While its simplicity makes it an ideal tool for proving meta-logical properties, sequent calculus is not expressive enough for constructing analytic calculi for many logics of interest. The case of modal logic is particularly problematic, since sequent systems for such logics are usually not modular, and they mostly lack relevant properties such as separate left and right introduction rules for the modalities. These problems are often connected to the fact that the modal rules in such calculi usually introduce more than one connective at a time, e.g. as in the rule $\mathsf {k}$ for modal logic $\mathsf {K}$:

One way of solving this problem is by considering extensions of the sequent framework that are expressive enough for capturing these modalities using separate left and right introduction rules. This is possible e.g. in labelled sequents [18] or in nested sequents [1]. In the labelled sequent framework, usually the semantical characterisation is explicitly added to sequents. In the nested framework in contrast, a single sequent is replaced with a tree of sequents, where successors of a sequent (nestings) are interpreted under a given modality. The nesting rules of these calculi govern the transfer of formulae between the different sequents, and they are local, in the sense that it is sufficient to transfer only one formula at a time. As an example, the labelled and nested versions for the necessity right rule ($\Box _R$) are

where y is a fresh variable in the $\Box _R^l$ rule. Reading bottom up, while the labelled system creates a new variable y related to x via a relation R and changes the label of A to y, in $\Box _R^n$ a new nesting is created, and A is moved there. It seems clear that nestings and semantical structures are somehow related. Indeed, a direct translation between proofs in labelled and nested systems for the modal logic of provability (a.k.a. the Gödel-Löb provability logic) is presented in [6], while in [4] it is shown how to relate nestings with Kripke structures for intuitionistic logic (via indexed tableaux systems). In this work, we show this relationship for intuitionistic logic and some normal modal logics, using only sequent based systems.

Since nested systems have been also proposed for other modalities, such as the non-normal ones [2], an interesting question is whether this semantical interpretation can be generalised to other systems as well. In [15] a labelled approach was used for setting the grounds for proof theory of some non-normal modal systems based on neighbourhood semantics. In parallel, we have proposed [10] modular systems based on nestings for several non-normal modal logics. We will relate these two approaches for the logics $\mathsf {M}$ and $\mathsf {E}$, hence clarifying the nesting-semantics relationship for such logics.

Finally, in [11], we showed that a class of nested systems can be transformed into sequent systems via a linearisation procedure, where sequent rules can be seen as nested macro-rules. By relating nested and sequent systems, we are able to extend the semantical interpretation also to the sequent case, hence closing the relationship between systems and shedding light on the semantical interpretation of several sequent based systems.

Organisation and Contributions. Section 2 presents the basic notation for sequent systems; Sect. 3 presents nested systems and summarizes the results for their sequentialisation; Sect. 4 presents the basic notation for labelled systems; Sects. 5, 6 and 7 show the results under the particular views of intuitionistic, normal and non-normal logics; Sect. 8 concludes the paper.

2 Sequent Systems

Contemporary proof theory started with Gentzen’s work [5], and it has had a continuous development with the proposal of several proof systems for many logics.

Definition 1

A sequent is an expression of the form $\varGamma \vdash \varDelta$ where $\varGamma$ (the antecedent) and $\varDelta$ (the succedent) are finite sets of formulae. A sequent calculus ($\mathsf {SC}$) consists of a set of rule schemas, of the form

where the sequent S is the conclusion inferred from the premise sequents $S_1,\ldots ,S_k$ in the rule r. If the set of premises is empty, then r is an axiom. An instance of a rule is a rule application.

A derivation is a finite directed tree with nodes labelled by sequents and a single root, axioms at the top nodes, and where each node is connected with the (immediate) successor nodes (if any) according to the application of rules. The height of a derivation is the greatest number of successive applications of rules in it, where an axiom has height 0.

In this work we will consider only fully structural sequent systems, i.e. allowing freely applications of the schemas $\mathsf {init}$ and $\mathsf {W}$ bellow

where P is atomic.

As an example, Fig. 1 presents $\mathsf {SC}_\mathsf {mLJ}$ [12], a multiple conclusion sequent system for propositional intuitionistic logic. The rules are exactly the same as in classical logic, except for the implication right rule, that forces all formulae in the succedent of the conclusion sequent to be previously weakened. This guarantees that, on applying the ($\rightarrow _R$) rule on $A\rightarrow B$, the formula B should be proved assuming only the pre-existent antecedent context extended with the formula A, creating an interdependency between A and B.

Fig. 1.

Multi-conclusion intuitionistic calculus $\mathsf {SC}_\mathsf {mLJ}$.

3 Nested Systems

Nested systems [1, 16] are extensions of the sequent framework where a single sequent is replaced with a tree of sequents.

Definition 2

A nested sequent is defined inductively as follows:

• (i) if $\varGamma \vdash \varDelta$ is a sequent, then it is a nested sequent;

• (ii) if $\varGamma \vdash \varDelta$ is a sequent and $G_1,\ldots ,G_k$ are nested sequents, then $\varGamma \vdash \varDelta ,[G_1],\ldots ,[G_k]$ is a nested sequent.

A nested system ($\mathsf {NS}$ ) consists of a set of inference rules acting on nested sequents.

For readability, we will denote by $\varGamma ,\varDelta$ sequent contexts and by $\varLambda$ sets of nestings. In this way, every nested sequent has the shape $\varGamma \vdash \varDelta , \varLambda$ where elements of $\varLambda$ have the shape $[\varGamma '\vdash \varDelta ', \varLambda ']$ and so on. We will denote by $\varUpsilon$ an arbitrary nested sequent.

Application of rules and schemas in nested systems will be represented using holed contexts.

Definition 3

A nested-holed context is a nested sequent that contains a hole of the form $\{ \; \}$ in place of nestings. We represent such a context as $\mathcal {S}\left\{ \;\right\}$. Given a holed context and a nested sequent $\varUpsilon$, we write $\mathcal {S}\left\{ \varUpsilon \right\}$ to stand for the nested sequent where the hole $\{\;\}$ has been replaced by $\left[ \varUpsilon \right]$, assuming that the hole is removed if $\varUpsilon$ is empty and if $\mathcal {S}$ is empty then $\mathcal {S}\left\{ \varUpsilon \right\} =\varUpsilon$. The depth of $\mathcal {S}\left\{ \;\right\}$, denoted by $\mathsf {dp}\left( \mathcal {S}\left\{ \;\right\} \right)$, is the number of nodes on a branch of the nesting tree of $\mathcal {S}\left\{ \;\right\}$ of maximal length.

For example, $(\varGamma \vdash \varDelta ,\{\;\})\{\varGamma '\vdash \varDelta '\}= \varGamma \vdash \varDelta ,\left[ \varGamma '\vdash \varDelta '\right]$ while $\{\;\}\{\varGamma '\vdash \varDelta '\}= \varGamma '\vdash \varDelta '$.

The definition of application of nested rules and derivations in a $\mathsf {NS}$ are natural extensions of the one for $\mathsf {SC}$, only replacing sequents by nested sequents. In this work we will assume that nested systems are fully structural, i.e., including the following nested versions for the initial axiom and weakening¹

Figure 2 presents the $\mathsf {NS}_{\mathsf {mLJ}}$ [4], a nested system for $\mathsf {mLJ}$.

Fig. 2.

Nested system $\mathsf {NS}_{\mathsf {mLJ}}$.

3.1 Sequentialising Nested Systems

In [11] we identified general conditions under which a nested calculus can be transformed into a sequent calculus by restructuring the nested sequent derivation (proof) and shedding extraneous information to obtain a derivation of the same formula in the sequent calculus. These results were formulated generally so that they apply to calculi for intuitionistic, normal and non-normal modal logics. Here we will briefly explain the main ideas in that work.

First of all, we restrict our attention to shallow directed nested systems, in with rules are restricted so to falling in one of the following mutually exclusive schemas:

• i. sequent-like rules

  

• ii nested-like rules

  • ii.a creation rules

    

  • ii.b upgrade rules

    

The nesting in the premise of a creation rule is called the auxiliary nesting.

The following extends the definition of permutability to the nested setting.

Definition 4

Let $\mathsf {NS}$ be shallow directed, $r_1,r_2$ be applications rules and $\varUpsilon$ be a nested sequent. We say that $r_2$ permutes down $r_1$ ($r_2 \downarrow r_1$) if, for every derivation in which $r_1$ operates on $\varUpsilon$ and $r_2$ operates on one or more of $r_1$’s premises (but not on auxiliary formulae/nesting of $r_1$), there exists another derivation of $\varUpsilon$ in which $r_2$ operates on $\varUpsilon$ and $r_1$ operates on zero or more of $r_2$’s premises (but not on auxiliary formulae/nesting of $r_2$). If $r_2\downarrow r_1$ and $r_1 \downarrow r_2$ we will say that $r_1,r_2$ are permutable, denoted by $r_1 \updownarrow r_2$. Finally, $\mathsf {NS}$ is said fully permutable if $r_1 \updownarrow r_2$ for any pair of rules.

Finally, the next result shows that fully permutable, shallow directed systems can be sequentialised.

Theorem 5

Let $\mathsf {NS}$ be fully permutable, shallow and directed. There is a normalisation procedure of proofs in $\mathsf {NS}$ transforming maximal blocks of applications of nested-like rules into sequent rules.

Next an example of such procedure.

Example 6

In $\mathsf {NS}_{\mathsf {mLJ}}$, a nested block containing the creation rule $\rightarrow ^n_R$ and the upgrade rule $\texttt {lift}^n$ has the shape

Observe that $\texttt {lift}^n$ maps a left formula into itself and there are no context relations on right formulae. Hence the corresponding sequent rule is

which is the implication right rule for $\mathsf {mLJ}$. That is, sequentialising the nested system $\mathsf {NS}_{\mathsf {mLJ}}$ (Fig. 2) results in the sequent system $\mathsf {mLJ}$ (Fig. 1).

4 Labelled Proof Systems

While it is widely accepted that nested systems carry the Kripke structure on nestings for intuitionistic and normal modal logics, it is not clear what is the relationship between nestings and semantics for other systems. For example, in [9] we presented a linear nested system [8] for linear logic, but the interpretation of nestings for this case is still an open problem.

In this work we will relate labelled nested systems [6] with labelled systems [18]. While the results for intuitionistic and some normal modal logics are not new [4, 6], we give a complete different approach for these results, and present the first semantical interpretation for nestings in non-normal modal logics. In this section we shall recall some of the terminology for labelled systems.

Labelled Nested Systems. Let $\texttt {SV}$ a countable infinite set of state variables (denoted by $x, y, z, \ldots$), disjoint from the set of propositional variables. A labelled formula has the form x : A where $x\in \texttt {SV}$ and A is a formula. If $\varGamma = \{A_1,\ldots , A_k\}$ is a set of formulae, then $x :\varGamma$ denotes the set $\{x : A_1,\ldots , x : A_k\}$ of labelled formulae. A (possibly empty) set of relation terms (i.e. terms of the form xRy, where $x,y\in \texttt {SV}$) is called a relation set. For a relation set $\mathcal{R}$, the frame $Fr(\mathcal{R})$ defined by $\mathcal{R}$ is given by $(|\mathcal{R}|,\mathcal{R})$ where $|\mathcal{R}| = \{x\; |\; xRy \in \mathcal{R} \text{ or } yRx \in \mathcal{R} \text{ for } \text{ some } y\in \texttt {SV}\}$. We say that a relation set $\mathcal{R}$ is treelike if the frame defined by $\mathcal{R}$ is a tree or $\mathcal{R}$ is empty.

Definition 7

A labelled nested sequent $\mathsf {LbNS}$ is a labelled sequent $\mathcal{R},X\vdash Y$ where

• 1. $\mathcal{R}$ is treelike;

• 2. if $\mathcal{R}=\emptyset$ then X has the form $x\!:\!A_1,\ldots ,x\!:\!A_k$ and Y has the form $x \!:\!B_1,\ldots , x \!:\!B_m$ for some $x\in \texttt {SV}$;

• 3. if $\mathcal{R}\not =\emptyset$ then every state variable y that occurs in either X or Y also occurs in $\mathcal{R}$.

A labelled nested sequent calculus is a labelled calculus whose initial sequents and inference rules are constructed from $\mathsf {LbNS}$.

As in [6], labelled nested systems can be automatically generated from nested systems.

Definition 8

Given $\varGamma \vdash \varDelta$ and $\varGamma '\vdash \varDelta '$ sequents, we define $(\varGamma \vdash \varDelta )\otimes (\varGamma '\vdash \varDelta ')$ to be $\varGamma ,\varGamma '\vdash \varDelta ,\varDelta '$. For a state variable x, define the mapping $\mathbb {TL}_{x}$ from $\mathsf {NS}$ to $\mathsf {LbLNS}$ as follows

with all state variables pairwise distinct.

For the sake of readability, when the state variable is not important, we will suppress the subscript, writing $\mathbb {TL}$ instead of $\mathbb {TL}_{x}$. We will shortly illustrate the procedure of constructing labelled nestings using the mapping $\mathbb {TL}$. Consider the following application of the rule $\rightarrow _R$ of Fig. 2:

Applying $\mathbb {TL}$ to the conclusion we obtain $\mathcal{R},X\vdash Y,x\!:\!A\rightarrow B$ where the variable x label formulae in two components of the $\mathsf {NS}$, and X, Y are sets of labelled formulae. Applying $\mathbb {TL}$ to the premise we obtain $\mathcal{R},xRy,X,y\!:\!A\vdash Y,y\!:\!B$ where y is a fresh variable (i.e. different from x and not occurring in X, Y). We thus obtain an application of the $\mathsf {LbLNS}$ rule

Some rules of the labelled nested system $\mathsf {LbNS}_\mathsf {mLJ}$ are depicted in Fig. 3.

The following result follows readily by transforming derivations bottom-up [6].

Theorem 9

The mapping $\mathbb {TL}_{x}$ preserves open derivations, that is, there is a 1-1 correspondence between derivations in a nested sequent system $\mathsf {NS}$ and in its labelled translation $\mathsf {LbNS}$.

Labelled Sequent Systems. In the labelled sequent framework, a semantical characterisation of a logic is explicitly added to sequents via the labelling of formulae [3, 13,14,15, 18]. In the case of world based semantics, the forcing relation $x\Vdash A$ is represented as the labelled formula $x \!:\!A$ and sequents have the form $\mathcal{R},X\vdash Y$, where $\mathcal {R}$ is a relation set and X, Y are multisets of labelled formulae.

The rules of the labelled calculus $\mathsf {G3I}$ are obtained from the inductive definition of validity in a Kripke frame (Fig. 4a), together with the rules describing a partial order, presented in Fig. 4b. Note that the anti-symmetry rule does not need to be stated directly since, for any x, the formula $x=x$ is equivalent to true and hence can be erased from the left side of a sequent.

Fig. 3.

Labelled nested system $\mathsf {LbNS}_{\mathsf {mLJ}}$.

Fig. 4.

Some rules of the labelled system $\mathsf {G3I}$

5 Intuitionistic Logic

In this section we will relate various proof systems for intuitionistic logic by applying the results presented in the last sections.

Theorem 10

All rules in $\mathsf {NS}_{\mathsf {mLJ}}$ are height-preserving invertible and $\mathsf {NS}_{\mathsf {mLJ}}$ is fully permutable.

Proof

The proofs of invertibility are by induction on the depth of the derivation, distinguishing cases according to the last applied rule. Permutability of rules is proven by a case-by-case analysis, using the invertibility results.     $\square$

The results in the previous sections entail the following.

Theorem 11

Systems $\mathsf {NS}_{\mathsf {mLJ}}$, $\mathsf {mLJ}$ and $\mathsf {LbNS}_{\mathsf {mLJ}}$ are equivalent.

Observe that the proof uses syntactical arguments only, differently from e.g. [4, 8].

For establishing a comparison between labels in $\mathsf {G3I}$ and $\mathsf {LbNS}_{\mathsf {mLJ}}$, first observe that applications of rule Trans in $\mathsf {G3I}$ can be restricted to the leaves (i.e. just before an instance of the initial axiom). Also, since weakening is admissible in $\mathsf {G3I}$ and the monotonicity property: $x \Vdash A \text{ and } x\le y \text{ implies } y\Vdash A$ is derivable in $\mathsf {G3I}$ (Lemma 4.1 in [3]), the next result follows.

Lemma 12

The following rules are derivable in $\mathsf {G3I}$ up to weakening.

Moreover, the rule

is admissible in $\mathsf {G3I}$.

Proof

For the derivable rules, just note that

and

Using an argument similar to the one in [6], it is easy to see that, in the presence of the primed rules shown above, the relational rules are admissible. Moreover, labels are preserved.

Theorem 13

$\mathsf {G3I}$ is label-preserving equivalent to $\mathsf {LbNS}_{\mathsf {mLJ}}$.

That is, nestings in $\mathsf {NS}_{\mathsf {mLJ}}$ and $\mathsf {LNS}_{\mathsf {mLJ}}$ correspond to worlds in the Kripke structure where the sequent is valid and this is the semantical interpretation of the nested system for intuitionistic logic [4].

Observe that, since $\mathsf {mLJ}$ derivations are equivalent to normal $\mathsf {NS}_{\mathsf {mLJ}}$ derivations, the semantical analysis for $\mathsf {LNS}_{\mathsf {mLJ}}$ also hold for $\mathsf {mLJ}$, that is, an application of the $\rightarrow _R$ rule over $\varGamma \vdash A\rightarrow B$ in $\mathsf {mLJ}$ corresponds to creating a new world w in the Kripke structure and setting the forcing relation to A, B and all the formulae in $\varGamma$.

In what follows, we will show how this approach on different proof systems can be smoothly extended to normal as well as non-normal modalities, using propositional classical logic as the base logic.

6 Normal Modal Logics

The next natural step on investigating the relationship between frame semantics and nested sequent systems is to consider modal systems.

The normal modal logic $\mathsf {K}$ is obtained from classical propositional logic by adding the unary modal connective $\Box$ to the set of classical connectives, together with the necessitation rule and the $\mathsf {K}$ axiom (see Fig. 5 for the Hilbert-style axiom schemata) to the set of axioms for propositional classical logic.

Fig. 5.

Modal axiom $\mathsf {K}$, necessitation rule $\mathsf {nec}$ and extensions $\mathsf {D},\mathsf {T},\mathsf {4}$.

The nested framework provides an elegant way of formulating modal systems, since no context restriction is imposed on rules. Figure 6 presents the modal rules for the nested sequent calculus $\mathsf {NS}_{\mathsf {K}}$ for the modal logic $\mathsf {K}$ [1, 16].

Observe that there are two rules for handling the box operator ($\Box _L$ and $\Box _R$), which allows the treatment of one formula at a time. Being able to separate the left/right behaviour of the modal connectives is the key to modularity for nested calculi [8, 17]. Indeed, $\mathsf {K}$ can be modularly extended by adding to $\mathsf {NS}_{\mathsf {K}}$ the nested corresponding to other modal axioms. In this paper, we will consider the axioms $\mathsf {D}, \mathsf {T}$ and $\mathsf {4}$ (Fig. 5). Figure 7 shows the modal nested rules for such extensions: for a logic $\mathsf {K}\mathcal {A}$ with $\mathcal {A} \subseteq \{\mathsf {D}, \mathsf {T}, \mathsf {4}\}$ the calculus $\mathsf {NS}_{\mathsf {K}\mathcal {A}}$ extends $\mathsf {NS}_\mathsf {K}$ with the corresponding nested modal rules.

Fig. 6.

Nested system $\mathsf {NS}_{\mathsf {K}}$. The rules $\rightarrow _L^n,\wedge _R^n,\wedge _L^n, \vee _R^n,\vee _L^n$ and $\perp ^n_L$ are the same as in Fig. 2.

Note that rule $\mathsf {t}^n$ is actually a sequent-like rule. On the other hand, $\Box _R^n$ and $\mathsf {d}^n$ are creation rules while $\Box _L^n$ and $\mathsf {4}^n$ are upgrade rules. It is straightforward to verify that $\mathsf {NS}_{\mathsf {K}\mathcal {A}}$ is shallow directed and fully permutable. Moreover, a nested block containing the application of one of the creation rules and possible several applications of the upgrade rules has one of the following shapes

where $\Box _L^n$ acted in the context $\varGamma _{\mathsf {K}}$ and $\mathsf {4}^n$ in the context $\varGamma _{\mathsf {4}}$. Observe that $\mathsf {4}^n$ maps a boxed left formula into itself, $\Box _L^n$ maps left formulae into the boxed versions and there are no context relations on right formulae. Hence sequentialising the nested system $\mathsf {NS}_{\mathsf {K}\mathcal {A}}$ (Fig. 7) results in the sequent system $\mathsf {SC}_{\mathsf {K}\mathcal {A}}$ (shown as rule schemas in Fig. 8).

Finally, Definition 8 of Sect. 4 can be extended to the normal modal case in a trivial way, resulting in the labelled nested system $\mathsf {LbNS}_{\mathsf {K}\mathcal {A}}$ (Fig. 9).

Theorem 14

Systems $\mathsf {NS}_{\mathsf {K}\mathcal {A}}$, $\mathsf {SC}_{\mathsf {K}\mathcal {A}}$ and $\mathsf {LbNS}_{\mathsf {K}\mathcal {A}}$ are equivalent.

Fig. 7.

Nested sequent rules for extensions of $\mathsf {K}$.

Fig. 8.

Modal sequent rules for normal modal logics $\mathsf {SC}_{\mathsf {K}\mathcal {A}}$, for $\mathcal {A} \subseteq \{ \mathsf {T}, \mathsf {D},\mathsf {4} \}$.

Figures 10a and b present the modal and relational rules of $\mathsf {G3K}\mathcal {A}$ [14], a sound and complete labelled sequent system for $\mathsf {K}\mathcal {A}$.

The next results follow the same lines as the ones in Sect. 5.

Lemma 15

The rules $\mathbb {TL}(\mathsf {d}^n),\mathbb {TL}(\mathsf {t}^n), \mathbb {TL}(\mathsf {4}^n)$ are derivable in $\mathsf {G3K}\mathcal {A}$.

Proof

The proof is straightforward. For example, for $\mathsf {K}\mathsf {D}$

    $\square$

Theorem 16

$\mathsf {G3K}\mathcal {A}$ is label-preserving equivalent to $\mathsf {LbNS}_{\mathsf {K}\mathcal {A}}$.

Proof

That every provable sequent in $\mathsf {LbNS}_{\mathsf {K}\mathcal {A}}$ is provable in $\mathsf {G3K}\mathcal {A}$ is a direct consequence of Lemma 15. For the other direction, observe that rule relational rules can be restricted so to be applied just before a $\Box _L^t$ rule.     $\square$

This means that labels in $\mathsf {NS}_{\mathsf {K}\mathcal {A}}$ represent worlds in a Kripke-frame, and this extends the results in [6] for modal logic of provability to normal modal logics $\mathsf {K}\mathcal {A}$.

7 Non-normal Modal Systems

We now move our attention to non-normal modal logics, i.e., modal logics that are not extensions of $\mathsf {K}$. In this work, we will consider the classical modal logic $\mathsf {E}$ and the monotone modal logic $\mathsf {M}$. Although our approach is general enough for considering nested, linear nested and sequent systems for several extensions of such logics (such as the classical cube or the modal tesseract – see [10]), there are no satisfactory labelled sequent calculi in the literature for such extensions.

Fig. 9.

Modal rules for labelled indexed nested system $\mathsf {LbNS}_{\mathsf {K}\mathcal {A}}$.

Fig. 10.

Some rules of the labelled system $\mathsf {G3K}\mathcal {A}$.

For constructing nested calculi for these logics, the sequent rules should be decomposed into their different components. However, there are two complications compared to the case of normal modal logics: the need for (1) a mechanism for capturing the fact that exactly one boxed formula is introduced on the left hand side; and (2) a way of handling multiple premises of rules. The first problem is solved by introducing the indexed nesting $\left[ \cdot \right] ^\mathsf {e}$ to capture a state where a sequent rule has been partly processed; the second problem is solved by making the nesting operator $\left[ \cdot \right] ^\mathsf {e}$ binary, which permits the storage of more information about the premises. Figure 11 presents a unified nested system for logics $\mathsf {NS}_{\mathsf {E}}$ and $\mathsf {NS}_{\mathsf {M}}$.

$\mathsf {NS}_{\mathsf {E}}$ and $\mathsf {NS}_\mathsf {M}$ are fully permutable but, since the nested-like rule $\Box _L^{\mathsf {e}n}$ has two premises, it does not fall into the definitions of shallowness/directedness. However, since propositional rules cannot be applied inside the indexed nestings, the modal rules naturally occur in blocks. Hence the nested rules correspond to macro-rules equivalent to the sequent rules in Fig. 12 for $\mathsf {SC}_\mathsf {E}$ and $\mathsf {SC}_\mathsf {M}$.

Finally, using the labelling method in Sect. 4, the rules in Fig. 11 correspond to the rules in Fig. 13, where xNy and $xN_\mathsf {e}(y_1,y_2)$ are relation terms capturing the behaviour of the nestings $\left[ \cdot \right]$ and $\left[ \cdot \right] ^\mathsf {e}$ respectively.

The semantical interpretation of non-normal modalities $\mathsf {E},\mathsf {M}$ can be given via neighbourhood semantics, that smoothly extends the concept of Kripke frames in the sense that accessibility relations are substituted by a family of neighbourhoods.

Definition 17

A neighbourhood frame is a pair $\mathcal{F}=(W,N)$ consisting of a set W of worlds and a neighbourhood function $N:W\rightarrow \wp (\wp W)$. A neighbourhood model is a pair $\mathcal{M}=(\mathcal{F},\mathcal{V})$, where $\mathcal{V}$ is a valuation. We will drop the model symbol when it is clear from the context.

The truth description for the box modality in the neighbourhood framework is

$$\begin{aligned} w\Vdash \Box A \text{ iff } \exists X\in N(w).[(X\Vdash ^{\forall }A)\wedge (A\lhd X)] \end{aligned}$$

(1)

where $X\Vdash ^{\forall }A$ is $\forall x\in X.x\Vdash A$ and $A\lhd X$ is $\forall y.[(y\Vdash A)\rightarrow y\in X]$. The rules for $\Vdash ^{\forall }$ and $\lhd$ are obtained using the geometric rule approach [15] and are depicted in Fig. 14.

Fig. 11.

Modal rules for systems $\mathsf {NS}_{\mathsf {E}}$ and $\mathsf {NS}_\mathsf {M}$.

Fig. 12.

Modal sequent rules for non-normal modal logics $\mathsf {SC}_\mathsf {E}$ and $\mathsf {SC}_\mathsf {M}$.

If the neighbourhood frame is monotonic (i.e. $\forall X\subseteq W$, if $X\in N(w)$ and $X\subseteq Y\subseteq W$ then $Y \in N(w)$), it is easy to see [15] that (1) is equivalent to

$$\begin{aligned} w\Vdash \Box A \text{ iff } \exists X\in N(w).X\Vdash ^{\forall }A. \end{aligned}$$

(2)

This yields the set of labelled rules presented in Fig. 15, where the rules are adapted from [15] by collapsing invertible proof steps. Intuitively, while the box left rules create a fresh neighbourhood to x, the box right rules create a fresh world in this new neighbourhood and move the formula to it.

Theorem 18

$\mathsf {G3E}$ (resp. $\mathsf {G3M}$) is label-preserving equivalent to $\mathsf {LbNS}_{\mathsf {E}}$ (resp. $\mathsf {LbNS}_\mathsf {M}$).

Proof

Let $\pi$ be a normal proof of $\mathcal{N}, X \vdash Y$ in $\mathsf {LbNS}_{\mathsf {E}}$. An instance of the blocked derivation

is transformed into the labelled derivation

Observe that, in $\pi _1$, the label $y_2$ will no longer be active, hence the formula $y_2:B$ can be weakened. The same with $y_1$ in $\pi _2$. Hence $\pi _1/\pi _2$ corresponds to $\pi _1'/\pi _2 '$ and the “only if” part holds. The “if” part uses similar proof theoretical arguments as in the intuitionistic or normal modal case, observing that applications of the forcing rules can be restricted so to be applied immediately after the modal rules.    $\square$

Observe that the neighbourhood information is “hidden” in the nested approach. That is, creating of a nesting has a two-step interpretation: one of creating a neighbourhood and another of creating a world in it. These steps are separated in Negri’s labelled systems, but the nesting information becomes superfluous after the creation of the related world. This indicates that the nesting approach is more efficient proof theoretically speaking when compared to labelled systems. Also, it is curious to note that this “two-step” interpretation makes the nested system external, in the sense that nestings cannot be interpreted inside the syntax of the logic. In fact, it makes use of the $\langle \,]$ modality [2].

Fig. 13.

Modal rules for $\mathsf {LbNS}_\mathsf {E}$ and $\mathsf {LbNS}_\mathsf {M}$ with $y_1,y_2$ fresh in $\Box _R^\mathsf {e}$.

Fig. 14.

Forcing rules, with z arbitrary in $\lhd _L$.

Fig. 15.

Labelled systems $\mathsf {G3E}$ and $\mathsf {G3M}$. a fresh in $\Box _L^\mathsf {e},\Box _L^\mathsf {m}$ and y, z fresh in $\Box _R^\mathsf {e},\Box _R^\mathsf {m}$.

8 Conclusion and Future Work

In this work we showed a semantical characterisation of intuitionistic, normal and non-normal modal systems, via a case-by-case translation between labelled nested to labelled sequent systems. In this way, we closed the cycle of syntax/semantic characterisation for a class of logical systems.

While some of the presented results are expected (or even not new as the semantical interpretation of nestings in intuitionistic logic), our approach is, as far as we know, the first done entirely using proof theoretical arguments. Indeed, the soundness and completeness results are left to the case of labelled systems, that carry within the syntax the semantic information explicitly. Using the results in [11], we were able to extend all the semantic discussion to the sequent case.

This work can be extended in a number of ways. First, it seems possible to propose nested and labelled systems for some paraconsistent systems and systems with negative modalities [7]. Our approach, both for sequentialising nested systems and for relating the so-called internal and external calculi could then be applied in such cases.

Another natural direction to follow is to complete this syntactical/semantical analysis for the classical cube [10]. This is specially interesting since $\mathsf {M}\mathsf {N}\mathsf {C}=\mathsf {K}$, that is, we should be able to smoothly collapse the neighbourhood approach into the relational one. We observe that nestings play an important role in these transformations, since it enables to modularly building proof systems.

Finally, it would be interesting to analyse to what extent the methodology of the present paper might be applied to shed light on the problem of finding intuitive semantics for substructural logics, like linear logic and its modal extensions [9].