Remote Sensing Image Fusion Based on Shearlet and Genetic Algorithm

Abstract

Image fusion is a technology which can effectively enhance the utilization ratio of image information, the accuracy of target recognition and the interpretation ability of image. However, traditional fusion methods may lead to the information loss and image distortion. Hence a novel remote sensing image fusion method is proposed in this paper. As one of the multi-scale geometric analysis tools, Shearlet has been widely used in image processing. In this paper, Shearlet is used to decompose the image. Genetic Algorithm, a intelligent optimization algorithm, is also applied to image fusion and it aims to optimize the weighted factors in order to improve the quality of fusion. Experimental results prove the superiority and feasibility of this method.

1 Introduction

With the development of image processing technologies, image fusion has been widely applied to each area. Remote sensing image fusion is a kind of technology which aims at fusing the image data of the same region obtained by multi-sensor platforms into a more comprehensive, accurate and informative image. Both higher spatial resolution and hyper-spectral information are reserved in fused image.

Remote sensing image has a wide application range, such as military, geological prospecting, mapping, environment and agriculture. In recent years, there are some common fusion methods, such as linear weighting method [1], HSI transform method [1], PCA [1], pyramid-based fusion method [2], and Discrete Wavelet Transform [3]. However, it is difficult for these traditional fusion methods to get a satisfactory result.

As one of the multi-scale geometric analysis tools, Shearlet overcomes the deficiency of information loss when Wavelet Transform is applied into image fusion. Besides, compared with Contourlet [4], the limitation of the number of directions has been successfully eliminated by Shearlet. Moreover, as a new optimal tool, intelligent optimization algorithms play a vital role in solving optimization problems. Among them, Genetic Algorithm [5] is now getting more attention for its powerful searching ability.

In this paper, a novel image fusion method based on Shearlet [6–13] and Genetic Algorithm is discussed. It mainly focuses on the application of Genetic Algorithm into image fusion. The experimental results prove the effectiveness of the proposed method. This paper is organized as follows. The basic theory of Shearlet is introduced in Sect. 2. In Sect. 3, Genetic Algorithm is described. The novel algorithm is presented in Sect. 4 and experimental results are shown in Sect. 5. Finally, this paper is concluded in Sect. 6.

2 Shearlet

K. Guo et al. had proposed the wavelet theory [14, 15].

In dimension $n=2$, the affine system with composite dilations can be described as $\{{{\psi }_{AB}}(\psi )\}$, where $\psi \in {{L}^{2}}({{R}^{2}})$. A, B are $2\times 2$ invertible matrices with $|\det B|=1$. Its specific expression is shown as follows:

$$\begin{aligned} {{\psi }_{AB}}(\psi )= \{{{\psi }_{j,k,l}}(x)= |\det A|^{j/2}\psi ({{B}^{l}}{{A}^{j}}x-k):j,l\in Z, k \in Z^2 \} \end{aligned}$$

(1)

The element in ${{\psi }_{AB}}(\psi )$, are defined as composite wavelet if ${{\psi }_{AB}}(\psi )$ forms a tight frame.

Shearlet is a special example of affine systems with composite wavelets in ${{L}^{2}}({{R}^{2}})$. Shearlet can be described as Eq. (1) if $A={{A}_{0}}$, $B={{B}_{0}}$.${A}_{0}$ and ${B}_{0}$ are defined as follows: ${{A}_{0}}=\left( \begin{matrix} 4 &{} 0 \\ 0 &{} 2 \\ \end{matrix} \right) ,\quad {{B}_{0}}=\left( \begin{matrix} 1 &{} 1 \\ 0 &{} 1 \\ \end{matrix} \right)$.

For $\xi =({{\xi }_{1}},{{\xi }_{2}})\in {{\hat{R}}^{2}},{{\xi }_{1}}\ne 0$, let ${{\psi }^{(0)}}$ be given by

$$\begin{aligned} {{\hat{\psi }}^{(0)}}(\xi )={{\hat{\psi }}^{(0)}}({{\xi }_{1}}, {{\xi }_{2}})={{\hat{\psi }}_{1}}({{\xi }_{1}}){{\hat{\psi }}_{2}}({{{\xi }_{2}}}/{{{\xi }_{1}}}) \end{aligned}$$

(2)

where ${{\hat{\psi }}_{1}}, {{\hat{\psi }}_{2}}\in {{C}^{\infty }}(\hat{R})$, $\text {supp}{{\hat{\psi }}_{1}}\subset [-1\text {/2},-1\text {/1}6]\bigcup [1\text {/1}6,1\text {/2}]$, and $\text {supp}{{\hat{\psi }}_{2}}\subset [-1\text {,1}]$. It can be proved that ${{\hat{\psi }}^{(0)}}$ is ${{C}^{\infty }}$ and compactly supported with $\text {supp} {{\hat{\psi }}^{(0)}}\subset {{[-1\text {/2},1\text {/2}]}^{2}}$.

$$\begin{aligned} \sum \limits _{j\ge 0}{|{{{\hat{\psi }}}_{1}}({{2}^{-2j}}\omega ){{|}^{2}}}=1,|\omega |\ge 1\text {/8} \end{aligned}$$

(3)

Then for $j\ge 0$,

$$\begin{aligned} \sum \limits _{l=-{{2}^{j}}}^{{{2}^{j}}-1}{|{{{\hat{\psi }}}_{2}}({{2}^{j}}\omega -l){{|}^{2}}}=1,|\omega |\le 1 \end{aligned}$$

(4)

The support set of ${{\psi }_{j,k,l}}$ in frequency domain is obtained as follows:

$$\begin{aligned} \{({{\xi }_{1}},{{\xi }_{2}}):{{\xi }_{1}}\in [-{{2}^{2j-1}},-{{2}^{2j-4}}]\bigcup [{{2}^{2j-4}},{{2}^{2j-1}}],|\frac{{{\xi }_{2}}}{{{\xi }_{1}}}+l{{2}^{-j}}|\le {{2}^{-j}}\} \end{aligned}$$

(5)

This support set is shown in Fig. 1(a). It can be seen that each element ${{\hat{\psi }}_{j,k,l}}$ is supported on a pair of trapezoids, approximate size ${{2}^{2j}}\times {{2}^{j}}$, oriented along lines of slope $l{{2}^{-j}}$.

Fig. 1.

(a) A single frequency support of Shearlet; (b) The tiling of the frequency using Shearlet.

According to Eqs. (3) and (4), the compact support of ${{D}_{0}}$ is formed by $\{{{\hat{\psi }}^{(0)}}(\xi A_{0}^{-j}B_{0}^{-l})\}$, where ${{D}_{0}}=\{({{\xi }_{1}},{{\xi }_{2}})\in {{\overset{\wedge }{\mathop {R}}\,}^{2}}:|{{\xi }_{1}}|\ge 1\text {/8},|{{{\xi }_{2}}}/{{{\xi }_{1}}}\;|\le 1\}$.

For $\text {(}{{\xi }_{\text {1}}}\text {,}{{\xi }_{\text {2}}}\text {)}\in {{\text {D}}_{\text {0}}}$,

$$\begin{aligned} \sum \limits _{j\ge 0}{\sum \limits _{l=-{{2}^{j}}}^{{{2}^{j}}-1}{|{{{\hat{\psi }}}^{(0)}}(\xi A_{0}^{-j}B_{0}^{-l}){{|}^{2}}}=}\sum \limits _{j\ge 0}{\sum \limits _{l=-{{2}^{j}}}^{{{2}^{j}}-1}{|{{{\hat{\psi }}}_{1}}({{2}^{-2j}}{{\xi }_{1}}){{|}^{2}}|{{{\hat{\psi }}}_{2}}({{2}^{j}}{{{\xi }_{2}}}/{{{\xi }_{1}}}\;-l){{|}^{2}}}}=1 \end{aligned}$$

(6)

The tiling of frequency using Shearlet transform is shown in Fig. 1(b). A Parseval frame for ${{L}^{2}}{{({{D}_{0}})}^{\vee }}$ can be defined as follows:

$$\begin{aligned} \{\psi _{j,k\text {,}l}^{(0)}(x)={{2}^{{3j}/{2}\;}}{{\psi }^{(0)}}(B_{0}^{l}A_{0}^{j}x-k):j\ge 0,-{{2}^{j}}\le l\le {{2}^{j}}-1,k\in {{Z}^{2}}\} \end{aligned}$$

(7)

where ${{L}^{2}}{{({{D}_{0}})}^{\vee }}$ is the set of function $f\in {{L}^{2}}({{R}^{2}})$, and the support set of ${{\hat{\psi }}^{(0)}}$ is included in ${{[-1/2,1/2]}^{2}}$. Similarly we can construct a Parseval frame for ${{L}^{2}}{{({{D}_{1}})}^{\vee }}$, where ${{D}_{1}}$ is the vertical cone ${{D}_{1}}=\{({{\xi }_{1}},{{\xi }_{2}})\in {{\overset{\wedge }{\mathop {R}}\,}^{2}}:|{{\xi }_{2}}|\ge 1\text {/8},|{{{\xi }_{1}}}/{{{\xi }_{2}}}\;|\le 1\}$. Let

$$\begin{aligned} {{A}_{1}}=\left( \begin{matrix} 2 &{} 0 \\ 0 &{} 4 \\ \end{matrix} \right) , {{B}_{1}}=\left( \begin{matrix} 1 &{} 0 \\ 1 &{} 1 \\ \end{matrix} \right) \end{aligned}$$

(8)

$$\begin{aligned} {{\hat{\psi }}^{(1)}}(\xi )={{\hat{\psi }}^{(1)}}({{\xi }_{1}},{{\xi }_{2}})={{\hat{\psi }}_{1}}({{\xi }_{2}}){{\hat{\psi }}_{2}}({{{\xi }_{1}}}/{{{\xi }_{2}}}\;) \end{aligned}$$

(9)

Then the Parseval frame is defined as

$$\begin{aligned} \{\psi _{j,k\text {,}l}^{(1)}(x)={{2}^{{3j}/{2}\;}}{{\psi }^{(1)}}(B_{1}^{l}A_{1}^{j}x-k):j\ge 0,-{{2}^{j}}\le l\le {{2}^{j}}-1,k\in {{Z}^{2}}\} \end{aligned}$$

(10)

The decomposition process of discrete Shearlet is shown in Fig. 2.

Fig. 2.

Decomposition of Shearlet

3 Genetic Algorithm

Genetic Algorithm (GA) [16, 17] was proposed by John Holland in 1975. It is an evolutionary computational method based on evolutionism. Starting with a group of random solutions, GA optimizes the solutions through selection, crossover, and mutation. These initial solutions are called initial population. Every individual called chromosome in this group is a solution of the question. Chromosomes are all coded based on some certain rules according to the requirements of the question. Selections are mainly based on the values of fitness function, which means that the individual with a higher fitness will be selected in the subsequent genetic process. Finally, when the algorithm converges to one certain fitness, the corresponding individual is the optimal chromosome. And the decoded chromosome is the optimum solution of the question.

The flow diagram for GA is shown in Fig. 3.

Fig. 3.

Flow diagram of GA

The detail of the steps in Genetic Algorithm is given below.

• 1. Coding. There are several coding schemes such as binary coding, gray coding, large character set coding, real coding and multi-parameter cascade coding. Among them, we perform binary coding to express the solution of the question as the genotype string structure data. Coding plays a vital role in genetic research because the quality of coding directly influences the results obtained by the subsequent genetic iterations.

• 2. Selection. As one of the most important steps in GA, selection determines the convergence of the population. Meanwhile, it aims to improve the convergence and heighten the optimization efficiency. A common method for selection is roulette wheel selection. It is defined as follows:

  $$\begin{aligned} P_i=\frac{f_i}{\sum \limits _{j=1}^{N}f_j} \end{aligned}$$

  (11)

  where N is the size of the population, $f_i$ is the fitness of the individual i. The probability $P_i$ reflects the proportion of the individual fitness in the whole population. Therefore, it can be seen that the higher the individual fitness is, the greater the probability for selection is.

• 3. Crossover. Crossover, similar with the genetic recombination, can generate new individuals by swapping or recombining the fragments of a pair of parent individuals. This operation can improve the searching ability and efficiency. There are three crossover methods: Single Point Crossover, Multipoint Crossover and Uniform Crossover.

• 4. Mutation. Mutation aims to maintain the diversity of the population by randomly disturbing the chromosome. The process of mutation is determined by the mutation probability $P_m$.

• 5. Fitness function. Fitness function is used to evaluate the quality of individuals. In general, individuals with higher fitness are more likely to be selected and generated. On the other hands, majorities of individuals with lower fitness are either eliminated or mutated. Consequently, the average fitness and performance of the population will be advanced gradually. It is undoubtedly that it is significant to choose a suitable fitness function for the question since the fitness function will directly influence the rate of convergence and the optimizing results.

• 6. Termination. There are different ways to set the terminal conditions. For instance, fix the number of generations and the step size in search.

4 Image Fusion Method Based on Shearlet and Genetic Algorithm

In this section, a novel image fusion method for remote sensing image based on Shearlet and Genetic Algorithm is presented. Genetic Algorithm is mainly used to optimize the weight factors among the fusion strategy of the high frequency coefficients. In this algorithm, the fitness function is constructed by using specific objective evaluation index. The following evaluation indexes are applied to this paper.

4.1 Evaluation Criteria

• 1. Entropy (EN). EN is used to measure the amount of the information in the fused image because it reflects the ability to preserve detail information. EN is defined as follows:

  $$\begin{aligned} EN=-\sum _{i=0}^{i-1}P_{i}ln{P_{i}} \end{aligned}$$

  (12)

  where $P_i$ is the probability of gray level i on each pixel. The larger the EN is, the higher the quality of fusion is.

• 2. Mean Cross Entropy (MCE). CE is the cross entropy of images and given below.

  $$\begin{aligned} {\left\{ \begin{array}{ll} CE_{(f_A,f)}=\sum \limits _{i=0}^{255}P_{f_{A}}(i)log|\frac{P_{f_{A}}(i)}{P_f(i)}| \quad \ \\ CE_{(f_B,f)}=\sum \limits _{i=0}^{255}P_{f_{B}}(i)log|\frac{P_{f_{B}}(i)}{P_f(i)}| \end{array}\right. } \end{aligned}$$

  (13)

  where $f_A$,$f_B$ are the original images, and f is the fused image. Then MCE can be described as follows:

  $$\begin{aligned} MCE=\frac{CE_{(f_{A},f)}+CE_{(f_{B},f)}}{2} \end{aligned}$$

  (14)

  The smaller the MCE is, the less the difference between the original images and fused image is.

• 3. Average Grads (AG). AG can reflect the blurring level of images and the expressing ability of minor details. The calculation formula of AG is given as follows:

  $$\begin{aligned} AG=\frac{1}{M\times N}\sum _{i=1}^{M-1}\sum _{j=1}^{N-1}\sqrt{\frac{(F(i,j)-F(i+1,j))^2+F(i,j)-F(i,j+1))^2}{2}} \end{aligned}$$

  (15)

  where F(i, j) is the pixel value of image in row i, column j. M,N are the total row and total column. The larger the AG is, the clearer the fused image is.

• 4. Standard Deviation (STD). STD indicates the dispersion degree of comparison between the pixel value and the average pixel value of the image.

  $$\begin{aligned} STD=\sqrt{\frac{\sum \limits _{i=0}^{N-1}\sum \limits _{j=0}^{M-1}[(x,y)-\mu ]^2}{M\times N}} \end{aligned}$$

  (16)

  The larger the STD is, the worse the fusion result is.

• 5. Structure Similarity (Qw). Given the original image X(X can be $f_A$,$f_B$), the fusion image is f. The size of each image is $M\times N$.

  $$\begin{aligned} \sigma _{X}^2=\frac{1}{MN-1}\sum \limits _{m=1}^M\sum \limits _{n=1}^N (X(m,n)-\overline{X}^2) \end{aligned}$$

  (17)
  $$\begin{aligned} \sigma _{Xf}=\frac{1}{MN-1}\sum \limits _{m=1}^M\sum \limits _{n=1}^N (X(m,n)-\overline{X})(f(m,n)-\overline{f}) \end{aligned}$$

  (18)

  where $X=\{x_i|i=1,2,...,N\}$,$f=\{f_i|i=1,2,...,N\}$. The mean value of X and f are $\overline{X}$ and $\overline{f}$, respectively. Define Q as the following formula.

  $$\begin{aligned} Q=\frac{4\sigma _{Xf}\overline{Xf}}{\overline{X}^2+\overline{f}^2}= \frac{\sigma _{Xf}}{\sigma _{X}\sigma _{f}}\cdot \frac{2\overline{X}\overline{f}}{\overline{X}^2+\overline{f}^2}\cdot \frac{2\sigma _X\sigma _f}{\sigma _X^2+\sigma _f^2} \end{aligned}$$

  (19)

  In image processing, sliding window is usually used to calculate the value of Q in the local region so that we could synthesis an overall index. The overall index can be described as follows:

  $$\begin{aligned} Q= \frac{1}{M}\sum ^{M}_{i=1}Q_i(X,f|\lambda ) \end{aligned}$$

  (20)

  where $\lambda$ is the size of the sliding window, and M is the calculation times. Then Qw is constructed.

  $$\begin{aligned} Qw= \lambda _AQ(f_A,f)+\lambda _BQ(f_B,f) \end{aligned}$$

  (21)

  where $\lambda _A=\frac{\sigma _{f_{A}}^2}{\sigma _{f_{A}}^2+\sigma _{f_{B}}^2}$,$\lambda _B=1-\lambda _A$. Qw is used to measure the level of similarity between two original images and the fused image. Its value belongs to [0, 1]. The larger the value of Qw is, the better the fusion result is.

• 6. Degree of Distortion (DD). DD reflects the degree of spectral distortion and the differences of spectral information between the original image and fused image. The smaller the value of DD is, the better the preservation of spectral information is.

  $$\begin{aligned} {\left\{ \begin{array}{ll} DD_{f_A,f}=\frac{1}{M\times N}\sum \limits _{i=1}^{M}\sum \limits _{j=1}^{N}|f(i,j)-f_A(i,j)| \quad \ \\ DD_{f_B,f}=\frac{1}{M\times N}\sum \limits _{i=1}^{M}\sum \limits _{j=1}^{N}|f(i,j)-f_B(i,j)| \end{array}\right. } \end{aligned}$$

  (22)

• 7. Correlation Coefficient (CC). The degree of correlation between the original image and the fused image can be described by CC. It can reflect the preserving ability of spectral information by comparing the correlation coefficients.

  $$\begin{aligned} CC_{X,f}=\frac{\sum \limits _{i=1}^{M}\sum \limits _{j=1}^{N}[f(i,j)-\mu _f][X(i,j)-\mu _X]}{\sqrt{\sum \limits _{i=1}^{M}\sum \limits _{j=1}^{N}[f(i,j)-\mu _f]^2[X(i,j)-\mu _X]^2}} \end{aligned}$$

  (23)

  $\mu _f$, $\mu _X$ are the gray average value of the fused image X and the original image X. The larger the CC is, the better the quality of the fused image is.

4.2 Image Fusion Algorithm

According to the requirements and the data characteristics of remote sensing image, GA and Shearlet are applied into image fusion.

The basic steps of our proposed method are as follows:

• Step 1: Image Decomposition. Decompose the original image in multi-scale and multi-direction by Shearlet. The high frequency coefficients and low frequency coefficients are obtained through this step. The window function of shear filter used in this step is formed by Meyer wavelet.

• Step 2: Process the coefficients. The coefficients are processed based on some certain fusion rules.

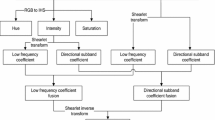
• Step 3: Image reconstruction. The fused image is obtained using inverse Shearlet transform. The fusion framework of the proposed method is shown in Fig. 4. In Step 2, the low frequency coefficients are fused based on the rule given below.

  $$\begin{aligned} f_{low}=0.5f_{A-low}+0.5f_{B-low} \end{aligned}$$

  (24)

The most important part of image fusion is to determine the fusion rule for the high frequency coefficients. In the proposed method, we choose weighting method to fuse the high frequency coefficients. Its formula is shown as follows:

$$\begin{aligned} f=\alpha f_A+(1-\alpha f_B) \end{aligned}$$

(25)

Fig. 4.

Image fusion framework based on Shearlet and GA

The weighted factor is optimized by GA. In order to get the high performance of algorithm, the population of GA cannot be oversize. However, the limitation of the number of the population will easily result in the local optimum and influence the quality of fusion. Therefore, the original images are cut into blocks before decomposition. Then the blocks are decomposed and the corresponding coefficients are fused. Finally, all of the blocks are reconstructed by inverse Shearlet transform.

Fitness function is an important part of GA. On the basis of the data features of remote sensing image, it can be seen that the fused image is required to contain rich spectral information and high resolution information. Hence the evaluation criteria CC, DD, EN and AG are applied to construct the fitness function. It is defined as follows:

$$\begin{aligned} fit=\frac{CC-\beta DD}{\gamma }+EN+\eta AG \end{aligned}$$

(26)

where $\beta ,\gamma ,\eta$ are parameters. We set $\beta =10,\gamma =\eta =100$.

5 Experiments and Analysis

In our experiment, the size of the original images is $512\times 512$. Many different methods, including averaging method, Laplacian pyramid, Wavelet-GA, Contourlet-PCNN, Shearlet-PCNN, are used to compare with our proposed approach. The parameters in GA are set as follows.

• 1. The length of individual strings: $bn=22$;

• 2. The number of initial population: $inn=50$;

• 3. Maximum iterations: $gn max=15$;

• 4. The probability of crossover and mutation: $pc=0.75,pm=0.05$;

• 5. Step size in search: 0.001.

Fig. 5.

Image fusion results by different methods

The original image, Fig. 5(a), (b), are the multi-band remote sensing images. From Fig. 5(c) to (h) are the fusion results using different methods. Figure 5 indicates that the proposed method gets a better performance in image fusion than any other methods. The information of rivers and roads obtained by our method are clear in the fused image. For example, Fig. 5(f), (g) show that the information of rivers, cities and roads are blurring.

The values of evaluation criteria are shown in Table 1. We choose seven evaluation criteria to assess the quality of fusion results. From Table 1 we can see that most evaluation index values using by proposed method are better than other methods do.

Table 1. The value of evaluation criteria

6 Conclusion

The theory of Shearlet and GA is introduced in this paper, and a new algorithm of image fusion based on them is proposed. As a multi-scale geometric analysis tool, Shearlet is equipped with a rich mathematical structure similar to wavelet and can capture the information in any direction. We take full advantage of multi-direction of Shearlet to fuse image. Moreover, GA is used to get a better performance in image fusion by the process of selection, crossover and mutation. The experimental results illustrate the effectiveness and feasibility of the proposed method, and improve the quality of the fusion.