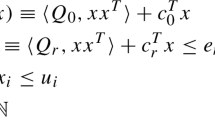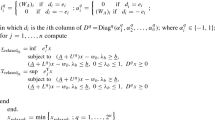Using Quadratic Approximations in an Interval Method for Solving Underdetermined and Well-Determined Nonlinear Systems

Abstract

This paper considers quadratic approximation as a narrowing tool in an interval branch-and-prune method. We seek the roots of such an approximate equation – a quadratic equation with interval parameters. Heuristics to decide, when to use the developed operator, are proposed. Numerical results for some benchmark problems are presented and analyzed.

1 Introduction

In the paper [11] the author considered an interval solver for nonlinear systems – targeted mostly at underdetermined equations systems – and its shared-memory parallelization. In subsequent papers several improvements have been considered, including various parallelization tools [12] and using sophisticated tools and heuristics to increase the efficiency of the solver [13]. As indicated in [13] and [14], the choice of proper tools and the proper heuristic, for their selection and parameterization, appeared to have a dramatic influence on the efficiency of the algorithm.

2 Generic Algorithm

The solver uses interval methods.They are based on interval arithmetic operations and basic functions operating on intervals instead of real numbers (so that result of an operation on numbers belong to the result of operation on intervals, containing the arguments). We shall not define interval operations here; the interested reader is referred to several papers and textbooks, e.g., [8, 9, 19].

The solver is based on the branch-and-prune (B&P) schema that can be expressed by the following pseudocode:

The “rejection/reduction tests”, mentioned in the algorithm are described in previous papers (specifically [13] and [14]), i.e.:

• switching between the componentwise Newton operator (for larger boxes) and Gauss-Seidel with inverse-midpoint preconditioner, for smaller ones,

• the sophisticated heuristic to choose the bisected component [13],

• an initial exclusion phase of the algorithm (deleting some regions, not containing solutions) – based on Sobol sequences [14].

Other possible variants (see, e.g., [11]) are not going to be considered.

3 Quadratic Approximations

3.1 Motivation

As stated above, the main tools used to narrow boxes in the branch-and-prune process are various forms of the Newton operator. This operator requires the computation of derivatives of (at least some of) the functions $f_i(\cdot )$. This computation – usually performed using the automatic differentiation process – is relatively costly. Because of that, in [14] the author proposed a heuristic using the Newton operator only for boxes that can be suspected to lie in the vicinity of a solution (or the solution manifold – in the underdetermined case). For other areas we try to base on 0th-order information only, i.e., function values and not gradients (or other derivatives). In [14] an “initial exclusion phase” was proposed, when regions are deleted using Sobol sequences, inner solution of the tolerance problem [19] and $\varepsilon$-inflation.

In [16] a similar approach (not using Sobol sequences, though) was considered for another problem – seeking Pareto sets of a multicriterion problem. Both papers show that this approach can improve the branch-and-bound type algorithms’ efficiency dramatically – at least for some problems.

However, as for some areas the Newton operators do not perform well, we can try to use 2nd (or even higher) order information there. Obviously, this requires Hesse matrix computations, which is very costly, but can be worthwhile.

3.2 Quadratic Approximation

Each of the functions $f_i(x_1, \ldots , x_n)$ can be approximated by the 2nd order Taylor polynomial:

$$\begin{aligned} x \in \mathbf {x}\, \rightarrow \, f_i(x) \in {\mathsf {f}}_i (\check{x}) + {\mathsf {g}}(\check{x})^T \cdot (x - \check{x}) + \frac{1}{2} \cdot (x - \check{x})^T \cdot {\mathsf {H}}(\mathbf {x}) \cdot (x - \check{x})\text{, } \end{aligned}$$

(1)

where $\mathsf g(\cdot )$ and $\mathsf H(\cdot )$ are interval extensions of the gradient and Hesse matrix of $f_i(\cdot )$, respectively.

By choosing a variable $x_j$, we can obtain a univariate formula: $x \in \mathbf {x}\, \rightarrow \, f_i(x) \in \mathbf {a}{\varvec{v}}_j^2 + \mathbf {b}\cdot {\varvec{v}}_j + \mathbf {c}$, where $v_j = x - \check{x}_j$.

Obviously:

$$\begin{aligned} \mathbf {a}&= \frac{1}{2} \mathsf H_{jj}(\mathbf {x})\text{, }\\ \mathbf {b}&= \mathsf g_j(\check{x}) + \sum _{k \ne j} \mathsf H_{jk}(\mathbf {x}) \cdot (\mathbf {x}_k - \check{x}_k)\text{, }\\ \mathbf {c}&= \frac{1}{2} \sum _{k \ne j} \Big ( \mathsf g_k(\check{x}) \cdot (\mathbf {x}_k - \check{x}_k) + \mathsf H_{jk}(\mathbf {x}) \cdot (\mathbf {x}_k - \check{x}_k)^2 \Big )\\&\ \ \ + \sum _{k=1, k \ne j}^{n} \sum _{l = k + 1}^{n} \mathsf H_{jk}(\mathbf {x}) \cdot (\mathbf {x}_k - \check{x}_k) \cdot (\mathbf {x}_l - \check{x}_l)\text{. } \end{aligned}$$

3.3 Interval Quadratic Equations

A quadratic equation is a well-known equation type of the form $a x^2 + b x + c = 0$. Methods of solving this equation in real numbers are common knowledge, nowadays.

How can such methods be generalized to the case when $\mathbf {a}$, $\mathbf {b}$ and $\mathbf {c}$ are intervals and we have an interval $\mathbf {x}$ of possible values of the variable? Below, we present two solutions: a straightforward one and a more sophisticated one, based on the algorithm, described by Hansen [8].

The Straightforward Approach. This approach is a simple (yet not naïve) “intervalization” of the point-wise algorithm. It is provided by the author, but it also resembles techniques of [6].

Please note, it is assumed that the interval $\mathbf {a}$ is either strictly positive or strictly negative; for $a = 0$ the formulae for the quadratic equation do not make sense – even using extended interval arithmetic is of little help.

So, as for the non-interval case, we start with computing the discriminant of the equation: $\varvec{\varDelta } = \mathbf {b}^{2} - 4 \mathbf {a}\mathbf {c}$. If all possible values of $\varvec{\varDelta }$ are guaranteed to be negative, i.e., $\overline{\varDelta }< 0$ then for no quadratic approximation can there be any solutions, and we can discard the box $\mathbf {x}$. Otherwise, we set: $\varvec{\varDelta } \leftarrow \varvec{\varDelta } \cap [0, +\infty ]$ and compute the values:

$$\begin{aligned} \mathbf {x}^{(1)} = \frac{-\mathbf {b}- \sqrt{\varvec{\varDelta }}}{2 \mathbf {a}}, \qquad \mathbf {x}^{(2)} = \frac{-\mathbf {b}+ \sqrt{\varvec{\varDelta }}}{2 \mathbf {a}}\text{. } \end{aligned}$$

(2)

Please note, we cannot use the Viete formula $x^{(1)} x^{(2)} = \frac{c}{a}$ to compute one of the roots – $\mathbf {c}$ (and the other root) will often contain zero. However, we can use the Viete formula for narrowing:

$$\begin{aligned} \mathbf {x}^{(1)} \leftarrow \mathbf {x}^{(1)} \cap \frac{\mathbf {c}}{\mathbf {a}\mathbf {x}^{(2)}}, \qquad \mathbf {x}^{(2)} \leftarrow \mathbf {x}^{(2)} \cap \frac{\mathbf {c}}{\mathbf {a}\mathbf {x}^{(1)}}\text{. } \end{aligned}$$

(3)

The two “interval solutions $\mathbf {x}^{(1)}$ and $\mathbf {x}^{(2)}$ can either be disjoint or not (if $0 \in \varvec{\varDelta }$ then they always coincide, but for strictly positive $\varvec{\varDelta }$ they can coincide, also). Now we can have the following possibilities:

• two disjoint intervals, both having nonempty intersections with $\mathbf {x}$ – the domain has been split, as for the Newton operator with extended arithmetic,

• two disjoint intervals, but only one of them has a nonempty intersection with $\mathbf {x}$ – then we can contract the domain; if the interval solution belongs to the interior of $\mathbf {x}$, we can prove the existence of a solution (as for the Newton operator),

• two coinciding intervals and at least one of them coincides with $\mathbf {x}$ – we narrow the domain, but cannot prove the existence or uniqueness of a solution,

• intervals disjoint with $\mathbf {x}$ – then we can discard this area, obviously.

Hansen’s Approach. The book of Hansen and Walster [8] presents a sophisticated and efficient approach to solve quadratic equations with interval coefficients. This approach is applicable if $0 \in \mathbf {a}$, also.

The essence is to consider upper and lower functions of $\mathsf f(x) = [\underline{f}(x), \overline{f}(x)]$ and find $x$’s, where $\underline{f}(x) \le 0 \le \overline{f}(x)$. It is assumed that $\overline{a} > 0$; if it is not, we can multiply both sides of the equation by $(-1)$.

Please note, the upper and lower functions can be expressed as follows:

$$\begin{aligned} \underline{f}(x)&= \left\{ \begin{array}{rcl} \underline{a} x^2 + \underline{b} x + \underline{c} &{} \text{ for } &{} x \ge 0 \\ \underline{a} x^2 + \overline{b} x + \underline{c} &{} \text{ for } &{} x < 0 \\ \end{array} \right. \text{, }\end{aligned}$$

(4)

$$\begin{aligned} \overline{f}(x)&= \left\{ \begin{array}{rcl} \overline{a} x^2 + \overline{b} x + \overline{c} &{} \text{ for } &{} x \ge 0 \\ \overline{a} x^2 + \underline{b} x + \overline{c} &{} \text{ for } &{} x < 0 \\ \end{array} \right. \text{. } \end{aligned}$$

(5)

The condition $\overline{a} > 0$ implies that the upper function $\overline{f}(x)$ is convex. The lower function can be either convex, concave or neither convex nor concave.

The algorithm can be presented as follows:

In [8] it is specified that double roots should be stored twice on the list. Our implementation does not distinguish the cases when the discriminant $\varDelta > 0$ or $\varDelta = 0$, as it would be very difficult from the numerical point of view. So, the double root can be represented by two very close, probably coinciding, but different intervals.

Also, it is proven in the book that other numbers of solutions are not possible. The case of three interval solutions can occur when $\underline{f}(x)$ is nonconvex and it has four roots – two positive and two negative ones.

3.4 When to Use the Quadratic Approximation?

As stated above, crucial for designing successful interval algorithms is the choice of a proper heuristic to choose, arrange and parameterize interval tools for a specific box.

It seems reasonable to formulate the following advice a priori:

• not to use it when traditional (less costly) Newton operators, perform well,

• not to use it on too wide boxes – the ranges of approximations will grow at least in a quadratic range with the size,

• probably, also not to use it on too narrow boxes – higher order Taylor models do not have a better convergence than 1st order centered forms [18],

• if the Newton operator could not reduce one of the components as there were zeros in both the nominator and the denominator of the formula (see, e.g., [13]); this indicates that the box might contain a singular (or near-singular) point – we assume the Newton operator sets the flag singular in such a case.

In particular, the following heuristic appeared to perform well:

The above procedure does not take singularities into account. We can modify it, by changing the proper line to:

Both versions of the heuristic will be called: “basic” and “singularity checking” respectively, in the remainder.

4 Computational Experiments

Numerical experiments were performed on a computer with 16 cores, i.e., 8 Dual-Core AMD Opterons 8218 with 2.6 GHz clock. The machine ran under control of a Fedora 15 Linux operating system with the GCC 4.6.3, glibc 2.14 and the Linux kernel 2.6.43.8.

The solver is written in C++ and compiled using GCC compiler. The C-XSC library (version 2.5.3) [1] was used for interval computations. The parallelization (8 threads) was done with TBB 4.0, update 3 [2]. OpenBLAS 0.1 alpha 2.2 [3] was linked for BLAS operations.

According to previous experience (see [12]), 8 parallel threads were used to decrease computation time. Please note that parallelization does not affect the number of iterations, but the execution time only.

The following test problems were considered.

The first one is called the Hippopede problem [11, 17] – two equations in three variables. Accuracy $\varepsilon = 10^{-7}$ was set.

The second problem, called Puma, arose in the inverse kinematics of a 3R robot and is one of typical benchmarks for nonlinear system solvers [4]. In the above form it is a well-determined (8 equations and 8 variables) problem with 16 solutions that are easily found by several solvers. To make it underdetermined the two last equations were dropped (as in [11]). The variant with 6 equations was considered in numerical experiments as the third test problem. Accuracy $\varepsilon = 0.05$ was set.

The third problem is well-determined – it is called Box3 [4] and has three equations in three variables. Accuracy $\varepsilon$ was set to $10^{-5}$.

The fourth one is a set of two equations – a quadratic one and a linear one – in five variables [7]. It is called the Academic problem. Accuracy $\varepsilon = 0.05$

The fifth problem is called the Brent problem – it is a well-determined algebraic problem, supposed to be “difficult” [5]. Presented results have been obtained for $N = 10$; accuracy was set to $10^{-7}$.

And the last one is a well-determined one – the well-known Broyden-banded system [4, 11]. In this paper we consider the case of $N = 16$. The accuracy $\varepsilon = 10^{-6}$ was set.

Results are given in Tables 1–4. The following notation is used in the tables:

• fun.evals, grad.evals, Hesse evals – numbers of functions evaluations, its gradients and Hesse matrices evaluations,

• bisecs – the number of boxes bisections,

• preconds – the number of preconditioning matrix computations (i.e., performed Gauss-Seidel steps),

• bis. Newt, del. Newt – numbers of boxes bisected/deleted by the Newton step,

• q.solv – the number of quadratic equations the algorithm was trying to solve,

• q.del.delta – the number of boxes deleted, because the discriminant of the quadratic equation was negative,

• q.del.disj. – the number of boxes deleted, because the solutions of a quadratic equation were disjoint with the original box,

• q.bisecs – the number of boxes bisected by the quadratic equations solving procedure,

• pos.boxes, verif.boxes – number of elements in the computed lists of boxes containing possible and verified solutions,

• Leb.pos., Leb.verif. – total Lebesgue measures of both sets,

• time – computation time in seconds.

Table 1. Computational results for the algorithm version from [14]

Table 2. Computational results for the algorithm version using the quadratic approximation as described in Sect. 3

Table 3. Computational results for the algorithm version using the quadratic approximation solved by the Hansen method [8] and the basic heuristic

Table 4. Computational results for the algorithm version using the Hansen method [8] and the singularity checking version of the heuristic

5 Analysis of the Results

The proposed new version of our B&P algorithm resulted in an excellent speedup for the Brent problem (for one of the algorithm versions – for the Hippopede problem, also) and a significant one for Broyden16. For Puma6 the improvement was marginal and for problems Box3 and Academic, the new algorithm performed slightly worse than the version from [14]. It is worth noting that for the Academic problem, although the computation time was slightly worse, the accuracy was a bit better.

It seems, it is difficult to improve the performance of the algorithm, using the 2nd order information – yet possible, at least for some problems.

It is worth noting that the algorithm cannot improve the performance on bilinear problems – like the Rheinboldt problem, considered in the author’s earlier papers (e.g., [11, 13, 14]). In such cases, we can try to transform the problem using symbolic techniques, e.g., the Gröbner basis theory (see, e.g., [15] and the references therein), but performance of this approach has yet to be investigated.

Performance of the method for the Hippopede problem is surprising – the algorithm version using the straightforward approach is the best there and the “singularity checking” heuristic version performs the worst. This remains to be carefully investigated in the future.

6 Conclusions

The proposed additional tool for interval branch-and-prune procedures, using quadratic approximations, allows us to improve the performance for some problems. The obtained improvement was minor for some cases, but significant, e.g., for the Broyden-banded problem and dramatic for the hard Brent problem. When the use of this tool is crucial, is going to be the subject of future research.