Cavity Enhanced Absorption Spectroscopy with Optical Feedback

Morville, Jérôme; Romanini, Daniele; Kerstel, Erik

doi:10.1007/978-3-642-40003-2_5

Jérôme Morville¹³,
Daniele Romanini¹⁴ &
Erik Kerstel¹⁴

Part of the book series: Springer Series in Optical Sciences ((SSOS,volume 179))

4273 Accesses
17 Citations

Abstract

In general, Cavity-Enhanced Absorption Spectroscopy (CEAS) suffers from inefficient and noisy cavity injection when using an unstabilized laser source with a linewidth exceeding that of the cavity resonances. The solution is to tightly frequency lock the laser to the cavity resonance, and drastically reduce its emission linewidth. This has been possible using either the Pound-Drever-Hall technique, giving the NICE-OHMS scheme, or Optical Feedback (OF). Here we review the OF-CEAS method that has the advantage of allowing simple self-locking of the laser to successive cavity modes during a frequency scan. OF-CEAS also produces a stronger linewidth reduction compared to an all-electronic locking loop, and works well with semiconductor lasers possessing a broad emission spectrum modulated by high-frequency phase noise that are difficult or impossible to lock using electronic control. The efficient laser linewidth narrowing and the locking onto successive TEM _0,0 cavity modes provides spectra with both a high S/N and an intrinsically precise and linear frequency scale over the short time of a single laser frequency scan.

Access provided by Autonomous University of Puebla. Download chapter PDF

Optical-feedback cavity-enhanced absorption spectroscopy in a linear cavity: model and experiments

Article 02 June 2015

Actively frequency-stabilized external cavity diode laser with a linewidth of 2.9 kHz

Article 18 December 2015

Dynamic Fabry-Pérot cavity stabilization technique for atom-cavity experiments

Article Open access 30 January 2024

Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

In this chapter we present absorption spectroscopy techniques that rely on self-locking of the laser to an optical cavity containing the sample under study. Following the success of Cavity Ring-Down Spectroscopy using CW lasers (CW-CRDS), the principle of laser self-locking to a cavity by providing spectrally filtered optical feedback (OF) was introduced to mitigate the problem of injecting the spectrally fluctuating emission of a diode laser into the narrow cavity resonances. The cavity-enhanced spectrum obtained using OF can be recorded in either of two ways. The first involves a ring-down measurement, based on recording the light decay following the abrupt interruption of the cavity injection. This is then repeated for different laser wavelengths in order to construct the sample absorption spectrum. The second involves recording the light intensity at the cavity output during a laser frequency scan. In the first case the technique is generally referred to as Optical Feedback Cavity Ring-Down Spectroscopy (OF-CRDS), whereas the second technique corresponds to the narrow interpretation of the term Optical-Feedback Cavity-Enhanced Absorption Spectroscopy (OF-CEAS). The term OF-CEAS is sometimes (but not here) used in a wider sense, as to also include OF-CRDS (a similar remark was made concerning CRDS and CEAS in the introduction chapter of this book). While OF-CEAS was introduced almost a decade ago [1], after some developments involving OF-CRDS [2–7], previous experience with OF from an optical cavity to a diode laser existed with applications in atomic physics, rather than in molecular spectroscopy (see e.g. [8, 9]).

Although it may be usual for a review to begin with a historical overview, we have decided to first present a basic description of the experimental implementation of OF-CEAS (Sect. 5.2) in its currently most common configuration, before proceeding with the theoretical foundation of OF-CEAS (Sect. 5.3). This approach should facilitate the reading of more fundamental aspects of laser physics. The theoretical section, all along illustrated with experimental results, identifies the constraints posed by OF-CEAS on the laser source and the type of cavity, and allows the reader to appreciate the different experimental implementations of OF-CEAS described in Sect. 5.4. Section 5.5 presents technical aspect of the technique, with a close look at the calibration procedure that enables the measurement of absolute cavity losses. Typical OF-CEAS performance figures are presented in Sect. 5.6, and limitations and prospects are discussed. An historical overview is then given in Sect. 5.7. We conclude with an overview, as complete as possible, of OF-CRDS and OF-CEAS applications.

5.2 An Intuitive Picture of the Technique

Inefficient cavity injection is one of the major problems in CEAS/CRDS, due to the fact that the laser linewidth is usually much larger than the cavity mode width (typically in the kHz range). Concretely, we will consider a typical semiconductor (SC) laser with a Distributed Feed-Back grating in the laser structure (DFB diode laser or Quantum Cascade Laser, QCL) stabilizing its single mode emission, yielding a short term (ms) linewidth of around 1 MHz. This leads to an injection efficiency that is orders of magnitude lower than for an ideal monochromatic laser, and a very noisy cavity output signal when the laser goes through resonance with one of the cavity modes, for example when frequency-tuned by a ramp applied to its injection current (see Fig. 5.1). As discussed in the introduction chapter, the laser linewidth ultimately results from an instantaneous monochromatic wave emission suffering random phase fluctuations due to spontaneous emission, which is an unavoidable quantum effect intrinsic to laser emission. The result of these random phase jumps is that over a millisecond time scale, the laser emission frequency traces out a power spectral density with a characteristic Lorentzian profile. For a DFB diode laser or QCL, typical widths are measured in MHz. However, for a QCL this value may, in practice, not correspond to the intrinsic spontaneous emission effect (which in this case results in a linewidth as low as a few tens of kHz), but rather to a non-negligible injection current noise.^{Footnote 1}

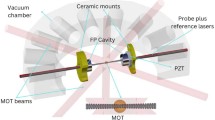
OF-CEAS exploits the sensitivity of SC lasers to OF in order to optimize the injection of a high-finesse cavity by returning to the laser light that has been spectrally filtered by the optical cavity. Without loss of generality, we will consider the experimental scheme depicted in Fig. 5.2, where a V-shaped cavity made of three, usually identical, concave mirrors is used to produce OF at resonance (i.e., when the laser emission frequency coincides with a cavity mode). Other cavity schemes have been used for OF-CEAS and will be presented in detail in Sect. 5.4.2. The important point is that no light is able to return to the laser directly from the input cavity mirror. This is of course in contrast to the case of on-axis injection of a two-mirror cavity, in which case there is always feedback to the laser, whether on or off resonance (actually, the OF decreases as the cavity becomes transmissive). The cavity mirrors are labeled M _a for the folding mirror at the apex of the cavity, and M ₁ and M ₂ for the two end mirrors. The laser output is focused by a single (aspheric) lens to have its waist coincide with one of the two waists centered between the cavity mirrors. A reference detector monitors the laser power, while a signal detector behind one of the cavity mirrors records the cavity output. As the laser is frequency tuned and approaches a cavity resonance, its radiation can build up inside the cavity, and a fraction of the intracavity field returns to the laser. An adjustable attenuator is used to reduce the OF level experienced by the laser, while a piezo-mounted steering mirror allows precise adjustment of the laser-to-cavity distance, and therewith the phase of the OF signal. If specific conditions (further discussed below) concerning the phase and intensity of the OF beam are respected, the SC laser will lock its frequency to the cavity resonance and its emission linewidth will collapse to below the resonance width. This spectral collapse is intuitively understood by considering that the OF signal coming from inside the cavity is spectrally filtered by the cavity resonance profile on each passage of photons traveling back and forth between the laser and the cavity during the period that the OF locking is active and before a steady state is reached.

The frequency locking mechanism that is thus established allows all the laser power to be admitted inside the resonance width and at the same time increases the residence time of the laser at resonance: As long as laser tuning is not too fast a complete build-up of the intracavity field is attained. In particular, this injection scheme eliminates the above mentioned amplitude noise that accompanies the passage through resonance of a free-running (optically isolated) laser. It is important to understand that with OF-locking the laser frequency does not come to a full stop, but its tuning speed is strongly reduced so that the laser remains much longer in resonance, as shown in Fig. 5.3 [1]. This figure will be discussed in detail further down. For the moment we mention that the slowing down of the tuning is proportional to the OF level, which can be adjusted by the attenuator placed between the laser and the cavity. An ideal level of OF is reached when the slow-down factor is equal to the cavity finesse, so that tuning across a resonance takes as long as it would take the free-running laser to tune over a full cavity free spectral range (FSR). We will refer to the spectral width of the locking region as “locking range”. In order to obtain the “true” cavity mode profile at this reduced speed, an adiabatic condition must be respected: In practice one finds that in order to obtain “adiabatic” transmission profiles the time for tuning across the resonance (with frequency locking) should be some 50 to 100 times longer than the cavity response time. Faster tuning induces visible distortion and fluctuation of these profiles (after having accounted for the different time scale associated with slower locked-frequency tuning). For a cavity with a 20 μs ring-down, the tuning speed should then be of the order of one FSR per ms considering the optimal locking range of 1 FSR. With a 50 cm V-shaped cavity the FSR is 150 MHz, such that it should take approximately 200 ms to cover the 200 FSRs that correspond to 1 cm⁻¹, the typical current scan range of a SC laser.

Another important requirement is that the OF wave returning to the laser arrives in phase with the laser field, in order to obtain constructive interference in the laser cavity. Normally, this would require that the distance between laser and cavity be adjusted continuously while the laser scans over successive cavity resonances. It is, however, possible to choose a laser-to-cavity distance such that the OF phase remains the same for all these resonances. Indeed each cavity standing wave has nodes on the two cavity output mirrors. This standing wave is composed of a travelling wave propagating back and forth between these end mirrors, changing sign upon reflection, which produces the nodal surfaces coinciding with the mirrors surfaces. It is easy to see that the fraction of this wave propagating out of the cavity through M _a and in the direction of the laser, will then have a fixed phase relationship with the laser field if the laser-cavity distance is chosen to be equal to the length of the other cavity arm relative to the arm to which the laser beam is aligned. A more rigorous insight into this point is provided later. Once the above condition is realized, a piezo-mounted mirror between laser and cavity enables the adjustment of the phase to obtain optimal injection of all resonances and requires only sub-wavelength adjustments during the laser scan, mainly to compensate for thermal drift and vibrations. A control signal for the piezo-mounted mirror is obtained by a real-time (analogue or digital [13]) analysis of the mode profiles in transmission, and the goal is to stabilize symmetric-looking profiles.

In the most practical and common situation considered here, with the laser-cavity distance matching the length of the cavity arms, OF-CEAS produces spectra sampled at all the longitudinal cavity modes inside the laser scan (with frequency interval given by the cavity FSR). A minor disadvantage of this scheme is that cavity modes for which the round trip cavity length is an even or an odd multiple of the wavelength (from here, named even and odd cavity modes), experience a slightly different reflection coefficient at the folding mirror [1]. This results in a slight and constant offset between the spectra registered by the odd and even modes that, however, is easily included in the data analysis procedure.

With minimal spatial mode matching, this scheme enables the successive injection of all longitudinal cavity modes that are within the laser frequency tuning range. Indeed, a welcome advantage of OF-CEAS is that it suffices to align the laser beam onto the optical axis of one of the cavity arms, and focus it to a point somewhere inside the cavity, to obtain OF predominantly from the TEM _0,0 mode, which then produces OF locking preferentially. One factor helping in this automatic mode matched injection, is that the locking range can be adjusted to be close to the cavity FSR. Then, higher-order transverse modes do not get a chance to be injected, since the laser jumps from one to the next longitudinal cavity mode rather than scanning continuously the whole cavity FSR. The above is illustrated in Fig. 5.4: In (a) the laser does not receive OF from the cavity (an optical isolator is placed between laser and cavity). Linear tuning of the laser frequency results in a periodic re-occurrence of resonances over one cavity FSR with the cavity mode structure that appears very noisy. The average intensity transmitted by the cavity is also orders of magnitude lower than in the case of Fig. 5.4(b), in which the laser receives in-phase OF, forcing it to lock to successive longitudinal modes of the cavity, and to simultaneously narrow its emission bandwidth to below that of the cavity resonance. As is shown, higher order transverse modes do not become excited in this case. We will see that there are other factors that also favor this “automatic mode matching”.

An OF-CEAS spectrum is finally obtained by considering maxima of the successive TEM _0,0 cavity mode profiles, determined by a software routine that takes as input the ratio of the cavity output signal over the reference signal. Since the signal is determined at the cavity mode profile maxima, instead of by integration of the entire profile, the cavity enhancement factor equals $2\mathcal{F}/\pi$ (as explained in the introduction chapter to this book). The TEM _0,0 mode maxima are then determined with a typical S/N in excess of 1000, without any need for averaging over several frequency scans. For a 20 μs ring-down time as assumed above, this S/N corresponds to a noise equivalent absorption of about 10⁻⁹/cm obtained over 200 spectral points from the acquisition of a single 200 ms scan, which in other CEAS schemes may be attained only after seconds to minutes averaging.

Thus, OF efficiently solves the problem of light injection into a high-finesse optical cavity. The alternative would be to force the laser frequency to match that of a cavity mode by an electronic feedback loop acting on the laser injection current, which is the only frequency control parameter in the system with a sufficiently high bandwidth. Still, in order to squeeze the emission of a SC laser and keep it inside a narrow cavity resonance, a servo loop with high bandwidth would be required, given the wide noise spectrum extending up to GHz frequencies for some of these lasers [14]. Even the most advanced of the electronic locking schemes, such as the one introduced by Pound, Drever and Hall [15]), have a hard time to narrow a diode laser linewidth to much below 10 kHz [16], whereas the highest finesse cavities exhibit modes with a width of the order of a few hundred Hz. As recently demonstrated [17], laser linewidth narrowing using the PDH scheme is more effective with a QCL than with a diode laser. Even then, it is necessary to force the locked laser to quickly jump between successive cavity modes and to subsequently re-establish the electronic lock.

On the other hand, even though OF-CEAS also requires an active control for the optical feedback phase, a bandwidth of 100 Hz is sufficient [18]. As will become clear later, reasonably small residual fluctuations in the OF-phase do affect the shape, and in particular the symmetry of the cavity transmission profiles. However, the maxima of these profiles continue to coincide with those of the true cavity resonances, such that the CEAS spectrum remains unperturbed.

As a last important aspect we mention that OF-CEAS provides an intrinsically precise frequency scale by sampling a molecular absorption spectrum on the uniform frequency grid of the cavity modes. At the timescale of spectra acquisition (∼100 ms), the cavity frequency comb stability is mainly affected by high-frequency acoustic and mechanical vibrations. Using a stiff cavity construction this jitter of the cavity mode frequencies can be reduced to sub-MHz levels (corresponding to fluctuations of a few nm for a 50 cm cavity length at λ=1 μm). Thus, while laser linewidth narrowing provides low amplitude noise at the cavity output, frequency locking to successive cavity modes comes along with a low level of frequency noise, and both aspects contribute to a high quality of the absorption spectra.

5.3 Theoretical Foundations of OF-CEAS

In this section, we give the theoretical ingredients enabling the understanding of the particular cavity transmission patterns induced by OF. A rigorous treatment should take into account the dynamic behavior of the coupled system composed of the SC laser and the external optical cavity, considering that a current ramp is applied to the SC laser injection current to induce frequency tuning. This interaction is rather complex, as it is described by differential equations including an integral term due to the cavity memory of past field evolution. However, a detailed understanding can still be obtained by considering only stationary solutions of the coupled system. In this limit, the reasonable requirement is that the injection current variations (or, equivalently, the free-laser frequency variations) should belong to the adiabatic regime. The tuning speed should then stay below Δν _cav/τ _RD, such that the time of passage over a cavity resonance (FWHM Δν _cav) is longer than the cavity response time (the ring-down time τ _RD). This would, in turn, impose very long acquisition times. Experimental observations show that cavity transmission patterns obtained with frequency scanning speeds several orders of magnitude higher than this theoretical limit still agree perfectly with patterns calculated from the stationary model, in the adiabatic limit. In Sect. 5.3.6 we will give a simple interpretation of this welcome behavior.

5.3.1 Optical Feedback: Model Equations

In order to interpret specific effects induced by the resonant OF, it is useful to identify the coupled system as a single laser with an output coupler formed by the combination of the laser chip facet and the cavity response function in reflection (see Fig. 5.5). The cavity system has an amplitude and phase defined by the cavity OF transfer function h _OF(ω). Therewith, when the free running laser frequency ω _free is far from a cavity resonance the effective output coupler reflectivity is given by the facet only, since OF from the cavity is absent. On the other hand, close to a resonance the effective amplitude reflectivity increases if the OF phase is “constructive”. Consequently, the losses of the effective laser decrease, which favors emission at the cavity resonant frequency. This is the effect of frequency locking induced by the resonant feedback. However, the locking depends on how the reflected wave interferes in the gain medium with the outgoing wave, and therefore the sum of the phase of h _OF(ω) and the phase accumulated throughout the propagation between the laser and the cavity will also determine how the effective laser losses are affected.

The stationary solutions of the coupled system could be obtained by writing the lasing condition of the coupled laser. However, it is preferable to start with the isolated LD. The field after one LD cavity round trip should be preserved, which can be written in the following manner:

$$ \sqrt{\mathcal{R}_1\mathcal{R}_2} \exp(-ik2L_{d})=1 , $$

(5.1)

where $\mathcal{R}_{1,2}$ are the diode facet reflection coefficients supposed equal in the following, L _d its length and k the complex wave vector:

$$ k={{n}}_{\mathrm{free}}\frac{\omega_{\mathrm{free}}}{c}+i\frac {1}{2}(g_{\mathrm{free}}-a) , $$

(5.2)

where ω _free, g _free and n _free are the laser stationary frequency, gain, and refractive index without optical feedback, while a stands for the distributed losses of the gain medium.

The OF from the cavity modifies the output facet reflectivity of the diode and a new lasing condition is obtained as:

$$ \sqrt{\mathcal{R}_1\mathcal{R}_{\mathrm{2eff}}( \omega_{L})} \exp\biggl(-i\frac{\omega_{L}}{c}2{{n}}_{L}L_{d} \biggr) \exp\bigl((g_{L}-a)L_{d}\bigr)=1 , $$

(5.3)

where the frequency ω _L, the gain g _L and the refractive index n _L are the stationary values of the coupled (locked) laser and $\mathcal{R}_{\mathrm{2eff}}(\omega_{L})$ is the effective reflection coefficient. In order to work in the low coupling regime, an optical system is placed between the laser and the cavity to attenuate the intensity fraction returning to the laser, by a factor β<1. The effective facet reflectivity has thus the following expression:

$$ \sqrt{\mathcal{R}_{\mathrm{2eff}}}=\sqrt{\mathcal{R}_2} \biggl(1-\sqrt{\beta} \frac{1-\mathcal{R}_2}{\sqrt{\mathcal {R}_2}} h_{\mathrm{OF}}(\omega)\exp \biggl(-i\frac{\omega}{c} 2L_a \biggr) \biggr), $$

(5.4)

corresponding to the sum of the field reflected by the facet and the field coming from the cavity with the complex amplitude h _OF(ω) attenuated by $\sqrt{\beta}$, phase shifted by propagation over the length L _a from the laser to the cavity input mirror and finally transmitted by the facet.

Inserting Eq. (5.4) in the lasing condition Eq. (5.3), and developing the gain to first order, g _L=g _free+Δg, one obtains the product (1−ϵ ₁)(1−ϵ ₂)(1−ϵ ₃)=1 where:

$$\begin{aligned} \epsilon_1 =& \sqrt{\beta} \frac{1-\mathcal{R}_2}{\sqrt{\mathcal {R}_2}} h_{\mathrm{OF}}(\omega_{L})\exp\biggl(-i\frac{\omega_{L}}{c} 2L_a \biggr) \\ \epsilon_2 =& ({{n}}_{L}\omega_{L}- {{n}}_{\mathrm{free}}\omega_{\mathrm{free}}) \frac{2L_{d}}{c} \\ \epsilon_3 =& \Delta g L_{d} \end{aligned}$$

are all small quantities in case of weak OF rates. This justifies keeping only the first order of the product. Expressing the refractive index as n _L=n _free+Δn and introducing the Henry factor [19], which expresses the dependence of the SC refractive index variation with the gain variation^{Footnote 2} , $\alpha_{H} = -2 \frac{\omega}{c} \frac{\partial{{n}}}{\partial g}$, then separating the real and imaginary parts, one obtains general expressions for the stationary shift of the laser gain and of the lasing frequency in the presence of weak OF:

$$\begin{aligned} \Delta g =& -\sqrt{\beta} \frac{{{n}}_{\mathrm{free}}}{c \tau_{d}} \biggl[P( \omega_{L}) \cos\biggl(\frac{\omega_{L}}{c}2L_{a} \biggr)+Q( \omega_{L}) \sin\biggl(\frac{\omega_{L}}{c}2L_{a} \biggr) \biggr] \\ \omega_{L}-\omega_{\mathrm{free}} =& -\frac{\sqrt{\beta (1+\alpha _{H}^{2} )}}{2 \tau_{d}} \\ &{}\times\biggl[P(\omega_{L}) \sin\biggl(\frac{\omega_{L}}{c}2L_{a}+ \theta\biggr)-Q(\omega_{L}) \cos\biggl(\frac{\omega_{L}}{c}2L_{a}+ \theta\biggr) \biggr], \end{aligned}$$

(5.5)

where θ=arctan(α _H), and $\tau_{d}=({{n}}_{\mathrm{free}}L_{d}/c) \sqrt{\mathcal{R}_{2}}/(1-\mathcal{R}_{2})$ is the photon lifetime of the isolated laser diode. P(ω) and Q(ω) are respectively the real and imaginary part of the field transfer function h _OF(ω). Expressions Eq. (5.5) formalize what has been mentioned above: in addition to the amplitude response associated with a resonance, the role of the phase associated to the dispersive response is also crucial. It should also be noted that the role of the phase acquired over the cavity-to-laser distance is expressed by the cosine and sine terms in these equations.

All things being equal, considering the factors in front of the square brackets in Eq. (5.5), we see that the gain change and frequency shift (thus the locking range) both increase with β and decrease with the isolated laser photon lifetime τ _d. On the other hand, the Henry factor α _H has a positive impact only on the frequency shift, where it also induces a phase shift θ relative to the gain response as a function of the laser to cavity distance L _a.

The expressions given by Eq. (5.5) are general for any kind of feedback generated by an optical system with a linear response, allowing for the use of the transfer function in reflection h _OF(ω). In particular, they can be used with a simple reflector (mirror), characterized by its amplitude reflection coefficient $\mathcal{R}$, in which case $h_{\mathrm{OF}}(\omega)=\sqrt{\mathcal{R}}$. In the case of a V-shaped cavity with equal mirror coefficients $\mathcal{R}$, the expression of the field transfer function is given by:

$$ h_{\mathrm{OF}}(\omega)=\frac{(1-\mathcal{R})\sqrt {\mathcal{R}} \exp (-i\frac{\omega}{c} 2L_{1} )}{ 1-\mathcal{R}^{2} \exp(-i\frac{\omega}{c} 2(L_{1}+L_{2}) )} , $$

(5.6)

where L _1,2 are the lengths of the two arms of the V-cavity, L ₁ being the arm along which the laser beam is aligned. The exponential phase factor in the numerator of h _OF(ω) can be grouped with the exponential phase factor of ϵ ₁, by defining a new transfer function taking its origin after one round trip in the arm L ₁:

$$ h'_{\mathrm{OF}}(\omega)= \frac{(1-\mathcal{R})\sqrt{\mathcal{R}}}{1-\mathcal{R}^{2} \exp (-i\frac{\omega}{c} 2(L_{1}+L_{2}) )} , $$

(5.7)

which allows to write the gain and frequency shift as modified expressions:

$$\begin{aligned} \Delta g =& -\sqrt{\beta} \frac{n_{\mathrm{free}}}{c \tau_{d}} \biggl[P'( \omega_{L}) \cos\biggl(\frac{\omega_{L}}{c}2(L_{a}+L_{1}) \biggr) \\ &{}+Q'(\omega_{L}) \sin\biggl(\frac{\omega_{L}}{c}2(L_{a}+L_{1}) \biggr) \biggr], \end{aligned}$$

(5.8)

$$\begin{aligned} \omega_{L}-\omega_{\mathrm{free}} =& -\frac{\sqrt{\beta (1+\alpha _{H}^{2})}}{2 \tau_{d}} \biggl[P'(\omega_{L}), \sin\biggl(\frac{\omega_{L}}{c}2(L_{a}+L_{1})+ \theta\biggr) \\ &{}-Q'(\omega_{L}) \cos\biggl(\frac{\omega_{L}}{c}2(L_{a}+L_{1})+ \theta\biggr) \biggr] , \end{aligned}$$

(5.9)

where $h'_{\mathrm{OF}}(\omega)=P'(\omega)+i Q'(\omega)$ for the modified transfer function. This expression clearly shows that the effect of the phase acquired during propagation should take into account the first round trip in the cavity arm L ₁. Also, when the laser frequency is outside a resonance, P′ and Q′ are both close to zero and the laser frequency equals the free laser frequency, irrespective of the values of L ₁ and L _a.

As explained before, cavity modes are standing-waves with nodes on mirrors M ₁ and M ₂. The same phase condition for all cavity modes is obtained when the OF wave that propagates out of M _a towards the laser presents an integer number of cycles counting from the node at M ₁ all the way to the laser output facet. This condition is met if the laser-to-cavity distance L _a matches a length L ₂+k(L ₁+L ₂) where k is an integer ≥0. Indeed, the arguments of the sine and cosine functions in Eq. (5.9) will then become synchronized to the argument of the exponential in the denominator of the Airy function in Eq. (5.7), which generates the comb of cavity resonances.

Before discussing the consequence of Eq. (5.9), it is convenient to introduce here the “feedback rate” of the coupled system. This is commonly defined as the optical power returning back to the laser and coupled to the laser active region divided by the emitted power. It is proportional to the attenuation factor β previously defined, squared because of the double pass, and to the square of the spatial coupling coefficient for the intensity ϵ ₀₀, which is itself the square modulus of the superposition integral of the laser beam field with the TEM _0,0 cavity field [20]. The square originates from the forward coupling of the laser beam to the cavity mode followed by the backward coupling of the cavity OF beam to the laser mode, which give the same superposition integral. Lastly, the feedback rate must include the square modulus of the maximum of the field transfer function, H _OF,max=|h _OF,max|², which depends on the cavity geometry and its losses and sets the maximum optical power that can return back to the laser. These three independent factors define the feedback rate as $\beta'=\epsilon _{00}^{2}H_{\mathrm{OF},\max}\beta$ which is in practice adjustable by acting on the attenuation factor β. It should be noted that accurate measurement of all these factors is not trivial.

5.3.2 The Locked Frequency Behavior and the Resulting Cavity Transmission Pattern

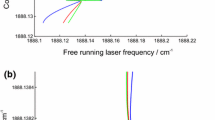
To aid the discussion of the laser behavior as it scans through a resonance at frequency ω _res, we plot in Fig. 5.6(a) the real and imaginary parts of the transfer function $h'_{\mathrm{OF}}$ for a lossless V-shaped cavity.^{Footnote 3} In addition we represent in Fig. 5.6(b) the stationary solution Eq. (5.9) as a plot of the coupled laser frequency ω _L against the free laser frequency ω _free.^{Footnote 4} Since ω _free is proportional (almost linearly) to the SC laser injection current, this is the free driving parameter when considering the evolution of the system and of the locked laser frequency ω _L. If we consider applying an increasing linear current ramp, the horizontal axis is then equivalent to a time axis.

To start with, we have chosen L _a satisfying the condition ω _res2(L _a+L ₁)/c=−θ, which makes the sine term in Eq. (5.9) to vanish. It is then the imaginary part of $h'_{\mathrm{OF}}$ that determines the behavior of the coupled frequency, as shown in Fig. 5.6(b). Its dispersion-like shape generates regions where three mathematical solutions coexist for a given ω _free. With reference to this figure, if we consider an increasing ω _free, then ω _L evolves first along a positive slope section before entering a region where two other solutions are possible. Still, the system cannot jump to any of these other solutions, since that would correspond to a spontaneous change of the intracavity field frequency: A long-lived intracavity field (even if in the wing of the cavity resonance) tends to maintain a given frequency in the coupled system. Frequency jumps can only occur at the turning points, where the system passes from three solutions back to only one available solution: At these turning points, if the driving parameter ω _free moves towards the point where 2 solutions collapse, then the system frequency ω _L may perform a forced jump if it was previously evolving according to one of the disappearing solutions. Inspection of the figure and considering also the case of a decreasing ω _L ramp, will confirm that actually only the positive slope regions are accessible, while the negative slope regions are unreachable and represent unphysical solutions. It is also easy to see that the regions with three solutions generate a hysteresis effect, with a different ω _L evolution depending on whether ω _free is tuned towards lower or higher frequencies. This also produces an asymmetric cavity transmission mode profile as visible in Fig. 5.6(c) for the case of a positive going ramp, since the locked laser frequency jumps directly close to the center of the resonance profile, which is also plotted (dashed line) as a function of ω _L in (b) and is thus referenced to the vertical axis.

As a consequence, in response to a large free laser frequency excursion, the locked laser frequency scans only a small spectral range lying inside the cavity mode linewidth. Then, the laser frequency exits the resonance with a sudden jump to a value equal to the free running frequency (the 1:1 dotted reference line in the figure). Neglecting for the moment the OF effect on the laser output power, the cavity transmission plotted in Fig. 5.6(c) will reflect this laser frequency evolution. In particular, the strong reduction of the scanning speed corresponds to an apparent broadening the transmission profile of the mode. It should also be mentioned that, given the hysteresis, a scan in the opposite direction will not produce the same profile.

These simulations are based on typical DFB multiple-quantum-wells near-IR laser parameters reported in the caption of Fig. 5.6. For clarity, the coupled laser frequency as a function of the free-laser frequency following (Eq. (5.9)) is computed with a moderate cavity finesse ($\mathcal{F}\sim200$). As shown by the behavior of the cavity transmission, in this case a feedback rate as small as 2.5×10⁻⁸ is already sufficient to broaden the transmission peak and give a locking range of more than 4 % of the FSR. As Eq. (5.9) shows, using a cavity with a much higher finesse ($\mathcal{F}\sim20\,000$) does not change the locking range, whereas increasing the feedback rate to around 2.5×10⁻⁵ (keeping all other parameters fixed), will increase the locking range to roughly one FSR, i.e. ∼150 MHz for a 50 cm base-length V-shaped cavity.

5.3.3 Optical Feedback Phase and the Cavity Transmission Beating Patterns

In the previous paragraph, the value of the propagation term ω _res2(L _a+L ₁)/c of the OF phase was adjusted in order to null the real part of the field transfer function for a given cavity resonance. As we have seen, this is a favorable case, as the transmitted mode profile in time will appear as a horizontal zoom-in around the top of that cavity resonance spectral response. But, in general, if this is the case for a given mode, adjacent modes may have different phases resulting in different frequency behaviors and different transmission profiles.

The propagation phase associated with the n-th cavity mode with resonant frequency ω _n=nπc/(L ₁+L ₂) is given by ϕ _n=n2π(L ₁+L _a)/(L ₁+L ₂) which implies a fixed phase increment of 2π(L ₁+L _a)/(L ₁+L ₂) between successive resonances. Considering a sequence of cavity modes starting from n, there exists a mode m such that ϕ _m−ϕ _n becomes larger than or equal to 2π. The cavity transmission over successive cavity modes thus exhibits a quasi-periodic beating structure imposed by the value of L _a (and strictly periodic if (ϕ _m−ϕ _n)[2π]=0). If L _a=(q/N)(L ₁+L ₂)−L ₁, where q/N is an irreducible ratio of integer numbers, the transmission profiles of a succession of modes will present a beating structure with period N=m−n (expressed in number of modes). In Fig. 5.7 we plot a measured pattern of cavity modes where eight beating periods are scanned. A zoom over one period shows the different mode profiles obtained for successive OF phase conditions. A simulated profile of the same region obtained with the same parameters given previously is also shown. The OF phase condition of the central mode corresponds roughly to the previously determined optimal condition ϕ _n=−θ, where the locked frequency has a symmetric trajectory around the exact resonance, determined by the imaginary part of the transfer function (plotted in Fig. 5.6(a)). The transmission profile in the presence of OF is, however, not symmetric, given the hysteresis effect shown in Figs. 5.6(b) and (c). Away from this central mode, the stationary solution of the laser frequency is determined by both the real and imaginary parts of the transfer function, and the peaked real part pushes the locked frequency trajectory away from the center of the resonance, in a direction determined by the relative sign of the sine and cosine terms in Eq. (5.9). Sufficiently far away from the center (see inset of Fig. 5.7), the resonance frequency does not even fall inside the small spectral range covered by the locked frequency, the transmission maxima are reduced in amplitude, and the transmission profiles become peaked and strongly asymmetric. For phase conditions where the real part of the transfer function dominates in Eq. (5.9), the laser frequency is then pushed away from the resonance, producing a repulsive OF and resulting in zero cavity transmission.

5.3.4 The OF-CEAS Operating Conditions

In order to obtain OF-CEAS spectra, L _a must then be adjusted to have the same OF phase for all successive cavity resonances in the laser scan, for instance by choosing L _a=L ₂. To this end the laser-to-cavity distance is first adjusted roughly, e.g. by a delay line, until the transmission profiles for all resonances appear to have the same shape. The precision of this adjustment must be such that the phase error from the first to the last resonance in the scan is small enough to induce an almost undetectable change in the corresponding transmission profiles. For a typical OF-CEAS setup with a 1 cm⁻¹ laser scan and a 50 cm cavity, the precision of this adjustment is of the order of 100 μm. Subsequent, sub-wavelength fine-adjustment of the optical path length, e.g. using a piezo-actuated translating mirror in the optical path between laser and cavity, then insures that the OF phase remains at the value that yields symmetric mode profiles for all resonances. An example of cavity transmission measured under these conditions is given in Fig. 5.8. The amplitudes of the transmitted peaks clearly correspond to what could be obtained in the ideal case of a monochromatic wave injecting a high finesse cavity as described in the introduction of this book. In addition, the locking onto each resonance results in wide and symmetric top sections of the transmission profiles, as described in the previous section, which allows an easy determination of the maximum of each peak. In particular, absorption lines are directly observable by their effect on the mode amplitudes.

Also clearly visible in Fig. 5.8 are the variations of the laser power induced by the OF, as expected from the gain modification in Eq. (5.9). This effect is particularly marked here given the use of an External-Cavity Diode Laser (ECDL). Due to this effect, the cavity output should be normalized by the incident power in order to obtain a correct estimate of the cavity transmission (the transfer function) and hence quantitative absorption measurements. It should be underlined that for modes falling inside an absorption line, the OF level decreases together with the cavity output, thus the effect on the laser power also decreases. For this reason, it is generally not possible to approximate the normalization function by a low-order polynomial.

We have derived the model equations accounting for the behavior of the stationary laser frequency and the peculiar features of cavity transmission patterns (asymmetric profiles and OF phase beatings). Both Fig. 5.7 and Fig. 5.8 include experimental observations. Clearly, a good agreement is obtained with the model equations despite the fact that the laser linewidth and the relatively high frequency scanning speed are, as remarked earlier (see Sect. 5.3), outside the validity range of the model. However, the observed agreement justifies a posteriori the validity of the adiabatic limit, and the low noise level on the profiles recorded at cavity output is an empirical confirmation that the laser spectrum is narrowing down well below the resonance width.

5.3.5 Locked-Laser Linewidth and Optical Feedback Phase Tolerance

A rigorous frequency noise analysis of the coupled laser is quite complex and analytical expressions are derived only for particular values of the OF phase. The interested reader will find all derivations in [21]. Notably, it is shown that for the in-phase optimal condition ϕ _n=−θ, the flat spectral density of the laser frequency noise, obtained when only spontaneous emission is considered, is strongly reduced over the cavity bandwidth. More specifically, the reduction factor inside the cavity bandwidth is given by the square of the reduced slope p=dω _L/dω _free. This derivative is obtained using expression Eq. (5.9). It is then shown that the laser linewidth is reduced by the same factor such that the locked laser linewidth is given by:

$$ \Delta\nu_{\mathrm{locked}} = {\Delta\nu_{\mathrm{free}}\over\beta '(1+\alpha _{H}^{2})} \biggl( {\tau_{d}\over{\tau_{\mathrm{RD}}}} \biggr)^{2} , $$

(5.10)

for a high finesse cavity. This actually holds only with white noise sources (flat noise spectral density), such as spontaneous emission. However, for a more realistic situation where 1/f noise is present, it is shown that the square-dependence reduces to a linear dependence on τ _d/τ _RD, and the locked laser linewidth is given by:

$$ [\Delta\nu_{\mathrm{locked}} ]_{1/f}= \frac{\Delta\nu_{\mathrm{free}}}{\sqrt{\beta'(1+\alpha_{H}^{2})}} \frac{\tau_{d}}{{\tau_{\mathrm{RD}}}} , $$

(5.11)

where Δν _free is the free laser linewidth. The linewidth reduction factor in this last case is equal to the slope reduction factor defining the locked-laser tuning speed relative to the free tuning speed: This also acts to reduce all spectral fluctuations, even of technical origin, e.g. those induced by injection current noise. Applying the parameter values used in Fig. 5.6 (τ _d∼3 ps, α _H=2) to Eq. (5.11), but with feedback rate β=10⁻⁴, a reduction of five orders of magnitude is obtained with a cavity possessing a ring-down time of 10 μs. Starting with a 1 MHz linewidth (typical for a DFB diode laser), a 10 Hz locked laser linewidth should result. Of course, this linewidth is relative to the cavity resonance, which has a width of 15 kHz and should also be stabilized, actively or passively.

In the end, the relevant point is that the locked laser linewidth is easily orders of magnitude below the cavity resonance linewidth. Moreover, cavity transmission patterns measured when the laser-to-cavity distance is such that the OF phase condition changes as a function of the mode number, agree extremely well with simulations. This demonstrates that the linewidth narrowing is sufficient to produce an essentially monochromatic laser as soon as the OF phase value enables a non-zero cavity injection.

Finally, we note that our model calculations confirm that OF-CEAS is tolerant of small OF phase fluctuations, typically up to about 2π/10, which do not have an impact on the CEAS spectra. As Fig. 5.7 shows, for one full phase beating period, 3 out of 30 modes reach the maximum transmission level.

5.3.6 The High Frequency Scanning Speed of OF-CEAS

We already remarked that OF allows to achieve full excitation of a cavity resonance within a surprisingly short time scale. As shown in Fig. 5.8, low-noise mode profiles are acquired in less than 1 ms, under typical conditions. If we consider instead a perfectly monochromatic laser continuously scanning over one FSR during the same time interval Δt, in the absence of OF its emitted field would interact with the cavity mode during a time $\Delta t/\mathcal{F}$. For a typical cavity finesse $\mathcal{F}= 10^{4}$ this time equals 100 ns, corresponding to a few tens of cavity round-trips, allowing for a very partial cavity field build-up, which occurs over the same time as a ring-down event. Comparing the scanning speed W to the adiabatic scanning speed defined in Sect. 5.3, we find W≈100×Δν _cav/τ _RD, which places the situation in the impulsive regime of cavity excitation. Turning to the particular situation with feedback, let us first recall the different timescales of the coupled system. Starting with the laser alone, the gain medium polarization relaxes on the timescale of intra-band relaxation (∼10⁻¹³ s), the inverted population relaxes on the timescale of the carrier lifetime (∼10⁻⁹ s) and the photon lifetime equals a few times 10⁻¹² s for a diode laser or a QCL. A coupled system is then formed by adding a cavity with a photon lifetime of tens of μs. It is thus clear that any variation of the intracavity field is adiabatically followed by the laser dynamics. Moreover, the shortest delay of the feedback field (the time for light to make a single cavity round-trip and then to return to the laser) is already an order of magnitude longer than the longest timescale for the isolated laser dynamics. We can thus expect the laser to follow any cavity field variation even on the shortest timescale. It appears that a reasonable condition to define the onset of OF locking, is that the re-injected field amplitude exceeds the incoherent effect of spontaneous emission which fundamentally drives laser field fluctuations and is responsible for its intrinsic linewidth (in the Schawlow–Townes limit).

Cavity excitation by a passage through resonance in the presence of OF may then be described as follows. The instantaneous laser frequency, subject to fluctuations and noise defining its free linewidth Δν _free, is initially out of resonance and scanned at a rate W. At a given time, the laser field distribution starts to overlap with the resonance and to build-up a small intracavity field (as a random process). A fraction of the intracavity buildup field feeds back to the laser and is re-amplified. If the build-up is sufficient to obtain an OF amplitude inside the laser cavity which surpasses the spontaneous emission in the laser mode, OF starts affecting the laser emission frequency, inducing linewidth narrowing. These effects increase the time interval during which the laser field is able to contribute to the cavity field buildup, and improve the laser field injection in the cavity, resulting in a self-amplifying process as the frequency scanning slows down more and more, while frequency fluctuations reduce which in turn strengthens the build-up and the locking effect. This finally converges to a stationary regime in which the previously introduced slope p=dω _L/dω _free defines the reduced scanning speed W/p and linewidth Δν _free/p.

We can understand now why the maximum frequency scanning rate at which cavity modes may become fully excited by OF locking does not correspond to the adiabatic scanning speed Δν _cav/τ _RD. A faster critical scanning speed W _c exists, for which it is no longer possible to buildup a sufficient field in the cavity for starting up the dynamic transition to the coupled laser regime. Above this limit, no locking occurs, the laser is undisturbed, and light transmitted by the cavity has the same low intensity and temporal profile as described earlier and shown in Fig. 5.4. In practice, a transient regime occurs for W∼W _c, where the OF locking works occasionally, as the onset of locking depends on a cavity injection which may randomly attain the buildup threshold level, due to the preexistent fluctuations of the laser field. This regime is quite easy to be observed experimentally either by decreasing β or by increasing W. For a given laser sensitivity, depending on the photon lifetime τ _d and Henry factor α _H, the critical frequency scanning speed W _c increases with the feedback rate β′. In Fig. 5.9, we report measurements of the injection efficiency (maximum cavity output at resonance, for an optimized OF phase, normalized to maximum cavity output for low W) as a function of W for different feedback rates, clearly illustrating this dependency.

In a more general way, Fig. 5.9 summarizes the relevance of using resonant feedback to inject all longitudinal cavity modes in rapid succession.

First of all, the linewidth narrowing enables to fully excite the cavity mode and to use its transfer function to describe its amplitude as it would be obtained with an ideal monochromatic laser. Thus, losses present inside the cavity may be determined quantitatively by their influence on the mode amplitude.

Second, the time of scanning is (to first order) not limited by the cavity response time, which would lead to a prohibitive acquisition time. For instance, without OF, a cavity with a ring-down time τ _RD around 20 μs and a FSR of 150 MHz (finesse $\mathcal{F}=2 \times10^{4}$), injected by an ideal monochromatic laser, requires a minimum acquisition time T _acq=N⋅FSR/(Δν _cav/τ _RD)=2πN⋅FSR⋅τ _RD ², or several tens of seconds to cover N=100 cavity modes. With resonant feedback, the acquisition time is reduced by several orders of magnitude, depending on the laser sensitivity and its robustness to OF. For a given laser, the locking range is adjusted by the feedback rate to optimally approach one FSR, while the free scanning speed can be set to a value just below the critical scanning speed. With a DFB diode laser, for example, a locking range of about one FSR implies a feedback rate of around 10⁻⁴, and the acquisition time required to cover N=100 modes is only about 100 ms. As discussed in the next section, some lasers do not manifest sufficient sensitivity to OF as needed to extend the locking range over one FSR or are not sufficiently robust to OF to tolerate such level of feedback rate while maintaining single frequency emission, the locking range and scanning speed must consequently be kept at a lower level than optimal.

Last, in addition to the effect of locking range discussed in Sect. 5.2, the dependency of the critical scanning speed with the feedback rate β′ also enables to selectively excite fundamental TEM _0,0 modes with no particular attention to the mode-matching. As long as the laser beam is aligned onto the cavity optical axis and focused at the cavity waist, the intensity spatial coupling coefficient onto the TEM _0,0 mode, ϵ ₀₀, dominates over high order mode coupling coefficients. As this coefficient participates (squared) to the feedback rate (see end of Sect. 5.3.1), the critical scanning speed for the high order transverse modes is always below the actual scanning speed and excitation with resonant OF can not operate. The fundamental TEM _0,0 modes are then selectively excited even in case of reduced locking range or for modes close to the center of a strong absorption line (which also have a reduced locking range induced by the reduced H _OF,max). This situation is somewhat idealized since a significantly lower scanning speed is required in practice to obtain mode transmission profiles which are really close to those of the adiabatic model. High order transverse cavity modes could then appear in correspondence of a strong absorption line if mode matching is too coarse. However, their amplitude may be easily kept low by optimizing the on-axis alignment of the laser beam, and they can be selectively neglected by using a threshold scheme in the analysis software.

In Fig. 5.10 an experimental registration of the cavity output is shown, together with a low-finesse etalon trace. The regular sine trace from a continuous, smooth laser scan, normally obtained with such an etalon, is here replaced by a step-sine trace, showing that practically most of the time the laser is effectively injecting cavity modes, in a rapid succession.

5.4 Implementation

5.4.1 Different Laser Sources for OF-CEAS

The use of optical feedback in the OF-CEAS technique limits the choice of laser sources. In addition, the range of optical feedback rates accessible with a given cavity is a function of its geometry and its losses (see Sect. 5.4.2). With typical V-shaped cavities, OF rates up to several percent are easily accessible. This corresponds to no attenuation (β=1) and roughly to the higher limit of the low coupling regime for “OF-robust” lasers like DFB diodes lasers or QCLs. It is often seen that even lower OF rates drive a laser out of single mode emission and eventually into a chaotic behavior. A laser ideally suited for OF-CEAS should have an OF sensitivity enabling locking ranges up to one cavity FSR (of the order of one hundred to several hundred MHz) with accessible OF rates, while maintaining stable, single mode operation. At the same time, the laser output power should ideally be affected as little as possible.

With regard to Eqs. (5.9), the laser sensitivity is governed by both the laser photon lifetime τ _d and the Henry factor $\alpha _{H} = -2 \frac{\omega}{c} \frac{\partial{{n}}}{\partial g}$, describing the degree of coupling between gain and refractive index variations. This amplitude-phase coupling depends on the specific energy bands involved in the laser transition. In a SC laser, optical transitions take place between carrier energy levels whose non-uniform density induces an asymmetric shape of the real part of the susceptibility (the gain) as a function of frequency. Thus, any small change of carrier density induces both vertical and horizontal shifts of the gain bands [12]. One consequence is that the lasing frequency, determined by the maximum gain amplitude, varies with carrier fluctuations induced by spontaneous emission. This explains why SC lasers exhibit an increased linewidth, roughly equal to ($1+\alpha _{H}^{2}$) times the Schawlow–Townes linewidth limit [23, 24]. For this reason, the Henry factor is also known as the linewidth enhancement factor. For a diode laser with an hetero-junction gain, typical values of α _H lie between 3 and 8 [25]. Values in the range of 1 to 3 are obtained with multiple-quantum-wells gain structures [26], normally used for DFB diode lasers. In QCLs, transitions occur between discrete states, the gain has a symmetric shape, and expected values for α _H are close to zero. However, while some authors confirm extremely low values [27, 28], others measure values as low as −0.5 and up to 3 for high injection currents [29]. To conclude, the range of variation of the Henry factor for SC laser roughly span over one order of magnitude whereas laser photon lifetimes for general laser system easily range from ps to hundreds of ns. The predominant parameter affecting sensitivity to OF is thus the photon lifetime and up to now, only mm or sub-mm range laser cavity lengths with high output coupling factors have been used for OF-CEAS.

The second crucial laser property for OF-CEAS application is its robustness to OF which is governed by the spectral selectivity of its single-mode emission. Single mode emission means that almost all the optical power is closely concentrated around the carrier frequency, defining the laser linewidth. However, some residual optical power is still present far away from the emission line and may then overlap with different cavity resonances. This usually negligible effect could be amplified by the laser gain if: (i) the feedback rate (at the first order equal for all cavity resonances) is sufficiently high and (ii) the laser spectral selectivity sufficiently low. The parasitic OF could then drive the laser emission out of its principal emitting mode, creating instable frequency jumps and ultimately collapse of coherence. When looking at the cavity output, the first sign indicating the route to instability appears on the top of the transmitted mode profile where a large dip occurs when the optical power starts to leak out of the main optical carrier frequency.

First applications of OF coupling for laser frequency stabilization employed double hetero-structure Fabry-Perot type diode lasers, demonstrating an extremely high OF sensitivity. However, their single-mode emission, when it exists (photorefractive effects must counteract spatial gain hole-burning), is generally not sufficiently robust for most OF-CEAS applications. In fact, the first OF-CEAS demonstration used a DFB diode laser [1] for which the spectral selectivity of the guided gain, index modulated structure, reinforces the single-mode emission. These lasers are extremely robust with respect to OF, with rates up to 10⁻² still not inducing instabilities. Observed locking ranges extending over almost 500 MHz (more than three cavity FSRs) are easily observed. Laser power variations induced by OF are generally below the 1 % level.

ECDLs have also been successfully employed, with both Littrow [30] and Litmann-Metcalf geometries [31]. Their longer photon lifetime reduces sensitivity to OF and their single-mode robustness appears to be lower. This is particularly evident in the case of a Litmann-Metcalf configuration, in which case locking ranges of more than 100 MHz are hardly ever reached before instabilities appear. For this last type of source the reduced OF sensitivity in the frequency domain is also accompanied by a larger OF effect on the output power. As evidenced by Fig. 5.8, power variations of several percent are observed.

With respect to application of Vertical-External-Cavity Surface-Emitting Lasers (VECSEL) to OF-CEAS [32], the low output coupler transmission (∼1 %) may be compensated by a short laser cavity (275 μm in air), which maintains a short photon lifetime in the laser cavity. However, locking ranges are still limited to several tens of MHz.

Finally, QCL lasers have a cavity length in the millimeter range. This, together with an output coupling made by facet cleaving, guarantees extremely short photon lifetimes, making these lasers well suited for OF-CEAS. Three applications have already been reported [33–35]. Although those studies used a V-shaped cavity, they reported significantly different laser behavior in terms of sensitivity to OF and the magnitude of the OF effect on intensity. Contrary to [33], in [34] no attenuator was placed between the laser and the cavity to control the locking range. At the same time, the power effect was observed to be in the percent range in [34], whereas it surpassed ten percent in [33]. These observations appear to call for more investigations relatively to the response of a QCL to resonant optical feedback.

5.4.2 OF-CEAS Schemes

Since the earliest developments, several OF-CEAS schemes have been developed combining different laser sources (as already discussed in Sect. 5.4.1) with different cavity geometries. Here we present a brief review of these cavity geometries. All have in common an ability to produce selective optical feedback at resonance. However, they differ by several important parameters relating to the laser-cavity coupling. The maximum feedback rate they can produce ($\beta'_{\max}=H_{\mathrm{OF},\max}$ when $\beta=\epsilon_{00}^{2}=1$) determines, together with the laser sensitivity to OF, whether a particular laser source may be employed or not. Their polarization eigenstates determine the acceptable incident laser polarization(s). Also, this may have impact on the way the feedback rate β′ is adjusted in practice. Lastly, some specific artifacts, discussed below, induced by the presence of a standing wave in a linear or folded cavity, will not be present in the case of a traveling-wave ring-shaped cavity.

The first cavity employed for OF-CEAS was a V-shaped cavity formed by three mirrors, as in Fig. 5.11(a). Here, injection occurs through the folding (apex) mirror, so that the direct reflection from the incident beam is not coupled back to the laser. On the other hand, one of the “exit ports” from the cavity is in the direction of the incident beam and generates the resonant OF. It is easily shown that with four exit ports through which light can leak out of the cavity, the maximum transmission of one port is 25 % for a lossless, V-shaped cavity with equal mirrors (see Eq. (5.16) in Sect. 5.5). However, typical values for a real, high-finesse cavity are closer to 5 %, which corresponds to the common case of mirrors that have equal loss and transmission coefficients. Furthermore, as we discussed in Sect. 5.3.1, the squared value of the mode-matching coefficient also contributes to β′. Taking all together, maximum OF rates obtained with a V-shaped cavity are typically in the range of 10⁻², and a variable attenuator placed before the cavity is generally the preferred method of adjusting β′. This has the drawback of lowering the incident power and hence the level of useful signal for the cavity transmission measurement, but may have the advantage to reduce the danger of power saturation of the molecular transitions, which is generally a nuisance and would be favored by the large intra-cavity power buildup allowed by OF injection. If desired, however, it is possible to exploit most of the laser power for cavity injection by using a more complex optical attenuation scheme. For instance, one could employ an optical isolator (a 45^∘Faraday rotator sandwiched between two crossed polarizers) with an adjustable output polarizer. This would allow an adjustable fraction of the OF field to be returned to the laser with little effect on the forward transmission level.

Whatever the scheme of feedback rate adjustment, the polarization of the incident light should match the polarization eigenstate of the cavity modes. If we consider the V-shaped cavity, the non-normal reflection at the folding mirror induces slightly different phase shifts for the s-polarization and the p-polarization. This breaks the polarization degeneracy present in a linear cavity and induces a slight spectral shift of the polarization modes. As the reflection coefficient too depends on the polarization orientation, each family of polarization modes is associated with a different cavity finesse.

Even when a V-shaped cavity is injected using either vertical or horizontal linear polarization, another effect modulates the TEM _0,0 mode losses. Let us consider a cavity TEM _0,0 mode with its transverse Gaussian profile. This standing wave, when it reflects at the folding mirror, produces vertical fringes on the mirror surface (we suppose the cavity laying in the horizontal plane). The period of these fringes is given by the inverse of the projection of the field wave vector k along the mirror plane, and thus is rather large when the V-cavity angle is small. For a cavity with a half-angle of 1^∘, the fringe period would be on the order of 100 μm for near-IR wavelengths. Small mirror defects or dust particles will then induce more or less losses depending on whether they are located near a fringe a maximum field line or a nodal line (zero field). The mode losses will then contain a term given by the sum of losses by all localized surface defects weighted by the fringe pattern. The observed even-odd loss modulation is then associated with the fact that the fringe pattern translates horizontally by a quarter of a period when going from a mode to the next, so that nodal lines exchange with maximum-field lines. In practice it is easily observed that deposition of dust on the folding mirror strongly increases the even-odd effect while also producing an overall decrease of the cavity finesse. This even-odd loss modulation is rather constant over a laser tuning range, only if the cavity arms are exactly matched, since a change in wavelength will increase the fringe spacing while maintaining the central fringe position on the mirror surface. If these have different lengths, the fringe pattern will then shift as a function of wavelength producing a sinusoidal modulation of the even-odd modes loss. Its period, in units of mode number, is given by (L ₁−L ₂)/(L ₁+L ₂). Most often, considering the small spectral scan achievable by current tuning of a SC laser, the even-odd difference can be included as a linear sloping baseline in a fitting routine for the spectral line profiles. Signals shown in Fig. 5.10 were obtained with a V-shaped cavity for which the odd and even modes families are barely distinguishable one from another.

A Brewster-plate cavity has also been used with OF-CEAS. It consists of a linear two-mirror cavity, containing a superpolished flat glass plate at its center, oriented close to the Brewster angle with respect to the cavity axis. The cavity is injected trough the weak reflection obtained on this plate when the incident light is p-polarized. The plate produces 4 output beams, one returning to the laser and creating the desired OF as illustrated in Fig. 5.11(b). For given mirror coefficients and given Brewster-plate losses, the signal level obtained through the mirror, the maximum OF level (H _OF,max) and the cavity finesse are all a function of the incident angle over the Brewster plate. In the study reported in [31], cavity finesses range from 10³ to 10⁴ and OF values are at the percent level. Here, polarization modes are highly discriminated by the near-Brewster reflection. Also, and contrary to the case of the V-shaped cavity, the cavity modes are entirely free of astigmatism. However, the standing wave, in combination with the intra-cavity plate surfaces, still introduces an even-odd like mode structure. Its pattern and dependence on the plate position inside the cavity may be quite complex because of the two plate interfaces. However by using a thin microscope slide (0.15 mum typically), which turns out to possess highly polished surfaces, it is possible to reduce this loss pattern to the noise level of a single OF-CEAS scan [31]. We have noted that the advantage of this cavity is the ability to modify the finesse by a simple adjustment of the plate orientation, which allows widely increasing the dynamic range of OF-CEAS measurements. On the other hand, the use of a thin microscope cover plate inside the cavity complicates the setup and makes it more sensitive to vibrations and temperature drift.

Mirror birefringence was also exploited to produce a resonant OF [36]. Birefringence results in a modified polarization state after cavity excitation which can be used to feed back selectively a small fraction of the resonant field against the strong background of the directly reflected linearly polarized input field. The advantage is that a simple linear 2 mirrors cavity configuration can be used, as depicted in Fig. 5.11(c). The mirror birefringence is principally linear and originates from the stress acquired during the coating process. Typical values of the phase shift at reflection between the birefringence axes are in the μrad range and can be easily increased by adding controlled mechanical stress to the mirror substrate. As long as the mirrors phase shifts are small, by rotating the mirrors it is possible to control the orientation and strength of the resulting round-trip phase, and therefore the orientation of the polarization eigenmodes, which are almost linearly polarized (and orthogonal). However, the principle of operation of this scheme requires that the resulting cavity phase shift does not exceed a critical value $\phi_{c}=2\pi/\mathcal{F}$, in order not to split the polarization modes. Under this condition, and by placing an optical system in front of the cavity, such as a polarizer followed by a 45^∘ Faraday rotator, or a quarter-wave plate (this enables to filter out the direct input mirror reflection, while any other polarization is partly transmitted), the maximum OF level H _OF,max is given by $(\phi_{c}\mathcal{F}/2\pi)^{2}$. For a cavity with a finesse of 10⁴ and ϕ _c≃10⁻⁵ rad, a feedback rate of 2.5×10⁻⁴ may be attained. Given the use of only 2 mirrors, this scheme is not affected by the even-odd modes loss structure, but the low level of feedback rate limits its application to lasers that are extremely sensitive to OF, such as DFB diode lasers. Lastly, the optical system used to filter out the direct input mirror reflection is the critical part of the scheme, as it must be selective at a sub-ppm level. This requires high quality optical components and high stability of the opto-mechanical setup, which constitutes the main drawback of this approach.

More recently, in order to avoid the even-odd modes loss structure, Hamilton and co-workers [37] used a ring cavity composed of three mirrors with the same radius of curvature, as depicted in Fig. 5.11(d). In principle, as a traveling wave is injected inside the ring and detected in transmission, no spatially selective losses can be produced. In order to create the desired OF, a mirror placed behind one of the cavity exiting ports reflects back the transmitted beam, which re-enters the cavity and creates new transmitted beams, one of is returning back to the laser. Adjustment of the feedback rate is done through the slight misalignment of the returning beam. It is straightforward to show that for equal mirrors $H_{\max}=(\mathcal{T}/(1-\mathcal{R}^{3/2}))^{2}$ (which has a maximum value of ∼4/9 in the limit of negligible losses). It is interesting to note that with this approach, the transfer function of the feedback field is not proportional to the transfer function describing a single exit port, but rather is proportional to the square of this expression. This point has not been discussed by the authors, but could reveal interesting potential for laser stabilization, as the linewidth reducing factor is now given by the square of the slope, even in the case of 1/f noise. A second consequence of the consecutive passage is that the photon dynamics of the feedback field may be longer than the single cavity photon lifetime. However, absorption lines by the sample will have a stronger negative impact on the available OF level, probably inducing a limited dynamic range for this configuration. Lastly, the even-odd modes loss could re-emerge if small imperfections are present somewhere on the mirrors surfaces probed by the laser beam. This is potentially sufficient to excite the counter-propagating wave [38] and to create a standing wave, as the scattering imposes a phase relation between the two traveling waves. For sufficient scattering a strong coupling takes place between the two traveling waves, which would cause a frequency splitting of the cavity resonances. However, such effect was found to be quite small by Hamilton et al., and with careful cleaning of the mirrors its contribution could be kept negligible [37].

5.5 Absorption Scale Calibration by a Single Ring-Down

We present a simple and direct calibration procedure used to convert normalized transmission signals into absorption spectra, following the derivation introduced in 2006 by Kerstel et al. [39]. An experimental verification of its validity was provided by Motto-Ross et al. [40]. Although the derivation is specific for a V-shaped cavity, we will see that its adaptation to other cavity geometries is straightforward. A major advantage of this approach is that it provides an absolute estimation of the total cavity losses including the molecular absorption, without the need for an independent measurement of the empty cavity losses (i.e.without absorption by the sample).

Let us consider the transmission function of the V-shaped cavity setup of Fig. 5.2 with arms of length L ₁ and L ₂, in the case of slow passage through resonance by a very narrow bandwidth laser. As explained above, these conditions are fulfilled in the case of OF-CEAS, because the optically self-locked laser linewidth narrows to below the width of the cavity resonance, while its emission is forced to scan slowly through the peak of the resonance. The resulting transmission profile would have the shape of an Airy function in the case of a laser that is optically isolated from the cavity (see, e.g., the Introductory chapter), but is altered by optical feedback as shown in Fig. 5.6 and as discussed in Sect. 5.3.2. The important point is that controlling the optical feedback phase insures that the transmission profile corresponds to a zoomed section of the Airy function around its maximum, such that the measured peak transmission corresponds to the maximum transmission of the resonance.

The peak transmission at resonance is easily obtained by squaring the sum of the amplitudes of the constructively interfering electric fields after each passage at the output mirror (M₁ in Fig. 5.2):

$$\begin{aligned} H_{\max} =&\biggl\vert \frac{{E_{\mathrm{out}}}}{{E_{\mathrm{in}}}}\biggr\vert ^2 = \Biggl(\mathbf{t}^2 a_1\sum_{n=0}^{\infty} \bigl(a_1^2 a_2^2 \mathbf{r}^4 \bigr)^{n} \Biggr)^2 \\ =& \biggl(\frac{\mathbf{t}^2 a_1}{1-a_1^2 a_2^2 \mathbf{r}^4 } \biggr)^2 . \end{aligned}$$

(5.12)

Here $\mathbf{t}=\sqrt{t_{a}t_{1}}$, where t _a and t ₁ are, respectively, the field transmission coefficients of the apex mirror M_a and of the output mirror, while r collects the field reflection coefficients over one round-trip, $\mathbf {r}=(r_{1}r_{2}r_{a}^{2})^{1/4}$. The single pass field transmissions by the sample in the two arms of the V-cavity are given by a ₁ and a ₂, and can be expressed in terms of the absorption coefficient α. The latter is defined for the field intensity, whose one pass transmission would be exp(−αL _i), and can be applied to the field amplitude by taking the square root of this expression, while we will neglect the corresponding imaginary part that contributes only to dispersion:

$$ a_{i} = e^{-\alpha L_{i} /2} \quad (i=1,2). $$

(5.13)

This is analogous to Eq. (8) obtained for a linear cavity in the introduction chapter.

Likewise, if we neglect reflection phase change, the field transmission and reflection coefficients of the mirrors can be replaced by the corresponding intensity coefficients (“averaged” over one round-trip) in the following manner:

$$ \begin{aligned} &{\mathcal{T}=\mathbf{t}^2 =\sqrt{\mathcal{T}_a \mathcal{T}_1 } }, \\ &{\mathcal{R} =\mathbf{r}^2 =\sqrt{\mathcal{R}_a } \sqrt[{4}]{\mathcal{R}_1 \mathcal{R}_2 } };. \end{aligned} $$

(5.14)

We should note that the reflectivity of the three mirrors usually does not differ noticeably, since in most instances they are taken from the same production batch, and because the angle between the two cavity arms is small enough to not appreciably affect the reflectivity of M _a.

We thus obtain for the peak of the transmission transfer function for a V-shaped cavity:

$$ H(\alpha)= \biggl( \frac{\mathcal{T} \;e^{-\alpha{L_{1}/2}}}{1-\mathcal{R}^2 e^{-\alpha(L_{1} +L_{2} )} } \biggr)^2. $$

(5.15)

Conservation of energy then requires that $\mathcal{L}+\mathcal {R}+\mathcal{T}=1$, where $\mathcal{L}$ represents the combined losses (scattering and absorption) of the mirrors. It is now straightforward to show, by setting α and $\mathcal{L}$ equal to zero in Eq. (5.15), that the maximum transmission for a completely lossless cavity reaches 25 %, reflecting the fact that light will leak out of the cavity in four different directions:

$$ H(\alpha\to0, \mathcal{L}+\mathcal{T}\ll1) \approx \frac{1}{4} \frac{1}{(1+\frac{\mathcal{L}}{\mathcal{T}} )^2 }. $$

(5.16)

As discussed in the introduction chapter, a derivation based on the summation of the intensities would miss the resonance effect and yield a much lower cavity transmission of only $\mathcal{T}/4$, corresponding to the case of a broadband incoherent light source or that of integrated cavity enhanced absorption spectroscopy. Also, as other cavity enhanced techniques, OF-CEAS benefits from an increased dynamic range compared to traditional direct absorption, as is seen by comparing Eq. (5.15) to the Beer-Lambert absorption, as a function of α, for the same effective absorption path length.

Direct inversion of Eq. (5.15), in order to determine the intracavity absorption coefficient α from the measured intensity ratio H(α), requires knowledge of the mirror transmission and reflection coefficients. In addition, it is difficult to measure the value of H(α) accurately since it depends on the ratio of photodiode signals, one monitoring the spatially filtered cavity output, the other monitoring a fraction of the laser intensity at cavity input from a beamsplitter. This would require not only accurate knowledge of the response of both detectors, but also the efficiency of the coupling of the laser mode to the cavity TEM _0,0 mode, as well as the exact beam splitting ratio. We will show here that knowledge of all these parameters is conveniently replaced by a single ring-down measurement, carried out once per spectral scan. This measurement, obtained in the presence of sample absorption, suffices to calibrate the absorption scale with a high degree of accuracy.

To this end we approximate the exponential factor in the numerator of Eq. (5.15) by unity, which allows to extract an approximation of α as a function of the other parameters, in particular the measured H _k, where the index k is for the specific cavity mode that we consider:

$$ \tilde{\alpha}(H_k)=\frac{1}{L_{1}+L_{2}} \biggl( \ln\bigl(\mathcal{R}^2 \bigr)+\ln\biggl(1-\frac {\mathcal{T}}{\sqrt {H_k}} \biggr) \biggr) . $$

(5.17)

Other approximate expression can be derived, but having numerically compared different possibilities we believe this one is the simplest and most effective.

The first r.h.s. term of Eq. (5.17) is recognized as the empty-cavity baseline absorption α ₀=γ ₀/c, where γ ₀ is the empty cavity loss rate, which can be obtained by considering that the exponential decay of intracavity light must amount to $\mathcal{R}^{2}$ (as defined above for a V-shaped cavity) after one pass in the cavity:

$$ \exp(-\gamma_0 t) |_{ (t=\frac{L_1+L_2}{c} )}=\mathcal {R}^{2} . $$

(5.18)

Thus Eq. (5.17) can be rewritten as:

$$ \tilde{\alpha}(H_k)= -\frac{\gamma_0}{c} - \frac{1}{L_{1}+L_{2}}\ln\biggl(1-\frac{\mathcal{T}}{\sqrt{H_k}} \biggr). $$

(5.19)

On the other hand, the absorption coefficient of mode k can be written in a highly recognizable way to anyone familiar with CRDS:

$$ \alpha_k = \frac{1}{c} \biggl(\frac{1}{\tau_k } -\frac{1}{\tau_0 } \biggr) =\frac{1}{c} ( \gamma_k -\gamma_0 ), $$

(5.20)

where τ ₀=1/γ ₀ is the ring-down time for the empty cavity, while τ _k=1/γ _k is the ring-down time (the inverse of the corresponding loss rate) for mode k. This can be determined experimentally by performing a ring-down measurement following an abrupt termination of the laser once the maximum injection for mode k has been reached, which is necessary for the simultaneous measurement of H _k.

Comparing the last two equations gives:

$$ {\gamma_k\over c} = {-1\over L_{1}+L_{2}}\ln\biggl(1- {\mathcal{T}\over\sqrt{H_k}} \biggr) \simeq{1\over L_{1}+L_{2}} {\mathcal{T}\over\sqrt{H_k}}, $$

(5.21)

which is generally a very good approximation since $\mathcal{T}/\sqrt {H}\ll 1$, considering that large sample absorptions will be avoided such that H _k should normally be larger than 1 %, while $\mathcal{T}$ is typically smaller than 100 ppm.

This last approximation allows writing:

$$ \gamma_k\sqrt{H_k} = {c\mathcal{T}\over L_{1}+L_{2}} = \gamma_m\sqrt{H_m}, $$

(5.22)

where we observe that over a small laser scan we can indeed consider $\mathcal{T}$ as a constant and write the last equality, as the expression is valid for any mode m. Thus, after γ _k has been measured, together with all H _m in the laser scan including m=k, this simple expression permits to calculate directly the γ _m values for all cavity modes. This way an OF-CEAS spectrum composed of the values H _m, can be “calibrated”, i.e. converted to values γ _m=cα _m (which include the baseline γ ₀) in absolute absorption units.

As mentioned before, this expression can be expected to be very precise in the limit of $\mathcal{T}\ll\sqrt{H}$, but we should also underline that the result is almost exact for mode number k for which the ring-down measurement is performed. This has been experimentally verified by comparing the measured ratio H _k/H _m with a registration of the ring-down rate γ _m for all modes in the spectral range being considered [40].

We should also note that the presence of an alternance of intensities between “even” and “odd” longitudinal cavity modes, explained elsewhere in this chapter, does not conflict with this normalization procedure. This effect is due to variations of intracavity losses occurring on the input mirror surface, which can be considered equivalent to sample absorption. The same can be stated concerning broad band intracavity losses produced, e.g., by particles or by Rayleigh scattering.

In order to investigate the accuracy of the normalization approach we compare the result of Eq. (5.22) to the exact result of Eq. (5.15) for a model case, where we assume to know all parameter values ($\mathcal {T}, L_{1}, L_{2}$, etc.). Although the latter can be solved analytically in the case that L ₁=L ₂=L (which requires solving a fourth order polynomial in x=exp(−αL)), it is straightforward to solve the equation numerically, as was done here to produce Fig. 5.12. This figure shows the relative error $\tilde{\alpha}/\alpha-1$ of the total absorption (with baseline) for a number of scenarios: low and high mirror reflectivity/transmission, and low and high absorption at the ring-down mode number k. The high-reflectivity mirror case ($\mathcal{T}=5$ ppm and $\mathcal{L}=3~\mbox{ppm}$) corresponds to a cavity with 130 μs ring-down time, whereas the (relatively!) low-reflectivity mirrors ($\mathcal{T}=50~\mbox{ppm}$ and $\mathcal{L}=35~\mbox{ppm}$) give a ring-down time of 20 μs (the cavity arm length equals 50 cm in both cases). For each case, the fractional error is determined for two different choices of the mode for which the ring-down normalization is carried out. In the one case the normalization is carried out for a mode at which the intracavity absorption results in a cavity transmission of 50 % of the maximum value, in the other case the cavity transmission at the ring-down normalization mode equals 95 %. For comparison, the relative error has also been calculated for the case that the approximate Eq. (5.17) is used with the true values of $\mathcal{T}$ and $\mathcal{R}$ (assuming that one could determine these independently). It is clear that the normalization procedure simply shifts this error curve to cross zero at the value used for H _k.

Figure 5.12 also shows that even for a typical OF-CEAS cavity with a ring-down time of ∼20 μs, the relative error associated with the normalization of the absorption scale is smaller than 1 part in 10⁴, provided that the transmission of the cavity remains higher than 10 % of its maximum value (H>0.1). This value of transmission corresponds to an absorption coefficient of ∼4×10⁻⁶/cm or, considering the typical noise floor below 10⁻¹⁰/cm, a dynamic range of 4 decades. The analysis also shows that there is no obvious advantage of performing the ring-down normalization on a cavity mode that shows a high transmission (close to the empty cavity limit), i.e., away from strong intra-cavity absorption features, other than that a long ring-down time recording will be composed of more samples with larger signal levels, and thus allow for the ring-down time to be determined with a higher signal-to-noise ratio. In the particular case where isotope ratios are determined by directly comparing absorption line intensities of different isotopologues within a single spectral recording, the error associated with the absorption scale normalization can be safely ignored if the sample used as reference material has similar concentration, thus similar intensities for the absorption lines. But also in the case of trace gas concentration measurements, this source of error is usually negligibly small, and could potentially be further reduced by about one order of magnitude with a simple linear correction based on the calculated error.

Finally, the derivation presented here is specifically for the case of a V-shaped cavity. However, it is straightforward to apply the same analysis to other cavity geometries by replacing Eq. (5.15) with the transmission function of the cavity geometry in question. Indeed, the experimental validation presented in [40] was done with a Brewster cavity injection scheme.

5.6 Typical Performance of OF-CEAS

In this section we present examples of data obtained with OF-CEAS and discuss its performance in terms of typical sensitivity, acquisition time and dynamic range. As already pointed out, uncertainties related to both the frequency and the intensity axis contribute to sensitivity and accuracy of acquired spectra. We will consider different sources of noise limiting the ultimate sensitivity and indicate the direction for future improvement. As it is an important issue for the precision of the frequency scale, we also discuss the effect of intracavity dispersion induced by molecular absorption itself.

The principal feature of the OF-CEAS technique is its ability to obtain high sensitivity spectra with a linear frequency scale in a fraction of a second. Typical duration for a tuning range covering approximately hundred cavity modes is 100 ms and for a cavity length L=L ₁+L ₂ generally not exceeding one meter, the tuned spectral range is a few tens of GHz. The minimum detectable absorption coefficient δα _min is for a single spectrum given by the smallest measurable normalized intensity variation δH/H divided by the cavity-enhanced effective absorption length at resonance (see Eq. (17) of the Introduction chapter), which can be written as:

$$ \delta\alpha_{\min}=\frac{\pi}{2\mathcal{F}L} \frac{\delta H}{H} . $$

(5.23)

This δα _min should correspond to the baseline noise of a single spectrum when care is taken to maintain parasitic optical fringes below this level. As already pointed out, the smoothed cavity mode profile and the high signal level, both induced by the optical self-locking, enable the recording of the normalized amplitude with an uncertainty at the per mille level. For a cavity of finesse 10 000 and length 1 m, δα _min is about 10⁻⁹/cm. If this noise level is further normalized by accounting for the single point acquisition rate, we deduce a figure of merit around $3\times10^{-11}/\mbox{cm}/\sqrt{\mathrm{Hz}}$.^{Footnote 5} Indeed, such a performance for a single spectrum acquisition have been reached with a DFB diode laser in the near-IR [36], with an ECDL in the visible [40], and recently with a QCL in the mid-IR [35].

When considering averaging of several spectra, a more refined expression is required. As the product $\mathcal{F}L$ is generally determined for each single spectrum, its uncertainty should be taken into account. Following our calibration procedure (Sect. 5.5), which uses the simultaneous measurement of the ring-down time and the normalized intensity of a single cavity mode, a basic model for the minimum detectable absorption is given by:

$$ \delta\alpha_{\min}=\frac{\pi }{2\mathcal{F} L}\sqrt{ \biggl({\delta\tau_{\mathrm{RD}}\over\tau_{\mathrm{RD}}} \biggr)^{2}+2 \biggl( {\delta H\over H} \biggr)^{2}} , $$

(5.24)

where uncertainties of the ring-down time and of the normalized intensities of different modes (according to Eq. (5.22)) are all assumed to be uncorrelated. The full power build-up offered by the self-locking effect also makes that an uncertainty on the ring-down time determination at the per mille level may be achieved. This multiplies the previous limit expressed by 5.23 by a factor smaller than 2. In other terms, the shot-to-shot variation of a single spectral point (on the spectrum baseline), will have a standard deviation given by expression 5.24. For spectral points close to an absorption line α(ν), a contribution to shot-to-shot intensity variations also comes from fluctuations of the cavity frequency comb. These are translated into amplitude fluctuations proportionally to the slope on the sides of the absorption line. Applying some basic algebra to Eq. (5.22) and still considering uncorrelated noise, this adds to the root of Eq. (5.24) the square of the term $\frac{2}{\alpha(\nu)+\gamma_{k}/c}\frac {d\alpha}{d\nu}\delta\nu$, where γ _k is the loss rate of the mode used for calibration, δν is the root mean square value of the mode frequency fluctuation (at the time scale of a single spectrum acquisition) and $\frac{d\alpha}{d\nu}$ is the derivative of the absorption line.

As long as white noise sources are dominant in the experiment, we expect to increase the sensitivity by averaging spectra. For a typical OF-CEAS system, this is true, at best, up to a few seconds, with about hundred spectra averaged before reaching an ultimate sensitivity of typically a few times 10⁻¹⁰/cm (for a ring-down of around 10 μs). At that point, the noise on the averaged spectrum converges to a fixed pattern, which may contain a few recognizable optical interference fringes (regular oscillations), which can be associated to etaloning caused by diffused light on specific optical surfaces. This fixed pattern noise evolves slowly with further averaging and has rms fluctuations across spectral datapoints which do not decrease. The origin of this fixed pattern noise is still at present unclear, but it is universally present in all OF-CEAS setups that the authors have experience with.

Figure 5.13 provides an example of a OF-CEAS spectrum of air at ambient conditions, with the oxygen B-band ^R Q ₁ line at 14 532.900 cm⁻¹. This is obtained with an ECDL and a Brewster cavity with a ring-down time of 12 μs. 50 spectra are averaged over 5 s and result in a baseline rms noise of 3×10⁻¹⁰/cm, as shown in the figure. This is determined by calculating the standard deviation (on a baseline section) of the residuals of a multi-Lorentzian line fit which includes the main strong line (7×10⁻⁶/cm peak absorption) plus other extremely weak lines (∼10⁻⁹/cm). The lower panel of the figure displays the relative absorption uncertainty for each cavity mode (from the shot-to-shot rms variations divided by the square root of the number of averaged spectra), indicating a relative baseline noise level just above 4×10⁻⁵.^{Footnote 6} In absolute value this corresponds to a δα _min of about 10⁻¹⁰/cm, 3 times lower than the above fixed-pattern baseline noise of an averaged spectrum. We see therefore that this pattern noise is limiting the quality of OF-CEAS spectra after just a few seconds averaging.

Nevertheless, considering the averaged spectrum noise level relative to the strong line intensity, the above example illustrates that a dynamic range of a few time 10⁴ is readily attained. Also, as expected, an increase of the relative loss rate uncertainty due to insufficient cavity stability is observed for cavity modes close to the absorption line (bottom trace in Fig. 5.13). However, the signal reduction induced by absorption also contributes to this increase, which explains why the uncertainty does not drop at line center (zero spectral slope). With a noise analysis as a function of the mode position relative to the absorption line, the cavity stability can be deduced. In the work presented in [40], where a non-monolithic Brewster-angle cavity is used, a RMS value of δν at the MHz level at the time scale of a single spectrum acquisition (100 ms) is deduced. On the other hand, OF-CEAS systems with monolithic cavities as described in [41] do not manifest excess noise on the wings of strong absorption lines, indicating negligible fluctuations of the mode positions over a single laser scan.

Let us consider now the shot-noise limit for OF-CEAS absorption measurements. This is expressed by:

$$ \delta\alpha^{\mathrm{SN}}_{\min}= \frac{\pi}{\mathcal{F}L}\sqrt{\frac{eB}{\eta P}} , $$

(5.25)

where e [C] is the electron charge; B and η are the bandwidth [Hz] and responsivity [A/W] of the detector, respectively; P [W] is the optical power received by the photodetectors. This expression takes into account the incident power normalization, and for simplicity it is assumed that both the signal and the reference detector receive equal power. The latter is a reasonable hypothesis as usually the fraction of laser power used for the normalization corresponds well to a cavity mode transmission of several percent. With typically 10 μW on the photodetectors, a bandwidth around 1 MHz as needed to record ring-down times in the several μs range, and a detector responsivity of 0.5 A/W, $\delta\alpha^{\mathrm{SN}}_{\min}$ is estimated to be a few times 10⁻¹⁰/cm. This is close to the performance described in Fig. 5.13 obtained however after averaging and limited by fringes and fixed pattern noise. Therefore we can state that, on one hand, improvement on photodetectors down to the shot noise level should allow achieving the current ultimate noise level with a single OF-CEAS scan. On the other hand, further improvement can only be expected after overcoming the parasitic optical fringes and pattern noise effects. With respect to spectral fringes caused by scattering from optical surfaces (for more details see Sect. 3 of the introduction chapter), we should underline that, thanks to the linear frequency scale of OF-CEAS and its fast acquisition time, these appear as perfectly periodic sinusoidal perturbations of the spectral baseline. In more conventional spectroscopy techniques, periodic fringes are obtained only after linearization of the frequency scale of acquired spectra, which is often a complex and imperfect procedure. Thanks to this, after a preliminary fit of a OF-CEAS spectrum, fringe periods are readily determined from the positions of peaks present in the Fourier transform of the fit residuals. A refined fit may be then executed with inclusion of sine functions of the predetermined periods in the fitting routine, which enables automatic subtraction of the fringes from the absorption spectrum. The price to pay is an increase in the number of fitting parameters and a (usually modest) increase of the indetermination associated with the resulting fit parameters values.

Improvements to the technique would also include the active stabilization of the cavity length and the temperature of the whole optical system. This allows having stable fringes and pattern noise and to obtain reproducible spectral fit results on the long term, which, combined with calibration procedures (periodic injection of reference gas samples) may still deliver high accuracy concentration or isotope ratio measurements. Of course, choosing high quality optical surfaces and assuring a careful alignment and choice of the distances separating the optical components would also help reducing the effect of optical fringes. Further gain in sensitivity is also possible by using higher reflectivity cavity mirrors. Nowadays, a cavity finesse in excess of 10⁵ is easily available at certain wavelengths (e.g. the telecom range [42]), thanks to advances in dielectric mirror coatings.

As a last issue relevant to precision of OF-CEAS measurements, it is interesting to consider the effect of cavity mode frequency shift induced by dispersion intrinsically associated with molecular absorption. Indeed, the resonant absorption of light is accomplished with a phase delay that leads to a dispersive perturbation of the refractive index of gas sample. Considering the absorption coefficient of a single absorption line described by a Lorentzian profile α(ν−ν _c) where ν _c is the transition frequency (see top panel of Fig. 5.14), the refractive index variation is given by [12]:

$$ \delta n(\nu)=-\frac{c}{2\pi\nu} \frac{\nu-\nu_{c}}{\varGamma}\alpha(\nu-\nu_{c}) , $$

(5.26)

where Γ is the Half Width at Half Maximum (HWHM) of the Lorentzian profile. The cavity mode frequency of order m is now given by:

$$ \nu'_{m}=\nu_{m} \biggl(1- \frac{\delta n(\nu'_{m})}{n_{\mathrm{nr}}} \biggr), $$

(5.27)

where ν _m=mc/2n _nr L is the empty cavity mode frequency and n _nr is the non-resonant refractive index of the gas sample. This implicit equation for $\nu'_{m}$ is numerically solved and the difference with the empty cavity mode frequency is plotted in the middle panel of Fig. 5.14 for an absorption coefficient of 10⁻⁵/cm at the line center. This maximum value α _max is approximately equal to the largest absorption that the typical cavity considered here can tolerate, and still produce a reasonable level of transmission and feedback. Mode frequency shifts are largest at 1 HWHM from line center, reaching a few tens of kHz. This is sufficiently small to replace $\nu'_{m}$ by ν _m in the argument of δn(ν) in Eq. (5.27). In that case, it is easy to show that the largest frequency shift is given by (ν′−ν)_max=cα _max/4π and depends only on α _max. However, if a constant frequency increment is assumed between OF-CEAS spectral data points, given by the cavity FSR (in the absence of dispersion effects), it is pertinent to consider the variation of the FSR induced by absorption, $\mathit{FSR}'_{m}-\mathit{FSR}=(\nu '_{m+1}-\nu'_{m})-c/2n_{\mathrm{nr}}L$. As expected, the middle panel of Fig. 5.14 shows that this variation is largest at the transition frequency where δn(ν) has the largest slope. Using the same approximation, and in the restricted case FSR≪Γ, the largest FSR variation is given by $\Delta \mathit{FSR}_{\max}= (\frac {\mathit{FSR}}{2\pi} )\cdot(\frac{c \alpha_{\max}}{\varGamma})$, which depends both on α _max and Γ. Even with α _max=10⁻⁵/cm and a HWHM of 1 GHz, the largest variation is just a few kHz. If datapoints in spectra acquired mode-by-mode are assumed to have a constant spacing, the effect induces a defect on the intensity of the absorption line, which is plotted for our example in the bottom panel of Fig. 5.14. We see then, that a detection limit below 10⁻¹⁰/cm around the absorption line would be required to resolve this effect. In other words, a signal-to-noise ratio (S/N) of 10⁵ is necessary. As confirmed by Fig. 5.14, the largest deviation of the residuals appears at about 1 HWHM from the line center, which enables to derive a simple analytical expression for it. Indeed, $\alpha(\nu'_{m})-\alpha(\nu_{m})=\frac{\partial \alpha}{\partial\nu}(\nu'_{m}-\nu_{m})$ and $(\alpha(\nu '_{m})-\alpha(\nu_{m}))_{\max}\simeq\frac{\partial\alpha }{\partial\nu}|\nu'_{m}-\nu_{m}|_{\max}$, which gives at the 1 HWHM position: Δα _max=c(α _max)²/8πΓ. In particular, this expression shows that the largest deviation of the residuals scales with the square of the absorption coefficient. A quadratically lower detection limit of 10⁻¹²/cm would occur for a more typical absorption coefficient of 10⁻⁶/cm.

To conclude, we see that the current performance of OF-CEAS is not far from the level that would enable the observations of this small effect. Using a narrower absorption line at lower sample pressure (close to the Doppler limit) would allow to make the effect stronger. However, in order to observe this effect a high-accuracy knowledge of the absorption line profile must be provided. Conversely, the equations above would allow correcting OF-CEAS spectral profiles in case high precision measurements are needed.

5.7 Precursory Works on OF-Locking of a Semiconductor Laser to an Optical Cavity

5.7.1 Laser Stabilization

The first application of OF-locking of a SC laser to an optical cavity appears to have occurred in atomic physics [8, 43]. The goal was to obtain a spectrally narrow and stable laser emission without a high bandwidth electronic feedback loop. It was discovered that with a low level of optical feedback coming from the resonant field of an optical cavity a SC laser is able to self-lock to the cavity resonance, even as its injection current would be driving its free running frequency away from the resonance. As it was readily noticed, this locking effect is accompanied by a dramatic reduction of the laser linewidth and of its relative intensity noise. The locking range could reach hundreds of MHz and be controlled by the feedback phase and level. By synchronized sweeping of the laser current and the reference cavity length, all the while controlling the feedback phase, a continuous narrow-linewidth scan of the laser frequency could be obtained over small spectral windows (∼1 GHz). The potential of this experimental approach led to several studies, providing a solid theoretical basis for this coupled optical system [21, 44–47]. Even though the main motivation was to obtain a stabilized laser, it was also recognized that the power buildup inside the reference cavity could be exploited for atomic beam collimation [48] or intracavity frequency doubling [38].

In the aforementioned studies, several optical cavity geometries were investigated. The first demonstration of Dahmani et al. [8] used a confocal cavity with a tilted injection providing the resonant optical feedback from an intracavity stable V-shaped light trajectory (produced as a superposition of frequency-degenerate transverse cavity modes, as discussed in the introductory chapter of this book). Shortly thereafter, Li et al. [47] used a V-shaped cavity as described in the previous section. This eliminates the need for a precise adjustment of the cavity length imposed by the confocal condition. Tanner et al. [48] used the small mirror birefringence and a polarization filter to discriminate the direct input mirror reflection from the resonant field. In the work of Hemmerich et al. [38], OF was obtained in a ring-cavity configuration: The parasitic diffusion on optical surfaces is sufficient to weakly excite the counter-propagating mode in a ring-cavity. This fact is actually not as surprising as it may seem at first, considering that intracavity scattering is enhanced by the large intracavity field and constitutes a light source internal to the cavity, directly seeding the counter-propagating cavity mode.

In all these applications, the stabilized laser was not intended, nor readily exploitable, for molecular spectroscopy, which requires a wide and fast tunability. In addition, stiff and short cavities with moderate finesse (about 100) were employed. Indeed, OF locking drives the laser linewidth to orders of magnitude below the width of the cavity resonance, thus a moderate finesse is already sufficient to attain sub-kHz laser emission.

5.7.2 Optical-Feedback Cavity Ring-Down Spectroscopy

Historically, before it could be established that OF is exploitable to obtain CEAS spectra injecting longitudinal cavity modes in rapid succession, another, experimentally simpler configuration was introduced. This uses ring-down events to measure the intracavity sample absorption [7, 49]. In this early implementation of OF-CRDS, a ring-down signal is obtained by applying a square current pulse to the SC laser. The pulse instantaneously induces laser emission as soon as the lasing threshold is exceeded, but the thermal equilibrium of the laser chip is abruptly modified. The initial heat-up of the laser induces a fast chirp in the emitted wavelength before a steady state with a constant temperature is reached. In other words, the abrupt laser current injection initiates a fast frequency sweep which progressively slows down. The entire frequency range spanned by this process depends on the current step, but can be easily on the order of ten GHz or more, or about hundred cavity FSRs. At the beginning of the pulse, the scanning speed is so high that the optical feedback (resulting from the extremely low transient intracavity build up) is not sufficient to affect the laser emission, and no light is detected behind the cavity. As the scanning speed reaches sufficiently low values to make the optical feedback operate, signals appear behind the cavity corresponding to the cavity modes which start to appear “enlarged” by the frequency locking effect. By adjusting a feedback rate in such a way that the locking range exceeds the free spectral range, the cavity is almost always injected at the end of the pulse. The abrupt current drop at pulse end is thus likely followed by a ring-down event at the frequency of the last injected mode. To construct a ring-down spectrum, it is sufficient to scan the current pulse amplitude. In order to correctly map a spectral window, the pulse duration and its amplitude increment are roughly optimized. For a typical feedback rate of 10⁻⁴ used with a DFB diode laser, the pulse duration is typically a few hundred μs, giving a ring-down acquisition rate in the kHz range.

This OF-CRDS scheme is simple and robust since no special adjustment nor active control of the laser-cavity distance is required. Actually, vibrations are welcome since they favor shot-to-shot variations of the OF phase at the end of the laser pulse. This induces an averaging over the selection of the last cavity mode to which the laser is locked when the ring-down event occurs. If mode matching is not good, this last mode may even fluctuate among different transverse modes, which require different OF phases for optimal laser locking. As it is well known that the ring-down time is different for different transverse modes, it is clear that this OF-CRDS scheme not only provides spectra with a frequency uncertainty of more than one cavity FSR, but can easily suffer of an excess amplitude noise associated with bad selectivity in transverse mode excitation.

Nonetheless, as mentioned before, the simplicity of this OF-CRDS scheme, its insensitivity to vibrations, and the high ring-down acquisition rate have led to the development and successful application of low cost transportable trace gas analyzers. Detection of methane, water vapor, and hydrogen fluoride has been demonstrated both in the laboratory and in field measurements [7, 49]. A typical absorption baseline noise of a few 10⁻⁸/cm may be obtained on a single spectrum, and averaging over a few minutes enables a sub-10⁻⁹/cm absorption limit with a ring-down time just above 10 μs. More recently, the high acquisition rate has been exploited for aerosols extinction measurements [50, 51] and precise measurement of an ultra-high mirror reflectivity was shown to be possible with an equally simple optical layout [52] (see next section).

5.8 Applications

OF-CEAS has been used in a number of different applications that will be reviewed in this section. We group them by applications area: trace gas detection, isotope ratio analyses, aerosol studies, and finally other applications such as mirror reflectivity measurements. At the same time, different techniques will be looked over: OF-CRDS and OF-CEAS; near-IR DFB diode lasers and ECDLs, as well as mid-IR laser sources; photoacoustic detection; V-shaped, birefringent linear, Brewster-angle, and ring cavity configurations.

5.8.1 Trace Gas Detection

The first spectroscopic applications of OF-CRDS were the detection of trace gases in the near-IR region of the spectrum. Romanini and co-workers demonstrated sensitive detection of H₂O and HF near 1.3 μm and CH₄ at 1.65 μm with at the time a performance only slightly inferior to that of CW-CRDS, but with a greatly simplified and lower cost experimental setup [7, 49, 53]. In 2005 the group demonstrated OF-CEAS with a noise equivalent absorption sensitivity (NEAS) of $5\times10^{-10}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$ for a spectral recording over ∼1 cm⁻¹. This was for a cavity with a ring-down time of 17 μs, yielding a sub-ppb detection limit for HF at 1.312 μm in an open V-shaped cavity [1]. Courtillot et al. extended the OF-CEAS method to ECDLs and to the blue region of the optical spectrum, by measuring NO₂ at 411 nm with an estimated detection limit below 1 ppb (with few seconds averaging) [30].

Measurements of atmospheric methane concentrations using an OF-CEAS instrument on board of NASA’s DC-8 research platform served to demonstrate the relative insensitivity of the technique to environmental factors, in particular vibrations, but also changing ambient temperature and pressure [18]. Operating at 1.6 μm, the airborne spectrometer was able to resolve fast (0.3 s, limited by the gas cell exchange time) methane concentration changes of 1 ppb. This instrument was not temperature controlled, still its stability was established to be about 20 ppb (pk-pk) during a 10-days long direct comparison with a half-hourly automatically calibrated gas chromatograph.

An extension of the technique towards the mid-IR was first demonstrated using a DFB diode laser emitting near 2.33 μm for the detection of CO and CH₄ in fumarolic gases (in the presence of about 98 % CO₂) [41]. The instrument achieved a relatively poor NEAS of $3\times10^{-9}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$, attributed partly to a short cavity ring-down time τ ₀ of 6.5 μs, partly to residual optical interference fringes. An improved version of the instrument was applied to exhaled breath analysis for CO and CH₄, as well as NH₃, in a hospital setting [54]. With better mirrors (τ ₀=30 μs) and fringe suppression, a tenfold reduction in NEAS was realized in this case.

A rather different approach to the same multiple gas analysis was taken by Cermak et al. [32], who combined the OF-CEAS V-shaped cavity with a VECSEL operating near 2.33 μm. The short and stiff external cavity design of the optically pumped laser enabled broad tuning over as much as 50 cm⁻¹ with low frequency noise, resulting in a spectrometer that exhibited a NEAS comparable to that of more common near-IR DFB diode laser OF-CEAS setups.

The high potential of combining OF-CEAS with thermo-electrically cooled DFB QCLs was illustrated by Maisons et al. [33] and by Hamilton et al. [34]. The first study used a 4.46 μm-QCL to construct a spectrometer that achieved a NEAS of $3\times 10^{-9}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$ for the registration of a ∼1 cm⁻¹ wide spectrum of diluted (1:25) atmospheric air. The corresponding detection sensitivities were 35 pptv for N₂O and 15 ppbv for CO₂ with τ ₀=8.5 μs. The second group used a QCL operating near 7.78 μm for the simultaneous detection of CH₄ and N₂O with a spectrometer NEAS of $5.5\times10^{-8}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$ and τ ₀=3.5 μs. These experiments serve to highlight the high cavity throughput advantage in the mid-IR of OF-CEAS over alternative CEAS-based techniques in this part of the optical spectrum, considering that the QCL used in this study exhibited a modest output power level of, respectively, 15 and 4 mW maximum (comparable to near-IR DFB diode laser output powers), while the detector sensitivities in the mid-IR are typically two to three orders of magnitude lower than those used in the near-IR. As mirror quality continues to improve and cavity transmission to decrease, this is likely to become an even larger advantage (see more recent results in [35]).

Motto-Ros et al. investigated the B-band of molecular oxygen at 688 nm using a novel optical layout consisting of a linear cavity with a microscope cover plate at a near-to-Brewster angle with respect to the cavity symmetry axis and approximately centered between the end-mirrors [40]. The Brewster plate serves to couple the laser light into the cavity, while simultaneously enabling an adjustment of the cavity finesse. This in turn offers the possibility to increase the dynamic range of the technique by up to one order of magnitude. Conceivably, the microscope plate also provides a convenient way to introduce a liquid or solid absorber, ad- or ab-sorbed on its surface.

Another interesting optical layout was investigated by Hamilton et al. [37]. They used a three-mirror ring cavity to record weak transitions of two molecular oxygen isotopologues in the A-band near 762 nm, demonstrating a NEAS of ${\sim}2 \times 10^{-9}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$. Potential advantages of the ring configuration are the ability to easily modulate the optical feedback level by means of a retro-reflecting mirror placed after one of the cavity high-reflectivity mirrors, without introducing an attenuating optical element in the beam path between laser and cavity, and the absence of the even odd mode structure.

Yet another interesting development for trace gas detection has been the combination of OF-CEAS with photoacoustic detection, demonstrated with the sensitive detection of high overtones of the water molecule near 635 nm [55]. The NEAS scales linearly with laser power and in this study was demonstrated to reach of $4.4\times 10^{-9}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$ for 1.7 mW of incoming laser power. The technique shares the principal advantages (such as its zero-base-line character), as well as disadvantages (among others, the dependence of its sensitivity on the gas matrix composition), with more common photoacoustic implementations.

5.8.2 Isotope Ratio Analyses

Isotope ratio measurements are particularly prone to benefit from a sensitive technique as CEAS to access the generally weak absorption lines of the isotopologues (see [56] and [57] for an introduction and review of the application of laser-based techniques in this field of research). We have therefore been an early adopter of OF-CEAS for water isotope ratio measurements. In early 2004 a spectrometer flew on the NASA DC-8 (together with the above mentioned CH₄ analyzer), demonstrating the feasibility of measuring isotope ratios with an airborne instrument operating in the near-IR and with good precision, even at the low water concentration encountered at an altitude of 13 km in the upper troposphere. This first water isotope spectrometer was characterized by a NEAS of $4\times10^{-10}~\mbox{cm}^{-1}/\sqrt{\mathrm{Hz}}$ for a spectral recording over 200 modes (∼1 cm⁻¹), a τ ₀ of 20 μs, and a cavity base length of 50 cm. It measured the ²H/¹H, ¹⁷O/¹⁶O, and ¹⁸O/¹⁶O isotopic ratios with a precision of 9 ‰, 3 ‰, and 1 ‰ after averaging over 30 s [39]. A second generation of this spectrometer was flown on the European M55-Geophysica high-altitude research aircraft during the 2006 AMMA/SCOUT-03 (African Monsoon Multidisciplinary Analysis/Stratospheric Climate links with emphasis on the Upper Troposphere and lower stratosphere) campaign in Burkina Faso [58, 59]. The same instrument was used to measure near-surface tropospheric water moisture at two orders of magnitude higher water mixing ratios [60]. More recently we have carried out high-precision isotope measurements of moisture at the Antarctic station of Troll with a spectrometer much improved in terms of cavity temperature and pressure stabilization, and with an increased empty cavity ring-down τ ₀ of 130 μs. [61]

Wehr et al. have used a DFB diode laser at 2.007 μm to access the $\nu_{1}+2\nu_{2}^{0}+\nu_{3}$ combination band of CO₂ [62]. This band is almost two orders of magnitude stronger than the $\nu_{1}+4\nu_{2}^{0}+\nu_{3}$ combination band at 1.6 μm. Despite this, the demonstrated performance on the ¹³CO₂/¹²CO₂ isotopic ratio determination was somewhat disappointing and attributed to mechanical instability in the setup and a relatively strong residual optical fringe due to the use of a flat, non-anti-reflection coated mirror substrate.

Currently, in the Grenoble laboratory, efforts are underway to miniaturize the water isotope spectrometer for it to be embarked on a novel ice-core drilling device to be deployed in 2015 at Dome Concordia in central Antarctica. The goal is to measure in-situ the isotopic composition of the melted ice, while the probe drills down to bedrock at about 3 km under the ice surface in one Antarctic summer season (∼70 days). At the same time, a QCL-equipped OF-CEAS system is being developed for the accurate measurement of carbon dioxide isotopologues recovered from tiny air bubbles contained in ice-cores that have been drilled in the traditional manner. The sensitivity boast required to deal with the very small sample size is to come from exciting strong CO₂ isotopologue transitions in the 4.35 μm region, while maintaining a small cavity volume of about 20 mL.

5.8.3 Aerosol Studies

Orr-Ewing and co-workers realized the potential of OF-CEAS for aerosol measurements, in particular its capability to perform CRDS measurements with a high repetition rate (1.25 kHz). This enabled multiple measurements of the extinction by single spherical polymer beads, revealing the dependence of light scattering on the position of a particle within the laser beam. A model is proposed to explain quantitatively this phenomenon [50]. Further studies show that the linear relation between the extinction coefficient and its variance, predicted by a Poisson statistical model, allows for the determination of the extinction cross-section without prior knowledge of the particle number density [51].

5.8.4 Other Applications

Morville and Romanini demonstrated that the weak birefringence of high-reflectivity dielectric mirrors can be measured with good spatial resolution and a sensitivity better than 10⁻⁷ radians by mapping the optical feedback rate as a function of the mirror rotation around the cavity symmetry axis [36]. More recently[63] a similar scheme was used to obtain the static Kerr effect in a gas by lock-in detection of the birefringence induced by a modulated transverse electric field. The state-of-the-art detection limit of 3×10⁻¹³ radians was attained by averaging shot-noise-limited measurements as long as one hour.

Gong and colleagues [64] used OF with a very simple linear cavity optical layout in combination with a spectrally wide, multi-mode Fabry-Perot diode laser, to measure an ultra-high mirror reflectivity with a precision of 0.3 ppm. This presents a gain in sensitivity of two-orders of magnitude compared with previous phase-shift CRDS mirror reflectivity measurements, at a significantly reduced cost. In this particular application, the direct OF from the mirror back surface is acceptable as the resulting perturbed laser frequency remains within the high-reflectivity optical bandwidth of the mirrors. More recently Tong-Kai et al. repeated the same experiment, but with both a linear and a V-shaped cavity configuration, and found the two to give comparable results [65].

5.9 Conclusions

In this chapter we have presented in detail the technique of cavity enhanced absorption spectroscopy exploiting selective optical feedback from the cavity resonances to the laser. The technique has several advantages over CEAS schemes that rely on an electronic control of the laser emission frequency to achieve sufficient spectral overlap between the laser emission and a cavity resonance. Its implementation is straightforward and requires few optical components. The spectral narrowing and frequency locking to TEM _0,0 cavity modes induced by the optical feedback achieve a higher level of performance than accessible with complex, high-performance electronic feedback circuitry. This results in a fast and complete light injection of the cavity on a well-defined grid of equally spaced frequencies, and provides clear advantages in terms of acquisition time and signal-to-noise ratio of the measurement of absorption lines as both absorption and frequency scales are precisely defined. Although the technique requires that the laser exhibits a certain level of sensitivity to optical feedback, it has been shown to work with a large variety of modern semi-conductor lasers, including DFB diode lasers, ECDLs, VECSELs, and QCLs, together spanning the spectral range from 400 nm to beyond 8 μm. Admittedly, successful application of the technique requires a good understanding of its underlying physical principles, which are arguably more complex than those of competing techniques.

We have started the chapter with an intuitive description of the OF-CEAS technique in order to ease the reader through the following more detailed description of the time and frequency behavior of a coupled diode-laser-cavity system, which is reasonably simple in the quasi stationary approximation. Model equations have been derived and used to analyze the cavity transmission when optical feedback modifies the laser frequency during a scan of the free laser frequency (or the injection current). In return, this analysis clearly identifies the configuration space of the system parameters (laser-cavity distance, feedback rate and feedback phase, frequency scanning speed) and their limits imposed by the cavity geometry and losses, and by the laser sensitivity and robustness to optical feedback.

After this general outline of the OF-CEAS working principle, we have discussed various implementations reported in the literature up to date, including the different laser sources as well as the cavity configurations that have been successfully applied to OF-CEAS.

We dedicated an entire section to a calibration procedure that we developed, based on the measurement of a single ring-down event during the laser scan, which confers to the technique the advantage of absolute loss measurements.

We then presented typical performance arising from this procedure when combined with the property of equally spaced frequency data points provided by the cavity comb sampling of OF-CEAS spectra. Limiting factors on both scales of a spectrum (absorption and frequency) have been discussed including perspectives of improvement. Absorption baseline noise on single spectra covering 1 cm⁻¹ acquired in 100 ms is presently around 10⁻⁹/cm, as obtained with cavities of moderate finesse ($\mathcal{F}\sim10\,000$) from the blue range to the IR range using DFB multiple-quantum-wells diode lasers, ECDLs, and DFB room-temperature QCLs.

We have provided a brief historical overview of developments leading to the currently most common implementation of OF-CEAS. The last section is devoted to the different fields of application of OF-CEAS, from trace to isotope ratio analysis, to birefringence, aerosols, or mirror reflectivity measurements.

Notes

1.
The Schawlow-Townes limit [10] expresses the laser linewidth when only spontaneous emission takes place. Its value scales with the inverse of the laser cavity photon lifetime, itself proportional to the laser length. For semiconductor lasers, this limit is increased by a factor ranging from 2 to 10, due to a coupling between gain and phase in the laser medium [11, 12]. QCL cavities are typically ten times longer than those of diode lasers and the coupling is expected to be practically zero, resulting in a smaller intrinsic linewidth. However, compared to diode lasers, QCLs have a similar current tuning coefficient but typically operate at an injection current level one order of magnitude higher, thus require a comparably higher fractional current stability. For instance, a current noise on the order of 10⁻⁶ is needed to obtain a 1 MHz laser linewidth.
2.
The Henry factor and its physical origin are discussed in Sect. 5.4.1.
3.
In this case, it is shown that the maximum cavity transmission H _OF,max is equal to 0.25 which corresponds well to the sum P′²+Q′² at exact resonance.
4.
In practice it is trivial to plot ω _free as a function of ω _L and exchange axes in the plot.
5.
This “figure of merit” is discussed in the introduction chapter (Sect. 1.3) together with detection-limit-related issues. It is not to be considered as a true detection limit since 1/f and fringe noise are not taken into account in its definition.
6.
We recall that the absorption baseline is not zero and corresponds to the empty cavity losses.

References

J. Morville, S. Kassi, M. Chenevier, D. Romanini, Appl. Phys. B, Lasers Opt. 80(8), 1027 (2005). doi:10.1007/s00340-005-1828-z. http://www.springerlink.com/index/10.1007/s00340-005-1828-z
Article ADS Google Scholar
A. Kachanov, D. Romanini, M. Chenevier, A. Garnache, F. Stoeckel, in Part of SPIE Conference on Air Monitoring and Detection of Chemical and Biological Agents II, Boston, MA, 19–22 September 1999. Proc. SPIE, vol. 3855 (1999), p. 51
Chapter Google Scholar
D. Romanini, A.A. Kachanov, J. Morville, M. Chenevier, in Part of SPIE EUROPTO Conference on Environmental Sensing and Applications, CLEO-Europe, Munich, 14–17 June 1999. Proc. SPIE, vol. 3821 (1999), p. 94
Chapter Google Scholar
J. Morville, D. Romanini, Appl. Phys. B 74, 495 (2002)
Article ADS Google Scholar
J. Morville, D. Romanini, M. Chenevier, J. Phys. IV 12, 389 (2002)
Google Scholar
J. Morville, M. Chenevier, A.A. Kachanov, D. Romanini, in Optical Spectroscopic Techniques, Remote Sensing, and Instrumentation for Atmospheric and Space Research IV. Proc. SPIE, vol. 4485 (2002), p. 236
Chapter Google Scholar
J. Morville, D. Romanini, A.A. Kachanov, M. Chenevier, Appl. Phys. B, Lasers Opt. 78(3–4), 465 (2004). doi:10.1007/s00340-003-1363-8. http://www.springerlink.com/openurl.asp?genre=article&id=doi:10.1007/s00340-003-1363-8
Article ADS Google Scholar
B. Dahmani, L.W. Hollberg, R.E. Drullinger, Opt. Lett. 12(11), 876 (1987). doi:10.1364/OL.12.000876. http://www.ncbi.nlm.nih.gov/pubmed/19741901
Article ADS Google Scholar
H. Patrick, C.E. Wieman, Rev. Sci. Instrum. 62(11), 2593 (1991). doi:10.1063/1.1142236
Article ADS Google Scholar
A.L. Schawlow, C.H. Townes, Phys. Rev. 112, 1940 (1958)
Article ADS Google Scholar
C. Henry, R. Logan, K. Bertness, J. Appl. Phys. 52(7), 4457 (1981)
Article ADS Google Scholar
A. Yariv, Quantum Electronics, 3rd edn. (Wiley, New York, 1989)
Google Scholar
J.C. Habig, J. Nadolny, J. Meinen, H. Saathoff, T. Leisner, Appl. Phys. B, Lasers Opt. 106(2), 491 (2011). doi:10.1007/s00340-011-4804-9. http://www.springerlink.com/index/10.1007/s00340-011-4804-9
Article ADS Google Scholar
C.E. Wieman, L.W. Hollberg, Rev. Sci. Instrum. 62(1), 1 (1991)
Article ADS Google Scholar
R.W.P. Drever, J.L. Hall, F.V. Kowalski, J. Hough, G.M. Ford, A.J. Munley, H. Ward, Appl. Phys. B, Lasers Opt. 31(2), 97 (1983). doi:10.1007/BF00702605. http://www.springerlink.com/index/10.1007/BF00702605
Article ADS Google Scholar
D.A. Long, A. Cygan, R.D. van Zee, M. Okumura, C.E. Miller, D. Lisak, J.T. Hodges, Chem. Phys. Lett. 536, 1 (2012). doi:10.1016/j.cplett.2012.03.035. http://linkinghub.elsevier.com/retrieve/pii/S0009261412003466
Article ADS Google Scholar
M.S. Taubman, T.L. Myers, B.D. Cannon, R.M. Williams, Spectrochim. Acta, Part A, Mol. Biomol. Spectrosc. 60(14), 3457 (2004). doi:10.1016/j.saa.2003.12.057. http://www.ncbi.nlm.nih.gov/pubmed/15561632
Article ADS Google Scholar
D. Romanini, M. Chenevier, S. Kassi, M. Schmidt, C. Valant, M. Ramonet, J. Lopez, H.J. Jost, Appl. Phys. B, Lasers Opt. 83(4), 659 (2006). doi:10.1007/s00340-006-2177-2. http://www.springerlink.com/index/10.1007/s00340-006-2177-2
Article ADS Google Scholar
C.H. Henry, IEEE J. Quantum Electron. 18(2), 259 (1982). doi:10.1109/JQE.1982.1071522. http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=1071522
Article ADS Google Scholar
K.K. Lehmann, D. Romanini, J. Chem. Phys. 105(23), 10263 (1996). doi:10.1063/1.472955. http://link.aip.org/link/JCPSA6/v105/i23/p10263/s1&Agg=doi
Article ADS Google Scholar
P. Laurent, A. Clairon, C. Breant, IEEE J. Quantum Electron. 25(6), 1131 (1989)
Article ADS Google Scholar
I. Courtillot, J. Morville, V. Motto-Ros, D. Romanini, Appl. Phys. B 85, 407 (2006)
Article ADS Google Scholar
C.H. Henry, J. Appl. Phys. 52(7), 4457 (1981). doi:10.1063/1.329371. http://link.aip.org/link/?JAP/52/4457/1&Agg=doi
Article ADS Google Scholar
C.A. Green, N.K. Dutta, W. Watson, Appl. Phys. Lett. 50(20), 1409 (1987). doi:10.1063/1.97836. http://link.aip.org/link/APPLAB/v50/i20/p1409/s1&Agg=doi
Article ADS Google Scholar
K. Petermann, Laser Diode Modulation and Noise (Kluwer Scientific, Tokyo, 1991)
Google Scholar
Y. Arakawa, A. Yariv, IEEE J. Quantum Electron. QE-21(10), 1666 (1985)
Article ADS Google Scholar
T. Aellen, R. Maulini, R. Terazzi, N. Hoyler, M. Giovannini, J. Faist, Appl. Phys. Lett. 89, 091121 (2006)
Article ADS Google Scholar
S. Bartalini, S. Borri, P. Cancio, A. Castrillo, I. Galli, G. Giusfredi, D. Mazzotti, L. Gianfrani, P.D. Natale, Phys. Rev. Lett. 104, 083904 (2010)
Article ADS Google Scholar
J. von Staden, T. Gensty, W. Elsäßer, G. Giuliani, C. Mann, Opt. Lett. 31(17), 2574 (2006). doi:10.1364/OL.31.002574. http://ol.osa.org/abstract.cfm?URI=ol-31-17-2574
Article ADS Google Scholar
I. Courtillot, J. Morville, V. Motto-Ros, D. Romanini, Appl. Phys. B, Lasers Opt. 85(2–3), 407 (2006). doi:10.1007/s00340-006-2354-3. http://www.springerlink.com/index/10.1007/s00340-006-2354-3
Article ADS Google Scholar
V. Motto-Ros, J. Morville, P. Rairoux, Appl. Phys. B, Lasers Opt. 87(3), 531 (2007). doi:10.1007/s00340-007-2618-6. http://www.springerlink.com/index/10.1007/s00340-007-2618-6
Article ADS Google Scholar
P. Cermak, M. Triki, A. Garnache, L. Cerutti, D. Romanini, IEEE Photonics Technol. Lett. 22(21), 1607 (2010). doi:10.1109/LPT.2010.2075922. http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=5570899
Article ADS Google Scholar
G. Maisons, P. Gorrotxategi-Carbajo, M. Carras, D. Romanini, Opt. Lett. 35(21), 3607 (2010)
Article ADS Google Scholar
D.J. Hamilton, A.J. Orr-Ewing, Appl. Phys. B, Lasers Opt. 102(4), 879 (2010). doi:10.1007/s00340-010-4259-4. http://www.springerlink.com/index/10.1007/s00340-010-4259-4
Article ADS Google Scholar
P. Gorrotxategi-Carbajo, E. Fasci, I. Ventrillard, M. Carras, G. Maisons, D. Romanini, Appl. Phys. B, 309–314 (2013)
Google Scholar
J. Morville, D. Romanini, Appl. Phys. B, Lasers Opt. 74(6), 495 (2002). doi:10.1007/s003400200854. http://www.springerlink.com/Index/10.1007/s003400200854
Article ADS Google Scholar
D.J. Hamilton, M.G.D. Nix, S.G. Baran, G. Hancock, A.J. Orr-Ewing, Appl. Phys. B, Lasers Opt. 100(2), 233 (2009). doi:10.1007/s00340-009-3811-6. http://www.springerlink.com/index/10.1007/s00340-009-3811-6
Article ADS Google Scholar
A. Hemmerich, D.H. McIntyre, C. Zimmermann, T.W. Hänsch, Opt. Lett. 15(7), 372 (1990). doi:10.1364/OL.15.000372. http://www.opticsinfobase.org/abstract.cfm?URI=ol-15-7-372
Article ADS Google Scholar
E.R.T. Kerstel, R.Q. Iannone, M. Chenevier, S. Kassi, H.J. Jost, D. Romanini, Appl. Phys. B, Lasers Opt. 85(2–3), 397 (2006), doi:10.1007/s00340-006-2356-1. http://www.springerlink.com/index/10.1007/s00340-006-2356-1
Article ADS Google Scholar
V. Motto-Ros, M. Durand, J. Morville, Appl. Phys. B, Lasers Opt. 91(1), 203 (2008). doi:10.1007/s00340-008-2950-5. http://www.springerlink.com/index/10.1007/s00340-008-2950-5
Article ADS Google Scholar
S. Kassi, M. Chenevier, L. Gianfrani, A. Salhi, Y. Rouillard, A. Ouvrard, D. Romanini, Opt. Express 14(23), 11442 (2006)
Article ADS Google Scholar
S. Kassi, A. Campargue, J. Chem. Phys. 137(23), 234201 (2012). doi:10.1063/1.4769974. http://www.ncbi.nlm.nih.gov/pubmed/23267478
Article ADS Google Scholar
L.W. Hollberg, M. Ohtsu, Appl. Phys. Lett. 53(11), 944 (1988). doi:10.1063/1.100077. http://link.aip.org/link/APPLAB/v53/i11/p944/s1&Agg=doi
Article ADS Google Scholar
A. Clairon, B. Dahmani, P. Laurent, C. Breant, in Proceeding of EFTF88, Second European Frequency and Time Forum, Neuchatel, Switzerland (1988), p. 537
Google Scholar
H. Li, N.B. Abraham, Appl. Phys. Lett. 53(23), 2257 (1988). doi:10.1063/1.100271. http://link.aip.org/link/APPLAB/v53/i23/p2257/s1&Agg=doi
Article ADS Google Scholar
H. Li, N.B. Abraham, IEEE J. Quantum Electron. 25(8), 1782 (1989). doi:10.1109/3.34036. http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=34036
Article ADS Google Scholar
H. Li, H.R. Telle, IEEE J. Quantum Electron. 25(3), 257 (1989). doi:10.1109/3.18538. http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=18538
Article ADS Google Scholar
C.E. Tanner, B.P. Masterson, C.E. Wieman, Opt. Lett. 13(5), 357 (1988). doi:10.1364/OL.13.000357. http://www.opticsinfobase.org/abstract.cfm?URI=ol-13-5-357
Article ADS Google Scholar
J. Morville, M. Chenevier, A.A. Kachanov, D. Romanini, in Proceedings of SPIE, vol. 4485, ed. by A.M. Larar, M.G. Mlynczak (2002), pp. 236–243. doi:10.1117/12.454256
Google Scholar
T.J. Butler, J.L. Miller, A.J. Orr-Ewing, J. Chem. Phys. 126, 174302 (2007). doi:10.1063/1.2723735
Article ADS Google Scholar
T.J.A. Butler, D. Mellon, J. Kim, J. Litman, A.J. Orr-Ewing, J. Phys. Chem. A 113(16), 3963 (2009). doi:10.1021/jp810310b
Article Google Scholar
Y. Gong, B. Li, Y. Han, Appl. Phys. B, Lasers Opt. 93(2–3), 355 (2008),. doi:10.1007/s00340-008-3247-4. http://www.springerlink.com/index/10.1007/s00340-008-3247-4
Article ADS Google Scholar
D. Romanini, A.A. Kachanov, J. Morville, M. Chenevier, in Proc. SPIE, vol. 3821 (1999), p. 94. doi:10.1117/12.364170. http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Measurement+of+trace+gases+by+diode+laser+cavity+ringdown+spectroscopy+.#0
Google Scholar
I. Ventrillard, T. Gonthiez, C. Clerici, D. Romanini, J. Biomed. Opt. 14(6), 64026 (2009). doi:10.1117/1.3269677. http://www.ncbi.nlm.nih.gov/pubmed/20059264
Article Google Scholar
M. Hippler, C. Mohr, K.A. Keen, E.D. McNaghten, J. Chem. Phys. 133(4), 44308 (2010). doi:10.1063/1.3461061. http://www.ncbi.nlm.nih.gov/pubmed/20687651
Article Google Scholar
E.R.T. Kerstel, in Handbook of Stable Isotope Analytical Techniques, vol. 1, ed. by P.A. De Groot (Elsevier, Amsterdam, 2004), pp. 759–787
Google Scholar
E.R.T. Kerstel, L. Gianfrani, Appl. Phys. B, Lasers Opt. 92(3), 439 (2008). doi:10.1007/s00340-008-3128-x. <GotoISI>://000258703600017
Article ADS Google Scholar
R.Q. Iannone, S. Kassi, H.J. Jost, M. Chenevier, D. Romanini, H.A.J. Meijer, S. Dhaniyala, M. Snels, E.R.T. Kerstel, Isot. Environ. Health Stud. 45(4), 303 (2009). doi:10.1080/10256010903172715. http://www.ncbi.nlm.nih.gov/pubmed/19670069
Article Google Scholar
F. Cairo, J.P. Pommereau, K.S. Law, H. Schlager, A. Garnier, F. Fierli, M. Ern, M. Streibel, S. Arabas, S. Borrmann, J.J. Berthelier, C. Blom, T. Christensen, F. D’Amato, G. Di Donfrancesco, T. Deshler, A. Diedhiou, G. Durry, O. Engelsen, F. Goutail, N.R.P. Harris, E.R.T. Kerstel, S. Khaykin, P. Konopka, A. Kylling, N. Larsen, T. Lebel, X. Liu, A.R. MacKenzie, J. Nielsen, A. Oulanowski, D.J. Parker, J. Pelon, J. Polcher, J.A. Pyle, F. Ravegnani, E.D. Rivière, A.D. Robinson, T. Röckmann, C. Schiller, F. Simões, L. Stefanutti, F. Stroh, L. Some, P. Siegmund, N. Sitnikov, J.P. Vernier, C.M. Volk, C. Voigt, M. von Hobe, S. Viciani, V. Yushkov, Atmos. Chem. Phys. Discuss. 9(5), 19713 (2009)
Article ADS Google Scholar
R.Q. Iannone, D. Romanini, O. Cattani, H.A.J. Meijer, E.R.T. Kerstel, J. Geophys. Res. 115(D10), 1 (2010). doi:10.1029/2009JD012895. http://www.agu.org/pubs/crossref/2010/2009JD012895.shtml
Article Google Scholar
J. Ladsberg, E. Kerstel, D. Romanini, Appl. Phys. Lett. (2013 prepared for submission)
Google Scholar
R. Wehr, S. Kassi, D. Romanini, L. Gianfrani, Appl. Phys. B, Lasers Opt. 92(3), 459 (2008). doi:10.1007/s00340-008-3086-3. http://www.springerlink.com/index/10.1007/s00340-008-3086-3
Article ADS Google Scholar
M. Durand, J. Morville, D. Romanini, Phys. Rev. A 82(3), 031803(R) (2010). doi:10.1103/PhysRevA.82.031803. http://link.aps.org/doi/10.1103/PhysRevA.82.031803
Article ADS Google Scholar
Y. Gong, B. Li, Appl. Opt. 47(21), 3860 (2008). http://www.ncbi.nlm.nih.gov/pubmed/18641755
Article ADS Google Scholar
Z. Tong-Kai, Q. Zhe-Chao, H. Yan-Ling, L. Bin-Cheng, Chin. Phys. Lett. 27(10), 100701 (2010). doi:10.1088/0256-307X/27/10/100701
Article Google Scholar

Download references

Author information

Authors and Affiliations

Institut Lumière Matière, UMR 5306, Université Lyon 1, CNRS, Université de Lyon, 69622, Villeurbanne cedex, France
Jérôme Morville
Laboratoire Interdisciplinaire de Physique, UMR 5588, Université J. Fourier (Grenoble I), CNRS, 38402, Saint-Martin d’Hères, France
Daniele Romanini & Erik Kerstel

Authors

Jérôme Morville
View author publications
You can also search for this author in PubMed Google Scholar
Daniele Romanini
View author publications
You can also search for this author in PubMed Google Scholar
Erik Kerstel
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jérôme Morville .

Editor information

Editors and Affiliations

CNR-Istituto Nazionale di Ottica (INO), Pozzuoli, Italy
Gianluca Gagliardi
Dept. of Chemistry, Queen's University, Kingston, Ontario, Canada
Hans-Peter Loock

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Morville, J., Romanini, D., Kerstel, E. (2014). Cavity Enhanced Absorption Spectroscopy with Optical Feedback. In: Gagliardi, G., Loock, HP. (eds) Cavity-Enhanced Spectroscopy and Sensing. Springer Series in Optical Sciences, vol 179. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-40003-2_5

Download citation

DOI: https://doi.org/10.1007/978-3-642-40003-2_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-40002-5
Online ISBN: 978-3-642-40003-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)

Publish with us

Policies and ethics